Matematyka dyskretna 1/Wykład 9: Asymptotyka: Różnice pomiędzy wersjami
| (Nie pokazano 14 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
Widzieliśmy już, że wskazanie postaci zwartej dla ciągu zadanego równaniem rekurencyjnym jest często zadaniem niełatwym. Do tej pory nie jest znana zwarta postać wielu równań. Na szczęście często jesteśmy w sytuacji, w której zadowoli nas przybliżenie odpowiedzi. Wróćmy do rozważanej wielokrotnie sumy kolejnych kwadratów <math> | Widzieliśmy już, że wskazanie postaci zwartej dla ciągu zadanego równaniem rekurencyjnym jest często zadaniem niełatwym. Do tej pory nie jest znana zwarta postać wielu równań. Na szczęście często jesteśmy w sytuacji, w której zadowoli nas przybliżenie odpowiedzi. Wróćmy do rozważanej wielokrotnie sumy kolejnych kwadratów <math>\sum_{i=0}^ni^2</math>. Fakt, że jest to wielomian <math>3</math>-go stopnia zmiennej <math>n</math>, to już wartościowa informacja, często zupełnie wystarczająca. Spotkaliśmy się już nie raz z oszacowaniami poprzez zwykłe nierówności. To podejście często wymaga użycia narzędzi z analizy matematycznej, w szczególności znajdowania ekstremum funkcji. | ||
{{przyklad||| | {{przyklad||| | ||
| Linia 7: | Linia 7: | ||
<center><math> | <center><math>(n!)^2=(1\cdot\ldots\cdot n)(n\cdot\ldots\cdot1)=\prod_{i=1}^ni(n+1-i)</math>.</center> | ||
| Linia 13: | Linia 13: | ||
<center><math>n^n\leqslant(n!)^2\leqslant\left(\frac{1}{4}(n+1)^2\right)^n | <center><math>n^n\leqslant(n!)^2\leqslant\left(\frac{1}{4}(n+1)^2\right)^n</math>,</center> | ||
</math></center> | |||
| Linia 20: | Linia 19: | ||
<center><math>n^{\frac{n}{2}}\leq n!\leqslant\left(\frac{n+1}{2}\right)^n | <center><math>n^{\frac{n}{2}}\leq n!\leqslant\left(\frac{n+1}{2}\right)^n</math></center> | ||
</math></center> | |||
| Linia 32: | Linia 30: | ||
==Notacja asymptotyczna== | ==Notacja asymptotyczna== | ||
[[File:SW_7.1.svg|350x350px|thumb|right|SW_7.1.swf]] | |||
{{kotwica|funasymptw|'''Funkcja asymptotycznie niewiększa'''}} od funkcji <math>g(n)</math> to taka funkcja <math>f: \mathbb{N} \longrightarrow \mathbb{R}</math>, dla której istnieją <math>c>0</math> i <math>n_0\in\mathbb{N}</math>, że <math>\left\vert f(n)\right\vert\leq c\cdot\left\vert g(n)\right\vert</math> dla wszystkich <math>n\geq n_0</math>.<br> | {{kotwica|funasymptw|'''Funkcja asymptotycznie niewiększa'''}} od funkcji <math>g(n)</math> to taka funkcja <math>f: \mathbb{N} \longrightarrow \mathbb{R}</math>, dla której istnieją <math>c>0</math> i <math>n_0\in\mathbb{N}</math>, że <math>\left\vert f(n)\right\vert\leq c\cdot\left\vert g(n)\right\vert</math> dla wszystkich <math>n\geq n_0</math>.<br> | ||
| Linia 70: | Linia 65: | ||
Więcej przykładów i ogólniejszych obserwacji poznamy po prezentacji pozostałych pojęć i symboli notacji asymptotycznej. | Więcej przykładów i ogólniejszych obserwacji poznamy po prezentacji pozostałych pojęć i symboli notacji asymptotycznej. | ||
[[File:SW_7.2.svg|350x350px|thumb|right|SW_7.2.swf]] | |||
{{kotwica|funasymptm|'''Funkcja asymptotycznie niemniejsza'''}} od funkcji <math>g(n)</math> to taka funkcja <math>f: \mathbb{N} \longrightarrow \mathbb{R}</math>, dla której istnieją <math>c>0</math> i <math>n_0\in\mathbb{N}</math>, że <math>c\cdot\left\vert g(n)\right\vert\leq \left\vert f(n)\right\vert</math> dla wszystkich <math>n\geq n_0</math>.<br> | {{kotwica|funasymptm|'''Funkcja asymptotycznie niemniejsza'''}} od funkcji <math>g(n)</math> to taka funkcja <math>f: \mathbb{N} \longrightarrow \mathbb{R}</math>, dla której istnieją <math>c>0</math> i <math>n_0\in\mathbb{N}</math>, że <math>c\cdot\left\vert g(n)\right\vert\leq \left\vert f(n)\right\vert</math> dla wszystkich <math>n\geq n_0</math>.<br> | ||
| Linia 86: | Linia 78: | ||
{{kotwica|funasymptmn|'''Funkcja asymptotycznie mniejsza'''}} od funkcji <math>g(n)</math> to taka funkcja <math>f: \mathbb{N} \longrightarrow \mathbb{R}</math>, że dla każdego <math>c>0</math> istnieje <math>n_0\in\mathbb{N}</math>, przy którym <math>\left\vert f(n)\right\vert<c\cdot\left\vert g(n)\right\vert</math> dla wszystkich <math>n\geq n_0</math>.<br> | {{kotwica|funasymptmn|'''Funkcja asymptotycznie mniejsza'''}} od funkcji <math>g(n)</math> to taka funkcja <math>f: \mathbb{N} \longrightarrow \mathbb{R}</math>, że dla każdego <math>c>0</math> istnieje <math>n_0\in\mathbb{N}</math>, przy którym <math>\left\vert f(n)\right\vert<c\cdot\left\vert g(n)\right\vert</math> dla wszystkich <math>n\geq n_0</math>.<br> | ||
Zbiór funkcji asymptotycznie mniejszych niż <math>g(n)</math> oznaczamy przez <math>o(g(n))</math>. A zatem <math>f(n)= o(g(n))</math> wtedy i tylko wtedy, gdy <math> | Zbiór funkcji asymptotycznie mniejszych niż <math>g(n)</math> oznaczamy przez <math>o(g(n))</math>. A zatem <math>f(n)= o(g(n))</math> wtedy i tylko wtedy, gdy <math>\lim_{n \rightarrow \infty} \frac{f(n)}{g(n)}=0</math>. | ||
{{kotwica|funasymptwi|'''Funkcja asymptotycznie większa'''}} od funkcji <math>g(n)</math> to taka funkcja <math>f: \mathbb{N} \longrightarrow \mathbb{R}</math>, że dla każdego <math>c>0</math> istnieje <math>n_0\in\mathbb{N}</math>, przy którym <math>c\cdot\left\vert g(n)\right\vert<\left\vert f(n)\right\vert</math> dla wszystkich <math>n\geq n_0</math>.<br> | {{kotwica|funasymptwi|'''Funkcja asymptotycznie większa'''}} od funkcji <math>g(n)</math> to taka funkcja <math>f: \mathbb{N} \longrightarrow \mathbb{R}</math>, że dla każdego <math>c>0</math> istnieje <math>n_0\in\mathbb{N}</math>, przy którym <math>c\cdot\left\vert g(n)\right\vert<\left\vert f(n)\right\vert</math> dla wszystkich <math>n\geq n_0</math>.<br> | ||
Zbiór funkcji asymptotycznie większych niż <math>g(n)</math> oznaczamy przez <math>\omega(g(n))</math>. A zatem <math>f(n)=\omega(g(n))</math> wtedy i tylko wtedy, gdy <math> | Zbiór funkcji asymptotycznie większych niż <math>g(n)</math> oznaczamy przez <math>\omega(g(n))</math>. A zatem <math>f(n)=\omega(g(n))</math> wtedy i tylko wtedy, gdy <math>\lim_{n \rightarrow \infty} \frac{g(n)}{f(n)}=0</math>. | ||
Oto kilka prostych faktów wiążących kolejne symbole asymptotyczne. Pozostawiamy je bez dowodu. | Oto kilka prostych faktów wiążących kolejne symbole asymptotyczne. Pozostawiamy je bez dowodu. | ||
| Linia 111: | Linia 103: | ||
Symbole asymptotyczne mogą pojawić się w złożonych wyrażeniach arytmetycznych. | Symbole asymptotyczne mogą pojawić się w złożonych wyrażeniach arytmetycznych. | ||
Dla przykładu wspomnijmy jeszcze raz sumę kolejnych kwadratów: <math> | Dla przykładu wspomnijmy jeszcze raz sumę kolejnych kwadratów: <math>\sum_{i=0}^n i^2=\frac{1}{3}n^3+\frac{1}{2}n^2+\frac{1}{6}n</math>. Możemy teraz napisać <math>\sum_{i=0}^ni^2=O(n^3)</math>, ale także <math>\sum_{i=0}^ni^2=\frac{1}{3}n^2+O(n^2)</math>, co formalnie oznacza <math>\sum_{i=0}^ni^2-\frac{1}{3}n^3\in O(n^2)</math>. Co więcej okazuje się, że symbol <math>=</math> może pełnić nie tylko rolę <math>\in</math>, ale czasami także rolę <math>\subseteq</math>. Na przykład wyrażenie | ||
<center><math>\frac{1}{3}n^3+O(n^2)=O(n^3) | <center><math>\frac{1}{3}n^3+O(n^2)=O(n^3)</math>,</center> | ||
</math></center> | |||
| Linia 125: | Linia 116: | ||
{{obserwacja|9.2|obs 9.2| | {{obserwacja|9.2|obs 9.2| | ||
Dla funkcji <math> | Dla funkcji <math>f,g,f_1,f_2,g_1,g_2: \mathbb{N} \mathbb{R}</math> mamy: | ||
* <math> | * <math>f(n)=O(f(n))</math>, | ||
* <math> | * <math>f(n)=O(O(g(n)))</math> wtedy i tylko wtedy, gdy <math>f(n)=O(g(n))</math>, | ||
* <math> | * <math>f(n)=O\left\vert (g(n)) \right\vert</math> wtedy i tylko wtedy, gdy <math>f(n)= O(g(n))</math>, | ||
* <math> | * <math>f(n)=c\cdot O(g(n))</math> wtedy i tylko wtedy, gdy <math>f(n)=O(g(n))</math>, | ||
* jeśli <math> | * jeśli <math>f_1(n)= O(g_1(n))</math> i <math>f_2(n)=O(g_2(n))</math>, to <math>f_1(n)+f_2(n)=O(g_1(n))+O(g_2(n))</math>, | ||
* jeśli <math> | * jeśli <math>f_1(n)= O(g_1(n))</math> i <math>f_2 | ||
(n)=O(g_2(n))</math>, to <math> | (n)=O(g_2(n))</math>, to <math>f_1(n)\cdot f_2(n)=O(g_1(n)g_2(n))</math>. | ||
}} | }} | ||
{{przyklad||| | {{przyklad||| | ||
Pokażemy, że wielomiany <math> | Pokażemy, że wielomiany <math>k</math>-tego stopnia są <math>\Theta(n^k)</math>. | ||
Zauważmy najpierw, że jeśli <math> | Zauważmy najpierw, że jeśli <math>k<l</math> to <math>O(n^k)=O(n^l)</math>, czyli jeśli <math>f(n)\in O(n^k)</math> to <math>f(n)\in O(n^l)</math>. Rozważmy zatem dowolny wielomian <math>k</math>-tego stopnia <math>p(n)=a_kn^k+\ldots+a_1n+a_0</math>, gdzie <math>a_k\neq0</math>. Wtedy | ||
<center><math> \begin{array} {rlll} | <center><math>\begin{array} {rlll} | ||
\left\vert p(n) \right\vert &=\left\vert a_kn^k+\ldots+a_1n+a_0 \right\vert &&\\ | \left\vert p(n) \right\vert &=\left\vert a_kn^k+\ldots+a_1n+a_0 \right\vert &&\\ | ||
&\leqslant \left\vert a_k \right\vert n^k+\ldots+\left\vert a_1 \right\vert n+\left\vert a_0 \right\vert &\\ | &\leqslant \left\vert a_k \right\vert n^k+\ldots+\left\vert a_1 \right\vert n+\left\vert a_0 \right\vert &\\ | ||
&=a_k\cdot O(n^k)+\ldots+a_1\cdot O(n)+a_0\cdot O(1)&\ | &=a_k\cdot O(n^k)+\ldots+a_1\cdot O(n)+a_0\cdot O(1)&\text{bo}\quad n^i=O(n^i)\\ | ||
&=O(n^k)+\ldots+O(n)+O(1)&\ | &=O(n^k)+\ldots+O(n)+O(1)&\text{bo}\quad c\cdot O(n^i) = O(n^i)\\ | ||
&=O(n^k)+\ldots+O(n^k)+O(n^k)&\ | &=O(n^k)+\ldots+O(n^k)+O(n^k)&\text{bo}\quad O(n^i)=O(n^k), \text{dla}\quad i\leqslant k\\ | ||
&=O(n^k),&\ | &=O(n^k),&\text{bo}\quad O(n^k)+O(n^k)= O(n^k) | ||
\end{array} | \end{array} | ||
</math></center> | </math></center> | ||
co dowodzi, że <math> | co dowodzi, że <math>p(n)=O(n^k)</math>. | ||
Dla dowodu <math> | Dla dowodu <math>p(n)=\Omega(n^k)</math>, | ||
niech <math> | niech <math>a=\max(\left\vert a_{0} \right\vert,\left\vert a_{1} \right\vert,\ldots,\left\vert a_{k-1} \right\vert)</math>. | ||
Wtedy | Wtedy | ||
<center><math> | <center><math>\left\vert a_k \right\vert n^k\geq 2kan^{k-1}\geq 2(\left\vert a_{k-1} \right\vert n^{k-1}+\left\vert a_{k-2} \right\vert n^{k-2}+\ldots+\left\vert a_0 \right\vert) | ||
</math></center> | </math></center> | ||
dla <math> | dla <math>n\geq \frac{2ka}{\left\vert a_k \right\vert}</math>. | ||
Mamy zatem | Mamy zatem | ||
<center><math>\ | <center><math>\begin{align} \left\vert p(n) \right\vert &=\left\vert a_kn^k+a_{k-1}n^{k-1}+\ldots+a_0 \right\vert \geqslant\left\vert a_k \right\vert n^k-(\left\vert a_{k-1} \right\vert n^{k-1}+\ldots+\left\vert a_0 \right\vert)\\ | ||
&\geqslant\left\vert a_k \right\vert n^k-kan^{k-1}\geqslant\frac{\left\vert a_k \right\vert n^k}{2}, | &\geqslant\left\vert a_k \right\vert n^k-kan^{k-1}\geqslant\frac{\left\vert a_k \right\vert n^k}{2}, | ||
\ | \end{align}</math></center> | ||
co dowodzi <math> | co dowodzi <math>p(n)=\Omega(n^k)</math>. | ||
}} | }} | ||
{{przyklad||| | {{przyklad||| | ||
Często pojawiają się logarytmy o różnych podstawach. | Często pojawiają się logarytmy o różnych podstawach. | ||
Najczęściej są to <math> | Najczęściej są to <math>\lg{n},\ln{n},\log{n}</math>. | ||
Z asymptotycznego punktu widzenia wszystkie te funkcje są podobne tzn. | Z asymptotycznego punktu widzenia wszystkie te funkcje są podobne tzn. | ||
np. <math> | np. <math>\ln{n}=\Theta(\lg{n})</math> i <math>\log{n}=\Theta(\lg{n})</math>, lub ogólniej: | ||
<center><math> | <center><math>\log_a{n}=\Theta(\log_b{n}),\quad \text{dla}\quad a,b>1</math>.</center> | ||
| Linia 194: | Linia 185: | ||
<center><math> | <center><math>\log_a{n}=\frac{1}{\log_b{a}}\cdot\log_b{n}</math>,</center> | ||
</math></center> | |||
gdzie ta sama stała <math> | gdzie ta sama stała <math>\frac{1}{\log_b{a}}</math> jest dobra do dolnego i górnego ograniczenia. | ||
}} | }} | ||
{{przyklad||| | {{przyklad||| | ||
Dla wielomianów <math> | Dla wielomianów <math>f(n),g(n)</math> rząd ich wielkości wyznaczony jest przez stopień: | ||
<center><math> | <center><math>f = O(g)</math> wtedy i tylko wtedy, gdy <math>\deg(f)\leq \deg(g)</math></center>. | ||
| Linia 211: | Linia 201: | ||
<center><math> | <center><math>n, n^2, n^3, n^4, \ldots, n^d, n^{d+1}, \ldots | ||
</math></center> | </math></center> | ||
| Linia 218: | Linia 208: | ||
<center><math> | <center><math>n^a = O(n^b)</math> wtedy i tylko wtedy, gdy <math>a \leq b</math></center> | ||
Na przykład: | Na przykład: | ||
*<math> | *<math>\sqrt{n} \in O(n)</math>, | ||
* <math> | * <math>\sqrt[3]{n} \in O(\sqrt{n})</math>. | ||
}} | }} | ||
{{przyklad||| | {{przyklad||| | ||
Mamy <math> | Mamy <math>n \in O(2^n)</math>. | ||
Istotnie łatwo dowieść indukcyjnie, że <math> | Istotnie łatwo dowieść indukcyjnie, że <math>n \leq 2^n</math>. | ||
Podobnie <math> | Podobnie <math>n^2 \in O(2^n)</math>. Wiemy już, że każda funkcja liniowa jest w <math>O(2^n)</math>, | ||
istnieje więc stała <math> | istnieje więc stała <math>c</math> taka, że od pewnego miejsca <math>2n+1 \leq c\cdot 2^n</math>. | ||
<br> | <br> | ||
Pokażemy, że wtedy też <math> | Pokażemy, że wtedy też <math>n^2 \leq c\cdot 2^n</math>. | ||
Indukcyjnie | Indukcyjnie | ||
<center><math> | <center><math>(n+1)^2 = n^2 +2n +1 \leq c \cdot 2^n +(2n +1) \leq c \cdot 2^n + c \cdot 2^n = c \cdot 2^{n+1} | ||
</math></center> | </math></center> | ||
Analogicznie, wiedząc już, że każda funkcja kwadratowa jest w <math> | Analogicznie, wiedząc już, że każda funkcja kwadratowa jest w <math>O(2^n)</math>, | ||
czyli że dla pewnej stałej <math> | czyli że dla pewnej stałej <math>c</math> od pewnego miejsca mamy { <math>3n^2 +3n +1 \leq c \cdot 2^n</math>}, | ||
możemy pokazać indukcyjnie, że <math> | możemy pokazać indukcyjnie, że <math>n^3 \leq c \cdot 2^n</math>. | ||
Istotnie | Istotnie | ||
<center><math> | <center><math>(n+1)^3 = n^3 + 3n^2 +3n +1 \leq c \cdot 2^n + c \cdot 2^n = c \cdot 2^{n+1}</math></center> | ||
</math></center> | |||
Ogólnie, dla dowolnego stopnia <math> | Ogólnie, dla dowolnego stopnia <math>d</math> mamy <math>n^d \in O(a^n)</math>, o ile tylko <math>a>1</math>. | ||
}} | }} | ||
{{przyklad||| | {{przyklad||| | ||
Oczywiście <math> | Oczywiście <math>2^n \leq 3^n</math>, więc <math>2^n \in O(3^n)</math>. | ||
<br> | <br> | ||
Ale <math> | Ale <math>3^n \not\in O(2^n)</math>. | ||
Gdyby bowiem <math> | Gdyby bowiem <math>3^n \leq c \cdot 2^n</math> to | ||
<center><math> | <center><math>\left(\frac{3}{2}\right)^n = \frac{3^n}{2^n} \leq c</math>,</center> | ||
</math></center> | |||
podczas gdy funkcja wykładnicza <math> | podczas gdy funkcja wykładnicza <math>\left(\frac{3}{2}\right)^n</math> rośnie do nieskończoności. | ||
Nie może zatem być ograniczona przez żadną stałą <math> | Nie może zatem być ograniczona przez żadną stałą <math>c</math>. | ||
<br> | <br> | ||
Ogólnie dla <math> | Ogólnie dla <math>a,b >1</math>, mamy <math>a^n \in O(b^n)</math> wtedy i tylko wtedy, gdy <math>a\leq b</math>. | ||
}} | }} | ||
{{przyklad||| | {{przyklad||| | ||
Mamy <math> | Mamy <math>2^n \in O(n!)</math> oraz <math>n! \in O(n^n)</math>. | ||
<br> | <br> | ||
Istotnie | Istotnie | ||
<math> | <math>2^n \leq 2 \cdot 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n = 2 \cdot n!</math>, | ||
bo każdy czynnik (poza pierwszym) w <math> | bo każdy czynnik (poza pierwszym) w <math>n!</math> jest równy co najmniej <math>2</math>. | ||
Pokazuje to, że <math> | Pokazuje to, że <math>2^n \in O(n!)</math>. | ||
<br> | <br> | ||
<br> | <br> | ||
Podobnie | Podobnie | ||
<math> | <math>n! = 1 \cdot 2 \cdot 3 \cdot \ldots \cdot n \leq n \cdot n \cdot n \cdot \ldots \cdot n = n^n</math>, | ||
bo każdy czynnik w <math> | bo każdy czynnik w <math>n!</math> jest nie większy niż <math>n</math>. | ||
}} | }} | ||
| Linia 291: | Linia 279: | ||
{{obserwacja|9.3|obs 9.3| | {{obserwacja|9.3|obs 9.3| | ||
Oto ciąg funkcji, z których każda jest <math> | Oto ciąg funkcji, z których każda jest <math>O</math> od następnej, ale nie od poprzedniej: | ||
<center><math> | <center><math>\frac{1}{n^n}, \frac{1}{n!}, \ldots, \frac{1}{3^n}, \frac{1}{2^n}, \ldots, | ||
\frac{1}{n^3}, \frac{1}{n^2}, \frac{1}{n \lg n}, \frac{1}{n}, | \frac{1}{n^3}, \frac{1}{n^2}, \frac{1}{n \lg n}, \frac{1}{n}, | ||
\frac{\lg{n}}{n}, \frac{1}{\sqrt{n}}, \frac{1}{\sqrt[3]{n}}, \ldots, | \frac{\lg{n}}{n}, \frac{1}{\sqrt{n}}, \frac{1}{\sqrt[3]{n}}, \ldots, | ||
| Linia 304: | Linia 292: | ||
<center><math> | <center><math>1, \lg\lg{n}, \lg{n}, \ldots, | ||
\sqrt[3]{n}, \sqrt{n}, \frac{n}{\lg{n}}, n, n\lg{n}, n\sqrt{n}, n^2, n^3, \ldots, | \sqrt[3]{n}, \sqrt{n}, \frac{n}{\lg{n}}, n, n\lg{n}, n\sqrt{n}, n^2, n^3, \ldots, | ||
n^{\lg{n}}, 2^n, 3^n, n!, n^n, 2^{2^n} | n^{\lg{n}}, 2^n, 3^n, n!, n^n, 2^{2^n}</math></center> | ||
</math></center> | |||
W istocie, gdy <math> | W istocie, gdy <math>g(n)</math> występuje w tym ciagu wczesniej niż <math>f(n)</math>, to | ||
*<math> | *<math>g(n)=O(f(n))</math>, | ||
*<math> | *<math>f(n)=o(g(n))</math>. | ||
}} | }} | ||
| Linia 323: | Linia 310: | ||
<center><math> | <center><math>f(n)= | ||
\left\{ | \left\{ | ||
\begin{array} {cl} | \begin{array} {cl} | ||
n,& \ | n,& \text{dla} \quad n \quad \text{parzystych}\\ | ||
n^3,& \ | n^3,& \text{dla}\quad n\quad \text{nieparzystych} | ||
\end{array} | \end{array} | ||
\right. | \right.</math></center> | ||
</math></center> | |||
i <math> | i <math>g(n)=n^2</math> mamy <math>f(n)\neq\Omega(g(n))</math> i <math>f(n)\neq O(g(n))</math>. | ||
}} | }} | ||
| Linia 342: | Linia 328: | ||
w szczególności procedur rekurencyjnych, | w szczególności procedur rekurencyjnych, | ||
których złożoność łatwo opisać równaniem rekurencyjnym. | których złożoność łatwo opisać równaniem rekurencyjnym. | ||
Niech <math> | Niech <math>T(n)</math> będzie funkcją opisującą złożoność czasową pewnego programu, | ||
czyli zwracającą liczbę wykonywanych operacji dla danych wielkości <math> | czyli zwracającą liczbę wykonywanych operacji dla danych wielkości <math>n</math>. | ||
Zazwyczaj nie jesteśmy zainteresowani dokładną liczbą wykonywanych operacji, | Zazwyczaj nie jesteśmy zainteresowani dokładną liczbą wykonywanych operacji, | ||
a jedynie dobrym oszacowaniem z góry i czasem z dołu. | a jedynie dobrym oszacowaniem z góry i czasem z dołu. | ||
| Linia 349: | Linia 335: | ||
co na ogół jest zadaniem beznadziejnym, | co na ogół jest zadaniem beznadziejnym, | ||
dopuszczamy użycie notacji asymptotycznej | dopuszczamy użycie notacji asymptotycznej | ||
i szukamy pewnej "dobrze znanej" funkcji <math> | i szukamy pewnej "dobrze znanej" funkcji <math>g(n)</math> takiej, | ||
że <math> | że <math>T(n)=\Theta(g(n))</math>. | ||
Znając <math> | Znając <math>g(n)</math> wiemy w jaki sposób rośnie długość działania programu | ||
wraz z wzrostem wielkości danych. | wraz z wzrostem wielkości danych. | ||
Równania, o których mówimy często są postaci | Równania, o których mówimy często są postaci | ||
<math> | <math>T(n)=a\cdot T\left( \left\lfloor\frac{n}{b}\right\rfloor \right)+f(n)</math>, | ||
czyli aby rozwiązać problem dla danych wielkości <math> | czyli aby rozwiązać problem dla danych wielkości <math>n</math>, | ||
rozwiązujemy <math> | rozwiązujemy <math>a</math> podproblemów wielkości <math>\left\lfloor\frac{n}{b}\right\rfloor</math> | ||
i składamy z nich rozwiązanie całości w dodatkowym czasie <math> | i składamy z nich rozwiązanie całości w dodatkowym czasie <math>f(n)</math>. | ||
Twierdzenie o rekurencji uniwersalnej wskazuje funkcję asymptotycznie podobną do <math> | Twierdzenie o rekurencji uniwersalnej wskazuje funkcję asymptotycznie podobną do <math>T(n)</math> | ||
w bardzo wielu przypadkach. | w bardzo wielu przypadkach. | ||
{{twierdzenie|9.4 [o rekurencji uniwersalnej]|tw 9.4| | {{twierdzenie|9.4 [o rekurencji uniwersalnej]|tw 9.4| | ||
Dla funkcji <math> | Dla funkcji <math>T(n)</math> zadanej przez | ||
<center><math> | <center><math>T(n)= | ||
\left | \left | ||
\{\begin{array} {ll} | \{\begin{array} {ll} | ||
\Theta(1),& \ | \Theta(1),& \text{dla}\quad n\in \{0,1\}\\ | ||
a\cdot T\left( \left\lfloor\frac{n}{b}\right\rfloor \right)+f(n),& \ | a\cdot T\left( \left\lfloor\frac{n}{b}\right\rfloor \right)+f(n),& \text{dla}\quad n>1 | ||
\end{array} | \end{array} | ||
\right. | \right.</math></center> | ||
</math></center> | |||
zachodzi: | zachodzi: | ||
* jeśli <math> | * jeśli <math>f(n)=O(n^{\log_b{a}-\epsilon})</math> dla pewnego <math>\epsilon>0</math>, to <math>T(n)=\Theta(n^{\log_b{a}})</math>, | ||
* jeśli <math> | * jeśli <math>f(n)=\Theta(n^{\log_b{a}})</math>, to <math>T(n)=\Theta(n^{\log_b{a}}\lg{n})</math>, | ||
* jeśli <math> | * jeśli <math>f(n)=\Omega(n^{\log_b{a}+\epsilon})</math> dla pewnego <math>\epsilon>0</math> oraz <math>a f(\frac{n}{b})\leq c f(n)</math> dla pewnego <math>c<1</math> i prawie wszystkich <math>n</math>, to <math>T(n)=\Theta(f(n))</math>. | ||
}} | }} | ||
| Linia 388: | Linia 373: | ||
poczynimy kilka uwag i prześledzimy kilka przykładów. | poczynimy kilka uwag i prześledzimy kilka przykładów. | ||
W praktyce na ogół pomijamy opis początkowych wartości funkcji <math> | W praktyce na ogół pomijamy opis początkowych wartości funkcji <math>T(n)</math> | ||
domyślnie przyjmując, że są one <math> | domyślnie przyjmując, że są one <math>\Theta(1)</math>. | ||
Nie będziemy też używać podłóg w wyrażeniach typu <math> | Nie będziemy też używać podłóg w wyrażeniach typu <math>T(\frac{n}{b})</math>, | ||
traktując występujące tu dzielenie jako całkowito-liczbowe. | traktując występujące tu dzielenie jako całkowito-liczbowe. | ||
Twierdzenie o rekurencji uniwersalnej jest silnym i praktycznym narzędziem. | Twierdzenie o rekurencji uniwersalnej jest silnym i praktycznym narzędziem. | ||
Jednak trzeba podkreślić, że nie szacuje ono rozwiązań | Jednak trzeba podkreślić, że nie szacuje ono rozwiązań | ||
wszystkich równań typu <math> | wszystkich równań typu <math>T(n)=aT\left( \frac{n}{b} \right)+f(n)</math>. | ||
Taka niemożność oszacowania może mieć miejsce z jednego z trzech powodów, | Taka niemożność oszacowania może mieć miejsce z jednego z trzech powodów, | ||
przy czym drugi z nich jest istotny i zdarza się w praktyce: | przy czym drugi z nich jest istotny i zdarza się w praktyce: | ||
* W każdym z trzech przypadków opisanym w twierdzeniu, porównujemy funkcje <math> | * W każdym z trzech przypadków opisanym w twierdzeniu, porównujemy funkcje <math>n^{\log_b{a}}</math> i <math>f(n)</math>. Może się zdarzyć (jak widzieliśmy w jednym z przykładów), iż <math>n^{\log_b{a}}</math> i <math>f(n)</math> są asymptotycznie nieporównywalne i wobec tego nie będzie można zastosować żadnego z tych trzech przypadków. Na szczęście w praktyce takie funkcje raczej zdarzają się niezmiernie rzadko. | ||
* Po drugie, w przypadku pierwszym (i trzecim), tak naprawdę, porównujemy <math> | * Po drugie, w przypadku pierwszym (i trzecim), tak naprawdę, porównujemy <math>f(n)</math> z funkcją istotnie mniejszą (wiekszą) od <math>n^{\log_b{a}}</math>, tzn. z funkcją <math>n^{\log_b{a}\pm\epsilon}</math> dla pewnego <math>\epsilon</math>. Ten warunek już może przeszkadzać w praktyce. Dla przykładu <math>n\lg{n}\in\Omega(n)</math>, ale <math>n\lg{n}\notin\Omega(n^{1+\epsilon})</math> dla dowolnego <math>\epsilon>0</math>. Pełny przykład takiego równania przedstawimy poniżej. | ||
* Po trzecie, w ostatnim warunku dla <math> | * Po trzecie, w ostatnim warunku dla <math>f(n)\in\Omega(n^{\log_b{a}+\epsilon})</math> dla dowolnego <math>\epsilon>0</math> wymagamy dodatkowo, żeby <math>af(\frac{n}{b})\leq c f(n)</math> dla pewnego <math>c<1</math> i dla wszystkich <math>n\geq n_0</math> dla pewnego <math>n _0</math>. Znów, na szczęście, w większości spotykanych sytuacji ten warunek "regularności" jest spełniony. Jednak zawsze trzeba go sprawdzić. | ||
{{przyklad||| | {{przyklad||| | ||
| Linia 405: | Linia 390: | ||
<center><math> | <center><math>T(n)=16T\left( \frac{n}{4} \right)+n\lg{n}</math>,</center> | ||
</math></center> | |||
dostajemy kolejno: | dostajemy kolejno: | ||
* <math> | * <math>a=16</math>, <math>b=4</math>, <math>f(n)=n\lg{n}</math>, | ||
* <math> | * <math>n^{\log_4{16}}=n^2</math>, <math>f(n)=O(n^{2-\epsilon})</math>, np. dla <math>\epsilon=0.5</math>, | ||
* zatem z pierwszego punktu [[#tw 9.4|Twierdzenia 9.4]] mamy <math> | * zatem z pierwszego punktu [[#tw 9.4|Twierdzenia 9.4]] mamy <math>T(n)=\Theta(n^2)</math>. | ||
Podobnie dla funkcji | Podobnie dla funkcji | ||
<center><math> | <center><math>T(n)=2T\left( \frac{n}{2} \right)+5n-15</math>,</center> | ||
</math></center> | |||
mamy: | mamy: | ||
* <math> | * <math>a=2</math>, <math>b=2</math>, <math>f(n)=5n-15</math>, | ||
* <math> | * <math>n^{\log_2{2}}=n</math>, <math>f(n)=\Theta(n)</math>, | ||
* zatem z drugiego punktu [[#tw 9.4|Twierdzenia 9.4]] mamy <math> | * zatem z drugiego punktu [[#tw 9.4|Twierdzenia 9.4]] mamy <math>T(n)=\Theta(n\lg{n})</math>. | ||
Niech teraz | Niech teraz | ||
<center><math> | <center><math>T(n)=2T\left( \frac{n}{3} \right)+n\lg{n}</math></center> | ||
</math></center> | |||
Wtedy | Wtedy | ||
* <math> | * <math>a=2</math>, <math>b=3</math>, <math>f(n)=n\lg{n}</math>, | ||
* <math> | * <math>n^{\log_3{2}}\approx n^{0.6309}</math>, <math>f(n)\in\Omega(n^{\log_3{2}-\epsilon})</math> dla <math>\epsilon=0.1</math>, | ||
* <math> | * <math>af(\frac{n}{b})\leq 2\cdot \frac{n}{3}\lg{\frac{n}{3}}\leq \frac{2}{3}n\lg{n}=\frac{2}{3}f(n)</math>, | ||
* zatem z trzeciego punktu [[#tw 9.4|Twierdzenia 9.4]] mamy <math> | * zatem z trzeciego punktu [[#tw 9.4|Twierdzenia 9.4]] mamy <math>T(n)=\Theta(n\lg{n})</math>. | ||
Z kolei dla funkcji spełniającej | Z kolei dla funkcji spełniającej | ||
<center><math> | <center><math>T(n)=2T\left( \frac{n}{2} \right)+n\lg{n}</math>,</center> | ||
</math></center> | |||
dostajemy | dostajemy | ||
* <math> | * <math>a=2</math>, <math>b=2</math>, <math>f(n)=n\lg{n}</math>, | ||
* <math> | * <math>n^{\log_2{2}}=n</math>, | ||
* <math> | * <math>n\lg{n}\in\Omega(n)</math> ale dla dowolnego <math>\epsilon>0</math>, <math>n\lg{n}\notin\Omega(n^{1+\epsilon})</math>, | ||
* i ... nie można zaaplikować [[#tw 9.4|Twierdzenia 9.4]]. | * i ... nie można zaaplikować [[#tw 9.4|Twierdzenia 9.4]]. | ||
}} | }} | ||
| Linia 457: | Linia 438: | ||
{{dowod||| | {{dowod||| | ||
Rozumowanie nasze przeprowadzimy tylko w przypadku, | Rozumowanie nasze przeprowadzimy tylko w przypadku, | ||
gdy liczba <math> | gdy liczba <math>b</math> występująca w rekurencyjnym równaniu zadającym funkcję <math>T(n)</math> | ||
jest potęgą liczby naturalnej, czyli dla liczb postaci <math> | jest potęgą liczby naturalnej, czyli dla liczb postaci <math>1,b,b^2,\ldots</math>. | ||
Rozszerzenie tego rozumowania na cały zbiór <math> | Rozszerzenie tego rozumowania na cały zbiór <math>\mathbb{N}</math> jest dość techniczne | ||
i wymaga szacowania podłóg. | i wymaga szacowania podłóg. | ||
Ponadto, symboli asymptotycznych będziemy używać tylko dla <math> | Ponadto, symboli asymptotycznych będziemy używać tylko dla <math>n\in\left\lbrace 1,b,b^2,\ldots \right\rbrace</math>. | ||
To nieformalne nadużycie nie ogranicza poprawności rozumowania -- | To nieformalne nadużycie nie ogranicza poprawności rozumowania -- | ||
wymaga wszakże rozszerzenia notacji asymptotycznej na funkcje postaci | wymaga wszakże rozszerzenia notacji asymptotycznej na funkcje postaci | ||
<math> | <math>f: \mathbb{R} \mathbb{R}</math>. | ||
Rozwijając rekurencyjną formułę <math> | Rozwijając rekurencyjną formułę <math>T(n)</math> dla <math>n=b^k</math> otrzymujemy: | ||
<center><math>\ | <center><math>\begin{align} T(n)&=T(b^k)=f(b^k)+aT(b^{k-1})=f(n)+af(b^{k-1})+a^2T(b^{k-2})=\ldots\\ | ||
&=f(b^k)+af(b^{k-1})+a^2f(b^{k-2})+\ldots+a^{k-1}f(b)+a^kT(1). | &=f(b^k)+af(b^{k-1})+a^2f(b^{k-2})+\ldots+a^{k-1}f(b)+a^kT(1). | ||
\ | \end{align}</math></center> | ||
Ponieważ <math> | Ponieważ <math>a^k=a^{\log_b{n}}=a^{\frac{\log_a{n}}{\log_a{b}}}=n^{\log_b{a}}</math> możemy kontynuować: | ||
<center><math>\ | <center><math>\begin{align} T(n)&=f(b^k)+af(b^{k-1})+a^2f(b^{k-2})+\ldots+a^{k-1}f(b)+a^kT(1).\\ | ||
&=\Theta(n^{\log_b{n}})+\sum_{i=0}^{k-1}a^if(b^{k-i}). | &=\Theta(n^{\log_b{n}})+\sum_{i=0}^{k-1}a^if(b^{k-i}). | ||
\ | \end{align}</math></center> | ||
Dalsze szacowanie rozbijamy na <math> | Dalsze szacowanie rozbijamy na <math>3</math> przypadki zgodnie z warunkami na zachowanie | ||
funkcji <math> | funkcji <math>f(n)</math> wobec <math>n^{\log_b{a}}</math>: | ||
* <math> | * <math>f(n)=O(n^{\log_b{a}-\epsilon})</math>, | ||
<center><math>\ | <center><math>\begin{align} T(n)&=\Theta(n^{\log_b{n}})+\sum_{i=0}^{k-1}a^if(b^{k-i})\\ | ||
&=\Theta(n^{\log_b{a}})+\sum_{i=0}^{k-1}a^i\cdot O((b^{k-i})^{\log_b{a}-\epsilon})\\ | &=\Theta(n^{\log_b{a}})+\sum_{i=0}^{k-1}a^i\cdot O((b^{k-i})^{\log_b{a}-\epsilon})\\ | ||
&=\Theta(n^{\log_b{a}})+O\left( b^{k(\log_b{a}-\epsilon)}\sum_{i=0}^{k-1}\left( \frac{a}{b^{\log_b{a}-\epsilon}} \right)^i \right)\\ | &=\Theta(n^{\log_b{a}})+O\left( b^{k(\log_b{a}-\epsilon)}\sum_{i=0}^{k-1}\left( \frac{a}{b^{\log_b{a}-\epsilon}} \right)^i \right)\\ | ||
| Linia 493: | Linia 474: | ||
&=\Theta(n^{\log_b{a}})+n^{\log_b{a}-\epsilon}\cdot O\left( \frac{b^{k\epsilon}-1}{b^\epsilon-1} \right)\\ | &=\Theta(n^{\log_b{a}})+n^{\log_b{a}-\epsilon}\cdot O\left( \frac{b^{k\epsilon}-1}{b^\epsilon-1} \right)\\ | ||
&=\Theta(n^{\log_b{a}})+n^{\log_b{a}-\epsilon}\cdot O\left( \frac{n^{\epsilon}-1}{b^\epsilon-1} \right). | &=\Theta(n^{\log_b{a}})+n^{\log_b{a}-\epsilon}\cdot O\left( \frac{n^{\epsilon}-1}{b^\epsilon-1} \right). | ||
\ | \end{align}</math></center> | ||
Ponieważ <math> | Ponieważ <math>b</math> i <math>\epsilon</math> są stałymi, ostatni składnik redukuje się do | ||
<math> | <math>n^{\log_b{a}-\epsilon}\cdot O(n^{\epsilon})=O(n^{\log_b{a}})</math>. Zatem | ||
<center><math> | <center><math>T(n)=\Theta(n^{\log_b{a}})+O(n^{\log_b{a}})=\Theta(n^{\log_b{a}})</math></center> | ||
</math></center> | |||
* <math> | * <math>f(n)=\Theta(n^{\log_b{a}})</math>, | ||
<center><math>\ | <center><math>\begin{align} T(n)&=\Theta(n^{\log_b{a}})+\sum_{i=0}^{k-1}a^if(b^{k-i})\\ | ||
&=\Theta(n^{\log_b{a}})+\Theta\left( \sum_{i=0}^{k-1}\frac{a^ib^{k\lg_b{a}}}{b^{i\log_b{a}}} \right)\\ | &=\Theta(n^{\log_b{a}})+\Theta\left( \sum_{i=0}^{k-1}\frac{a^ib^{k\lg_b{a}}}{b^{i\log_b{a}}} \right)\\ | ||
&=\Theta(n^{\log_b{a}})+\Theta\left( n^{\log_b{a}}\sum_{i=0}^{k-1}1 \right)\\ | &=\Theta(n^{\log_b{a}})+\Theta\left( n^{\log_b{a}}\sum_{i=0}^{k-1}1 \right)\\ | ||
&=\Theta(n^{\log_b{a}})+\Theta\left( n^{\log_b{a}}\log_b{n} \right)\\ | &=\Theta(n^{\log_b{a}})+\Theta\left( n^{\log_b{a}}\log_b{n} \right)\\ | ||
&=\Theta\left( n^{\log_b{a}}\lg{n} \right). | &=\Theta\left( n^{\log_b{a}}\lg{n} \right). | ||
\ | \end{align}</math></center> | ||
* <math> | * <math>af(\frac{n}{b})\leq cf(n)</math> dla pewnego <math>c</math> i prawie wszystkich <math>n</math> <br> | ||
oraz <math> | oraz <math>f(n)=\Omega(n^{\log_b{a}})</math>. | ||
Z założeń tego przypadku mamy <math> | Z założeń tego przypadku mamy <math>a^if(b^{k-i})\leq c^if(n)</math>. Zatem | ||
<center><math>\ | <center><math>\begin{align} T(n)&=\Theta(n^{\log_b{a}})+\sum_{i=0}^{k-1}a^if(b^{k-i})\\ | ||
&\leqslant\Theta(n^{\log_b{a}})+\sum_{i=0}^{k-1}c^if(n)\\ | &\leqslant\Theta(n^{\log_b{a}})+\sum_{i=0}^{k-1}c^if(n)\\ | ||
&\leqslant\Theta(n^{\log_b{a}})+f(n)\sum_{i=0}^{\infty}c^i\\ | &\leqslant\Theta(n^{\log_b{a}})+f(n)\sum_{i=0}^{\infty}c^i\\ | ||
| Linia 524: | Linia 504: | ||
&=\Theta(n^{\log_b{a}})+\Theta{f(n)}\\ | &=\Theta(n^{\log_b{a}})+\Theta{f(n)}\\ | ||
&=\Theta({f(n)}). | &=\Theta({f(n)}). | ||
\ | \end{align}</math></center> | ||
| Linia 540: | Linia 520: | ||
<center><math>\ | <center><math>\begin{align} a_0&=1,\\ | ||
a_{n+1}&=\frac{1}{n^3}\sum_{i=0}^{n-1}a_i, | a_{n+1}&=\frac{1}{n^3}\sum_{i=0}^{n-1}a_i, | ||
\ | \end{align}</math></center> | ||
najpierw dowodzimy indukcyjnie, że <math> | najpierw dowodzimy indukcyjnie, że <math>0<a_n\leq 1</math>, czyli <math>a_n=O(1)</math>. | ||
Podstawiając uzyskane oszacowanie do równania rekurencyjnego otrzymujemy: | Podstawiając uzyskane oszacowanie do równania rekurencyjnego otrzymujemy: | ||
<center><math> | <center><math>a_n=\frac{1}{n^3}\sum_{i=0}^{n}a_i=\frac{1}{n^3}\cdot \sum_{i=0}^n O(1)=\frac{1}{n^3}\cdot O\left( \sum_{i=0}^n1 \right)=\frac{1}{n^3}\cdot O(n)=O\left( \frac{1}{n^2} \right)</math></center> | ||
</math></center> | |||
| Linia 556: | Linia 535: | ||
<center><math>\ | <center><math>\begin{align} a_n&=\frac{1}{n^3}\sum_{i=0}^na_i=\frac{1}{n^3}\left( a_0+\sum_{i=1}^na_i \right)=\frac{1}{n^3}+\frac{1}{n^3}\sum_{i=1}^{n}O\left( \frac{1}{n^2} \right)= \frac{1}{n^3}+\frac{1}{n^3}O(1)\\ | ||
&=O\left( \frac{1}{n^3} \right). | &=O\left( \frac{1}{n^3} \right). | ||
\ | \end{align}</math></center> | ||
Wykorzystaliśmy tu fakt, iż szereg <math> | Wykorzystaliśmy tu fakt, iż szereg <math>\sum_{i=0}^{\infty}\frac{1}{i^2}</math> jest zbieżny. | ||
Zauważmy też, że następne powtórzenie podobnej procedury szacującej już nam nic nie da. | Zauważmy też, że następne powtórzenie podobnej procedury szacującej już nam nic nie da. | ||
<center><math> | <center><math>a_n=\frac{1}{n^3}\sum_{i=0}^na_i=\frac{1}{n^3}+\frac{1}{n^3}\sum_{i=1}^nO\left( \frac{1}{n^3} \right)=\frac{1}{n^3}+\frac{1}{n^3}\cdot O\left( \frac{1}{n^2} \right)=O\left( \frac{1}{n^3} \right)</math></center> | ||
</math></center> | |||
| Linia 572: | Linia 550: | ||
{{przyklad||| | {{przyklad||| | ||
Niech ciąg <math> | Niech ciąg <math>b_n</math> spełnia | ||
<center><math> | <center><math>b_n\cdot\ln{b_n}=n</math></center> | ||
</math></center> | |||
Z monotoniczności funkcji <math> | Z monotoniczności funkcji <math>n\ln{n}</math> dostajemy, że <math>0<b_n<n</math>. | ||
Podstawiając to oszacowanie za drugie wystąpienie <math> | Podstawiając to oszacowanie za drugie wystąpienie <math>b_n</math> w równaniu otrzymujemy: | ||
<center><math> | <center><math>n=b_n\cdot\ln{b_n}< b_n\ln{n}</math>,</center> | ||
</math></center> | |||
czyli <math> | czyli <math>b_n>\frac{n}{\ln{n}}</math>. Podstawiając powtórnie dostajemy: | ||
<center><math> | <center><math>n=b_n\ln{b_n}>b_n\cdot\ln{\frac{n}{\ln{n}}}</math>,</center> | ||
</math></center> | |||
czyli <math> | czyli <math>b_n<\frac{n}{\ln{n}-\ln{\ln{n}}}</math>. | ||
Uzyskaliśmy zatem, że <math> | Uzyskaliśmy zatem, że <math>b_n=\Theta\left( \frac{n}{\ln{n}} \right)</math>. | ||
}} | }} | ||
Na zakończenie tego wykładu poznamy jeszcze jeden symbol asymptotyczny. | Na zakończenie tego wykładu poznamy jeszcze jeden symbol asymptotyczny. | ||
Jest on podobny do <math> | Jest on podobny do <math>\Theta</math> lecz znacznie precyzyjniejszy. | ||
{{kotwica|fasymprowne|'''Funkcje asymptotycznie równe'''|}} to takie funkcje <math> | {{kotwica|fasymprowne|'''Funkcje asymptotycznie równe'''|}} to takie funkcje <math>f(n)</math> i <math>g(n)</math>, że | ||
<center><math> | <center><math>\lim_{n\rightarrow\infty}\frac{f(n)}{g(n)}=1</math></center> | ||
</math></center> | |||
Fakt, że funkcje <math> | Fakt, że funkcje <math>f(n)</math> i <math>g(n)</math> są asymptotycznie równe zapisujemy jako <math>f(n)\sim g(n)</math>. | ||
Jednym z najbardziej znanych przybliżeń asymptotycznych jest | Jednym z najbardziej znanych przybliżeń asymptotycznych jest | ||
| Linia 616: | Linia 590: | ||
<center><math> | <center><math>n!\sim \sqrt{2\pi n}\left( \frac{n}{e} \right)^n</math></center> | ||
</math></center> | |||
| Linia 625: | Linia 598: | ||
<center><math> | <center><math>n!\sim c \cdot n^{n+1/2} e^{-n}</math>,</center> | ||
</math></center> | |||
dla pewnej stałej <math> | dla pewnej stałej <math>c</math>. | ||
Wkładem Jamesa Stirlinga było pokazanie, że stałą tą jest <math> | Wkładem Jamesa Stirlinga było pokazanie, że stałą tą jest <math>c=\sqrt{2\pi}</math>. | ||
Dowód tego oszacowania wykracza poza metody tego kursu. | Dowód tego oszacowania wykracza poza metody tego kursu. | ||
W oszacowaniach przez nierówności przydatna jest następująca wersja wzoru Stirlinga: | W oszacowaniach przez nierówności przydatna jest następująca wersja wzoru Stirlinga: | ||
<center><math> | <center><math>\sqrt{2\pi n}\left( \frac{n}{e} \right)^ne^{-(12n+1)}\leq n!\leq \sqrt{2\pi n}\left( \frac{n}{e} \right)^{n}e^{-12n} | ||
</math></center> | </math></center> | ||
Innym ważnym przybliżeniem asymptotycznym jest wzór na liczbę podziałów liczby naturalnej <math> | Innym ważnym przybliżeniem asymptotycznym jest wzór na liczbę podziałów liczby naturalnej <math>n</math> na sumy dodatnich liczb naturalnych, tzn. asymptotyczne przybliżenie funkcji <math>p_n = \sum_{k=1}^n P(n,k)</math> . | ||
{{twierdzenie|9.6|tw 9.6| | {{twierdzenie|9.6|tw 9.6| | ||
<center><math> | <center><math>p_n \sim \frac{e^{\pi\sqrt{\frac{2n}{3}}}}{4n\sqrt{3}} | ||
</math></center> | </math></center> | ||
| Linia 650: | Linia 622: | ||
}} | }} | ||
Podamy też asymptotyczne przybliżenie na liczbę liczb pierwszych nie większych niż <math> | Podamy też asymptotyczne przybliżenie na liczbę liczb pierwszych nie większych niż <math>n</math>. | ||
{{twierdzenie|9.7|tw .7| | {{twierdzenie|9.7|tw .7| | ||
Jeśli <math> | Jeśli <math>\pi(n)</math> oznacza liczbę liczb pierwszych w zbiorze <math>\left\lbrace 1,2,3,\ldots,n \right\rbrace</math>, to | ||
<center><math> | <center><math>\pi(n) \sim \frac{n}{\ln n} | ||
</math></center> | </math></center> | ||
}} | }} | ||
Aktualna wersja na dzień 09:09, 12 wrz 2023
Widzieliśmy już, że wskazanie postaci zwartej dla ciągu zadanego równaniem rekurencyjnym jest często zadaniem niełatwym. Do tej pory nie jest znana zwarta postać wielu równań. Na szczęście często jesteśmy w sytuacji, w której zadowoli nas przybliżenie odpowiedzi. Wróćmy do rozważanej wielokrotnie sumy kolejnych kwadratów . Fakt, że jest to wielomian -go stopnia zmiennej , to już wartościowa informacja, często zupełnie wystarczająca. Spotkaliśmy się już nie raz z oszacowaniami poprzez zwykłe nierówności. To podejście często wymaga użycia narzędzi z analizy matematycznej, w szczególności znajdowania ekstremum funkcji.
Przykład
Silnię liczby naturalnej można trywialnie oszacować przez . Przyjrzyjmy się delikatniejszemu oszacowaniu wskazującemu także dolne ograniczenie na .
Najpierw zauważmy, że
Potraktujmy jako wielomian drugiego stopnia zmiennej . Łatwo zauważyć, że dla przybiera on najmniejszą wartość w punkcie , a największą w punkcie . Zatem dla mamy i dalej
czyli
Nierówności w oszacowaniach bywają niepotrzebnie krępujące. Zaś wyniki w ten sposób otrzymane, często skupiają naszą uwagę na zbędnych i czasem nieinteresujących detalach. Często bowiem wystarczają nam przybliżone, asymptotyczne oszacowania ciągów lub ogólniej funkcji. Opisują one zachowanie funkcji wraz ze wzrostem argumentu. Podczas przekształceń rachunkowych celowo ograniczamy naszą wiedzę o funkcji, dzięki czemu łatwiej jest rachować i otrzymać zadowalającą postać przybliżającą.
W oszacowaniach asymptotycznych posługujemy się ogólnie przyjętymi symbolami opisującymi asymptotyczne zachowanie jednej funkcji wobec drugiej. Najpowszechniej używany jest symbol przydatny w analizie górnej granicy asymptotycznej. Po raz pierwszy tego symbolu użył niemiecki teorio-liczbowiec Paul Bachmann w 1894. Prace Edmunda Landau'a (także niemieckiego teorio-liczbowca) spopularyzowały tę notację, stąd czasami jest nazywany symbolem Landau'a. Notację asymptotyczną wprowadzimy jedynie dla funkcji zdefiniowanych na zbiorze (lub jego podzbiorach postaci ) o wartościach w .
Notacja asymptotyczna
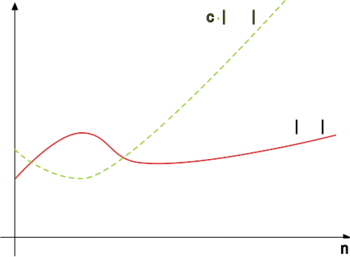
Funkcja asymptotycznie niewiększa od funkcji to taka funkcja , dla której istnieją i , że dla wszystkich .
Będziemy też często mówić, że zachodzi dla prawie wszystkich liczb naturalnych .
Zbiór funkcji asymptotycznie niewiększych niż oznaczamy przez .
Ponieważ jest zbiorem funkcji, poprawnie powinniśmy zapisywać , gdy spełnia warunek podany w definicji. Jednak przyjęło się zapisywać . Jest to pewne nadużycie symbolu równości . Jednak tradycja, a jak się niebawem okaże, również i wygoda użycia, są wystarczającym usprawiedliwieniem dla tego nadużycia. W związku z tym napis czytamy " jest -duże od ".
Przykład
- , to zbiór funkcji ograniczonych.
Istotnie warunek zachodzący dla prawie wszystkich łatwo jest, poprzez zamianę stałej na inną , sprowadzić do warunku zachodzącego już dla wszystkich , jako że skończenie wiele wartości dla początkowych daje się ograniczyć przez stałą.
- każda funkcja stała jest np. jest , bo dla dowolnego ,
- , bo dla dowolnego ,
- , bo dla dowolnego ,
- , bo dla , zatem dla .
- to zbiór funkcji ograniczonych przez funkcję liniową:
- wszystkie funkcje są też ,
- , bo dla ,
- , bo dla dowolnego .
-
- ,
- ,
- (funkcja ta jest także i ).
-
- , bo , a zatem dla dowolnego .
Więcej przykładów i ogólniejszych obserwacji poznamy po prezentacji pozostałych pojęć i symboli notacji asymptotycznej.
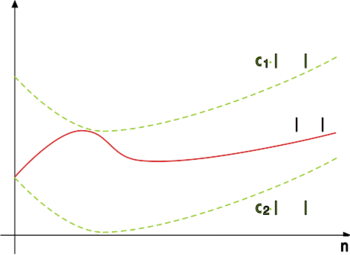
Funkcja asymptotycznie niemniejsza od funkcji to taka funkcja , dla której istnieją i , że dla wszystkich .
Zbiór funkcji asymptotycznie niemniejszych niż
oznaczamy przez .
Funkcja asymptotycznie podobna do funkcji to taka funkcja , dla której istnieją i , że
dla wszystkich .
Zbiór funkcji asymptotycznie podobnych do oznaczamy przez . A zatem .
Pozostałe dwa symbole: są rzadziej stosowane w informatyce. Wyznaczają one funkcje asymptotycznie, ściśle mniejsze [większe] od podanej funkcji.
Funkcja asymptotycznie mniejsza od funkcji to taka funkcja , że dla każdego istnieje , przy którym dla wszystkich .
Zbiór funkcji asymptotycznie mniejszych niż oznaczamy przez . A zatem wtedy i tylko wtedy, gdy .
Funkcja asymptotycznie większa od funkcji to taka funkcja , że dla każdego istnieje , przy którym dla wszystkich .
Zbiór funkcji asymptotycznie większych niż oznaczamy przez . A zatem wtedy i tylko wtedy, gdy .
Oto kilka prostych faktów wiążących kolejne symbole asymptotyczne. Pozostawiamy je bez dowodu.
Obserwacja 9.1
Dla funkcji mamy:
- jeśli , , to ,
- jeśli , , to ,
- jeśli , , to ,
- jeśli , , to ,
- wtedy i tylko wtedy, gdy ,
- wtedy i tylko wtedy, gdy ,
- wtedy i tylko wtedy, gdy .
Symbole asymptotyczne mogą pojawić się w złożonych wyrażeniach arytmetycznych. Dla przykładu wspomnijmy jeszcze raz sumę kolejnych kwadratów: . Możemy teraz napisać , ale także , co formalnie oznacza . Co więcej okazuje się, że symbol może pełnić nie tylko rolę , ale czasami także rolę . Na przykład wyrażenie
ma po obu stronach"równości" zbiory funkcji, przy czym po lewej stronie są to wszystkie funkcje postaci dla . W tej sytuacji znak powinien być formalnie rozumiany jako inkluzja .
Nadużywając znaku "równości" musimy jednak uważać i pamiętać, że w konwencji asymptotycznej taki nadużyty znak nie jest relacją symetryczną. Rzeczywiście, , gdyż np. funkcja , ale . Jednak pożytki płynące z takiego "przeciążenia" znaku równości sprawiedliwiają te nadużycia. W następnej Obserwacji w taki właśnie sposób sformułujemy (bez oczywistego dowodu) kilka własności notacji . Z nich mozna łatwo otrzymać analogiczne własności dla i .
Obserwacja 9.2
Dla funkcji mamy:
- ,
- wtedy i tylko wtedy, gdy ,
- wtedy i tylko wtedy, gdy ,
- wtedy i tylko wtedy, gdy ,
- jeśli i , to ,
- jeśli i , to .
Przykład
Pokażemy, że wielomiany -tego stopnia są .
Zauważmy najpierw, że jeśli to , czyli jeśli to . Rozważmy zatem dowolny wielomian -tego stopnia , gdzie . Wtedy
co dowodzi, że .
Dla dowodu , niech . Wtedy
dla .
Mamy zatem
co dowodzi .
Przykład
Często pojawiają się logarytmy o różnych podstawach. Najczęściej są to . Z asymptotycznego punktu widzenia wszystkie te funkcje są podobne tzn. np. i , lub ogólniej:
Rzeczywiście, jest to po prostu wzór na zamianę podstaw logarytmu,
gdzie ta sama stała jest dobra do dolnego i górnego ograniczenia.
Przykład
Dla wielomianów rząd ich wielkości wyznaczony jest przez stopień:
Ustala to hierarchię rzędów funkcji:
Również dla "stopni" będącymi dowolnymi liczbami dodatnimi mamy:
Na przykład:
- ,
- .
Przykład
Mamy . Istotnie łatwo dowieść indukcyjnie, że .
Podobnie . Wiemy już, że każda funkcja liniowa jest w ,
istnieje więc stała taka, że od pewnego miejsca .
Pokażemy, że wtedy też .
Indukcyjnie
Analogicznie, wiedząc już, że każda funkcja kwadratowa jest w ,
czyli że dla pewnej stałej od pewnego miejsca mamy { },
możemy pokazać indukcyjnie, że .
Istotnie
Ogólnie, dla dowolnego stopnia mamy , o ile tylko .
Przykład
Oczywiście , więc .
Ale .
Gdyby bowiem to
podczas gdy funkcja wykładnicza rośnie do nieskończoności.
Nie może zatem być ograniczona przez żadną stałą .
Ogólnie dla , mamy wtedy i tylko wtedy, gdy .
Przykład
Mamy oraz .
Istotnie
,
bo każdy czynnik (poza pierwszym) w jest równy co najmniej .
Pokazuje to, że .
Podobnie
,
bo każdy czynnik w jest nie większy niż .
Jako ćwiczenie pozostawiamy dowód następnej obserwacji.
Obserwacja 9.3
Oto ciąg funkcji, z których każda jest od następnej, ale nie od poprzedniej:
i dalej
W istocie, gdy występuje w tym ciagu wczesniej niż , to
- ,
- .
Przykład
Nie każde dwie funkcje są porównywalne asymptotycznie. Na przykład dla funkcji
i mamy i .
Twierdzenie o rekursji uniwersalnej
Podstawowym zastosowaniem notacji asymptotycznej w informatyce jest szacowanie długości działania programów, w szczególności procedur rekurencyjnych, których złożoność łatwo opisać równaniem rekurencyjnym. Niech będzie funkcją opisującą złożoność czasową pewnego programu, czyli zwracającą liczbę wykonywanych operacji dla danych wielkości . Zazwyczaj nie jesteśmy zainteresowani dokładną liczbą wykonywanych operacji, a jedynie dobrym oszacowaniem z góry i czasem z dołu. Dlatego zamiast szukać postaci zwartej rozwiązania rekurencyjnego, co na ogół jest zadaniem beznadziejnym, dopuszczamy użycie notacji asymptotycznej i szukamy pewnej "dobrze znanej" funkcji takiej, że . Znając wiemy w jaki sposób rośnie długość działania programu wraz z wzrostem wielkości danych.
Równania, o których mówimy często są postaci , czyli aby rozwiązać problem dla danych wielkości , rozwiązujemy podproblemów wielkości i składamy z nich rozwiązanie całości w dodatkowym czasie . Twierdzenie o rekurencji uniwersalnej wskazuje funkcję asymptotycznie podobną do w bardzo wielu przypadkach.
Twierdzenie 9.4 [o rekurencji uniwersalnej]
Dla funkcji zadanej przez
zachodzi:
- jeśli dla pewnego , to ,
- jeśli , to ,
- jeśli dla pewnego oraz dla pewnego i prawie wszystkich , to .
Zanim podamy dowód Twierdzenia 9.4, poczynimy kilka uwag i prześledzimy kilka przykładów.
W praktyce na ogół pomijamy opis początkowych wartości funkcji domyślnie przyjmując, że są one . Nie będziemy też używać podłóg w wyrażeniach typu , traktując występujące tu dzielenie jako całkowito-liczbowe. Twierdzenie o rekurencji uniwersalnej jest silnym i praktycznym narzędziem. Jednak trzeba podkreślić, że nie szacuje ono rozwiązań wszystkich równań typu . Taka niemożność oszacowania może mieć miejsce z jednego z trzech powodów, przy czym drugi z nich jest istotny i zdarza się w praktyce:
- W każdym z trzech przypadków opisanym w twierdzeniu, porównujemy funkcje i . Może się zdarzyć (jak widzieliśmy w jednym z przykładów), iż i są asymptotycznie nieporównywalne i wobec tego nie będzie można zastosować żadnego z tych trzech przypadków. Na szczęście w praktyce takie funkcje raczej zdarzają się niezmiernie rzadko.
- Po drugie, w przypadku pierwszym (i trzecim), tak naprawdę, porównujemy z funkcją istotnie mniejszą (wiekszą) od , tzn. z funkcją dla pewnego . Ten warunek już może przeszkadzać w praktyce. Dla przykładu , ale dla dowolnego . Pełny przykład takiego równania przedstawimy poniżej.
- Po trzecie, w ostatnim warunku dla dla dowolnego wymagamy dodatkowo, żeby dla pewnego i dla wszystkich dla pewnego . Znów, na szczęście, w większości spotykanych sytuacji ten warunek "regularności" jest spełniony. Jednak zawsze trzeba go sprawdzić.
Przykład
Dla funkcji zadanej przez:
dostajemy kolejno:
- , , ,
- , , np. dla ,
- zatem z pierwszego punktu Twierdzenia 9.4 mamy .
Podobnie dla funkcji
mamy:
- , , ,
- , ,
- zatem z drugiego punktu Twierdzenia 9.4 mamy .
Niech teraz
Wtedy
- , , ,
- , dla ,
- ,
- zatem z trzeciego punktu Twierdzenia 9.4 mamy .
Z kolei dla funkcji spełniającej
dostajemy
- , , ,
- ,
- ale dla dowolnego , ,
- i ... nie można zaaplikować Twierdzenia 9.4.
Po tych uwagach i przykładach podamy dowód Twierdzenia o rekurencji uniwersalnej.
Dowód
Rozumowanie nasze przeprowadzimy tylko w przypadku, gdy liczba występująca w rekurencyjnym równaniu zadającym funkcję jest potęgą liczby naturalnej, czyli dla liczb postaci . Rozszerzenie tego rozumowania na cały zbiór jest dość techniczne i wymaga szacowania podłóg. Ponadto, symboli asymptotycznych będziemy używać tylko dla . To nieformalne nadużycie nie ogranicza poprawności rozumowania -- wymaga wszakże rozszerzenia notacji asymptotycznej na funkcje postaci .
Rozwijając rekurencyjną formułę dla otrzymujemy:
Ponieważ możemy kontynuować:
Dalsze szacowanie rozbijamy na przypadki zgodnie z warunkami na zachowanie
funkcji wobec :
- ,
Ponieważ i są stałymi, ostatni składnik redukuje się do
. Zatem
- ,
- dla pewnego i prawie wszystkich
oraz .
Z założeń tego przypadku mamy . Zatem
Metoda przybliżeń
W pewnych sytuacjach łatwiejsze do uzyskania, ale słabsze oszacowanie zastosowane w odpowiedni sposób może prowadzić do lepszego końcowego szacowania zachowania asymptotycznego. Poznamy tę metodę w kilku kolejnych przykładach.
Przykład
Dla ciągu zadanego przez
najpierw dowodzimy indukcyjnie, że , czyli .
Podstawiając uzyskane oszacowanie do równania rekurencyjnego otrzymujemy:
Operację tę możemy powtórzyć uzyskując jeszcze lepsze oszacowanie
Wykorzystaliśmy tu fakt, iż szereg jest zbieżny.
Zauważmy też, że następne powtórzenie podobnej procedury szacującej już nam nic nie da.
Przykład
Niech ciąg spełnia
Z monotoniczności funkcji dostajemy, że .
Podstawiając to oszacowanie za drugie wystąpienie w równaniu otrzymujemy:
czyli . Podstawiając powtórnie dostajemy:
czyli .
Uzyskaliśmy zatem, że .
Na zakończenie tego wykładu poznamy jeszcze jeden symbol asymptotyczny. Jest on podobny do lecz znacznie precyzyjniejszy.
Funkcje asymptotycznie równe to takie funkcje i , że
Fakt, że funkcje i są asymptotycznie równe zapisujemy jako .
Jednym z najbardziej znanych przybliżeń asymptotycznych jest tzw. Wzór Stirlinga przybliżający zachowanie silni.
Twierdzenie 9.5 [wzór Stirlinga]
Wzór ten został odkryty przez Abrahama de Moivre w postaci
dla pewnej stałej .
Wkładem Jamesa Stirlinga było pokazanie, że stałą tą jest .
Dowód tego oszacowania wykracza poza metody tego kursu.
W oszacowaniach przez nierówności przydatna jest następująca wersja wzoru Stirlinga:
Innym ważnym przybliżeniem asymptotycznym jest wzór na liczbę podziałów liczby naturalnej na sumy dodatnich liczb naturalnych, tzn. asymptotyczne przybliżenie funkcji .
Twierdzenie 9.6
Podamy też asymptotyczne przybliżenie na liczbę liczb pierwszych nie większych niż .
Twierdzenie 9.7
Jeśli oznacza liczbę liczb pierwszych w zbiorze , to