GKIW Moduł 3 - Podstawowe operacje rastrowe: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 6 wersji utworzonych przez 3 użytkowników) | |||
| Linia 20: | Linia 20: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M3_Slajd1.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M3_Slajd1.png|thumb|500px]] | ||
|valign="top"|Jednym z podstawowych problemów tego typu jest '''zadanie narysowania odcinka na mapie pikseli'''. Najprostszym rozwiązaniem wydaje się poprowadzenie prostej przez końce odcinka i opisanie jej równaniem <math>y=m\cdot x</math>. Następnie wyznaczenie wartości <math>y_i\ | |valign="top"|Jednym z podstawowych problemów tego typu jest '''zadanie narysowania odcinka na mapie pikseli'''. Najprostszym rozwiązaniem wydaje się poprowadzenie prostej przez końce odcinka i opisanie jej równaniem <math>y=m\cdot x</math>. Następnie wyznaczenie wartości <math>y_i\ </math>, dla całkowitych wartości <math>x_i\ </math>, odpowiadających kolejnym kolumnom pikseli. Jeśli teraz przybliżymy współrzędne <math>y_i\ </math>, do wartości całkowitej, to otrzymamy współrzędne dla kolejnych pikseli tworzących odcinek tzn. <math>y_i=ROUND(m\cdot x_i)</math> , gdzie <math>ROUND()\,\ </math>, jest operacją zaokrąglania do najbliższej wartości całkowitej. Tak skonstruowany algorytm przyrostowy ma podstawową wadę. Wymaga operacji zmiennopozycyjnych (mnożenia, dodawania, zaokrąglania). | ||
|} | |} | ||
| Linia 35: | Linia 35: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M3_Slajd3_v4.png|thumb|500px]] | ||
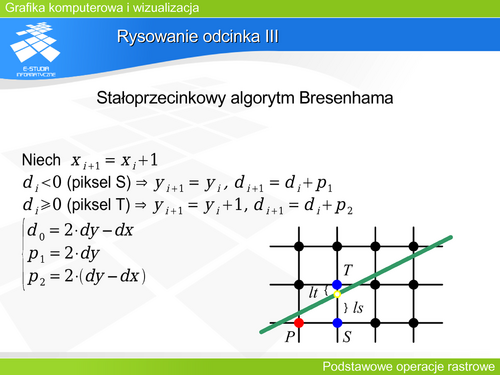
|valign="top"|Pełny algorytm Bresenhama dla x2>x1, y2>y1, 0<m<1 wyglądałby tak: | |valign="top"|Pełny algorytm Bresenhama dla x2>x1, y2>y1, 0<m<1 wyglądałby tak: | ||
'''procedure Bresline''' (x1,x2, | '''procedure Bresline''' (x1,x2, y1,y2,) | ||
'''begin''' | '''begin''' | ||
| Linia 70: | Linia 70: | ||
Pierwszym jest fakt, że odcinek może nie być symetryczny gdy zamienimy końce startowe. Problem ten wymaga korekty podejmowania decyzji dla d=0 w zależności od wzrostu lub spadku wartości współrzędnych. | Pierwszym jest fakt, że odcinek może nie być symetryczny gdy zamienimy końce startowe. Problem ten wymaga korekty podejmowania decyzji dla d=0 w zależności od wzrostu lub spadku wartości współrzędnych. | ||
Poważniejszym problemem jest zmiana jasności. Oba odcinki na rysunku składają się z 7 punktów. Tylko że odcinek po przekątnej rastra jest <math>\sqrt{2}\ | Poważniejszym problemem jest zmiana jasności. Oba odcinki na rysunku składają się z 7 punktów. Tylko że odcinek po przekątnej rastra jest <math>\sqrt{2}\ </math>, razy dłuższy od odcinka poziomego. Jest to problem związany ze skończoną rozdzielczością rastra i podobnie jak usuwanie wrażenia schodków odcinka rozwiązuje się go zmieniając barwy pikseli sąsiednich. | ||
|} | |} | ||
| Linia 180: | Linia 180: | ||
W takiej sytuacji należy rozważyć przypadek szczególny gdy kody obu końców są zerowe (punkty P1 i K1 na rysunku), wtedy cały rysunek leży wewnątrz okna. | W takiej sytuacji należy rozważyć przypadek szczególny gdy kody obu końców są zerowe (punkty P1 i K1 na rysunku), wtedy cały rysunek leży wewnątrz okna. | ||
Natomiast jeśli kody końców są niezerowe to określają one którymi prostymi należy przyciąć odcinek. Odcinek <math> | Natomiast jeśli kody końców są niezerowe to określają one którymi prostymi należy przyciąć odcinek. Odcinek <math>\overline{P2K2}\ </math>, należy przyciąć prostą prawą (K2=0010). Odcinek <math>\overline{P3K3}\ </math>, prostymi lewą i dolną (P3=0101) oraz prawą i górną (K3=1010). | ||
|} | |} | ||
| Linia 206: | Linia 206: | ||
Ma jednak jedną wadę. Często odcinki są przycinane kilka razy (różnymi prostymi) zanim uzyskają końcową postać. Z punktu widzenia wyznaczania przecięcia nie jest to efektywne. W 1978 roku Cyrus i Beck zaproponowali całkowicie inne podejście do problemu obcinania. | Ma jednak jedną wadę. Często odcinki są przycinane kilka razy (różnymi prostymi) zanim uzyskają końcową postać. Z punktu widzenia wyznaczania przecięcia nie jest to efektywne. W 1978 roku Cyrus i Beck zaproponowali całkowicie inne podejście do problemu obcinania. | ||
Jeśli opiszemy prostą parametrycznie to wzrost parametru określi naturalny zwrot prostej. Niech punkty P0 i Pk odpowiadają odpowiednio parametrom t=0 i t=tk dla k>0. Wektor <math> | Jeśli opiszemy prostą parametrycznie to wzrost parametru określi naturalny zwrot prostej. Niech punkty P0 i Pk odpowiadają odpowiednio parametrom t=0 i t=tk dla k>0. Wektor <math>\overline{P0Pk}\ </math>, określa zwrot prostej. Można przeanalizować iloczyn skalarny tego wektora i wektora normalnego (skierowanego na zewnątrz) do boku wielokąta. | ||
Jeśli <math> | Jeśli <math>\overline{P0Pk}\circ \overrightarrow{n}_i>0</math> to parametr tk określa punkt Pk.który może być „maksymalnym” punktem przecięcia z wielokątem (np. punkt dla t=t2 na rysunku). | ||
Jeśli <math> | Jeśli <math>\overline{P0Pk}\circ \overrightarrow{n}_i<0</math> to parametr tk określa punkt Pk.który może być „minimalnym” punktem przecięcia z wielokątem (np. punkt dla t=t1 na rysunku). | ||
Cyrus i Beck zaproponowali efektywny zestaw operacji parametrycznych do analizy całego wielokąta. Algorytm ten został w 1984 roku rozszerzony Lianga i Barsky’ego do ogólnego przypadku 2D obcinania prostymi równoległymi do osi układu współrzędnych oraz 3D obcinania płaszczyznami prostopadłymi do osi układu współrzędnych. | Cyrus i Beck zaproponowali efektywny zestaw operacji parametrycznych do analizy całego wielokąta. Algorytm ten został w 1984 roku rozszerzony Lianga i Barsky’ego do ogólnego przypadku 2D obcinania prostymi równoległymi do osi układu współrzędnych oraz 3D obcinania płaszczyznami prostopadłymi do osi układu współrzędnych. | ||
| Linia 261: | Linia 261: | ||
:reszta wielokąta to punkt jest wewnątrz. | :reszta wielokąta to punkt jest wewnątrz. | ||
Opisany algorytm należy w zależności od potrzeb uzupełnić o analizę samego wielokąta (przynależność lub nie do odpowiednich odcinków co jest zabiegiem technicznym i nie stanowi problemu. | Opisany algorytm należy w zależności od potrzeb uzupełnić o analizę samego wielokąta (przynależność lub nie do odpowiednich odcinków co jest zabiegiem technicznym i nie stanowi problemu). | ||
Podstawową wadą zaprezentowanego algorytmu jest fakt, że działa poprawnie tylko dla wielokątów wypukłych. Dla wielokątów wklęsłych będą proste wyznaczone przez kolejne wierzchołki, które będą przecinały wielokąt. | Podstawową wadą zaprezentowanego algorytmu jest fakt, że działa poprawnie tylko dla wielokątów wypukłych. Dla wielokątów wklęsłych będą proste wyznaczone przez kolejne wierzchołki, które będą przecinały wielokąt. | ||
| Linia 293: | Linia 293: | ||
Można założyć, że wierzchołki wielokąta są uporządkowane przeciwnie do ruchu wskazówek zegara. Z badanego punktu przez każdy wierzchołek wielokąta prowadzimy półprostą. Badany punkt oraz półproste przechodzące przez kolejne wierzchołki wyznaczają kąt, któremu można przypisać zorientowanie analogicznie jak zorientowanie wielokąta (+ jeśli kolejność ramion kąta jest przeciwna do ruchu wskazówek zegara, i – w sytuacji odwrotnej). Po przyjęciu takich założeń wystarczy zsumować wszystkie kąty związane z punktem badanym. Jeśli <math>suma = 360^\circ</math> to punkt jest wewnątrz wielokąta. Jeśli <math>suma = 0^\circ</math> to na zewnątrz. | Można założyć, że wierzchołki wielokąta są uporządkowane przeciwnie do ruchu wskazówek zegara. Z badanego punktu przez każdy wierzchołek wielokąta prowadzimy półprostą. Badany punkt oraz półproste przechodzące przez kolejne wierzchołki wyznaczają kąt, któremu można przypisać zorientowanie analogicznie jak zorientowanie wielokąta (+ jeśli kolejność ramion kąta jest przeciwna do ruchu wskazówek zegara, i – w sytuacji odwrotnej). Po przyjęciu takich założeń wystarczy zsumować wszystkie kąty związane z punktem badanym. Jeśli <math>suma = 360^\circ</math> to punkt jest wewnątrz wielokąta. Jeśli <math>suma = 0^\circ</math> to na zewnątrz. | ||
Oczywiście należy pamiętać o błędach zaokrąglenia i oczekiwanie np. dokładnie zerowej wartości byłoby nieporozumieniem. Jeśli jesteśmy pewni że w implementacji nie ma błędu, to warunki można postawić jako: <math>suma > | Oczywiście należy pamiętać o błędach zaokrąglenia i oczekiwanie np. dokładnie zerowej wartości byłoby nieporozumieniem. Jeśli jesteśmy pewni że w implementacji nie ma błędu, to warunki można postawić jako: <math>suma > 180^\circ</math> i <math>suma < 180^\circ</math>. | ||
|} | |} | ||
| Linia 302: | Linia 302: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M3_Slajd22_v4.png|thumb|500px]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Aktualna wersja na dzień 12:06, 5 wrz 2023
Wykład
 |
 |
Analogicznym zadaniem do wypełniania obszaru jest zmiana barwy w danym obszarze. Zadania są równoważne. Algorytm rozwiązujący jedno z nich może posłużyć do rozwiązania drugiego. |
Literatura
 |