|
|
| (Nie pokazano 14 wersji utworzonych przez 3 użytkowników) |
| Linia 1: |
Linia 1: |
| __TOC__ | | __TOC__ |
| = Wykład nowy = | | = Wykład = |
|
| |
|
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| Linia 114: |
Linia 114: |
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd12n.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd12n.png|thumb|500px]] |
| |valign="top"|Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, która będzie odkształcona. Analogicznie niech <math>B(u,v)=[x_B(u,v), y_B(u,v), z_B(u,v)]</math> opisuje zaburzenie (teksturę). Wektor normalny <math>\vec{N}\,</math> do powierzchni <math>S(u,v)\,</math> można wyznaczyć jako: | | |valign="top"|Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, która będzie odkształcona. Niech <math>B(u,v)</math> opisuje zaburzenie (teksturę). Wektor normalny <math>\vec{N}\ </math>, do powierzchni <math>S(u,v)\ </math>, można wyznaczyć jako: |
|
| |
|
| :<math>\displaystyle \vec{N}=\frac{\partial S(u,v)}{\partial u}\times\frac{\partial S(u,v)}{\partial v}</math> | | :<math>\vec{N}=\frac{\partial S(u,v)}{\partial u}\times\frac{\partial S(u,v)}{\partial v}</math> |
|
| |
|
| Jeśli nałożymy teksturę na powierzchnię to powstanie powierzchnia zniekształcona | | Jeśli nałożymy teksturę na powierzchnię to powstanie powierzchnia zniekształcona |
| Linia 124: |
Linia 124: |
| Wektor normalny do tak otrzymanej powierzchni można wyznaczyć analogicznie. Przy czym różniczkując równanie zniekształconej powierzchni otrzymuje się: | | Wektor normalny do tak otrzymanej powierzchni można wyznaczyć analogicznie. Przy czym różniczkując równanie zniekształconej powierzchni otrzymuje się: |
|
| |
|
| :<math>\displaystyle \frac{\partial S'(u,v)}{\partial u}=\frac{\partial S(u,v)}{\partial u}+\frac{\partial B(u,v)}{\partial u}\cdot \vec{N}+B(u,v)\cdot \frac{\partial \vec{N}}{\partial u}</math> | | :<math>\frac{\partial S'(u,v)}{\partial u}=\frac{\partial S(u,v)}{\partial u}+\frac{\partial B(u,v)}{\partial u}\cdot \vec{N}+B(u,v)\cdot \frac{\partial \vec{N}}{\partial u}</math> |
|
| |
|
| :<math>\displaystyle \frac{\partial S'(u,v)}{\partial v}=\frac{\partial S(u,v)}{\partial v}+\frac{\partial B(u,v)}{\partial v}\cdot \vec{N}+B(u,v)\cdot \frac{\partial \vec{N}}{\partial v}</math> | | :<math>\frac{\partial S'(u,v)}{\partial v}=\frac{\partial S(u,v)}{\partial v}+\frac{\partial B(u,v)}{\partial v}\cdot \vec{N}+B(u,v)\cdot \frac{\partial \vec{N}}{\partial v}</math> |
|
| |
|
| Blinn założył, że zaburzenie jest na tyle małe, że ostatnie wyrazy w tych równaniach można pominąć. Wtedy aproksymowany wektor normalny do zniekształconej powierzchni można opisać jako | | Blinn założył, że zaburzenie jest na tyle małe, że ostatnie wyrazy w tych równaniach można pominąć. Wtedy aproksymowany wektor normalny do zniekształconej powierzchni można opisać jako |
|
| |
|
| :<math>\displaystyle \vec{N}'\approx \left(\frac{\partial S(u,v)}{\partial u}+\frac{\partial B(u,v)}{\partial u}\cdot \vec{N}\ \right)\times \left(\frac{\partial S(u,v)}{\partial v}+\frac{\partial B(u,v)}{\partial v}\cdot \vec{N}\ \right)</math> | | :<math>\vec{N}'\approx \left(\frac{\partial S(u,v)}{\partial u}+\frac{\partial B(u,v)}{\partial u}\cdot \vec{N}\ \right)\times \left(\frac{\partial S(u,v)}{\partial v}+\frac{\partial B(u,v)}{\partial v}\cdot \vec{N}\ \right)</math> |
|
| |
|
| to oznacza, że | | to oznacza, że |
| Linia 136: |
Linia 136: |
| :<math>\vec{N}'=\vec{N}+\vec{D}</math> | | :<math>\vec{N}'=\vec{N}+\vec{D}</math> |
|
| |
|
| Przy czym <math>\vec{D}\,</math> jest wektorem zaburzenia: | | Przy czym <math>\vec{D}\ </math>, jest wektorem zaburzenia: |
|
| |
|
| :<math>\displaystyle \vec{D}=\frac{\partial B(u,v)}{\partial u}\cdot \vec{S}-\frac{\partial B(u,v)}{\partial v}\cdot \vec{T}</math> | | :<math>\vec{D}=\frac{\partial B(u,v)}{\partial u}\cdot \vec{S}-\frac{\partial B(u,v)}{\partial v}\cdot \vec{T}</math> |
|
| |
|
| gdzie <math>\vec{S}\,</math> i <math>\vec{T}\,</math> są wektorami stycznymi do powierzchni <math>S(u,v)\,</math>. | | gdzie <math>\vec{S}\ </math>, i <math>\vec{T}\ </math>, są wektorami stycznymi do powierzchni <math>S(u,v)\ </math>,. |
|
| |
|
| Takie rozwiązanie daje bardzo prostą możliwość definicji wektora normalnego odkształconej powierzchni za pomocą wektorów zaburzenia. Wadą zaproponowanej przez Blinna metody jest aproksymacja wektora normalnego. Stąd powstało wiele różnych realizacji tej metody, wykorzystujących różne warianty uproszczenia. Znane są również próby aplikacji sprzętowych mapowania nierówności Blinna. | | Takie rozwiązanie daje bardzo prostą możliwość definicji wektora normalnego odkształconej powierzchni za pomocą wektorów zaburzenia. Wadą zaproponowanej przez Blinna metody jest aproksymacja wektora normalnego. Stąd powstało wiele różnych realizacji tej metody, wykorzystujących różne warianty uproszczenia. Znane są również próby aplikacji sprzętowych mapowania nierówności Blinna. |
| Linia 158: |
Linia 158: |
| Techniką dającą dobre efekty w takiej sytuacji jest mapowanie przesunięć. | | Techniką dającą dobre efekty w takiej sytuacji jest mapowanie przesunięć. |
|
| |
|
| Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, <math>P\,</math> będzie punktem na tej powierzchni, a <math>\vec{N}\,</math> będzie wektorem normalnym do powierzchni <math>S(u,v)\,</math>. Niech funkcja <math>f(P)\,</math> opisuje przesunięcie punktu powierzchni <math>S(u,v)\,</math>. | | Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, <math>P\ </math>, będzie punktem na tej powierzchni, a <math>\vec{N}\ </math>, będzie wektorem normalnym do powierzchni <math>S(u,v)\ </math>,. Niech funkcja <math>f(P)\ </math>, opisuje przesunięcie punktu powierzchni <math>S(u,v)\ </math>,. |
|
| |
|
| Wtedy dla każdego punktu <math>P\,</math> | | Wtedy dla każdego punktu <math>P\ </math>, |
|
| |
|
| :<math>P'=P+f(P)\cdot \vec{N}</math> | | :<math>P'=P+f(P)\cdot \vec{N}</math> |
| Linia 230: |
Linia 230: |
|
| |
|
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_05.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:GKIW_M10v5_plus_05.png|thumb|500px]] |
| |valign="top"|Deformowanie obrazów (warping) w celu uzyskania określonego kształtu (poprzez zmianę barw rysunku) wymaga precyzyjnej definicji co i w jaki sposób ma zostać odkształcone. Najczęściej jest to określane za pomocą siatki punktów kontrolnych (czworokątnej lub trójkątnej). Wykorzystywane są przekształcenia afiniczne (translacje, obroty, skalowanie) lub dowolne. Przekształcenie może dotyczyć samej geometrii obiektu lub też jego atrybutów (barwa, tekstura, właściwości odbijające itd.). | | |valign="top"|Deformowanie obrazów (warping) w celu uzyskania określonego kształtu (poprzez zmianę barw rysunku) wymaga precyzyjnej definicji co i w jaki sposób ma zostać odkształcone. Najczęściej jest to określane za pomocą siatki punktów kontrolnych (czworokątnej lub trójkątnej). Wykorzystywane są przekształcenia afiniczne (translacje, obroty, skalowanie) lub dowolne. Przekształcenie może dotyczyć samej geometrii obiektu lub też jego atrybutów (barwa, tekstura, właściwości odbijające itd.). |
|
| |
|
| Linia 300: |
Linia 300: |
| |} | | |} |
|
| |
|
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd19n.png|thumb|500px]]
| |
| |valign="top"|Animacja oparta na klatkach kluczowych składa się z następujących etapów:
| |
|
| |
| *Wyszczególnienie i synteza klatek kluczowych charakteryzujących najważniejsze momenty ruchu lub sceny.
| |
| *Określenie sposobu przejścia pomiędzy klatkami – może to być realizowane w postaci równań ruchu.
| |
| *Wyznaczenie klatek pośrednich – na przykład za pomocą morfingu.
| |
| *Kontrola efektu końcowego i ewentualne poprawki.
| |
|
| |
| Animacja proceduralna polega na wydzieleniu parametrów sterujących przebiegiem zmian i wyznaczeniu zależności funkcyjnych między opisem parametrów a wyglądem klatki (lub sceny). Metoda ta jest wygodna do animacji procesów fizycznych i mechanicznych.
| |
|
| |
| Przykładem są kinematyka odwrotna i metoda deformacji swobodnych (FFD – Free Form Deformation).
| |
|
| |
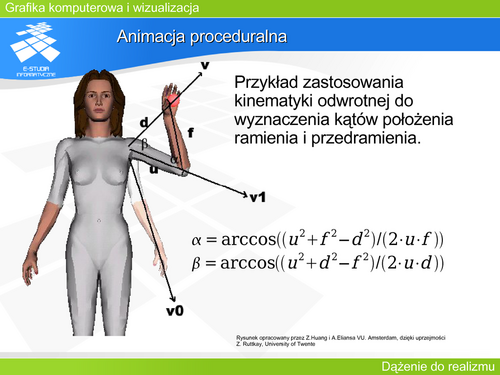
| Kinematyka odwrotna opisuje zależności ruchowe na podstawie wymaganych położeń obiektów. Jest bardzo wygodną forma dla uzyskania ruchu złożonych mechanicznie elementów, jest często wykorzystywana do animacji postaci.
| |
|
| |
| Metoda deformacji swobodnych ma wiele implementacji. Najczęściej stosuje się techniki szkieletowe lub siatkowe, w których pozycje odpowiednich punktów i zależności między węzłami siatki lub szkieletu opisane są równaniami parametrycznymi.
| |
|
| |
| Animacja symulacyjna wykorzystuje opis zachowania obiektów uzyskany na podstawie praw fizyki. Rozwiązanie tak uzyskanych równań daje poszukiwaną symulację. Metoda ta jest najbardziej złożona obliczeniowo, jest zatem czasochłonna jednak może dać bardzo dobre efekty. Wykorzystywana do modelowania i animacji zjawisk fizycznych.
| |
|
| |
| Przechwytywanie ruchu pozwala powielić schemat zachowania obiektu na podstawie naturalnego zachowania się obiektu rzeczywistego. Jest wygodna do modelowania ruchu postaci ludzkich, zwierzęcych a także postaci fantastycznych, którym można przypisać pewne właściwości ruchowe podobne do znanych cech zwierząt lub ludzi. Metoda ta daje bardzo dobre efekty, gdyż łatwiej jest skopiować ruch zwierząt niż opisać go równaniami matematycznymi. Wadą jest konieczność stosowania specjalistycznego sprzętu do przechwytywania ruchu. Stosuje się zestawy czujników położenia, skanery trójwymiarowe lub zdjęcia poklatkowe.
| |
|
| |
| |}
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd20.png|thumb|500px]]
| |
| |valign="top"|Uwzględnienie zjawisk fizycznych w zachowaniu się obiektów na scenie daje możliwość uzyskania realizmu odbieranej animacji. Nawet najlepiej zaprojektowane szczegóły postaci nie zagwarantują poprawnego odbioru jeśli zachowanie się postaci będzie odbiegało od naszych oczekiwań. Z drugiej strony odbiór tradycyjnych filmów animowanych pokazuje, że jesteśmy skłonni zaakceptować nawet bardzo duży poziom umowności szczegółów i uproszczeń postaci jeśli będzie się ona poruszała w sposób naturalny.
| |
|
| |
| Ponieważ opis zgodny z prawami fizyki jest bardzo złożony, więc stosuje się metody upraszczające obliczenia. Przykładem może być opis ruchu układu mechanicznego będący układem liniowych równań różniczkowych stopnia drugiego. Do rozwiązania stosuje się albo metodę wektorów stanu sprowadzającą równania do rzędu pierwszego, albo metodę różnic skończonych pozwalającą sprowadzić układ równań różniczkowych do układu równań nieliniowych.
| |
|
| |
| Zachowanie się obiektów zależy od ich typu. Wyróżnia się modelowanie obiektów sztywnych przegubowych i modelowanie obiektów deformowalnych.
| |
|
| |
| Obiekty sztywne przegubowe modeluje się w postaci zestawu prostych sztywnych elementów połączonych ze sobą złączami mechanicznymi o zadanym zestawie stopni swobody. Dla obiektów deformowalnych opisuje się odpowiednimi równaniami takie zjawiska jak sprężystość, plastyczność, zrywanie, topnienie, lepkość itd.
| |
| |}
| |
|
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd21n.png|thumb|500px]]
| |
| |valign="top"|Symulacja kolizji jest jednym z ważniejszych problemów pojawiających się w grach komputerowych i filmach animowanych. Rozwiązanie tego problemu wymaga rozwiązania kilku zagadnień. Najważniejszym jest wykrycie kolizji. Zadanie to jest podobne do wykrycia przecięcia w metodzie śledzenia promieni. Przy czym tam było to przecięcie prosta – obiekt, tutaj natomiast jest to obiekt – obiekt. Niemniej jednak metody przyspieszające są podobne. Stosowana jest metoda brył ograniczających, wykrycie przecięcia sfera – sfera jest równie łatwe jak prosta – sfera. Od rodzaju powierzchni (sztywne, odkształcalne) zależy geometria kolizji – odkształcenia obiektów. Od rodzaju powierzchni zależą także efekty kolizji. Zastosowanie odpowiedniego modelu fizycznego opisu zjawiska pozwoli uzyskać wrażenie zgodne z naszym wyobrażeniem i oczekiwaniem.
| |
| |}
| |
|
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd22n.png|thumb|500px]]
| |
| |valign="top"|W modelowaniu postaci wykorzystuje się modele mieszane. Sztywny szkielet jako typowy model obiektu sztywnego przegubowego. Szkielet jest otoczony warstwą deformowalną. Deformacja powierzchni tej warstwy zależy zarówno od struktury szkieletu i jego odkształcenia jak i bieżącego stanu warstwy deformowalnej. Kinematyka odwrotna jest stosowana do opisu ruchu kończyn.
| |
|
| |
| Zestaw składowych jednej postaci jest zazwyczaj modelowany w postaci hierarchicznej.
| |
|
| |
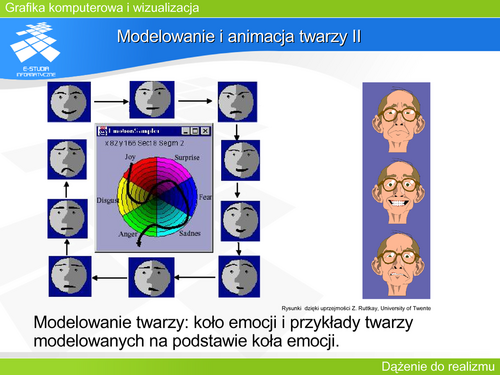
| Animacja twarzy jest traktowana jako odrębne zagadnienie ze względu na złożoność problemu oraz ze względu na fakt, że człowiek szybciej identyfikuje twarz na obrazie
| |
| |}
| |
|
| |
| ----
| |
|
| |
| = Literatura =
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_24.png|thumb|500px]]
| |
| |valign="top"|
| |
| |}
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_25.png|thumb|500px]]
| |
| |valign="top"|
| |
| |}
| |
| ----
| |
|
| |
| = Wykład =
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd1.png|thumb|500px]]
| |
| |valign="top"|
| |
| |}
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_01.png|thumb|500px]]
| |
| |valign="top"|
| |
| |}
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_02.png|thumb|500px]]
| |
| |valign="top"|Mapowanie nierówności Blinna (bump mapping) daje znakomite wrażenie nierówności powierzchni, ale nie zmienia w rzeczywistości jej kształtu. Takie postępowanie przynosi dobre efekty pod warunkiem, że nie występuje wzajemne zasłanianie między poszczególnymi nierównościami powierzchni (lub jest ono pomijalne z punktu widzenia obserwatora). Jeśli ten warunek nie jest spełniony wtedy pojawiają się problemy.
| |
|
| |
| Techniką dającą dobre efekty w takiej sytuacji jest mapowanie przesunięć.
| |
|
| |
| Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, <math>P\,</math> będzie punktem na tej powierzchni, a <math>\vec{N}\,</math> będzie wektorem normalnym do powierzchni <math>S(u,v)\,</math>. Niech funkcja <math>f(P)\,</math> opisuje przesunięcie punktu powierzchni <math>S(u,v)\,</math>.
| |
|
| |
| Wtedy dla każdego punktu <math>P\,</math>
| |
|
| |
| :<math>P'=P+f(P)\cdot \vec{N}</math>
| |
|
| |
| Taka modyfikacja kształtu daje możliwość uzyskania rzeczywistego przesunięcia i efektów z tym związanych (np. wzajemne zasłanianie).
| |
|
| |
| |}
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_03.png|thumb|500px]]
| |
| |valign="top"|Mapowanie przesunięć służy do modelowania faktury, to znaczy modelowania lokalnych kształtów powierzchni obiektu. Zakładamy przy tym, że powierzchnia obiektu jest zdefiniowana innymi metodami. Dobrym przykładem może być tworzenie zmarszczek na powierzchni twarzy. Głowa ma określony kształt - praktycznie niezmienny (poza np. ruchami żuchwy). Zmarszczki można traktować jako lokalne zmiany kształtu i zdefiniować wykorzystując mapowanie przesunięć.
| |
|
| |
| Prezentowany przykład pokazuje możliwość użycia mapowania przesunięć do modelowania obiektu. Jako kształt wyjściowy przyjęto sferę. Przesuwając punkty powierzchni wzdłuż promieni sfery, została ona odkształcona w taki sposób, że uzyskała kształt głowy. Oczywiście taki sposób ma podstawową wadę: nie można modelować dowolnego kształtu. A zatem ucho na pokazanym przykładzie będzie tylko pewnym przybliżeniem rzeczywistości. Dodatkowo warto zwrócić uwagę na dwa problemy. Pierwszym jest odpowiednie zdefiniowanie funkcji opisującej przesunięcie punktu. Drugim problemem jest rozdzielczość siatki uzyskanego obiektu. Równomierna siatka (południk/równoleżnik) sfery została przekształcona na nierównomierną, zależną od wysokości o dużych zmianach. Powoduje to, że tekstury muszą być indywidualnie dobierane do fragmentu, aby zachować odpowiedni poziom szczegółów.
| |
| |}
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_04.png|thumb|500px]]
| |
| |valign="top"|Deformacje dokonywane są:
| |
|
| |
| *W przestrzeni sceny, a więc deformacje obiektu (jego modelu).
| |
| Zmianie może podlegać geometria (kształt) obiektu oraz jego atrybuty (barwa, tekstura, właściwości odbijania światła itd.). Dobrym przykładem zmian geometrii są operacje ściskania, rozciągania lub skręcenia.
| |
|
| |
| *W przestrzeni rzutu – deformacje obrazu obiektu.
| |
| Zmiana dokonywana jest z wykorzystaniem transformacji afinicznych (lub dowolnych).
| |
|
| |
|
| |
| Warping jest przykładem operacji deformacji kształtu stosowanej zarówno w odniesieniu do obiektu jak i jego obrazu. Odbywa się to przez nałożenie siatki na obraz (lub obiekt trójwymiarowy – siatki przestrzennej) i przekształcenie położenia węzłów siatki zgodnie z określoną funkcją. Klasycznymi efektami uzyskiwanymi tą metodą jest zmiana wyrazu twarzy na zdjęciu – uśmiech, przymknięcie oczu itp.
| |
|
| |
| Morfing jest operacją pozwalającą wygenerować deformacje kształtu odpowiadające stanom pośrednim pomiędzy danymi obrazami.
| |
| |}
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_05.png|thumb|500px]]
| |
| |valign="top"|Deformowanie obrazów (warping) w celu uzyskania określonego kształtu (poprzez zmianę barw rysunku) wymaga precyzyjnej definicji co i w jaki sposób ma zostać odkształcone. Najczęściej jest to określane za pomocą siatki punktów kontrolnych (czworokątnej lub trójkątnej). Wykorzystywane są przekształcenia afiniczne (translacje, obroty, skalowanie) lub dowolne. Przekształcenie może dotyczyć samej geometrii obiektu lub też jego atrybutów (barwa, tekstura, właściwości odbijające itd.).
| |
|
| |
| Ponieważ obiekty wymagają zobrazowania (renderingu) to można złożyć tę operację z deformacjami w dowolnej kolejności. To znaczy najpierw jest deformowany model obiektu (np. jego geometria), a następnie odkształcony obiekt jest zobrazowany (renderowany), lub najpierw obiekt jest zobrazowany, a następnie przekształcany jest jego obraz. Do często stosowanych przekształceń geometrii obiektów trójwymiarowych należą ściskanie, skręcanie, wyginanie.
| |
|
| |
| Do deformacji i przekształcenia obiektów stosowana jest również morfologia matematyczna – dziedzina zajmująca się przetwarzaniem obrazów. Morfologia matematyczna powstała w latach sześćdziesiątych XX wieku w Ecole des Mines de Paris (Wyższej Szkole Górniczej w Paryżu). Twórcami morfologii byli Georges Matheron i Jean Serra. Podstawowymi przekształceniami morfologicznymi są: erozja (przypisanie pikselowi najmniejszej wartości spośród sąsiadów) i dylacja (przypisanie pikselowi największej wartości spośród sąsiadów). Wykorzystuje się także takie operacje jak: otwarcie (złożenie najpierw erozji potem dylacji), domknięcie (najpierw dylacja potem erozja), pogrubianie i ścienianie obiektów.
| |
|
| |
| Warto zwrócić uwagę także na zastosowanie geometrii rzutowej w deformacji obiektów. Zniekształcenia zapewniające korekcję perspektywy lub umożliwiające „nakładanie” płaskiego obrazu na krzywoliniową powierzchnię obiektu są operacjami wykorzystywanymi nie tylko w animacji. Posługujemy się nimi także w edytorach graficznych.
| |
|
| |
| Typowe wykorzystanie deformowania (warpingu) – wpłynięcie na kształt detali rysunku. W pokazanym przykładzie zmieniono wyraz twarzy przez zniekształcenie układu ust. Podobnie można „zmrużyć oczy” lub „zmarszczyć brwi”. Dzięki takim zabiegom można uzyskać, na przykład, zamierzony efekt zdjęć reklamowych.
| |
| |}
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_06.png|thumb|500px]]
| |
| |valign="top"|Uzyskanie większych zmian może być trudniejsze, mogą się bowiem pojawiać szczegóły, których nie było dotychczas widać. W takiej sytuacji samo deformowanie obrazu nic nie daje – należy użyć edytora graficznego i dodać odpowiednie detale. Łatwiej jednak często stworzyć wiarygodny obraz przez dodanie fragmentów do przekształconego zdjęcia niż namalować go w całości.
| |
| |}
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_07.png|thumb|500px]]
| |
| |valign="top"|Przekształcanie pozwala uzyskać stany pośrednie między obrazami. Jeśli wskażemy odpowiadające sobie punkty na obu obrazach, to za pomocą liniowej interpolacji można wyznaczyć pośrednie położenie między tymi punktami. Oczywiście operacja taka może zostać wykonana także na węzłach (punktach kontrolnych) nałożonej siatki. Wtedy zawartość każdego oczka jest deformowana zgodnie z liniową interpolacją względem brzegu takiego oczka. Stosuje się siatki czworokątów i trójkątów. W ogólnym przypadku przekształcenia mogą być wykonywane na obiektach wielowymiarowych – operację opisuje wtedy zestaw transformacji. W szczególności możemy mieć do czynienia z przekształceniem dwuwymiarowym obiektów jednowymiarowym (przekształcenia rysunku na płaszczyźnie), przekształceniem trójwymiarowym obiektów dwuwymiarowych (przekształcenia powierzchni trójwymiarowego obiektu), przekształceniem trójwymiarowym obiektów trójwymiarowych (przekształcenia obiektów wolumetrycznych).
| |
|
| |
| Zastosowanie morfologii matematycznej pozwala dokonywać przekształcania obrazów bez wykorzystywania siatek punktów kontrolnych
| |
|
| |
| Generowanie stanów pośrednich jest wygodnym sposobem uzyskania określonej liczby klatek pośrednich pomiędzy klatkami kluczowymi filmu. Operacja ta wymaga wstępnego dopasowania do siebie szczególnych cech klatek kluczowych. Oczywiście ze względu na sposób poruszania się obiektów lub zależności czasowe mogą być wymagane przekształcenia nieliniowe.
| |
| |}
| |
| ---- | | ---- |
|
| |
|
| Linia 489: |
Linia 334: |
|
| |
|
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_10.png|thumb|500px]][[Grafika:animA1v2.gif |'''Dziwne przygody Koziołka Matołka (1869-1971)'''|thumb|300px]] | | |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_10.png|thumb|500px]] |
| |valign="top"|Animacja poklatkowa jest najczęściej stosowaną metodą w tradycyjnych filmach rysunkowych. | | |valign="top"|Animacja poklatkowa jest najczęściej stosowaną metodą w tradycyjnych filmach rysunkowych. |
|
| |
|
| Pokazany przykład animacji Koziołka Matołka obejmuje 14 klatek pełnego cyklu ruchu. Bardzo często dla uproszczenia wykonywano mniej klatek (na przykład 7) obejmujących ten sam cykl ruchu i aby zachować odpowiedni czas trwania akcji każdą klatkę powielano dwukrotnie. Czasami mogło to prowadzić do pewnego, nienaturalnego „szarpania” ruchu, jednak przy wartkiej (zazwyczaj) akcji całego filmu było to praktycznie niezauważalne. | | Pokazany przykład animacji Koziołka Matołka obejmuje 14 klatek pełnego cyklu ruchu. Bardzo często dla uproszczenia wykonywano mniej klatek (na przykład 7) obejmujących ten sam cykl ruchu i aby zachować odpowiedni czas trwania akcji każdą klatkę powielano dwukrotnie. Czasami mogło to prowadzić do pewnego, nienaturalnego „szarpania” ruchu, jednak przy wartkiej (zazwyczaj) akcji całego filmu było to praktycznie niezauważalne. |
| Linia 548: |
Linia 393: |
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_15.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_15.png|thumb|500px]] |
| |valign="top"|Rozpatrzmy dwie kamery K1 i K2 śledzące poruszający się punkt P zgodnie z rysunkiem. Jeśli znane jest położenie kamer oraz ich ustawienie, to można określić rzuty <math>P'</math> i <math>P''</math> . Rzuty te definiują proste, których przecięciem jest szukany punkt P. Stąd jego współrzędne można wyznaczyć korzystając z prezentowanych równań. W praktyce, na skutek zakłóceń i błędów pomiarów może się okazać, że proste zdefiniowane przez rzuty <math>P'</math> i <math>P''</math> wcale się nie przecinają. W takiej sytuacji należy wyznaczyć punkt P będący punktem najbliższym obu prostych. | | |valign="top"|Rozpatrzmy dwie kamery <math>K_1</math> i <math>K_2</math> śledzące poruszający się punkt <math>P</math> zgodnie z rysunkiem. Jeśli znane jest położenie kamer oraz ich ustawienie, to można określić rzuty <math>P'</math> i <math>P''</math> . Rzuty te definiują proste, których przecięciem jest szukany punkt <math>P</math>. Stąd jego współrzędne można wyznaczyć korzystając z prezentowanych równań. W praktyce, na skutek zakłóceń i błędów pomiarów może się okazać, że proste zdefiniowane przez rzuty <math>P'</math> i <math>P''</math> wcale się nie przecinają. W takiej sytuacji należy wyznaczyć punkt <math>P</math> będący punktem najbliższym obu prostych. |
|
| |
|
| Do określenia położenia punktu wystarczą dwie kamery. Jednak aktor poruszając się może zasłaniać markery umieszczone na ubraniu. Na scenie może być także wielu aktorów, którzy zasłaniają się wzajemnie. Z tego powodu stosuje się wiele kamer, aby bez względu na pozę aktora, każdy marker był zawsze „widziany” przynajmniej przez dwie kamery. | | Do określenia położenia punktu wystarczą dwie kamery. Jednak aktor poruszając się może zasłaniać markery umieszczone na ubraniu. Na scenie może być także wielu aktorów, którzy zasłaniają się wzajemnie. Z tego powodu stosuje się wiele kamer, aby bez względu na pozę aktora, każdy marker był zawsze „widziany” przynajmniej przez dwie kamery. |
| Linia 572: |
Linia 417: |
| |valign="top"|Proces kreowania pojedynczej klatki nie odbiega w zasadzie od standardowego procesu powstawania obrazu w grafice komputerowej. Warto natomiast zwrócić uwagę na modelowanie obiektów na scenie filmu animowanego. Modelowane są te obiekty, które są widoczne. Pod uwagę brana jest przy tym nie tylko dana scena, ale cały film, lub przynajmniej pewna sekwencja klatek. Stąd na górnych rysunkach widoczna jest pełna siatka drzwi, chociaż są one otwarte i niewidoczne. Jednak w jednym z następnych ujęć będą one zamknięte (rysunek dolny) stąd potrzebny jest ich pełny model. Modelowanie obiektów filmu wymaga przeanalizowania całego scenopisu i określenia jakie obiekty i w jakim zakresie powinny zostać w określonej scenie zamodelowane. | | |valign="top"|Proces kreowania pojedynczej klatki nie odbiega w zasadzie od standardowego procesu powstawania obrazu w grafice komputerowej. Warto natomiast zwrócić uwagę na modelowanie obiektów na scenie filmu animowanego. Modelowane są te obiekty, które są widoczne. Pod uwagę brana jest przy tym nie tylko dana scena, ale cały film, lub przynajmniej pewna sekwencja klatek. Stąd na górnych rysunkach widoczna jest pełna siatka drzwi, chociaż są one otwarte i niewidoczne. Jednak w jednym z następnych ujęć będą one zamknięte (rysunek dolny) stąd potrzebny jest ich pełny model. Modelowanie obiektów filmu wymaga przeanalizowania całego scenopisu i określenia jakie obiekty i w jakim zakresie powinny zostać w określonej scenie zamodelowane. |
| |} | | |} |
| | ---- |
| | |
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd20.png|thumb|500px]] |
| | |valign="top"|Uwzględnienie zjawisk fizycznych w zachowaniu się obiektów na scenie daje możliwość uzyskania realizmu odbieranej animacji. Nawet najlepiej zaprojektowane szczegóły postaci nie zagwarantują poprawnego odbioru jeśli zachowanie się postaci będzie odbiegało od naszych oczekiwań. Z drugiej strony odbiór tradycyjnych filmów animowanych pokazuje, że jesteśmy skłonni zaakceptować nawet bardzo duży poziom umowności szczegółów i uproszczeń postaci jeśli będzie się ona poruszała w sposób naturalny. |
| | |
| | Ponieważ opis zgodny z prawami fizyki jest bardzo złożony, więc stosuje się metody upraszczające obliczenia. Przykładem może być opis ruchu układu mechanicznego będący układem liniowych równań różniczkowych stopnia drugiego. Do rozwiązania stosuje się albo metodę wektorów stanu sprowadzającą równania do rzędu pierwszego, albo metodę różnic skończonych pozwalającą sprowadzić układ równań różniczkowych do układu równań nieliniowych. |
| | |
| | Zachowanie się obiektów zależy od ich typu. Wyróżnia się modelowanie obiektów sztywnych przegubowych i modelowanie obiektów deformowalnych. |
| | |
| | Obiekty sztywne przegubowe modeluje się w postaci zestawu prostych sztywnych elementów połączonych ze sobą złączami mechanicznymi o zadanym zestawie stopni swobody. Dla obiektów deformowalnych opisuje się odpowiednimi równaniami takie zjawiska jak sprężystość, plastyczność, zrywanie, topnienie, lepkość itd. |
| | |} |
| | |
| | ---- |
| | |
| | {| border="0" cellpadding="4" width="100%" |
| | |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd21n.png|thumb|500px]] |
| | |valign="top"|Symulacja kolizji jest jednym z ważniejszych problemów pojawiających się w grach komputerowych i filmach animowanych. Rozwiązanie tego problemu wymaga rozwiązania kilku zagadnień. Najważniejszym jest wykrycie kolizji. Zadanie to jest podobne do wykrycia przecięcia w metodzie śledzenia promieni. Przy czym tam było to przecięcie prosta – obiekt, tutaj natomiast jest to obiekt – obiekt. Niemniej jednak metody przyspieszające są podobne. Stosowana jest metoda brył ograniczających, wykrycie przecięcia sfera – sfera jest równie łatwe jak prosta – sfera. Od rodzaju powierzchni (sztywne, odkształcalne) zależy geometria kolizji – odkształcenia obiektów. Od rodzaju powierzchni zależą także efekty kolizji. Zastosowanie odpowiedniego modelu fizycznego opisu zjawiska pozwoli uzyskać wrażenie zgodne z naszym wyobrażeniem i oczekiwaniem. |
| | |} |
| | |
| ---- | | ---- |
|
| |
|
| Linia 624: |
Linia 489: |
| ---- | | ---- |
|
| |
|
| = Wykład stary = | | = Literatura = |
|
| |
|
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd3.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_24.png|thumb|500px]] |
| |valign="top"|Nakładanie tekstury jest jednym z najważniejszych zadań grafiki realistycznej. Pozwala zwiększyć stopień realizmu generowanych obrazów, dodając pewne cechy obiektom, które bez tego wyglądałyby nienaturalnie. Jednocześnie ponieważ jest to nakładanie – odwzorowanie obrazu na powierzchni materiału, to jest to technika szybsza i efektywniejsza niż realizacja rzeczywistego definiowania właściwości powierzchni obiektu. | | |valign="top"| |
| | |
| Przedstawione zastosowania pokazują możliwości jakie daje tekstura. Nie jest to tylko nałożenie obrazu – zdjęcia, ale może to być także zmiana pewnych postrzeganych właściwości materiałowych. Możliwa jest także zmiana pewnych cech związanych z otoczeniem – tekstura jest także stosowana do przyspieszenia lub uproszczenia wyznaczania oświetlenia.
| |
| | |
| W tym zestawieniu warto wyróżnić trzy kategorie odwzorowania.
| |
| | |
| *Odwzorowanie wzoru – przeniesienie mapy barw (np. zdjęcia) na powierzchnię. Od takiej realizacji oczekujemy tylko, aby nałożona mapa była związana z obiektem.
| |
| *Odwzorowanie cech zależnych od obserwatora. W tym przypadku dodatkowo tekstura powinna zachowywać właściwości zależne od pewnych kierunków związanych ze sceną (np. położenie źródeł światła) i kierunków związanych z obiektem (np. anizotropia).
| |
| *Odwzorowanie zmieniające geometrię powierzchni materiału. Oczywiście zmiana może być w tym przypadku pozorna (np. przy zastosowaniu mapowania nierówności) ale realizacja powoduje powstanie wrażenia zgodnego z oczekiwaniem.
| |
| | |
| Jak widać nakładanie tekstury może obejmować szeroki zestaw zagadnień. Formalnie należałoby więc definiować teksturę jako pewną wektorowa funkcje wielu zmiennych. Liczba zmiennych jest zależna od właściwości odwzorowania.
| |
| | |
| |} | | |} |
| ---- | | ---- |
|
| |
|
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd4.png|thumb|500px]] | | |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_25.png|thumb|500px]] |
| |valign="top"|Pierwszym problemem jaki pojawia się przy odwzorowaniu tekstur jest pozyskiwanie tekstur. Znane są „banki” tekstur w Internecie zawierające wzory o różnej rozdzielczości i jakości (a także różnej cenie). Można także pokazać metody generowania wzorów. | | |valign="top"| |
| | |
| Odwzorowanie geometryczne jest operacją, która musi zapewnić możliwość nałożenia wzorca na powierzchnię, w taki sposób żeby nie stracić jakości wzorca.
| |
| | |
| Bezpośrednio z nakładaniem tekstury, a także z rzutowaniem perspektywicznym są związane problemy próbkowania, powodujące, że trudno jest w prosty sposób uzyskać zawsze dobrą jakość odwzorowanej tekstury mimo posiadania znakomitych wzorców. Problem ten można rozwiązać stosując filtrowanie tekstur.
| |
| | |
| |}
| |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd5.png|thumb|500px]]
| |
| |valign="top"|Tekstury dwuwymiarowe w postaci prostokątnego wzoru są najczęściej spotykane. Również właściwości trójwymiarowe materiałów spotykane są w postaci zestawów dwuwymiarowych wzorców – na przykład przecięć pod różnymi kątami.
| |
| | |
| |}
| |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd6.png|thumb|500px]]
| |
| |valign="top"|Opis proceduralny pozwala generować tekstury za pomocą odpowiednio dobranych funkcji matematycznych lub zestawu parametrów dla wybranej klasy funkcji.
| |
| Tablicowanie parametrów tekstury daje gotowy zestaw wartości dla realizacji obrazowania. Stosując opis proceduralny można dostosować wybrany podzbiór dziedziny dla konkretnego rozwiązania. Jest to bardzo istotne, gdyż gęstość próbkowania daje z jednej strony określony poziom szczegółów, a z drugiej strony zapewnia możliwość minimalizacji zniekształceń związanych z nakładaniem próbkowanego obrazu. Parametry tablicowane są realizacją funkcyjną dla określonej gęstości próbkowania. Ponieważ parametr ten nie może być zmieniany w trakcie odwzorowania, stosuje się zestawy takiej samej tekstury tablicowane dla różnej gęstości próbkowania.
| |
| | |
| Niezależny podział wyróżnia generowanie deterministyczne i stochastyczne. Deterministyczne, w którym istnieją reguły rozmieszczania wzorca tekstury na powierzchni materiału. Generowanie stochastyczne nie zapewnia informacji o ustalonej strukturze wzorca. Pozwala natomiast na tworzenie lokalnych zmian parametru (np. barwy) powierzchni wynikających z pewnego prawdopodobieństwa.
| |
| | |
| Często zachodzi potrzeba łączenia różnych technik aby uzyskany efekt jak najlepiej odpowiadał rzeczywistości. Przykładem może być generowanie trójwymiarowej tekstury słojów drewna. Można to zrobić przyjmując opis proceduralny deterministyczny opierając się na modelu zawierającym koncentrycznie umieszczone walce. Średnicę walca zmienia się dodatkowo przez deterministyczne zaburzenie w postaci harmonicznych. Ale aby zwiększyć podobieństwo do rzeczywistego obiektu dodaje się niewielkie zaburzenia stochastyczne zarówno do średnicy walców i położenia ich osi obrotu, jak również do barwy słojów.
| |
| | |
| |}
| |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd7.png|thumb|500px]]
| |
| |valign="top"|Modele deterministyczne można podzielić na cztery grupy.:
| |
| | |
| Modele okresowe, w których wzorzec jest nakładany na przestrzeń tekstury w ramach siatki. Okna siatki odpowiadają rozmiarom wzorca. Wzorzec może być powielony na wszystkie okna siatki lub tylko na ich część. Źródłem wzorca mogą być obiekty naturalne (skanowane, fotografowane) lub wygenerowane obrazy (edytory graficzne itp.).
| |
| | |
| W modelach o losowym rozmieszczeniu na powierzchni przestrzeni tekstury pojawiają się losowo rozmieszczone elementy (tzw. „bomby”) o określonej barwie i kształcie.
| |
| | |
| Modele mozaikowe są generowane bezpośrednio w przestrzeni tekstury w postaci rozrastających się, losowo ułożonych komórek. Każda z nich rozrasta się, aż do napotkania innej komórki.
| |
| | |
| Modele syntaktyczne generowane są bezpośrednio w przestrzeni tekstury z wykorzystaniem języków formalnych i reguł gramatycznych.
| |
| | |
| |}
| |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd8.png|thumb|500px]]
| |
| |valign="top"|Parametryzacja w przestrzeni obiektu zakłada, że obiekty są generowane w swoich własnych układach współrzędnych. Odwzorowanie tekstury jest opisem przekształcenia układu współrzędnych obiektu na układ współrzędnych tekstury. Takie odwzorowanie jest nazywane przekształceniem prosty.
| |
| | |
| Ten typ parametryzacji jest najwygodniejszy do stosowania w metodzie śledzenia promieni.
| |
| | |
| Parametryzacja w przestrzeni świata określa odwzorowanie przestrzeni tekstury na przestrzeń świata. Jest to nazywane często przekształceniem odwrotnym.
| |
| | |
| Projekcja jest przekształceniem przestrzeni obiektu na przestrzeń ekranu (rzutu). Ponieważ najczęściej w rzutowaniu jest wykorzystywane rzutowanie perspektywiczne więc również projekcja tekstury jest realizowana w postaci przekształcenia perspektywicznego.
| |
| |}
| |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd9.png|thumb|500px]]
| |
| |valign="top"|Prezentowane przykłady są parametryzacjami w przestrzeni obiektu. Pierwsza funkcja przekształca sferę obiektu na prostokąt tekstury.
| |
| | |
| Drugi przykład jest funkcją przekształcającą powierzchnię boczną walca (powierzchnia obiektu) na prostokąt tekstury.
| |
| |}
| |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd10.png|thumb|500px]]
| |
| |valign="top"|Prezentowane przykłady opisane są jako modele okresowe, przy czym w przypadku zdjęcia budynku Metropolita prostokąt tekstury jest nałożony dokładnie jeden raz, natomiast w pozostałych dwóch przypadkach prostokątny wzorzec jest powielany wielokrotnie.
| |
| | |
| |}
| |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd11n.png|thumb|500px]]
| |
| |valign="top"|Modelowanie nierówności powierzchni jest przykładem tekstury dwuwymiarowej. Metoda ta (ang. bump mapping) została zaproponowana przez Blinna w 1978 roku. Pozwala uzyskiwać widok powierzchni o zmodyfikowanym kształcie bez modyfikowania samej geometrii powierzchni.
| |
| | |
| Przy zastosowaniu tekstury Blinna zmianę kierunku wektora normalnego uzyskuje się przez dodatkową funkcje zaburzenia. Zmodyfikowany wektor normalny jest wykorzystywany w modelu oświetlenia, dzięki czemu są postrzegane lokalne zmiany oświetlenia. Oczywiście wektor zmieniony funkcją zaburzenia może, tak naprawdę, tworzyć dowolny kąt z powierzchnią obiektu, w związku z tym głównym problemem jest dobranie funkcji zaburzenia w taki sposób, aby zmiana wektora odpowiadała rzeczywistej zmianie kształtu powierzchni.
| |
| | |
| |}
| |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd12n.png|thumb|500px]]
| |
| |valign="top"|Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, która będzie odkształcona. Analogicznie niech <math>B(u,v)=[x_B(u,v), y_B(u,v), z_B(u,v)]</math> opisuje zaburzenie (teksturę). Wektor normalny <math>\vec{N}\,</math> do powierzchni <math>S(u,v)\,</math> można wyznaczyć jako:
| |
| | |
| :<math>\displaystyle \vec{N}=\frac{\partial S(u,v)}{\partial u}\times\frac{\partial S(u,v)}{\partial v}</math>
| |
| | |
| Jeśli nałożymy teksturę na powierzchnię to powstanie powierzchnia zniekształcona
| |
| | |
| :<math>S'(u,v)=S(u,v)+B(u,v)\cdot \vec{N}</math>
| |
| | |
| Wektor normalny do tak otrzymanej powierzchni można wyznaczyć analogicznie. Przy czym różniczkując równanie zniekształconej powierzchni otrzymuje się:
| |
| | |
| :<math>\displaystyle \frac{\partial S'(u,v)}{\partial u}=\frac{\partial S(u,v)}{\partial u}+\frac{\partial B(u,v)}{\partial u}\cdot \vec{N}+B(u,v)\cdot \frac{\partial \vec{N}}{\partial u}</math>
| |
| | |
| :<math>\displaystyle \frac{\partial S'(u,v)}{\partial v}=\frac{\partial S(u,v)}{\partial v}+\frac{\partial B(u,v)}{\partial v}\cdot \vec{N}+B(u,v)\cdot \frac{\partial \vec{N}}{\partial v}</math>
| |
| | |
| Blinn założył, że zaburzenie jest na tyle małe, że ostatnie wyrazy w tych równaniach można pominąć. Wtedy aproksymowany wektor normalny do zniekształconej powierzchni można opisać jako
| |
| | |
| :<math>\displaystyle \vec{N}'\approx \left(\frac{\partial S(u,v)}{\partial u}+\frac{\partial B(u,v)}{\partial u}\cdot \vec{N}\ \right)\times \left(\frac{\partial S(u,v)}{\partial v}+\frac{\partial B(u,v)}{\partial v}\cdot \vec{N}\ \right)</math>
| |
| | |
| to oznacza, że
| |
| | |
| :<math>\vec{N}'=\vec{N}+\vec{D}</math>
| |
| | |
| Przy czym <math>\vec{D}\,</math> jest wektorem zaburzenia:
| |
| | |
| :<math>\displaystyle \vec{D}=\frac{\partial B(u,v)}{\partial u}\cdot \vec{S}-\frac{\partial B(u,v)}{\partial v}\cdot \vec{T}</math>
| |
| | |
| gdzie <math>\vec{S}\,</math> i <math>\vec{T}\,</math> są wektorami stycznymi do powierzchni <math>S(u,v)\,</math>.
| |
| | |
| Takie rozwiązanie daje bardzo prostą możliwość definicji wektora normalnego odkształconej powierzchni za pomocą wektorów zaburzenia. Wadą zaproponowanej przez Blinna metody jest aproksymacja wektora normalnego. Stąd powstało wiele różnych realizacji tej metody, wykorzystujących różne warianty uproszczenia. Znane są również próby aplikacji sprzętowych mapowania nierówności Blinna.
| |
| |}
| |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd13n.png|thumb|500px]]
| |
| |valign="top"|Przykłady pokazują nałożenie tekstury Blinna (mapowania nierówności) na sferę. Warto zwrócić uwagę na linię brzegową rzutu sfery. W obu przypadkach jest ona okręgiem, niezniekształconym ! Mapowanie nierówności pozwala uzyskać wrażenie zmian krzywizny bez zmiany geometrii powierzchni. Możliwość niezależnego modelowania kształtu obiektu i drobnych zaburzeń powierzchni jest jedną z podstawowych zalet mapowania nierówności.
| |
| |}
| |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd14n.png|thumb|500px]]
| |
| |valign="top"|Mapowanie nierówności Blinna (bump mapping) daje znakomite wrażenie nierówności powierzchni, ale nie zmienia w rzeczywistości jej kształtu. Takie postępowanie przynosi dobre efekty pod warunkiem, że nie występuje wzajemne zasłanianie między poszczególnymi nierównościami powierzchni (lub jest ono pomijalne z punktu widzenia obserwatora). Jeśli ten warunek nie jest spełniony wtedy pojawiają się problemy.
| |
| | |
| Techniką dającą dobre efekty w takiej sytuacji jest mapowanie przesunięć.
| |
| | |
| Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, <math>P\,</math> będzie punktem na tej powierzchni, a <math>\vec{N}\,</math> będzie wektorem normalnym do powierzchni <math>S(u,v)\,</math>. Niech funkcja <math>f(P)\,</math> opisuje przesunięcie punktu powierzchni <math>S(u,v)\,</math>.
| |
| | |
| Wtedy dla każdego punktu <math>P\,</math>
| |
| | |
| :<math>P'=P+f(P)\cdot \vec{N}</math>
| |
| | |
| Taka modyfikacja kształtu daje możliwość uzyskania rzeczywistego przesunięcia i efektów z tym związanych (np. wzajemne zasłanianie).
| |
| | |
| |}
| |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd14.png|thumb|500px]]
| |
| |valign="top"|Rysunek ilustruje problem próbkowania, na który warto zwrócić uwagę, gdyż jest on jednym z poważniejszych problemów występujących w prawie wszystkich dziedzinach związanych z generacją i obróbką obrazów cyfrowych. Częściowo było to omawiane w związku z metodą śledzenia promieni w wariancie śledzenia stochastycznego.
| |
| | |
| Jeśli przeprowadzimy analizę próbkowania ciągłego sygnału dwuwymiarowego, jakim jest obraz, to okaże się, że w efekcie na przykład nakładania tekstury pojawiają się składowe o częstotliwości wyższej niż częstotliwość próbkowania (Nyquista). Może to być spowodowane zbyt dużą liczba szczegółów na danej powierzchni w efekcie rzutowania perspektywicznego lub nałożeniem tekstury o rozmiarach tekseli (pojedynczych elementów wzorca – pikseli tekstury) dużo mniejszych niż rozmiary piksela ekranu. Powszechnie rozwiązuje się ten problem za pomocą filtrowania dolnoprzepustowego i stosowania nadpróbkowania uśredniającego (rysunek b – szachownica pozbawiona większości artefaktów). Oczywiście efektywniejszym nadpróbkowaniem całego obrazu będzie nadpróbkowanie adaptacyjne, w którym gęstość próbkowania będzie uzależniona od szybkości zmian lokalnych.
| |
| |}
| |
| | |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd15.png|thumb|500px]]
| |
| |valign="top"|W przypadku nakładania tekstury zamiast filtrować cały obraz można zrobić tę operację na samej teksturze przed jej nałożeniem. Ponieważ konieczne jest przy tym uwzględnienie odwzorowania tekstury więc operacja staje się czasochłonna. Stosuje się techniki splotu bezpośredniego (filtrowanie w przestrzeni tekstury) lub filtrowanie w przestrzeni widma z wykorzystaniem analizy fourierowskiej.
| |
| | |
| Najefektywniejszą techniką jest mip-mapping – technika polegająca na przygotowaniu przefiltrowanych tekstur o różnych rozdzielczościach. Metodę tę zaproponował Williams w 1983 roku. W efekcie przefiltrowania dla każdej tekstury uzyskujemy zestaw wzorów odpowiadających przeskalowaniu z uwzględnieniem filtracji na odpowiednim poziomie rozdzielczości. Nakładanie takiej tekstury jest bardzo efektywne, gdyż nie wymaga bieżącego filtrowania. Jedyną operacją, jaka jest konieczna to wybór wzoru o właściwej rozdzielczości. W najprostszym przypadku celem jest nałożenie tekstury, której teksel będzie jak najmniejszy, ale większy od piksela.
| |
| |}
| |
| | |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd16n.png|thumb|500px]]
| |
| |valign="top"|Obiekty naturalne podlegają różnego typu metamorfozom. Dotyczy to zarówno przyrody ożywionej jak i nieożywionej.
| |
| | |
| Możemy mieć do czynienia ze zmianami kształtu i ze zmianami atrybutów wizualnych.
| |
| | |
| Czynnikiem decydującym dla obiektów ożywionych będzie proces wzrostu oraz proces starzenia się.
| |
| | |
| Dla przyrody nieożywionej decydującym czynnikiem będą zjawiska środowiskowe (erozje).
| |
| | |
| Obiekty sztuczne poza naturalnymi procesami starzenia się podlegają przede wszystkim czynnikom mechanicznym.
| |
| | |
| Warto zwrócić uwagę na rezultat działania czynników mechanicznych: może on być trwały (np. ściskanie obiektów nieelastycznych) oraz czasowy (np. ściskanie obiektów elastycznych).
| |
| |}
| |
| | |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd17n.png|thumb|500px]]
| |
| |valign="top"|Deformacje dokonywane są:
| |
| | |
| *W przestrzeni sceny, a więc deformacje obiektu (jego modelu).
| |
| Zmianie może podlegać geometria (kształt) obiektu oraz jego atrybuty (barwa, tekstura, właściwości odbijania światła itd.). Dobrym przykładem zmian geometrii są operacje ściskania, rozciągania lub skręcenia.
| |
| | |
| *W przestrzeni rzutu – deformacje obrazu obiektu.
| |
| Zmiana dokonywana jest z wykorzystaniem transformacji afinicznych (lub dowolnych).
| |
| | |
| | |
| Warping jest przykładem operacji deformacji kształtu stosowanej zarówno w odniesieniu do obiektu jak i jego obrazu. Odbywa się to przez nałożenie siatki na obraz (lub obiekt trójwymiarowy – siatki przestrzennej) i przekształcenie położenia węzłów siatki zgodnie z określoną funkcją. Klasycznymi efektami uzyskiwanymi tą metodą jest zmiana wyrazu twarzy na zdjęciu – uśmiech, przymknięcie oczu itp.
| |
| | |
| Morfing jest operacją pozwalającą wygenerować deformacje kształtu odpowiadające stanom pośrednim pomiędzy danymi obrazami.
| |
| |}
| |
| | |
| ----
| |
| | |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd18n.png|thumb|500px]]
| |
| |valign="top"|Definicja animacji jest dzisiaj bardzo szeroka. Obejmuje zarówno proces tworzenia jak i jego efekt. Odnosi się do filmu, przedstawień teatralnych, gier komputerowych reklam. Współczesna definicja animacji obejmuje także szereg różnych operacji wykonywanych na obrazach cyfrowych.
| |
| | |
| Wyróżnia się dwa rodzaje animacji.:
| |
| | |
| *Klasyczną (tradycyjną) polegającą na ręcznym wytworzeniu wszystkich elementów niezbędnych do powstania kolejnych klatek filmu, a następnie sfotografowaniu ich.
| |
| | |
| *Animację komputerową, wykonaną w całości lub częściowo technikami komputerowymi.
| |
| | |
| Warto zwrócić uwagę na fakt, że w animacji klasycznej każda klatka jest niezależnie realizowana, a każda scena filmu musi być konsekwentnie zbudowana klatka po klatce. W animacji komputerowej można spotkać realizacje wykonane na tej samej zasadzie, jednak częściej sposób i możliwości uzyskania pewnych efektów zmieniają całkowicie ten systematyczny schemat. Szczególnie ma to miejsce w grach komputerowych gdzie trudno mówić o tradycyjnym schemacie kolejnych scen i klatek, natomiast poszczególne obrazy są generowane na bieżąco w zależności od sytuacji, przy czy jednocześnie mogą wykorzystywać elementy wykreowane wcześniej, niezależnie od kolejności sekwencji obrazowych.
| |
| |} | | |} |
|
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd16.png|thumb|500px]]
| |
| |valign="top"|Podobnie jak w filmie aktorskim, film animowany zanim rozpocznie się jego produkcja powstaje w postaci szeregu różnych opisów. Dotyczy to zarówno akcji filmu, jak i bohaterów. W pierwszej fazie planuje się treść z wykorzystaniem przykładowych rysunków ilustrujących najważniejsze momenty akcji. Projektuje się postaci, scenografię, podział na plany pierwszy i dalsze. Ważne jest aby na tym etapie uwzględnić możliwości techniczne studia oraz jego wszystkich urządzeń (przede wszystkim rejestrujących).
| |
|
| |
| Animatorzy tworzą rysunki (lub sceny czy postaci np. kukiełkowe) kluczowe. Sceny pośrednie są wykonywane zgodnie z założeniami scenopisu – zgodnie z przebiegiem i tempem akcji.
| |
|
| |
| Po poprawkach i naniesieniu szczegółów obraz trafia na taśmę filmową lub video.
| |
|
| |
| Tradycyjny film jest wyświetlany z częstotliwością 24 klatek na sekundę, NTSC TV wyświetla 30 obrazów na sekundę, PAL TV – 25.
| |
|
| |
| Podstawy dzisiejszej animacji zawdzięczamy Disneyowi i jego pracom z lat trzydziestych XX wieku. Prace te pozwoliły uzyskać płynny przebieg akcji i naturalne ruchy bohaterów.
| |
|
| |
| Komputer jest wykorzystywany w animacji tradycyjnej do modelowania ruchu i tworzenia precyzyjnego planu, do sterowania urządzeniami laboratorium oraz w postprodukcji do prac związanych z montażem i synchronizacją dźwięku.
| |
| |}
| |
|
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd17.png|thumb|500px]]
| |
| |valign="top"|Pierwsza zasadnicza różnica charakteryzująca animację komputerową występuje już na etapie planowania filmu, gdyż możliwości techniczne odgrywają większą rolę niż w animacji tradycyjnej. Scenariusz powstaje tutaj na drodze kompromisu między oczekiwaniami, możliwościami realizacyjnymi, czasem wykonania i związanymi z tym kosztami. Wybór formy filmu jest wyborem konkretnych możliwości technicznych.
| |
|
| |
| Główny etap tworzenia filmu obejmuje cykl modelowania obiektów (bohaterów, scenografii), ruchu i oświetlenia oraz tworzenia obrazów w uproszczonej formie oraz oceny efektów. Postać uproszczona może obejmować zarówno mniejszą rozdzielczość, jak też brak mniej istotnych szczegółów, czy mniejszą liczbę klatek na sekundę. Ponieważ na tym etapie produkcji, w zasadzie, prawie wszystkie parametry można zmienić (w przeciwieństwie do filmu tradycyjnego), więc do końcowego generowania z docelową rozdzielczością przechodzi się dopiero po sprawdzeniu wszystkich istotnych elementów kompozycyjnych filmu.
| |
|
| |
| Innego znaczenia może nabierać postprodukcja, gdzie montaż końcowy filmu może obejmować łączenie obrazów czy scen pochodzących na przykład z sieci komputerowej zapewniającej szybkie tworzenie niezależnych fragmentów. Przy czym niezależność może oznaczać nie tylko podział na sceny filmu, ale także osobne tworzenia tła i scenografii, podział na plany, niezależne kreowanie postaci itp.
| |
| |}
| |
|
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd19n.png|thumb|500px]]
| |
| |valign="top"|Animacja oparta na klatkach kluczowych składa się z następujących etapów:
| |
|
| |
| *Wyszczególnienie i synteza klatek kluczowych charakteryzujących najważniejsze momenty ruchu lub sceny.
| |
| *Określenie sposobu przejścia pomiędzy klatkami – może to być realizowane w postaci równań ruchu.
| |
| *Wyznaczenie klatek pośrednich – na przykład za pomocą morfingu.
| |
| *Kontrola efektu końcowego i ewentualne poprawki.
| |
|
| |
| Animacja proceduralna polega na wydzieleniu parametrów sterujących przebiegiem zmian i wyznaczeniu zależności funkcyjnych między opisem parametrów a wyglądem klatki (lub sceny). Metoda ta jest wygodna do animacji procesów fizycznych i mechanicznych.
| |
|
| |
| Przykładem są kinematyka odwrotna i metoda deformacji swobodnych (FFD – Free Form Deformation).
| |
|
| |
| Kinematyka odwrotna opisuje zależności ruchowe na podstawie wymaganych położeń obiektów. Jest bardzo wygodną forma dla uzyskania ruchu złożonych mechanicznie elementów, jest często wykorzystywana do animacji postaci.
| |
|
| |
| Metoda deformacji swobodnych ma wiele implementacji. Najczęściej stosuje się techniki szkieletowe lub siatkowe, w których pozycje odpowiednich punktów i zależności między węzłami siatki lub szkieletu opisane są równaniami parametrycznymi.
| |
|
| |
| Animacja symulacyjna wykorzystuje opis zachowania obiektów uzyskany na podstawie praw fizyki. Rozwiązanie tak uzyskanych równań daje poszukiwaną symulację. Metoda ta jest najbardziej złożona obliczeniowo, jest zatem czasochłonna jednak może dać bardzo dobre efekty. Wykorzystywana do modelowania i animacji zjawisk fizycznych.
| |
|
| |
| Przechwytywanie ruchu pozwala powielić schemat zachowania obiektu na podstawie naturalnego zachowania się obiektu rzeczywistego. Jest wygodna do modelowania ruchu postaci ludzkich, zwierzęcych a także postaci fantastycznych, którym można przypisać pewne właściwości ruchowe podobne do znanych cech zwierząt lub ludzi. Metoda ta daje bardzo dobre efekty, gdyż łatwiej jest skopiować ruch zwierząt niż opisać go równaniami matematycznymi. Wadą jest konieczność stosowania specjalistycznego sprzętu do przechwytywania ruchu. Stosuje się zestawy czujników położenia, skanery trójwymiarowe lub zdjęcia poklatkowe.
| |
|
| |
| |}
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd20.png|thumb|500px]]
| |
| |valign="top"|Uwzględnienie zjawisk fizycznych w zachowaniu się obiektów na scenie daje możliwość uzyskania realizmu odbieranej animacji. Nawet najlepiej zaprojektowane szczegóły postaci nie zagwarantują poprawnego odbioru jeśli zachowanie się postaci będzie odbiegało od naszych oczekiwań. Z drugiej strony odbiór tradycyjnych filmów animowanych pokazuje, że jesteśmy skłonni zaakceptować nawet bardzo duży poziom umowności szczegółów i uproszczeń postaci jeśli będzie się ona poruszała w sposób naturalny.
| |
|
| |
| Ponieważ opis zgodny z prawami fizyki jest bardzo złożony, więc stosuje się metody upraszczające obliczenia. Przykładem może być opis ruchu układu mechanicznego będący układem liniowych równań różniczkowych stopnia drugiego. Do rozwiązania stosuje się albo metodę wektorów stanu sprowadzającą równania do rzędu pierwszego, albo metodę różnic skończonych pozwalającą sprowadzić układ równań różniczkowych do układu równań nieliniowych.
| |
|
| |
| Zachowanie się obiektów zależy od ich typu. Wyróżnia się modelowanie obiektów sztywnych przegubowych i modelowanie obiektów deformowalnych.
| |
|
| |
| Obiekty sztywne przegubowe modeluje się w postaci zestawu prostych sztywnych elementów połączonych ze sobą złączami mechanicznymi o zadanym zestawie stopni swobody. Dla obiektów deformowalnych opisuje się odpowiednimi równaniami takie zjawiska jak sprężystość, plastyczność, zrywanie, topnienie, lepkość itd.
| |
| |}
| |
|
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd21n.png|thumb|500px]]
| |
| |valign="top"|Symulacja kolizji jest jednym z ważniejszych problemów pojawiających się w grach komputerowych i filmach animowanych. Rozwiązanie tego problemu wymaga rozwiązania kilku zagadnień. Najważniejszym jest wykrycie kolizji. Zadanie to jest podobne do wykrycia przecięcia w metodzie śledzenia promieni. Przy czym tam było to przecięcie prosta – obiekt, tutaj natomiast jest to obiekt – obiekt. Niemniej jednak metody przyspieszające są podobne. Stosowana jest metoda brył ograniczających, wykrycie przecięcia sfera – sfera jest równie łatwe jak prosta – sfera. Od rodzaju powierzchni (sztywne, odkształcalne) zależy geometria kolizji – odkształcenia obiektów. Od rodzaju powierzchni zależą także efekty kolizji. Zastosowanie odpowiedniego modelu fizycznego opisu zjawiska pozwoli uzyskać wrażenie zgodne z naszym wyobrażeniem i oczekiwaniem.
| |
| |}
| |
|
| |
| ----
| |
|
| |
| {| border="0" cellpadding="4" width="100%"
| |
| |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd22n.png|thumb|500px]]
| |
| |valign="top"|W modelowaniu postaci wykorzystuje się modele mieszane. Sztywny szkielet jako typowy model obiektu sztywnego przegubowego. Szkielet jest otoczony warstwą deformowalną. Deformacja powierzchni tej warstwy zależy zarówno od struktury szkieletu i jego odkształcenia jak i bieżącego stanu warstwy deformowalnej. Kinematyka odwrotna jest stosowana do opisu ruchu kończyn.
| |
|
| |
| Zestaw składowych jednej postaci jest zazwyczaj modelowany w postaci hierarchicznej.
| |
|
| |
| Animacja twarzy jest traktowana jako odrębne zagadnienie ze względu na złożoność problemu oraz ze względu na fakt, że człowiek szybciej identyfikuje twarz na obrazie
| |
| |}
| |
|
| |
| ---- | | ---- |