GKIW Moduł 10 - Dążenie do realizmu: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
|||
| (Nie pokazano 45 wersji utworzonych przez 3 użytkowników) | |||
| Linia 13: | Linia 13: | ||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
| Linia 369: | Linia 114: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd12n.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M10_Slajd12n.png|thumb|500px]] | ||
|valign="top"|Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, która będzie odkształcona. | |valign="top"|Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, która będzie odkształcona. Niech <math>B(u,v)</math> opisuje zaburzenie (teksturę). Wektor normalny <math>\vec{N}\ </math>, do powierzchni <math>S(u,v)\ </math>, można wyznaczyć jako: | ||
:<math> | :<math>\vec{N}=\frac{\partial S(u,v)}{\partial u}\times\frac{\partial S(u,v)}{\partial v}</math> | ||
Jeśli nałożymy teksturę na powierzchnię to powstanie powierzchnia zniekształcona | Jeśli nałożymy teksturę na powierzchnię to powstanie powierzchnia zniekształcona | ||
| Linia 379: | Linia 124: | ||
Wektor normalny do tak otrzymanej powierzchni można wyznaczyć analogicznie. Przy czym różniczkując równanie zniekształconej powierzchni otrzymuje się: | Wektor normalny do tak otrzymanej powierzchni można wyznaczyć analogicznie. Przy czym różniczkując równanie zniekształconej powierzchni otrzymuje się: | ||
:<math> | :<math>\frac{\partial S'(u,v)}{\partial u}=\frac{\partial S(u,v)}{\partial u}+\frac{\partial B(u,v)}{\partial u}\cdot \vec{N}+B(u,v)\cdot \frac{\partial \vec{N}}{\partial u}</math> | ||
:<math> | :<math>\frac{\partial S'(u,v)}{\partial v}=\frac{\partial S(u,v)}{\partial v}+\frac{\partial B(u,v)}{\partial v}\cdot \vec{N}+B(u,v)\cdot \frac{\partial \vec{N}}{\partial v}</math> | ||
Blinn założył, że zaburzenie jest na tyle małe, że ostatnie wyrazy w tych równaniach można pominąć. Wtedy aproksymowany wektor normalny do zniekształconej powierzchni można opisać jako | Blinn założył, że zaburzenie jest na tyle małe, że ostatnie wyrazy w tych równaniach można pominąć. Wtedy aproksymowany wektor normalny do zniekształconej powierzchni można opisać jako | ||
:<math> | :<math>\vec{N}'\approx \left(\frac{\partial S(u,v)}{\partial u}+\frac{\partial B(u,v)}{\partial u}\cdot \vec{N}\ \right)\times \left(\frac{\partial S(u,v)}{\partial v}+\frac{\partial B(u,v)}{\partial v}\cdot \vec{N}\ \right)</math> | ||
to oznacza, że | to oznacza, że | ||
| Linia 391: | Linia 136: | ||
:<math>\vec{N}'=\vec{N}+\vec{D}</math> | :<math>\vec{N}'=\vec{N}+\vec{D}</math> | ||
Przy czym <math>\vec{D}\ | Przy czym <math>\vec{D}\ </math>, jest wektorem zaburzenia: | ||
:<math> | :<math>\vec{D}=\frac{\partial B(u,v)}{\partial u}\cdot \vec{S}-\frac{\partial B(u,v)}{\partial v}\cdot \vec{T}</math> | ||
gdzie <math>\vec{S}\ | gdzie <math>\vec{S}\ </math>, i <math>\vec{T}\ </math>, są wektorami stycznymi do powierzchni <math>S(u,v)\ </math>,. | ||
Takie rozwiązanie daje bardzo prostą możliwość definicji wektora normalnego odkształconej powierzchni za pomocą wektorów zaburzenia. Wadą zaproponowanej przez Blinna metody jest aproksymacja wektora normalnego. Stąd powstało wiele różnych realizacji tej metody, wykorzystujących różne warianty uproszczenia. Znane są również próby aplikacji sprzętowych mapowania nierówności Blinna. | Takie rozwiązanie daje bardzo prostą możliwość definicji wektora normalnego odkształconej powierzchni za pomocą wektorów zaburzenia. Wadą zaproponowanej przez Blinna metody jest aproksymacja wektora normalnego. Stąd powstało wiele różnych realizacji tej metody, wykorzystujących różne warianty uproszczenia. Znane są również próby aplikacji sprzętowych mapowania nierówności Blinna. | ||
| Linia 408: | Linia 153: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_02.png|thumb|500px]] | ||
|valign="top"|Mapowanie nierówności Blinna (bump mapping) daje znakomite wrażenie nierówności powierzchni, ale nie zmienia w rzeczywistości jej kształtu. Takie postępowanie przynosi dobre efekty pod warunkiem, że nie występuje wzajemne zasłanianie między poszczególnymi nierównościami powierzchni (lub jest ono pomijalne z punktu widzenia obserwatora). Jeśli ten warunek nie jest spełniony wtedy pojawiają się problemy. | |valign="top"|Mapowanie nierówności Blinna (bump mapping) daje znakomite wrażenie nierówności powierzchni, ale nie zmienia w rzeczywistości jej kształtu. Takie postępowanie przynosi dobre efekty pod warunkiem, że nie występuje wzajemne zasłanianie między poszczególnymi nierównościami powierzchni (lub jest ono pomijalne z punktu widzenia obserwatora). Jeśli ten warunek nie jest spełniony wtedy pojawiają się problemy. | ||
Techniką dającą dobre efekty w takiej sytuacji jest mapowanie przesunięć. | Techniką dającą dobre efekty w takiej sytuacji jest mapowanie przesunięć. | ||
Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, <math>P\ | Niech <math>S(u,v)=[x_S(u,v), y_S(u,v), z_S(u,v)]</math> opisuje parametrycznie powierzchnię, <math>P\ </math>, będzie punktem na tej powierzchni, a <math>\vec{N}\ </math>, będzie wektorem normalnym do powierzchni <math>S(u,v)\ </math>,. Niech funkcja <math>f(P)\ </math>, opisuje przesunięcie punktu powierzchni <math>S(u,v)\ </math>,. | ||
Wtedy dla każdego punktu <math>P\ | Wtedy dla każdego punktu <math>P\ </math>, | ||
:<math>P'=P+f(P)\cdot \vec{N}</math> | :<math>P'=P+f(P)\cdot \vec{N}</math> | ||
| Linia 421: | Linia 166: | ||
Taka modyfikacja kształtu daje możliwość uzyskania rzeczywistego przesunięcia i efektów z tym związanych (np. wzajemne zasłanianie). | Taka modyfikacja kształtu daje możliwość uzyskania rzeczywistego przesunięcia i efektów z tym związanych (np. wzajemne zasłanianie). | ||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_03.png|thumb|500px]] | |||
|valign="top"|Mapowanie przesunięć służy do modelowania faktury, to znaczy modelowania lokalnych kształtów powierzchni obiektu. Zakładamy przy tym, że powierzchnia obiektu jest zdefiniowana innymi metodami. Dobrym przykładem może być tworzenie zmarszczek na powierzchni twarzy. Głowa ma określony kształt - praktycznie niezmienny (poza np. ruchami żuchwy). Zmarszczki można traktować jako lokalne zmiany kształtu i zdefiniować wykorzystując mapowanie przesunięć. | |||
Prezentowany przykład pokazuje możliwość użycia mapowania przesunięć do modelowania obiektu. Jako kształt wyjściowy przyjęto sferę. Przesuwając punkty powierzchni wzdłuż promieni sfery, została ona odkształcona w taki sposób, że uzyskała kształt głowy. Oczywiście taki sposób ma podstawową wadę: nie można modelować dowolnego kształtu. A zatem ucho na pokazanym przykładzie będzie tylko pewnym przybliżeniem rzeczywistości. Dodatkowo warto zwrócić uwagę na dwa problemy. Pierwszym jest odpowiednie zdefiniowanie funkcji opisującej przesunięcie punktu. Drugim problemem jest rozdzielczość siatki uzyskanego obiektu. Równomierna siatka (południk/równoleżnik) sfery została przekształcona na nierównomierną, zależną od wysokości o dużych zmianach. Powoduje to, że tekstury muszą być indywidualnie dobierane do fragmentu, aby zachować odpowiedni poziom szczegółów. | |||
|} | |} | ||
---- | ---- | ||
| Linia 460: | Linia 213: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_04.png|thumb|500px]] | ||
|valign="top"|Deformacje dokonywane są: | |valign="top"|Deformacje dokonywane są: | ||
| Linia 474: | Linia 227: | ||
Morfing jest operacją pozwalającą wygenerować deformacje kształtu odpowiadające stanom pośrednim pomiędzy danymi obrazami. | Morfing jest operacją pozwalającą wygenerować deformacje kształtu odpowiadające stanom pośrednim pomiędzy danymi obrazami. | ||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v5_plus_05.png|thumb|500px]] | |||
|valign="top"|Deformowanie obrazów (warping) w celu uzyskania określonego kształtu (poprzez zmianę barw rysunku) wymaga precyzyjnej definicji co i w jaki sposób ma zostać odkształcone. Najczęściej jest to określane za pomocą siatki punktów kontrolnych (czworokątnej lub trójkątnej). Wykorzystywane są przekształcenia afiniczne (translacje, obroty, skalowanie) lub dowolne. Przekształcenie może dotyczyć samej geometrii obiektu lub też jego atrybutów (barwa, tekstura, właściwości odbijające itd.). | |||
Ponieważ obiekty wymagają zobrazowania (renderingu) to można złożyć tę operację z deformacjami w dowolnej kolejności. To znaczy najpierw jest deformowany model obiektu (np. jego geometria), a następnie odkształcony obiekt jest zobrazowany (renderowany), lub najpierw obiekt jest zobrazowany, a następnie przekształcany jest jego obraz. Do często stosowanych przekształceń geometrii obiektów trójwymiarowych należą ściskanie, skręcanie, wyginanie. | |||
Do deformacji i przekształcenia obiektów stosowana jest również morfologia matematyczna – dziedzina zajmująca się przetwarzaniem obrazów. Morfologia matematyczna powstała w latach sześćdziesiątych XX wieku w Ecole des Mines de Paris (Wyższej Szkole Górniczej w Paryżu). Twórcami morfologii byli Georges Matheron i Jean Serra. Podstawowymi przekształceniami morfologicznymi są: erozja (przypisanie pikselowi najmniejszej wartości spośród sąsiadów) i dylacja (przypisanie pikselowi największej wartości spośród sąsiadów). Wykorzystuje się także takie operacje jak: otwarcie (złożenie najpierw erozji potem dylacji), domknięcie (najpierw dylacja potem erozja), pogrubianie i ścienianie obiektów. | |||
Warto zwrócić uwagę także na zastosowanie geometrii rzutowej w deformacji obiektów. Zniekształcenia zapewniające korekcję perspektywy lub umożliwiające „nakładanie” płaskiego obrazu na krzywoliniową powierzchnię obiektu są operacjami wykorzystywanymi nie tylko w animacji. Posługujemy się nimi także w edytorach graficznych. | |||
Typowe wykorzystanie deformowania (warpingu) – wpłynięcie na kształt detali rysunku. W pokazanym przykładzie zmieniono wyraz twarzy przez zniekształcenie układu ust. Podobnie można „zmrużyć oczy” lub „zmarszczyć brwi”. Dzięki takim zabiegom można uzyskać, na przykład, zamierzony efekt zdjęć reklamowych. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_06.png|thumb|500px]] | |||
|valign="top"|Uzyskanie większych zmian może być trudniejsze, mogą się bowiem pojawiać szczegóły, których nie było dotychczas widać. W takiej sytuacji samo deformowanie obrazu nic nie daje – należy użyć edytora graficznego i dodać odpowiednie detale. Łatwiej jednak często stworzyć wiarygodny obraz przez dodanie fragmentów do przekształconego zdjęcia niż namalować go w całości. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_07.png|thumb|500px]] | |||
|valign="top"|Przekształcanie pozwala uzyskać stany pośrednie między obrazami. Jeśli wskażemy odpowiadające sobie punkty na obu obrazach, to za pomocą liniowej interpolacji można wyznaczyć pośrednie położenie między tymi punktami. Oczywiście operacja taka może zostać wykonana także na węzłach (punktach kontrolnych) nałożonej siatki. Wtedy zawartość każdego oczka jest deformowana zgodnie z liniową interpolacją względem brzegu takiego oczka. Stosuje się siatki czworokątów i trójkątów. W ogólnym przypadku przekształcenia mogą być wykonywane na obiektach wielowymiarowych – operację opisuje wtedy zestaw transformacji. W szczególności możemy mieć do czynienia z przekształceniem dwuwymiarowym obiektów jednowymiarowym (przekształcenia rysunku na płaszczyźnie), przekształceniem trójwymiarowym obiektów dwuwymiarowych (przekształcenia powierzchni trójwymiarowego obiektu), przekształceniem trójwymiarowym obiektów trójwymiarowych (przekształcenia obiektów wolumetrycznych). | |||
Zastosowanie morfologii matematycznej pozwala dokonywać przekształcania obrazów bez wykorzystywania siatek punktów kontrolnych | |||
Generowanie stanów pośrednich jest wygodnym sposobem uzyskania określonej liczby klatek pośrednich pomiędzy klatkami kluczowymi filmu. Operacja ta wymaga wstępnego dopasowania do siebie szczególnych cech klatek kluczowych. Oczywiście ze względu na sposób poruszania się obiektów lub zależności czasowe mogą być wymagane przekształcenia nieliniowe. | |||
|} | |||
---- | ---- | ||
| Linia 521: | Linia 303: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_08.png|thumb|500px]] | ||
|valign="top"|Scenariusz filmu animowanego przedstawia jego treść w postaci planu przebiegu akcji (szkicu fabuły) z uwzględnieniem opisu scenerii i charakterystyki bohaterów. Zawiera także pełny zestaw dialogów, jeśli film nie jest niemy. To wszystko musi zostać przełożone na język filmu ze wszystkimi ograniczeniami realizacyjnymi. Ułatwia to scenopis, zawierający opis kolejnych (lub czasem wybranych) ujęć filmu. Ujęcie jest najmniejszym, niezależnym (i niepodzielnym) fragmentem trwającym, w filmie animowanym, najczęściej kilka sekund. Scenopis zawiera uproszczony rysunek (projekt) danego ujęcia, oraz opis treści, dialogi i inne niezbędne szczegóły. Może zawierać także warianty projektu (ostatnie ujęcie prezentowanego przykładu), a także szczegóły związane na przykład ze scenerią lub tłem (rysunek szezlongu w prezentowanym scenopisie). | |||
Na podstawie scenopisu reżyser tworzy zestaw szkiców poszczególnych ujęć dla animatorów, którzy przygotują wstępne projekty ujęć. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_09.png|thumb|500px]] | |||
|valign="top"|Animacja oparta na klatkach kluczowych składa się z następujących etapów: | |valign="top"|Animacja oparta na klatkach kluczowych składa się z następujących etapów: | ||
| Linia 540: | Linia 330: | ||
Przechwytywanie ruchu pozwala powielić schemat zachowania obiektu na podstawie naturalnego zachowania się obiektu rzeczywistego. Jest wygodna do modelowania ruchu postaci ludzkich, zwierzęcych a także postaci fantastycznych, którym można przypisać pewne właściwości ruchowe podobne do znanych cech zwierząt lub ludzi. Metoda ta daje bardzo dobre efekty, gdyż łatwiej jest skopiować ruch zwierząt niż opisać go równaniami matematycznymi. Wadą jest konieczność stosowania specjalistycznego sprzętu do przechwytywania ruchu. Stosuje się zestawy czujników położenia, skanery trójwymiarowe lub zdjęcia poklatkowe. | Przechwytywanie ruchu pozwala powielić schemat zachowania obiektu na podstawie naturalnego zachowania się obiektu rzeczywistego. Jest wygodna do modelowania ruchu postaci ludzkich, zwierzęcych a także postaci fantastycznych, którym można przypisać pewne właściwości ruchowe podobne do znanych cech zwierząt lub ludzi. Metoda ta daje bardzo dobre efekty, gdyż łatwiej jest skopiować ruch zwierząt niż opisać go równaniami matematycznymi. Wadą jest konieczność stosowania specjalistycznego sprzętu do przechwytywania ruchu. Stosuje się zestawy czujników położenia, skanery trójwymiarowe lub zdjęcia poklatkowe. | ||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_10.png|thumb|500px]] | |||
|valign="top"|Animacja poklatkowa jest najczęściej stosowaną metodą w tradycyjnych filmach rysunkowych. | |||
Pokazany przykład animacji Koziołka Matołka obejmuje 14 klatek pełnego cyklu ruchu. Bardzo często dla uproszczenia wykonywano mniej klatek (na przykład 7) obejmujących ten sam cykl ruchu i aby zachować odpowiedni czas trwania akcji każdą klatkę powielano dwukrotnie. Czasami mogło to prowadzić do pewnego, nienaturalnego „szarpania” ruchu, jednak przy wartkiej (zazwyczaj) akcji całego filmu było to praktycznie niezauważalne. | |||
Warto zwrócić jeszcze uwagę na złożoność całego ujęcia. Ruch postaci musi być skorelowany z przesuwaniem się tła. W ten sposób widz będzie miał na przykład wrażenie, że Koziołek rzeczywiście biegnie przez miasto. Ale z drugiej strony fazy ruchu postaci i fazy ruchu tła (w tym przypadku domków miasta) są całkowicie niezależne – w prezentowanym przykładzie nie ma ciągłości ruch tła. Wynika stąd możliwość niezależnego generowania obrazu postaci i tła. W tradycyjnej animacji realizowane to było na kolejnych warstwach przezroczystego celuloidu. Najwygodniej jest operować niezależnie każdą postacią oraz często niezależnie różnymi fragmentami dekoracji. Taki zestaw (gruby) celuloidu dopiero w ostatniej fazie produkcji był kopiowany na taśmę filmową. W animacji komputerowej mamy do dyspozycji warstwy rysunku, każda animowana i edytowana niezależnie. Daje to bardzo duże możliwości manipulacji obrazem. | |||
Warto przypomnieć, że pomysły „rozwarstwienia” obrazu w technice filmowej pochodzą z początku XX wieku. W 1916 roku Frank Williams zaproponował metodę wędrującej maski (travelling matte), która została w latach 50 przekształcona w jedną z najważniejszych wykorzystywanych dzisiaj technik, występującą pod nazwą kluczowania (CSO – color separation overlay, także występuje jako chroma key, blue screen, lub czasami jako blue-box). Polega ona na filmowaniu aktora na tle jednolitej planszy (np. niebieskiej), a następnie zmontowaniu filmu wstawiając dowolne tło w miejsce barwy planszy. W czasach Williamsa wymagało to powtórnego filmowania, ewentualnie filmowania z wykorzystaniem tylnej projekcji. Dzisiaj wykonuje się to odpowiednim mikserem elektronicznym (kluczowaniem) lub programami komputerowymi na etapie postprodukcji. Dodatkowo współcześnie najczęściej realizuje się takie zadanie techniką grey-screen – tło ma kolor szary i dobre właściwości odbijające. Dzięki temu za pomocą odpowiedniego oświetlenia można uzyskać prawie dowolny kolor tła w zależności od potrzeb. Autorzy pełnej komputeryzacji tej techniki w 1995 roku otrzymali Oscara. | |||
Dodatkowo warto zwrócić uwagę na sposób rysowania określonych elementów poszczególnych klatek. Rysunki domków tła, w pokazanym przykładzie, są rozmazane w przeciwieństwie do postaci pierwszoplanowej (Koziołka Matołka) rysowanej wyraźną, ostrą kreską. Potęguje to wrażenie ruchu i jednocześnie daje namiastkę głębi ostrości obejmującej tylko pierwszoplanowego bohatera. | |||
Niezależnie od produkcji filmów animowanych, metoda animacji poklatkowej jest dzisiaj dość powszechnie stosowana w postaci prostych animacji wykorzystywanych w prezentacjach lub na stronach internetowych. Realizowane to jest na przykład w postaci animowanych gifów. Oczywiście wymaga to wygenerowania zestawu rysunków obejmujących pełny cykl ruchu i połączeniu ich w jedną animację. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_11.png|thumb|500px]] | |||
|valign="top"|Klatka kluczowa (keyframe) jest związana z charakterystycznym punktem scenariusza, momentem ruchu lub fazą ujęcia. Klatki kluczowe wyznaczają etapy rozwoju akcji filmu, ale także mogą charakteryzować postaci (na przykład przez mimikę twarzy). Klatki kluczowe zawsze planował i rysował główny animator („keyframer”). Natomiast klatki pośrednie traktowane były jako wypełnienie luk między klatkami kluczowymi – stąd animatorzy rysujący klatki pośrednie nazywani byli „inbetweenerami”. Ich zajęcie, chociaż niezbędne dla całego procesu powstania filmu, traktowane było zawsze jako prostsze i mniej ambitne. Dzisiaj zadanie generowania klatek pośrednich realizuje zazwyczaj komputer. | |||
Warto zwrócić uwagę na problem czasu, a właściwie jego kontroli, w powstawaniu filmu animowanego. Film o określonym czasie trwania przekłada się na określoną liczbę klatek, a to z kolei limituje możliwości rysowania określonych faz ruchu, aby sprawiał on wrażenie ciągłego. Zadanie planowania klatek kluczowych jest ściśle związane z rozwojem akcji i związanym z nią upływem czasu. Jest to jednym z najtrudniejszych zadań głównego animatora. Problem komplikuje fakt, że poszczególne etapy akcji, poszczególne fazy ruchu najczęściej nie dają się opisać prostymi zależnościami liniowymi. Rzeczą, która jest zawsze stała w filmie animowanym jest odstęp czasu pomiędzy poszczególnymi klatkami natomiast zawartość klatek musi być dopasowana do upływu czasu. W najprostszym przykładzie animacji odbijającej się piłeczki, jej położenia w określonych momentach określają prawa fizyki. Nieuwzględnienie ich spowoduje nienaturalny ruch, co na pewno zostanie zauważone przez odbiorcę. Aby rozwiązać tego typu problemy, w metodzie klatek kluczowych wykorzystuje się tzw. krzywe (ścieżki lub linie) ruchu. Określają one położenie obiektu w danym momencie. Współczesne programy animacyjne wspomagają realizację klatkami kluczowymi pozwalając na dowolne, nieliniowe manipulowanie krzywą ruchu, a tym samym położeniem obiektu w określonym momencie. | |||
Prezentowany rysunek pokazuje odbicie zakładając, że piłeczka nie odkształca się przy kontakcie z przedmiotem, od którego się odbija. Uwzględnienie tego typu parametrów znacznie poprawiłoby odbiór animacji. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_12.png|thumb|500px]] | |||
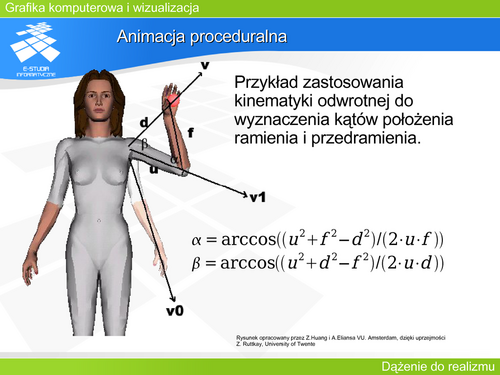
|valign="top"|Animacja proceduralna pozwala opisać zależnościami funkcyjnymi zmiany położeń lub kształtów. Stosuje się kinematykę (prostą i odwrotną) lub metodę deformacji swobodnych. | |||
Ruch złożonych mechanizmów lub postaci wymaga opisania zależności między poszczególnymi segmentami obiektu – powiązania „stawami” segmentów. Na przykład animacja ręki wymaga połączenia ruchów ramienia, przedramienia, dłoni i palców. Połączenie segmentów tworzy łańcuch kinematyczny o skończonej liczbie ogniw. Jest to łączenie hierarchiczne tzn. dla każdego segmentu można wyróżnić segment nadrzędny i podrzędny w łańcuchu. Warto przy tym zwrócić uwagę na sposób wydzielenia segmentów. W przypadku postaci ludzkich czy zwierzęcych znana jest ich budowa anatomiczna i na tej podstawie budowany jest łańcuch kinematyczny. Podobnie dla obiektów mechanicznych o znanej konstrukcji. Natomiast dla postaci fantastycznych lub innych nieznanych obiektów trzeba przeprowadzić modelowanie szkieletu – wydzielenie segmentów i opracowanie zależności mechanicznych pomiędzy nimi. Dla każdego połączenia (stawu) trzeba zdefiniować stopnie swobody segmentów. Stopnie swobody określają liczbę prostych ruchów możliwych do wykonania. Na przykład ciało swobodne ma 6 stopni swobody w układzie kartezjańskim (trzy translacje i trzy obroty). | |||
Kinematyka prosta (forward kinematic) opisuje zależności w łańcuchu kinematycznym od segmentu nadrzędnego do podrzędnego. | |||
Kinematyka odwrotna (inverse kinematic) opisuje zależności w łańcuchu kinematycznym od segmentu podrzędnego do nadrzędnego. W tym przypadku można rozpocząć analizę od docelowego położenia ostatniego (najbardziej podrzędnego w hierarchii) segmentu i na tej podstawie wyznaczyć położenie segmentów pozostałych – np. szukamy położenia ramienia i przedramienia, aby zapewnić położenie dłoni i palców w określonym punkcie. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_13.png|thumb|500px]] | |||
|valign="top"|Trudności w wiarygodnym pokazaniu ruchu postaci są znane twórcom filmowym od początku historii filmu animowanego. O wiele łatwiej zaakceptować widzowi umowność rysunku lub brak szczegółów niż, na przykład, nienaturalne poruszanie ręką – poruszanie niezgodne z naszym wyobrażeniem. Naturalnym pomysłem rozwiązania tego problemu było wzorowanie ruchów animowanych postaci na rzeczywistych ruchach ludzi. W tym celu zatrudniano modeli zastygających w pozach (często niewygodnych) odpowiadających klatkom kluczowym. Jeśli nie było to możliwe, animatorzy musieli wykonać perfekcyjne rysunki na podstawie wyobrażenia postaci. Pierwszą metodą ułatwiającą to zadanie była rotoskopia. Polega ona na filmowaniu aktora wykonującego sekwencję ruchu, a następnie wykonywaniu rysunków na podstawie zdjęć poklatkowych takiego filmu. Pierwszym znanym filmem, w którym wykorzystano rotoskopię była Królewna Śnieżka Walta Disneya. Metoda ta jest również stosowana współcześnie. | |||
W latach osiemdziesiątych XX wieku na Simon Fraser University podjęto badania nad automatycznym przechwytywaniem ruchów postaci (motion capture). W celach komercyjnych metodę tę zastosowano po raz pierwszy w technice filmowej w 1984 roku. Była to 30 sekundowa reklamówka – „Sexy robot” (“Brilliance”) - firmy National Canned Food Information Council. Do produktów firmy, głosem Kathleen Turner, zachęcał animowany robot. Aby zachować naturalność ruchów postaci, Robert Abel opracował optyczny system przechwytywania ruchu na podstawie położenia markerów umieszczonych na ciele aktora. Niepowodzenia w 1990 roku przy realizacji filmu „Pamięć absolutna” (Total Recall) z Arnoldem Schwarzeneggerem zahamowały rozwój systemów przechwytywania ruchu. Do problemu powrócono w 1997 roku podczas produkcji „Titanica”. Od tego czasu większość filmów wymagających efektów specjalnych, a także gier komputerowych, jest realizowana z wykorzystaniem techniki przechwytywania ruchu (motion capture). | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_14.png|thumb|500px]] | |||
|valign="top"|Najprostszym rozwiązaniem jest system elektromechaniczny. Aktor zakłada strój (egzoszkielet) w formie sztywnego stelażu. Egzoszkielet zawiera zestaw czujników, pozwalających monitorować wzajemne położenia między jego elementami. Jest to, oczywiście, tak skonstruowane, aby w jak najmniejszym stopniu ograniczać ruchy aktora. Analiza wzajemnych położeń między elementami egzoszkieletu pozwala, w czasie rzeczywistym, określać i rejestrować położenie ciała aktora. System elektromechaniczny jest najmniej dokładny spośród znanych rozwiązań przechwytywania ruchu. Wadą tego systemu jest także konieczność używania niewygodnego egzoszkieletu. Jest to jednak rozwiązanie praktycznie najtańsze, co jest jego podstawową zaletą. Dodatkowo jest to rozwiązanie niewymagające rozstawiania zestawu czujników zewnętrznych, tak jak w systemach optycznych. | |||
System elektromagnetyczny (magnetyczny) wykorzystuje rejestrację zmian strumienia magnetycznego wywołaną zmianą wzajemnego położenia czujników (nadajników i odbiorników). Aktor zakłada strój z zestawem czujników połączonych kablem (najczęściej) z komputerem. System zawiera zwykle stosunkowo małą liczbę czujników (kilkanaście). Dokładność pomiaru położenia jest lepsza niż systemów mechanicznych, ale gorsza niż optycznych. Analiza położenia jest jednak szybsza niż systemów optycznych. Do podstawowych wad systemu elektromagnetycznego należy zaliczyć wrażliwość na zakłócenia zewnętrzne – na zewnętrzne pole magnetyczne. | |||
Systemy optyczne oparte są na analizie położenia punktu (markera) na podstawie kilku niezależnych rzutów tego punktu. Na stroju aktora jest umieszczony zestaw od kilkunastu do kilkudziesięciu markerów. Kamery rozmieszczone wokół sceny rejestrują obraz aktora i markerów. W zależności od liczby aktorów na scenie stosuje się od kilku do kilkudziesięciu kamer. Kamery muszą objąć całą przestrzeń sceny i dawać możliwość rejestracji markerów także przy wzajemnym zasłanianiu się aktorów. Na podstawie rzutów markera komputer wyznacza jego położenie w przestrzeni. System optyczny jest najdroższym ze znanych rozwiązań przechwytywania ruchu. Daje jednak możliwość najbardziej dokładnego pomiaru położenia (rzędu ułamków milimetra). Strój z markerami optycznymi jest najmniej kłopotliwym rozwiązaniem dla aktora spośród wszystkich systemów przechwytywania ruchu. | |||
Wyróżnia się systemy optyczne pasywne i aktywne. W systemach pasywnych markery odbijają światło we wszystkich kierunkach – a przede wszystkim w kierunku źródła (odbicie powrotne – retroreflection). Markery są punktami pokrytymi farbą lub tworzywem o odpowiednich właściwościach odbijających. W pierwszych systemach optycznych stosowano piłeczki pingpongowe. W systemach aktywnych markery emitują światło. Najczęściej stosuje się diody elektroluminescencyjne emitujące promieniowanie podczerwone. Aby ułatwić analizę przy dużej liczbie czujników, często każdy z nich emituje impulsy (błyski) z inną częstotliwością. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_15.png|thumb|500px]] | |||
|valign="top"|Rozpatrzmy dwie kamery <math>K_1</math> i <math>K_2</math> śledzące poruszający się punkt <math>P</math> zgodnie z rysunkiem. Jeśli znane jest położenie kamer oraz ich ustawienie, to można określić rzuty <math>P'</math> i <math>P''</math> . Rzuty te definiują proste, których przecięciem jest szukany punkt <math>P</math>. Stąd jego współrzędne można wyznaczyć korzystając z prezentowanych równań. W praktyce, na skutek zakłóceń i błędów pomiarów może się okazać, że proste zdefiniowane przez rzuty <math>P'</math> i <math>P''</math> wcale się nie przecinają. W takiej sytuacji należy wyznaczyć punkt <math>P</math> będący punktem najbliższym obu prostych. | |||
Do określenia położenia punktu wystarczą dwie kamery. Jednak aktor poruszając się może zasłaniać markery umieszczone na ubraniu. Na scenie może być także wielu aktorów, którzy zasłaniają się wzajemnie. Z tego powodu stosuje się wiele kamer, aby bez względu na pozę aktora, każdy marker był zawsze „widziany” przynajmniej przez dwie kamery. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_16.png|thumb|500px]] | |||
|valign="top"|Duża szybkość pracy systemów przechwytywania ruchu (optycznych lub magnetycznych) pozwala wygenerować wirtualne postacie w czasie rzeczywistym. Prezentowane zdjęcia pokazują system optyczny aktywny, którego jednym z elementów jest stojący na scenie ekran. Dzięki niemu aktor może na bieżąco śledzić ruchy wirtualnej postaci. | |||
Mimo niezaprzeczalnych zalet stosowania systemów przechwytywania ruchu w kreowaniu realistycznie poruszających się wirtualnych postaci trzeba wspomnieć o ich wadach. | |||
*Występuje konieczność stosowania bardzo specjalistycznego sprzętu i oprogramowania. | |||
*Związane jest to z wysokimi kosztami (co najmniej kilkadziesiąt tysięcy dolarów). | |||
*Koszty te mogą utrudniać powstawanie małych, niskobudżetowych produkcji. | |||
*Powstają problemy skalowania postaci – wymiary wirtualnych postaci, szczególnie fantastycznych, nie zawsze odpowiadają budowie ciała aktorów, wymaga to dodatkowego przetwarzania ścieżek ruchu, | |||
*Podobny problem występuje w przypadku scenariusza przewidującego ruchy niezgodne z wyobrażeniami lub niezgodne z fizyką – co często występuje w filmach animowanych. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_17.png|thumb|500px]] | |||
|valign="top"|Proces kreowania pojedynczej klatki nie odbiega w zasadzie od standardowego procesu powstawania obrazu w grafice komputerowej. Warto natomiast zwrócić uwagę na modelowanie obiektów na scenie filmu animowanego. Modelowane są te obiekty, które są widoczne. Pod uwagę brana jest przy tym nie tylko dana scena, ale cały film, lub przynajmniej pewna sekwencja klatek. Stąd na górnych rysunkach widoczna jest pełna siatka drzwi, chociaż są one otwarte i niewidoczne. Jednak w jednym z następnych ujęć będą one zamknięte (rysunek dolny) stąd potrzebny jest ich pełny model. Modelowanie obiektów filmu wymaga przeanalizowania całego scenopisu i określenia jakie obiekty i w jakim zakresie powinny zostać w określonej scenie zamodelowane. | |||
|} | |} | ||
---- | ---- | ||
| Linia 565: | Linia 440: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_18.png|thumb|500px]] | ||
|valign="top"|W modelowaniu postaci wykorzystuje się modele mieszane. Sztywny szkielet jako typowy model obiektu sztywnego przegubowego. Szkielet jest otoczony warstwą deformowalną. Deformacja powierzchni tej warstwy zależy zarówno od struktury szkieletu i jego odkształcenia jak i bieżącego stanu warstwy deformowalnej. Kinematyka odwrotna jest stosowana do opisu ruchu kończyn. | |valign="top"|W modelowaniu postaci wykorzystuje się modele mieszane. Sztywny szkielet jako typowy model obiektu sztywnego przegubowego. Szkielet jest otoczony warstwą deformowalną. Deformacja powierzchni tej warstwy zależy zarówno od struktury szkieletu i jego odkształcenia jak i bieżącego stanu warstwy deformowalnej. Kinematyka odwrotna jest stosowana do opisu ruchu kończyn. | ||
| Linia 572: | Linia 447: | ||
Animacja twarzy jest traktowana jako odrębne zagadnienie ze względu na złożoność problemu oraz ze względu na fakt, że człowiek szybciej identyfikuje twarz na obrazie | Animacja twarzy jest traktowana jako odrębne zagadnienie ze względu na złożoność problemu oraz ze względu na fakt, że człowiek szybciej identyfikuje twarz na obrazie | ||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_19.png|thumb|500px]] | |||
|valign="top"|Kinematyka prosta lub odwrotna pozwala opisać zależności ruchowe w łańcuchu kinematycznym. Aby jednak było to możliwe trzeba zdefiniować taki łańcuch. Dla postaci tworzy się szkielet łączący poszczególne segmenty (kości – stąd metoda taka bywa nazywana modelowaniem opartym na systemie kostnym). Dla układu kostnego szkieletu budowana jest hierarchia połączeń między poszczególnymi segmentami. Szkielet nie jest rysowany jednak na podstawie jego kształtu (układu jego segmentów) jest rysowana zewnętrzna powierzchnia postaci. Kształt takiej powierzchni najczęściej opisuje odpowiednia siatka. Aby zatem ruch kości przekładał się na ruch na przykład kończyn, to położenie segmentów szkieletu musi być powiązane z siatką powierzchni postaci. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_20.png|thumb|500px]] | |||
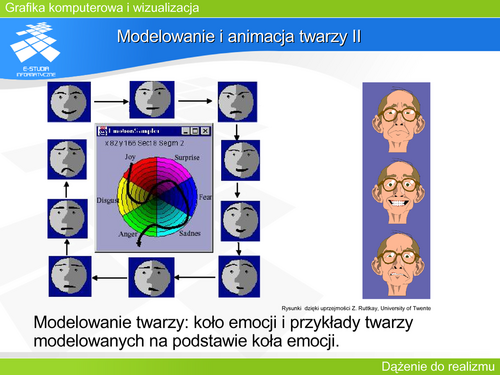
|valign="top"|Każdy z wymienionych sposobów modelowania twarzy pozwala uzyskać poprawne efekty. Zależnie jednak od potrzeb uzyskania odpowiedniego poziomu szczegółowości wybrane modele mogą być mniej lub bardziej przydatne. Wydaje się, że najlepszym rozwiązaniem byłby model anatomiczny opisujący budowę głowy w sposób jak najbardziej zbliżony do rzeczywistości. Uwzględnienie właściwości fizycznych poszczególnych warstw mięśni i skóry oraz ich wzajemnych powiązań powinno dać w efekcie końcowym rysunki odpowiadające rzeczywistości. Model taki jest jednak bardzo skomplikowany i manipulacja nim w celu uzyskania oczekiwanej mimiki twarzy staje się niezwykle trudna i pracochłonna, a co za tym idzie również kosztowna. Odwzorowanie kształtu samej powierzchni twarzy z wykorzystaniem systemów przechwytywania ruchu może dać równie dobre, a jednocześnie szybsze efekty. Przechwytywanie ruchu nie jest w ogóle związane z budową anatomiczną natomiast wymaga odpowiedniego „zagrania” sceny przez aktora, którego twarz jest odwzorowywana. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_21.png|thumb|500px]] | |||
|valign="top"|Prezentowany przykład pokazuje modelowanie twarzy wykorzystujące przekaz emocji. Warto podkreślić, że wszystkie uwagi dotyczące animacji w tym rozdziale były związane tylko ze sprawami technicznymi. A tak naprawdę film animowany, bez względu na to czy jest to animacja tradycyjna, czy komputerowa, jest środkiem wyrazu – sposobem wypowiedzi twórcy dzieła i sposobem przekazania pewnych treści odbiorcy. W tym momencie zaczynają odgrywać role emocje, uczucia i wrażliwości, a to nie musi być związane z bardzo wyrafinowaną technicznie formą przekazu. Znane są przykłady znakomitych dzieł sztuki filmowej realizowanych bardzo prostymi środkami. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_22.png|thumb|500px]] | |||
|valign="top"|Systemy przechwytywania ruchu są również stosowane do rejestracji mimiki twarzy (facial mocap). Wymaga to jednak o wiele większej precyzji niż w zwykłych zastosowaniach. Wykorzystuje się systemy optyczne pasywne. Nie wymagają one zasilania tak jak systemy aktywne, wystarczy umieszczenie od kilkunastu do kilkudziesięciu markerów (punktów odbijających światło) na twarzy aktora. Odpowiedni zestaw kamer pozwala wyznaczyć położenie każdego markera (punktu twarzy) z dokładnością do ułamków milimetra. | |||
Są to najdroższe systemy do przechwytywania ruchu, ale pozwalają najszybciej wykreować realistyczne wirtualne postacie i ich twarze. Systemów przechwytywania mimiki twarzy nie stosuje się do rejestracji ruchów języka oraz gałek ocznych i powiek. Prezentowane rysunki pokazują także siatkę opracowaną na podstawie danych uzyskanych z systemu przechwytywania. Siatka taka zostaje z reguły poddana obróbce: uzupełniane są punkty odpowiadające powiekom i ewentualnie językowi. Dodawane są siatki gałek ocznych i zębów, które w ogóle nie podlegają przechwytywaniu. Jednocześnie można wpłynąć na kształt twarzy poprzez dodatkowe odkształcenie siatki (uwydatnienie kości policzkowych na rysunku). | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_23.png|thumb|500px]] | |||
|valign="top"|Modelowanie i animacja twarzy jako przykład wykorzystania grafiki komputerowej w filmie fabularnym. | |||
Prezentowane rysunki pokazują, że nawet tak skomplikowane elementy jak ludzkie twarze mogą być „dorysowane” z pomocą grafiki komputerowej. Rysowanie realistycznej ludzkiej twarzy jest jednym z najtrudniejszych zadań. Każdy z nas, od dzieciństwa obcuje z widokiem twarzy i nawet najdrobniejsze błędy – niezgodności z oczekiwaniem będą natychmiast zauważone. Model wykorzystywany w Matrixie opierał się na siatce trójkątów (ok. 10 milionów) uzyskanej na podstawie trójwymiarowego skanowania twarzy aktora. Model składał się z dwóch warstw – warstwy geometrii (kształtu) o małej rozdzielczości i warstwy o dużej rozdzielczości opisującej właściwości odbiciowe powierzchni skóry. Na podstawie zdjęć z 30 kamer umieszczonych wokół głowy aktora zbudowano analityczny model BRDF opisujący odbicie dla każdego trójkąta siatki. Wykorzystano przy tym mapowanie przesunięć (displacement mapping) dla większych szczegółów i mapowanie nierówności (bump mapping) dla mniejszych szczegółów. | |||
Jednym z dodatkowych problemów, na który warto zwrócić uwagę jest rysowanie (i modelowanie) włosów postaci. W przypadku Matrixa każdy pojedynczy włos był w pierwszej fazie pracy zamodelowany niezależnie przy użyciu NURBS. Następnie zostały wykreowane prymitywy do modelowania i analizy cienia w rysowaniu układu włosów. Dodatkowo zostało użyte modelowanie wolumetryczne. | |||
Oczywiście warto byłoby wspomnieć także o innych filmach, w których wykorzystano grafikę komputerową. Jedną z najciekawszych realizacji jest trylogia Władca Pierścieni, a szczególnie postać Golluma. Efekt widoczny na ekranie uzyskano dzięki połączeniu zdjęć aktora i symulacji komputerowych. Wielkie sceny batalistyczne we współczesnych filmach powstają raczej dzięki symulacjom komputerowym. We wspomnianej trylogii, w jednej ze scen bitwy gdzie walczy sześciotysięczna armia orków zatrudnionych było tylko 175 statystów. | |||
Bez grafiki komputerowej nie mogłyby powstać nie tylko takie filmy jak Matrix i Władca Pierścieni, ale także Star Trek, Park Jurajski, Terminator 2, Głębia, Titanic, Wodny Świat, Obcy oraz wiele, wiele innych. I to nie tylko ze względu na kreowanie nieistniejących stworów lub rejestrowanie niemożliwych do wykonania ewolucji. Oglądając w kinie przepiękne widoki, niczym nieskażonej i bajecznie kolorowej roślinności, bezkresne tafle szmaragdowego morza czy perfekcyjnie romantyczne zachody słońca warto zastanowić się, kiedy kończy się filmowanie naturalnych krajobrazów, a zaczyna komputerowa wizja reżysera. | |||
|} | |||
---- | ---- | ||
| Linia 578: | Linia 492: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika: | |width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_24.png|thumb|500px]] | ||
|valign="top"| | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:GKIW_M10v4_plus_25.png|thumb|500px]] | |||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
---- | ---- | ||
Aktualna wersja na dzień 12:03, 5 wrz 2023
Wykład
 |
 |
Literatura
 |
 |