PEE Moduł 2

---

Parametry sygnału sinusoidalnego Sygnały sinusoidalne zwane również harmonicznymi są opisane w dziedzinie czasu następującym wzorem (w opisie przyjęto oznaczenie sygnału napięciowego) $u(t)=U_{m}sin(\omega t+\psi )$ Wielkości występujące w opisie mają następujące nazwy i oznaczenia: $u(t)$ - wartość chwilowa napięcia $U_m$ - wartość maksymalna (szczytowa) napięcia zwana również amplitudą $\psi$ - faza początkowa napięcia odpowiadająca chwili t=0 $\omega t+\psi$ - kąt fazowy napięcia w chwili t $f=1/T$ - częstotliwość mierzona w hercach (Hz) $T$ - okres przebiegu sinusoidalnego $\omega =2\pi f$ - pulsacja mierzona w radianach na sekundę. Wartości chwilowe sygnałów oznaczać będziemy małą literą a wartości maksymalne, skuteczne i wielkości operatorowe dużą. Rysunek na slajdzie obok przedstawia przebieg sygnału sinusoidalnego napięcia z oznaczeniami poszczególnych jego parametrów. Oś odciętych ma podwójne oznaczenie: czasu oraz fazy (aktualny kąt fazowy).

---

Przebiegi zmienne w czasie dobrze charakteryzuje wartość skuteczna. Dla przebiegu okresowego $f(t)$ o okresie $T$ jest ona definiowana w postaci Parser nie mógł rozpoznać (błąd składni): {\displaystyle F=\sqrt\left \frac{1}{T} \right \int_{t_0}^{t_o+T}f^2(t)dt} Łatwo udowodnić, że wartość skuteczna przebiegu okresowego nie zależy od wyboru fazy początkowej. W przypadku przebiegu sinusoidalnego napięcia $u(t)=U_{m}sin(\omega t+\psi )$ jest równa Parser nie mógł rozpoznać (błąd składni): {\displaystyle U=\left \frac{U_m}{\sqrt 2} \right} a w przypadku prądu sinusoidalnego $i(t)=U_{m}sin(\omega t+\psi )$ Parser nie mógł rozpoznać (błąd składni): {\displaystyle I=\left \frac{I_m}{\sqrt 2} \right} Dla sygnału sinusoidalnego wartość skuteczna jest więc $\sqrt{2}$ razy mniejsza niż jego wartość maksymalna. Należy zauważyć, że napięcie stałe $u(t)=U$ jest szczególnym przypadkiem sygnału sinusoidalnego, dla którego częstotliwość jest równa zeru $(f=0)$ a wartość chwilowa jest stała i równa $u(t)=U_{m}sin(\omega t+\psi )=U$. Jest to ważna właściwość, gdyż dzięki temu metody analizy obwodów o wymuszeniu sinusoidalnym mogą mieć zastosowanie również do wymuszeń stałych przy założeniu $f=0$. Dla sygnału stałego wartość maksymalna i skuteczna są sobie równe i równają się danej wartości stałej.

---

Metoda symboliczna liczb zespolonych analizy obwodów RLC w stanie ustalonym Analiza obwodów zawierających elementy RLC przy wymuszeniu sinusoidalnym napotyka na pewne trudności związane z wystąpieniem w opisie cewki i kondensatora równań różniczkowych. Trudności te łatwo jest pokonać w stanie ustalonym. Stanem ustalonym obwodu nazywać będziemy taki stan, w którym charakter odpowiedzi jest identyczny jak charakter wymuszenia, to znaczy odpowiedzią na wymuszenie sinusoidalne jest odpowiedź również sinusoidalna o tej samej częstotliwości choć o różnej amplitudzie i fazie początkowej. Dla stanu ustalonego obwodu wprowadzona zostanie metoda liczb zespolonych, zwana również metodą symboliczną, sprowadzająca wszystkie operacje różniczkowe i całkowe do działań algebraicznych na liczbach zespolonych.

---

Dla wprowadzenia tej metody przyjmijmy, że rozważany jest obwód szeregowy RLC zasilany ze źródła napięcia sinusoidalnego $u(t)=U_{m}sin(\omega t+\psi )$ Z prawa napięciowego Kirchhoffa wynika następujący związek między napięciami elementów tego obwodu $u(t)=u_R+u_L+u_C$ Biorąc pod uwagę podstawowe zależności definicyjne dla rezystora, cewki i kondensatora $u_R=Ri$ $u_c=\frac{1}{C}\int idt$ Parser nie mógł rozpoznać (błąd składni): {\displaystyle u_L=L \left \frac{di}{dt} \right} otrzymuje się Parser nie mógł rozpoznać (błąd składni): {\displaystyle U_m sin(\omega t+\psi)=R_i+ \left \frac{1}{C} \right \int idt+L \left \frac{di}{dt} \right}

---

Ostatni wzór przedstawia sobą równanie różniczkowo-całkowe opisujące zależności między wartościami chwilowymi prądu i napięcia wymuszającego w obwodzie. Pełne rozwiązanie tego równania sprowadza się do wyznaczenia dwu składowych prądu, stanowiących odpowiedź obwodu w stanie ustalonym i stanie przejściowym: składowej ustalonej, której charakter zmian w czasie jest taki sam jak sygnału wymuszającego (przy sinusoidalnym wymuszeniu odpowiedź również sinusoidalna o tej samej częstotliwości); jest to stan który zostanie osiągnięty przez obwód po czasie teoretycznie dążącym do nieskończoności. składowej przejściowej odpowiadającej różnicy między rozwiązaniem rzeczywistym równania różniczkowego a składową ustaloną. Składowa przejściowa zanika zwykle szybko w czasie i pozostaje jedynie składowa ustalona. Stan po zaniknięciu składowej przejściowej nazywamy stanem ustalonym obwodu.

---

Składową ustaloną prądu w obwodzie można otrzymać nie rozwiązując równania różniczkowego opisującego ten obwód a korzystając jedynie z metody liczb zespolonych (metody symbolicznej). Istotnym elementem tej metody jest zastąpienie przebiegów czasowych ich reprezentacją zespoloną. Przyjmijmy, że prąd $i(t)=I_{m}sin(\omega t+\psi )$ oraz napięcie $u(t)=U_{m}sin(\omega t+\psi )$ zastąpione zostały przez wektory wirujące w czasie, odpowiednio $I(t)$ oraz $U(t)$ określone w postaci $U(t)=U_m{e}^j{}^{\psi }{e}^j{}^{\omega }{}^t$ $I(t)=I_m{e}^j{}^{{\psi }_i}{e}^j{}^{\omega }{}^t$ Po zastąpieniu wartości czasowych prądu i napięcia poprzez ich reprezentację w postaci wektorów wirujących otrzymuje się Parser nie mógł rozpoznać (błąd składni): {\displaystyle U(t)=RI(t)+L \left \frac{dI(t)}{dt} \right+\frac{1}{C} \int I(t)dt}

---

Po wykonaniu operacji różniczkowania i całkowania równanie powyższe przyjmuje postać $\frac{U_m}{\sqrt{2}}{e}^j{}^{\psi }=R\frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}+j\omega L\frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}+\frac{1}{j\omega C}\frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}$ Oznaczmy przez $u=\frac{U_m}{\sqrt{2}}{e}^j{}^{\psi }$ wartość skuteczną zespoloną napięcia, a przez $I=\frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}$ wartość skuteczną zespoloną prądu. Wtedy równanie można zapisać w następującej postaci obowiązującej dla wartości skutecznych zespolonych $U=RI+j\omega LI+\frac{1}{j\omega C}I$

---

Wielkość $U_r=RI$ odpowiada napięciu skutecznemu zespolonemu na rezystorze, $U_L=j\omega LI$ reprezentuje wartość skuteczną zespoloną napięcia na cewce, $U_c=\frac{1}{j\omega C}I$ odpowiada wartości skutecznej zespolonej napięcia na kondensatorze. Wszystkie napięcia i prąd w obwodzie są wartościami zespolonymi.

---

Można zauważyć prostą analogię do równania opisującego obwód rezystancyjny. W tym celu wprowadzimy uogólnienie rezystancji w postaci pojęcia impedancji zespolonej wiążącej wartości skuteczne prądu i napięcia na elementach R, L, C w stanie ustalonym przy wymuszeniu sinusoidalnym. Z ostatnich równań na podstawie prawa Ohma można napisać następujące przyporządkowania: Dla rezystora $Z_R=R$ impedancja $Z_R$ jest równa rezystancji tego rezystora. Dla cewki $Z_L=j\omega L$ impedancja $Z_L$ jest liczbą zespoloną (urojoną) zależną liniowo od częstotliwości. Dla kondensatora $Z_C=\frac{1}{j\omega C}=-j\frac{1}{\omega C}$ impedancja $Z_C$ jest także zespolona i odwrotnie proporcjonalna do częstotliwości. $X_L=\omega L$ nosi nazwę reaktancji indukcyjnej, a $X_C=\frac{1}{\omega C}$ reaktancji pojemnościowej. W związku z powyższym można napisać $Z_L=j{X}_L,Z_C=-j{X}_C$.

---

Wprowadzając oznaczenie wypadkowej impedancji obwodu przez $Z$, gdzie $Z=Z_R+Z_L+Z_C$ zależność prądowo-napięciową w obwodzie szeregowym RLC można zapisać w postaci, znanej jako prawo Ohma dla wartości symbolicznych $U=ZL$ lub $I=\frac{U}{Z}=|I|e^j{}^w$ gdzie moduł prądu i kąt fazowy prądu dane są wzorami $|I|=\frac{|U|}{|Z|}=\frac{|U|}{{\sqrt{R}}^2+(\omega L-1/(\omega C){)}^2}$ ${\psi }_i=\psi -arctg\frac{\omega L-1/(\omega C)}{R}$ Faza początkowa wektora napięcia wymuszającego jest tu oznaczona przez $\psi$ , a faza początkowa wektora prądu – przez ${\psi }_i$ Różnica faz nazywana jest przesunięciem fazowym prądu względem napięcia i oznaczana literą $\phi$ , przy czym $\phi =\psi -{\psi }_i=arctg\frac{\omega L-1/(\omega C)}{R}$ Kąt ten jest uważany za dodatni dla obwodów o charakterze indukcyjnym a za ujemny dla obwodów o charakterze pojemnościowym. Zauważmy, że wartościom skutecznym zespolonym prądu oraz napięcia można przyporządkować funkcję czasu. Biorąc pod uwagę, że przejście z przebiegu czasowego na opis zespolony (symboliczny) odbywa się według schematu $u(t)=U_{m}sin(\omega t+\psi )\to \frac{U_m}{\sqrt{2}}{e}^j{}^{\psi }$ powrót z wartości zespolonej do postaci czasowej polega na pomnożeniu modułu wartości skutecznej przez $\sqrt{2}$ i uzupełnieniu wyniku przez dopisanie funkcji$sin(\omega t+\psi )$ Stąd przykładowo, jeśli wynik zespolony prądu dany jest w postaci $I=10e^{50^o}$ , to odpowiadający mu przebieg czasowy ma postać $i(t)=10\sqrt{2}sin(\omega t+50^o)$ Istnieje również ścisła analogia między konduktancją (odwrotność rezystancji) a odwrotnością impedancji. Analogicznie do pojęcia konduktancji w obwodzie rezystancyjnym wprowadza się pojęcie admitancji zespolonej dla obwodu RLC. Admitancja jest definiowana jako odwrotność impedancji. Oznaczana jest najczęściej literą $Y$, przy czym $Y=1/Z$. Admitancja kondensatora jest równa $Y_C=j\omega C$ , cewki $Y_L=\frac{1}{j\omega L}=-\frac{1}{\omega L}$ natomiast admitancja rezystora jest równa jego konduktancji $Y_R=G=1/R$.

---

Prawa Kirchhoffa dla wartości skutecznych zespolonych Przy zastąpieniu wartości rzeczywistych przez wartości zespolone równania różniczkowe zostały zastąpione przez równania algebraiczne. Nastąpiła zatem algebraizacja równań opisujących obwód. Wszystkie elementy RLC traktowane są w podobny sposób i reprezentowane przez swoje impedancje symboliczne w postaci zespolonej. Impedancje zespolone mogą być interpretowane jako uogólnienie rezystancji. Dla obwodu reprezentowanego w postaci symbolicznej obowiązują prawa Kirchhoffa, które mają identyczną postać jak dla obwodu rzeczywistego, z tą różnicą, że zamiast wielkości chwilowych używa się wielkości zespolonych. Prawo prądowe Kirchhoffa Suma algebraiczna prądów zespolonych w dowolnym węźle obwodu elektrycznego jest równa zeru, co zapiszemy w postaci $\sum _k{I}_k=0$ W równaniu tym wszystkie prądy dane są w postaci zespolonej. Prawo napięciowe Kirchhoffa Suma algebraiczna napięć zespolonych w każdym oczku obwodu elektrycznego jest równa zeru, co zapiszemy w postaci $\sum _k{U}_k=0$ W równaniu tym symbolem $U$ oznaczono wszystkie napięcia w postaci zespolonej, zarówno na gałęziach pasywnych jak i źródłowych obwodu. Sposób sumowania (znak plus lub minus) zarówno prądów jak i napięć jest taki sam jak w przypadku operowania wartościami rzeczywistymi.

---

Podsumowując, na metodę symboliczną analizy obwodu składa się Przejście z przebiegu czasowego na opis zespolony (symboliczny) dla źródeł prądu i napięcia $u(t)=U_{m}sin(\omega t+{\psi }_u)\to \frac{U_m}{\sqrt{2}}{e}^j{}^{{\psi }_u}$ $i(t)=I_{m}sin(\omega t+{\psi }_i)\to \frac{I_m}{\sqrt{2}}{e}^j{}^{{\psi }_i}$ Reprezentacja elementów poprzez ich impedancje zespolone Zastosowanie praw Kirchoffa dla wartości symbolicznych Rozwiązanie układu równań w postaci skutecznej zespolonej Ewentualnie (w miarę potrzeb) przedstawienie rozwiązania w postaci czasowej (odwrotna operacja) do wykonanej w punkcie pierwszym).

---

Jako przykład wyznaczymy rozpływy prądów w obwodzie z rysunku w stanie ustalonym. Przyjiemy następujące wartości parametrów: $i(t)=5\sqrt{2}sin(1000t)A,R=10\mathrm{\Omega },C=0,0001F,L=5mH$.

---

Rozwiązanie Wartości symboliczne elementów obwodu: $\omega =1000$ $I=5$ $Z_L=j\omega L=j5$ $Z_C=\frac{1}{j\omega C}=-j10$ Impedancje obwodu RLC: $Y=\frac{1}{R}+\frac{1}{Z_L}+\frac{1}{Z_C}=0,1-j0,1$ $Z=\frac{1}{Y}=\frac{10}{\sqrt{2}}{e}^j{}^{45^o}$

---

Prądy i napięcie w obwodzie: $U=ZI=\frac{50}{\sqrt{2}}{e}^j{}^{45^o}$ $I_R=\frac{U}{R}=\frac{5}{\sqrt{2}}{e}^j{}^{45^o}$ $I_L=\frac{U}{Z_L}=\frac{10}{\sqrt{2}}{e}^{-}{}^j{}^{45^o}$ $I_C=\frac{U}{Z_C}=\frac{5}{\sqrt{2}}{e}^j{}^{135^o}$

---

Wartości chwilowe prądów i napięcia otzrymuje się przechodząc z wartości zespolonych na postać rzeczywista opisaną funkcją sinusoidalną według schematu przedstawionego na slajdzie 13. $u(t)=50sin(1000t+45^o)$ $i_R(t)=5sin(1000t+45^o)$ $i_L(t)=10sin(1000t-45^o)$ $i_C(t)=5sin(1000t+135^o)$

---

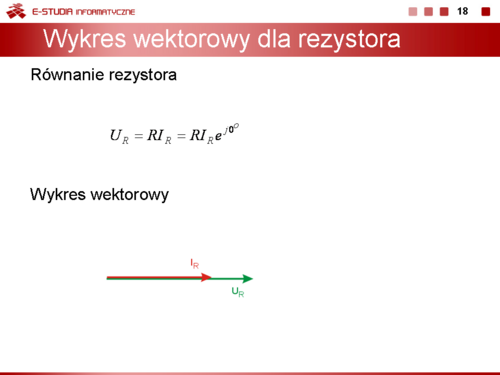
Wykresy wektorowe obwodu W przypadku analizy obwodów RLC w stanie ustalonym ważnym pojęciem jest wykres wektorowy, zwany również wykresem wskazowym, przedstawiający w sposób orientacyjny zależności między poszczególnymi wektorami prądu i napięcia w obwodzie. Jak wiadomo każdej liczbie zespolonej można przyporządkować reprezentację geometryczną w postaci odpowiedniej zależności wektorowej przedstawionej na płaszczyźnie, w której oś pozioma odpowiada części rzeczywistej a oś pionowa części urojonej liczby zespolonej. Konstruując wykres należy pamiętać, że pomnożenie wektora przez operator $j$ jest równoważne jego obrotowi o kąt 90 stopni przeciwnie do ruchu wskazówek zegara gdyż operator j jest równy $e^j{}^{90^o}$ Podobnie pomnożenie wektora przez operator $-j$ jest równoważne jego obrotowi o kąt 90 stopni zgodnie z ruchem wskazówek zegara gdyż operator -j jest równy $e^{-}{}^j{}^{90^o}$ Pomnożenie wektora przez liczbę rzeczywistą nie zmienia pozycji wektora w przestrzeni o ile jest to liczba dodatnia lub zmienia zwrot wektora o jeśli liczba ta jest ujemna. Z zależności prądowo-napięciowych dla rezystora jest oczywiste, że $U_R=R{I}_R$ co wobec rzeczywistych, dodatnich wartości R oznacza, że napięcie na rezystorze jest w fazie z prądem tego rezystora.

---

]

Przedstawione powyżej zasady konstruowania przesunięć kątowych między wektorami prądu i napięcia umożliwiają podanie ogólnych zasad postępowania przy konstruowaniu wykresu wektorowego dla dowolnego obwodu RLC. Dla cewki obowiązuje $U_L=j\omega L{I}_L$ co oznacza, że napięcie na cewce wyprzedza prąd o kąt $90^o$.

---

]	Podobnie napięcie na kondensatorze opóźnia się względem swojego prądu o kąt $90^o$, gdyż $U_C=-j\frac{1}{\omega C}{I}_C$

---

Wykres wektorowy z definicji uwzględnia przede wszystkim przesunięcia kątowe między poszczególnymi wektorami. Relacje ilościowe (długości) poszczególnych wektorów są mniej istotne i zwykle uwzględniane w sposób jedynie przybliżony. Wykres rozpoczyna się zwykle od końca obwodu (gałęzi najdalej położonej od źródła). Jeśli gałąź jest połączeniem szeregowym elementów rozpoczynamy od prądu tej gałęzi, a w przypadku połączenia równoległego – od napięcia. Następnie rysuje się na wykresie na przemian napięcia i prądy kolejnych gałęzi, dochodząc w ten sposób do źródła. Budowę wykresu kończy się w momencie dojścia do prądu i napięcia źródłowego obwodu. Relacja wektora prądu źródłowego względem napięcia decyduje o charakterze obwodu. Jeśli napięcie wypadkowe (źródłowe) wyprzedza prąd wypadkowy lub inaczej mówiąc prąd opóźnia się względem napięcia - obwód ma charakter indukcyjny. Jeśli natomiast napięcie opóźnia się względem prądu lub prąd wyprzedza napięcie - mówimy o charakterze pojemnościowym obwodu. Jeśli nie istnieje przesunięcie fazowe prądu wypadkowego względem napięcia (kąt fazowy równy zeru) mówimy o tzw. stanie rezonansu obwodu, lub po prostu charakterze rezystancyjnym danego obwodu. Charakter rezystancyjny obwodu może powstać nawet przy istnieniu w obwodzie indukcyjności i pojemności w przypadku gdy następuje kompensacja odpowiednich składowych indukcyjnej i pojemnościowej wektorów. Sposób postępowania przy sporządzaniu wykresów wektorowych przedstawimy na przykładzie konkretnego obwodu.

---

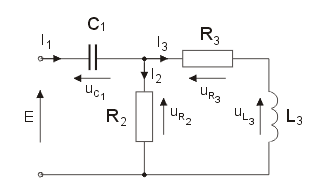
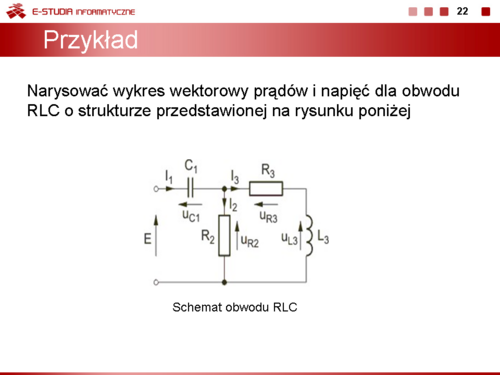
Kolejny przykład ilustruje sposób konstrukcji wykresu wektorowego prądów i napięć dla obwodu RLC o strukturze przedstawionej na rysunku:

---

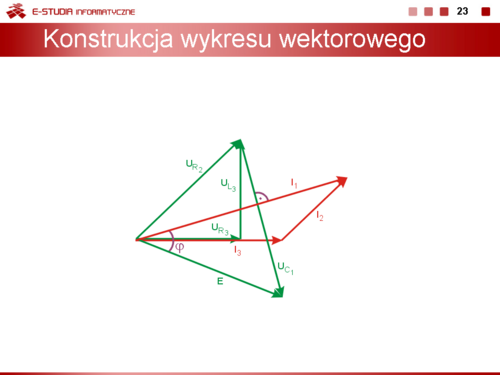
Konstrukcja wykresu wektorowego Na rysunku obok i animacji poniżej przedstawiono wykres wektorowy prądów i napięć w obwodzie RLC z z porzedniego slajdu Sporządzanie wykresu rozpoczyna się od prądu $I_3$ dobudowując kolejno wektory napięć i prądów gałęzi przesuwając się w stronę źródła: $U_{R_3},U_{L_3},U_{R_2},I_2,I_1,U_{C_1},E$. Jak widać obwód ma charakter pojemnościowy, gdyż napięcie wypadkowe $E$ opóźnia się względem odpowiadającego mu prądu $I_1$

---

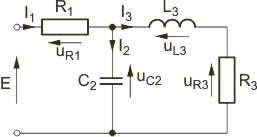
Zadania sprawdzające Zadanie 2.1 Wyznaczyć prądy i napięcia w obwodzie przedstawionym na rysunku. Przyjąć następujące wartości elementów: $e(t)=20\sqrt{2}sin(100t-90^o)V,R_1=10\mathrm{\Omega },R_2=5\mathrm{\Omega },C=0,001F,L=0,05H$. Rozwiązanie Wartości symboliczne elementów obwodu: $\omega =100$ $E=20e^{-}{}^{90^o}$ $Z_L=j\omega L=j5$ $Z_C=1/j\omega C=-j10$ Impedancje obwodu: $Z_{RL}=\frac{R_2{Z}_L}{R_2+Z_L}=2,5+j2,5$ $Z=Z_{RL}+R_1+Z_C=12,5-j7,5$ Prądy i napięcia w obwodzie: $I=E/Z=0,71-j1,18$ $U_{RL}=I{Z}_{RL}=4,71-J1,18$ $I_1=\frac{U_{RL}}{R_2}=-0,23-j0,94$ $I_2=\frac{U_{RL}}{R_2}=-0,94-j0,23$ $U_C=I{Z}_C=-11,76-j7,06$ $U_{R_1}=I{R}_1=7,1-j11,8$ 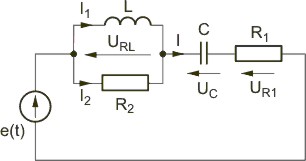Zadanie 2.2 Sporządzić wykres wektorowy prądów i napięć w obwodzie przedstawionym na rysunku Rozwiązanie Wykres rozpoczyna się od prądu $I_3$, dodając kolejno napięcia na $R_3$ i $L_3$, napięcie $U_C{}_2$, prąd $I_C{}_2$, prąd $I_1$ oraz napięcie $E$. Pełny wykres wektorowy przedstawiony jest na rysunku. Kąt fazowy przesunięcia prądu względem napięcia zasilającego jest równy $\phi$,. Biorąc pod uwagę, że napięcie wyprzedza prąd obwód ma charakter indukcyjny.

---