TTS Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „ </math>” na „</math>” |
||
| (Nie pokazano 4 wersji utworzonych przez 2 użytkowników) | |||
| Linia 159: | Linia 159: | ||
Przypomnijmy, że jednym z parametrów charakteryzujących falę elektromagnetyczną jest impedancja falowa, którą definiujemy jako stosunek wartości wzajemnie prostopadłych składowych wektorów natężeń pól elektrycznego i magnetycznego. Dodatkowo składowe te muszą być prostopadłe do kierunku rozchodzenia się fali. Ten ostatni warunek jest a priori spełniony dla fali typu TEM. | Przypomnijmy, że jednym z parametrów charakteryzujących falę elektromagnetyczną jest impedancja falowa, którą definiujemy jako stosunek wartości wzajemnie prostopadłych składowych wektorów natężeń pól elektrycznego i magnetycznego. Dodatkowo składowe te muszą być prostopadłe do kierunku rozchodzenia się fali. Ten ostatni warunek jest a priori spełniony dla fali typu TEM. | ||
Zauważmy, że we wzorze wyrażającym impedancję falową znak minus występuje tylko przed ilorazem składowych <math>E_y\,</math> i <math>H_y\,</math>. Zasadność istnienia przeciwnych znaków przed ilorazami odpowiednich składowych pól można wyjaśnić korzystając z podanych związków między polami. Przyjmując, że fala TEM rozchodzi się w kierunku +0z i zapisując wektor natężenia pola elektrycznego fali TEM jako <math>\vec{E}_T=\vec{i}_x E_x+\vec{i}_y E_y</math> otrzymamy to wektor natężenia pola magnetycznego w formie <math> | Zauważmy, że we wzorze wyrażającym impedancję falową znak minus występuje tylko przed ilorazem składowych <math>E_y\,</math> i <math>H_y\,</math>. Zasadność istnienia przeciwnych znaków przed ilorazami odpowiednich składowych pól można wyjaśnić korzystając z podanych związków między polami. Przyjmując, że fala TEM rozchodzi się w kierunku +0z i zapisując wektor natężenia pola elektrycznego fali TEM jako <math>\vec{E}_T=\vec{i}_x E_x+\vec{i}_y E_y</math> otrzymamy to wektor natężenia pola magnetycznego w formie <math>\vec{H}_T=\vec{i}_y H_y+\vec{i}_y H_y=-\vec{i}_x\frac{E_y}{Z}+\vec{i}_y\frac{E_x}{Z}</math>. | ||
Z powyższych postaci pól widać, że należy umieścić znak minus w definicji impedancji falowej. | Z powyższych postaci pól widać, że należy umieścić znak minus w definicji impedancji falowej. | ||
| Linia 276: | Linia 276: | ||
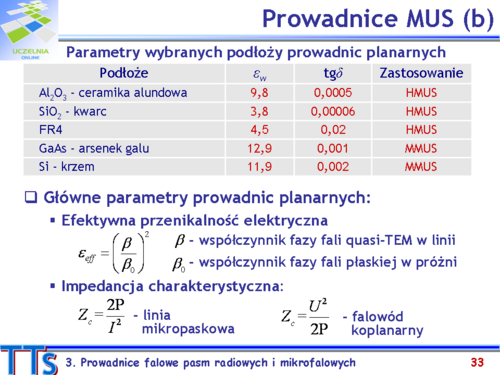
Impedancja charakterystyczna prowadnicy falowej <math>(Z_c)</math>, w której rozchodzi się fala w jednym kierunku, może być zdefiniowana jedną z zależności: | Impedancja charakterystyczna prowadnicy falowej <math>(Z_c)</math>, w której rozchodzi się fala w jednym kierunku, może być zdefiniowana jedną z zależności: | ||
:<math> | :<math>Z_{cUI}=\frac{U}{I}</math> | ||
:<math> | :<math>Z_{cPU}=\frac{U^2}{2P}</math> | ||
:<math> | :<math>Z_{cPI}=\frac{2P}{I^2}</math> | ||
w których: U, I – amplitudy napięcia i prądu (w ogólności wielkości zespolone); P – średnia w czasie moc przenoszona przez falę elektromagnetyczną w linii (wielkość rzeczywista). | w których: U, I – amplitudy napięcia i prądu (w ogólności wielkości zespolone); P – średnia w czasie moc przenoszona przez falę elektromagnetyczną w linii (wielkość rzeczywista). | ||
| Linia 301: | Linia 301: | ||
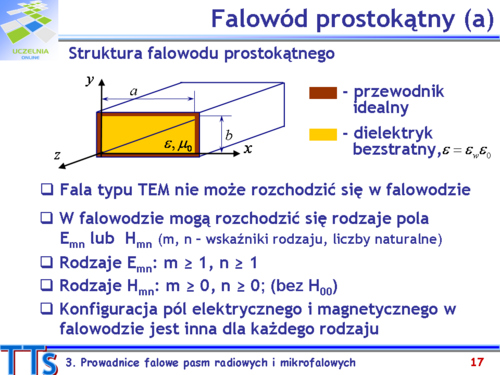
Falowód prostokątny jest prowadnicą falową, w której nie występują dwa niezależne przewody, a więc nie może rozchodzić się w nim fala elektromagnetyczna typu TEM. Do zbioru rodzajów pola elektromagnetycznego falowodu należą rodzaje typu E (TM) i H (TE). Dowolne pole elektromagnetyczne występujące w tym falowodzie można przedstawić jako superpozycję wymienionych rodzajów. | Falowód prostokątny jest prowadnicą falową, w której nie występują dwa niezależne przewody, a więc nie może rozchodzić się w nim fala elektromagnetyczna typu TEM. Do zbioru rodzajów pola elektromagnetycznego falowodu należą rodzaje typu E (TM) i H (TE). Dowolne pole elektromagnetyczne występujące w tym falowodzie można przedstawić jako superpozycję wymienionych rodzajów. | ||
Rodzaje pola, które mogą rozchodzić się w falowodzie prostokątnym oznaczamy jako <math>E_{mn}</math> i <math>H_{mn}</math>. Liczby naturalne m i n nazywamy wskaźnikami albo indeksami rodzaju. Z warunków brzegowych wynika, że zmiany składowych wektorów pól elektrycznego i magnetycznego w płaszczyźnie xy opisują funkcje sinus lub cosinus. Przykładowo, dla rodzaju <math>E_{mn}</math> składowa <math>E_z\,</math> w płaszczyźnie xy (dla z = 0) jest proporcjonalna do wyrażenia <math> | Rodzaje pola, które mogą rozchodzić się w falowodzie prostokątnym oznaczamy jako <math>E_{mn}</math> i <math>H_{mn}</math>. Liczby naturalne m i n nazywamy wskaźnikami albo indeksami rodzaju. Z warunków brzegowych wynika, że zmiany składowych wektorów pól elektrycznego i magnetycznego w płaszczyźnie xy opisują funkcje sinus lub cosinus. Przykładowo, dla rodzaju <math>E_{mn}</math> składowa <math>E_z\,</math> w płaszczyźnie xy (dla z = 0) jest proporcjonalna do wyrażenia <math>sin(\frac{m\pi}{a}x)sin(\frac{n\pi}{b}y)</math> (składowa ta musi przyjmować wartość równą zeru na ściankach falowodu). Natomiast dla rodzaju Hmn składowa <math>H_z\,</math> w płaszczyźnie z = 0 jest proporcjonalna do wyrażenia <math>sin(\frac{m\pi}{a}x)sin(\frac{n\pi}{b}y)</math> (składowa ta osiąga maksimum na ściankach falowodu). | ||
Wskaźnik m rodzaju pola oznacza więc liczbę zmian (liczbę połówek okresu funkcji sinus lub cosinus) pola wzdłuż dłuższego boku (a) falowodu, a wskaźnik n opisuje liczbę zmian pola wzdłuż któtszego boku (b) falowodu. Zmiany te dotyczą wszystkich składowych wektorów pól elektrycznego i magnetycznego występujących dla danego rodzaju pola. | Wskaźnik m rodzaju pola oznacza więc liczbę zmian (liczbę połówek okresu funkcji sinus lub cosinus) pola wzdłuż dłuższego boku (a) falowodu, a wskaźnik n opisuje liczbę zmian pola wzdłuż któtszego boku (b) falowodu. Zmiany te dotyczą wszystkich składowych wektorów pól elektrycznego i magnetycznego występujących dla danego rodzaju pola. | ||
| Linia 441: | Linia 441: | ||
*prądy płynące w kierunku +0y na krótszych bokach falowodu; | *prądy płynące w kierunku +0y na krótszych bokach falowodu; | ||
*prądy na dolnym dłuższym boku, które płyną w kierunku +0x dla </math>x < a/2</math> oraz w kierunku –0x dla <math>x > a/2</math>; | *prądy na dolnym dłuższym boku, które płyną w kierunku +0x dla</math>x < a/2</math> oraz w kierunku –0x dla <math>x > a/2</math>; | ||
*prądy na górnym dłuższym boku, ktore płyną w kierunkach przeciwnych niż prądy na dolnej ściance, a więc płyną one w kierunku –0x dla <math>x < a/2</math> i w +0x dla <math>x > a/2</math>. | *prądy na górnym dłuższym boku, ktore płyną w kierunkach przeciwnych niż prądy na dolnej ściance, a więc płyną one w kierunku –0x dla <math>x < a/2</math> i w +0x dla <math>x > a/2</math>. | ||
| Linia 480: | Linia 480: | ||
W falowodzie kołowym, tak jak to ma miejsce w falowodzie prostokątnym, mogą rozchodzić się rodzaje pola elektromagnetycznego typu E (TM) i H (TE). Dowolne pole elektromagnetyczne występujące w tym falowodzie można przedstawić jako superpozycję wymienionych rodzajów. | W falowodzie kołowym, tak jak to ma miejsce w falowodzie prostokątnym, mogą rozchodzić się rodzaje pola elektromagnetycznego typu E (TM) i H (TE). Dowolne pole elektromagnetyczne występujące w tym falowodzie można przedstawić jako superpozycję wymienionych rodzajów. | ||
Opis matematyczny pola elektromagnetycznego w przekroju poprzecznym falowodu kołowego, który analizujemy w cylindrycznym układzie współrzędnych, jest inny niż dla falowodu prostokątnego i jest to konsekwencja innego kształtu przekroju poprzecznego prowadnicy. Rodzaje pola w falowodzie kołowym oznaczamy jako <math>E_{mn}\,</math> i <math>H_{mn}\,</math>. Liczby naturalne m i n to wskaźniki (indeksy) rodzaju. Z rozwiązania równania Helmholtz’a we współrzędnych cylindrycznych z uwzględnieniem warunków brzegowych wynika, że zmiany składowej z wektora pola elektrycznego (rodzaje typu E), a także wektora pola magnetycznego (rodzaje typu H) w płaszczyźnie poprzecznej do kierunku rozchodzenia się fali (płaszczyzna <math>\rho \varphi</math>) są zgodne z funkcją Bessela m-tego rzędu wzdłuż promienia (zmienna <math></math>) oraz następują według funkcji cosinus ze zmianą kąta (zmienna <math>\varphi\,</math>). | Opis matematyczny pola elektromagnetycznego w przekroju poprzecznym falowodu kołowego, który analizujemy w cylindrycznym układzie współrzędnych, jest inny niż dla falowodu prostokątnego i jest to konsekwencja innego kształtu przekroju poprzecznego prowadnicy. Rodzaje pola w falowodzie kołowym oznaczamy jako <math>E_{mn}\,</math> i <math>H_{mn}\,</math>. Liczby naturalne m i n to wskaźniki (indeksy) rodzaju. Z rozwiązania równania Helmholtz’a we współrzędnych cylindrycznych z uwzględnieniem warunków brzegowych wynika, że zmiany składowej z wektora pola elektrycznego (rodzaje typu E), a także wektora pola magnetycznego (rodzaje typu H) w płaszczyźnie poprzecznej do kierunku rozchodzenia się fali (płaszczyzna <math>\rho \varphi</math>) są zgodne z funkcją Bessela m-tego rzędu wzdłuż promienia (zmienna <math>\rho</math>) oraz następują według funkcji cosinus ze zmianą kąta (zmienna <math>\varphi\,</math>). | ||
Dla rodzaju Emn składowa Ez przyjmuje wartość równą zeru na ściankach falowodu i w płaszczyźnie <math>\rho \varphi</math>) (dla z = 0) jest proporcjonalna do wyrażenia <math> | Dla rodzaju Emn składowa Ez przyjmuje wartość równą zeru na ściankach falowodu i w płaszczyźnie <math>\rho \varphi</math>) (dla z = 0) jest proporcjonalna do wyrażenia <math>J_m\left (\frac{\kappa_{mn}}{a}\right)cos(m\varphi)</math> , przy czym <math>J_m</math> to funkcja Bessela pierwszego rodzaju m-tego rzędu, a <math>\kappa_m</math> to n-ty pierwiastek tej funkcji. Natomiast dla rodzaju <math>H_{mn}</math> składowa <math>H_z</math> osiąga maksimum na ściankach falowodu i w płaszczyźnie z = 0 jest proporcjonalna do wyrażenia <math>J_m\left (\frac{\kappa'_{mn}}{a}\right)cos(m\varphi)</math> , gdzie <math>\kappa'</math> to n-ty pierwiastek pierwszej pochodnej funkcji <math>J_m</math>. Znając składową z, pozostałe składowe pola elektromagnetycznego wyznaczamy korzystając z równań Maxwella. | ||
W oparciu o powyżej przedstawione zależności możemy zauważyć, że wskaźnik m rodzaju pola oznacza rząd funkcji Bessela oraz liczbę całkowitych okresów funkcji funkcji cosinus, a wskaźnik n określa numer pierwiastka funkcji <math>J_m</math> (dla rodzajów E) albo pierwszej pochodnej tej funkcji (dla rodzajów H). | |||
W falowodzie kołowym rozkłady pola elektromagnetycznego rodzajów, dla których wskaźnik m jest równy zeru charakteryzują się symetrią osiową (względem osi 0z) bo pola nie zależą od zmiennej <math>\varphi\,</math>. | |||
|} | |} | ||
| Linia 492: | Linia 494: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd29.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd29.png|thumb|500px]] | ||
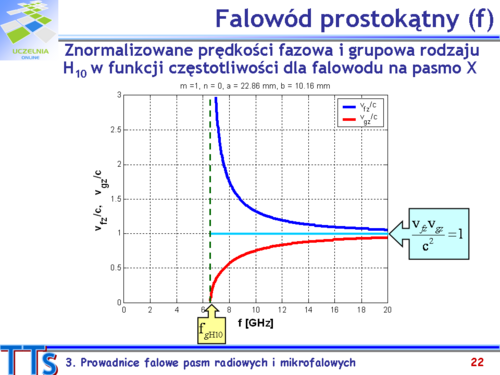
|valign="top"| | |valign="top"|Tak jak to ma miejsce w falowodzie prostokątnym, dla danego rodzaju pola w falowodzie kołowym rozchodzącego się w kierunku +0z, zależność wszystkich występujących w nim składowych pól elektrycznego i magnetycznego wzdłuż kierunku propagacji jest opisana przez czynnik <math>exp(–\gamma_zz), przy czym <math>\gamma_z\,</math> to współczynnik propagacji fali wzdłuż osi z. Współczynnik ten określa się w oparciu o równanie dyspersyjne, które pokazane jest na slajdzie. | ||
Rola i znaczenie granicznego współczynnika fazy <math>\beta_g\,</math> dla falowodu kołowego są analogiczne jak to miało miejsce dla falowodu prostokątnego, a istotna różnica między tymi falowodami polega na sposobie obliczania tej wielkości. Zależności, według których wyznaczamy <math>\beta_g\,</math> dla zadanych rodzajów pola w falowodzie kołowym są podane i opisane na slajdzie. Zaznaczyć należy, że w falowodzie kołowym graniczne współczynniki fazy nie mają tej samej wartości dla rodzajów E i H o identycznych wskaźnikach m, n. | |||
|} | |} | ||
| Linia 500: | Linia 504: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd30.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd30.png|thumb|500px]] | ||
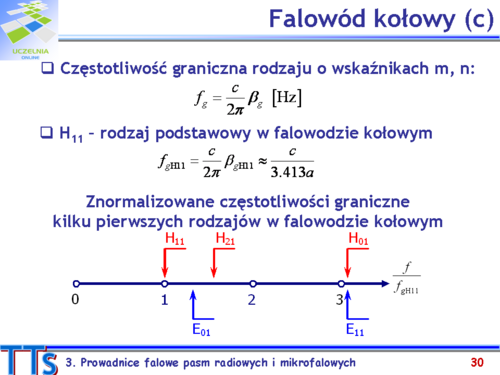
|valign="top"| | |valign="top"|Przypomnijmy, że częstotliwość graniczna rodzaju o wskaźnikach m, n w bezstratnym falowodzie kołowym to taka częstotliwość, dla której o współczynnik propagacji γz tego rodzaju jest równy zeru. Jest ona powiązana z granicznym współczynnikiem fazy oraz parametrami ośrodka wypełniającego falowód. Fala elektromagnetyczna określonego rodzaju rozchodzi się w falowodzie dla częstotliwości większych od częstotliwości granicznej. | ||
Wśród pierwiastków, tak funkcji Bessela pierwszego rodzaju jak i pierwszej pochodnej tych funkcji, najmniejszą wartość ma pierwszy pierwiastek pochodnej funkcji <math>J_1\,</math> <math>\kappa'_{11}=1.811</math> . Oznacza to, że najmniejszy graniczny współczynnik fazy, a tym samym i najmniejsza częstotliwość graniczna, odpowiada rodzajowi <math>H_{11}\,</math>, który jest rodzajem podstawowym w falowodzie kołowym. | |||
Na slajdzie pokazano graficznie rozkład częstotliwości granicznych znormalizowanych do częstotliwości granicznej rodzaju podstawowego dla kilku pierwszych rodzajów wzbudzanych w falowodzie kołowym. Warto zauważyć, że pasmo pracy falowodu kołowego (gdy rozchodzi się tylko rodzaj podstawowy) wynosi około 25% i jest znacznie mniejsze niż dla falowodu prostokątnego. | |||
Znając częstotliwość graniczną zadanego rodzaju pola w falowodzie kołowym możemy wyznaczyć jego współczynnik propagacji posługując się zależnościami podanymi wcześniej dla falowodu prostokątnego (slajd 20). Przypomnijmy, że poniżej częstotliwości granicznej współczynnik propagacji dowolnego rodzaju pola w bezstratnym falowodzie kołowym jest wielkością rzeczywistą, czyli staje się współczynnikiem tłumienia. Natomiast dla częstotliwości większych niż częstotliwość graniczna współczynnik propagacji jest urojony, a jego wartość to współczynnik fazy. Wiemy także, że znając współczynnikiem fazy można określić długość fali w falowodzie oraz prędkości fazową i grupową, a przedstawione wcześniej zależności dla falowodu prostokątnego są słuszne również dla falowodu kołowego. Także częstotliwościowe charaktrystyki współczynnika propagacji i prędkości prezentowane przy omawianiu falowodu prostokątnego oddają jakościowe zmiany tych parametrów z częstotliwością dla rodzajów pola falowodu kołowego. Podsumowując, parametry pola elektromagnetycznego w falowodach prostokątnym i kołowym są identycznie definiowane i jedyną różnicą jest sposób oblicznia granicznego współczynnika fazy. Natomiast rozkłady pól poszczególnych rodzajów pola elektromagnetycznego są zdecydowanie różne. | |||
|} | |} | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd31.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd31.png|thumb|500px]] | ||
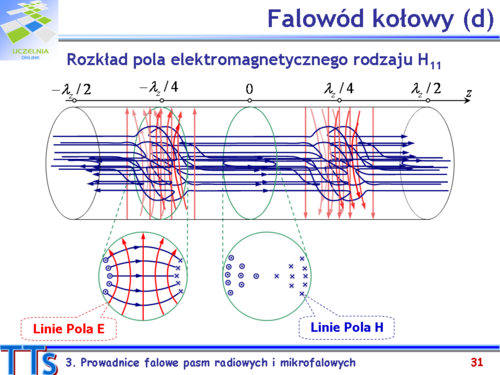
|valign="top"| | |valign="top"|Na slajdzie przedstawiono konfigurację linii sił pól elektrycznego i magnetycznego rodzaju podstawowego w bezstratnym falowodzie kołowym dla fali rozchodzącej się w kierunku +0z w chwili t = 0. Jest to graficzna ilustracja rzeczywistych wektorów pól rodzaju <math>H_{11}\,</math> o następujących składowych: | ||
:<math>H_z(\rho,\varphi, z,t)=H_{z0}J_1(\beta_{gH11}\rho)cos\varphi cos(\omega t-\beta_z z)</math> | |||
:<math>H_{\rho}(\rho,\varphi, z,t)=-\frac{\beta_z}{\beta_{gH11}}H_{z0}J'_1(\beta_{gH11}\rho)cos\varphi sin(\omega t-\beta_z z)</math> | |||
:<math>H_{\varphi}(\rho,\varphi, z,t)=-\frac{\beta_z}{\rho \beta_{gH11}}H_{z0}J_1(\beta_{gH11}\rho)sin\varphi sin(\omega t-\beta_z z)</math> | |||
:<math>E_{\rho}(\rho,\varphi, z,t)=-\frac{Z\beta_z}{\rho \beta^2_{gH11}}H_{z0}J_1(\beta_{gH11}\rho)sin\varphi sin(\omega t-\beta_z z)</math> | |||
:<math>E_{\varphi}(\rho,\varphi, z,t)=-\frac{Z\beta_z}{\\beta_{gH11}}H_{z0}J'_1(\beta_{gH11}\rho)cos\varphi sin(\omega t-\beta_z z)</math> | |||
gdzie <math>\beta_{gH11}=\frac{\kappa'_{11}}{a}=\frac{1.811}{a}</math> , <math>J_1\,</math> to funkcja Bessela pierwszego rodzaju rzędu 1, a <math>J'_1\,</math> – pierwsza pochodna tej funkcji, Z to impedancja właściwa ośrodka wypełniającego falowód. | |||
Wyrażenia określające składowe pól rodzaju <math>H_{11}\,</math> wskazują, że spełnione są warunki brzegowe na ściance falowodu (dla <math>\rho = a</math>), czyli zerowanie składowych <math>E_{\varphi}\,</math> i <math>H_{\rho}</math>. Ze składową <math>E_{\rho}</math> związane są powierzchniowe ładunki elektryczne, a składowe <math>H_z</math> i <math>H_{\varphi}</math> określają gęstości prądów powierzchniowych. Związki między polami a ładunkami i prądami na powierzchni przewodnika omówiono szczegółowo dla falowodu prostokątnego. Poprzestaniemy tu na stwierdzeniu, że analogiczne relacje dotyczą falowodu kołowego. | |||
Falowody kołowe znalazły zastosowanie w systemach antenowych oraz w konstrukcjach niektórych tłumików, rezonatorów i filtrów (będzie o tym mowa w jednym z dalszych wykładów). | |||
|} | |} | ||
| Linia 581: | Linia 606: | ||
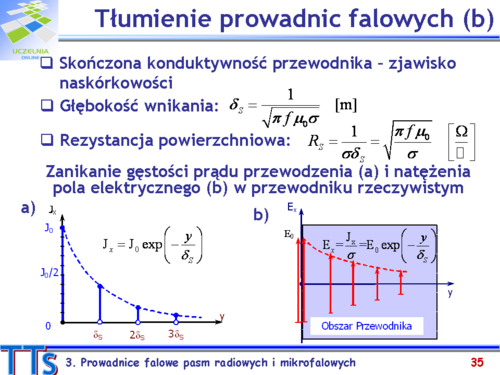
Współczynnik tłumienia można wyrazić w Neperach na metr albo z decybelach na metr. Związek między tymi jednostkami, który wynika z defincji Nepera i decybela, jest dla współczynnika tłumienia następujący: | Współczynnik tłumienia można wyrazić w Neperach na metr albo z decybelach na metr. Związek między tymi jednostkami, który wynika z defincji Nepera i decybela, jest dla współczynnika tłumienia następujący: | ||
:<math> | :<math>\alpha\left[\frac{dB}{m}\right]=20lge\cdot \alpha \left[\frac{Np}{m}\right]=8.686\alpha \left[\frac{Np}{m}\right]</math> | ||
Współczynnik tłumienia fali wynikający ze strat dielektrycznych αd można przedstawić w formie analogicznej do postaci współczynnika αm. W tym przypadku, niezależnie od rodzaju pola i prowadnicy, współczynnik tłumienia jest wprostproporcjonalny do tangensa kąta stratności dielektryka. Komentarz dotyczący funkcji <math>F_d</math> można sformułować podobnie jak dla funkcji <math>F_m</math>. Warto zwrócić uwagę na prostotę funkcji <math>F_d</math> dla linii współosiowej oraz na fakt, że <math>\alpha_d</math> rośnie liniowo z częstotliwością. | Współczynnik tłumienia fali wynikający ze strat dielektrycznych αd można przedstawić w formie analogicznej do postaci współczynnika αm. W tym przypadku, niezależnie od rodzaju pola i prowadnicy, współczynnik tłumienia jest wprostproporcjonalny do tangensa kąta stratności dielektryka. Komentarz dotyczący funkcji <math>F_d</math> można sformułować podobnie jak dla funkcji <math>F_m</math>. Warto zwrócić uwagę na prostotę funkcji <math>F_d</math> dla linii współosiowej oraz na fakt, że <math>\alpha_d</math> rośnie liniowo z częstotliwością. | ||
| Linia 665: | Linia 690: | ||
#Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8. | #Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8. | ||
#Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3. | #Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3. | ||
#Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2 | #Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2</math>. | ||
Aktualna wersja na dzień 10:45, 5 wrz 2023
Wykład
Pytania sprawdzające
(jeśli potrafisz na nie odpowiedzieć, to znaczy, że opanowałeś/aś materiał wykładu)
- Wymień i scharakteryzuj najważniejsze parametry prowadnicy falowej.
- Przypomnij sobie jakie mody mogą rozchodzić się w falowodach i scharakteryzuj je.
- Co to jest dyspersja, w jakich warunkach i dlaczego dyspersja utrudnia transmisję sygnału.
- Przeanalizuj przyczyny powstawania strat przy transmisji mocy prowadnicami falowymi.
- Na czym polega efekt naskórkowości?
- Opisz kolejno prowadnice typu TEM.
- Narysuj konfigurację pól E i H dla modu podstawowego i naszkicuj kierunki przepływu prądów w ściankach falowodu prostokątnego.
- Dlaczego nie stosujemy falowodów prostokątnych, dla których stosunek a/b=1?
- W jakim pasmie częstotliwości może pracować falowód prostokątny?
- W jakim pasmie może pracować falowód cylindryczny?
- Jak uzasadnisz fakt, że obwodem zastępczym odcinka falowodu prostokątnego jest odcinek linii dwuprzewodowej?
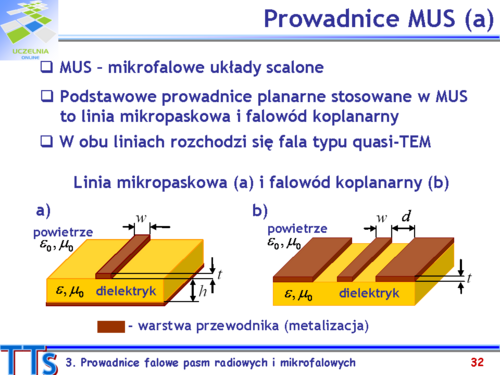
- Jak zbudowana jest i jakie ma właściwości prowadnica mikropaskowa?
- Jak zbudowana jest i jakie ma właściwości linia koplanarna?
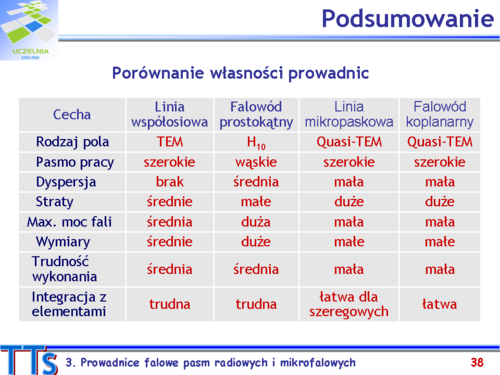
- Jakie są obszary zastosowań linii współosiowej, linii mikropaskowej i falowodu prostokątnego? Aby to uzasadnić porównaj parametry wymienionych typów prowadnic.
- Wymień argumenty przemawiające za rozwojem technologii i konstrukcji Mikrofalowych Monolitycznych Układów Scalonych na krzemie i arsenku galu.
Słownik
Częstotliwość graniczna - częstotliwość powyżej której może się propagować fala w falowodzie. Poniżej tej częstotliwości fala jest silnie tłumiona.
Zestawienie typów fal:
- Fala typu TEM - wektory pola E i H leżą w płaszczyźnie prostopadłej do kierunku propagacji.
- Fala typu TE (zwana też H) - pole E posiada składowe tylko w płaszczyźnie prostopadłej do kierunku propagacji. Pole H posiada składowe w kierunku propagacji fali.
- Fala typu TM (zwana też E) - pole H posiada składowe tylko w płaszczyźnie prostopadłej do kierunku propagacji. Pole E posiada składowe w kierunku propagacji fali.
- Fala typu EH - zarówno pole E jak i pole H tej fali posiadają składowe w kierunku propagacji.
Linie TEM:
- Linia współosiowa.
- Linia dwuprzewodowa.
- Symetryczna linia paskowa.
Linie Quasi-TEM:
- Niesymetryczna linia paskowa:
- Linia koplanarna (falowód koplanarny).
- Linia koplanarna paskowa.
Linie falowodowe:
- Falowód prostokątny. Mod podstawowy typu TE10 (H10).
- Falowód kołowy (cylindryczny). Mod podstawowy typu TE11 (H11).
Mod (rodzaj) podstawowy dla danego falowodu - to mod fali o najmniejszej
Bibliografia
- Bogdan Galwas. Miernictwo mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1985, Rozdział 1, 2 i 3.
- Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8.
- Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3.
- Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2</math>.