TTS Moduł 3: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „ </math>” na „</math>” |
||
| (Nie pokazano 5 wersji utworzonych przez 2 użytkowników) | |||
| Linia 159: | Linia 159: | ||
Przypomnijmy, że jednym z parametrów charakteryzujących falę elektromagnetyczną jest impedancja falowa, którą definiujemy jako stosunek wartości wzajemnie prostopadłych składowych wektorów natężeń pól elektrycznego i magnetycznego. Dodatkowo składowe te muszą być prostopadłe do kierunku rozchodzenia się fali. Ten ostatni warunek jest a priori spełniony dla fali typu TEM. | Przypomnijmy, że jednym z parametrów charakteryzujących falę elektromagnetyczną jest impedancja falowa, którą definiujemy jako stosunek wartości wzajemnie prostopadłych składowych wektorów natężeń pól elektrycznego i magnetycznego. Dodatkowo składowe te muszą być prostopadłe do kierunku rozchodzenia się fali. Ten ostatni warunek jest a priori spełniony dla fali typu TEM. | ||
Zauważmy, że we wzorze wyrażającym impedancję falową znak minus występuje tylko przed ilorazem składowych <math>E_y\,</math> i <math>H_y\,</math>. Zasadność istnienia przeciwnych znaków przed ilorazami odpowiednich składowych pól można wyjaśnić korzystając z podanych związków między polami. Przyjmując, że fala TEM rozchodzi się w kierunku +0z i zapisując wektor natężenia pola elektrycznego fali TEM jako <math>\vec{E}_T=\vec{i}_x E_x+\vec{i}_y E_y</math> otrzymamy to wektor natężenia pola magnetycznego w formie <math> | Zauważmy, że we wzorze wyrażającym impedancję falową znak minus występuje tylko przed ilorazem składowych <math>E_y\,</math> i <math>H_y\,</math>. Zasadność istnienia przeciwnych znaków przed ilorazami odpowiednich składowych pól można wyjaśnić korzystając z podanych związków między polami. Przyjmując, że fala TEM rozchodzi się w kierunku +0z i zapisując wektor natężenia pola elektrycznego fali TEM jako <math>\vec{E}_T=\vec{i}_x E_x+\vec{i}_y E_y</math> otrzymamy to wektor natężenia pola magnetycznego w formie <math>\vec{H}_T=\vec{i}_y H_y+\vec{i}_y H_y=-\vec{i}_x\frac{E_y}{Z}+\vec{i}_y\frac{E_x}{Z}</math>. | ||
Z powyższych postaci pól widać, że należy umieścić znak minus w definicji impedancji falowej. | Z powyższych postaci pól widać, że należy umieścić znak minus w definicji impedancji falowej. | ||
| Linia 276: | Linia 276: | ||
Impedancja charakterystyczna prowadnicy falowej <math>(Z_c)</math>, w której rozchodzi się fala w jednym kierunku, może być zdefiniowana jedną z zależności: | Impedancja charakterystyczna prowadnicy falowej <math>(Z_c)</math>, w której rozchodzi się fala w jednym kierunku, może być zdefiniowana jedną z zależności: | ||
:<math> | :<math>Z_{cUI}=\frac{U}{I}</math> | ||
:<math> | :<math>Z_{cPU}=\frac{U^2}{2P}</math> | ||
:<math> | :<math>Z_{cPI}=\frac{2P}{I^2}</math> | ||
w których: U, I – amplitudy napięcia i prądu (w ogólności wielkości zespolone); P – średnia w czasie moc przenoszona przez falę elektromagnetyczną w linii (wielkość rzeczywista). | w których: U, I – amplitudy napięcia i prądu (w ogólności wielkości zespolone); P – średnia w czasie moc przenoszona przez falę elektromagnetyczną w linii (wielkość rzeczywista). | ||
| Linia 301: | Linia 301: | ||
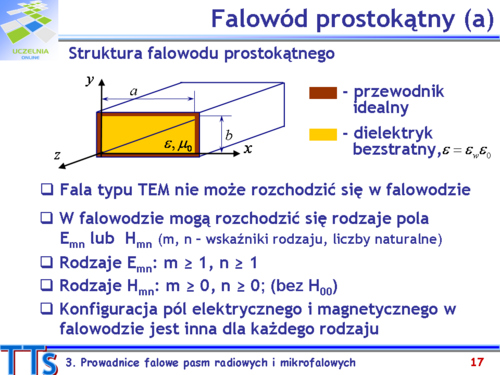
Falowód prostokątny jest prowadnicą falową, w której nie występują dwa niezależne przewody, a więc nie może rozchodzić się w nim fala elektromagnetyczna typu TEM. Do zbioru rodzajów pola elektromagnetycznego falowodu należą rodzaje typu E (TM) i H (TE). Dowolne pole elektromagnetyczne występujące w tym falowodzie można przedstawić jako superpozycję wymienionych rodzajów. | Falowód prostokątny jest prowadnicą falową, w której nie występują dwa niezależne przewody, a więc nie może rozchodzić się w nim fala elektromagnetyczna typu TEM. Do zbioru rodzajów pola elektromagnetycznego falowodu należą rodzaje typu E (TM) i H (TE). Dowolne pole elektromagnetyczne występujące w tym falowodzie można przedstawić jako superpozycję wymienionych rodzajów. | ||
Rodzaje pola, które mogą rozchodzić się w falowodzie prostokątnym oznaczamy jako <math>E_{mn}</math> i <math>H_{mn}</math>. Liczby naturalne m i n nazywamy wskaźnikami albo indeksami rodzaju. Z warunków brzegowych wynika, że zmiany składowych wektorów pól elektrycznego i magnetycznego w płaszczyźnie xy opisują funkcje sinus lub cosinus. Przykładowo, dla rodzaju <math>E_{mn}</math> składowa <math>E_z\,</math> w płaszczyźnie xy (dla z = 0) jest proporcjonalna do wyrażenia <math> | Rodzaje pola, które mogą rozchodzić się w falowodzie prostokątnym oznaczamy jako <math>E_{mn}</math> i <math>H_{mn}</math>. Liczby naturalne m i n nazywamy wskaźnikami albo indeksami rodzaju. Z warunków brzegowych wynika, że zmiany składowych wektorów pól elektrycznego i magnetycznego w płaszczyźnie xy opisują funkcje sinus lub cosinus. Przykładowo, dla rodzaju <math>E_{mn}</math> składowa <math>E_z\,</math> w płaszczyźnie xy (dla z = 0) jest proporcjonalna do wyrażenia <math>sin(\frac{m\pi}{a}x)sin(\frac{n\pi}{b}y)</math> (składowa ta musi przyjmować wartość równą zeru na ściankach falowodu). Natomiast dla rodzaju Hmn składowa <math>H_z\,</math> w płaszczyźnie z = 0 jest proporcjonalna do wyrażenia <math>sin(\frac{m\pi}{a}x)sin(\frac{n\pi}{b}y)</math> (składowa ta osiąga maksimum na ściankach falowodu). | ||
Wskaźnik m rodzaju pola oznacza więc liczbę zmian (liczbę połówek okresu funkcji sinus lub cosinus) pola wzdłuż dłuższego boku (a) falowodu, a wskaźnik n opisuje liczbę zmian pola wzdłuż któtszego boku (b) falowodu. Zmiany te dotyczą wszystkich składowych wektorów pól elektrycznego i magnetycznego występujących dla danego rodzaju pola. | Wskaźnik m rodzaju pola oznacza więc liczbę zmian (liczbę połówek okresu funkcji sinus lub cosinus) pola wzdłuż dłuższego boku (a) falowodu, a wskaźnik n opisuje liczbę zmian pola wzdłuż któtszego boku (b) falowodu. Zmiany te dotyczą wszystkich składowych wektorów pól elektrycznego i magnetycznego występujących dla danego rodzaju pola. | ||
| Linia 441: | Linia 441: | ||
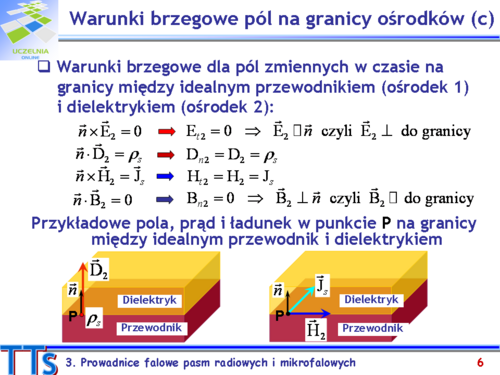
*prądy płynące w kierunku +0y na krótszych bokach falowodu; | *prądy płynące w kierunku +0y na krótszych bokach falowodu; | ||
*prądy na dolnym dłuższym boku, które płyną w kierunku +0x dla </math>x < a/2</math> oraz w kierunku –0x dla <math>x > a/2</math>; | *prądy na dolnym dłuższym boku, które płyną w kierunku +0x dla</math>x < a/2</math> oraz w kierunku –0x dla <math>x > a/2</math>; | ||
*prądy na górnym dłuższym boku, ktore płyną w kierunkach przeciwnych niż prądy na dolnej ściance, a więc płyną one w kierunku –0x dla <math>x < a/2</math> i w +0x dla <math>x > a/2</math>. | *prądy na górnym dłuższym boku, ktore płyną w kierunkach przeciwnych niż prądy na dolnej ściance, a więc płyną one w kierunku –0x dla <math>x < a/2</math> i w +0x dla <math>x > a/2</math>. | ||
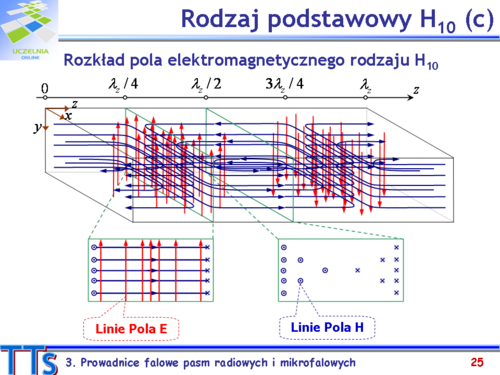
Podano rozpływy prądów w dwóch szczególnych przekrojach poprzecznych. Prądy na ściankach falowodu w innych płaszczyznach przekroju będą miały tak składową wzdłużną jak i odpowiednie składowe poprzeczne. | Podano rozpływy prądów w dwóch szczególnych przekrojach poprzecznych. Prądy na ściankach falowodu w innych płaszczyznach przekroju będą miały tak składową wzdłużną jak i odpowiednie składowe poprzeczne. | ||
Poza prądem powierzchniowym w falowodzie występuje również prąd przesunięcia. Dla pokazanego na rysunku przypadku (t = 0) wektor gęstości prądu przesunięcia opisuje zależność <math>-\vec{i}_y</math> . Prąd ten „płynie” między dłuższymi bokami falowodu, linie tego prądu są tak skierowane jak linie pola elektrycznego, ale są przesunięte względem tego pola o ćwierć długości fali w falowodzie. W płaszczyźnie z = | Poza prądem powierzchniowym w falowodzie występuje również prąd przesunięcia. Dla pokazanego na rysunku przypadku (t = 0) wektor gęstości prądu przesunięcia opisuje zależność <math>-\vec{i}_y \omega\varepsilon_0 E_{y0}sin(\pi x/a)cos(-\beta_z z) [A/m^2]</math> . Prąd ten „płynie” między dłuższymi bokami falowodu, linie tego prądu są tak skierowane jak linie pola elektrycznego, ale są przesunięte względem tego pola o ćwierć długości fali w falowodzie. W płaszczyźnie <math>z = \lambda_z/4</math>, gdzie składowe poprzeczne wektorów nateżeń pól elektrycznego i magnetycznego osiągają wartości maksymalne, prąd przesunięcia jest równy zeru. Gęstość prądu przesunięcia wzdłuż osi z jest maksymalna w płaszczyźnie <math>z = \lambda_z/2</math>, gdzie prąd przesunięcia płynie od dolnej do górnej ścianki falowodu. | ||
|} | |} | ||
| Linia 453: | Linia 453: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd26.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd26.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Omawiając linię współosiową wprowadziliśmy parametry obwodowe tej prowadnicy TEM. Teraz zdefiniujemy dla falowodu prostokątnego z rodzajem podstawowym wielkości obwodowe, czyli napięcie, prąd i impedancję charakterystyczną. | ||
Napięcie między ściankami falowodu nie jest określone jednoznacznie, zależy od wybranej drogi całkowania. Jest to sytuacja inna niż dla prowadnic TEM, ponieważ pole elektryczne w przekroju poprzecznym falowodu z rodzajem <math>H_{10}\,</math> nie jest potencjalne. Maksymalne napięcie w falowodzie jest między środkami ścianek dolnej i górnej. Definiujemy amplitudę napięcia dla falowodu z rodzajem <math>H_{10}\,</math> jako całkę amplitudy natężenie pola elektrycznego (dla rodzaju <math>H_{10}\,</math> istnieje tylko składowa Ey) wzdłuż prostej łączącej środki wymienionych ścianek. Napięcie obliczamy wybierając płaszczyznę poprzeczną, w której pole elektryczne jest rzeczywiste. | |||
Również definicja prądu dla falowodu jest umowna. Traktując falowód jako linię transmisyjną, na ogół przyjmujemy, że prąd tej linii płynie wzdłuż kierunku rozchodzenia się fali. Jak wiemy, w falowodzie prostokątnym z rodzajem <math>H_{10}\,</math> prądy przewodzenia płyną po ściankach tak wzdłuż jak i w poprzek falowodu. Do obliczenia prądu w falowodzie bierzemy pod uwagę tylko gęstość prądu powierzchniowego płynącego wzdłuż falowodu na jednym z dłuższych boków (na górnej albo dolnej ściance), czyli prądy związane ze składową x wektora natężenia pola magnetycznego. | |||
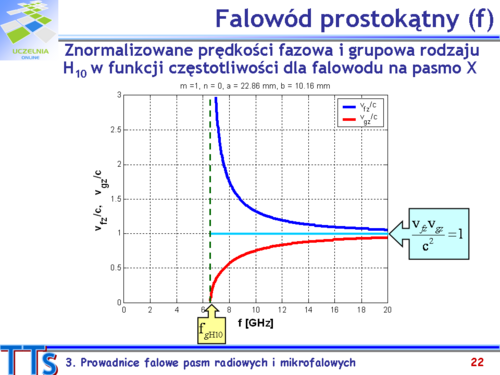
Patrząc na pokazane na slajdzie zależności określające napięcie i prąd zauważamy, że dla ustalonej amplitudy składowej y natężenia pola elektrycznego napięcie ma stałą wartość dla falowodu o określonych bokach, a natężenie prądu zmienia się z częstotliwością (impedancja falowa jest funkcją częstotliwości). Zauważmy również, że podobnie jak to miało miejsce dla linii współosiowej, napięcie i prąd są wielkościami rzeczywistymi dla falowodu wypełnionego ośrodkiem bezstratnym. Gdy dielektryk w falowodzie jest stratny (o zespolonej impedancji właściwej) to impedancja falowa i w konsekwencji także amplituda prądu są wielkościami zespolonymi. | |||
|} | |} | ||
| Linia 461: | Linia 466: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd27.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd27.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Po wyznaczeniu obwodowych wielkości, a mianowicie amplitud napięcia i prądu, dla bezstratnego falowodu prostokątnego z rodzajem podstawowym obliczamy uśrednioną w czasie moc przenoszoną w falowodzie jako połowę iloczynu tych amplitud. Porównanie uzyskanego rezultatu z wynikiem dla mocy fali <math>H_{10}\,</math> uzyskanym na drodze polowej (całkowanie wektora Poyntinga w przekroju poprzecznym falowodu) wskazuje, że obie moce nie są identyczne. Który rezultat jest prawidłowy? Wiarygodną wartość mocy przepływającej przez falowód, co potwierdzono eksperymentalnie, wyznacza się stosując polową technikę. Pole elektromagnetyczne fali <math>H_{10}\,</math> w falowodzie jest określone jednoznacznie, czego nie można powiedzieć o napięciu i prądzie. | ||
Konsekwencją różnych wartości mocy fali uzyskanych na drodze polowej i obwodowej jest niejednoznaczność impedancji charakterystycznej. Wartość tego parametru zależy od definicji, według której ją obliczamy. Sytuację tę zilustrowano na slajdzie podając trzy zależności opisujące impedancje charakterystyczne dla falowodu prostokątnego z rodzajem <math>H_{10}\,</math>. Nie można wskazać, która wartość jest prawdziwa. W przypadku falowodu prostokątnego z rodzajem podstawowym najczęściej posługujemy się impedancją charakterystyczną wyznaczoną w oparciu o moc i napięcie <math>(Z_{cPU})</math>. | |||
|} | |} | ||
| Linia 469: | Linia 476: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd28.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd28.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Zajmijmy się falowodem kołowym, czyli cylindrem, którego przekrój poprzeczny jest kołem. Przyjmujemy założenia idealizujące, które stosowaliśmy przy analizie falowodu prostokątnego, a zatem ścianki falowodu są doskonale przewodzące, a dielektryk wypełniający falowód jest liniowy, jednorodny, izotropowy i bezstratny. Pole elektromagnetyczne w falowodzie kołowym spełnia równania Maxwella, wynikające z nich równania Helmholtz’a oraz warunki brzegowe na granicy dielektryk – przewodnik. | ||
W falowodzie kołowym, tak jak to ma miejsce w falowodzie prostokątnym, mogą rozchodzić się rodzaje pola elektromagnetycznego typu E (TM) i H (TE). Dowolne pole elektromagnetyczne występujące w tym falowodzie można przedstawić jako superpozycję wymienionych rodzajów. | |||
Opis matematyczny pola elektromagnetycznego w przekroju poprzecznym falowodu kołowego, który analizujemy w cylindrycznym układzie współrzędnych, jest inny niż dla falowodu prostokątnego i jest to konsekwencja innego kształtu przekroju poprzecznego prowadnicy. Rodzaje pola w falowodzie kołowym oznaczamy jako <math>E_{mn}\,</math> i <math>H_{mn}\,</math>. Liczby naturalne m i n to wskaźniki (indeksy) rodzaju. Z rozwiązania równania Helmholtz’a we współrzędnych cylindrycznych z uwzględnieniem warunków brzegowych wynika, że zmiany składowej z wektora pola elektrycznego (rodzaje typu E), a także wektora pola magnetycznego (rodzaje typu H) w płaszczyźnie poprzecznej do kierunku rozchodzenia się fali (płaszczyzna <math>\rho \varphi</math>) są zgodne z funkcją Bessela m-tego rzędu wzdłuż promienia (zmienna <math>\rho</math>) oraz następują według funkcji cosinus ze zmianą kąta (zmienna <math>\varphi\,</math>). | |||
Dla rodzaju Emn składowa Ez przyjmuje wartość równą zeru na ściankach falowodu i w płaszczyźnie <math>\rho \varphi</math>) (dla z = 0) jest proporcjonalna do wyrażenia <math>J_m\left (\frac{\kappa_{mn}}{a}\right)cos(m\varphi)</math> , przy czym <math>J_m</math> to funkcja Bessela pierwszego rodzaju m-tego rzędu, a <math>\kappa_m</math> to n-ty pierwiastek tej funkcji. Natomiast dla rodzaju <math>H_{mn}</math> składowa <math>H_z</math> osiąga maksimum na ściankach falowodu i w płaszczyźnie z = 0 jest proporcjonalna do wyrażenia <math>J_m\left (\frac{\kappa'_{mn}}{a}\right)cos(m\varphi)</math> , gdzie <math>\kappa'</math> to n-ty pierwiastek pierwszej pochodnej funkcji <math>J_m</math>. Znając składową z, pozostałe składowe pola elektromagnetycznego wyznaczamy korzystając z równań Maxwella. | |||
W oparciu o powyżej przedstawione zależności możemy zauważyć, że wskaźnik m rodzaju pola oznacza rząd funkcji Bessela oraz liczbę całkowitych okresów funkcji funkcji cosinus, a wskaźnik n określa numer pierwiastka funkcji <math>J_m</math> (dla rodzajów E) albo pierwszej pochodnej tej funkcji (dla rodzajów H). | |||
W falowodzie kołowym rozkłady pola elektromagnetycznego rodzajów, dla których wskaźnik m jest równy zeru charakteryzują się symetrią osiową (względem osi 0z) bo pola nie zależą od zmiennej <math>\varphi\,</math>. | |||
|} | |} | ||
| Linia 477: | Linia 494: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd29.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd29.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Tak jak to ma miejsce w falowodzie prostokątnym, dla danego rodzaju pola w falowodzie kołowym rozchodzącego się w kierunku +0z, zależność wszystkich występujących w nim składowych pól elektrycznego i magnetycznego wzdłuż kierunku propagacji jest opisana przez czynnik <math>exp(–\gamma_zz), przy czym <math>\gamma_z\,</math> to współczynnik propagacji fali wzdłuż osi z. Współczynnik ten określa się w oparciu o równanie dyspersyjne, które pokazane jest na slajdzie. | ||
Rola i znaczenie granicznego współczynnika fazy <math>\beta_g\,</math> dla falowodu kołowego są analogiczne jak to miało miejsce dla falowodu prostokątnego, a istotna różnica między tymi falowodami polega na sposobie obliczania tej wielkości. Zależności, według których wyznaczamy <math>\beta_g\,</math> dla zadanych rodzajów pola w falowodzie kołowym są podane i opisane na slajdzie. Zaznaczyć należy, że w falowodzie kołowym graniczne współczynniki fazy nie mają tej samej wartości dla rodzajów E i H o identycznych wskaźnikach m, n. | |||
|} | |} | ||
| Linia 485: | Linia 504: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd30.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd30.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Przypomnijmy, że częstotliwość graniczna rodzaju o wskaźnikach m, n w bezstratnym falowodzie kołowym to taka częstotliwość, dla której o współczynnik propagacji γz tego rodzaju jest równy zeru. Jest ona powiązana z granicznym współczynnikiem fazy oraz parametrami ośrodka wypełniającego falowód. Fala elektromagnetyczna określonego rodzaju rozchodzi się w falowodzie dla częstotliwości większych od częstotliwości granicznej. | ||
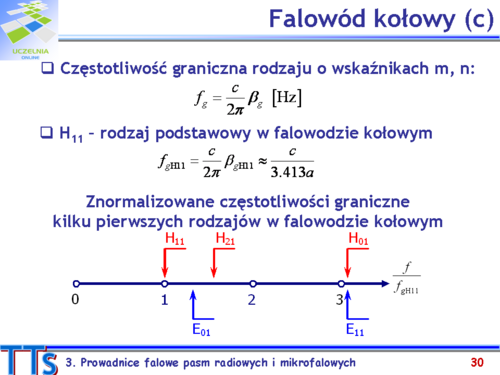
Wśród pierwiastków, tak funkcji Bessela pierwszego rodzaju jak i pierwszej pochodnej tych funkcji, najmniejszą wartość ma pierwszy pierwiastek pochodnej funkcji <math>J_1\,</math> <math>\kappa'_{11}=1.811</math> . Oznacza to, że najmniejszy graniczny współczynnik fazy, a tym samym i najmniejsza częstotliwość graniczna, odpowiada rodzajowi <math>H_{11}\,</math>, który jest rodzajem podstawowym w falowodzie kołowym. | |||
Na slajdzie pokazano graficznie rozkład częstotliwości granicznych znormalizowanych do częstotliwości granicznej rodzaju podstawowego dla kilku pierwszych rodzajów wzbudzanych w falowodzie kołowym. Warto zauważyć, że pasmo pracy falowodu kołowego (gdy rozchodzi się tylko rodzaj podstawowy) wynosi około 25% i jest znacznie mniejsze niż dla falowodu prostokątnego. | |||
Znając częstotliwość graniczną zadanego rodzaju pola w falowodzie kołowym możemy wyznaczyć jego współczynnik propagacji posługując się zależnościami podanymi wcześniej dla falowodu prostokątnego (slajd 20). Przypomnijmy, że poniżej częstotliwości granicznej współczynnik propagacji dowolnego rodzaju pola w bezstratnym falowodzie kołowym jest wielkością rzeczywistą, czyli staje się współczynnikiem tłumienia. Natomiast dla częstotliwości większych niż częstotliwość graniczna współczynnik propagacji jest urojony, a jego wartość to współczynnik fazy. Wiemy także, że znając współczynnikiem fazy można określić długość fali w falowodzie oraz prędkości fazową i grupową, a przedstawione wcześniej zależności dla falowodu prostokątnego są słuszne również dla falowodu kołowego. Także częstotliwościowe charaktrystyki współczynnika propagacji i prędkości prezentowane przy omawianiu falowodu prostokątnego oddają jakościowe zmiany tych parametrów z częstotliwością dla rodzajów pola falowodu kołowego. Podsumowując, parametry pola elektromagnetycznego w falowodach prostokątnym i kołowym są identycznie definiowane i jedyną różnicą jest sposób oblicznia granicznego współczynnika fazy. Natomiast rozkłady pól poszczególnych rodzajów pola elektromagnetycznego są zdecydowanie różne. | |||
|} | |} | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd31.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd31.png|thumb|500px]] | ||
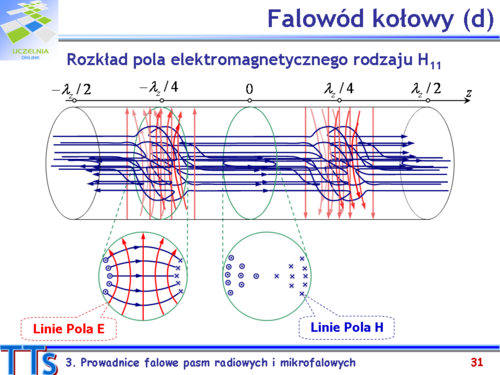
|valign="top"| | |valign="top"|Na slajdzie przedstawiono konfigurację linii sił pól elektrycznego i magnetycznego rodzaju podstawowego w bezstratnym falowodzie kołowym dla fali rozchodzącej się w kierunku +0z w chwili t = 0. Jest to graficzna ilustracja rzeczywistych wektorów pól rodzaju <math>H_{11}\,</math> o następujących składowych: | ||
:<math>H_z(\rho,\varphi, z,t)=H_{z0}J_1(\beta_{gH11}\rho)cos\varphi cos(\omega t-\beta_z z)</math> | |||
:<math>H_{\rho}(\rho,\varphi, z,t)=-\frac{\beta_z}{\beta_{gH11}}H_{z0}J'_1(\beta_{gH11}\rho)cos\varphi sin(\omega t-\beta_z z)</math> | |||
:<math>H_{\varphi}(\rho,\varphi, z,t)=-\frac{\beta_z}{\rho \beta_{gH11}}H_{z0}J_1(\beta_{gH11}\rho)sin\varphi sin(\omega t-\beta_z z)</math> | |||
:<math>E_{\rho}(\rho,\varphi, z,t)=-\frac{Z\beta_z}{\rho \beta^2_{gH11}}H_{z0}J_1(\beta_{gH11}\rho)sin\varphi sin(\omega t-\beta_z z)</math> | |||
:<math>E_{\varphi}(\rho,\varphi, z,t)=-\frac{Z\beta_z}{\\beta_{gH11}}H_{z0}J'_1(\beta_{gH11}\rho)cos\varphi sin(\omega t-\beta_z z)</math> | |||
gdzie <math>\beta_{gH11}=\frac{\kappa'_{11}}{a}=\frac{1.811}{a}</math> , <math>J_1\,</math> to funkcja Bessela pierwszego rodzaju rzędu 1, a <math>J'_1\,</math> – pierwsza pochodna tej funkcji, Z to impedancja właściwa ośrodka wypełniającego falowód. | |||
Wyrażenia określające składowe pól rodzaju <math>H_{11}\,</math> wskazują, że spełnione są warunki brzegowe na ściance falowodu (dla <math>\rho = a</math>), czyli zerowanie składowych <math>E_{\varphi}\,</math> i <math>H_{\rho}</math>. Ze składową <math>E_{\rho}</math> związane są powierzchniowe ładunki elektryczne, a składowe <math>H_z</math> i <math>H_{\varphi}</math> określają gęstości prądów powierzchniowych. Związki między polami a ładunkami i prądami na powierzchni przewodnika omówiono szczegółowo dla falowodu prostokątnego. Poprzestaniemy tu na stwierdzeniu, że analogiczne relacje dotyczą falowodu kołowego. | |||
Falowody kołowe znalazły zastosowanie w systemach antenowych oraz w konstrukcjach niektórych tłumików, rezonatorów i filtrów (będzie o tym mowa w jednym z dalszych wykładów). | |||
|} | |} | ||
| Linia 499: | Linia 539: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd32.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd32.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Mikrofalowe systemy, układy i elementy budowane do końca lat czterdziestych oparte były na linii współosiowej oraz falowodzie prostokątnym. Elementami aktywnymi w ówczesnych konstrukcjach były prawie wyłącznie mikrofalowe lampy elektronowe, a jedynym przyrządem półprzewodnikowym była krzemowa dioda ostrzowa. | ||
Zapoczątkowany w latach pięćdziesiątych burzliwy rozwój techniki półprzewodnikowej, doskonalenie technologii materiałów elektronicznych oraz wprowadzenie do obwodów mikrofalowych linii paskowych w zasadniczy sposób wpłynęły na metody realizacji elementów i układów pracujących powyżej częstotliwości 300 MHz. Diody półprzewodnikowe i tranzystory wypierają lampy elektronowe z elementów pasm mikrofalowych i milimetrowych, co pozwala uzyskać - obok zredukowanej mocy zasilania - ich większą niezawodność i trwałość. Stosując linię mikropaskową w miejsce falowodu prostokątnego czy linii współosiowej uzyskuje się znaczne zmniejszenie wymiarów oraz ciężaru pasywnych i aktywnych elementów. W rezultacie prac prowadzonych nad połączeniem poszczególnych elementów mikrofalowych w konkretne, pewnie działąjące urządzenie powstają hybrydowe, a następnie monolityczne mikrofalowe układy scalone. | |||
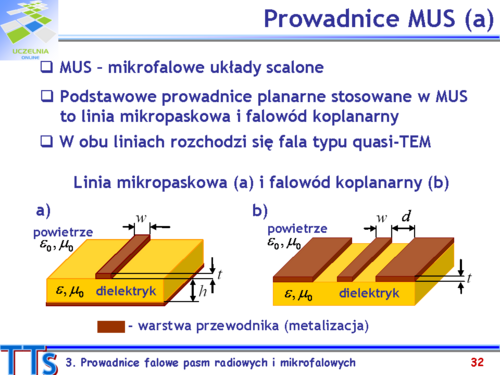
Linia mikropaskowa stała się podstawową prowadnicą mikrofalowych układów scalonych (MUS) pracujących w pasmach decymetrowych i centymetrowych. Falowód koplanarny, który opracowano pod koniec lat sześćdziesiątych, znalazł zastosowanie w monolitycznych układach scalonych dzięki łatwości integrowania z przyrządami półprzewodnikowymi. | |||
W dobie łączy światłowodowych, sygnałów nie przesyła się na duże odległości prowadnicami falowymi. Z punktu widzenia miejsca występowania prowadnicy można wyróżnić dwie grupy linii transmisyjnych: wewnętrzne i zewnętrzne. | |||
Do prowadnic zewnętrznych, które występują pomiędzy elementami czy podzespołami w przyrządach i systemach funkcjonalnych lub pomiarowych, należy zaliczyć linię współosiową oraz falowód prostokątny. Podstawowe prowadnice wewnętrzne, które znajdują się w hybrydowych i monolitycznych mikrofalowych układach scalonych (HMUS i MMUS), to linia mikropaskowa i falowód koplanarny. | |||
Struktury obu planarnych prowadnic falowych przedstawiono na slajdzie. W linii mikropaskowej występują przewodniki po obu stronach warstwy dielektryka o grubości h. Po jednej stronie dielektrycznego podłoża jest pasek metalizacji o szerokości w i grubości t, a drugą stronę pokrywa płaszczyzna przewodząca. Falowód koplanarny jest określany mianem prowadnicy uniplanarnej ponieważ metalizacja występuje po jednej stronie podłoża. Formuje ona trzy obszary przewodzące: pasek oraz dwie półpłaszczyzny, które są symetrycznie odsunięte od paska o szerokość szczelin d. | |||
Fala elektromagnetyczna prowadzona w linii mikropaskowej albo falowodzie koplanarnym występuje w dielektryku oraz w powietrzu, czyli ośrodkach o różnych przenikalnościach elektrycznych. Nie może zatem być falą typu TEM, dla której prędkość rozchodzenia się fali jest ściśle określona przez parametry ośrodka. W oparciu o pierwsze dwa równania Maxwella można wykazać, że spełnienie warunków brzegowych na granicy dwóch dielektryków występujących w omawianych prowadnicach wymaga istnienia składowych wzdłużnych tak pola elektrycznego jak i magnetycznego. | |||
W linii mikropaskowej, prowadnicy mającej dwa przewody, występuje jeden, podstawowy rodzaj pola elektromagnetycznego o zerowej częstotliwości granicznej. Rodzaj ten nie jest czystą falą TEM (ma składowe wzdłużne pól elektrycznego i magnetycznego) i określany jest mianem quasi-TEM. Stosunek składowych poprzecznych do składowych wzdłużnych zmienia się z częstotliwością. W rezultacie prędkość fazowa nie jest stała w funkcji częstotliwości. Mamy więc do czynienia z nieznaczną dyspersją rodzaju podstawowego tej prowadnicy. | |||
W strukturze falowodu koplanarnego mamy trzy przewody i linia ta ma dwa rodzaje pola z zerową częstotliwością graniczną, tzw. rodzaj parzysty i rodzaj nieparzysty. Dla rodzaju nieparzystego pola elektryczne w szczelinach skierowane są w przeciwne strony, a w tę samą stronę dla rodzaju nieparzystego. Rodzaj nieparzysty, typu quasi-TEM, jest rodzajem podstawowym, pożądanym w transmisji mocy fali. Jest to rodzaj z stosunkowo małą dyspersją. Rodzaj parzysty jest rodzajem pasożytniczym. Aby go wyeliminować półpłaszczyzny przewodzące winny mieć ten sam potencjał. W mikrofalowych układach scalonych z falowodem koplanarnym wytwarza się mostki przewodzące zwierające w określonych odstępach metalizacje boczne prowadnicy. Konieczność stosowania mostków jest komplikacją technologiczną. | |||
|} | |} | ||
| Linia 508: | Linia 563: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd33.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd33.png|thumb|500px]] | ||
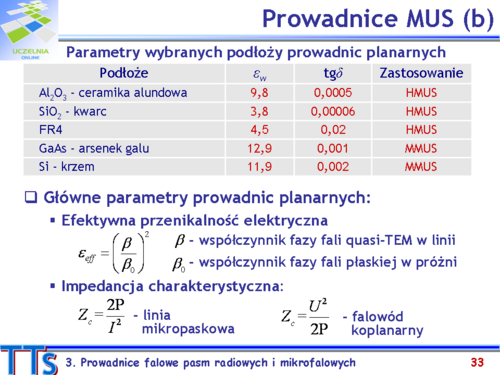
|valign="top"| | |valign="top"|W tabeli pokazano parametry dielektryczne typowych dielektryków stosowanych w technice planarnych prowadnic falowych. | ||
Wśród dielektryków stosowanych w hybrydowych mikrofalowych układach scalonych jedną z najbardziej popularnych jest ceramika alundowa. Ceramika ta ze względu na swoje bardzo małe straty, niski współczynnik rozszerzalności temperaturowej oraz dobre przewodnictwo cieplne szczególnie dobrze nadaje się do układów oscylatorów i wzmacniaczy. Stosunkowo duża wartość względnej przenikalności elektrycznej ceramiki alundowej sprawia, że bardzo dobrze nadaje się do układów pracujących w pasmach decymetrowych i centymetrowych. W zakresie fal milimetrowych używane są podłoża o znacznie mniejszych <math>\varepsilon_w</math>, np. materiał RT/Duroid 5880 o <math>\varepsilon_w = 2.22</math>. Najtańszym podłożem jest FR4, laminat szklano-epoksydowy, który ze względu na duże straty można stosować w układach pracujących na pojedynczych gigahertzach. Do wytwarzania obwodów HMUS stosuje się klasyczną metodę fotolitografii. | |||
Podłoża półprzewodnikowe, czyli arsenek galu oraz krzem, występują w monolitycznych mikrofalowych układach scalonych. Straty tych materiałów są większe niż niskostratnych podłoży dielektrycznych. W konsekwencji, współczynniki tłumienia prowadnic na podłożach półprzewodnikowych są odpowiednio większe niż analogicznych prowadnic z dobrymi dielektrykami. Nie jest to istotne ograniczenie dla zastosowań prowadnic planarnych na podłożach półprzewodnikowych ponieważ długości prowadnic w układach MMUS są rzędu pojedynczych milimetrów, podczas gdy w układach HMUS mamy znacznie dłuższe odcinki prowadnic. Wielką zaletą układów monolitycznych jest wykonanie całego układu (prowadnice, elementy bierne i aktywne) w trakcie procesu technologicznego właściwego dla typu zastosowanych tranzystorów. | |||
Przypomnijmy, że prowadnicę falową, dla jej podstawowego rodzaju pola elektromagnetycznego, charakteryzują dwa podstawowe parametry współczynnik propagacji oraz impedancja charakterystyczna. | |||
Dla linii mikropaskowej i falowodu koplanarnego definiujemy efektywną przenikalność elektryczną, która jest równa kwadratowi znormalizowanego współczynnika fazy fali quasi-TEM do współczynnika fazy fali płaskiej w próżni. Wartość tego parametru dla linii mikropaskowej jest większa niż dla falowodu koplanarnego ponieważ pole elektromagnetyczne fali w linii mikropaskowej znajduje się głównie w dielektryku. Dokładne wyznaczenie efektywnej przenikalności elektrycznej fali quasi-TEM w danej prowadnicy wiąże sie z rozwiązaniem równań Maxwella dla tej linii przy określonych warunkach brzegowych i jest dosyć skomplikowanym zagadnieniem matematycznym tak dla linii mikropaskowej jak i falowodu koplanarnego. W literaturze dotyczącej prowadnic planarnych można znaleść szereg przybliżonych zależności analitycznych dla <math>\varepsilon_{eff}</math>, które z wystarczającą dla celów projektowych dokładnością pozwalają obliczyć ten parametr dla każdej z dwu omawianych linii transmisyjnych. Zaznaczyć należy, że <math>\varepsilon_{eff}</math> jest funkcją względnej przenikalności elektrycznej podłoża, wymiarów geometrycznych (dla linii mikropaskowej są to: grubość podłoża, szerokość i grubość paska) oraz częstotliwości. Zależność od częstotliwości nie jest zbyt silna i zazwyczaj zmiana wartości εeff nie przekracza kilkunastu procent w całym pasmie pracy prowadnicy. | |||
Głównym obwodowym parametrem prowadnicy falowej jest impedancja charakterystyczna. Precyzyjne wyznaczenie mocy fali oraz napięcia i prądu w prowadnicy jest możliwe gdy znamy rozkłady pól fali quasi-TEM, co jest dla linii mikropaskowej i falowodu koplanarnego złożonym i trudnym zadaniem. Pamiętamy, że impedancję charakterystyczną można definiować na trzy sposoby. Dla linii mikropaskowej najczęściej stosujemy definicję opartą na mocy fali i prądzie w pasku płynącym wzdłuż kierunku rozchodzenia się fali. Stwierdzono, że tak zdefiniowana impedancja charakterystyczna linii mikropaskowej najsłabiej zależy od częstotliwości. W przypadku falowodu koplanarnego posługujemy się z reguły imedancją charakterystyczną obliczoną na bazie mocy i napięcia w jednej ze szczelin. Analityczne wzory empiryczne dla impedancji charakterystycznych obu prowadnic można znaleść w literaturze. Realizowane impedancje charakterystyczne planarnych prowadnic zawierają się w szerokich granicach: | |||
20 – 100 <math>\Omega\,</math> dla linii mikropaskowej i 25 – 150 <math>\Omega\,</math> dla falowodu koplanarnego. | |||
Dla potrzeb technologii mikrofalowych układów scalonych opracowano techniki wytwarzania planarnych rezystorów, kondensatorów, cewek indukcyjnych, a także diod i tranzystorów. W HMUS elementy te montowane są na powierzchni układu, a łączą je odcinki prowadnic falowych. W MMUS wszystkie elementy, łącznie z prowadnicami falowymi wykonuje się w procesach technologicznych na podłożu krzemu lub arsenku galu. | |||
|} | |} | ||
| Linia 516: | Linia 584: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd34.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd34.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Dotychczas, omawiając prowadnice falowe zakładaliśmy, że przewodniki występujące w ich strukturach są idealne i nie powodują tłumienia mocy rozchodzących się fal. Rzeczywiste przewodniki, o dużej ale skończonej konduktywności, są źródłem strat mocy. Wiemy już, że w wyniku istnienia strat dielektrycznych następuje tłumienie fali elektromagnetycznej prowadzonej w linii transmisyjnej. Trzecim źródłem strat mocy fali jest zjawisko promieniowania. Występuje ono w strukturach otwartych, którymi są wśród omawianych prowadnic linia mikropaskowa i falowód koplanarny. Intensywność promieniowania rośnie ze wzrostem częstotliwości. Straty wywołane promieniowaniem są trudne do oszacowania i nie będą tutaj omawiane. | ||
Straty występujące w przewodnikach i dielektryku sumują się i współczynnik tłumienia fali w prowadnicy możemy wyrazić jako superpozycję współczynników tłumienia wynikających z obydwu źródeł strat. | |||
|} | |} | ||
| Linia 524: | Linia 593: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd35.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd35.png|thumb|500px]] | ||
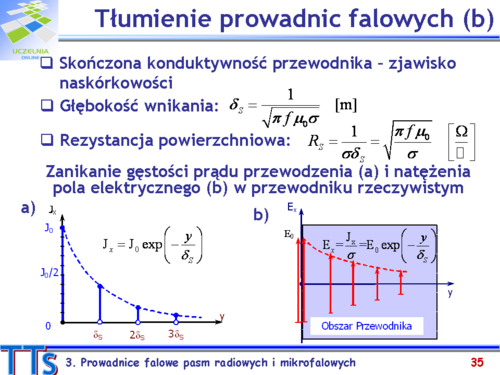
|valign="top"| | |valign="top"|W prowadnicy falowej z idealnymi przewodnikami występuje na granicy dielektryk – metal składowa styczna pola magnetycznego i zgodnie z warunkami brzegowymi związany z nią prąd powierzchniowy. Dla rzeczywistego przewodnika składowa styczna pola magnetycznego jest ciągła na granicy dielektryk – metal, nie ma prądu powierzchniowego, pole magnetyczne wnika w przewodnik i jest związane z przestrzennym prądem przewodzenia zgodnie z drugim prawem Maxwella (prąd przesunięcia możemy zaniedbać). Prąd ten związany jest również z natężeniem pola elektrycznego według prawa Ohma: <math>\vec{J}=\sigma\vec{E}</math> . W rezultacie powstaje fala elektro-magnetyczna kierująca się w głąb przewodnika. Ze względu na bardzo silne tłumienie fali, pole wnika w przewodnik na niewielką głebokość. Zjawisko to nazywa się naskórkowością. Miarą tego zjawiska jest wielkość zwana głębokością wnikania, której wartość równa jest drodze, na której amplituda fali maleje e-krotnie. Oznacza to, że na długości równej głębokości wnikaniae-krotnie zmaleją amplitudy tak gęstości prądu przewodzenia jak i natężeń pól elektrycznego i magnetycznego. Dla przykładu, głębokość wnikania dla miedzi fali o częstotliwości 10 GHz wynosi <math>0.66\mu m</math>. | ||
Do obliczania tłumienia fali w prowadnicy falowej wywołanej stratami w przewodnikach wygodnie jest wprowadzić pojęcie rezystancji powierzchniowej, która jest w prosty sposób powiązana z głębokością wnikania. Dla tej rezystancji tradycyjnie używamy jednoski Ohm na kwadrat, przy czym „kwadrat” jest bezwymiarowy i podkreśla jedynie, że pojęcie związane jest z cienką warstwą materiału. Łatwo sprawdzić, że wartość rezystancji powierzchniowej jest równa części rzeczywistej impedancji właściwej metalu. | |||
|} | |} | ||
| Linia 532: | Linia 602: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd36.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd36.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Współczynnik tłumienia fali w prowadnicy związany ze stratami w przewodniku <math>\alpha_m</math> jest wprostproporcjonalny do rezystancji powierzchniowej materiału, z którego wykonano warstwy przewodzące. Zauważmy, że rezystancja powierzchniowa wzrasta proporcjonalnie do pierwiastka kwadratowego z częstotliwości. We wzorze pokazanym na slajdzie wprowadzono pewną ogólną funkcję <math>F_m</math>, której postać zależy od rozważanej prowadnicy z uwzględnieniem rodzaju pola elektromagnetycznego. Dla linii współosiowej z falą TEM wartość <math>F_m</math> zależy od impedancji charakterystycznej (<math>Z_c</math>) i promieni przewodów linii, a nie zmienia się z częstotliwością. Natomiast, w przypadku falowodu prostokątnego z rodzajem H10 Fm jest dodatkowo funkcją częstotliwości. | ||
Współczynnik tłumienia można wyrazić w Neperach na metr albo z decybelach na metr. Związek między tymi jednostkami, który wynika z defincji Nepera i decybela, jest dla współczynnika tłumienia następujący: | |||
:<math>\alpha\left[\frac{dB}{m}\right]=20lge\cdot \alpha \left[\frac{Np}{m}\right]=8.686\alpha \left[\frac{Np}{m}\right]</math> | |||
Współczynnik tłumienia fali wynikający ze strat dielektrycznych αd można przedstawić w formie analogicznej do postaci współczynnika αm. W tym przypadku, niezależnie od rodzaju pola i prowadnicy, współczynnik tłumienia jest wprostproporcjonalny do tangensa kąta stratności dielektryka. Komentarz dotyczący funkcji <math>F_d</math> można sformułować podobnie jak dla funkcji <math>F_m</math>. Warto zwrócić uwagę na prostotę funkcji <math>F_d</math> dla linii współosiowej oraz na fakt, że <math>\alpha_d</math> rośnie liniowo z częstotliwością. | |||
|} | |} | ||
| Linia 540: | Linia 616: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd37.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd37.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Na rysunku pokazano częstotliwościowe charakterystyki współczynnika tłumienia rodzajów podstawowych pola elektromagnetycznego w omawianych prowadnicach falowych. Uwzględniono straty dielektryczne oraz straty w przewodnikach. | ||
Dla linii mikropaskowej i falowodu koplanarnego wybrano ceramikę alundową (<math>\varepsilon_w = 9.8</math>, | |||
<math>tg\delta = 0.0005</math>) o grubości h = 0.508 mm oraz warstwy miedzi (<math>\sigma = 5.88\cdot 10^7 S/m</math>) o grubości <math>t = 35\mu m</math>. Przyjęto, że obie prowadnice mają mieć zbliżone impedancje charakterystyczne równe ok. <math>50 \Omega</math> dla częstotliwości 10 GHz. Przy powyższych założeniach dla linii mikropaskowej szerokość paska wynosi w = 0.5 mm. Dla falowodu koplanarnego wybrano tę samą szerokość paska w = 0.5 mm i wyznaczono szerokość obu szczelin, która wynosi d = 0.225 mm. Współczynniki tłumienia obu prowadnic są prawie identyczne w całym zakresie częstotliwości. Falowód koplanarny tłumi nieco bardziej falę dla niskich i średnich częstotliwości. Zauważmy, że nachylenie charakterystyk tłumienia obu prowadnic zmienia się nieznacznie z częstotliwością. Dla niskich częstotliwości dominują straty w przewodnikach wzrastające proporcjonalnie do <math>\sqrt{f}</math> . Dla wysokich częstotliwości straty dielektryczne, które rosną proporcjonalnie do f, są porównywalne ze stratami w przewodnikach i w rezultacie wzrasta nachylenie charakterystyki tłumienia. | |||
W linii współosiowej o impedancji charakterystycznej równej 50 Ω, dla której wyznaczono współczynnik tłumienia, przestrzeń między przewodami z miedzi o promieniach a = 1.75 mm i b = 0.502 mm wypełniona jest teflonem o <math>\varepsilon_w = 2.1</math> i <math>tg\delta = 0.0005</math>. Tłumienie linii współosiowej jest wyraźnie mniejsze niż planarnych prowadnic. | |||
Na rysunku pokazano również charakterystyki tłumienia rodziny standardowych falowodów prostokątnych wypełnionych powietrzem w ich pasmach pracy. Przy charakterystykach podano stosowane powszechnie oznaczenia falowodów. Przyjęto, że falowody od WR-1000 do WR-62 wykonane są z aluminium (<math>\sigma = 3.58\cdot 10^7 S/m</math>), a pozostałe ze srebra (<math>\sigma = 6.14\cdot 10^7 S/m</math>). Współczynniki tłumienia fali <math>H_{10}</math> w falowodach maleją w funkcji częstotliwości. Jest to spowodowane tym, że przy ustalonej wartości mocy przenoszonej przez falowód ze wzrostem częstotliwości zmniejsza się wartość składowej <math>H_z\,</math>, a więc i wartość prądów w ściankach, które wywołują straty mocy. W pasmie pracy falowodu zjawisko to jest silniejsze niż wzrost strat wywołany naskórkowością. Z prezentowanych prowadnic falowody mają wyrażnie najniższe straty. | |||
|} | |} | ||
| Linia 548: | Linia 630: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M3_Slajd38.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M3_Slajd38.png|thumb|500px]] | ||
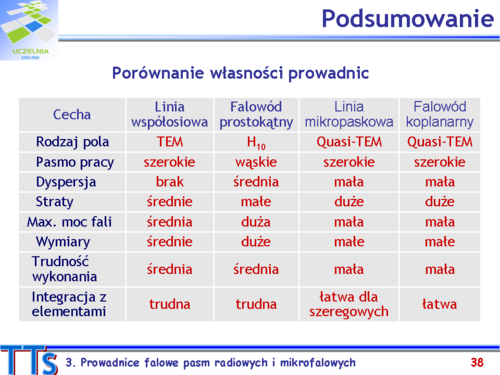
|valign="top"| | |valign="top"|W podsumowaniu jakościowo porównano własności prezentowanych prowadnic falowych. | ||
Tytułem komentarza należy dodać, że dla odpowiednio dużej częstotliwości w linii współosiowej poza rodzajem TEM mogą rozchodzić się również rodzaje falowodowe, z których każdy ma określoną częstotliwość graniczną. Z tego względu pasmo pracy tej prowadnicy falowej nie jest nieograniczone i rozciąga się od DC do częstotliwości o kilka procent niższej od wartości częstotliwości granicznej pierwszego rodzaju falowodowego w linii współosiowej, którym jest rodzaj <math>H_{11}</math>. Przykładowo, dla wypełnionej powietrzem linii współosiowej o promieniach 3.5 mm i 1.5 mm pasmo pracy wynosi od 0 do 18 GHz. Również w linii mikropaskowej i falowodzie koplanarnym mogą rozchodzić się falowodowe rodzaje | |||
i ograniczają one pasma pracy tych prowadnic. | |||
|} | |} | ||
| Linia 604: | Linia 690: | ||
#Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8. | #Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8. | ||
#Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3. | #Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3. | ||
#Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2 | #Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2</math>. | ||
Aktualna wersja na dzień 10:45, 5 wrz 2023
Wykład
Pytania sprawdzające
(jeśli potrafisz na nie odpowiedzieć, to znaczy, że opanowałeś/aś materiał wykładu)
- Wymień i scharakteryzuj najważniejsze parametry prowadnicy falowej.
- Przypomnij sobie jakie mody mogą rozchodzić się w falowodach i scharakteryzuj je.
- Co to jest dyspersja, w jakich warunkach i dlaczego dyspersja utrudnia transmisję sygnału.
- Przeanalizuj przyczyny powstawania strat przy transmisji mocy prowadnicami falowymi.
- Na czym polega efekt naskórkowości?
- Opisz kolejno prowadnice typu TEM.
- Narysuj konfigurację pól E i H dla modu podstawowego i naszkicuj kierunki przepływu prądów w ściankach falowodu prostokątnego.
- Dlaczego nie stosujemy falowodów prostokątnych, dla których stosunek a/b=1?
- W jakim pasmie częstotliwości może pracować falowód prostokątny?
- W jakim pasmie może pracować falowód cylindryczny?
- Jak uzasadnisz fakt, że obwodem zastępczym odcinka falowodu prostokątnego jest odcinek linii dwuprzewodowej?
- Jak zbudowana jest i jakie ma właściwości prowadnica mikropaskowa?
- Jak zbudowana jest i jakie ma właściwości linia koplanarna?
- Jakie są obszary zastosowań linii współosiowej, linii mikropaskowej i falowodu prostokątnego? Aby to uzasadnić porównaj parametry wymienionych typów prowadnic.
- Wymień argumenty przemawiające za rozwojem technologii i konstrukcji Mikrofalowych Monolitycznych Układów Scalonych na krzemie i arsenku galu.
Słownik
Częstotliwość graniczna - częstotliwość powyżej której może się propagować fala w falowodzie. Poniżej tej częstotliwości fala jest silnie tłumiona.
Zestawienie typów fal:
- Fala typu TEM - wektory pola E i H leżą w płaszczyźnie prostopadłej do kierunku propagacji.
- Fala typu TE (zwana też H) - pole E posiada składowe tylko w płaszczyźnie prostopadłej do kierunku propagacji. Pole H posiada składowe w kierunku propagacji fali.
- Fala typu TM (zwana też E) - pole H posiada składowe tylko w płaszczyźnie prostopadłej do kierunku propagacji. Pole E posiada składowe w kierunku propagacji fali.
- Fala typu EH - zarówno pole E jak i pole H tej fali posiadają składowe w kierunku propagacji.
Linie TEM:
- Linia współosiowa.
- Linia dwuprzewodowa.
- Symetryczna linia paskowa.
Linie Quasi-TEM:
- Niesymetryczna linia paskowa:
- Linia koplanarna (falowód koplanarny).
- Linia koplanarna paskowa.
Linie falowodowe:
- Falowód prostokątny. Mod podstawowy typu TE10 (H10).
- Falowód kołowy (cylindryczny). Mod podstawowy typu TE11 (H11).
Mod (rodzaj) podstawowy dla danego falowodu - to mod fali o najmniejszej
Bibliografia
- Bogdan Galwas. Miernictwo mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1985, Rozdział 1, 2 i 3.
- Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8.
- Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3.
- Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2</math>.