GKIW Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 3 wersji utworzonych przez 2 użytkowników) | |||
| Linia 95: | Linia 95: | ||
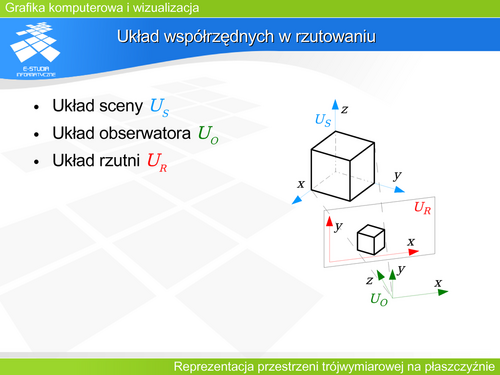
Rozpatrzmy rzutowanie perspektywiczne w przestrzeni obserwatora. Współrzędne opisują położenie w lewoskrętnym układzie współrzędnych obserwatora 0XYZ. | Rozpatrzmy rzutowanie perspektywiczne w przestrzeni obserwatora. Współrzędne opisują położenie w lewoskrętnym układzie współrzędnych obserwatora 0XYZ. | ||
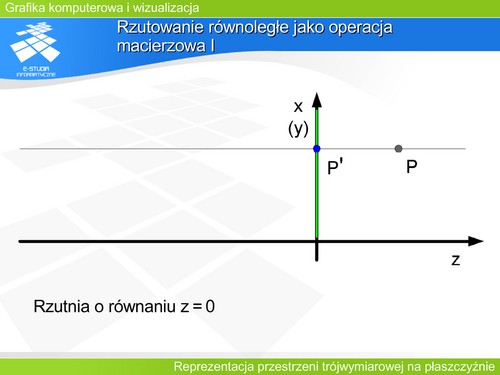
Niech obserwator (środek rzutowania) znajduje się w punkcie <math>(0,0,-d)</math> dla <math>d>0</math> a płaszczyzna rzutni ma równanie <math>z=0\ | Niech obserwator (środek rzutowania) znajduje się w punkcie <math>(0,0,-d)</math> dla <math>d>0</math> a płaszczyzna rzutni ma równanie <math>z=0\ </math>, - jak na rysunku. Macierz rzutowania będzie wtedy miała postać: | ||
:<math>M_{RP1}=\begin{bmatrix} | :<math>M_{RP1}=\begin{bmatrix} | ||
| Linia 111: | Linia 111: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M5_Slajd_8.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M5_Slajd_8.png|thumb|500px]] | ||
|valign="top"|Warto zwrócić uwagę na to, że macierz <math>M_{RP1}\ | |valign="top"|Warto zwrócić uwagę na to, że macierz <math>M_{RP1}\ </math>, definiuje operację wymagającą normalizacji. | ||
|} | |} | ||
| Linia 121: | Linia 121: | ||
|valign="top"|Rzutowanie perspektywiczne można również prosto zdefiniować w nieco inny sposób. | |valign="top"|Rzutowanie perspektywiczne można również prosto zdefiniować w nieco inny sposób. | ||
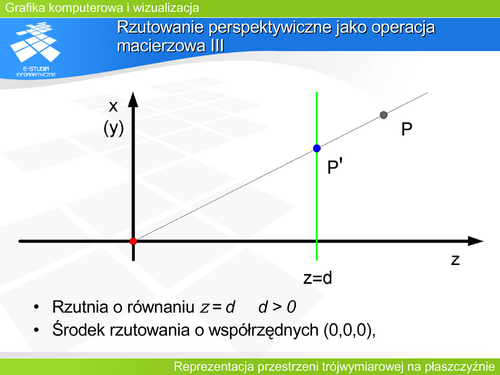
Niech w analogicznym układzie współrzędnych obserwator (środek rzutowania) znajduje się w początku układu współrzędnych, a rzut jest dokonywany na płaszczyznę <math>z=d\ | Niech w analogicznym układzie współrzędnych obserwator (środek rzutowania) znajduje się w początku układu współrzędnych, a rzut jest dokonywany na płaszczyznę <math>z=d\ </math>, dla <math>d>0</math> (rysunek). Rzutem punktu P o współrzędnych <math>(x_P, y_P, z_P )</math> będzie punkt <math>P'\ </math>, o współrzędnych <math>(x'_P, y'_P, z'_P )</math> , który zgodnie z definicją rzutu perspektywicznego będzie należał do płaszczyzny rzutni i jednocześnie do prostej przechodzącej przez środek rzutowania i punkt . Uwzględniając proste zależności geometryczne można pokazać, że macierz opisująca tak zdefiniowane rzutowanie perspektywiczne ma następującą postać: | ||
:<math>M_{RP2}=\begin{bmatrix} | :<math>M_{RP2}=\begin{bmatrix} | ||
| Linia 178: | Linia 178: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M5_Slajd_15.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M5_Slajd_15.png|thumb|500px]] | ||
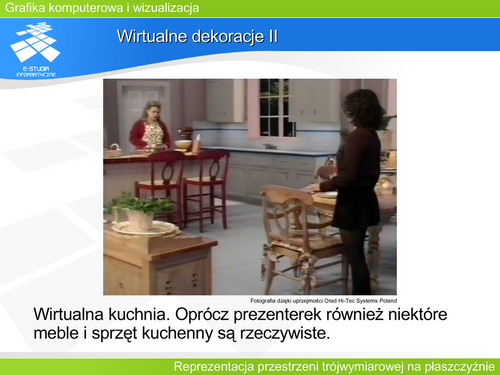
|valign="top"| | |valign="top"|Patrząc na rzutowanie poprzez analogię do aparatu fotograficznego warto zwrócić uwagę na parametry decydujące o obrazie, który powstanie. Fotograf, wybierając temat do zdjęcia, określa położenie aparatu i kierunek fotografowania. Określa także ogniskową obiektywu (funkcja zoom) czyli kąt „widzenia” aparatu. Warto przy tym pamiętać, że zdjęcie wykonane obiektywem szerokokątnym z bliskiej odległości jest inne niż obiektywem wąskokątnym (teleobiektywem) z dużej odległości, pomimo pozornego podobieństwa wybranych fragmentów. Dobranie właściwego ostrosłupa widzenia jest szczególnie istotne w grach komputerowych i zastosowaniach filmowych grafiki komputerowej. Przekładając parametry ruchu aparatu (fotografa) na parametry rzutowania definiujemy '''wirtualną kamerę'''. Jaki jest minimalny zestaw operacji, zapewniający pełną swobodę manipulacji taką kamerą? | ||
|} | |} | ||
| Linia 185: | Linia 186: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M5_Slajd_14.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M5_Slajd_14.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Realizacja rzutowania perspektywicznego wymaga definicji parametrów tak, aby jednoznacznie określić bryłę widzenia. Najczęściej używa się do definicji trójki wektorów <math>\vec{u}</math>, <math>\vec{v}</math>, <math>\overrightarrow{VPN}\ </math>,. Wektor <math>\overrightarrow{VPN}\ </math>, definiuje oś widzenia (kierunek patrzenia prostopadły do płaszczyzny rzutni). Jednocześnie długość tego wektora określa wysokość ostrosłupa widzenia. Stosowane są dwa podejścia do określenia zwrotu tego wektora. Przyjęty wariant na rysunku powoduje, że kierunek patrzenia wzdłuż osi optycznej jest przeciwny do wektora <math>\overrightarrow{VPN}\ </math>, . Wektory <math>\vec{u}</math>, <math>\vec{v}</math> definiują płaszczyznę rzutni, a także prostokąt rzutni gdzie będzie powstawał obraz (poprzez długości tych wektorów). Jednocześnie kierunki wektorów określają obrót rzutni wokół osi optycznej. Zestaw wektorów <math>\vec{u}</math>, <math>\vec{v}</math>, <math>\overrightarrow{VPN}\ </math>, definiuje jednoznacznie ostrosłup prawidłowy o podstawie prostokąta. Daje to możliwość określenia kąta patrzenia w rzutowaniu perspektywicznym. Komplet parametrów rzutowania wymaga definicji: środka rzutowania (punkt VPR) oraz trzech odległości wzdłuż osi optycznej względem środka rzutowania. Pierwszą jest odległość do płaszczyzny rzutni (VPD). Dwie pozostałe (FPD i BPD) definiują położenie dwóch płaszczyzn (przedniej <math>S_1\ </math>, i tylnej <math>S_2\ </math>,), które określają ostrosłup ścięty - wyznaczają fragment przestrzeni, która będzie rzutowana. | ||
|} | |} | ||
| Linia 212: | Linia 213: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:GKIW_M5_Slajd_18.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:GKIW_M5_Slajd_18.png|thumb|500px]] | ||
|valign="top"|*Translacja obiektu kamery w układzie współrzędnych świata, odpowiadająca przesuwaniu aparatu w dowolnym kierunku (przemieszczanie się fotografa). | |valign="top"| | ||
*Translacja obiektu kamery w układzie współrzędnych świata, odpowiadająca przesuwaniu aparatu w dowolnym kierunku (przemieszczanie się fotografa). | |||
*Obroty wokół osi własnego układu współrzędnych kamery, pozwalające symulować skierowanie aparatu w dowolnie wybranym kierunku. | *Obroty wokół osi własnego układu współrzędnych kamery, pozwalające symulować skierowanie aparatu w dowolnie wybranym kierunku. | ||
*Zmiany kątów ostrosłupa widzenia np. poprzez definicję odległości rzutni o zadanym prostokącie obrazu od środka rzutowania (obserwatora). Odpowiada to zmianie ogniskowej (kąta „widzenia”) obiektywu. | *Zmiany kątów ostrosłupa widzenia np. poprzez definicję odległości rzutni o zadanym prostokącie obrazu od środka rzutowania (obserwatora). Odpowiada to zmianie ogniskowej (kąta „widzenia”) obiektywu. | ||
Aktualna wersja na dzień 12:04, 5 wrz 2023
Wykład
 |
 |
 |
Warto zwrócić uwagę na to, że macierz , definiuje operację wymagającą normalizacji. |
 |
W tym wariancie opisu rzutowania perspektywicznego macierz wynikowa również wymaga normalizacji.
Oba warianty definicji rzutowania perspektywicznego mogą być stosowane zamiennie zależnie od sytuacji. |
 |
Macierz opisująca rzutowanie równoległe będzie miała następującą postać:
Operacja w tym przypadku nie wymaga normalizacji. |
 |
 |
Literatura
 |