PEE Moduł 12: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 7 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd1.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd1.png|thumb|500px]] | ||
|valign="top"|''' | |valign="top"|'''Podstawowe elementy półprzewodnikowe''' | ||
|} | |} | ||
| Linia 50: | Linia 50: | ||
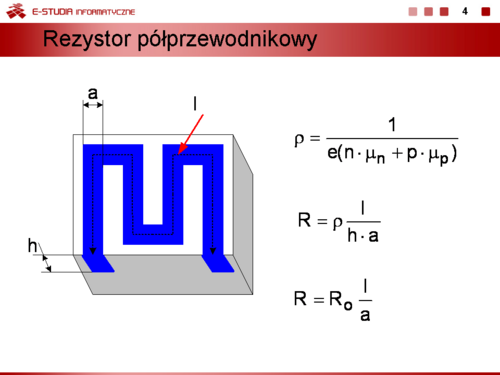
|valign="top"|'''Rezystor półprzewodnikowy. '''Jednym z podstawowych elementów każdego obwodu elektronicznego jest rezystor. W monolitycznych układach scalonych wytwarzanych na bazie kryształu krzemu także rezystory są wykonane z półprzewodnika. Ponieważ rezystywność półprzewodnika odpowiednio domieszkowanego jest opisana zależnością | |valign="top"|'''Rezystor półprzewodnikowy. '''Jednym z podstawowych elementów każdego obwodu elektronicznego jest rezystor. W monolitycznych układach scalonych wytwarzanych na bazie kryształu krzemu także rezystory są wykonane z półprzewodnika. Ponieważ rezystywność półprzewodnika odpowiednio domieszkowanego jest opisana zależnością | ||
:<math> | :<math>\rho=\frac{1}{e(n\cdot \mu_n+p\cdot \mu_p)}</math> | ||
to jej wartość może być w czasie trwania procesu technologicznego odpowiednio uformowana przez dobór koncentracji i rozkładu domieszek. W ten sposób w warstwie półprzewodnika samoistnego o dużej rezystywności można wytworzyć ścieżkę | to jej wartość może być w czasie trwania procesu technologicznego odpowiednio uformowana przez dobór koncentracji i rozkładu domieszek. W ten sposób w warstwie półprzewodnika samoistnego o dużej rezystywności można wytworzyć ścieżkę | ||
o wymaganej przewodności. Jeżeli ścieżka ma wymiary długość – l, szerokość – a oraz grubość – h to rezystancja warstwowego rezystora półprzewodnikowego jest równa: | o wymaganej przewodności. Jeżeli ścieżka ma wymiary długość – l, szerokość – a oraz grubość – h to rezystancja warstwowego rezystora półprzewodnikowego jest równa: | ||
:<math> | :<math>R=\rho \frac{l}{h\cdot a}</math> | ||
Grubość – h ścieżki rezystora wykonanego w konkretnym procesie technologicznym jest stała, zatem rezystancja rezystora zależy oprócz rezystywności ρ także od długości i szerokości wykonanej ścieżki. | Grubość – h ścieżki rezystora wykonanego w konkretnym procesie technologicznym jest stała, zatem rezystancja rezystora zależy oprócz rezystywności ρ także od długości i szerokości wykonanej ścieżki. | ||
:<math> | :<math>R_0=\rho \frac{l}{a}</math> | ||
gdzie <math> | gdzie <math>R_0= \frac{\rho}{h}</math> - rezystywność powierzchniowa warstwy. | ||
Wartość <math>R_0\ | Wartość <math>R_0\ </math>, jest stała dla danego procesu technologicznego i w zależności od domieszkowania waha się w zakresie 50 ÷ 250 <math>\Omega\ </math>,. Istotne znaczenie praktyczne ma także kształt ścieżki. Często rezystory półprzewodnikowe wykonuje się w postaci meandra co pozwala ograniczyć powierzchnię, którą zajmują oraz zmniejszyć ich indukcyjność własną. | ||
|} | |} | ||
| Linia 81: | Linia 81: | ||
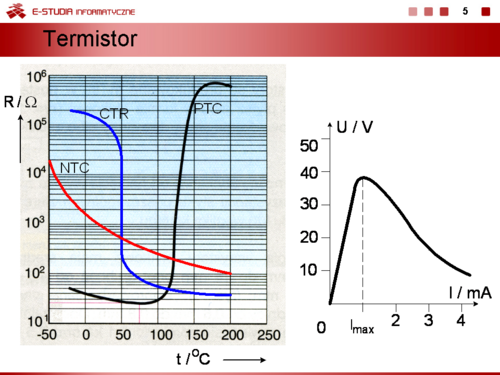
Rezystancja termistora NTC zmniejsz się ze wzrostem temperatury zgodnie z zależnością | Rezystancja termistora NTC zmniejsz się ze wzrostem temperatury zgodnie z zależnością | ||
:<math> | :<math>R_T=A\cdot e^{\frac{B}{T}}</math> | ||
gdzie A i B stałe materiałowe, T temperatura bezwzględna (K). | gdzie A i B stałe materiałowe, T temperatura bezwzględna (K). | ||
| Linia 89: | Linia 89: | ||
Ponieważ | Ponieważ | ||
:<math> | :<math>R_{T0}=A\cdot e^{\frac{B}{T_0}}</math> | ||
to po wyliczeniu A i wstawieniu do zależności | to po wyliczeniu A i wstawieniu do zależności | ||
<math> | <math>R_T=A\cdot e^{\frac{B}{T}}</math> otrzymujemy <math>R_T=R_{T_0}\cdot e^{(\frac{B}{T}-\frac{B}{T_0})}</math> | ||
Temperaturowy współczynnik rezystancji termistora definiowany następująco | Temperaturowy współczynnik rezystancji termistora definiowany następująco | ||
:<math> | :<math>d_T\left[\frac{\%}{C}\right]=\frac{1}{R_T}\frac{dR_T}{dT}</math> | ||
jest dla termistorów typu NTC ujemny i zawiera się w przedziale wartości od -3,5 do -6. | jest dla termistorów typu NTC ujemny i zawiera się w przedziale wartości od -3,5 do -6. | ||
Charakterystyka prądowo-napięciowa termistora NTC jest także nieliniowa. W zakresie małych prądów przebiega liniowo (tak jak w zwykłym liniowym rezystorze), ale już dla prądów większych od <math>I_{max}\ | Charakterystyka prądowo-napięciowa termistora NTC jest także nieliniowa. W zakresie małych prądów przebiega liniowo (tak jak w zwykłym liniowym rezystorze), ale już dla prądów większych od <math>I_{max}\ </math>,, pomimo zwiększenia wartości prądu płynącego przez termistor NTC napięcie na jego zaciskach zmniejsza się. Jest to efekt samo podgrzewania się elementu, które powoduje zmniejszanie się jego rezystancji. | ||
Termistory stosuje się jako czujniki temperatury w układach termoregulacji, w klimatyzacji, chłodnictwie, wentylacji oraz układach automatycznej regulacji. | Termistory stosuje się jako czujniki temperatury w układach termoregulacji, w klimatyzacji, chłodnictwie, wentylacji oraz układach automatycznej regulacji. | ||
| Linia 112: | Linia 112: | ||
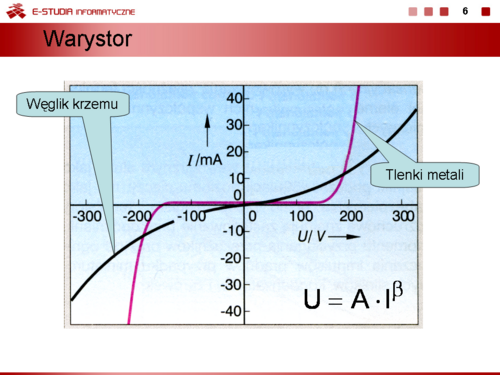
|valign="top"|'''Warystor''' często nazywany jest rezystorem VDR (Voltage Dependent Resistor) zmniejsza rezystancję, gdy napięcie na jego zaciskach rośnie. Charakterystyka prądowo-napięciowa warystora jest opisana zależnością | |valign="top"|'''Warystor''' często nazywany jest rezystorem VDR (Voltage Dependent Resistor) zmniejsza rezystancję, gdy napięcie na jego zaciskach rośnie. Charakterystyka prądowo-napięciowa warystora jest opisana zależnością | ||
:<math>U=A\cdot I^{ | :<math>U=A\cdot I^{\beta}</math> | ||
A – stałam materiałowa, <math>\beta\ | A – stałam materiałowa, <math>\beta\ </math>, – współczynnik nieliniowości. Stałe A i <math>\beta\ </math>, zależą od rodzaju materiału półprzewodnikowego, technologii wykonania i rodzaju warystora. W praktyce warystory mają konstrukcję walcową lub dyskową i są stosowane do ochrony przepięciowej, ograniczania i stabilizacji napięcia oraz w układach automatyczne regulacji. | ||
Typowym parametrem warystora jest napięcie stabilizacji podawane dla typowej wartości prądu przewodzenia np. 1, 10, 100 mA. Ponadto podaje się dopuszczalną moc strat lub częściej energię impulsu przepływającego przez warystor prądu. | Typowym parametrem warystora jest napięcie stabilizacji podawane dla typowej wartości prądu przewodzenia np. 1, 10, 100 mA. Ponadto podaje się dopuszczalną moc strat lub częściej energię impulsu przepływającego przez warystor prądu. | ||
| Linia 123: | Linia 123: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd7.png|thumb|500px]] | ||
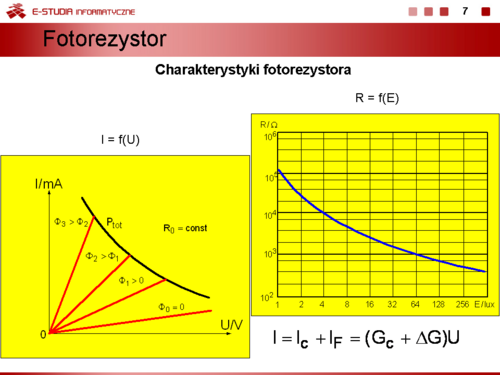
|valign="top"|'''Fotorezystor''' nazywany także rezystorem LDR (Light Dependent Resistor) zmienia rezystancję pod wpływem światła (zarówno w zakresie promieniowania widzialnego jak i niewidzialnego). Poprzez oświetlanie fotorezystora powstają w nim dodatkowe nośniki ładunku, wskutek czego jego rezystancja maleje. Tzw. rezystancja ciemna (bez oświetlenia) jest zwykle równa kilka <math>M\Omega\ | |valign="top"|'''Fotorezystor''' nazywany także rezystorem LDR (Light Dependent Resistor) zmienia rezystancję pod wpływem światła (zarówno w zakresie promieniowania widzialnego jak i niewidzialnego). Poprzez oświetlanie fotorezystora powstają w nim dodatkowe nośniki ładunku, wskutek czego jego rezystancja maleje. Tzw. rezystancja ciemna (bez oświetlenia) jest zwykle równa kilka <math>M\Omega\ </math>,, zaś rezystancja jasna, przy określonym natężeniu oświetlenia jest zwykle mniejsza niż <math>1\,k\Omega\ </math>,. | ||
Charakterystyki prądowo-napięciowe fotorezystora to pęk prostych przechodzących przez początek układu współrzędnych o nachyleniu zależnym od wartości strumienia świetlnego <math>\phi\ | Charakterystyki prądowo-napięciowe fotorezystora to pęk prostych przechodzących przez początek układu współrzędnych o nachyleniu zależnym od wartości strumienia świetlnego <math>\phi\ </math>,. Można je opisać równaniem | ||
:<math>I=I_c+I_F=(G_c+\Delta G)U</math> | :<math>I=I_c+I_F=(G_c+\Delta G)U</math> | ||
gdzie | gdzie | ||
:<math>I_c\ | :<math>I_c\ </math>, – prąd ciemny | ||
:<math>I_F\ | :<math>I_F\ </math>, – prąd fotoelektryczny | ||
:<math>G_c\ | :<math>G_c\ </math>, – konduktancja ciemna | ||
:<math>\Delta G\ | :<math>\Delta G\ </math>, – przyrost konduktancji pod wpływem oświetlenia. | ||
|} | |} | ||
| Linia 143: | Linia 143: | ||
|valign="top"|'''Piezorezystor''' to element, którego rezystancja zależy od siły nacisku, jaki wywierany jest w osi poprzecznej elementu. Często zastępuje, w przypadku niewielkich odkształceń, klasyczny tensometr wykonany ze stopu oporowego. Czułość piezorezystora jest definiowana jako | |valign="top"|'''Piezorezystor''' to element, którego rezystancja zależy od siły nacisku, jaki wywierany jest w osi poprzecznej elementu. Często zastępuje, w przypadku niewielkich odkształceń, klasyczny tensometr wykonany ze stopu oporowego. Czułość piezorezystora jest definiowana jako | ||
:<math> | :<math>k=\frac{\frac{R}{R_0}}{\frac{I}{I_0}}</math> | ||
gdzie | gdzie | ||
:<math>R\ | :<math>R\ </math>, – rezystancja płytki po przyłożeniu siły, | ||
:<math>R_0\ | :<math>R_0\ </math>, – rezystancja początkowa (bez działania siły) | ||
:<math>l\ | :<math>l\ </math>, – długość płytki po przyłożeniu siły | ||
:<math>l_0\ | :<math>l_0\ </math>, – początkowa długość płytki (bez działania siły) | ||
Czułość piezorezystora jest bardzo duża 20-200, podczas gdy tensometr oporowy ma czułość tylko 2-6. Piezorezystory stosuje się jako czujniki w pomiarach sił oraz naprężeń statycznych i dynamicznych. | Czułość piezorezystora jest bardzo duża 20-200, podczas gdy tensometr oporowy ma czułość tylko 2-6. Piezorezystory stosuje się jako czujniki w pomiarach sił oraz naprężeń statycznych i dynamicznych. | ||
| Linia 162: | Linia 162: | ||
|valign="top"|'''Magnetorezystor''' nazywany także gaussotronem to rezystor o rezystancji zależnej od pola magnetycznego, w którym go umieszczono. Zależność rezystancji od indukcji magnetycznej opisana jest wzorem | |valign="top"|'''Magnetorezystor''' nazywany także gaussotronem to rezystor o rezystancji zależnej od pola magnetycznego, w którym go umieszczono. Zależność rezystancji od indukcji magnetycznej opisana jest wzorem | ||
:<math> | :<math>R_B=R_0\cdot \frac{\rho_B}{\rho_0}\cdot f(\mu, B, a, b)</math> | ||
gdzie <math>R_0, \rho_0</math> – rezystancja i rezystywność elementu przy <math>B = 0\, T</math> | gdzie <math>R_0, \rho_0</math> – rezystancja i rezystywność elementu przy <math>B = 0\, T</math> | ||
| Linia 168: | Linia 168: | ||
<math>R_B , \rho_B</math> – rezystancja i rezystywność elementu przy <math>B \neq 0\, T</math> | <math>R_B , \rho_B</math> – rezystancja i rezystywność elementu przy <math>B \neq 0\, T</math> | ||
<math>f(\mu, B, a, b)</math> – funkcja zależna od indukcji magnetycznej B i parametrów płytki: wymiarów a, b oraz ruchliwości nośników większościowych <math>\mu\ | <math>f(\mu, B, a, b)</math> – funkcja zależna od indukcji magnetycznej B i parametrów płytki: wymiarów a, b oraz ruchliwości nośników większościowych <math>\mu\ </math>,. | ||
Podstawową charakterystyką magnetorezystora jest zależność <math>R_B = f(B)</math>. Magnetorezystory są wrażliwe na temperaturę co oznacza, że mają duży temperaturowy współczynnik rezystancji. Najczęściej nie należy przekraczać temperatury pracy płytki, <math>95^\circ C</math> . Typowe zastosowanie magnetorezystorów to czujniki do pomiaru indukcji magnetycznej, mocy i skutecznej wartości prądów odkształconych. | Podstawową charakterystyką magnetorezystora jest zależność <math>R_B = f(B)</math>. Magnetorezystory są wrażliwe na temperaturę co oznacza, że mają duży temperaturowy współczynnik rezystancji. Najczęściej nie należy przekraczać temperatury pracy płytki, <math>95^\circ C</math> . Typowe zastosowanie magnetorezystorów to czujniki do pomiaru indukcji magnetycznej, mocy i skutecznej wartości prądów odkształconych. | ||
| Linia 179: | Linia 179: | ||
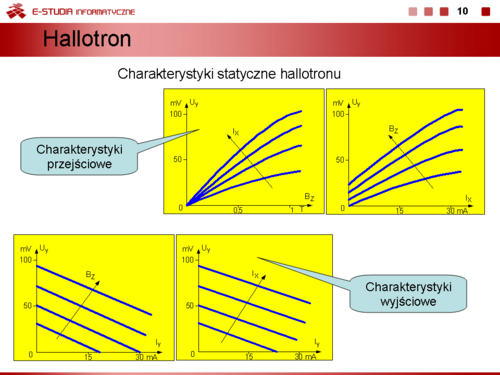
|valign="top"|'''Hallotrony''' są wykonane najczęściej w postaci płytek w kształcie krzyża z litych materiałów półprzewodnikowych lub z płytek mikowych z naparowanym półprzewodnikiem (Ge, InSb, InAs). Często wytwarza się je w technologii hybrydowych układów scalonych w jednej obudowie ze wzmacniaczem operacyjnym. Tego typu układy są szczególnie przydatne do pomiarów i badań pól magnetycznych, wielkości elektrycznych i nie elektrycznych oraz jako elementy mnożące i modulatory sygnałów wolnozmiennych. Właściwości elektryczne hallotronu opisują rodziny charakterystyk statycznych: przejściowych i wyjściowych. | |valign="top"|'''Hallotrony''' są wykonane najczęściej w postaci płytek w kształcie krzyża z litych materiałów półprzewodnikowych lub z płytek mikowych z naparowanym półprzewodnikiem (Ge, InSb, InAs). Często wytwarza się je w technologii hybrydowych układów scalonych w jednej obudowie ze wzmacniaczem operacyjnym. Tego typu układy są szczególnie przydatne do pomiarów i badań pól magnetycznych, wielkości elektrycznych i nie elektrycznych oraz jako elementy mnożące i modulatory sygnałów wolnozmiennych. Właściwości elektryczne hallotronu opisują rodziny charakterystyk statycznych: przejściowych i wyjściowych. | ||
Charakterystyki statyczne przejściowe to funkcje zmian napięcia Halla <math>U_y\ | Charakterystyki statyczne przejściowe to funkcje zmian napięcia Halla <math>U_y\ </math>, od parametru sterującego: poprzecznego pola magnetycznego <math>B_z\ </math>, lub prądu przewodzenia <math>I_x\ </math>,. Charakterystyki statyczne wyjściowe to funkcje zmian napięcia Halla <math>U_y\ </math>, od prądu obciążenia <math>I_y\ </math>, przy stałych parametrach sterujących <math>B_z\ </math>,, <math>I_x\ </math>,. | ||
|} | |} | ||
| Linia 201: | Linia 201: | ||
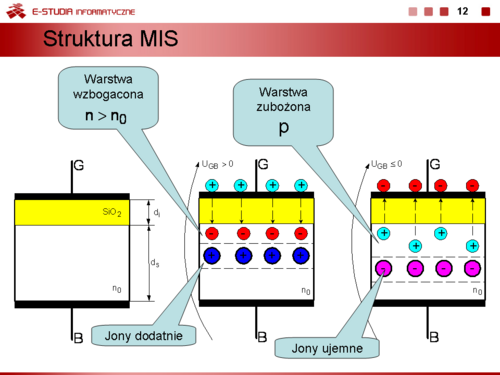
'''Struktura MIS (Metal-Insulator-Semiconductor)''' | '''Struktura MIS (Metal-Insulator-Semiconductor)''' | ||
Na slajdzie przedstawiono strukturę MIS. Podłoże '''B''' (''Bulk'') o grubości <math>100-300 \mu m</math> stanowi często krzem samoistny lub słabo domieszkowany typu n lub p. Metalem, czyli elektrodą przewodzącą jest najczęściej cienka warstwa napylonego aluminium, a dielektrykiem warstwa tlenku <math>SiO_2\ | Na slajdzie przedstawiono strukturę MIS. Podłoże '''B''' (''Bulk'') o grubości <math>100-300 \mu m</math> stanowi często krzem samoistny lub słabo domieszkowany typu n lub p. Metalem, czyli elektrodą przewodzącą jest najczęściej cienka warstwa napylonego aluminium, a dielektrykiem warstwa tlenku <math>SiO_2\ </math>,. Elektrodę metalową nazywamy bramką G (''Gate''). | ||
Załóżmy, że podłoże wykonano z półprzewodnika typu n o koncentracji elektronów <math>n_0\ | Załóżmy, że podłoże wykonano z półprzewodnika typu n o koncentracji elektronów <math>n_0\ </math>,. | ||
Pomiędzy bramkę i podłoże przykładamy napięcie UGB wytwarzające słabe pole elektryczne. Jeżeli dla uproszczenia podłoże B umieścimy na potencjale zerowym, to napięcie UGB będzie mogło mieć wartość dodatnią lub ujemną. | Pomiędzy bramkę i podłoże przykładamy napięcie UGB wytwarzające słabe pole elektryczne. Jeżeli dla uproszczenia podłoże B umieścimy na potencjale zerowym, to napięcie UGB będzie mogło mieć wartość dodatnią lub ujemną. | ||
#Jeżeli <math>U_{GB} > 0\, V</math> to dodatnie pole elektryczne wnika do półprzewodnika i powoduje tzw. akumulację nośników tzn. przyciąganie nośników większościowych (elektronów) do warstwy przypowierzchniowej i utworzenie w niej ładunku przestrzennego ujemnego o wzbogaconej koncentracji <math>n > n_0</math>. Pod tą warstwą znajdują się nieruchome dodatnie jony domieszek tworzące warstwę zubożoną. Ponieważ nastąpiło rozdzielenie ładunków strukturę MIS (w tym wypadku, ponieważ dielektrykiem jest tlenek krzemu strukturę MOS, '''Metal-Oxide-Semiconductor''') można traktować jak kondensator o pojemności C. | #Jeżeli <math>U_{GB} > 0\, V</math> to dodatnie pole elektryczne wnika do półprzewodnika i powoduje tzw. akumulację nośników tzn. przyciąganie nośników większościowych (elektronów) do warstwy przypowierzchniowej i utworzenie w niej ładunku przestrzennego ujemnego o wzbogaconej koncentracji <math>n > n_0</math>. Pod tą warstwą znajdują się nieruchome dodatnie jony domieszek tworzące warstwę zubożoną. Ponieważ nastąpiło rozdzielenie ładunków strukturę MIS (w tym wypadku, ponieważ dielektrykiem jest tlenek krzemu strukturę MOS, '''Metal-Oxide-Semiconductor''') można traktować jak kondensator o pojemności C. | ||
#<math>U_{GB} \le 0\, V</math>. Jeżeli zmniejszamy napięcie <math>U_{GB}\ | #<math>U_{GB} \le 0\, V</math>. Jeżeli zmniejszamy napięcie <math>U_{GB}\ </math>, od wartości dodatnich do zera zmniejsza się ładunek indukowany w warstwie przypowierzchniowej i koncentracja elektronów powraca do wartości <math>n_0\ </math>,. Jeżeli nadal będziemy zmniejszać napięcie <math>U_{GB}\ </math>, i będzie spełniony warunek <math>U_{GB} < 0\, V</math> z warstwy przypowierzchniowej będą wypierane elektrony i pojawi się w niej ładunek mniejszościowy, czyli dziury. Nastąpi wzrost koncentracji dziur <math>p > p_0</math> w tej warstwie. W momencie, gdy <math>n < p</math> następuje zmiana znaku ładunku przestrzennego, czyli inwersja ładunku na którym kończą się linie pola elektrycznego. | ||
|} | |} | ||
| Linia 215: | Linia 215: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd13.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd13.png|thumb|500px]] | ||
|valign="top"|Głębokość wnikania pola, a zatem i grubość warstwy inwersyjnej, a także ładunek elektryczny zgromadzony w warstwie inwersyjnej zależy od wartości napięcia <math>U_GB\ | |valign="top"|Głębokość wnikania pola, a zatem i grubość warstwy inwersyjnej, a także ładunek elektryczny zgromadzony w warstwie inwersyjnej zależy od wartości napięcia <math>U_GB\ </math>, | ||
:<math> | :<math>C_s=\frac{dQ_S}{dU_{GB}}</math> | ||
W tej sytuacji pojemność <math>C_s\ | W tej sytuacji pojemność <math>C_s\ </math>, jest połączona szeregowo ze stałą pojemnością warstwy dielektryka <math>C_i\ </math>,, zależną od rozmiarów geometrycznych struktury i stałej elektrycznej dielektryka. Wypadkowa pojemność struktury jest równa | ||
:<math> | :<math>C=\frac{C_i\cdot C_s(U_{GB})}{C_i + C_s(U_{GB})}</math> | ||
|} | |} | ||
| Linia 231: | Linia 231: | ||
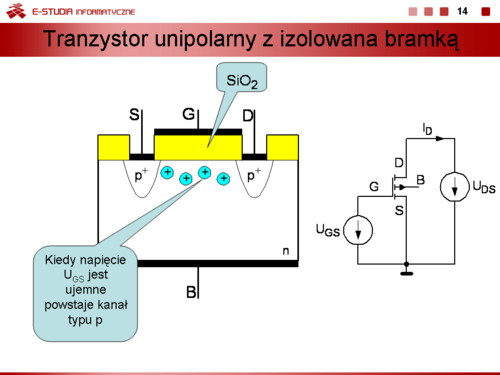
|valign="top"|'''Tranzystor unipolarny z izolowana bramką'''. Jeżeli strukturę przedstawiona na slajdzie 12 uzupełnić dwoma obszarami bardzo silnie domieszkowanymi typu <math>p^{+}</math> to przy przypowierzchniowa warstwa inwersyjna (tutaj typu p) będzie tworzyła pomiędzy tymi obszarami tzw. kanał. Rezystancja kanału będzie w tym wypadku zależała od jego rozmiarów geometrycznych i koncentracji nośników mniejszościowych i jest znacznie mniejsza od rezystancji podłoża. | |valign="top"|'''Tranzystor unipolarny z izolowana bramką'''. Jeżeli strukturę przedstawiona na slajdzie 12 uzupełnić dwoma obszarami bardzo silnie domieszkowanymi typu <math>p^{+}</math> to przy przypowierzchniowa warstwa inwersyjna (tutaj typu p) będzie tworzyła pomiędzy tymi obszarami tzw. kanał. Rezystancja kanału będzie w tym wypadku zależała od jego rozmiarów geometrycznych i koncentracji nośników mniejszościowych i jest znacznie mniejsza od rezystancji podłoża. | ||
Koncentracja nośników w kanale inwersyjnym zależy od natężenia pola elektrycznego wytworzonego przez elektrodę bramkową. Zmieniając napięcie <math>U_{GB}\ | Koncentracja nośników w kanale inwersyjnym zależy od natężenia pola elektrycznego wytworzonego przez elektrodę bramkową. Zmieniając napięcie <math>U_{GB}\ </math>, zmieniamy natężenie pola elektrycznego, a co za tym idzie także koncentrację nośników i w konsekwencji rezystancję kanału. Można zatem powiedzieć, że rezystancja kanału jest sterowana polowo (napięciowo). Ponieważ prąd płynący pomiędzy dodatkowymi elektrodami tworzą dziury to taki element nazywamy tranzystorem unipolarnym z izolowaną bramką z kanałem typu p. Oczywiście można wytworzyć także strukturę tranzystora z kanałem typu n. Tranzystory unipolarne bezzłączowe, do których zaliczamy tranzystory z izolowana bramką, oznacza się angielskim skrótem IGFET (''Insulated Gate Field Effect Transistor'') lub w przypadku, kiedy dielektrykiem jest tlenek krzemu '''MOSFET''' ('''''Metal-Oxide-Semiconductor-Field-Effect-Transistor'''''). Elektrody stanowiące wyprowadzenia z dodatkowych bardzo silnie domieszkowanych obszarów nazywamy drenem '''D''' (''Drain'') i źródłem '''S''' (''Sourcs''). Taka struktura jest symetryczna i dlatego przypisanie poszczególnym elektrodom funkcji drenu i źródła jest umowne. Najczęściej źródło i podłoże są ze sobą połączone (przyjmuje się, że mają potencjał zerowy), a zatem napięciem sterującym tranzystor jest napięcie <math>U_{GS}\ </math>,. Dla opisanej wyżej struktury tranzystora MOSFET warunkiem koniecznym do tego, aby można było sterować rezystancją kanału jest <math>U_{GS} < 0\, V</math>. Ponadto przyjmuje się, że napięcie <math>U_{DS}\ </math>, jest także ujemne. W opisanym tranzystorze poprzez zmianę napięcia UGS kanał jest wzbogacany w nośniki ładunku typu p, zatem można go nazwać także tranzystorem z kanałem wzbogaconym. Napięcie UGS, przy którym kanał inwersyjny zaczyna przewodzić prąd drenu nazywa się napięciem progowym <math>U_P\ </math>,. | ||
Jeżeli dodatkowo poprzez dyfuzję lub implantację jonów do podłoża będzie wytworzony w tranzystorze specjalnie przewodzący kanał to taki tranzystor przy <math>U_{DS} \neq 0\, V</math> nawet przy napięciu <math>U_{GS} = 0\, V</math> będzie przewodził prąd drenu. W tym wypadku, aby wstrzymać przepływ prądu należy wprowadzić pole zubożające kanał wbudowany, a taki tranzystor będziemy nazywali tranzystorem z kanałem zubożonym. Napięcie UGS, przy którym kanał przestaje przewodzić prąd nazywa się napięciem odcięcia i dla uproszczenia oznaczmy go podobnie jak napięcie progowe symbolem <math>U_P\ | Jeżeli dodatkowo poprzez dyfuzję lub implantację jonów do podłoża będzie wytworzony w tranzystorze specjalnie przewodzący kanał to taki tranzystor przy <math>U_{DS} \neq 0\, V</math> nawet przy napięciu <math>U_{GS} = 0\, V</math> będzie przewodził prąd drenu. W tym wypadku, aby wstrzymać przepływ prądu należy wprowadzić pole zubożające kanał wbudowany, a taki tranzystor będziemy nazywali tranzystorem z kanałem zubożonym. Napięcie UGS, przy którym kanał przestaje przewodzić prąd nazywa się napięciem odcięcia i dla uproszczenia oznaczmy go podobnie jak napięcie progowe symbolem <math>U_P\ </math>,. | ||
|} | |} | ||
| Linia 253: | Linia 253: | ||
:<math>I_D=f(U_{GS}) \, dla \, U_{DS}=const</math> | :<math>I_D=f(U_{GS}) \, dla \, U_{DS}=const</math> | ||
Rodzina charakterystyk wyjściowych ma taki sam przebieg dla tranzystorów z kanałem wzbogaconym jak i zubożonym. Dla małych wartości napięcia <math>U_{DS}\ | Rodzina charakterystyk wyjściowych ma taki sam przebieg dla tranzystorów z kanałem wzbogaconym jak i zubożonym. Dla małych wartości napięcia <math>U_{DS}\ </math>, charakterystyka jest praktycznie liniowa, prąd drenu <math>I_D\ </math>, rośnie w przybliżeniu proporcjonalnie do napięcia <math>U_{DS}\ </math>,, a nachylenie charakterystyki tzn. wartość rezystancji kanału można zadawać napięciem <math>U_{GS}\ </math>,. Dla napięć trochę większych, ale mniejszych od tzw. napięcia kolana <math>│U_{DS}│ < U_K = │U_{GS} - U_P│</math> rodzinę charakterystyk wyjściowych można opisać równaniem | ||
:<math> | :<math>I_D=\frac{I_{DSS}}{U_P^2}[2\cdot |U_{GS}-U_P|\cdot |U_{DS}|-U_{DS}^2]</math> | ||
Ten zakres pracy nazywamy liniowym, nienasycenia lub triodowym. | Ten zakres pracy nazywamy liniowym, nienasycenia lub triodowym. | ||
| Linia 263: | Linia 263: | ||
<math>U_{DS}</math> i jest opisany równaniem | <math>U_{DS}</math> i jest opisany równaniem | ||
:<math> | :<math>I_D=I_{DSS}\left(1-\left|\frac{U_{GS}}{U_P}\right| \right)^2</math> | ||
a niewielką zależność ID od napięcia UDS charakteryzuje dynamiczna rezystancja wyjściowa | a niewielką zależność ID od napięcia UDS charakteryzuje dynamiczna rezystancja wyjściowa | ||
:<math> | :<math>r_{DS}=\frac{\delta U_{DS}}{\delta I_D}</math> dla <math>U_{GS}=const</math>. | ||
Prąd IDSS wyznaczyć można z charakterystyk bramkowych: dla tranzystorów z kanałem zubożonym przy <math>U_{GS} = 0\, V</math>, dla tranzystorów z kanałem wzbogaconym przy <math>U_{GS} = 2U_P</math>. | Prąd IDSS wyznaczyć można z charakterystyk bramkowych: dla tranzystorów z kanałem zubożonym przy <math>U_{GS} = 0\, V</math>, dla tranzystorów z kanałem wzbogaconym przy <math>U_{GS} = 2U_P</math>. | ||
| Linia 273: | Linia 273: | ||
Rodzina charakterystyk bramkowych (przejściowych) tranzystorów z kanałem typu n w zakresie napięć sterujących <math>U_{GS} > U_P</math> oraz z kanałem typu p w zakresie napięć <math>U_{GS} < U_P</math> opisana jest wzorem | Rodzina charakterystyk bramkowych (przejściowych) tranzystorów z kanałem typu n w zakresie napięć sterujących <math>U_{GS} > U_P</math> oraz z kanałem typu p w zakresie napięć <math>U_{GS} < U_P</math> opisana jest wzorem | ||
:<math> | :<math>I_D=I_{DSS}\left(1-\left|\frac{U_{GS}}{U_P}\right| \right)^2</math> | ||
Z charakterystyki bramkowej można wyznaczyć istotny z punktu widzenia wzmacniania sygnałów elektrycznych parametr tranzystora tzw. transkonduktancję gm lub inaczej nachylenie charakterystyki bramkowej S | Z charakterystyki bramkowej można wyznaczyć istotny z punktu widzenia wzmacniania sygnałów elektrycznych parametr tranzystora tzw. transkonduktancję gm lub inaczej nachylenie charakterystyki bramkowej S | ||
:<math> | :<math>g_m=S=\frac{\delta I_D}{\delta U_{GS}}</math> dla <math>U_{DS}=const</math>. | ||
Obserwując kształt charakterystyki bramkowej można stwierdzić, wśród tranzystorów z izolowaną bramką możemy wydzielić grupę tranzystorów normalnie załączonych, tzn. takich które przy <math>U_{DS} \neq 0\, V</math> i <math>U_{GS} = 0\, V</math>, przewodzą prąd drenu i grupę tranzystory normalnie wyłączonych, tzn. takich które w tych samych warunkach (<math>U_{DS} \neq 0\, V</math> i <math>U_{GS} = 0\, V</math>) nie przewodzą prądu drenu. | Obserwując kształt charakterystyki bramkowej można stwierdzić, wśród tranzystorów z izolowaną bramką możemy wydzielić grupę tranzystorów normalnie załączonych, tzn. takich które przy <math>U_{DS} \neq 0\, V</math> i <math>U_{GS} = 0\, V</math>, przewodzą prąd drenu i grupę tranzystory normalnie wyłączonych, tzn. takich które w tych samych warunkach (<math>U_{DS} \neq 0\, V</math> i <math>U_{GS} = 0\, V</math>) nie przewodzą prądu drenu. | ||
| Linia 324: | Linia 324: | ||
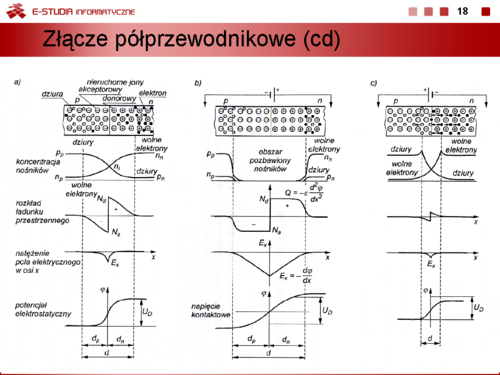
Nawet przy braku polaryzacji złącza na skutek ruchów cieplnych sieci krystalicznej półprzewodnika nośniki większościowe-elektrony z obszar typu n przenikają do obszaru o przewodnictwie dziurowym typu p i stają się tam nośnikami mniejszościowymi, a nośniki większościowe-dziury z obszaru p przenikają do obszaru typu n. W obszarze złącza następuje rekombinacja par elektron-dziura i w związku z tym w obszarze tym nie występuje swobodny ładunek. W pobliżu obszaru złącza w półprzewodniku typu n pozostają praktycznie nieruchome jony dodatnie, a w materiale typu p nieruchome jony ujemne. Te ładunki powodują, że na złączu wystąpi napięcie bariery potencjału lub krótko bariera potencjału | Nawet przy braku polaryzacji złącza na skutek ruchów cieplnych sieci krystalicznej półprzewodnika nośniki większościowe-elektrony z obszar typu n przenikają do obszaru o przewodnictwie dziurowym typu p i stają się tam nośnikami mniejszościowymi, a nośniki większościowe-dziury z obszaru p przenikają do obszaru typu n. W obszarze złącza następuje rekombinacja par elektron-dziura i w związku z tym w obszarze tym nie występuje swobodny ładunek. W pobliżu obszaru złącza w półprzewodniku typu n pozostają praktycznie nieruchome jony dodatnie, a w materiale typu p nieruchome jony ujemne. Te ładunki powodują, że na złączu wystąpi napięcie bariery potencjału lub krótko bariera potencjału | ||
:<math> | :<math>U_D=\frac{k\cdot T}{e}ln\frac{N_a\cdot N_d}{n_i}=\frac{e}{2\varepsilon}\left(N_d\cdot d_n^2+N_a\cdot d_p^2\right)</math> | ||
która zapobiega dalszemu przenikaniu ładunków przez obszar złącza. Warstwa ta staje się warstwą zaporową. Wychodząc z warunku równowagi ładunku w obszarze złącza | która zapobiega dalszemu przenikaniu ładunków przez obszar złącza. Warstwa ta staje się warstwą zaporową. Wychodząc z warunku równowagi ładunku w obszarze złącza | ||
| Linia 332: | Linia 332: | ||
można wyznaczenia szerokość tej warstwy zaporowej (szerokości złącza) | można wyznaczenia szerokość tej warstwy zaporowej (szerokości złącza) | ||
:<math> | :<math>d=d_p+d_n=\sqrt{\frac{2\varepsilon \cdot U_D\cdot (N_d+N_a)}{e\cdot N_d\cdot N_a}}</math> | ||
Warto zauważyć, że | Warto zauważyć, że | ||
:<math> | :<math>\frac{d_n}{d_p}=\frac{N_a}{N_d}</math> | ||
co oznacza, że ładunek jonowy wnika głębiej w obszar słabiej domieszkowany. | co oznacza, że ładunek jonowy wnika głębiej w obszar słabiej domieszkowany. | ||
| Linia 348: | Linia 348: | ||
i zależą od bariery potencjału <math>U_D</math> | i zależą od bariery potencjału <math>U_D</math> | ||
:<math> | :<math>Q_0=S\cdot e\cdot d_n\cdot N_d=S\cdot e\cdot d_p\cdot N_a=S\cqrt{2e\frac{N_d\cdot N_a}{N_d+N_a}U_D}</math> | ||
Pojemność takiego niespolaryzowanego napięciem zewnętrznym złącza jest równa | Pojemność takiego niespolaryzowanego napięciem zewnętrznym złącza jest równa | ||
:<math> | :<math>C_{T0}=\frac{Q_0}{2U_D}</math> | ||
Po spolaryzowaniu złącza w kierunku zaporowym szerokość złącza zwiększa się | Po spolaryzowaniu złącza w kierunku zaporowym szerokość złącza zwiększa się | ||
:<math> | :<math>d=d_p+d_n=\sqrt{\frac{2\varepsilon \cdot( U_D+U)\cdot (N_d+N_a)}{e\cdot N_d\cdot N_a}}</math> | ||
Złącze takie można traktować jak kondensator. Pojemność warstwy zaporowej jest w tym wypadku równa | Złącze takie można traktować jak kondensator. Pojemność warstwy zaporowej jest w tym wypadku równa | ||
:<math> | :<math>C_T=\frac{dQ}{dU}=C_{T0}\sqrt{\frac{U_D}{U_D+U}}</math> | ||
Przy polaryzacji złącza w kierunku przewodzenia bariera potencjału znacznie obniża się ponieważ oba rodzaje nośników swobodnych dziury i elektrony poruszają się w kierunku złącza. Zmniejsza się szerokość i ładunek zgromadzony w warstwie zaporowej, maleje natężenie pola elektrycznego. W tym stanie rośnie gwałtownie dyfuzja nośników. Wzrasta liczba dziur przechodzących z obszaru półprzewodnika typu p do n i elektronów z obszaru n do p. Po przejściu przez złącze nośniki te stają się nośnikami mniejszościowymi | Przy polaryzacji złącza w kierunku przewodzenia bariera potencjału znacznie obniża się ponieważ oba rodzaje nośników swobodnych dziury i elektrony poruszają się w kierunku złącza. Zmniejsza się szerokość i ładunek zgromadzony w warstwie zaporowej, maleje natężenie pola elektrycznego. W tym stanie rośnie gwałtownie dyfuzja nośników. Wzrasta liczba dziur przechodzących z obszaru półprzewodnika typu p do n i elektronów z obszaru n do p. Po przejściu przez złącze nośniki te stają się nośnikami mniejszościowymi | ||
| Linia 367: | Linia 367: | ||
Ponieważ ładunek mniejszościowy wstrzykiwany do obszarów p i n w pobliżu złącza nie od razu rekombinuje zatem można mu przypisać pewną pojemność elektryczną zwana pojemnością dyfuzyjną. Ładunek dyfuzyjny wstrzykiwanych nośników mniejszościowych jest proporcjonalny do prądu I płynącego przez złącze, a ponieważ prąd I jest funkcja napięcia zasilania U to pojemność dyfuzyjną można obliczyć z zależności | Ponieważ ładunek mniejszościowy wstrzykiwany do obszarów p i n w pobliżu złącza nie od razu rekombinuje zatem można mu przypisać pewną pojemność elektryczną zwana pojemnością dyfuzyjną. Ładunek dyfuzyjny wstrzykiwanych nośników mniejszościowych jest proporcjonalny do prądu I płynącego przez złącze, a ponieważ prąd I jest funkcja napięcia zasilania U to pojemność dyfuzyjną można obliczyć z zależności | ||
:<math> | :<math>C_D=\frac{dQ}{dU}=\frac{\tau}{U_D}\cdot I</math> | ||
gdzie <math>\tau\ | gdzie <math>\tau\ </math>, – czas życia nośników mniejszościowych (zakłada się, że czasy życia dziur | ||
i elektronów są jednakowe). | i elektronów są jednakowe). | ||
| Linia 423: | Linia 423: | ||
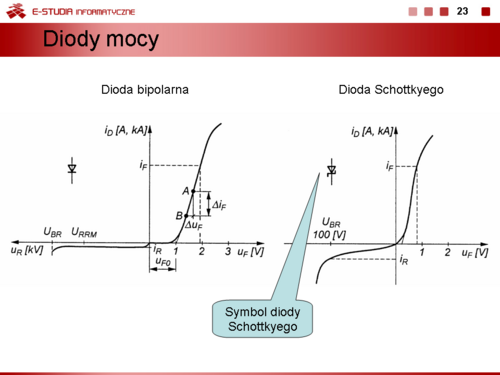
Parametry i charakterystyki statyczne. Właściwości statyczne diod w ustalonych stanach pracy tj. w stanie zaporowym i w stanie przewodzenia, przedstawia charakterystyka napięciowo - prądowa. Podstawową cechą diody jest jej działanie zaworowe co oznacza, że przewodzi prąd tylko wtedy, kiedy anoda jest spolaryzowana dodatnio względem katody. Stan ten odpowiada odcinkowi charakterystyki zawartemu w I kwadrancie układu współrzędnych. Często w katalogach ta część charakterystyki diody prezentowana jest w skali półlogarytmicznej. Umożliwia to dokładny odczyt wartości prądów i napięć w odniesieniu do dużego obejmującego kilka dekad zakresu zmian prądu przewodzenia diody. | Parametry i charakterystyki statyczne. Właściwości statyczne diod w ustalonych stanach pracy tj. w stanie zaporowym i w stanie przewodzenia, przedstawia charakterystyka napięciowo - prądowa. Podstawową cechą diody jest jej działanie zaworowe co oznacza, że przewodzi prąd tylko wtedy, kiedy anoda jest spolaryzowana dodatnio względem katody. Stan ten odpowiada odcinkowi charakterystyki zawartemu w I kwadrancie układu współrzędnych. Często w katalogach ta część charakterystyki diody prezentowana jest w skali półlogarytmicznej. Umożliwia to dokładny odczyt wartości prądów i napięć w odniesieniu do dużego obejmującego kilka dekad zakresu zmian prądu przewodzenia diody. | ||
Charakterystycznym parametrem diody w stanie przewodzenia jest <math>I_F\ | Charakterystycznym parametrem diody w stanie przewodzenia jest <math>I_F\ </math>, - maksymalny prąd przewodzenia. | ||
Jeżeli anoda jest spolaryzowana ujemnie względem katody to dioda jest w stanie nie przewodzenia (złącze jest spolaryzowane w kierunku zaporowym, wstecznie). Prąd płynący przez diodę jest pomijalnie mały i jest wyłącznie spowodowany ruchem ładunków przewodnictwa samoistnego (generacja termiczna). Charakterystycznym parametrem diody w stanie polaryzacji wstecznej jest dopuszczalne napięcie wsteczne <math>U_R\ | Jeżeli anoda jest spolaryzowana ujemnie względem katody to dioda jest w stanie nie przewodzenia (złącze jest spolaryzowane w kierunku zaporowym, wstecznie). Prąd płynący przez diodę jest pomijalnie mały i jest wyłącznie spowodowany ruchem ładunków przewodnictwa samoistnego (generacja termiczna). Charakterystycznym parametrem diody w stanie polaryzacji wstecznej jest dopuszczalne napięcie wsteczne <math>U_R\ </math>,. | ||
Pozostałe istotne parametry diody to moc znamionowa <math>P_{tot}\ | Pozostałe istotne parametry diody to moc znamionowa <math>P_{tot}\ </math>, oraz temperatura złącza tj. | ||
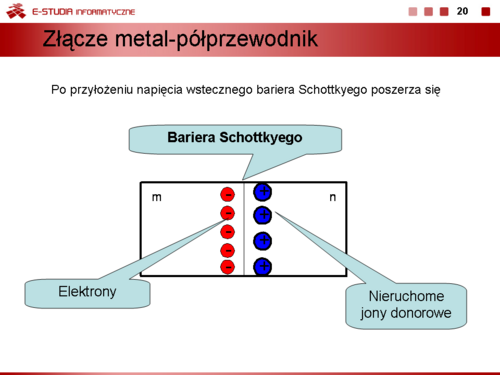
''Diody Schottkyego'' to elementy ze złączem metal – półprzewodnik m-n. Metal stanowi anodę A, półprzewodnik katodę K. Mają one podobnie jak diody bipolarne właściwości prostownicze. W obszarze złącza gromadzi się w stanie przewodzenia ładunek elektryczny, a ponieważ w złączu metal-półprzewodnik jest on bardzo mały to czas potrzebny na odprowadzenie go w czasie przejścia diody ze stanu przewodzenia do stanu zaporowego (nie przewodzenia) jest bardzo krótki rzędu kilkudziesięciu pikosekund i o kilka rzędów mniejszy niż w diodach bipolarnych. Diody Schottkyego maja ponad to mniejsze napięcia progu załączenia, ok. 0,3 V. | ''Diody Schottkyego'' to elementy ze złączem metal – półprzewodnik m-n. Metal stanowi anodę A, półprzewodnik katodę K. Mają one podobnie jak diody bipolarne właściwości prostownicze. W obszarze złącza gromadzi się w stanie przewodzenia ładunek elektryczny, a ponieważ w złączu metal-półprzewodnik jest on bardzo mały to czas potrzebny na odprowadzenie go w czasie przejścia diody ze stanu przewodzenia do stanu zaporowego (nie przewodzenia) jest bardzo krótki rzędu kilkudziesięciu pikosekund i o kilka rzędów mniejszy niż w diodach bipolarnych. Diody Schottkyego maja ponad to mniejsze napięcia progu załączenia, ok. 0,3 V. | ||
| Linia 451: | Linia 451: | ||
|valign="top"|'''Parametry diod w kierunku przewodzenia''' | |valign="top"|'''Parametry diod w kierunku przewodzenia''' | ||
<math>I_{F(AV)}\ | <math>I_{F(AV)}\ </math>, - wartość średnia prądu przewodzenia, określana za okres napięcia sieci (20 ms), dla sinusoidalnego przebiegu prądu, | ||
<math>I_{F(RMS)}\ | <math>I_{F(RMS)}\ </math>, - wartość skuteczna prądu przewodzenia za okres napięcia sieci (20 ms) dla dowolnego przebiegu prądu, | ||
<math>I_{FSM}\ | <math>I_{FSM}\ </math>, - niepowtarzalny szczytowy prąd przewodzenia, | ||
<math>I_{FRM}\ | <math>I_{FRM}\ </math>, - powtarzalny szczytowy prąd przewodzenia, | ||
<math>I_{F(0V)}\ | <math>I_{F(0V)}\ </math>, - przeciążeniowy prąd przewodzenia. | ||
'''Parametry diody w stanie zaworowym''' | '''Parametry diody w stanie zaworowym''' | ||
<math>U_{RSM}\ | <math>U_{RSM}\ </math>, - niepowtarzalne szczytowe napięcie wsteczne, które może pojawić się na diodzie przypadkowo w znacznych odstępach czasu, | ||
<math>U_{RMAX},\ , U_{RRM}\ | <math>U_{RMAX},\ , U_{RRM}\ </math>, - powtarzalne napięcie wsteczne, które może cyklicznie pojawiać się na przyrządzie. | ||
'''Właściwości dynamiczne diod'''. Proces przełączania diody mocy ze stanu przewodzenia do stanu zaworowego i odwrotnie nazywa się komutacją. Proces komutacji składa się z dwóch części: procesu załączania i procesu wyłączania. W obu tych procesach na przez diodę płynie prąd znacznie większy od prądu wstecznego, i jednocześnie na jej zaciskach występuje napięcie znaczne większe od napięcia przewodzenia. W efekcie impuls mocy chwilowej jaka wydziela się w diodzie ma znaczną amplitudę i przy częstych przełączeniach kumulacja energii może być tak duża, że dioda ulegnie zniszczeniu w wyniku przegrzania struktury półprzewodnikowej. W procesie załączania istotna jest także szybkość narastania prądu przewodzenia ponieważ na występującej w strukturze płytki krzemowej indukcyjności oraz na indukcyjności wyprowadzeń będą indukowały się napięcia, które dodając się do napięcia zasilania spowodują wystąpienie przepięcia i w konsekwencji uszkodzenie diody. W procesie wyłączania istotny jest natomiast prąd wsteczny diody ponieważ przewodząca wstecznie dioda może spowodować po załączeniu innego elementu niekontrolowane zwarcie w układzie przekształtnika. | '''Właściwości dynamiczne diod'''. Proces przełączania diody mocy ze stanu przewodzenia do stanu zaworowego i odwrotnie nazywa się komutacją. Proces komutacji składa się z dwóch części: procesu załączania i procesu wyłączania. W obu tych procesach na przez diodę płynie prąd znacznie większy od prądu wstecznego, i jednocześnie na jej zaciskach występuje napięcie znaczne większe od napięcia przewodzenia. W efekcie impuls mocy chwilowej jaka wydziela się w diodzie ma znaczną amplitudę i przy częstych przełączeniach kumulacja energii może być tak duża, że dioda ulegnie zniszczeniu w wyniku przegrzania struktury półprzewodnikowej. W procesie załączania istotna jest także szybkość narastania prądu przewodzenia ponieważ na występującej w strukturze płytki krzemowej indukcyjności oraz na indukcyjności wyprowadzeń będą indukowały się napięcia, które dodając się do napięcia zasilania spowodują wystąpienie przepięcia i w konsekwencji uszkodzenie diody. W procesie wyłączania istotny jest natomiast prąd wsteczny diody ponieważ przewodząca wstecznie dioda może spowodować po załączeniu innego elementu niekontrolowane zwarcie w układzie przekształtnika. | ||
| Linia 471: | Linia 471: | ||
Dla procesu załączania istotnymi parametrami są zatem: | Dla procesu załączania istotnymi parametrami są zatem: | ||
:<math> | :<math>\frac{di_F}{dt}</math> – maksymalna stromość narastania prądu przewodzenia oraz | ||
:<math>t_{fr}</math> - czas ustalania się napięcia przewodzenia. | :<math>t_{fr}</math> - czas ustalania się napięcia przewodzenia. | ||
| Linia 482: | Linia 482: | ||
|valign="top"|'''Diody specjalne''' | |valign="top"|'''Diody specjalne''' | ||
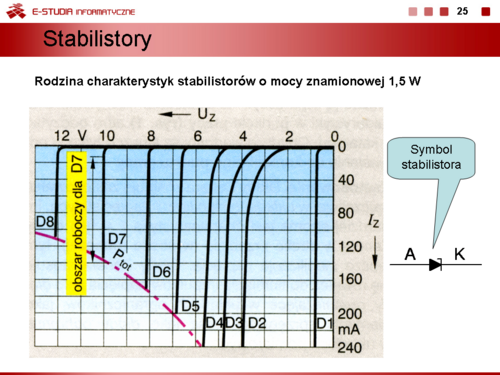
'''Stabilistory''' (diody Zenera i diody lawinowe) są diodami krzemowymi, które stosuje się do stabilizacji napięć stałych. Pracując jako stabilizatory stabilistory są zawsze spolaryzowane w kierunku wstecznym (III kwadrant charakterystyki). Przy polaryzacji złącza w kierunku zaporowym przewodzą prąd, tylko wtedy, gdy napięcie na ich zaciskach przekroczy napięcie przebicia <math>U_{Z0}\ | '''Stabilistory''' (diody Zenera i diody lawinowe) są diodami krzemowymi, które stosuje się do stabilizacji napięć stałych. Pracując jako stabilizatory stabilistory są zawsze spolaryzowane w kierunku wstecznym (III kwadrant charakterystyki). Przy polaryzacji złącza w kierunku zaporowym przewodzą prąd, tylko wtedy, gdy napięcie na ich zaciskach przekroczy napięcie przebicia <math>U_{Z0}\ </math>,. Napięcie to nazywamy napięciem Zenera. Stabilistory produkuje się w szeregach o stałej mocy strat na napięcie przebicia od 1 V do 200 V. Jeżeli napięcie na zaciskach stabilistora jest mniejsze od napięcia przebicia stabilistor nie przewodzi. Jeżeli złącze jest spolaryzowane w kierunku przewodzenia stabilistor działa jak zwykła dioda prostownicza. Stabilistory o napięciu przebicia <math>U_{Z0} < 6\, V</math> mają ujemny współczynnik temperaturowy napięcia przebicia i dominującym jest w nich zjawisko Zenera, a w stabilistorach o <math>U_{Z0} > 6\, V</math> współczynnik temperaturowy napięcia przebicia jest dodatni i dominującym zjawiskiem jest zjawisko lawinowe. Najlepsze z punktu widzenia stabilizacji napięcia (stroma charakterystyka prądowo - napięciowa i zerowy współczynnik temperaturowy napięcia przebicia) są diody Zenera o napięciu przebicia około 6 V. | ||
Do podstawowych parametrów stabilistorów zaliczamy: | Do podstawowych parametrów stabilistorów zaliczamy: | ||
| Linia 488: | Linia 488: | ||
<math>U_{Z0}</math> – napięcie przebicia (napięcie Zenera) | <math>U_{Z0}</math> – napięcie przebicia (napięcie Zenera) | ||
<math>r_Z\ | <math>r_Z\ </math>, – rezystancję dynamiczną, gdzie <math>r_Z=\frac{\Delta U_Z}{\Delta I_Z}</math> | ||
<math>P_{tot}\ | <math>P_{tot}\ </math>, – moc strat | ||
<math>\alpha_{Uz}</math> – temperaturowy współczynnik napięcia przebicia | <math>\alpha_{Uz}</math> – temperaturowy współczynnik napięcia przebicia | ||
| Linia 560: | Linia 560: | ||
'''Złączowe tranzystory unipolarne ''' | '''Złączowe tranzystory unipolarne ''' | ||
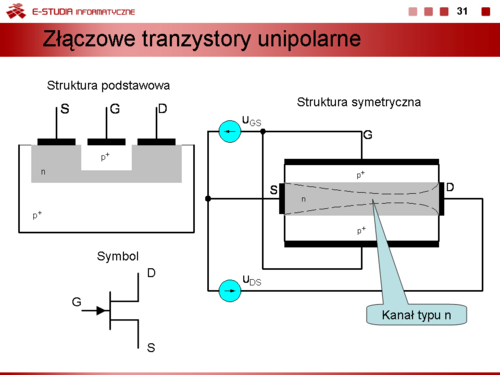
Złączowy tranzystor unipolarny JFET (Junction Field Effect Transistor) ma właściwości podobne do tranzystora unipolarnego z izolowana bramką. Na slajdzie przedstawiono model struktury takiego tranzystora. Na podłożu B np. z półprzewodnika typu <math>p^{+}\ | Złączowy tranzystor unipolarny JFET (Junction Field Effect Transistor) ma właściwości podobne do tranzystora unipolarnego z izolowana bramką. Na slajdzie przedstawiono model struktury takiego tranzystora. Na podłożu B np. z półprzewodnika typu <math>p^{+}\ </math>, wytwarza się obszar o przewodnictwie typu n, w którym z kolei jest wytworzona ponownie warstwa <math>p^{+}\ </math>,, która jest wyprowadzona na zewnątrz (bramka G). Obydwa końce kanału n są wyposażone w elektrody drenu D i źródła S. Struktura jest symetryczna, a zatem przypisanie elektrodom funkcji drenu i źródła jest umowne. Jeżeli bramka tranzystora nie jest zasilana to pod wpływem zewnętrznego źródła napięcia polaryzującego elektrody D i S w kanale popłynie prąd drenu <math>I_D\ </math>,. Przy zwiększaniu napięcia <math>U_{DS}\ </math>, w zakresie od zerowej do wartości <math>U_{DS} < U_P</math> rezystancja drenu jest praktycznie stała i prąd <math>I_D\ </math>, jest proporcjonalny do napięcia <math>U_{DS}\ </math>,. Dla napięcia <math>U_{DS} \approx U_P</math> kanał zwęża się, rezystancja zaczyna rosnąć i prąd <math>I_D\ </math>, rośnie wolniej niż napięcie <math>U_{DS}</math>. Jeżeli napięcie <math>U_{DS}</math> będzie większe od napięcia <math>U_P\ </math>, zwanego napięciem zaciśnięcia kanału (pinch-off) prąd drenu jest praktycznie stały i nie zależy od napięcia <math>U_{DS}</math>. | ||
Kiedy pomiędzy bramkę i źródło przyłożymy napięciem <math>U_{GS}</math> tak, że złącze bramka-kanał będzie spolaryzowane w kierunku zaporowym szerokość i kształt kanału będzie zależał tym razem od obu napięć <math>U_{GS}</math> oraz <math>U_{DS}</math>. Silniej będzie zaciskany kanał w pobliżu tej elektrody (drenu lub źródła), której potencjał względem bramki będzie większy. Dla napięć <math>U_{DS} > U_P</math>, gdzie <math>U_P = U_{DS} - U_{GS}</math> (przy <math>U_{GS} < 0\, V</math>) kanał będzie całkowicie zaciśnięty. Obraz takiego kanału w symetrycznej strukturze tranzystora przedstawiono na rysunku. W tym wypadku prąd drenu zależy wyłącznie od napięcia <math>U_{GS}</math>. | Kiedy pomiędzy bramkę i źródło przyłożymy napięciem <math>U_{GS}</math> tak, że złącze bramka-kanał będzie spolaryzowane w kierunku zaporowym szerokość i kształt kanału będzie zależał tym razem od obu napięć <math>U_{GS}</math> oraz <math>U_{DS}</math>. Silniej będzie zaciskany kanał w pobliżu tej elektrody (drenu lub źródła), której potencjał względem bramki będzie większy. Dla napięć <math>U_{DS} > U_P</math>, gdzie <math>U_P = U_{DS} - U_{GS}</math> (przy <math>U_{GS} < 0\, V</math>) kanał będzie całkowicie zaciśnięty. Obraz takiego kanału w symetrycznej strukturze tranzystora przedstawiono na rysunku. W tym wypadku prąd drenu zależy wyłącznie od napięcia <math>U_{GS}</math>. | ||
| Linia 574: | Linia 574: | ||
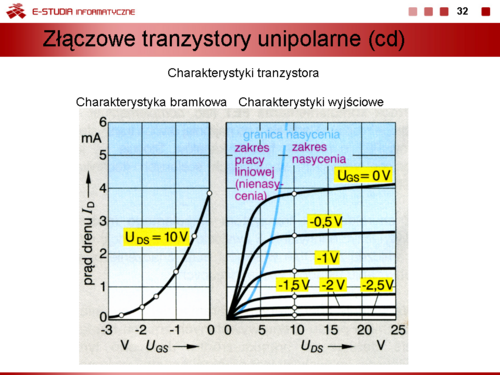
*charakterystykę wyjściową <math>I_D=f(U_{DS})</math> dla <math>U_{GS} = const</math> oraz | *charakterystykę wyjściową <math>I_D=f(U_{DS})</math> dla <math>U_{GS} = const</math> oraz | ||
*charakterystykę przejściową (bramkową) <math>I_D=f(U_{GS})</math> dla <math>U_{DS} = const | *charakterystykę przejściową (bramkową) <math>I_D=f(U_{GS})</math> dla <math>U_{DS} = const</math>. | ||
Podobnie jak dla tranzystorów z izolowana bramką występują tutaj dwa zakresy pracy: liniowy (triodowy) i nasycenia (pentodowy). Granicę obu obszarów wyznacza napięcie <math>U_P = U_{DS} - U_{GS}</math>. | Podobnie jak dla tranzystorów z izolowana bramką występują tutaj dwa zakresy pracy: liniowy (triodowy) i nasycenia (pentodowy). Granicę obu obszarów wyznacza napięcie <math>U_P = U_{DS} - U_{GS}</math>. | ||
| Linia 580: | Linia 580: | ||
Z charakterystyki wyjściowej można wyznaczyć rezystancją dynamiczną tranzystora | Z charakterystyki wyjściowej można wyznaczyć rezystancją dynamiczną tranzystora | ||
:<math> | :<math>r_{DS}=\frac{\delta U_{DS}}{\delta I_D}</math> dla <math>U_{GS} = const</math>. | ||
a z charakterystyki bramkowej istotny z punktu widzenia wzmacniania sygnałów elektrycznych parametr tzw. transkonduktancję <math>g_m\ | a z charakterystyki bramkowej istotny z punktu widzenia wzmacniania sygnałów elektrycznych parametr tzw. transkonduktancję <math>g_m\ </math>, lub inaczej nachylenie charakterystyki bramkowej S | ||
:<math> | :<math>g_m=S=\frac{\delta I_D}{\delta U_{GS}}</math> przy <math>U_{DS} = const</math>. | ||
Charakterystyka bramkowa (przejściowa) tranzystora jest opisana wzorem | Charakterystyka bramkowa (przejściowa) tranzystora jest opisana wzorem | ||
| Linia 590: | Linia 590: | ||
:<math>I_D=I_{DSS}\left(1-\left|\frac{U_{GS}}{U_P} \right|\right)^2</math> | :<math>I_D=I_{DSS}\left(1-\left|\frac{U_{GS}}{U_P} \right|\right)^2</math> | ||
przy czym prąd <math>I_{DSS}\ | przy czym prąd <math>I_{DSS}\ </math>, wyznacza się z charakterystyki bramkowej przy <math>U_{GS} = 0\, V</math>. | ||
|} | |} | ||
| Linia 606: | Linia 606: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd34.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd34.png|thumb|500px]] | ||
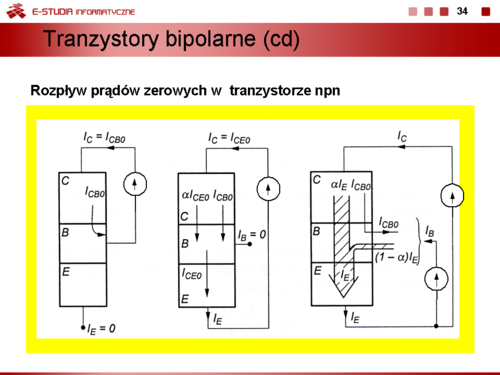
|valign="top"|Zakładając wstępnie, że baza tranzystora nie jest zasilana <math>I_B = 0\, A</math> sytuacja się nie zmieni nadal złącze baza-emiter będzie spolaryzowane w kierunku przewodzenia, a złącze kolektor-baza w kierunku zaporowym. Oba złącza połączone są szeregowo i zasilane ze źródła zewnętrznego napięcia <math>U_{CE}\ | |valign="top"|Zakładając wstępnie, że baza tranzystora nie jest zasilana <math>I_B = 0\, A</math> sytuacja się nie zmieni nadal złącze baza-emiter będzie spolaryzowane w kierunku przewodzenia, a złącze kolektor-baza w kierunku zaporowym. Oba złącza połączone są szeregowo i zasilane ze źródła zewnętrznego napięcia <math>U_{CE}\ </math>,, przy czym należy zauważyć, że poza niewielką częścią polaryzującą złącze baza-emiter w kierunku przewodzenia, praktycznie całe napięcie źródła zasilania <math>U_{CE}\ </math>, odkłada się na wstecznie spolaryzowanym złączu kolektor-baza. Przez tranzystor płynie niewielki prąd generacji termicznej, tzw. prąd zerowy <math>I_{CE0}\ </math>,, który składa się z dwóch części prądu zerowego <math>I_{CB0}\ </math>, płynącego we wstecznie spolaryzowanym złączu kolektor-baza oraz części <math>\alpha_0\cdot I_{CE0}\ </math>, wynikający z efektu tranzystorowego polegającego na przechwytywaniu przez kolektor części elektronów (ładunek mniejszościowy) wstrzykiwanych z emitera do bazy tworzących w złączu baza-emiter prąd <math>I_{CE0}\ </math>,. Pozostała część elektronów tworzących prąd <math>I_{CE0}\ </math>, rekombinuje w bazie równoważąc składową <math>I_{CB0}\ </math>,. Można zatem napisać | ||
:<math>\alpha_0\cdot I_{CE0}+I_{CB0}=I_{CE0}</math> | :<math>\alpha_0\cdot I_{CE0}+I_{CB0}=I_{CE0}</math> | ||
| Linia 612: | Linia 612: | ||
Zatem prądy zerowe w tranzystorze wiąże równanie | Zatem prądy zerowe w tranzystorze wiąże równanie | ||
:<math> | :<math>I_{CE0}=I_{CB0}\frac{1}{1-\alpha_0}</math> | ||
Prądy zerowe w tranzystorze są efektem zjawiska generacji termicznej nośników mniejszościowych. W wypadku złącza kolektor-baza jest to prąd wsteczny tego złącza. Można go zmierzyć przy odłączonym emiterze w układzie jak na rysunku. | Prądy zerowe w tranzystorze są efektem zjawiska generacji termicznej nośników mniejszościowych. W wypadku złącza kolektor-baza jest to prąd wsteczny tego złącza. Można go zmierzyć przy odłączonym emiterze w układzie jak na rysunku. | ||
Kiedy baza tranzystora jest dodatkowo zasilana ze źródła napięcia <math>U_{BE}\ | Kiedy baza tranzystora jest dodatkowo zasilana ze źródła napięcia <math>U_{BE}\ </math>, w emiterze popłynie prąd o wartości znacznie większej niż prąd zerowy <math>I_{CE0}</math>. Część elektronów wstrzykiwanych do bazy podobnie jak poprzednio będzie rekombinowała z dziurami, a pozostała część <math>\alpha_0\cdot I_E</math> , która nie zdąży zrekombinować, pod wpływem silnego pola elektrycznego w złączu kolektorowym, będzie przechwycona przez kolektor. Zatem prąd jaki płynie w spolaryzowanym zaporowo złączu kolektor-baza nie jest wynikiem wstrzykiwania nośników do kolektora, lecz przechwytywania ich z bazy. Zjawisko to nosi nazwę efektu tranzystorowego i występuje tylko wtedy, gdy obszar bazy jest odpowiednio wąski. | ||
|} | |} | ||
| Linia 627: | Linia 627: | ||
:<math>I_C=\alpha_0\cdot I_E+I_{CB0}</math> | :<math>I_C=\alpha_0\cdot I_E+I_{CB0}</math> | ||
Współczynnik <math>\alpha_0\ | Współczynnik <math>\alpha_0\ </math>, nazywamy statycznym współczynnikiem wzmocnienia prądowego w układzie wspólnej bazy. | ||
:<math> | :<math>\alpha_0=\frac{I_C-I_{CB0}}{I_E}\cong \frac{I_C}{I_E}</math> | ||
Dla układu wspólnego emitera statyczny współczynnik wzmocnienia prądowego jest definiowany jako | Dla układu wspólnego emitera statyczny współczynnik wzmocnienia prądowego jest definiowany jako | ||
:<math> | :<math>\beta_0=\frac{I_C-I_{CB0}}{I_B+I_{CB0}}=\frac{\alpha_0\cdot I_E}{I_B+I_C-\alpha_0\cdot I_E}=\frac{1}{1-\alpha_0}\cong \frac{I_C}{I_B}</math> | ||
a zatem | a zatem | ||
:<math> | :<math>\beta_0+1=\frac{1}{1-\alpha_0}</math> | ||
Uwzględniając prąd bazy równanie prądu kolektora przyjmie postać | Uwzględniając prąd bazy równanie prądu kolektora przyjmie postać | ||
| Linia 645: | Linia 645: | ||
Oprócz statycznych współczynników wzmocnienia prądowego (inaczej dla dużych sygnałów lub dla prądu stałego) stosuje się także dynamiczne (małosygnałowe, przyrostowe lub dla składowej zmiennej) współczynniki wzmocnienia prądowego | Oprócz statycznych współczynników wzmocnienia prądowego (inaczej dla dużych sygnałów lub dla prądu stałego) stosuje się także dynamiczne (małosygnałowe, przyrostowe lub dla składowej zmiennej) współczynniki wzmocnienia prądowego | ||
:<math> | :<math>\alpha=\frac{i_C}{i_E}\bigg|_{u_{CB}=0}=\frac{\Delta I_C}{\Delta I_E}\bigg|_{U_{CB}=const</math> | ||
:<math> | :<math>\beta=\frac{i_C}{i_B}\bigg|_{u_{CE}=0}=\frac{\Delta I_C}{\Delta I_B}\bigg|_{U_{CE}=const</math> | ||
| Linia 658: | Linia 658: | ||
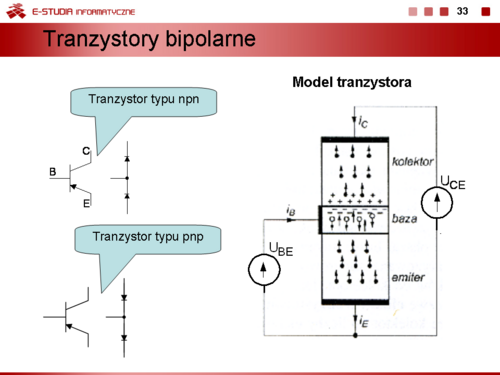
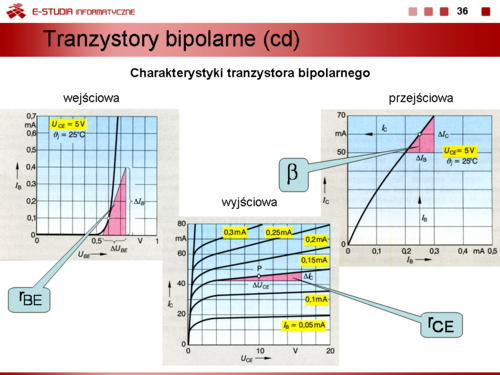
|valign="top"|Podstawowe charakterystyki tranzystora. Przyjmując, że emiter jest elektrodą wspólna można wyróżnić w tranzystorze bipolarnym dwa obwody: obwód baza-emiter, zwany często wejściowym (sterującym) i obwód kolektor-emiter zwany wyjściowym. | |valign="top"|Podstawowe charakterystyki tranzystora. Przyjmując, że emiter jest elektrodą wspólna można wyróżnić w tranzystorze bipolarnym dwa obwody: obwód baza-emiter, zwany często wejściowym (sterującym) i obwód kolektor-emiter zwany wyjściowym. | ||
Dla obwodu wejściowego wyznacza się charakterystykę wejściową. Jest to zależność <math>I_B = f(U_{BE})</math> przy <math>U_{CE} = const | Dla obwodu wejściowego wyznacza się charakterystykę wejściową. Jest to zależność <math>I_B = f(U_{BE})</math> przy <math>U_{CE} = const</math>. Ponieważ wpływ napięcia <math>U_{CE}</math> na przebieg tej charakterystyki jest znikomy w szerokim zakresie zmienności tego napięcia rodzinę tych charakterystyk wyznacza linia przedstawiona na rysunku. Z charakterystyki tej można wyznaczyć dynamiczną rezystancję wejściową tranzystora <math>r_{BE}</math> | ||
:<math> | :<math>r_{BE}=\frac{u_{BE}}{i_B}\bigg|_{u_{CE}=0}=\frac{\Delta U_{BE}}{\Delta I_B}\bigg|_{U_{CE}=const</math> | ||
Dla obwodu wyjściowego wyznacza się rodzinę charakterystyk wyjściowych. Jest to zależność <math>I_C = f(U_{CE})</math> przy <math>I_B = const | Dla obwodu wyjściowego wyznacza się rodzinę charakterystyk wyjściowych. Jest to zależność <math>I_C = f(U_{CE})</math> przy <math>I_B = const</math>. | ||
Rzadziej parametrem jest napięcie <math>U_{BE} = const | Rzadziej parametrem jest napięcie <math>U_{BE} = const</math>. | ||
Z charakterystyki wyjściowej można wyznaczyć dynamiczną rezystancję wyjściową tranzystora <math>r_{CE}</math> | Z charakterystyki wyjściowej można wyznaczyć dynamiczną rezystancję wyjściową tranzystora <math>r_{CE}</math> | ||
:<math> | :<math>r_{CE}=\frac{u_{CE}}{i_C}\bigg|_{i_B=0}=\frac{\Delta U_{CE}}{\Delta I_C}\bigg|_{I_B=const</math> | ||
Zależność <math>I_C = f(I_B)</math> przy </math>U_{CE} = const</math> przedstawia charakterystykę przejściową tranzystora. Z tej charakterystyki można wyznaczyć statyczny i dynamiczny współczynnik wzmocnienia prądowego. | Zależność <math>I_C = f(I_B)</math> przy</math>U_{CE} = const</math> przedstawia charakterystykę przejściową tranzystora. Z tej charakterystyki można wyznaczyć statyczny i dynamiczny współczynnik wzmocnienia prądowego. | ||
| Linia 691: | Linia 691: | ||
*częstotliwość <math>f_{\alpha}</math> – częstotliwość przy której wartość współczynnika <math>\alpha</math> zmniejszy się o 3 dB w stosunku do wartości <math>\alpha_0</math> | *częstotliwość <math>f_{\alpha}</math> – częstotliwość przy której wartość współczynnika <math>\alpha</math> zmniejszy się o 3 dB w stosunku do wartości <math>\alpha_0</math> | ||
*częstotliwość <math>f_{\beta}</math> – częstotliwość przy której wartość współczynnika <math>\beta</math> zmniejszy się o 3 dB w stosunku do wartości <math>\beta_0</math> | *częstotliwość <math>f_{\beta}</math> – częstotliwość przy której wartość współczynnika <math>\beta</math> zmniejszy się o 3 dB w stosunku do wartości <math>\beta_0</math> | ||
*częstotliwość <math>f_T\ | *częstotliwość <math>f_T\ </math>, – częstotliwość przy której wartość współczynnika <math>\beta</math> zmniejszy się do wartości 1 | ||
Dla częstotliwości granicznych zachodzi nierówność | Dla częstotliwości granicznych zachodzi nierówność | ||
| Linia 709: | Linia 709: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd38.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd38.png|thumb|500px]] | ||
|valign="top"|Wpływ temperatury na parametry tranzystora. Prądy zerowe w tranzystorze bipolarnym rosną wraz z temperaturą <math>T_j\ | |valign="top"|Wpływ temperatury na parametry tranzystora. Prądy zerowe w tranzystorze bipolarnym rosną wraz z temperaturą <math>T_j\ </math>, struktury półprzewodnikowej | ||
:<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot e^{ | :<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot e^{b\cdot (T-T_j)}</math> | ||
gdzie b = 0,07 dla Ge, b = 0,12 dla Si | gdzie b = 0,07 dla Ge, b = 0,12 dla Si | ||
| Linia 719: | Linia 719: | ||
dla germany | dla germany | ||
:<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot 2^{ | :<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot 2^{\frac{(T-T_j)}{6}}</math> | ||
lub dla krzemu | lub dla krzemu | ||
:<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot 2^{ | :<math>I_{CB0}(T)=I_{CB0}(T_j)\cdot 2^{\frac{(T-T_j)}{10}}</math> | ||
Także napięcie na złączu baza-emiter zmienia się w funkcji temperatury. Współczynnik temperaturowy tego napięcia jest ujemny (napięcie maleje ze wzrostem temperatury) i ma wartość 2,3 mV/ K. | Także napięcie na złączu baza-emiter zmienia się w funkcji temperatury. Współczynnik temperaturowy tego napięcia jest ujemny (napięcie maleje ze wzrostem temperatury) i ma wartość 2,3 mV/ K. | ||
Temperatura struktury półprzewodnikowej (złącza) <math>T_j\ | Temperatura struktury półprzewodnikowej (złącza) <math>T_j\ </math>, zależy od trzech czynników: | ||
*mocy traconej w tranzystorze <math>P_C = U_{CE}\cdot I_C + U_{BE}\cdot I_B \approx U_{CE}\cdot I_C</math> | *mocy traconej w tranzystorze <math>P_C = U_{CE}\cdot I_C + U_{BE}\cdot I_B \approx U_{CE}\cdot I_C</math> | ||
*temperatury otoczenia <math>T_0\ | *temperatury otoczenia <math>T_0\ </math>, | ||
*rezystancji termicznej Rth przejścia złącze-obudowa-radiator-otoczenie | *rezystancji termicznej Rth przejścia złącze-obudowa-radiator-otoczenie | ||
| Linia 750: | Linia 750: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M12_Slajd40.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M12_Slajd40.png|thumb|500px]] | ||
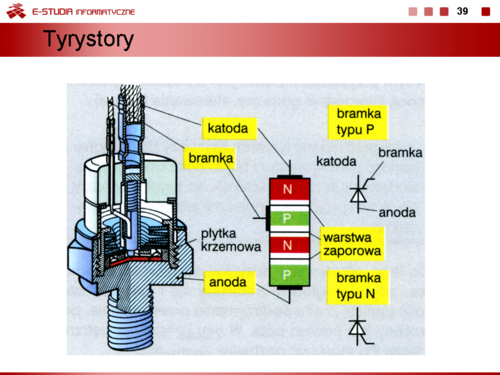
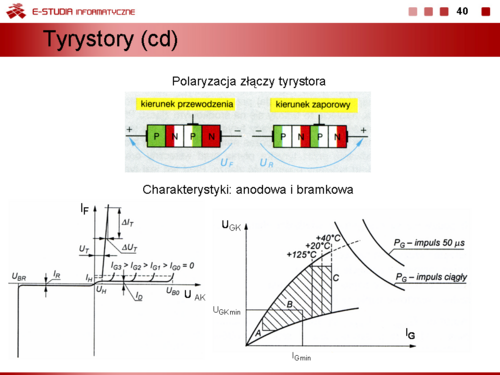
|valign="top"|Wewnętrzna struktura tyrystora zawiera trzy złącza półprzewodnikowe. Jeżeli pomiędzy anodę i katodę przyłoży się napięcie to zawsze któreś złącze będzie spolaryzowane w kierunku zaporowym i przez tyrystor nie będzie płynął prąd. Gdy napięcie <math>U_{AK} > 0\, V</math>, tzn. anoda ma wyższy potencjał niż katoda, tylko jedno złącze jest spolaryzowane zaporowo i stan w którym znajduje się tyrystor nazywamy stanem blokowania. W tym stanie, po wymuszeniu w obwodzie bramkowym prądu o odpowiedniej wartości można załączyć tyrystor i wymusić w obwodzie anoda-katoda prąd roboczy <math>I_F\ | |valign="top"|Wewnętrzna struktura tyrystora zawiera trzy złącza półprzewodnikowe. Jeżeli pomiędzy anodę i katodę przyłoży się napięcie to zawsze któreś złącze będzie spolaryzowane w kierunku zaporowym i przez tyrystor nie będzie płynął prąd. Gdy napięcie <math>U_{AK} > 0\, V</math>, tzn. anoda ma wyższy potencjał niż katoda, tylko jedno złącze jest spolaryzowane zaporowo i stan w którym znajduje się tyrystor nazywamy stanem blokowania. W tym stanie, po wymuszeniu w obwodzie bramkowym prądu o odpowiedniej wartości można załączyć tyrystor i wymusić w obwodzie anoda-katoda prąd roboczy <math>I_F\ </math>,. Przy polaryzacji przeciwnej tj. <math>U_{AK} < 0\, V</math> dwa złącza są spolaryzowane w kierunku zaporowym i stan w którym znajduje się tyrystor nazywamy stanem zaworowym. Tyrystor zachowuje się zatem jak sterowana dioda półprzewodnikowa dlatego można je zastosować w układach prostowników sterowanych lub łącznikach bezstykowych. Po załączeniu tyrystora, żeby przerwać przepływ prądu głównego (obciążenia) i odzyskać własności zaworowe przyrządu należy zmienić kierunek przepływu prądu głównego. Tyrystor wyłączy się tzn. odzyska właściwości zaworowe wtedy kiedy prąd główny zmniejszy swoją wartość poniżej prądu podtrzymania <math>I_H\ </math>,. Jeżeli tyrystor pracuje w obwodzie prądu przemiennego to przy końcu każdej dodatniej półfali napięcia zasilającego prąd przewodzenia w sposób naturalny jest mniejszy od prądu <math>I_H\ </math>, i tyrystor wyłączy się. W obwodach, w których nie występuje komutacja naturalna należy zastosować specjalne obwody zwane obwodami komutacyjnymi, które wymuszają przez odpowiednio długi czas przepływ prądu wstecznego w tyrystorze i w ten sposób zmniejszają prąd przewodzenia poniżej wartości prądu podtrzymania i wyłączają tyrystor. Czas wyłączania tyrystora potrzebny na odprowadzenie ładunku z wewnętrznego złącza przyrządu jest stosunkowo długi od <math>100\, \mu s</math> do <math>300\, \mu s</math>. W tyrystorach szybkich może być mniejszy rzędu <math>5\, \mu s</math>. | ||
Podczas narastania napięcia blokowania przez tyrystor płynie prąd ładujący pojemność złącza. Prąd ten jest tym większy im szybciej narasta napięcie blokowania. Wewnętrzne złącze może być tak silnie wzbogacane ładunkiem, że tyrystor bez udziału prądu bramki samoczynnie załączy się. Aby temu zapobiec szybkość narastania napięcia blokowania nie może być większa od wartości dopuszczalnej. Wartość ta leży w zakresie od <math>50 V/ {\mu s}</math> do <math>1000 V/ {\mu s}</math>. Podczas załączania prąd główny (anodowy) tyrystora również nie może narastać zbyt szybko, np. przy złączaniu obciążenia o charakterze pojemnościowym lub rezystancyjnym, ponieważ w tym wypadku pastylka krzemowa może ulec uszkodzeniu przez punktowe przegrzanie struktury. Dopuszczalne wartości prędkości narastania prądu anodowego w zależności od typu tyrystora zmieniają się w zakresie od <math>100 A/ {\mu s}</math> do <math>1000 A/ {\mu s}</math>. | Podczas narastania napięcia blokowania przez tyrystor płynie prąd ładujący pojemność złącza. Prąd ten jest tym większy im szybciej narasta napięcie blokowania. Wewnętrzne złącze może być tak silnie wzbogacane ładunkiem, że tyrystor bez udziału prądu bramki samoczynnie załączy się. Aby temu zapobiec szybkość narastania napięcia blokowania nie może być większa od wartości dopuszczalnej. Wartość ta leży w zakresie od <math>50 V/ {\mu s}</math> do <math>1000 V/ {\mu s}</math>. Podczas załączania prąd główny (anodowy) tyrystora również nie może narastać zbyt szybko, np. przy złączaniu obciążenia o charakterze pojemnościowym lub rezystancyjnym, ponieważ w tym wypadku pastylka krzemowa może ulec uszkodzeniu przez punktowe przegrzanie struktury. Dopuszczalne wartości prędkości narastania prądu anodowego w zależności od typu tyrystora zmieniają się w zakresie od <math>100 A/ {\mu s}</math> do <math>1000 A/ {\mu s}</math>. | ||
| Linia 779: | Linia 779: | ||
---- | ---- | ||
'''Literatura''' | |||
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, | |||
Oficyna Wydawnicza PW, Warszawa 2005 | |||
J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, | |||
WNT, Warszawa 1981 | |||
P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976 | |||
Aktualna wersja na dzień 12:02, 5 wrz 2023
 |
Podstawowe elementy półprzewodnikowe |
 |
Elementy jednozłączowe
Wyróżnia się: Złącza półprzewodnikowe Złącza metal-półprzewodnik |
Literatura
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza PW, Warszawa 2005
J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, WNT, Warszawa 1981
P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976