PF Moduł 4a

Zasady dynamiki Newtona stanowią podstawę opisu wszelkich ruchów obiektów makroskopowych. W wielu przypadkach warto jednak skorzystać z innych zasad fizyki. Sa to tzw. zasady zachowania stwierdzające, że w danym procesie nie ulega zmianie określona wielkość fizyczna. Zasady te pozostają w zgodności z prawami dynamiki Newtona, chociaż ich sformułowanie nie odwołuje się do tych zasad bezpośrednio. W oparciu o zasady zachowania, bardzo łatwo jest zrozumieć np. istotę napędu odrzutowego lub rakietowego czy utrzymywanie pozycji pionowej pojazdów jednośladowych w ruchu i wiele innych procesów i zjawisk fizycznych. Jako wstęp do omówienia zasad zachowania wprowadzimy pojęcia pracy, mocy i energii mechanicznej. Omówimy też kilka przykładów zjawisk, których własności wynikają bezpośrednio z określonych zasad zachowania.

---

Praca w fizyce zdefiniowana jest jako iloczyn skalarny wektora siły i wektora przesunięcia wskutek działania tej siły. Z definicji tej wynika natychmiast, że tylko składowa siły równoległa do wektora przesunięcia wykonuje pracę. Kiedy w czasie ruchu zmianie ulega wartość siły lub jej kierunek względem kierunku przesunięcia, wówczas praca musi być wyznaczona jako całka oznaczona na określonym, skończonym odcinku drogi.

---

Kiedy na ciało działa równocześnie kilka sił, wówczas sumaryczna praca jest sumą prac wykonanych przez poszczególne siły. Praca wykonana w jednostce czasu przez daną siłę, to moc przypisywana układowi, który jest źródłem tej siły.

---

Jednostką pracy jest dżul. Jest to praca wykonana przez siłę o jednostkowej wartości tzn. jednego Newtona na odcinku równym jednej jednostce długości tzn jednego metra. Popularną w energetyce jednostką pracy jest kilowatogodzina. Dla jej zdefiniowania trzeba określić jednostkę mocy, którą jest jeden wat. Jest to moc urządzenia, które wykonuje pracę jednego dżula w czasie jednej sekundy. Kilowatogodzina, to praca wykonana przez urządzanie o mocy tysiąca watów w czasie jednej godziny, lub innej równoważnej kombinacji mocy i czasu.

---

Kiedy wchodzimy na górę, wykonujemy pracę przeciwko siłom grawitacji. (Można też powiedzieć, że siły grawitacji wykonują w tym przypadku pracę ujemną.) Zauważamy natychmiast, że wykonanie tej pracy umożliwia nam pokonanie drogi powrotnej bez wkładu pracy z naszej strony. (Siły grawitacji wykonują pracę dodatnią.) Możemy np. zjechać na nartach i nie tylko bez wysiłku znaleźć się w punkcie wyjścia, ale także posiadać sporą prędkość nabyta podczas zjazdu. Kiedy jednak posuwamy się po terenie płaskim, możliwości takiej nie nabywamy pomimo, że wykonujemy zwykle pewną pracę pokonując oporu ruchu.

---

Można pokazać, żę sumaryczna praca sił grawitacji w cyklu zamkniętym równa jest zeru. Jeśli dana siła spełnia ten warunek, wówczas sile taką nazywamy siłą zachowawczą. Siły nie spełniające tego warunku nazywamy siłami dyssypatywnymi lub rozpraszającymi. Siłami takimi są właśnie siły oporów ruchu.

---

Można pokazać także, że w przypadku działania sił zachowawczych praca przy przemieszczeniu ciała pomiędzy dwoma punktami zależy wyłącznie od położenia tych punktów, a nie zależy od drogi, po której odbywało się przemieszczenie pomiędzy tymi punktami.

---

Konsekwencją wykonanej pracy jest przemieszczenie ciała, ale mogą być również i inne skutki, np. ogrzanie ciała lub zmiany w jego otoczeniu (ślady na śniegu). Jeśli praca dotyczy sił zachowawczych, wówczas jej wykonanie powoduje zmianę wielkości zwanej energią. Energia z kolei umożliwia wykonanie pracy. W mechanice wyróżniamy dwa rodzaje energii: energię potencjalną i energię kinetyczną. Energia potencjalna związana jest z położeniem ciała, energia kinetyczna – z jego ruchem. Dla zdefiniowania energii potencjalnej ciała musimy najpierw określić położenie punktu odniesienia względem którego energię tę będziemy definiować. Energię potencjalną określamy za pomocą wprowadzonego już pojęcia pracy. Energia potencjalna ciała w danym punkcie, względem określonego punktu odniesienia, równa jest pracy jaką wykonują siły zachowawcze przy przemieszczeniu ciała z danego punktu do punktu odniesienia. Nie bez powodu zaznaczamy, że chodzi tu o pracę sił zachowawczych. Praca wykonywana przez siły dyssypatywne powoduje wydzielenie się ciepła, wywołuje różnorodne skutki zewnętrzne i zamienia się na inne niż mechaniczne rodzaje energii. Ta rozproszona energia nie stanowi energii potencjalnej ciała.

---

Energia kinetyczna, która wiąże się z ruchem ciała proporcjonalne jest do masy ciała i kwadratu jego prędkości. Zwróćmy uwagę, na ważną zależność pomiędzy pracą ciała (lub pracą otoczenia nad ciałem) a jego energią; potencjalną lub kinetyczną. Wykonana praca zmienia energię ciała. Ale nie stanowi jego energii całkowitej. Dlatego energię określamy względem danego punktu odniesienia, z którym wiążemy współrzędne położenia ciała i stan jego ruchu (wektor prędkości).

---

Jeśli na ciało działają tylko siły zachowawcze, to energia mechaniczna ciała pozostaje stała, niezależnie od ruchu tego ciała. Zachodzą jedynie przemiany energii potencjalnej w energię kinetyczną i na odwrót. Kiedy na ciało działają siły dyssypatywne zasada zachowania energii mechanicznej nie jest spełniona. Siły te zmieniają energię mechaniczną ciała. Następuje zamiana energii mechanicznej na inne rodzaje energii, np. energię cieplną, chemiczną, elektryczną, jądrową itp. Zasada zachowania energii może być jednak sformułowana bardziej ogólnie. Rozpatrzmy układ odosobniony, czyli taki, który w żaden sposób nie oddziałuje z otoczeniem, a więc nie wymienia ani energii ani masy z otoczeniem i weźmy pod uwagę sumę wszystkich postaci energii w dowolnych procesach zachodzących w tym układzie. Nazwijmy tę energię - całkowitą energią układu. Zasadę zachowania energii możemy sformułować wtedy w sposób ogólny: Energia całkowita układu odosobnionego jest stała. Zasada zachowania energii należy do fundamentalnych zasad fizyki, chociaż sformułowana została na podstawie faktów doświadczalnych i może być obalona przez stwierdzenie faktów przeczących jej słuszności. Faktów takich dotychczas nie znaleziono. Ich poszukiwania doprowadziły natomiast do odkrycia wielu efektów fizycznych, których nieuwzględnienie interpretowano początkowo jako niezgodność z zasadą zachowania energii.

---

Druga zasada dynamiki dla układu punktów materialnych wyraża związek pomiędzy pochodną względem czasu całkowitego pędu układu a wypadkową sił zewnętrznych działających na układ. Kiedy wypadkowa tych sił wynosi zero, to równa jest także zeru pochodna całkowitego pędu względem czasu, co oznacza, że sam pęd nie zmienia się, tzn. pozostaje stały co do wartości, kierunku i zwrotu. Stwierdzenie to wyraża zasadę zachowania pędu. Jeżeli na układ nie działają siły zewnętrzne lub działa układ sił zrównoważonych, to pęd układu pozostaje stały. Na szczególne podkreślenie zasługuje niezależność całkowitego pędu układu od wszelkich oddziaływań wewnętrznych pomiędzy jego elementami. Kiedy więc jakiś element układu uzyskuje pęd w wyniku zachodzących w układzie procesów, pozostała część układu uzyskuje pęd o tej samej wartości, lecz przeciwnie skierowany. To właśnie zachowanie pędu jest podstawą działania silników odrzutowych i rakietowych, jest też powodem odrzutu przy strzałach z broni palnej itd.

---

Przykładem wykorzystania zasady zachowania pędu w praktyce jest efektowne i łatwe do wykonania doświadczenie, w którym z butelki wyrzucana jest woda pod ciśnieniem, wskutek czego butelka wzlata na znaczna wysokość w powietrzu. Jest to bezpośrednią konsekwencją zasady zachowania pędu.

---

Analogiczną do zasady zachowania pędu jest dla ruchów obrotowych zasada zachowania momentu pędu. Warto dodać, że nawet kiedy układ jest pod działaniem siły zewnętrznej, ale tak działającej, że jej moment będzie równy zeru, to moment pędu również pozostanie stały.

---

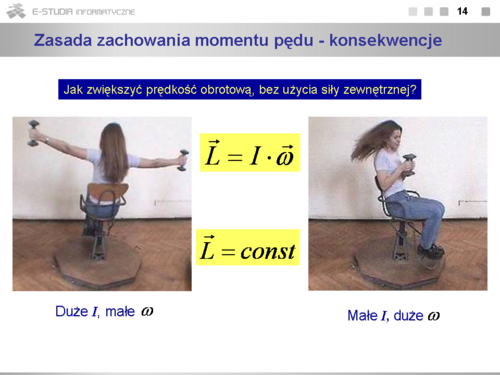Efektowny przykład demonstrujący zasadę zachowania momentu pędu. Na tej samej zasadzie opiera się pokaz piruetów w jeździe figurowej na lodzie.

---