PF Moduł 4: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „<math> ” na „<math>” |
||
| (Nie pokazano 7 wersji utworzonych przez 2 użytkowników) | |||
| Linia 6: | Linia 6: | ||
W mechanice uważa się, że materia składa się z cząstek obdarzonych masą, które poruszają się pod wpływem sił. Ruch takiej cząstki określony jest jej energią i wektorem pędu. | W mechanice uważa się, że materia składa się z cząstek obdarzonych masą, które poruszają się pod wpływem sił. Ruch takiej cząstki określony jest jej energią i wektorem pędu. | ||
W myśl teorii Maxwella zjawiska elektromagnetyczne można opisać za pomocą pola elektrycznego i pola magnetycznego. Pola te rozchodzą się w przestrzeni jako fale elektromagnetyczne charakteryzowane częstotliwością | W myśl teorii Maxwella zjawiska elektromagnetyczne można opisać za pomocą pola elektrycznego i pola magnetycznego. Pola te rozchodzą się w przestrzeni jako fale elektromagnetyczne charakteryzowane częstotliwością \nu i wektorem propagacji k. Cząstki i fale są odrębnymi składnikami przyrody. | ||
Taki obraz, w którym materia składa się cząstek a promieniowanie z fal stanowi podstawe do zadowalającego opisu makroświata. Okazuje się jednak, że opis taki jest zawodny w przypadku zjawisk zachodzących na poziomie mikrocząstek. Wobec tego należało zasadniczo zreformować teorię tak aby poglądy klasyczne, które są prawdziwe były naturalną konsekwencją teorii ogólniejszej, która nazywamy teorią kwantową. | Taki obraz, w którym materia składa się cząstek a promieniowanie z fal stanowi podstawe do zadowalającego opisu makroświata. Okazuje się jednak, że opis taki jest zawodny w przypadku zjawisk zachodzących na poziomie mikrocząstek. Wobec tego należało zasadniczo zreformować teorię tak aby poglądy klasyczne, które są prawdziwe były naturalną konsekwencją teorii ogólniejszej, która nazywamy teorią kwantową. | ||
| Linia 15: | Linia 15: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd2.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd2.png|thumb|500px]] | ||
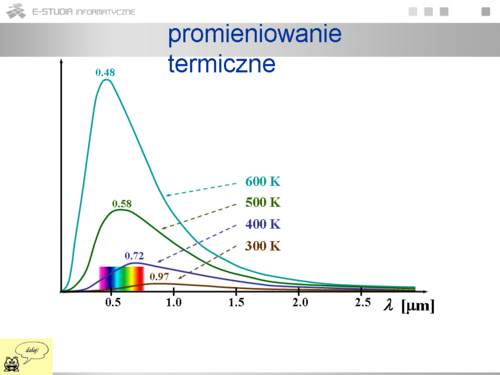
|valign="top"|Świecenie ciał czyli wypromieniowywanie fal elektromagnetycznych odbywa się kosztem różnego rodzaju energii. Najbardziej typowym jest promieniowanie termiczne odbywające się kosztem energii wewnętrznej ciał. Promieniowanie to emitowane jest w każdej temperaturze chociaż w niewielkich temperaturach ciała wysyłają jedynie długofalowe promieniowanie zwane podczerwonym. Jednocześnie zachodzi zjawisko odwrotne czyli absorbcja promieniowania przez ciało. Gdy ciało ma określoną temperaturę następuje równowaga między promieniowaniem a ciałem. Wówczas mamy do czynienia z charakterystycznym, zależnym od temperatury widmem promieniowania termicznego czyli rozkładem względnym natężeniem odpowiadającym różnym długościom fal elektromagnetycznych. Jeżeli temperatura jest odpowiednio wysoka (1500 K) w widmie pojawiają się nie tylko fale podczerwone ale również widzialne ( | |valign="top"|Świecenie ciał czyli wypromieniowywanie fal elektromagnetycznych odbywa się kosztem różnego rodzaju energii. Najbardziej typowym jest promieniowanie termiczne odbywające się kosztem energii wewnętrznej ciał. Promieniowanie to emitowane jest w każdej temperaturze chociaż w niewielkich temperaturach ciała wysyłają jedynie długofalowe promieniowanie zwane podczerwonym. Jednocześnie zachodzi zjawisko odwrotne czyli absorbcja promieniowania przez ciało. Gdy ciało ma określoną temperaturę następuje równowaga między promieniowaniem a ciałem. Wówczas mamy do czynienia z charakterystycznym, zależnym od temperatury widmem promieniowania termicznego czyli rozkładem względnym natężeniem odpowiadającym różnym długościom fal elektromagnetycznych. Jeżeli temperatura jest odpowiednio wysoka (1500 K) w widmie pojawiają się nie tylko fale podczerwone ale również widzialne (\lambda = 380 ÷ 550 nm), ciało zaczyna świecić. Istnieją dokładne metody pomiarowe wyznaczające widma promieniowania ciał w zależności od temperatury. Teoretyczne wyjaśnienie praw promieniowania miało doniosłe znaczenie w historii fizyki i doprowadziło do powstania pojęcia kwantów energii. | ||
|} | |} | ||
---- | ---- | ||
| Linia 29: | Linia 29: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd4.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd4.png|thumb|500px]] | ||
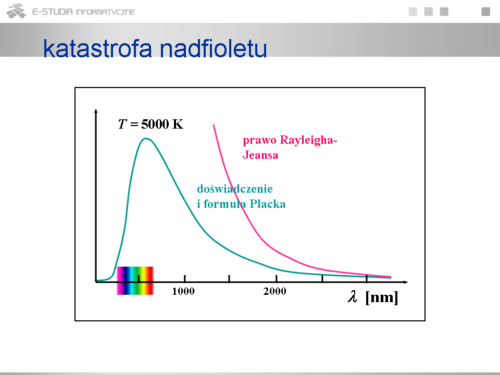
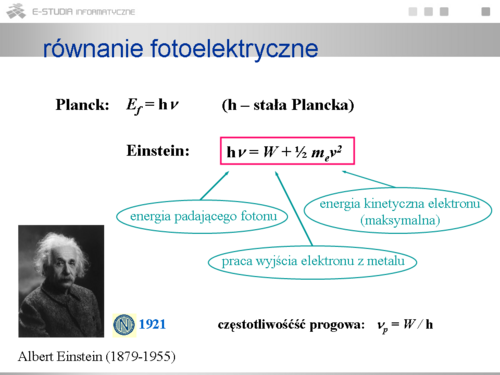
|valign="top"|W roku 1900 Planck znalazł funkcyjną postać gęstości wypromieniowanej energii w zależności od częstotliwości promieniowania i temperatury promieniującego ciała. Musiał w tym celu zrobić założenie, które było całkowicie sprzeczne z klasycznymi wyobrażeniami, a mianowicie musiał przyjąć, że promieniowanie elektromagnetyczne emitowane jest w postaci osobnych porcji energii, tzw. kwantów energii, o wartości proporcjonalnej do częstotliwości promieniowania: E = | |valign="top"|W roku 1900 Planck znalazł funkcyjną postać gęstości wypromieniowanej energii w zależności od częstotliwości promieniowania i temperatury promieniującego ciała. Musiał w tym celu zrobić założenie, które było całkowicie sprzeczne z klasycznymi wyobrażeniami, a mianowicie musiał przyjąć, że promieniowanie elektromagnetyczne emitowane jest w postaci osobnych porcji energii, tzw. kwantów energii, o wartości proporcjonalnej do częstotliwości promieniowania: <math>E = h\nu</math>. Współczynnik proporcjonalności h, nazwany później stałą Plancka został wyznaczony przez porównanie z danymi doświadczalnymi, <math>h = 6.626 \cdot 10^{-34} Js</math>. Otrzymany przez Plancka wzór daje wyczerpujący i w pełni zgodny z pomiarami opis zrównoważonego promieniowania termicznego. Jednocześnie wykracz poza granicę rozumienia promieniowania wyłącznie jako fali elektromagnetycznej. | ||
'''Słowa kluczowe''' | '''Słowa kluczowe''' | ||
| Linia 58: | Linia 58: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd6.png|thumb|500px]] | ||
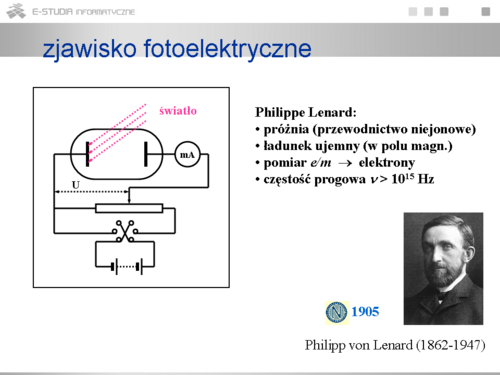
|valign="top"|Zjawisko fotoelektryczne było zbadane przez Lenarda. W bańce próżniowej są zatopione dwie elektrody. Na jedną z nich (fotoelektrodę) skierowany jest strumień światła. Wytwarzając napięcie między elektrodami obserwuje się przepływ prądu. Czym są nośniki tego prądu płynącego przez próżnię? W polu magnetycznym odchylają się jak ładunki ujemne. Zmierzony stosunek ładunku do masy tych nośników wynosi: <math> e/m = 1.76 \cdot 10^{-11} C/kg</math>, co dowodzi że są to elektrony i niewątpliwie są to elektrony wybite z fotoelektrody. Ważną cechą zjawiska jest występowanie częstotliwości progowej. Światło wywołuje zjawisko fotoelektryczne tylko wówczas gdy jego częstotliwość przekracza pewną wartość charakterystyczną dla materiału, z którego zrobiona jest fotoelektroda. Dlaczego? | |valign="top"|Zjawisko fotoelektryczne było zbadane przez Lenarda. W bańce próżniowej są zatopione dwie elektrody. Na jedną z nich (fotoelektrodę) skierowany jest strumień światła. Wytwarzając napięcie między elektrodami obserwuje się przepływ prądu. Czym są nośniki tego prądu płynącego przez próżnię? W polu magnetycznym odchylają się jak ładunki ujemne. Zmierzony stosunek ładunku do masy tych nośników wynosi: <math>e/m = 1.76 \cdot 10^{-11} C/kg</math>, co dowodzi że są to elektrony i niewątpliwie są to elektrony wybite z fotoelektrody. Ważną cechą zjawiska jest występowanie częstotliwości progowej. Światło wywołuje zjawisko fotoelektryczne tylko wówczas gdy jego częstotliwość przekracza pewną wartość charakterystyczną dla materiału, z którego zrobiona jest fotoelektroda. Dlaczego? | ||
|} | |} | ||
---- | ---- | ||
| Linia 106: | Linia 106: | ||
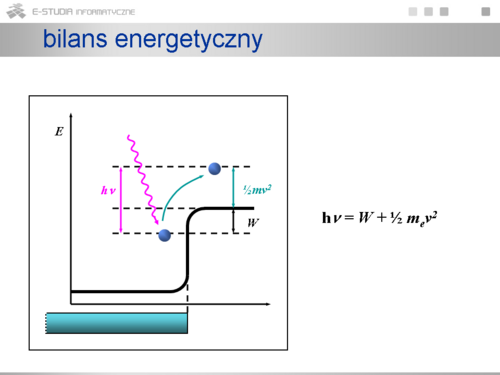
• oszacowanie pracy wyjścia W dla różnych materiałów, | • oszacowanie pracy wyjścia W dla różnych materiałów, | ||
• jednakowe nachylenie prostych niezależnie od materiału czyli uniwersalny | • jednakowe nachylenie prostych niezależnie od materiału czyli uniwersalny charakter stałej Plancka. Doświadczenie pozwoliło na dokładne wyznaczenie tej stałej. | ||
| Linia 116: | Linia 115: | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd11.png|thumb|500px]] | ||
|valign="top"|W swym ważnym doświadczeniu Millikan wykazał poprawność równania fotoelektrycznego | |valign="top"|W swym ważnym doświadczeniu Millikan wykazał poprawność równania fotoelektrycznego | ||
Einsteina, które z kolei bazuje na hipotezie kwantowej Plancka. Dowodzi to fundamentalnej dwoistości natury światła. Jest ono z jednej strony falą elektromagnetyczną o czym świadczą zjawiska interferencji, dyfrakcji i polaryzacji. Z drugiej strony jest ono strumieniem bezmasowych kwantów energii promienistej, zwanych fotonami, o czym świadczą zjawiska związane z emisją i absorpcją światła. Jak wynika z tych pomiarów „granulacja” energii promienistej jest związana ze stałą Plancka. Wartość tej fundamentalnej stałej definiuje nam gdzie zaczyna się świat kwantowy. Stała ta jest bardzo mała i wynika z tego, że kwantowe jest to co jest małe, tak małe jak stała Planka. Należy podkreślić, że własności falowe fotonu nie są związane z jego występowaniem w intensywnych wiązkach. Jak wykazano w późniejszych badaniach własności falowe przejawia nawet pojedynczy foton (taki foton też doznaje dyfrakcji). To, że stała Planka jest stałą fundamentalną, definiującą nasz Świat oznacza, że nie wiemy dlaczego wynosi ona <math>h = 6.67 \cdot 10^{-32} Js</math>, możemy ją tylko zmierzyć i zrozumieć jakie znaczenia ma wartość tej stałej w budowie Świata. Często używa się we wzorach zmodyfikowanej stałej <math>ħ = h/2\pi</math>. Wówczas energia fotonu wyraża się jako <math>ħ\omega</math>, gdzie<math> \omega</math> to tzw. częstość kołowa. | Einsteina, które z kolei bazuje na hipotezie kwantowej Plancka. Dowodzi to fundamentalnej dwoistości natury światła. Jest ono z jednej strony falą elektromagnetyczną o czym świadczą zjawiska interferencji, dyfrakcji i polaryzacji. Z drugiej strony jest ono strumieniem bezmasowych kwantów energii promienistej, zwanych fotonami, o czym świadczą zjawiska związane z emisją i absorpcją światła. Jak wynika z tych pomiarów „granulacja” energii promienistej jest związana ze stałą Plancka. Wartość tej fundamentalnej stałej definiuje nam gdzie zaczyna się świat kwantowy. Stała ta jest bardzo mała i wynika z tego, że kwantowe jest to co jest małe, tak małe jak stała Planka. Należy podkreślić, że własności falowe fotonu nie są związane z jego występowaniem w intensywnych wiązkach. Jak wykazano w późniejszych badaniach własności falowe przejawia nawet pojedynczy foton (taki foton też doznaje dyfrakcji). To, że stała Planka jest stałą fundamentalną, definiującą nasz Świat oznacza, że nie wiemy dlaczego wynosi ona <math>h = 6.67 \cdot 10^{-32} Js</math>, możemy ją tylko zmierzyć i zrozumieć jakie znaczenia ma wartość tej stałej w budowie Świata. Często używa się we wzorach zmodyfikowanej stałej <math>ħ = h/2\pi</math>. Wówczas energia fotonu wyraża się jako <math>ħ\omega</math>, gdzie<math>\omega</math> to tzw. częstość kołowa. | ||
|} | |} | ||
| Linia 156: | Linia 155: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PF_M4_Slajd13.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PF_M4_Slajd13.png|thumb|500px]] | ||
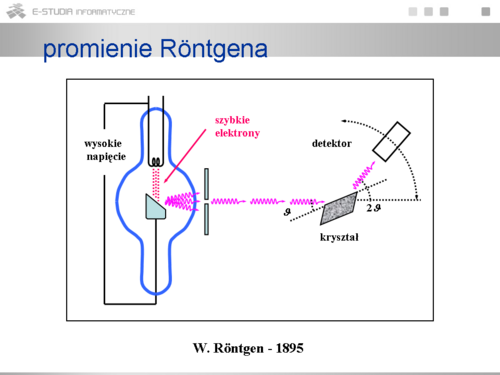
|valign="top"|Promienie rentgenowskie, odkryte przypadkowo a następnie zbadane przez W.Röntgena, powstają w lampie w której między żarzoną katodą a anodą przyłożone jest wysokie napięcie rzędu kilowoltów. Elektrony, które są emitowane z katody na skutek jej żarzenia są przyspieszane do dużych prędkości przez silne pole elektryczne. Następnie zderzają się z anodą i w wyniku tego powstają promienie o specyficznych własnościach. Są to promienie bardzo przenikliwe, nie posiadające ładunku. Promienie te mają naturę fali elektromagnetycznej o bardzo małej długości fali, w przedziale (5 \cdot 10^{-9} \div 1 \cdto 10^{-11} ) m, czyli kilka rzędów wielkości krótsze niż widzialne. Stwierdzenie falowej natury tak krótkich fal wymaga zastosowania szczególnych obiektów na których można zaobserwować efekty dyfrakcyjne. Chodzi mianowicie o rozpraszanie na krysztale. Typowe odległości między regularnie rozmieszczonymi w krysztale molekułami są rzędu <math>10^{-10}</math> m a więc odpowiadają zakresowi długości fal rentgenowskich. Przy odbiciu od kryształu obserwuje się typowe dla fal sekwencje maksimów i można wyznaczyć długości fal i ich widma. Ale jaki mechanizm odpowiada za powstanie promieni rentgenowskich? | |valign="top"|Promienie rentgenowskie, odkryte przypadkowo a następnie zbadane przez W.Röntgena, powstają w lampie w której między żarzoną katodą a anodą przyłożone jest wysokie napięcie rzędu kilowoltów. Elektrony, które są emitowane z katody na skutek jej żarzenia są przyspieszane do dużych prędkości przez silne pole elektryczne. Następnie zderzają się z anodą i w wyniku tego powstają promienie o specyficznych własnościach. Są to promienie bardzo przenikliwe, nie posiadające ładunku. Promienie te mają naturę fali elektromagnetycznej o bardzo małej długości fali, w przedziale <math>(5 \cdot 10^{-9} \div 1 \cdto 10^{-11} )</math> m, czyli kilka rzędów wielkości krótsze niż widzialne. Stwierdzenie falowej natury tak krótkich fal wymaga zastosowania szczególnych obiektów na których można zaobserwować efekty dyfrakcyjne. Chodzi mianowicie o rozpraszanie na krysztale. Typowe odległości między regularnie rozmieszczonymi w krysztale molekułami są rzędu <math>10^{-10}</math> m a więc odpowiadają zakresowi długości fal rentgenowskich. Przy odbiciu od kryształu obserwuje się typowe dla fal sekwencje maksimów i można wyznaczyć długości fal i ich widma. Ale jaki mechanizm odpowiada za powstanie promieni rentgenowskich? | ||
|} | |} | ||
---- | ---- | ||
| Linia 194: | Linia 193: | ||
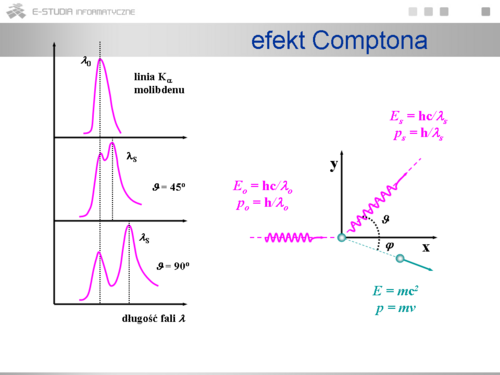
<math>h\nu_o + m_ec^2 = h\nu_s + m_ec^2 + Ee </math> <math>\rightarrow</math> <math>Ee = h(\nu_o - \nu_s) = (p_o - p_s)c</math> | <math>h\nu_o + m_ec^2 = h\nu_s + m_ec^2 + Ee </math> <math>\rightarrow</math> <math>Ee = h(\nu_o - \nu_s) = (p_o - p_s)c</math> | ||
zasada zachowania pędu: | zasada zachowania pędu: | ||
składowa y: <math> | składowa y: <math>p_s sin = pe sin\omega</math> | ||
składowa x: <math> | składowa x: <math>p_o = p_s cos + pe cos\omega</math> <math>\rightarrow</math> <math>p_o^2 - 2p_op_scos + p_s^2 = p_e^2</math> | ||
relatywistyczne wzory na całkowitą energię elektronu: | relatywistyczne wzory na całkowitą energię elektronu: | ||
| Linia 206: | Linia 205: | ||
<math>\lambda_s - \lambda_o = h/m_ec \cdot (1 - cos)</math> | <math>\lambda_s - \lambda_o = h/m_ec \cdot (1 - cos)</math> | ||
<math>\Delta\lambda = lambda_s - \lambda_o = \lambda_c(1 - cos)</math> | <math>\Delta \lambda = \lambda_s - \lambda_o = \lambda_c(1 - cos)</math> | ||
gdzie <math>\lambda_c</math> to stała zwana komptonowską długością fali: | gdzie <math>\lambda_c</math> to stała zwana komptonowską długością fali: | ||
<math>\lambda_c = h/m_ec = 2.426 \cdot 10^{-12} m | <math>\lambda_c = h/m_ec = 2.426 \cdot 10^{-12} m</math>. | ||
uwaga: jeśli elektron, na którym rozprasza się foton jest elektronem silnie związanym w atomie to cały, ciężki atom doznaje odrzutu i masa w mianowniku jest masą atomu w rezultacie czego <math>\Delta\lambda</math> jest znikome. Stąd jest obecność fotonów o długości fali pierwotnej <math>\lambda_o</math>. | uwaga: jeśli elektron, na którym rozprasza się foton jest elektronem silnie związanym w atomie to cały, ciężki atom doznaje odrzutu i masa w mianowniku jest masą atomu w rezultacie czego <math>\Delta\lambda</math> jest znikome. Stąd jest obecność fotonów o długości fali pierwotnej <math>\lambda_o</math>. | ||