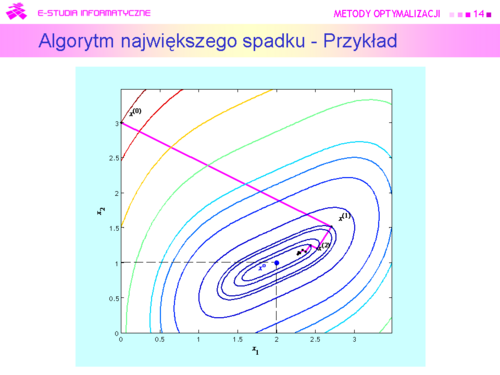
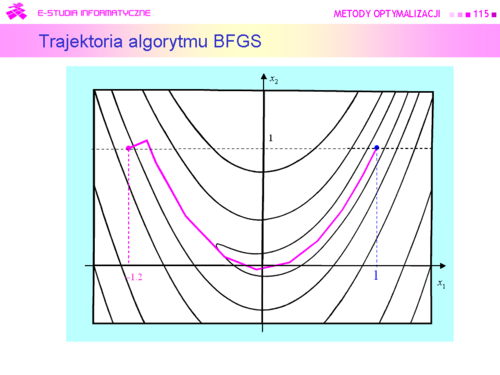
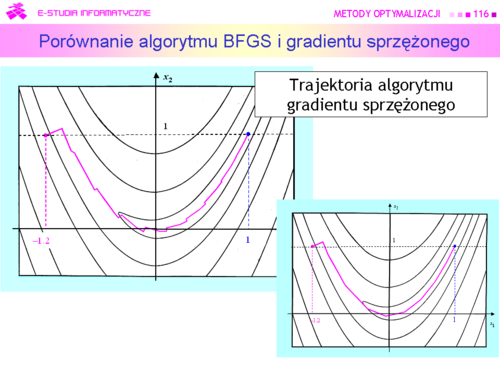
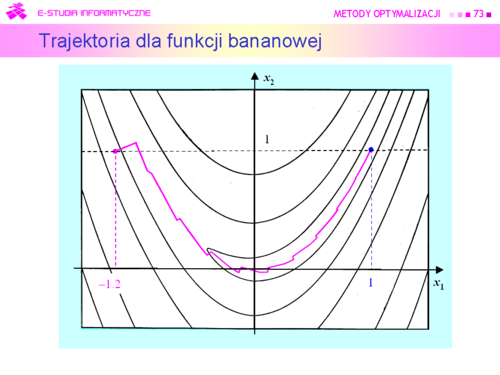
| |valign="top"|Na rysunku zaznaczono kolorem zielonym „drogę” algorytmu gradientu sprzężonego z metodą interpolacji kwadratowej użytą do minimalizacji w kierunku, który wystartował z tego samego co poprzednio punktu początkowego <math>x^{(0)}=(0,3)</math> i miał znaleźć rozwiązanie z dokładnością <math>\varepsilon = 0.05</math> (przypominamy, że dla algorytmu gradientu prostego wybrana dokładność była 2 razy mniejsza i wynosiła 0.1). Dla porównania kroki algorytmu największego spadku zaznaczono na czerwono.<br>Algorytm wykonał siedem kroków i zatrzymał się w punkcie <math>x^{(7)} = (2.185,\,1.094)</math> w którym <math>||\nabla f(2.185,\,1.094)||=0.02</math> . Wartość funkcji celu <math>f (2.185,\,1.094) = 0.0012</math>, a odległość proponowanego rozwiązania od punktu optymalnego jest równa<center><math>||x^{(7)}-x^o||= 0.208</math>.</center> | | |valign="top"|Na rysunku zaznaczono kolorem zielonym „drogę” algorytmu gradientu sprzężonego z metodą interpolacji kwadratowej użytą do minimalizacji w kierunku, który wystartował z tego samego co poprzednio punktu początkowego <math>x^{(0)}=(0,3)</math> i miał znaleźć rozwiązanie z dokładnością <math>\varepsilon = 0.05</math> (przypominamy, że dla algorytmu gradientu prostego wybrana dokładność była 2 razy mniejsza i wynosiła 0.1). Dla porównania kroki algorytmu największego spadku zaznaczono na czerwono.<br>Algorytm wykonał siedem kroków i zatrzymał się w punkcie <math>x^{(7)} = (2.185,\,1.094)</math> w którym <math>||\nabla f(2.185,\,1.094)||=0.02</math> . Wartość funkcji celu <math>f (2.185,\,1.094) = 0.0012</math>, a odległość proponowanego rozwiązania od punktu optymalnego jest równa<center><math>||x^{(7)}-x^o||= 0.208</math>.</center> |
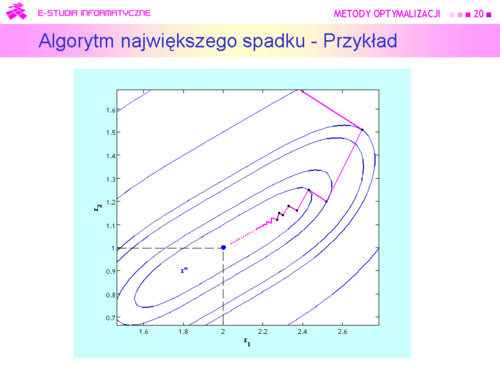
| Krok pierwszy z <math>x^{(0)}=(0,\,3)</math> do <math>x^{(1)}=(2.70,\,1.51)</math> był oczywiście taki sam jak dla metody gradientu prostego. Przejście z kroku szóstego do siódmego jest na rysunku niezauważalne, ponieważ <math>x^{(6)} = (2.190,\,1.090)</math>. Zadanie jest dwuwymiarowe, zatem odnowa (ruch w kierunku antygradientu) nastąpiła w kroku trzecim, piątym i ostatnim – siódmym. Ponieważ punkty <math> x^{(2)}</math> wyznaczone w drugim kroku przez oba algorytmy leżą jeszcze blisko siebie to i antygradienty są prawie równe, więc ruch obu algorytmów w trzecim kroku musi dać punkty <math>x^{(3)}</math>, które też będą leżały blisko siebie. Lecz antygradient policzony w punkcie <math>x^{(3)}</math> wyliczonym przez algorytm najszybszego spadku jest równy <math>[-0.18\,\vdots -0.28]</math>, a kierunek poprawy wyznaczony w swoim punkcie <math>x^{(3)}</math> przez algorytm gradientu sprzężonego jest równy <math>[-0.30\,\vdots -0.25]</math>. Ta różnica spowodowała, że algorytm gradientu sprzężonego wyznaczył jako punkt <math>x^{(4)}</math> punkt o współrzędnych <math>(2.25,\,1.10)</math>, co dało wartość funkcji celu <math>f (2.25,\,1.10) = 0.0064</math>, a algorytm gradientu prostego – punkt o współrzędnych <math>(2.37,\,1.16)</math> z wartością funkcji celu <math>f(2.37,\,1.16) = 0.02</math>. W piątym kroku algorytm gradientu sprzężonego wyznaczył punkt <math>x^{(5)} = (2.23,\,1.12)</math> dający wartość funkcji celu <math>f(2.23,\,1.12) = 0.003</math> i wartość normy gradientu <math>||\nabla f(2.23,\,1.12)||=0.05</math> , a więc punkt lepszy niż ostatni (ósmy) punkt uzyskany przez algorytm najszybszego spadku (przypominamy był to punkt <math>(2.27,\,1.12)</math> w którym <math>f (2.27,\,1.12) = 0.0062</math>, oraz <math>||\nabla f(2.27,\,1.12)||=0.09</math> . | | Krok pierwszy z <math>x^{(0)}=(0,\,3)</math> do <math>x^{(1)}=(2.70,\,1.51)</math> był oczywiście taki sam jak dla metody gradientu prostego. Przejście z kroku szóstego do siódmego jest na rysunku niezauważalne, ponieważ <math>x^{(6)} = (2.190,\,1.090)</math>. Zadanie jest dwuwymiarowe, zatem odnowa (ruch w kierunku antygradientu) nastąpiła w kroku trzecim, piątym i ostatnim – siódmym. Ponieważ punkty <math>x^{(2)}</math> wyznaczone w drugim kroku przez oba algorytmy leżą jeszcze blisko siebie to i antygradienty są prawie równe, więc ruch obu algorytmów w trzecim kroku musi dać punkty <math>x^{(3)}</math>, które też będą leżały blisko siebie. Lecz antygradient policzony w punkcie <math>x^{(3)}</math> wyliczonym przez algorytm najszybszego spadku jest równy <math>[-0.18\,\vdots -0.28]</math>, a kierunek poprawy wyznaczony w swoim punkcie <math>x^{(3)}</math> przez algorytm gradientu sprzężonego jest równy <math>[-0.30\,\vdots -0.25]</math>. Ta różnica spowodowała, że algorytm gradientu sprzężonego wyznaczył jako punkt <math>x^{(4)}</math> punkt o współrzędnych <math>(2.25,\,1.10)</math>, co dało wartość funkcji celu <math>f (2.25,\,1.10) = 0.0064</math>, a algorytm gradientu prostego – punkt o współrzędnych <math>(2.37,\,1.16)</math> z wartością funkcji celu <math>f(2.37,\,1.16) = 0.02</math>. W piątym kroku algorytm gradientu sprzężonego wyznaczył punkt <math>x^{(5)} = (2.23,\,1.12)</math> dający wartość funkcji celu <math>f(2.23,\,1.12) = 0.003</math> i wartość normy gradientu <math>||\nabla f(2.23,\,1.12)||=0.05</math> , a więc punkt lepszy niż ostatni (ósmy) punkt uzyskany przez algorytm najszybszego spadku (przypominamy był to punkt <math>(2.27,\,1.12)</math> w którym <math>f (2.27,\,1.12) = 0.0062</math>, oraz <math>||\nabla f(2.27,\,1.12)||=0.09</math> . |