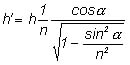PF Moduł 15: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 2 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 24: | Linia 24: | ||
|valign="top"|'''Propagacja fal elektromagnetycznych''' | |valign="top"|'''Propagacja fal elektromagnetycznych''' | ||
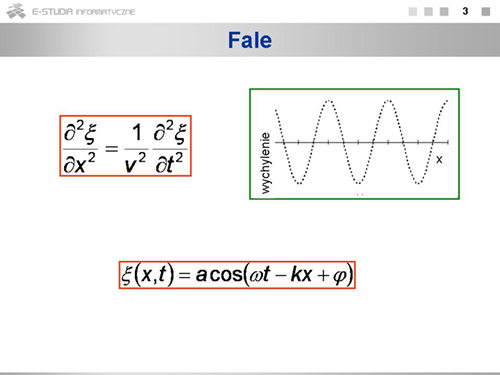
Przypomnijmy sobie podstawowe fakty o propagacji fal. Fala to rozchodzenie się w ośrodku drgań cząsteczek. Wychylenie <math>\xi\ | Przypomnijmy sobie podstawowe fakty o propagacji fal. Fala to rozchodzenie się w ośrodku drgań cząsteczek. Wychylenie <math>\xi\ </math>, z położenia równowagi cząstek biorących udział w ruchu falowym, opisuje wzór: <math>\xi (x,t)=acos(\omega t-kx+\varphi)</math>, gdzie <math>k=\frac{2\pi}{\lambda}</math> jest liczbą falową, <math>\omega=\frac{2\pi}{T}</math> częstością, a <math>\varphi\ </math>, - fazą początkową. Funkcja <math>\xi (x,t)=acos(\omega t-kx+\varphi)</math> jest rozwiązaniem równania falowego: | ||
: <math>\frac{\partial^2 \xi}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \xi}{\partial t^2}</math>. | : <math>\frac{\partial^2 \xi}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \xi}{\partial t^2}</math>. | ||
| Linia 42: | Linia 42: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd5.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd5.png]] | ||
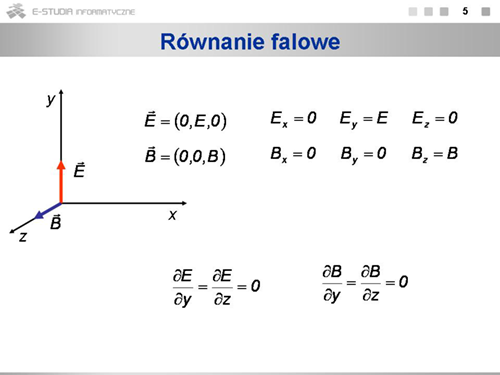
|valign="top"|Zapiszmy równania Maxwella dla przypadku, kiedy w przestrzeni nie ma ładunków ani ośrodków materialnych, to jest dla próżni. Kiedy rozważamy rozchodzenie się zaburzeń pola elektrycznego w określonym kierunku, na przykład wzdłuż osi <math>X\ | |valign="top"|Zapiszmy równania Maxwella dla przypadku, kiedy w przestrzeni nie ma ładunków ani ośrodków materialnych, to jest dla próżni. Kiedy rozważamy rozchodzenie się zaburzeń pola elektrycznego w określonym kierunku, na przykład wzdłuż osi <math>X\ </math>,, to z równań Maxwella wynika, że będzie mu towarzyszyło pole magnetyczne skierowane prostopadle do pola elektrycznego i kierunku propagacji. Przyjmijmy, że kierunek pola elektrycznego pokrywa się z osią <math>Y\ </math>, prostokątnego układu współrzędnych, a pola magnetycznego z osią <math>Z\ </math>,. Zapiszemy to w postaci: <math>\overrightarrow{E}=(0,E,0), \overrightarrow{B}=(0,0,B)\ </math>,. | ||
Będziemy rozważali propagację zaburzeń pól w jednym kierunku, wzdłuż osi <math>x\ | Będziemy rozważali propagację zaburzeń pól w jednym kierunku, wzdłuż osi <math>x\ </math>,, z czego wynika, że pola te są jednorodne w kierunkach prostopadłych do kierunku propagacji. Oznacza to, że pochodne <math>\frac{\partial E}{\partial y}, \frac{\partial E}{\partial z}, \frac{\partial B}{\partial y}, \frac{\partial B}{\partial z}</math> równe są zeru, czyli że wartości <math>E\ </math>, i <math>B\ </math>, nie zależą od położenia punktu w kierunkach <math>Y\ </math>, i <math>Z\ </math>,, to znaczy w każdym momencie mają te same wartości we wszystkich punktach leżących w płaszczyźnie <math>YZ\ </math>,; zależą natomiast od <math>X\ </math>, oraz <math>t\ </math>,. | ||
|} | |} | ||
| Linia 52: | Linia 52: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd6.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd6.png]] | ||
|valign="top"|Zapiszmy równania Maxwella dla przyjętych założeń. Po obliczeniu pochodnych cząstkowych <math>\frac{\partial}{\partial x}\ | |valign="top"|Zapiszmy równania Maxwella dla przyjętych założeń. Po obliczeniu pochodnych cząstkowych <math>\frac{\partial}{\partial x}\ </math>, z obu stron pierwszego równania i <math>\frac{\partial}{\partial t}\ </math>, z drugiego, widzimy, że każde z równań zawiera równe sobie wyrażenia: <math>-\frac{\partial^2 B}{\partial x\partial t}\ </math>, oraz <math>\frac{\partial^2 B}{\partial t\partial x}\ </math>,. Przyrównanie do siebie drugich stron równań daje bardzo ciekawy rezultat! Równanie <math>\frac{\partial^2 E}{\partial t^2}=\frac{1}{\varepsilon_0 \mu_0}\frac{\partial^2 E}{\partial x^2}</math> ma postać podobną do postaci równania falowego. Wykonując różniczkowanie względem czasu dla pierwszego równania oraz względem <math>x\ </math>, dla równania drugiego otrzymujemy analogiczny związek dla pola magnetycznego: <math>\frac{\partial^2 B}{\partial t^2}=\frac{1}{\varepsilon_0 \mu_0}\frac{\partial^2 B}{\partial x^2}</math>. Oznacza to, że zaburzenia pola elektrycznego i magnetycznego rozchodzą się w postaci fal elektromagnetycznych. | ||
|} | |} | ||
| Linia 60: | Linia 60: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd7.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd7.png]] | ||
|valign="top"|Porównując otrzymane równanie z równaniem falowym, widzimy, że wielkość <math>\frac{1}{\varepsilon_0 \mu_0}\ | |valign="top"|Porównując otrzymane równanie z równaniem falowym, widzimy, że wielkość <math>\frac{1}{\varepsilon_0 \mu_0}\ </math>, jest kwadratem prędkości fazowej <math>v\ </math>, fali elektromagnetycznej. Podstawiając wartości przenikalności elektrycznej i magnetycznej próżni <math>(\varepsilon_0\, i\, \mu_0)\ </math>, otrzymujemy wartość prędkości <math>v=3\cdot 10^8 m/s\ </math>,. Jest to wartość prędkości światła! W ten sposób Maxwell pierwszy odkrył naturę fizyczną światła, uświadamiając nam, że światło jest falą elektromagnetyczną. Wniosek ten uznawany jest za największe osiągniecie teorii Maxwella! Widzimy, że prędkość światła jest niezależna od częstości drgań czy długości fali. Jest to uniwersalna stała związana bezpośrednio z przenikalnością elektryczną i magnetyczną próżni - podstawowymi charakterystykami pól: elektrycznego i magnetycznego. Wiedząc, że prędkość światła w próżni: <math>c=\frac{1}{\sqrt{\varepsilon_0 \mu_0}}</math>, rozumiemy, że nie może ona zależeć od układu odniesienia, w którym jest mierzona, bowiem <math>\varepsilon_0\, i\, \mu_0\ </math>, są stałymi uniwersalnymi. Jest to zgodne z wynikami doświadczeń i stanowi podstawowe założenie szczególnej teorii względności. W ośrodku materialnym o względnej przenikalności elektrycznej <math>\varepsilon\ </math>, i magnetycznej <math>\mu\ </math>, prędkość światła jest mniejsza od prędkości światła w próżni <math>\frac{1}{\sqrt{\varepsilon \mu}}\ </math>, razy. | ||
|} | |} | ||
| Linia 68: | Linia 68: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd8.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd8.png]] | ||
|valign="top"|Podsumujmy: zmiany prostopadłych wzajemnie pól elektrycznego i magnetycznego rozchodzą się w kierunku prostopadłym do kierunku obu tych pól z prędkością światła jako fala elektromagnetyczna. Fale elektromagnetyczne są więc falami poprzecznymi. Rozchodzenie się fali elektromagnetycznej ilustruje rysunek. Zwróćmy uwagę, że drgania wektora elektrycznego <math>\overrightarrow{E}\ | |valign="top"|Podsumujmy: zmiany prostopadłych wzajemnie pól elektrycznego i magnetycznego rozchodzą się w kierunku prostopadłym do kierunku obu tych pól z prędkością światła jako fala elektromagnetyczna. Fale elektromagnetyczne są więc falami poprzecznymi. Rozchodzenie się fali elektromagnetycznej ilustruje rysunek. Zwróćmy uwagę, że drgania wektora elektrycznego <math>\overrightarrow{E}\ </math>, i magnetycznego <math>\overrightarrow{B}\ </math>, zachodzą w tej samej fazie: w tych samych punktach przestrzeni oba wektory osiągają wartość maksymalną, czy równą zeru. | ||
|} | |} | ||
| Linia 76: | Linia 76: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd9.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd9.png]] | ||
|valign="top"|Rozwiązaniem równania falowego są funkcje <math>E(x, t)\ | |valign="top"|Rozwiązaniem równania falowego są funkcje <math>E(x, t)\ </math>, i <math>B(x, t)\ </math>, opisujące propagację fali elektromagnetycznej. Amplitudy <math>E_0\ </math>, i <math>B_0\ </math>, nie są od siebie niezależne. Rzeczywiście, gdy obliczymy odpowiednie pochodne cząstkowe <math>E\ </math>, i <math>B\ </math>, i wstawimy do równania Maxwella <math>\frac{\partial E}{\partial x}=-\frac{\partial B}{\partial t}</math>, otrzymamy związek <math>E_0=cB_0\ </math>,. Mając na uwadze, że zmiany obu pól przebiegają w ten sam sposób dany powyższymi równaniami, możemy związek pomiędzy amplitudami przenieść na relacje pomiędzy wartościami pól: <math>E=cB\ </math>,. | ||
|} | |} | ||
| Linia 89: | Linia 89: | ||
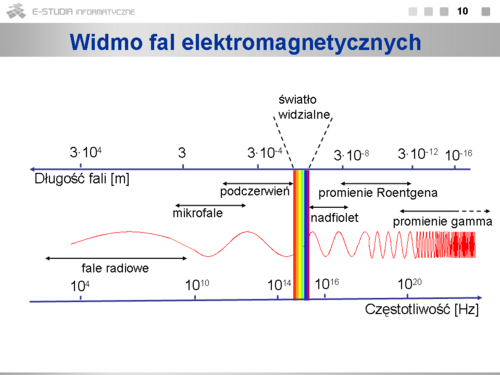
* '''Fale radiowe''' to fale o długości mierzonej w metrach, a nawet w kilometrach. Fale te generowane są w układach elektrycznych wytwarzających drgania elektromagnetyczne (obwody LC), i charakteryzują się określoną fazą generowanej fali. | * '''Fale radiowe''' to fale o długości mierzonej w metrach, a nawet w kilometrach. Fale te generowane są w układach elektrycznych wytwarzających drgania elektromagnetyczne (obwody LC), i charakteryzują się określoną fazą generowanej fali. | ||
* Ten sposób generacji dotyczy także '''mikrofal''', których długość fali wynosi od <math>10^{-4}\ | * Ten sposób generacji dotyczy także '''mikrofal''', których długość fali wynosi od <math>10^{-4}\ </math>,m do 0,3 m (0,1 mm do 30 cm). Do ich wytwarzania używa się lamp mikrofalowych: elektrony krążąc w polu magnetycznym po spiralach, emitują mikrofale. | ||
* Promieniowanie podczerwone w zakresie od <math>7\cdot 10^{-7}\ | * Promieniowanie podczerwone w zakresie od <math>7\cdot 10^{-7}\ </math>,m do <math>2\cdot 10^{-3}\ </math>,m emitowane jest przez rozgrzane ciała w wyniku wzbudzeń cieplnych elektronów wewnątrz substancji. Im niższa temperatura ciała tym mniejsze natężenie promieniowania i większa długość fali. Ciała o temperaturze do około <math>400^\circ C\ </math>, wysyłają praktycznie tylko promieniowanie podczerwone. Fale w obszarze podczerwieni, które emitowane są wskutek chaotycznych wzbudzeń termicznych atomów i cząsteczek nie zachowują stałej fazy, to znaczy, że nie są spójne. Fale spójne w tym obszarze widmowym mogą być generowane przez lasery. Podobna sytuacja jest także w obszarze światła widzialnego i nadfioletu. | ||
* '''Światło widzialne''' to bardzo wąski zakres długości fal od około <math>4\cdot 10^{-7}\ | * '''Światło widzialne''' to bardzo wąski zakres długości fal od około <math>4\cdot 10^{-7}\ </math>,m do około <math>7\cdot 10^{-7}\ </math>,m. Światło o największej długości fali widzimy jako czerwone, a o najmniejszej – fioletowe. Naturalnymi źródłami są ciała ogrzane do temperatury ponad <math>700^\circ C\ </math>,. Na skutek ruchów cieplnych następuje wtedy wzbudzenie elektronów wewnątrz substancji i przy powrocie do niższych stanów energetycznych następuje emisja światła. | ||
* '''Promieniowanie nadfioletowe''' obejmuje zakres długości fal od <math>4\cdot 10^{-7}\ | * '''Promieniowanie nadfioletowe''' obejmuje zakres długości fal od <math>4\cdot 10^{-7}\ </math>,m do <math>10^{-8}\ </math>,m (od 400 do 10 nm). Naturalnymi źródłami są ciała o dostatecznie wysokiej temperaturze. Znikome, ale zauważalne ilości tego promieniowania wysyłają już ciała o temperaturze 3000K i ze wzrostem temperatury natężenie wzrasta. Silnym źródłem jest Słońce, którego temperatura powierzchni wynosi 6000K. Promieniowanie nadfioletowe ma silne działanie fotochemiczne. Przy długości fali poniżej 300 nm wywołuje już jonizację i jest zabójcze dla organizmów żywych, wywołuje lub przyspiesza szereg reakcji chemicznych. | ||
* '''Promieniowanie rentgenowskie''' emitowane jest, gdy przejścia elektronów w atomie dotyczą wewnętrznych powłok elektronowych. Jest to możliwe, gdy elektrony wybijane są przez przyspieszone silnym polem elektrycznym cząstki naładowane. Również podczas hamowania swobodnych elektronów przyspieszonych do dużych prędkości, emitowane jest promieniowanie z zakresu rentgenowskiego. | * '''Promieniowanie rentgenowskie''' emitowane jest, gdy przejścia elektronów w atomie dotyczą wewnętrznych powłok elektronowych. Jest to możliwe, gdy elektrony wybijane są przez przyspieszone silnym polem elektrycznym cząstki naładowane. Również podczas hamowania swobodnych elektronów przyspieszonych do dużych prędkości, emitowane jest promieniowanie z zakresu rentgenowskiego. | ||
* Źródłem '''promieniowania <math>\gamma\ | * Źródłem '''promieniowania <math>\gamma\ </math>,''' o długości fali mniejszej od <math>10^{-10}\ </math>,m są procesy zachodzące w jądrze atomowym (np. rozpad pierwiastków promieniotwórczych zawartych w skorupie ziemskiej lub reakcje jądrowe). Promieniowanie to powstaje również podczas procesów jądrowych zachodzących w gwiazdach i galaktykach. Do wielkich zagadek współczesnej nauki należą tak zwane błyski <math>\gamma\ </math>,. To dochodzące z głębi Wszechświata impulsy promieniowania <math>\gamma\ </math>,, o energii porównywalnej z energią, jaką wydzieli Słońce w ciągu całego swego istnienia (10 mld lat). | ||
|} | |} | ||
| Linia 112: | Linia 112: | ||
|valign="top"|'''Energia fal elektromagnetycznych''' | |valign="top"|'''Energia fal elektromagnetycznych''' | ||
Jeśli fala elektromagnetyczna jest w stanie pobudzić do działania telewizor, czy telefon komórkowy, to musi przenosić energię z jednego miejsca przestrzeni do drugiego. Skorzystajmy ze wzorów na gęstość energii pola elektrycznego oraz na gęstość energii pola magnetycznego. Gęstość energii, to energia przypadająca na jednostkę objętości. Całkowita energia fali elektromagnetycznej zmagazynowana w jednostce objętości jest sumą energii pola elektrycznego i pola magnetycznego. Po uwzględnieniu związku między wartościami <math>E\ | Jeśli fala elektromagnetyczna jest w stanie pobudzić do działania telewizor, czy telefon komórkowy, to musi przenosić energię z jednego miejsca przestrzeni do drugiego. Skorzystajmy ze wzorów na gęstość energii pola elektrycznego oraz na gęstość energii pola magnetycznego. Gęstość energii, to energia przypadająca na jednostkę objętości. Całkowita energia fali elektromagnetycznej zmagazynowana w jednostce objętości jest sumą energii pola elektrycznego i pola magnetycznego. Po uwzględnieniu związku między wartościami <math>E\ </math>, i <math>B\ </math>, dla fali elektromagnetycznej <math>E=cB\ </math>,, otrzymujemy wzór na gęstość energii fali: <math>w=\varepsilon_0 E^2</math>. | ||
|} | |} | ||
| Linia 128: | Linia 128: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd14.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd14.png]] | ||
|valign="top"|Określmy teraz energię transportowaną przez falę elektromagnetyczną w próżni w jednostce czasu. Kierunek transportu energii pokrywa się z kierunkiem rozchodzenia się fali i jest prostopadły do kierunków wektorów <math>\overrightarrow{E}\ | |valign="top"|Określmy teraz energię transportowaną przez falę elektromagnetyczną w próżni w jednostce czasu. Kierunek transportu energii pokrywa się z kierunkiem rozchodzenia się fali i jest prostopadły do kierunków wektorów <math>\overrightarrow{E}\ </math>, i <math>\overrightarrow{B}\ </math>,. W czasie <math>dt\ </math>, fala przesuwa się o odcinek <math>c\dot dt\ </math>,. Przez powierzchnię <math>S\ </math>, prostopadłą do kierunku rozchodzenia się fali przetransportowana jest energia zawarta w objętości <math>S\cdot c \cdot dt\ </math>,. Energia ta wynosi: <math>dW=wdV\ </math>, Energia przenoszona przez jednostkową powierzchnię <math>w\ </math>, jednostce czasu wynosi więc: <math>P=\frac{1}{S}\frac{dW}{dt}=\varepsilon_0 cE^2</math> | ||
|} | |} | ||
| Linia 136: | Linia 136: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd15.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd15.png]] | ||
|valign="top"|Wykorzystując związki: <math>E=cB</math> oraz <math>c=\frac{1}{\sqrt{\varepsilon_0 \mu_0}}</math> możemy wzór na energię przenoszona przez jednostkową powierzchnię w jednostce czasu przedstawić jako: <math>P=\frac{EB}{\mu_0}</math>. Ponieważ, jak to już stwierdziliśmy, energia ta przenoszona jest w kierunku prostopadłym do wektorów <math>\overrightarrow{E}\ | |valign="top"|Wykorzystując związki: <math>E=cB</math> oraz <math>c=\frac{1}{\sqrt{\varepsilon_0 \mu_0}}</math> możemy wzór na energię przenoszona przez jednostkową powierzchnię w jednostce czasu przedstawić jako: <math>P=\frac{EB}{\mu_0}</math>. Ponieważ, jak to już stwierdziliśmy, energia ta przenoszona jest w kierunku prostopadłym do wektorów <math>\overrightarrow{E}\ </math>, i <math>\overrightarrow{B}\ </math>,, możemy zdefiniować wektor, którego wartość określa energię przenoszoną przez jednostkową powierzchnię w jednostce czasu, a kierunek wskazuje kierunek przenoszenia tej energii. Pamiętając, że wektory <math>\overrightarrow{E}\ </math>, i <math>\overrightarrow{B}\ </math>, są do siebie prostopadłe zapisujemy wzór w postaci wektorowej: <math>\overrightarrow{P}=\frac{1}{\mu_0}\overrightarrow{E}\times \overrightarrow{B}</math>. Określony tym wzorem wektor nosi nazwę wektora Poyntinga. | ||
|} | |} | ||
| Linia 146: | Linia 146: | ||
|valign="top"|'''Optyka geometryczna''' | |valign="top"|'''Optyka geometryczna''' | ||
Rozchodzenie się światła, podobnie jak i fal elektromagnetycznych o innych długościach, polega na przemieszczaniu się w czasie i przestrzeni drgań wektorów natężeń pól: elektrycznego i magnetycznego. Prędkość światła w próżni oznaczyliśmy symbolem <math>c\ | Rozchodzenie się światła, podobnie jak i fal elektromagnetycznych o innych długościach, polega na przemieszczaniu się w czasie i przestrzeni drgań wektorów natężeń pól: elektrycznego i magnetycznego. Prędkość światła w próżni oznaczyliśmy symbolem <math>c\ </math>,. Jak stwierdziliśmy, w innych ośrodkach prędkość ta jest mniejsza, co wynika z równań Maxwella, i zależy od względnej przenikalności elektrycznej <math>\varepsilon\ </math>, i magnetycznej <math>\mu\ </math>, ośrodka. Współczynnik załamania światła w ośrodku definiujemy wzorem <math>n=\frac{c}{v}</math>, a więc prędkość światła w danym ośrodku można wyrazić następująco: <math>n=\sqrt{\varepsilon \mu}\approx \sqrt{\varepsilon}</math>. Przybliżona równość w tym wzorze wynika z faktu, że dla większości ośrodków, w których rozważamy rozchodzenie się światła, wartość przenikalności magnetycznej jest na tyle bliska jedności, że można ją tu pominąć. Otrzymujemy w ten sposób wynikającą z równań Maxwella interesującą zależność między współczynnikiem załamania i przenikalnością elektryczną dla większości (nie ferromagnetycznych) ośrodków <math>n\approx \sqrt{\varepsilon}</math>. Dodajmy do tego jeszcze, że chociaż w falach elektromagnetycznych mamy do czynienia z drganiami wektorów <math>\overrightarrow{E}\ </math>, i <math>\overrightarrow{B}\ </math>,, to doświadczalnie stwierdzono decydującą rolę drgań pola elektrycznego dla reakcji fotochemicznych, fotoelektrycznych czy również fizjologicznych. Dlatego w rozważaniach naszych będziemy mówić o drganiach wektora natężenia pola elektrycznego jako o drganiach wektora świetlnego. Stosunek prędkości światła w próżni do prędkości światła w danym ośrodku oznaczyliśmy symbolem <math>n\ </math>, i nazywamy współczynnikiem załamania. Często nazywa się go także bezwzględnym współczynnikiem załamania, gdyż określa załamanie światła przy przejściu z próżni do ośrodka. Jeśli światło przechodzi z ośrodka <math>1\ </math>,, gdzie rozchodzi się z prędkością <math>v_1\ </math>, do ośrodka <math>2\ </math>,, gdzie prędkość światła wynosi <math>v_2\ </math>,, załamanie jest określone przez współczynnik załamania ośrodka drugiego względem ośrodka pierwszego <math>n_{2,1}=\frac{n_2}{n_1}=\frac{v_1}{v_2}</math>. | ||
Pod pojęciem natężenia lub intensywności fali świetlnej będziemy tu rozumieć wielkość proporcjonalną nie do amplitudy drgań wektora <math>\overrightarrow{E}\ | Pod pojęciem natężenia lub intensywności fali świetlnej będziemy tu rozumieć wielkość proporcjonalną nie do amplitudy drgań wektora <math>\overrightarrow{E}\ </math>,, a do kwadratu tej amplitudy, bowiem, jak pamiętamy, energia fali elektromagnetycznej jest proporcjonalna do kwadratu natężenia pola elektrycznego. Pod sformułowaniem "amplituda fali" będziemy więc rozumieli, amplitudę drgań elektrycznych zaś w celu wyznaczenia intensywności lub natężenia światła będziemy wyznaczać wielkość proporcjonalną do kwadratu amplitudy. | ||
Wszystkie omawiane tu zjawiska mogą być opisane z użyciem formalizmu równań Maxwella. Zjawiska te i prawidłowości nimi rządzące zostały jednak zaobserwowane znacznie wcześniej. Zostały one opisane w ramach fenomenologicznych zasad, które umożliwiały w prosty sposób zrozumienie zjawisk falowych nie rozpatrując elektromagnetycznej natury samych fal, z czego nie zdawano sobie wcześniej sprawy. Jak już powiedzieliśmy, dopiero Maxwell pokazał, że światło ma naturę fal elektromagnetycznych. | Wszystkie omawiane tu zjawiska mogą być opisane z użyciem formalizmu równań Maxwella. Zjawiska te i prawidłowości nimi rządzące zostały jednak zaobserwowane znacznie wcześniej. Zostały one opisane w ramach fenomenologicznych zasad, które umożliwiały w prosty sposób zrozumienie zjawisk falowych nie rozpatrując elektromagnetycznej natury samych fal, z czego nie zdawano sobie wcześniej sprawy. Jak już powiedzieliśmy, dopiero Maxwell pokazał, że światło ma naturę fal elektromagnetycznych. | ||
| Linia 171: | Linia 171: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd18.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd18.png]] | ||
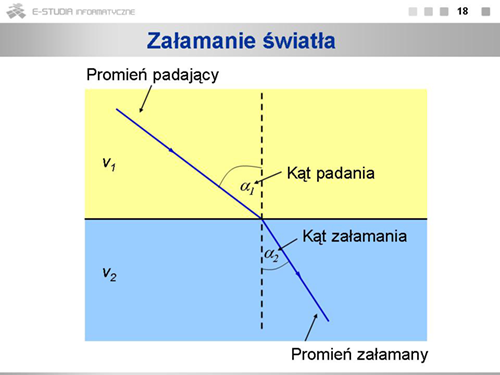
|valign="top"|Zastosujmy zasadę Huyghensa do zjawiska załamania światła na granicy dwóch ośrodków. W pierwszym prędkość światła wynosi <math>v_1\ | |valign="top"|Zastosujmy zasadę Huyghensa do zjawiska załamania światła na granicy dwóch ośrodków. W pierwszym prędkość światła wynosi <math>v_1\ </math>,, w drugim <math>v_2\ </math>,. Kąty padania i załamania definiujemy jako kąty między normalną do granicy ośrodków a odpowiednio, promieniem padającym i załamanym. | ||
|} | |} | ||
| Linia 179: | Linia 179: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd19.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd19.png]] | ||
|valign="top"|Niech czoło fali rozchodzącej się w prędkością <math>v_1\ | |valign="top"|Niech czoło fali rozchodzącej się w prędkością <math>v_1\ </math>, w pierwszym ośrodku o współczynniku załamania <math>n_1\ </math>,, pada na granicę z drugim ośrodkiem o współczynniku załamania <math>n_2\ </math>, i rozchodzi się dalej z prędkością <math>v_2\ </math>,. Zgodnie z zasadą Huyghensa, w ośrodku tym rozchodzą się fale kuliste, które na rysunku pokazane są kolorem czerwonym. W czasie, kiedy światło przebiegnie w ośrodku pierwszym odcinek <math>AA'\ </math>,, fala w ośrodku drugim przebiegnie odcinek <math>BB'\ </math>,: <math>t_{AA'}=t_{BB'}</math>. Wyrażając czas jako iloraz drogi i prędkości mamy: <math>\frac{AA'}{v_1}=\frac{BB'}{v_2}</math> Pamiętamy przy tym, że współczynnik załamania wiąże się z prędkością fali związkiem <math>n=\frac{c}{v}</math>. | ||
Wykorzystując zależności geometryczne: <math>AA'=BA'sin\alpha_1</math> i <math>BB'=BA'sin\alpha_2</math>, otrzymujemy prawo Sneliusa: <math>n_1 sin\alpha_1=n_2 sin\alpha_2</math>, które można też wyrazić jako: stosunek sinusa kąta padania do sinusa kąta załamania jest stały i równy współczynnikowi załamania ośrodka drugiego względem pierwszego. | Wykorzystując zależności geometryczne: <math>AA'=BA'sin\alpha_1</math> i <math>BB'=BA'sin\alpha_2</math>, otrzymujemy prawo Sneliusa: <math>n_1 sin\alpha_1=n_2 sin\alpha_2</math>, które można też wyrazić jako: stosunek sinusa kąta padania do sinusa kąta załamania jest stały i równy współczynnikowi załamania ośrodka drugiego względem pierwszego. | ||
| Linia 189: | Linia 189: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd20.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd20.png]] | ||
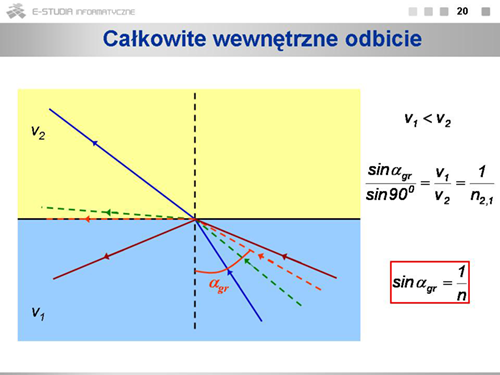
|valign="top"|Jeśli promień padający biegnie w ośrodku gęstszym optycznie (czyli <math>v_1<v_2</math>), to kąt załamania jest większy niż kąt padania. Zwiększając kąt padania dochodzimy do sytuacji, gdy kąt załamania równy jest <math>90^\circ\ | |valign="top"|Jeśli promień padający biegnie w ośrodku gęstszym optycznie (czyli <math>v_1<v_2</math>), to kąt załamania jest większy niż kąt padania. Zwiększając kąt padania dochodzimy do sytuacji, gdy kąt załamania równy jest <math>90^\circ\ </math>,. Taki kąt padania nazywamy kątem granicznym. Sinus kąta granicznego jest odwrotnością współczynnika załamania ośrodka gęstszego optyczne względem ośrodka rzadszego optycznie. Jeśli światło padnie na granicę ośrodków pod kątem większym od granicznego, odbije się w całości od granicy. Jest to zjawisko całkowitego wewnętrznego odbicia. Wykorzystywane jest ono w konstrukcji światłowodów. | ||
|} | |} | ||
| Linia 212: | Linia 212: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd22.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd22.png]] | ||
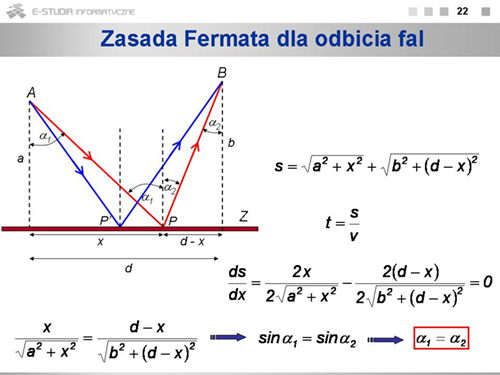
|valign="top"|Warunki geometryczne dla odbicia promieni świetlnych od granicy dwóch ośrodków pokazane są na rysunku. "Próbny" promień pokazany jest kolorem czerwonym. Ośrodek jest wciąż ten sam, więc światło porusza się cały czas z tą samą prędkością. Minimum czasu odpowiada więc najkrótszej drodze. Długość drogi pomiędzy punktami <math>A\ | |valign="top"|Warunki geometryczne dla odbicia promieni świetlnych od granicy dwóch ośrodków pokazane są na rysunku. "Próbny" promień pokazany jest kolorem czerwonym. Ośrodek jest wciąż ten sam, więc światło porusza się cały czas z tą samą prędkością. Minimum czasu odpowiada więc najkrótszej drodze. Długość drogi pomiędzy punktami <math>A\ </math>, i <math>B\ </math>,, określonej tak, że promień świetlny musi w jakimś punkcie odbić się od zwierciadła <math>Z\ </math>,, może być zapisana w postaci: <math>s=\sqrt{a^2+x^2}+\sqrt{b^2+(d-x)^2}</math>. Poszukujemy takiej wartości <math>x\ </math>,, dla której droga <math>s\ </math>, mieć będzie wartość minimalną. W tym celu obliczamy pochodną ds/dx i przyrównujemy ją do zera. Otrzymujemy: <math>\frac{x}{\sqrt{a^2+x^2}}=\frac{d-x}{\sqrt{b^2+(d-x)^2}}</math>, czyli <math>sin\alpha_1=sin\alpha_2</math>. Oznacza to, że kąt odbicia równy jest kątowi padania. Oba promienie padający i odbity oraz normalna leżą w jednej płaszczyźnie. Światło pobiegnie więc od punktu <math>A\ </math>, do punktu <math>B\ </math>, po takiej drodze, by spełniony był warunek minimalnego czasu, a wiec nie po drodze <math>APB\ </math>,, ale <math>AP'B\ </math>,. | ||
|} | |} | ||
| Linia 228: | Linia 228: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd24.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd24.png]] | ||
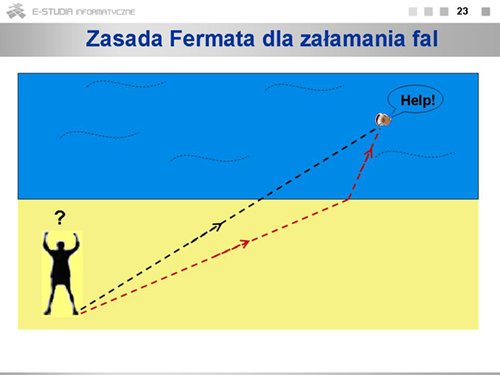
|valign="top"|Zastosujmy zasadę Fermata do zjawiska załamania fali na granicy dwóch ośrodków o współczynnikach załamania <math>n_1\ | |valign="top"|Zastosujmy zasadę Fermata do zjawiska załamania fali na granicy dwóch ośrodków o współczynnikach załamania <math>n_1\ </math>, i <math>n_2\ </math>,. Relacje geometryczne przedstawia rysunek. Pamiętając, że współczynnik załamania jest stosunkiem prędkości światła w próżni do prędkości w danym ośrodku <math>n=\frac{c}{v}</math>, otrzymujemy wyrażenie na czas przebycia przez światło drogi od <math>A\ </math>, do <math>B\ </math>,: <math>t=\frac{n_1 l_1+n_2 l_2}{c}</math>. Wielkość <math>l=n_1 l_1+n_2 l_2</math> nosi nazwę drogi optycznej. Poszukujemy więc takiej wartości <math>x\ </math>,, przy ustalonych położeniach punktów <math>A\ </math>, i <math>B\ </math>,, by droga optyczna była minimalna. W tym celu obliczamy pochodną wyrażenia, w którym drogę optyczną określamy w funkcji <math>x\ </math>,: <math>l=n_1\sqrt{a^2+x^2}+n_2\sqrt{b^2+(c-x)^2}</math>. Po przyrównaniu pochodnej <math>dl/dx\ </math>, do zera otrzymujemy: <math>n_1\cdot\frac{x}{\sqrt{a^2+x^2}}=n_2\cdot\frac{c-x}{\sqrt{b^2+(c-x)^2}}</math>, czyli znane prawo załamania: <math>n_1 sin\alpha_1=n_2 sin\alpha_2</math>. | ||
|} | |} | ||
| Linia 238: | Linia 238: | ||
|valign="top"|'''Polaryzacja fali''' | |valign="top"|'''Polaryzacja fali''' | ||
W świetle naturalnym, czyli emitowanym przez naturalne źródła takie jak żarówka lub słońce, wektor drga we wszystkich możliwych kierunkach prostopadłych do promienia. Na promieniowanie ciała świecącego składają się fale emitowane przez poszczególne atomy. Ponieważ emisja atomów odbywa się niezależnie od siebie, płaszczyzna drgań wektora <math>\overrightarrow{E}\ | W świetle naturalnym, czyli emitowanym przez naturalne źródła takie jak żarówka lub słońce, wektor drga we wszystkich możliwych kierunkach prostopadłych do promienia. Na promieniowanie ciała świecącego składają się fale emitowane przez poszczególne atomy. Ponieważ emisja atomów odbywa się niezależnie od siebie, płaszczyzna drgań wektora <math>\overrightarrow{E}\ </math>, zorientowana zupełnie przypadkowo. W fali wypadkowej drgania o różnych kierunkach występują z jednakowym prawdopodobieństwem. Taką falę nazywamy falą niespolaryzowaną. Jeśli kierunki drgań wektora <math>\overrightarrow{E}\ </math>, są w jakiś sposób uporządkowane, falę nazywamy spolaryzowaną. Polaryzacja może być liniowa, gdy drgania zachodzą tylko w jednej przechodzącej przez promień płaszczyźnie. Kiedy z zachowaniem wzajemnych relacji kierunkowych, układ wektorów <math>\overrightarrow{E}\ </math>, i <math>\overrightarrow{B}\ </math>, wykonuje obrót wokół kierunku propagacji, to mówimy, że fala jest spolaryzowana kołowo. W zależności od kierunku tego obrotu fala może być spolaryzowana prawo- lub lewoskrętnie. W przypadku fali spolaryzowanej kołowo składowe <math>Y\ </math>, i <math>Z\ </math>, wektorów <math>\overrightarrow{E}\ </math>, i <math>\overrightarrow{B}\ </math>, będą różne w różnych punktach na osi <math>X\ </math>,, przy zachowaniu bezwzględnych ich wartości. Kiedy bezwzględne wartości zmieniają się, mówimy o polaryzacji eliptycznej. | ||
|} | |} | ||
| Linia 248: | Linia 248: | ||
|valign="top"|Czy można "spolaryzować" światło? Gdybyśmy umieli z przypadkowo zorientowanych ciągów falowych wydzielić tylko takie, które mają zadaną stałą płaszczyznę drgań wektora elektrycznego, to moglibyśmy otrzymać światło spolaryzowane. Intuicja podpowiada nam, że w tym celu musimy światło skierować na obiekt mający własności kierunkowe w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali świetlnej. Sposobów uzyskania światła spolaryzowanego jest wiele i omówimy tu niektóre z nich. | |valign="top"|Czy można "spolaryzować" światło? Gdybyśmy umieli z przypadkowo zorientowanych ciągów falowych wydzielić tylko takie, które mają zadaną stałą płaszczyznę drgań wektora elektrycznego, to moglibyśmy otrzymać światło spolaryzowane. Intuicja podpowiada nam, że w tym celu musimy światło skierować na obiekt mający własności kierunkowe w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali świetlnej. Sposobów uzyskania światła spolaryzowanego jest wiele i omówimy tu niektóre z nich. | ||
'''Polaroid''' - to płytka lub błona, w której cząsteczki ułożone są tak, że tworzą strukturę łańcuchową, która po zabiegach mechanicznych i chemicznych, przepuszcza jedynie składową wektora <math>\overrightarrow{E}\ | '''Polaroid''' - to płytka lub błona, w której cząsteczki ułożone są tak, że tworzą strukturę łańcuchową, która po zabiegach mechanicznych i chemicznych, przepuszcza jedynie składową wektora <math>\overrightarrow{E}\ </math>, równoległą do wyróżnionego kierunku w płytce. Kiedy drugą taką płytkę będziemy obracać wokół osi równoległej do kierunku padania światła zauważymy, że światło zostało spolaryzowane, bo natężenie światła przepuszczonego będzie się zmieniać. Kiedy płytki ustawimy tak, że ich kierunki polaryzacji będą się krzyżować pod kątem prostym uzyskamy wygaszenie fal, kiedy kierunki te będą równoległe, uzyskamy maksymalne przepuszczanie światła. Oznacza to, że w pierwszej płytce światło zostało liniowo spolaryzowane. | ||
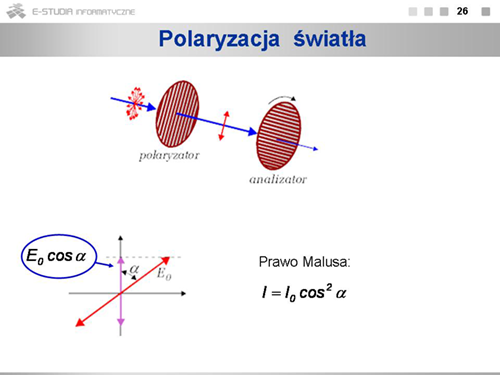
Przy kątach pośrednich natężenie przechodzącego światła będzie się zmieniać zgodnie z tzw. '''prawem Malusa'''. Sens tego prawa wyjaśnia schemat pokazany na rysunku. Jeśli czerwona strzałka pokazuje kierunek drgań wektora pola elektrycznego po przejściu światła przez polaryzator, to przy ustawieniu analizatora zgodnie ze strzałką fioletową składowa drgań po przejściu przez niego będzie <math>E_0 cos\alpha\ | Przy kątach pośrednich natężenie przechodzącego światła będzie się zmieniać zgodnie z tzw. '''prawem Malusa'''. Sens tego prawa wyjaśnia schemat pokazany na rysunku. Jeśli czerwona strzałka pokazuje kierunek drgań wektora pola elektrycznego po przejściu światła przez polaryzator, to przy ustawieniu analizatora zgodnie ze strzałką fioletową składowa drgań po przejściu przez niego będzie <math>E_0 cos\alpha\ </math>,. Natężenie promieniowania proporcjonalne jest do kwadratu amplitudy drgań, więc zależność natężenia (intensywności) promieniowania od kąta może być wyrażona w postaci <math>l=l_0 cos^2 \alpha</math>. | ||
|} | |} | ||
| Linia 258: | Linia 258: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M15_Slajd27.png]] | |width="450px" valign="top"|[[Grafika:PF_M15_Slajd27.png]] | ||
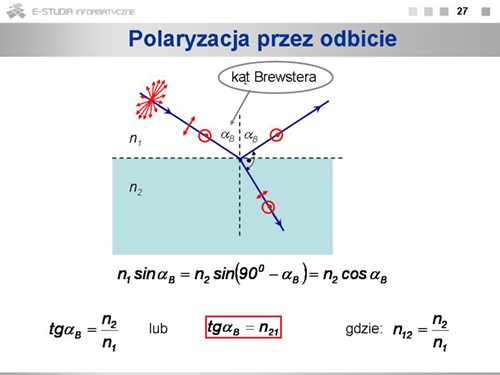
|valign="top"|Kiedy nie spolaryzowane światło pada na granicę dwóch ośrodków to światło odbite wykazuje pewien stan polaryzacji. Całkowita polaryzacja jest wtedy, kiedy kąt pomiędzy wiązką odbitą i załamaną jest kątem prostym. Kąt padania <math>\alpha\ | |valign="top"|Kiedy nie spolaryzowane światło pada na granicę dwóch ośrodków to światło odbite wykazuje pewien stan polaryzacji. Całkowita polaryzacja jest wtedy, kiedy kąt pomiędzy wiązką odbitą i załamaną jest kątem prostym. Kąt padania <math>\alpha\ </math>,, dla którego warunek ten jest spełniony nosi nazwę '''kąta Brewstera'''. Światło załamane jest spolaryzowane w dużym stopniu w kierunku prostopadłym do kierunku polaryzacji światła odbitego. Jednak nawet przy kącie padania równym kątowi Brewstera światło to nie jest spolaryzowane całkowicie. Kiedy kąt padania równy jest kątowi Brewstera, to wykorzystując prawo załamania Sneliusa otrzymujemy: <math>tg\alpha_B=n_{21}</math>. Wielkość <math>n_{21}\ </math>, określa współczynnik załamania ośrodka drugiego względem pierwszego. Określenie kąta Brewstera umożliwia znalezienie warunków, w jakich następuje całkowita polaryzacja promienia odbitego. | ||
|} | |} | ||
| Linia 278: | Linia 278: | ||
= Podsumowanie = | = Podsumowanie = | ||
Z równań Maxwella można wyprowadzić równanie falowe <math>\frac{\partial^2 E}{\partial t^2}=\frac{1}{\varepsilon_0 \mu_0}\frac{\partial^2 E}{\partial x^2}</math> opisujące falę elektromagnetyczną rozchodzącą się z prędkością światła: <math>c=\frac{1}{\sqrt{\varepsilon_0 \mu_0}}</math>. Fala elektromagnetyczna jest falą poprzeczną, w której drgania wzajemnie prostopadłych wektorów <math>\overrightarrow{E}\ | Z równań Maxwella można wyprowadzić równanie falowe <math>\frac{\partial^2 E}{\partial t^2}=\frac{1}{\varepsilon_0 \mu_0}\frac{\partial^2 E}{\partial x^2}</math> opisujące falę elektromagnetyczną rozchodzącą się z prędkością światła: <math>c=\frac{1}{\sqrt{\varepsilon_0 \mu_0}}</math>. Fala elektromagnetyczna jest falą poprzeczną, w której drgania wzajemnie prostopadłych wektorów <math>\overrightarrow{E}\ </math>, i <math>\overrightarrow{B}\ </math>, zachodzą w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali. Rodzaje fal elektromagnetycznych różnią się długością fali. Zaczynając od fal o największej długości są to: fale radiowe, mikrofale, promieniowanie podczerwone, światło widzialne, promieniowanie nadfioletowe, promieniowanie rentgenowskie i promieniowanie <math>\gamma\ </math>,. Całkowita energia fali elektromagnetycznej zmagazynowana w jednostce objętości jest sumą energii pola elektrycznego i pola magnetycznego i wynosi <math>w=\varepsilon_0 E^2</math>. Wektor Poyntinga to wektor, którego wartość określa energię przenoszoną przez jednostkową powierzchnię w jednostce czasu, a kierunek wskazuje kierunek przenoszenia tej energii. Wyraża się on wzorem: <math>\overrightarrow{P}=\frac{1}{\mu_0}\overrightarrow{E}\times \overrightarrow{B}</math>. | ||
Z równań Maxwella wynika, że prędkość światła w ośrodku materialnym jest <math>\sqrt{\varepsilon \mu}\ | Z równań Maxwella wynika, że prędkość światła w ośrodku materialnym jest <math>\sqrt{\varepsilon \mu}\ </math>, razy mniejsza niż prędkość światła w próżni (<math>\varepsilon\ </math>, i <math>\mu\ </math>, to względna przenikalność elektryczna i magnetyczna ośrodka). Optyka geometryczna opiera się na dwóch prawach: prawu odbicia i prawu załamania światła. Prawo odbicia mówi, że kąty padania i odbicia są sobie równe, natomiast prawo załamania, zwane też prawem Sneliusa brzmi: stosunek kątów padania i załamania jest stały i równy odwrotności stosunku współczynników załamania <math>\frac{sin\alpha_1}{sin\alpha2}=\frac{n_2}{n_1}</math>. | ||
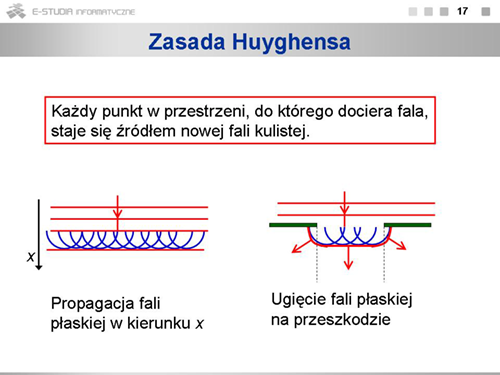
Oba te prawa wynikają z ogólniejszych zasad rządzących propagacją światła: zasady Huyghensa (każdy punkt w przestrzeni, do którego dociera fala, staje się źródłem nowej fali kulistej) oraz zasady Fermata (światło biegnie po takiej drodze, na pokonanie której potrzebny jest ekstremalny czas). | Oba te prawa wynikają z ogólniejszych zasad rządzących propagacją światła: zasady Huyghensa (każdy punkt w przestrzeni, do którego dociera fala, staje się źródłem nowej fali kulistej) oraz zasady Fermata (światło biegnie po takiej drodze, na pokonanie której potrzebny jest ekstremalny czas). | ||
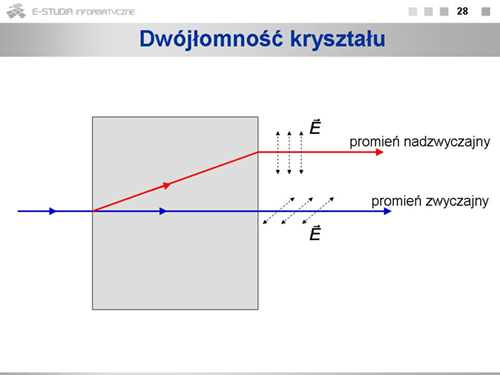
Światło o uporządkowanych kierunkach drgań wektora <math>\overrightarrow{E}\ | Światło o uporządkowanych kierunkach drgań wektora <math>\overrightarrow{E}\ </math>, nazywamy światłem spolaryzowanym. Polaryzacja może być liniowa, kołowa lub eliptyczna. Polaryzację światła można uzyskać odbijając je od granicy ośrodków pod kątem Brewstera lub przepuszczając przez polaryzator. Zjawisko dwójłomności to rozdzielenie światła padającego na kryształ o strukturze nieregularnej na dwa promienie rozchodzące się z różnymi prędkościami. Promienie te są spolaryzowane w płaszczyznach wzajemnie prostopadłych. | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 292: | Linia 292: | ||
'''Zadanie 1''' | '''Zadanie 1''' | ||
Obwód LC zawiera pojemność <math>C = 9 pF\ | Obwód LC zawiera pojemność <math>C = 9 pF\ </math>, i indukcyjność <math>L = 4 \mu H\ </math>,. Do jakiego zakresu fal elektromagnetycznych zaliczymy fale generowane w tym obwodzie? | ||
| Linia 313: | Linia 313: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
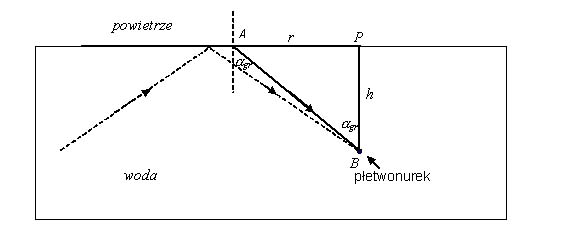
Płetwonurek może zobaczyć przedmioty na powierzchni znajdujące się wewnątrz okręgu o promieniu <math>r\ | Płetwonurek może zobaczyć przedmioty na powierzchni znajdujące się wewnątrz okręgu o promieniu <math>r\ </math>,, wyznaczonym przez kąt graniczny (rysunek). Jeśli spojrzy pod kątem większym niż <math>\alpha_{gr}\ </math>,, to zobaczy obraz dna w świetle odbitym od powierzchni wody. Z trójkąta <math>APB\ </math>, mamy: <math>r=htg\alpha_{gr}</math>. Warunek na kąt graniczny: | ||
: <math>\frac{sin90^\circ}{sin\alpha_{gr}}=n</math>, stąd <math>sin\alpha_{gr}=\frac{1}{n}</math> | : <math>\frac{sin90^\circ}{sin\alpha_{gr}}=n</math>, stąd <math>sin\alpha_{gr}=\frac{1}{n}</math> | ||
| Linia 329: | Linia 329: | ||
'''Zadanie 3''' | '''Zadanie 3''' | ||
Ryba znajduje się w punkcie P na głębokości h = 1,5 m. Na jakiej głębokości <math>h'\ | Ryba znajduje się w punkcie P na głębokości h = 1,5 m. Na jakiej głębokości <math>h'\ </math>, widzi ją wędkarz, który spogląda pod kątem <math>45^\circ\ </math>, ? Współczynnik załamania wody n = 1,33. | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
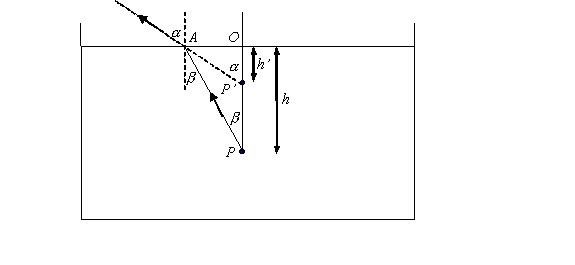
Wędkarz widzi rybę na przedłużeniu promienia załamanego, w punkcie <math>P'\ | Wędkarz widzi rybę na przedłużeniu promienia załamanego, w punkcie <math>P'\ </math>, (rysunek). Z trójkąta AOP mamy: <math>\frac{AO}{h}=tg\beta</math>, a z trójkąta <math>AOP'\ </math>,: <math>\frac{AO}{h'}=tg\alpha</math>. Dzieląc stronami równania otrzymujemy: <math>\frac{h'}{h}=\frac{tg\beta}{tg\alpha}</math>, czyli <math>h'=h\frac{sin\beta}{sin\alpha}\cdot \frac{cos\alpha}{cos\beta}=h\cdot \frac{1}{n}\cdot \frac{cos\alpha}{cos\beta}</math>. Korzystamy ze wzoru trygonometrycznego: <math>cos\beta=\sqrt{1-sin^2 \beta}</math>, z prawa załamania: <math>sin\beta=\frac{sin\alpha}{n}</math>. | ||
: [[Grafika:PF1_M15_Wzor2.jpg]] | : [[Grafika:PF1_M15_Wzor2.jpg]] | ||
| Linia 350: | Linia 350: | ||
'''Zadanie 4''' | '''Zadanie 4''' | ||
Dwa polaryzatory ustawione są tak, że płaszczyzny, w których polaryzują światło, są nierównoległe. Każdy z polaryzatorów oprócz polaryzowania światła pochłania <math>p = 5\%\ | Dwa polaryzatory ustawione są tak, że płaszczyzny, w których polaryzują światło, są nierównoległe. Każdy z polaryzatorów oprócz polaryzowania światła pochłania <math>p = 5\%\ </math>, promieniowania padającego. Na polaryzator pierwszy pada wiązka światła spolaryzowanego liniowo tak, że kąt między płaszczyzną polaryzacji światła a płaszczyzną polaryzatora wynosi <math>\alpha =30^\circ\ </math>,. Natężenie tego światła jest równe <math>I_0 = 6 mW/sr\ </math>,. Pod jakim kątem skrzyżowane są polaryzatory, jeśli po przejściu przez obydwa światło ma natężenie <math>I_k = 1,015 mW/Sr</math> ? | ||
| Linia 360: | Linia 360: | ||
#przepuszczeniu światła spolaryzowanego przez pierwszy polaryzator, zgodnie z prawem Malusa: <math>I_2=I_1 cos^2 \alpha</math> ; | #przepuszczeniu światła spolaryzowanego przez pierwszy polaryzator, zgodnie z prawem Malusa: <math>I_2=I_1 cos^2 \alpha</math> ; | ||
#absorpcji światła w drugim polaryzatorze: <math>I_3 = (1-p)I_2</math> ; | #absorpcji światła w drugim polaryzatorze: <math>I_3 = (1-p)I_2</math> ; | ||
#przepuszczeniu światła spolaryzowanego przez drugi polaryzator: <math>I_4=I_3 cos^2 \beta</math>, gdzie <math>\beta\ | #przepuszczeniu światła spolaryzowanego przez drugi polaryzator: <math>I_4=I_3 cos^2 \beta</math>, gdzie <math>\beta\ </math>, to szukany kąt. | ||
Pamiętając, że <math>I_4 = I_k</math>, otrzymujemy: <math>I_k=I_0(1-p)^2cos^2\alpha cos^2 \beta</math> , stąd: <math>cos^2 \beta=\frac{I_k}{I_0 (1-p)^2 cos^2 \alpha}=0,25</math>. | Pamiętając, że <math>I_4 = I_k</math>, otrzymujemy: <math>I_k=I_0(1-p)^2cos^2\alpha cos^2 \beta</math> , stąd: <math>cos^2 \beta=\frac{I_k}{I_0 (1-p)^2 cos^2 \alpha}=0,25</math>. | ||
Odp. Płaszczyzny polaryzacji polaryzatorów ustawione są pod kątem <math>\beta=60^\circ\ | Odp. Płaszczyzny polaryzacji polaryzatorów ustawione są pod kątem <math>\beta=60^\circ\ </math>,. | ||
</div></div> | </div></div> | ||
| Linia 377: | Linia 377: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | ||
:<math>\alpha=36^\circ 56'\ | :<math>\alpha=36^\circ 56'\ </math>, | ||
</div></div> | </div></div> | ||
Aktualna wersja na dzień 12:05, 5 wrz 2023
Wykład

|

|
Nasze rozważania rozpoczniemy od przypomnienia równań Maxwella, które przedstawiają relacje pomiędzy zmianami pól: elektrycznego i magnetycznego w czasie i przestrzeni. |

|
Możemy też gęstość energii fali elektromagnetycznej przedstawić w postaci: lub . |
Podsumowanie
Z równań Maxwella można wyprowadzić równanie falowe opisujące falę elektromagnetyczną rozchodzącą się z prędkością światła: . Fala elektromagnetyczna jest falą poprzeczną, w której drgania wzajemnie prostopadłych wektorów , i , zachodzą w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali. Rodzaje fal elektromagnetycznych różnią się długością fali. Zaczynając od fal o największej długości są to: fale radiowe, mikrofale, promieniowanie podczerwone, światło widzialne, promieniowanie nadfioletowe, promieniowanie rentgenowskie i promieniowanie ,. Całkowita energia fali elektromagnetycznej zmagazynowana w jednostce objętości jest sumą energii pola elektrycznego i pola magnetycznego i wynosi . Wektor Poyntinga to wektor, którego wartość określa energię przenoszoną przez jednostkową powierzchnię w jednostce czasu, a kierunek wskazuje kierunek przenoszenia tej energii. Wyraża się on wzorem: .
Z równań Maxwella wynika, że prędkość światła w ośrodku materialnym jest , razy mniejsza niż prędkość światła w próżni (, i , to względna przenikalność elektryczna i magnetyczna ośrodka). Optyka geometryczna opiera się na dwóch prawach: prawu odbicia i prawu załamania światła. Prawo odbicia mówi, że kąty padania i odbicia są sobie równe, natomiast prawo załamania, zwane też prawem Sneliusa brzmi: stosunek kątów padania i załamania jest stały i równy odwrotności stosunku współczynników załamania .
Oba te prawa wynikają z ogólniejszych zasad rządzących propagacją światła: zasady Huyghensa (każdy punkt w przestrzeni, do którego dociera fala, staje się źródłem nowej fali kulistej) oraz zasady Fermata (światło biegnie po takiej drodze, na pokonanie której potrzebny jest ekstremalny czas).
Światło o uporządkowanych kierunkach drgań wektora , nazywamy światłem spolaryzowanym. Polaryzacja może być liniowa, kołowa lub eliptyczna. Polaryzację światła można uzyskać odbijając je od granicy ośrodków pod kątem Brewstera lub przepuszczając przez polaryzator. Zjawisko dwójłomności to rozdzielenie światła padającego na kryształ o strukturze nieregularnej na dwa promienie rozchodzące się z różnymi prędkościami. Promienie te są spolaryzowane w płaszczyznach wzajemnie prostopadłych.
Materiały do ćwiczeń
Zadanie 1
Obwód LC zawiera pojemność , i indukcyjność ,. Do jakiego zakresu fal elektromagnetycznych zaliczymy fale generowane w tym obwodzie?
Zadanie 2
Na głębokości h = 2 m pod punktem P na powierzchni wody znajduje się płetwonurek o bardzo złych zamiarach. Zbliża się do niego James Bond na swojej bezszelestnej lodzi. Na jaką odległość może podpłynąć do punktu P, aby złowieszczy płetwonurek go nie zauważył? Współczynnik załamania wody n =1,33.
Zadanie 3
Ryba znajduje się w punkcie P na głębokości h = 1,5 m. Na jakiej głębokości , widzi ją wędkarz, który spogląda pod kątem , ? Współczynnik załamania wody n = 1,33.
Zadanie 4
Dwa polaryzatory ustawione są tak, że płaszczyzny, w których polaryzują światło, są nierównoległe. Każdy z polaryzatorów oprócz polaryzowania światła pochłania , promieniowania padającego. Na polaryzator pierwszy pada wiązka światła spolaryzowanego liniowo tak, że kąt między płaszczyzną polaryzacji światła a płaszczyzną polaryzatora wynosi ,. Natężenie tego światła jest równe ,. Pod jakim kątem skrzyżowane są polaryzatory, jeśli po przejściu przez obydwa światło ma natężenie ?
Zadanie 5
Pod jakim kątem w stosunku do horyzontu powinno znajdować się słońce, aby jego promienie odbite od gładkiej powierzchni jeziora były maksymalnie spolaryzowane. Współczynnik załamania światła w wodzie wynosi n =1,33.
Słowa kluczowe
- fala elektromagnetyczna
- wektor Poyntinga
- widmo fal elektromagnetycznych
- zasada Hyughensa
- zasada Fermata
- kąt padania
- kąt odbicia
- kąt załamania
- droga optyczna
- prawo Sneliusa
- polaryzacja liniowa
- polaryzacja kołowa
- polaryzacja eliptyczna
- kąt Brewstera
- dwójłomność
Bibliografia
- J. Orear, Fizyka, WNT, Warszawa (1998);
- R. Resnick, D. Halliday, Fizyka 1, PWN, Warszawa (1994);
- I.W. Sawieliew, Wykłady z fizyki, PWN, Warszawa (1994).