PEE Moduł 1: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 1 pośredniej wersji utworzonej przez tego samego użytkownika) | |||
| Linia 15: | Linia 15: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd3.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd3.png|500px]] | ||
|valign="top"|Teoria obwodów stanowi jedną z dziedzin elektrotechniki zajmującą się stroną teoretyczną zjawisk występujących w obwodach elektrycznych, w tym metodami analizy rozpływu prądów i rozkładu napięć obwodu w stanie ustalonym i nieustalonym. Przyjmuje się, że nośnikami elektryczności są cząstki elementarne: elektrony i protony występujące w atomie. W przypadku przewodników elektrycznych najważniejszą rolę odgrywają elektrony swobodne, stanowiące trwałe nośniki ujemnego ładunku <math>q</math>, wyzwolone z przyciągania jądra atomu oraz jony, stanowiące cząsteczki naładowane dodatnio lub ujemnie. Ładunek elektryczny elektronu, oznaczany jest literą <math>e\ | |valign="top"|Teoria obwodów stanowi jedną z dziedzin elektrotechniki zajmującą się stroną teoretyczną zjawisk występujących w obwodach elektrycznych, w tym metodami analizy rozpływu prądów i rozkładu napięć obwodu w stanie ustalonym i nieustalonym. Przyjmuje się, że nośnikami elektryczności są cząstki elementarne: elektrony i protony występujące w atomie. W przypadku przewodników elektrycznych najważniejszą rolę odgrywają elektrony swobodne, stanowiące trwałe nośniki ujemnego ładunku <math>q</math>, wyzwolone z przyciągania jądra atomu oraz jony, stanowiące cząsteczki naładowane dodatnio lub ujemnie. Ładunek elektryczny elektronu, oznaczany jest literą <math>e\ </math>, a jego wartość <math>e=1,602 \cdot 10^{-19}C</math>. | ||
'''Prąd elektryczny''' powstaje jako uporządkowany ruch ładunków elektrycznych i jest utożsamiany w teorii obwodów z pojęciem natężenia prądu elektrycznego. W ogólności definiowany jest jako granica stosunku ładunku elektrycznego przepływającego przez przekrój poprzeczny elementu do rozpatrywanego czasu, gdy czas ten dąży do zera. Prąd elektryczny oznaczany będzie literą <math>i\ | '''Prąd elektryczny''' powstaje jako uporządkowany ruch ładunków elektrycznych i jest utożsamiany w teorii obwodów z pojęciem natężenia prądu elektrycznego. W ogólności definiowany jest jako granica stosunku ładunku elektrycznego przepływającego przez przekrój poprzeczny elementu do rozpatrywanego czasu, gdy czas ten dąży do zera. Prąd elektryczny oznaczany będzie literą <math>i\ </math>, (dużą lub małą). Jest wielkością skalarną a jej jednostką w układzie SI jest '''amper''' (<math>A\ </math>,). Prąd mierzymy przyrządem zwanym amperomierzem, włączanym szeregowo do gałęzi, której prąd chcemy zmierzyć. Przyjmuje się, że amperomierz ma impedancję wewnętrzną równą zeru, a więc nie wpływa na rozpływy prądów w obwodzie. | ||
Każdemu punktowi w środowisku przewodzącym prąd elektryczny można przyporządkować pewien potencjał mierzony względem punktu odniesienia. Różnica potencjałów między dwoma punktami tego środowiska nazywana jest '''napięciem elektrycznym'''. Jednostką napięcia elektrycznego jest '''volt''' (<math>V</math>). Napięcie pomiędzy dwoma punktami obwodu elektrycznego mierzymy zwykle przyrządem zwanym woltomierzem, włączanym równolegle między punkty, których różnicę potencjałów chcemy mierzyć. Przyjmuje się przy tym, że impedancja wewnętrzna woltomierza jest bliska nieskończoności, a więc woltomierz pomiarowy nie wpływa na rozkład napięć i rozpływ prądów w obwodzie. | Każdemu punktowi w środowisku przewodzącym prąd elektryczny można przyporządkować pewien potencjał mierzony względem punktu odniesienia. Różnica potencjałów między dwoma punktami tego środowiska nazywana jest '''napięciem elektrycznym'''. Jednostką napięcia elektrycznego jest '''volt''' (<math>V</math>). Napięcie pomiędzy dwoma punktami obwodu elektrycznego mierzymy zwykle przyrządem zwanym woltomierzem, włączanym równolegle między punkty, których różnicę potencjałów chcemy mierzyć. Przyjmuje się przy tym, że impedancja wewnętrzna woltomierza jest bliska nieskończoności, a więc woltomierz pomiarowy nie wpływa na rozkład napięć i rozpływ prądów w obwodzie. | ||
| Linia 59: | Linia 59: | ||
|valign="top"|'''Rezystor''' | |valign="top"|'''Rezystor''' | ||
Rezystor, zwany również opornikiem należy do klasy elementów pasywnych rozpraszających energię. W teorii obwodów rezystor uważa się za element idealny i przypisuje mu tylko jedną cechę (parametr), zwaną '''rezystancją''' lub oporem. W dalszej części rozważać będziemy wyłącznie rezystor liniowy. Rezystancję (oporność) oznaczać będziemy literą <math>R\ | Rezystor, zwany również opornikiem należy do klasy elementów pasywnych rozpraszających energię. W teorii obwodów rezystor uważa się za element idealny i przypisuje mu tylko jedną cechę (parametr), zwaną '''rezystancją''' lub oporem. W dalszej części rozważać będziemy wyłącznie rezystor liniowy. Rezystancję (oporność) oznaczać będziemy literą <math>R\ </math>, a jej odwrotność jest nazywana '''konduktancją''' i oznaczana literą <math>G\ </math>,, przy czym <math>R = 1/G</math>. Symbol graficzny rezystora liniowego przedstawiony jest na rysunku obok. | ||
Opis matematyczny rezystora wynika z prawa Ohma, zgodnie z którym | Opis matematyczny rezystora wynika z prawa Ohma, zgodnie z którym | ||
| Linia 67: | Linia 67: | ||
Wartość rezystancji rezystora liniowego przyjmuje określoną wartość (często stałą). Jednostką rezystancji jest '''om''' (<math>\Omega</math>) a konduktancji '''siemens''' (<math>S</math>). | Wartość rezystancji rezystora liniowego przyjmuje określoną wartość (często stałą). Jednostką rezystancji jest '''om''' (<math>\Omega</math>) a konduktancji '''siemens''' (<math>S</math>). | ||
W realizacji praktycznej opornik jest wykonywany często z drutu metalowego o długości <math>l\ | W realizacji praktycznej opornik jest wykonywany często z drutu metalowego o długości <math>l\ </math>,, polu przekroju poprzecznego <math>S\ </math>, i rezystancji właściwej <math>\rho</math>. Rezystancja takiego opornika jest wprost proporcjonalna do <math>l\ </math>, i <math>\rho</math> a odwrotnie proporcjonalna do <math>S\ </math>,, stąd <math>R = \rho l/S</math>. | ||
|} | |} | ||
| Linia 76: | Linia 76: | ||
|valign="top"|'''Cewka''' | |valign="top"|'''Cewka''' | ||
Cewka zwana również induktorem należy również do klasy elementów pasywnych. Ma zdolność gromadzenia energii w polu magnetycznym. Cewce idealnej przypisuje się tylko jedną właściwość, zwaną '''indukcyjnością''' własną (w skrócie indukcyjnością) <math>L\ | Cewka zwana również induktorem należy również do klasy elementów pasywnych. Ma zdolność gromadzenia energii w polu magnetycznym. Cewce idealnej przypisuje się tylko jedną właściwość, zwaną '''indukcyjnością''' własną (w skrócie indukcyjnością) <math>L\ </math>,. W przypadku cewki liniowej indukcyjność definiuje się jako stosunek strumienia <math>\Psi</math> skojarzonego z cewką do prądu płynącego przez nią, to znaczy | ||
: <math>L={\Psi \over i_L}</math> | : <math>L={\Psi \over i_L}</math> | ||
Strumień skojarzony <math>\Psi</math> cewki o z zwojach jest równy sumie strumieni wszystkich zwojów cewki, to jest <math>\Psi = z\phi</math> (<math>\phi\ | Strumień skojarzony <math>\Psi</math> cewki o z zwojach jest równy sumie strumieni wszystkich zwojów cewki, to jest <math>\Psi = z\phi</math> (<math>\phi\ </math>, - strumień skojarzony z jednym zwojem cewki, <math>z\ </math>, – liczba zwojów). Jednostką indukcyjności jest '''henr''' (<math>H\ </math>,), przy czym <math>1H = 1\Omega s</math>. Napięcie cewki wyrażone jest jako pochodna strumienia względem czasu | ||
: <math>u_L={d\Psi \over dt}</math> | : <math>u_L={d\Psi \over dt}</math> | ||
W przypadku cewki liniowej o indukcyjności <math>L\ | W przypadku cewki liniowej o indukcyjności <math>L\ </math>, niezależnej od czasu, dla której strumień jest iloczynem prądu <math>i\ </math>, indukcyjności <math>L\ </math>,, <math>\Psi=Li_L</math>, relacja napięciowo-prądowa upraszcza się do postaci | ||
: <math>u_L=L{di_L \over dt}</math> | : <math>u_L=L{di_L \over dt}</math> | ||
Zauważmy, że przy stałej wartości prądu cewki i stałej wartości indukcyjności <math>L\ | Zauważmy, że przy stałej wartości prądu cewki i stałej wartości indukcyjności <math>L\ </math>, napięcie na niej jest równe zeru, gdyż pochodna wartości stałej względem czasu jest równa zeru. Stąd cewka w stanie ustalonym obwodu przy prądzie stałym zachowuje się jak zwarcie (napięcie między końcówkami elementu równe zeru). | ||
|} | |} | ||
| Linia 97: | Linia 97: | ||
|valign="top"|'''Kondensator''' | |valign="top"|'''Kondensator''' | ||
Kondensator jest elementem pasywnym, w którym istnieje możliwość gromadzenia energii w polu elektrycznym. Kondensatorowi idealnemu przypisuje się tylko jedną właściwość zwaną '''pojemnością''' <math>C\ | Kondensator jest elementem pasywnym, w którym istnieje możliwość gromadzenia energii w polu elektrycznym. Kondensatorowi idealnemu przypisuje się tylko jedną właściwość zwaną '''pojemnością''' <math>C\ </math>,. W przypadku kondensatora liniowego pojemność <math>C\ </math>, jest definiowana jako stosunek ładunku <math>q\ </math>, zgromadzonego w kondensatorze do napięcia między okładzinami tego kondensatora | ||
: <math>C={q \over u_C}</math> | : <math>C={q \over u_C}</math> | ||
W układzie SI jednostką ładunku jest '''kulomb''' (<math>C\ | W układzie SI jednostką ładunku jest '''kulomb''' (<math>C\ </math>,), a pojemności '''farad''' (<math>F\ </math>,), przy czym <math>1 F = 1 C/V</math>. Zależność wiążąca napięcie i prąd kondensatora dana jest w postaci równania różniczkowego | ||
: <math>i_C={dq \over dt}=C{du_C \over dt}</math> | : <math>i_C={dq \over dt}=C{du_C \over dt}</math> | ||
| Linia 118: | Linia 118: | ||
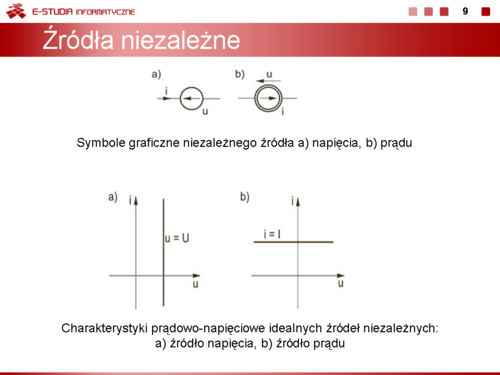
Rysunek na slajdzie przedstawia charakterystyki prądowo-napięciowe obu rodzajów idealnych źródeł niezależnych: napięcia (a) i prądu (b). | Rysunek na slajdzie przedstawia charakterystyki prądowo-napięciowe obu rodzajów idealnych źródeł niezależnych: napięcia (a) i prądu (b). | ||
Dla źródła napięciowego charakterystyka jest równoległa do osi prądowej (wartość napięcia <math>u\ | Dla źródła napięciowego charakterystyka jest równoległa do osi prądowej (wartość napięcia <math>u\ </math>, stała), a dla źródła prądowego równoległa do osi napięciowej (wartość prądu <math>i\ </math>, stała). Tak podane charakterystyki odnoszą się do źródeł stałych. W przypadku źródeł sinusoidalnych idealność jest rozumiana jako stałość parametrów źródła (amplituda, faza początkowa oraz częstotliwość niezależne od obciążenia). | ||
Przykładami źródła napięcia stałego jest akumulator, źródła napięcia zmiennego - generator synchroniczny, źródła prądowego - elektroniczny zasilacz prądowy o stabilizowanym, niezależnym od obciążenia prądzie, itp. | Przykładami źródła napięcia stałego jest akumulator, źródła napięcia zmiennego - generator synchroniczny, źródła prądowego - elektroniczny zasilacz prądowy o stabilizowanym, niezależnym od obciążenia prądzie, itp. | ||
| Linia 129: | Linia 129: | ||
|valign="top"|Niezależne źródła prądu i napięcia mają następujące właściwości: | |valign="top"|Niezależne źródła prądu i napięcia mają następujące właściwości: | ||
*Napięcie na zaciskach idealnego źródła napięcia nie zależy od prądu przepływającego przez to źródło, a zatem nie zależy od jego obciążenia. | *Napięcie na zaciskach idealnego źródła napięcia nie zależy od prądu przepływającego przez to źródło, a zatem nie zależy od jego obciążenia. | ||
*Przy stałym napięciu <math>u\ | *Przy stałym napięciu <math>u\ </math>, panującym na zaciskach oraz prądzie <math>i\ </math>, wynikającym z obciążenia, rezystancja wewnętrzna idealnego źródła napięciowego, definiowana jest w postaci zależności różniczkowej <math>R_W={du \over di}=0</math>. Stąd idealne źródło napięcia charakteryzuje się rezystancją wewnętrzna równą zeru (zwarcie z punktu widzenia rezystancyjnego). | ||
*Prąd idealnego źródła prądu nie zależy od obciążenia tego źródła, a więc od napięcia panującego na jego zaciskach. | *Prąd idealnego źródła prądu nie zależy od obciążenia tego źródła, a więc od napięcia panującego na jego zaciskach. | ||
*Przy stałym prądzie płynącym przez idealne źródło prądowe i dowolnym (bliżej nieokreślonym) napięciu panującym na jego zaciskach rezystancja wewnętrzna idealnego źródła prądowego jest równa nieskończoności. Stąd idealne źródło prądowe z punktu widzenia rezystancyjnego reprezentuje sobą przerwę. | *Przy stałym prądzie płynącym przez idealne źródło prądowe i dowolnym (bliżej nieokreślonym) napięciu panującym na jego zaciskach rezystancja wewnętrzna idealnego źródła prądowego jest równa nieskończoności. Stąd idealne źródło prądowe z punktu widzenia rezystancyjnego reprezentuje sobą przerwę. | ||
| Linia 162: | Linia 162: | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd12.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd12.png|500px]] | ||
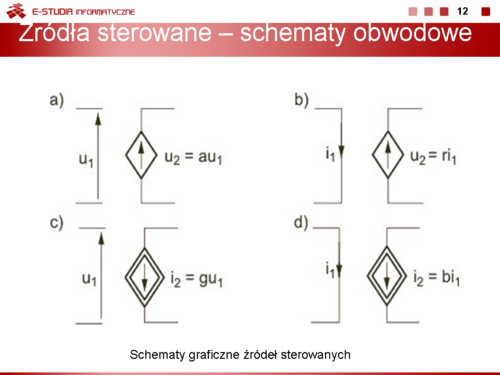
|valign="top"|Schematy graficzne wszystkich wymienionych tu rodzajów źródeł sterowanych prądu i napięcia przedstawione są na rysunku (slajd obok). | |valign="top"|Schematy graficzne wszystkich wymienionych tu rodzajów źródeł sterowanych prądu i napięcia przedstawione są na rysunku (slajd obok). | ||
Wielkości <math>r\ | Wielkości <math>r\ </math>,, <math>g\ </math>, oraz <math>a\ </math>, i <math>b\ </math>, stanowią współczynniki proporcjonalności między wielkością sterująca i sterowaną tych źródeł. Przyjmują one najczęściej wartości rzeczywiste, choć w różnego rodzaju modelach mogą być również opisane funkcją zespoloną. Należy nadmienić, że źródła sterowane stanowią bardzo popularne modele wielu elementów elektrycznych i elektronicznych, takich jak transformatory idealne, maszyny elektryczne, tranzystory bipolarne i polowe, wzmacniacze operacyjne napięciowe i prądowe, itp. | ||
|} | |} | ||
| Linia 177: | Linia 177: | ||
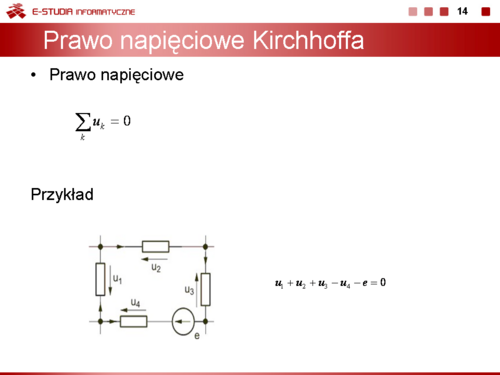
Suma prądów w każdym węźle obwodu elektrycznego jest równa zeru | Suma prądów w każdym węźle obwodu elektrycznego jest równa zeru | ||
: <math>\sum_{k}=i_k=0\ | : <math>\sum_{k}=i_k=0\ </math>, | ||
Sumowanie dotyczy wszystkich prądów, które dopływają lub odpływają z danego oczka, przy czym wszystkie prądy wpływające do węzła brane są z jednakowym znakiem a wszystkie prądy wypływające z węzła ze znakiem przeciwnym (nie jest istotne czy znak plus dotyczy prądów wpływających czy wypływających). Sposób tworzenia równania prądowego Kirchhoffa zilustrujemy dla jednego węzła obwodu przedstawionego na rysunku obok. | Sumowanie dotyczy wszystkich prądów, które dopływają lub odpływają z danego oczka, przy czym wszystkie prądy wpływające do węzła brane są z jednakowym znakiem a wszystkie prądy wypływające z węzła ze znakiem przeciwnym (nie jest istotne czy znak plus dotyczy prądów wpływających czy wypływających). Sposób tworzenia równania prądowego Kirchhoffa zilustrujemy dla jednego węzła obwodu przedstawionego na rysunku obok. | ||
| Linia 189: | Linia 189: | ||
: <math>i_1+i_2+i_3=i_4+i_5</math> | : <math>i_1+i_2+i_3=i_4+i_5</math> | ||
Dla każdego obwodu można napisać dokładnie <math>n-1\ | Dla każdego obwodu można napisać dokładnie <math>n-1\ </math>, niezależnych równań prądowych, gdzie <math>n\ </math>, oznacza całkowitą liczbę węzłów a <math>(n-1)</math> liczbę węzłów niezależnych. Bilans prądów w pozostałym <math>n\ </math>,-tym węźle obwodu wynika z równań prądowych napisanych dla <math>n-1\ </math>, węzłów (jest to węzeł zależny zwany węzłem odniesienia). Wybór węzła odniesienia jest całkowicie dowolny. | ||
|} | |} | ||
| Linia 306: | Linia 306: | ||
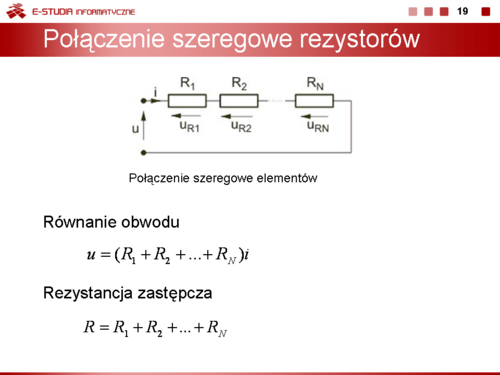
W '''połączeniu szeregowym''' elementów koniec jednego elementu jest bezpośrednio połączony z początkiem następnego. Rysunek na slajdzie obok przedstawia schemat ogólny połączenia szeregowego rezystorów. | W '''połączeniu szeregowym''' elementów koniec jednego elementu jest bezpośrednio połączony z początkiem następnego. Rysunek na slajdzie obok przedstawia schemat ogólny połączenia szeregowego rezystorów. | ||
Prąd każdego elementu obwodu jest jednakowy i równy <math>i\ | Prąd każdego elementu obwodu jest jednakowy i równy <math>i\ </math>,, natomiast napięcie na zaciskach zewnętrznych obwodu jest równe sumie napięć poszczególnych elementów tworzących połączenie. Napięciowe równanie Kirchhoffa dla obwodu (z rysunku na slajdzie obok) przyjmuje więc postać: | ||
: <math>u=(R_1+R_2+...+R_N)i</math> | : <math>u=(R_1+R_2+...+R_N)i</math> | ||
Przy oznaczeniu sumy rezystancji przez <math>R\ | Przy oznaczeniu sumy rezystancji przez <math>R\ </math>, | ||
: <math>R=R_1+R_2+...+R_N</math> | : <math>R=R_1+R_2+...+R_N</math> | ||
otrzymuje się uproszczenie <math>N\ | otrzymuje się uproszczenie <math>N\ </math>, rezystorów połączonych szeregowo do jednego rezystora zastępczego o rezystancji <math>R\ </math>, opisanej wzorem na slajdzie. Rezystancja wypadkowa połączenia szeregowego rezystorów jest równa sumie rezystancji poszczególnych elementów tworzących to połączenie. | ||
|} | |} | ||
| Linia 327: | Linia 327: | ||
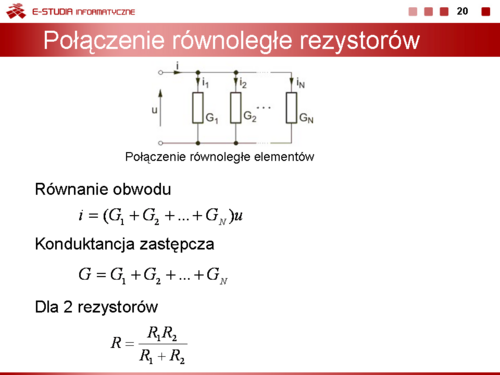
: <math>i=(G_1+G_2+...+G_N)u</math> | : <math>i=(G_1+G_2+...+G_N)u</math> | ||
przy czym <math>G_i (i = 1, 2, ..., N)</math> stanowią konduktancje rezystorów, <math>G_i=1/R_i</math>. Przy oznaczeniu sumy konduktancji przez <math>G\ | przy czym <math>G_i (i = 1, 2, ..., N)</math> stanowią konduktancje rezystorów, <math>G_i=1/R_i</math>. Przy oznaczeniu sumy konduktancji przez <math>G\ </math>,, gdzie | ||
: <math>G=G_1+G_2+...+G_N</math> | : <math>G=G_1+G_2+...+G_N</math> | ||
otrzymuje się uproszczenie <math>N\ | otrzymuje się uproszczenie <math>N\ </math>, rezystorów połączonych równolegle do jednego rezystora zastępczego o konduktancji <math>G\ </math>, opisanej wzorem na slajdzie. Jak widać w połączeniu równoległym rezystorów konduktancja wypadkowa jest równa sumie konduktancji poszczególnych rezystorów. | ||
Szczególnie prosty jest wzór na rezystancję zastępczą dla 2 rezystorów połączonych równolegle. W tym przypadku <math>G=G_1+G_2</math>. Uwzględniając, że <math>G=1/R</math> po prostych przekształceniach otrzymuje się | Szczególnie prosty jest wzór na rezystancję zastępczą dla 2 rezystorów połączonych równolegle. W tym przypadku <math>G=G_1+G_2</math>. Uwzględniając, że <math>G=1/R</math> po prostych przekształceniach otrzymuje się | ||
| Linia 398: | Linia 398: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M1_Slajd23.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M1_Slajd23.png|500px]] | ||
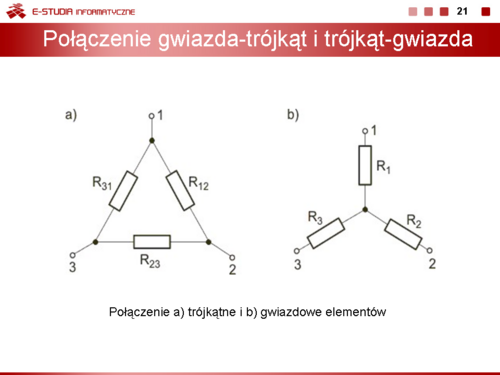
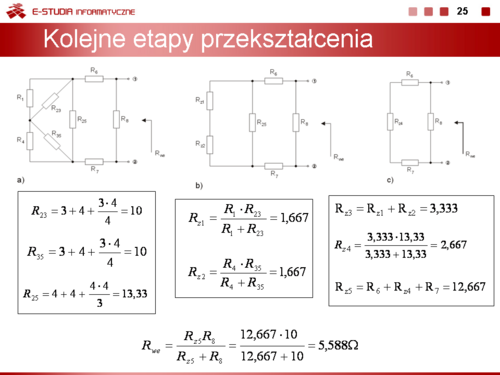
|valign="top"|Zamieniając gwiazdę złożoną z rezystorów <math>R_2\ | |valign="top"|Zamieniając gwiazdę złożoną z rezystorów <math>R_2\ </math>,, <math>R_3\ </math>,, i <math>R_5\ </math>, na równoważny jej trójkąt otrzymuje się: | ||
: <math>R_{23}=3+4+{3 \cdot 4 \over4}=10</math> | : <math>R_{23}=3+4+{3 \cdot 4 \over4}=10</math> | ||
Aktualna wersja na dzień 12:01, 5 wrz 2023

|

|
| Zadania sprawdzające
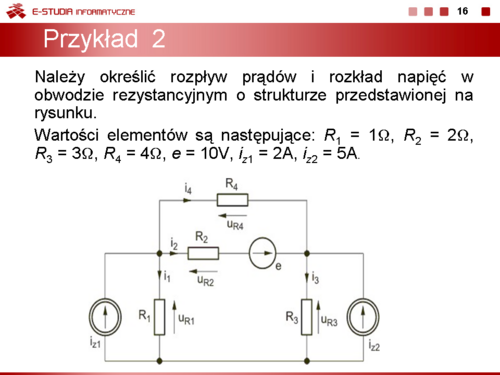
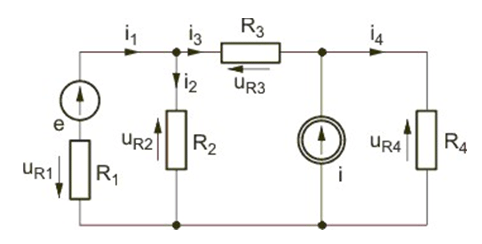
Stosując prawa Kirchhoffa wyznaczyć prądy w obwodzie przedstawionym na rysunku poniżej, jeśli , , , , a wartości źródeł są następujące: , . Rozwiązanie Korzystając z praw Kirchhoffa otrzymuje się układ równań opisujących obwód w postaci Po wstawieniu wartości liczbowych parametrów i rozwiązaniu układu równań otrzymuje się: , , oraz .
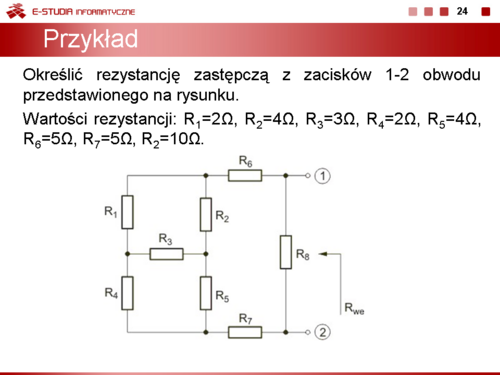
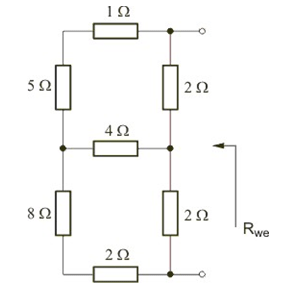
Zadanie 1.2 Wyznaczyć rezystancję wypadkową obwodu przedstawionego na rysunku poniżej. Rozwiązanie Po likwidacji połączenia szeregowego rezystorów ( i oraz i ) należy zastosować transformację trójkąt-gwiazda lub gwiazda-trójkąt w odniesieniu do wybranych trzech rezystorów obwodu, a następnie wykorzystać uproszczenia wynikające z powstałych połączeń szeregowych i równoległych w obwodzie. Po wykonaniu tych działań otrzymuje się . |