TTS Moduł 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
|||
| (Nie pokazano 3 wersji utworzonych przez 2 użytkowników) | |||
| Linia 35: | Linia 35: | ||
|valign="top"|Przypomnijmy podstawowe wielkości charakteryzujące pole elektromagnetyczne będące kompozycją pól elektrycznego i magnetycznego: | |valign="top"|Przypomnijmy podstawowe wielkości charakteryzujące pole elektromagnetyczne będące kompozycją pól elektrycznego i magnetycznego: | ||
*Natężenie pola elektrycznego <math> | *Natężenie pola elektrycznego <math>\overrightarrow{E}\,</math> jest wektorem (ma swoją wartość i kierunek), funkcją miejsca i czasu. Natężenie pola elektrycznego mierzymy w woltach na metr <math>[V/m]\,</math>. | ||
*Natężenie pola magnetycznego <math> | *Natężenie pola magnetycznego <math>\overrightarrow{H}\,</math> jest także wektorem, mierzymy jego wartość w amperach na metr <math>[A/m]\,</math>. | ||
*Indukcja elektryczna <math> | *Indukcja elektryczna <math>\overrightarrow{D}\,</math> jest wektorem, mierzymy jej wartość w amperach razy sekunda na metr kwadratowy <math>[As/m^2]\,</math>, czyli kulombach na <math>m^2\,</math> <math>[C/m^2]\,</math>. | ||
*Indukcja magnetyczna <math> | *Indukcja magnetyczna <math>\overrightarrow{B}\,</math> jest wektorem, mierzymy jej wartość w voltach razy sekunda na metr kwadratowy <math>[Vs/m^2]\,</math>. | ||
Ładunek elektryczny jest skalarnym źrodłem pola elektrycznego. W punkcie przestrzeni miarą ładunku jest jego gęstość objętościowa <math>\rho\,</math>, której jednostką jest kulomb na metr sześcienny <math>[C/m^3]\,</math>. | Ładunek elektryczny jest skalarnym źrodłem pola elektrycznego. W punkcie przestrzeni miarą ładunku jest jego gęstość objętościowa <math>\rho\,</math>, której jednostką jest kulomb na metr sześcienny <math>[C/m^3]\,</math>. | ||
Prądy elektryczne są wektorowymi źródłami pola magnetycznego. Wektor gęstości prądu <math> | Prądy elektryczne są wektorowymi źródłami pola magnetycznego. Wektor gęstości prądu <math>\overrightarrow{J}\,</math> opisuje prąd w punkcie przestrzeni. Wartość <math>\overrightarrow{J}\,</math> mierzymy w amperach na metr kwadratowy <math>[A/m^2]\,</math>. | ||
Wymienione powyżej pięć pól wektorowych i skalarne pole gęstości ładunku są funkcjami położenia (w prostokątnym układzie współrzędnych zależą od <math>(x, y, z)\,</math> oraz czasu <math>t\,</math>. Wzajemne relacje między tymi polami określają równania Maxwella. | Wymienione powyżej pięć pól wektorowych i skalarne pole gęstości ładunku są funkcjami położenia (w prostokątnym układzie współrzędnych zależą od <math>(x, y, z)\,</math> oraz czasu <math>t\,</math>. Wzajemne relacje między tymi polami określają równania Maxwella. | ||
| Linia 57: | Linia 57: | ||
Drugie równanie Maxwella stanowi, że rotacja wektora natężenia pola magnetycznego w punkcie przestrzeni jest równa wektorowi gęstości całkowitego prądu występującego w tym punkcie. Prawa strona równania zawiera dwa składniki: | Drugie równanie Maxwella stanowi, że rotacja wektora natężenia pola magnetycznego w punkcie przestrzeni jest równa wektorowi gęstości całkowitego prądu występującego w tym punkcie. Prawa strona równania zawiera dwa składniki: | ||
*wektor gęstości prądu elektrycznego <math> | *wektor gęstości prądu elektrycznego <math>\overrightarrow{J}\,</math> , który jest sumą wektora gęstości prądu przewodzenia wynikającego z ruchu ładunków w materiale i wektora gęstości prądu unoszenia polegającego na ruchu naładowanych ciał; | ||
*wprowadzony przez Maxwella prąd przesunięcia związany ze zmianami indukcji elektrycznej w czasie, którego wektor gęstości to <math> | *wprowadzony przez Maxwella prąd przesunięcia związany ze zmianami indukcji elektrycznej w czasie, którego wektor gęstości to <math>\partial \overrightarrow{D}/{\partial t}</math> . Miarą gęstości prądu przesunięcia jest amper na metr kwadratowy <math>[A/m^2]\,</math>. | ||
Pomijając prąd przesunięcia stwierdzimy, że przepływ prądu elektrycznego powoduje powstanie wirowego pola magnetycznego o rotacji równej gęstości tego prądu. Prąd elektryczny jest więc źródłem wektorowym pola magnetycznego. | Pomijając prąd przesunięcia stwierdzimy, że przepływ prądu elektrycznego powoduje powstanie wirowego pola magnetycznego o rotacji równej gęstości tego prądu. Prąd elektryczny jest więc źródłem wektorowym pola magnetycznego. | ||
| Linia 85: | Linia 85: | ||
|valign="top"|Rozwiązanie szeregu zagadnień elektrodynamiki upraszcza się gdy zastosuje się rachunek symboliczny wykorzystujący operacje na funkcjach zespolonych. | |valign="top"|Rozwiązanie szeregu zagadnień elektrodynamiki upraszcza się gdy zastosuje się rachunek symboliczny wykorzystujący operacje na funkcjach zespolonych. | ||
Wektorem zespolonym <math> | Wektorem zespolonym <math>\overrightarrow{E}\,</math> nazywamy wektor, którego trzy składowe mogą być liczbami zespolonymi. Taki wektor jest jednoznacznie określony przez podanie sześciu uporządkowanych liczb lub dwóch wektorów rzeczywistych: <math>Re(\overrightarrow{E})\,</math> oraz <math>Im(\overrightarrow{E})\,</math> ; <math>\overrightarrow{E}= Re(\overrightarrow{E})+jIm(\overrightarrow{E})</math> . | ||
Działania na wektorach zespolonych wykonujemy tak jak na wektorach rzeczywistych, przy czym należy pamiętać, że kwadrat jednostki urojonej należy zastąpić przez minus jeden. | Działania na wektorach zespolonych wykonujemy tak jak na wektorach rzeczywistych, przy czym należy pamiętać, że kwadrat jednostki urojonej należy zastąpić przez minus jeden. | ||
| Linia 95: | Linia 95: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd6.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M2_Slajd6.png|thumb|500px]] | ||
|valign="top"|Układ zespolonych równań Maxwella jest analogiczny do układu dla wektorów rzeczywistych, przy czym różniczkowanie po czasie <math> | |valign="top"|Układ zespolonych równań Maxwella jest analogiczny do układu dla wektorów rzeczywistych, przy czym różniczkowanie po czasie <math>\partial /{\partial t}</math> zastąpiono mnożeniem przez <math>j\omega\,</math> . | ||
Rozwiązaniem układu równań są amplitudy zespolone zależne od zmiennych przestrzeni, na podstawie których wyznacza się pola rzeczywiste. | Rozwiązaniem układu równań są amplitudy zespolone zależne od zmiennych przestrzeni, na podstawie których wyznacza się pola rzeczywiste. | ||
Przykładowo, znamy amplitudę zespoloną <math> | Przykładowo, znamy amplitudę zespoloną <math>\overrightarrow{E}(x,y,z)=\overrightarrow{i}_x|E_x(x,y,z)|exp(jArgE_x)</math> | ||
Mnożymy ją przez <math>exp(j\omega t)\,</math> i wyznaczamy część rzeczywistą, która jest poszukiwanym wektorem rzeczywistym, czyli | Mnożymy ją przez <math>exp(j\omega t)\,</math> i wyznaczamy część rzeczywistą, która jest poszukiwanym wektorem rzeczywistym, czyli | ||
<math> | <math>\overrightarrow{E}(x,y,z,t)=Re[\overrightarrow{E}(x,y,z)e^{j\omega t}=\overrightarrow{i}_x|E_x(x,y,z)|cos(\omega t+ArgE_x)</math> | ||
|} | |} | ||
| Linia 110: | Linia 110: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd7.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M2_Slajd7.png|thumb|500px]] | ||
|valign="top"|Dotychczas mówilismy o wektorach <math> | |valign="top"|Dotychczas mówilismy o wektorach <math>\overrightarrow{E},\overrightarrow{D},\overrightarrow{H},\overrightarrow{B}\,</math> określających pole elektromagnetyczne w taki sposób, jakby były one niezależne od siebie. Pierwsze dwa równania materiałowe wiążą ze sobą wymienione wektory w szekokiej klasie ośrodków (istnieją ośrodki, np. bianizotropowe, dla których związki między wektorami natężeń i indukcji pól są bardziej skomplikowane). | ||
Trzecie równanie materiałowe, nazywane wektorowym prawem Ohma, wiąże wektor gęstości prądu przewodzenia z wektorem natężeniam pola elektrycznego. | Trzecie równanie materiałowe, nazywane wektorowym prawem Ohma, wiąże wektor gęstości prądu przewodzenia z wektorem natężeniam pola elektrycznego. | ||
| Linia 162: | Linia 162: | ||
|valign="top"|Podział ośrodków na próżnię i ośrodki materialne nie jest przypadkowy. Jedynie próżnia jest ośrodkiem bezstratnym. | |valign="top"|Podział ośrodków na próżnię i ośrodki materialne nie jest przypadkowy. Jedynie próżnia jest ośrodkiem bezstratnym. | ||
Konduktywność ośrodków występujących w przyrodzie zawiera się w bardzo szerokich granicach od <math>\ | Konduktywność ośrodków występujących w przyrodzie zawiera się w bardzo szerokich granicach od <math>\sim 10^{-17} S/m\,</math> dla kwarcu do <math>6,1\cdot 10^7 S/m\,</math> dla srebra. Należy zadać pytanie, które ośrodki można uznać za bezstratne. | ||
Konduktywność ośrodka jest właściwym kryterium jego bezstratności tylko dla niskich częstotliwości. Dla wyższych częstotliwości poza stratami przewodzenia mamy do czynienia z tzw. stratami polaryzacji, które omówimy w dalszej części wykładu. | Konduktywność ośrodka jest właściwym kryterium jego bezstratności tylko dla niskich częstotliwości. Dla wyższych częstotliwości poza stratami przewodzenia mamy do czynienia z tzw. stratami polaryzacji, które omówimy w dalszej części wykładu. | ||
| Linia 191: | Linia 191: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd11.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M2_Slajd11.png|thumb|500px]] | ||
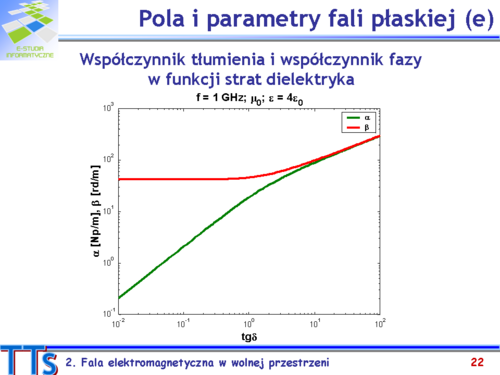
|valign="top"|Źródłem strat przewodzenia w dielektryku jest prąd przewodzenia o gęstości określonej przez tzw. wektorowe prawo Ohma: <math> | |valign="top"|Źródłem strat przewodzenia w dielektryku jest prąd przewodzenia o gęstości określonej przez tzw. wektorowe prawo Ohma: <math>\overrightarrow{J}=\sigma \overrightarrow{E}</math>. | ||
W oparciu o drugie prawo Maxwella wyznaczamy gęstość całkowitego prądu w dielektryku jako sumę prądów przewodzenia i przesunięcia. Z zapisu tego prądu widać, że straty związane z tłumienia oscylacji dipoli <math>(\omega \varepsilon'')\,</math> i straty wynikające z istnienia prądu przewodzenia <math>(\sigma)\,</math> są nierozróżnialne. Wielkość <math>(\sigma+\omega \varepsilon'')\,</math> nazywamy zastępczą konduktywnością ośrodka i mówi ona o całkowitych stratach cieplnych. | W oparciu o drugie prawo Maxwella wyznaczamy gęstość całkowitego prądu w dielektryku jako sumę prądów przewodzenia i przesunięcia. Z zapisu tego prądu widać, że straty związane z tłumienia oscylacji dipoli <math>(\omega \varepsilon'')\,</math> i straty wynikające z istnienia prądu przewodzenia <math>(\sigma)\,</math> są nierozróżnialne. Wielkość <math>(\sigma+\omega \varepsilon'')\,</math> nazywamy zastępczą konduktywnością ośrodka i mówi ona o całkowitych stratach cieplnych. | ||
| Linia 372: | Linia 372: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd24.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M2_Slajd24.png|thumb|500px]] | ||
|valign="top"|Do poprawnej interpretacji zjawisk związanych z propagacją fal elektromagnetycznych należy wprowadzić dwie prędkości. Jedną z nich jest prędkość fazowa, a drugą prędkość grupowa. Przypomnijmy, że w procesie modulacji „nakładamy” informację na falę nośną. W najprostszym przypadku modulacji amplitudowej jedną częstotliwością otrzymujemy dwie częstotliwości prążków bocznych, różniące się od nośnej o <math>\Delta \omega\,</math>. Superpozycję kilku fal o zbliżonych częstotliwościach, <math>\Delta \omega \to 0\,</math>, i współczynnikach fazowych, <math>\Delta \beta \to 0\,</math>, zwana jest fizyce grupą fal. Obserwując ruch płaszczyzny stałej fazy obwiedni (np. płaszczyzny, w której superpozycja dwóch fal osiąga maksimum) można zapisać warunek <math>\Delta \omega t | |valign="top"|Do poprawnej interpretacji zjawisk związanych z propagacją fal elektromagnetycznych należy wprowadzić dwie prędkości. Jedną z nich jest prędkość fazowa, a drugą prędkość grupowa. Przypomnijmy, że w procesie modulacji „nakładamy” informację na falę nośną. W najprostszym przypadku modulacji amplitudowej jedną częstotliwością otrzymujemy dwie częstotliwości prążków bocznych, różniące się od nośnej o <math>\Delta \omega\,</math>. Superpozycję kilku fal o zbliżonych częstotliwościach, <math>\Delta \omega \to 0\,</math>, i współczynnikach fazowych, <math>\Delta \beta \to 0\,</math>, zwana jest fizyce grupą fal. Obserwując ruch płaszczyzny stałej fazy obwiedni (np. płaszczyzny, w której superpozycja dwóch fal osiąga maksimum) można zapisać warunek <math>\Delta \omega t- \Delta \beta z=const.\,</math> , z którego wynika, podana na slajdzie, zależność opisująca prędkość grupową. | ||
Dla omawianego przypadku, prędkość grupową interpretujemy jako prędkość poruszania się obwiedni grupy fal, a więc jest to również prędkość przesyłania informacji zawartych w tej obwiedni. | Dla omawianego przypadku, prędkość grupową interpretujemy jako prędkość poruszania się obwiedni grupy fal, a więc jest to również prędkość przesyłania informacji zawartych w tej obwiedni. | ||
| Linia 488: | Linia 488: | ||
*'''Warunki brzegowe na granicy dielektryk idealny przewodnik:''' W idealnym przewodniku pole elektryczne jest równe 0 i z tego wynikają następujące jego właściwości: | *'''Warunki brzegowe na granicy dielektryk idealny przewodnik:''' W idealnym przewodniku pole elektryczne jest równe 0 i z tego wynikają następujące jego właściwości: | ||
**Pole elektryczne musi być prostopadłe do przewodnika. | **Pole elektryczne musi być prostopadłe do przewodnika. | ||
**Ta prostopadła (normalna) składowa pola indukuje na powierzchni przewodnika ładunek o gęstości <math>\rho\,\</math> równej indukcji elektrycznej <math>D\,</math>. | **Ta prostopadła (normalna) składowa pola indukuje na powierzchni przewodnika ładunek o gęstości <math>\rho\,\ </math> równej indukcji elektrycznej <math>D\,</math>. | ||
**Pole magnetyczne musi być styczne do przewodnika. | **Pole magnetyczne musi być styczne do przewodnika. | ||
**Pole magnetyczne wywołuję na powierzchni przewodnika prąd o gęstości powierzchniowej <math>j\,</math> równej <math>H\,</math>. | **Pole magnetyczne wywołuję na powierzchni przewodnika prąd o gęstości powierzchniowej <math>j\,</math> równej <math>H\,</math>. | ||
Aktualna wersja na dzień 12:03, 5 wrz 2023
Wykład
 |
Słownik
- Częstotliwość graniczna - częstotliwość powyżej której może się propagować fala w falowodzie. Poniżej tej częstotliwości fala jest silnie tłumiona.
- Mikrofale - zakres częstotliwości fal elektromagnetycznych od 300 MHz do 1000 GHz.
- Równania Maxwella - fundamentalne równania techniki mikrofalowej opisujące pole elektromagnetyczne w czasie i przestrzeni.
- Przenikalność dielektryczna i magnetyczna -Podstawowe parametry opisujące właściwości przestrzeni odpowiednio dla pola elektrycznego i magnetycznego.
- Podstawowe parametry pola elektromagnetycznego:
- Natężenie pola elektrycznego .
- Natężenie pola magnetycznego .
- Indukcja pola elektrycznego - wielkość wektorowa proporcjonalna do natężenia pola elektrycznego i przenikalności dielektrycznej.
- Indukcja pola magnetycznego - wielkość wektorowa proporcjonalna do natężenia pola magnetycznego i przenikalności magnetycznej.
- I prawo Maxwella - z pierwszego równania Maxwella widać że zmienne pole magnetyczne jest źródłem zmiennego pola elektrycznego
- W postaci całkowej jest zapisem prawa Faradaya i wiąże ze sobą zmianę strumienia indukcji magnetycznej przenikającego powierzchnię z polem elektrycznym całkowanym wzdłuż zamkniętego konturu otaczającego tą powierzchnię (zal. 2-1).
- W postaci różniczkowej I prawo Maxwella mówi, że rotacja pola elektrycznego jest równa pochodnej indukcji magnetycznej po czasie (zal.2-6).
- II prawo Maxwella - z drugiego równania Maxwella widać że źródłem zmiennego pola magnetycznego jest zmienny w czasie prąd lub zmienne pole elektryczne.
- W postaci całkowej jest zapisem prawa Ampera i wiąże ze sobą zmianę strumienia indukcji elektrycznej i prąd przenikający powierzchnię z polem magnetycznym całkowanym wzdłuż zamkniętego konturu otaczającego tą powierzchnię (zal. 2-2).
- W postaci różniczkowej II prawo Maxwella mówi nam że rotacja pola magnetycznego jest równa pochodnej indukcji elektrycznej i prądu po czasie (zal.2-6).
- III prawo Maxwella - jest zapisem prawa Gaussa dla pola elektrycznego i mówi, że źródłem pola indukcji elektrycznej są ładunki elektryczne.
- W postaci całkowej prawo to mówi że strumień wektora indukcji pola elektrycznego wypływający z objętości przez zamkniętą powierzchnię równy jest zgromadzonemu w tej objętości ładunkowi (zal 2-3).
- W postaci różniczkowej prawo to mówi że divergencja (rozbieżność) wektora indukcji elektrycznej jest równa gęstości ładunku elektrycznego (zal.2-6).
- IV prawo Maxwella - jest zapisem prawa Gaussa dla pola magnetycznego i mówi, że pole magnetyczne jest bezźródłowe.
- W postaci całkowej prawo to mówi że strumień wektora indukcji pola magnetycznego wypływający z objętości przez zamkniętą powierzchnię jest równy 0 co znaczy że pole magnetyczne jest bezźródłowe (zal. 2-4).
- W postaci różniczkowej prawo to mówi, że divergencja (rozbieżność) wektora indukcji magnetycznej jest równa 0, co również znaczy że pola magnetyczne jest bezźródłowe (zal1-6).
- Równanie ciągłości prądu - opisuje relacje między prądem i ładunkiem elektrycznym.
- W postaci całkowej prawo to mówi nam, że prąd przewodzenia wypływający przez powierzchnię zamkniętej objętości V równy jest szybkości zmian ładunku w tej objętości (zal.2-5).
- W postaci różniczkowej prawo to mówi nam, że źródłem pola gęstości prądów jest zmiana gęstości ładunku w czasie (zal 2-6).
- Parametry materiałowe ośrodka dla pola elektromagnetycznego:
- Przenikalność dielektryczna - określa relację między natężeniem pola elektrycznego a jego indukcją (zal. 2-11)
- Przenikalność magnetyczna - określa relację między natężeniem pola magnetycznego a jego indukcją (zal. 2-11)
- Konduktywność - określa relację między natężeniem pola elektrycznego a gęstością prądu przewodzenia ( zal 2-11).
- Rodzaje ośrodków pod katem właściwości dla pola elektromagnetycznego:
- Ośrodki liniowe i nieliniowe.
- Ośrodki jednorodne i niejednorodne.
- Ośrodki dyspersyjne i niedyspersyjne. Parametry materiałowe ośrodka dyspersyjnego zależą a ośrodka niedyspersyjnego nie zależą od częstotliwości.
- Ośrodki izotropowe i anizotropowe. Parametry materiałowe ośrodka izotropowego nie zależą zaś ośrodka anizotropowego zależą od kierunku pola
- Warunki brzegowe na granicy dwóch dielektryków:
- Nie ma prądów i ładunków powierzchniowych.
- Składowe normalne wektorów indukcji i oraz składowe styczne wektorów natężenia pól i są ciągłe.
- Warunki brzegowe na granicy dielektryk idealny przewodnik: W idealnym przewodniku pole elektryczne jest równe 0 i z tego wynikają następujące jego właściwości:
- Pole elektryczne musi być prostopadłe do przewodnika.
- Ta prostopadła (normalna) składowa pola indukuje na powierzchni przewodnika ładunek o gęstości równej indukcji elektrycznej .
- Pole magnetyczne musi być styczne do przewodnika.
- Pole magnetyczne wywołuję na powierzchni przewodnika prąd o gęstości powierzchniowej równej .
- Równania Helmholtza - równania falowe dla pól harmonicznych w zapisie zespolonym.
- Stała propagacji – funkcja parametrów materiałowych ośrodka (zal 2-38). Wartość decyduje o szybkości zmian parametrów fali wzdłuż kierunku propagacji.
- Stała tłumienia część rzeczywista stałej propagacji, decyduje o szybkości strat mocy fali wzdłuż kierunku jej propagacji (zal. 2-51a)
- Stała fazowa część urojona stałej propagacji, decyduje o szybkości zmian fazy fali ( zal. 2-51b, 2-52b).
- Prędkość fazowa fali - prędkość z jaką przesuwa się płaszczyzna stałej fazy fali.
- Prędkość grupowa fali - jest prędkością przepływu energii.
- Fala płaska - Wartości chwilowe wektorów pól elektrycznego i magnetycznego tej fali są takie same w każdym punkcie płaszczyzny prostopadłej do kierunku rozchodzenia się fali. Powierzchnia ekwifazowa fali płaskiej jest płaszczyzna prostopadłą do kierunku propagacji.
- Właściwości fali płaskiej - fala płaska jest falą typu TEM (Transverse Electro-Magnetic)
- Wektory i fali TEM leżą w płaszczyźnie prostopadłej do kierunku propagacji i są prostopadłe względem siebie.
- Zwrot iloczynu wektorowego pola razy pole wyznacza kierunek propagacji a jego moduł gęstość mocy fali.
- Impedancja falowa (stosunek wartości wzajemnie prostopadłych składowych pola i ) fali płaskiej jest równy impedancji właściwej ośrodka.
Bibliografia
- Bogdan Galwas. Miernictwo mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1985, Rozdział 1, 2 i 3.
- Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8.
- Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3.
- Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2.