Architektura Komputerów/Wykład 2: Dane: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
Nie podano opisu zmian |
||
| (Nie pokazano 12 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 16: | Linia 16: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S03.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S03.png]] | ||
|valign="top"| | |valign="top"| | ||
. | Komputer musi być zaprojektowany tak, aby był zdolny do przetwarzania danych zgodnie z potrzebami użytkownika. Współczesne komputery są używane do przetwarzania danych różnych typów – liczbowych, logicznych, tekstowych, a także obrazów i dźwięków. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 22: | Linia 22: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S04.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S04.png]] | ||
|valign="top"| | |valign="top"| | ||
... | Współczesne komputery działają w systemie binarnym. Wszystkie dane, na których operuje komputer, są zapisane w postaci ciągów cyfr binarnych – bitów (BInary Digit), interpretowanych najczęściej jako liczby binarne. | ||
Wszelkie dane o charakterze nieliczbowym muszą być zapisane (zakodowane) w postaci liczb lub grup liczb. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 28: | Linia 30: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S05.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S05.png]] | ||
|valign="top"| | |valign="top"| | ||
... | Dane alfanumeryczne – tekstowe mają postać znaków pisarskich – liter, cyfr, znaków przestankowych i innych symboli . W komputerze są one reprezentowane przez liczby, określające pozycję danego symbolu w tablicy kodowej. We współczesnych komputerach używa się kilku standardów kodowania znaków pisarskich. | ||
Kod ASCII został opracowany w pierwszej połowie XX wieku dla urządzeń dalekopisowych. Zawiera on cyfry, znaki przestankowe, podstawowe symbole matematyczne oraz małe i wielkie litery alfabetu łacińskiego, mieszczące się na 128 pozycjach kodowych. | |||
Kody rodziny EBCDIC są używane w systemach firmy IBM. Bazują one na binarnym kodowaniu liczb dziesiętnych reprezentujących pozycje kodowe znaków. | |||
Kod UNICODE jest uniwersalnym kodem znakowym, umożliwiającym reprezentację wszystkich znaków pisarskich zapisu fonetycznego (głoskowego) używanych na całym świecie. Liczba pozycji kodowych jest praktycznie nieograniczona, obecnie jest zdefiniowanych kilkadziesiąt tysięcy znaków | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 40: | Linia 48: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S07.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S07.png]] | ||
|valign="top"| | |valign="top"| | ||
... | Symbole ASCII o kodach 0..31 nie są znakami pisarskimi, lecz kodami formatującymi oraz kodami sterującymi wymianą informacji. Wśród nich znajdują się m.in. kody: CR – przejście na początek wiersza, LF – przejście do następnego wiersza, FF – rozpoczęcie nowej strony, HT – tabulacja pozioma, BSP – cofnięcie o jeden znak, BEL – sygnał dźwiękowy, VT – tabulacja pionowa i wiele innych. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 46: | Linia 54: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S08.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S08.png]] | ||
|valign="top"| | |valign="top"| | ||
... | Na bazie kodu ASCII zaprojektowano wiele kodów rozszerzonych, zawierających 256 pozycji kodowych. W kodach tych pierwsze 128 pozycji jest identyczne, jak w kodzie ASCII, a następne 128 pozycji zawiera znaki dodatkowe, np. litery akcentowane, rozszerzony zestaw symboli matematycznych, litery alfabetów narodowych. Istnieje wiele kodów tej rodziny, używanych w różnych częściach świata. W Polsce najpowszechniej używa się kodów ISO8859-2 oraz Microsoft CP1250. Jeszcze kilkanaście lat temu w naszym kraju używano ponad 12 różnych standardów kodowanie polskich znaków. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 70: | Linia 78: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S12.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S12.png]] | ||
|valign="top"| | |valign="top"| | ||
... | Najprostszy typ danych stanowią dane logiczne. Mogą one przyjmować dwie wartości. Bajtowe adresowanie danych używane w komputerach oraz fakt, że wiele komputerów traktuje jako podstawowy format danych słowo 32-bitowe powodują, że dane logiczne są zwykle zapisywane w postaci bajtów lub słów, pomimo, że do ich zapisu wystarczyłby pojedynczy bit. | ||
Należy zwrócić uwagę na reprezentację wartości PRAWDA w różnych językach programowania. Różne wzorce bitowe używane w różnych językach oraz korzystanie z operatorów (np. negacji) bitowych zamiast logicznych mogą być przyczyną błędów w programach, w których poszczególne moduły są pisane w różnych językach. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 76: | Linia 86: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S13.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S13.png]] | ||
|valign="top"| | |valign="top"| | ||
... | W dalszej części do opisu różnych reprezentacji danych liczbowych będziemy posługiwali się założeniem, że dane reprezentowane są przez słowo komputera, w którym poszczególne bity zostały ponumerowane od prawej do lewej strony. | ||
W naturalnym kodzie binarnym numer bitu jest równy wykładnikowi jego wagi binarnej. | |||
Zapis BCD polega na oddzielnym zakodowaniu w postaci binarnej (w kodzie NKB) każdej cyfry zapisu dziesiętnego, w postaci czterech bitów (tetrady). Zapis ten był dawniej używany do reprezentacji danych w języku COBOL. Obecnie jest on bardzo rzadko stosowany, głównie w mikrokontrolerach. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 82: | Linia 96: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S14.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S14.png]] | ||
|valign="top"| | |valign="top"| | ||
... | Ekran przedstawia kilka najważniejszych zapisów liczb ze znakiem. | ||
Zapis U2 jest najczęściej stosowanym zapisem liczb całkowitych. Jest on podobny do NKB, z tą różnicą, że najbardziej znaczący bit ma wagę ujemną. Typ int jest we współczesnych komputerach implementowany jako zapis U2. | |||
Zapis U1 był popularny kilkadziesiąt lat temu. Zapis ten jest podobny do U2, ale wartość bezwzględna najbardziej znaczącego bitu jes tu o jeden mniejsza. Obecnie wyszedł on z użycia. | |||
Zapis znak-moduł wydaje się być najbardziej intuicyjnym – jeden bit jest interpretowany jako znak liczby, pozostałe bity – jako wartość bezwzględna w kodzie NKB. Jest on jednak niewygodny dla jednostek arytmetycznych i współczesne komputery nie obsługują danych całkowitoliczbowych w tym zapisie. | |||
Zapis spolaryzowany umożliwia reprezentację licz ze znakiem jako licz bez znaku, z odpowiednim przesunięciem wartości 0. Liczby ujemne zapisywane są jako bliskie zeru,a zero – jako wartość w połowie zakresu reprezentacji NKB. Zapis powstaje przez dodanie do zapisywanej wartości stałej – podkładu, a następnie zapisanie tak uzyskanej liczby w kodzie NKB. Jako wartość podkładu przyjmuje się zwykle wartość leżącą tuż poniżej połowy zakresu w NKB. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 88: | Linia 110: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S15.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S15.png]] | ||
|valign="top"| | |valign="top"| | ||
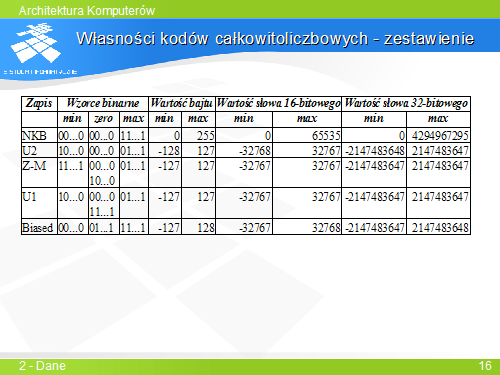
... | Kody całkowitoliczbowe charakteryzują się zestawem własności, które decydują o wygodzie ich stosowania. Istotne własności to m.in.: | ||
Reprezentacja zera – wpływa na łatwość wykrywania wartości 0 przy użyciu prostego układu logicznego. | |||
Reprezentacja znaku – wpływa na łatwość rozróżnienia liczb ujemnych od dodatnich. | |||
Operacja, jaką należy wykonać w celu zmiany znaku liczby – może to być prosta operacja logiczna, prosta lub złożona operacja arytmetyczna. | |||
Łatwość wykonywania operacji arytmetycznych – dodawanie i odejmowanie w U2 jest realizowane tak samo, jak w NKB. Mnożenie i dzielenie w U2 jest niewygodne, za to liczby zapisane w kodzie znak-moduł można mnożyć i dzielić niemal tak samo, jak w NKB. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 100: | Linia 130: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S17.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S17.png]] | ||
|valign="top"| | |valign="top"| | ||
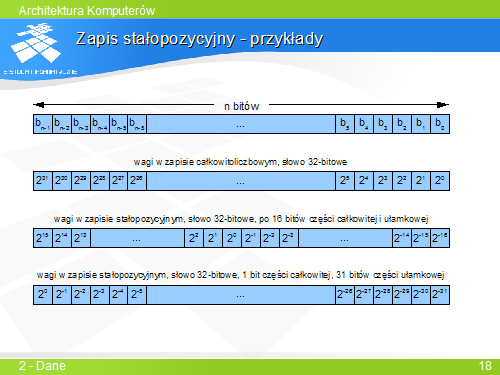
... | Do zapisywania liczb ułamkowych i mieszanych można użyć zapisu stałopozycyjnego. W zapisie tym liczba jest reprezentowany przez słowo binarne, w którym pewne, z góry określone liczby bitów reprezentują część całkowitą i część ułamkową liczby. Odpowiada to interpretacji zapisu całkowitoliczbowego, pomnożonej przez wartość będącą ujemną potęgą liczby 2. | ||
Do zapisu liczb bez znaku używa się jako bazowej postaci NKB, a do zapisu liczb ze znakiem – U2. Komputery zazwyczaj nie obsługują w szczególny sposób zapisów stałopozycyjnych. Podstawowe operacje są wykonywane tak samo, jak na liczbach całkowitych, odmienna jest jedynie interpretacja zapisu, za którą jest odpowiedzialny wyłącznie programista. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 112: | Linia 144: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S19.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S19.png]] | ||
|valign="top"| | |valign="top"| | ||
... | Zapis zmiennopozycyjny umożliwia zapisywanie liczb całkowitych i ułamkowych o bardzo dużym zakresie dynamiki wartości bezwzględnych. Do wprowadzenie zapisu binarnego posłużymy się najpierw obserwacjami związanymi z dziesiętnym zapisem zmiennopozycyjnym. | ||
Każda liczba może być zapisana na kilka sposobów, różniących się położeniem przecinka oddzielającego część całkowitą od ułamkowej i wartością wykładnika | |||
Zwykle posługujemy się jedną z możliwych postaci jako preferowaną. Postać tę nazywamy znormalizowaną. Postać znormalizowana ma część całkowitą części znaczącej wyrażoną przez pojedynczą cyfrę różną od zera. | |||
Aby zapisać (przechować) liczbę, musimy zapisać jej znak, część znaczącą oraz wykładnik, który jest liczbą całkowitą ze znakiem. | |||
W postaci znormalizowanej nie da się zapisać zera, bo zero nie ma żadnej cyfry znaczącej różnej od 0. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 118: | Linia 158: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S20.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S20.png]] | ||
|valign="top"| | |valign="top"| | ||
... | W przeszłości w różnych rodzinach komputerów używano różnych zapisów zmiennopozycyjnych. Od początku lat 80-tych XX wieku nastąpiła w tej dziedzinie standaryzacja. Obecnie niemal wszystkie komputery posługują się binarnym zapisem zmiennopozycyjnym zgodnym ze standardem IEEE754. | ||
Standard zakłada, że, o ile tylko jest to możliwe, liczby zapisuje się w postaci znormalizowanej. | |||
Bazą systemu jest liczba 2 – wykładnik określa potęgę liczby 2. | |||
Ponieważ w systemie binarnym jedyną cyfrą różną od zera jest jedynka, każda liczba w postaci znormalizowanej ma część cakowitą równą 1 – nie ma więc potrzeby zapisywania jej – zapisuje się tylko część ułamkową. | |||
Wykładnik jest liczbą całkowitą ze znakiem. W IEEE754 wykładnik jest zapisywany w kodzie spolaryzowanym, w którym wartość podkładu jest określona wzorcem bitowym 01....11, o liczbie bitów równej szerokości pola wykładnika. Dwie wartości pola wykładnika są zarezerwowane i oznaczają, że zapis nie reprezentuje postaci znormalizowanej. | |||
Pole wykładnika o wzorcu 00...00 oznacza zapis zdenormalizowany. Wartość wykładnika jest w tym przypadku taka sama, jak przy zapisie znormalizowanym z wzorcem wykładnika 00...01, a część całkowita części znaczącej ma wartość 0 (a nie 1 jak w postaci znormalizowanej). | |||
Pole wykładnika o wzorcu 11...11 oznacza nie-liczby – nieskończoności i wartości błędne. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 124: | Linia 175: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S21.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S21.png]] | ||
|valign="top"| | |valign="top"| | ||
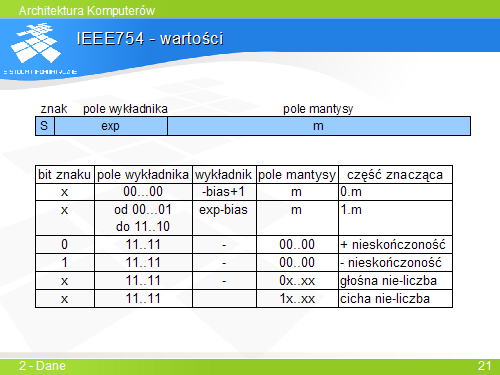
... | Wartość pola wykładnika równa 0 oznacza postać zdenormalizowaną. Jeżeli pole mantysy ma wartość 0 – zapis reprezentuje liczbę 0. W przeciwnym przypadku jest to liczba o bardzo małej wartości bezwzględnej. | ||
Wartość pola wykładnika złożona z bitów o wartości 1 oznacza tzw. nie-liczby. Pole mantysy równe 0 identyfikuje nieskończoność. Wzorzec bitowy, w którym najbardziej znaczący bit jkest równy 0, a wśród pozostałych jest co najmniej jedna jedynka jest zapisem głośnej nie-liczby, czyli wartości, która ni e może być argumentem operacji. Najbardziej znaczący bit mantysy o wertości 1 identyfikuje cichą nie-liczbę. Wynikiem operacji na cichej nie-liczbie jest zawsze cicha nie-liczba. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 130: | Linia 183: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S22.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S22.png]] | ||
|valign="top"| | |valign="top"| | ||
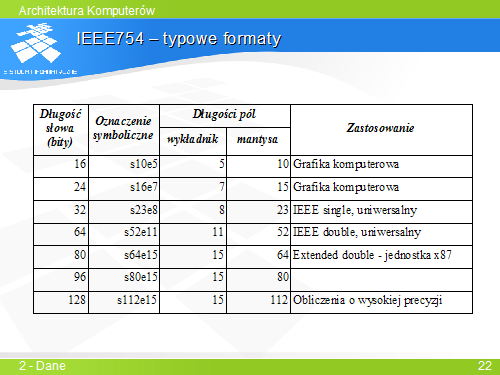
... | Podstawowym formatem jest format double – 64-bitowy. | ||
Format 32-bitowy jest używany w zastosowaniach, gdzie wymagana precyzja jest niewielka – ma on tylko 24 bity znaczące. | |||
Format 80-bitowy był używany w starszych jednostkach zmiennopozycyjnych procesorów rodziny x86. Obecnie wychodzi on z użycia. | |||
Format 128-bitowy jest formatem „przyszłościowym” dla liczb o dużej precyzji. | |||
W grafice komputerowej używa się niekiedy formatów krótszych, o mniejszej precyzji – 16- i 24-bitowego. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 136: | Linia 197: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S23.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S23.png]] | ||
|valign="top"| | |valign="top"| | ||
... | Posługując się liczbami zmiennpozycyjnymi należy pamiętać o ich specyficznych własnościach. | ||
Liczby o skończonej reprezentacji dziesiętnej mogą mieć nieskończoną reprezentację binarną (np. 0.1, 0.3). Reprezentacja zmiennopozycyjna jest reprezentacją przybliżoną, a wyniki operacji są w rzeczywistości przybliżeniami. Oznacza to, że w praktyce nie można stosować relacji równości w odniesieniu do liczb zmiennopozycyjnych. | |||
Operacja dodawania liczb różniących się znacznie rzędem wielkości daje w wyniku liczbę równą składnikowi o większej wartości bezwzględnej. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 142: | Linia 207: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S24.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S24.png]] | ||
|valign="top"| | |valign="top"| | ||
... | Podstawowa adresowalna komórka pamięci ma rozmiar jednego bajtu. Dane o rozmiarach przekraczających jeden bajt są przechowywane w kilku kolejnych komórkach, pod kilkoma kolejnymi adresami. | ||
Fizyczna organizacja pamięci współczesnych komputerów jest nieco odmienna od organizacji logicznej. Bajty są pogrupowane w słowa pamięci, których długość jest najczęściej dwukrotnie większa od długości słów danych przetwarzanych przez procesor. Taka konstrukcja pamięci umożliwia zwiększenie jej wydajności poprzez transmitowanie większej porcji danych podczas pojedynczego dostępu. | |||
Współczesne procesory 64-bitowe współpracują z pamięcią o szerokości 128 bitów. | |||
Pierwsze mikroprocesory 16- i 32-bitowe, produkowane w latach 70-tych i 80-tych XX wieku były często przystosowane do współpracy z pamięcią o szerokości 8 lub 16 bitów. W tamtym okresie wydajność procesorów była porównywalna z wydajnością pamięci, a pamięć o mniejszej szerokości słowa była tańsza w implementacji. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 148: | Linia 219: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S25.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S25.png]] | ||
|valign="top"| | |valign="top"| | ||
. | Istnieją dwa sposoby zapisu danej wielobajtowej w pamięci, zwane konwencjami adresowania danych. Nazwy konwencji pochodzą z powieści „Podróże Guliwera”, w której odnosiły się one do dwóch społeczności, różniących się zasadami jedzenia gotowanych jaj. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 160: | Linia 231: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S27.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S27.png]] | ||
|valign="top"| | |valign="top"| | ||
... | W konwencji Little-Endian adres bajtu odzwierciedla wagę bajtu w liczbie. Jest to konwencja naturalna dla komputera, chociaż dla człowieka na pierwszy rzut oka wydaje się dziwna – jesteśmy przyzwyczajeni do zapisywania liczb począwszy od najbardziej znaczących cyfr. | ||
Istotną cechą tej konwencji jest to, że jeżeli zapiszemy w pamięci daną całkowitoliczbową w długim formacie (np. 64 bity), to przy dostępach do jej mniej znaczącej części o mniejszej długości (np. jednego, dwóch lub czterech bajtów) adres danej będzie w każdym przypadku ten sam. Jest to wygodne przy częstym rzutowaniu typów całkowitoliczbowych, ca ma miejsce w programach pisanych w języku C. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 166: | Linia 239: | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S28.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S28.png]] | ||
|valign="top"| | |valign="top"| | ||
... | Zapis Big-Endian, naturalny dla człowieka, jest zwykle mniej wygodny dla komputera. Dostęp do danej całkowitoliczbowej w pamięci wymaga zmiany wartości adresu w zależności od długości danej. Jeżeli liczba 32-bitowa zostanie zapisana pod adresem A, to jej wartość w postaci jednobajtowej ma adres A+3. | ||
Istotną zaletą konwencji Big-Endian jest możliwość szybkiego porównywania łańcuchów tekstowych przy użyciu instrukcji operujących na liczbach całkowitych o długości 32 lub 64 bitów. Wektor znaków (bajtów) interpretowany jako liczba ma w najbardziej znaczącym bajcie pierwszy bajt łańcucha. Zamiast więc prowadzić operację porównywania łańcuchów znak po znaku, można ją wykonać posługując się grupami znaków o długości słowa procesora. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:ASK_M2_S29.png]] | |valign="top" width="500px"|[[Grafika:ASK_M2_S29.png]] | ||
|valign="top"| | |||
Dane powinny być umieszczone w pamięci w taki sposób, aby dostęp do danej, której rozmiar nie przekracza długości słowa pamięci następował w pojedynczym cyklu dostępu do pamięci. | |||
W nowszych architekturach komputerów rozmieszczenie danych gwarantujące dostęp w jednym cyklu transmisji jest obligatoryjne – próba dostępu do danej położonej inaczej generuje błąd. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:ASK_M2_S30.png]] | |||
|valign="top"| | |||
Dostęp w jednym cyklu przesłania można zagwarantować, umieszczając każdą daną skalarną pod adresem podzielnym przez jej długość. Dane 32-bitowe powinny być położone pod adresami podzielnymi przez 4, a 16-bitowe – pod adresami parzystymi. Takie umieszczenie danych w pamięci nazywa się wyrównaniem naturalnym. | |||
Nawet jeśli model programowy procesora nie narzuca takiego wymagania, wyrównanie naturalne jest zwykle wymuszane przez kompilatory (np. w x86). | |||
Dane strukturalne muszą być wyrównane w taki sposób, aby każde pole struktury było wyrównane naturalnie. Oznacza to, że początek struktury powinien być wyrównany zgodnie z wymaganiami najdłuższego typu danych obsługiwanego przez procesor. Należy zauważyć, że wyrównanie wpływa na rozmiar struktury, zwracany przez operator sizeof – rozmiar jest „zaokrąglany w górę” do granicy wyrównania struktur. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:ASK_M2_S31.png]] | |||
|valign="top"| | |valign="top"| | ||
... | ... | ||
| Linia 176: | Linia 269: | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:ASK_M2_S32.png]] | ||
|valign="top"| | |valign="top"| | ||
... | ... | ||
|} | |} | ||
Aktualna wersja na dzień 23:07, 5 paź 2006

|
... |

|
... |

|
... |

|
... |

|
... |

|
... |
|
... |
|
... |

|
... |

|
... |

|
... |