PF Moduł 8: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 7 wersji utworzonych przez 2 użytkowników) | |||
| Linia 49: | Linia 49: | ||
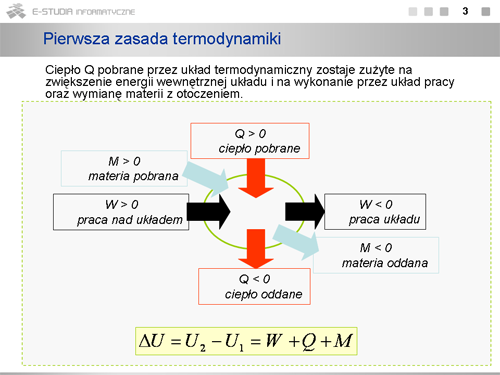
Wprowadzamy tu konwencję, którą będziemy stosować w dalszych rozważaniach dla układów nie wymieniających materii z otoczeniem. | Wprowadzamy tu konwencję, którą będziemy stosować w dalszych rozważaniach dla układów nie wymieniających materii z otoczeniem. | ||
Praca <math>W\ | Praca <math>W\ </math>, jest dodatnia <math>(W > 0)</math>, jeżeli jest wykonywana przez siły zewnętrzne (otoczenie) nad układem fizycznym. Kiedy układ fizyczny wykonuje pracę nad otoczeniem (kosztem swej energii wewnętrznej) praca ta jest ujemna <math>(W < 0)</math>. Podobnie, ciepło jest dodatnie <math>(Q > 0)</math>, jeśli przepływa z otoczenia do układu, a ujemne <math>(Q < 0)</math>, jeśli przepływa z układu do otoczenia. Dla przykładu, kiedy siły zewnętrzne (otoczenie) wykonują pracę sprężając gaz <math>(\Delta V < 0)</math>, to wykonana praca jest dodatnia, kiedy gaz wykonuje pracę nad otoczeniem rozprężając się <math>(\Delta V > 0)</math>, praca jest ujemna. | ||
|} | |} | ||
| Linia 61: | Linia 61: | ||
: <math>dU=\delta Q + \delta W</math> | : <math>dU=\delta Q + \delta W</math> | ||
'''UWAGA:''' Symbolami <math>\delta Q</math> i <math>\delta W</math> oznaczamy różniczkowe porcje (a nie skończone przyrosty) wymienianego przez układ ciepła i wykonanej pracy przy nieskończenie małych (infinitezymalnych) zmianach parametrów stanu układu. Wynika, to z faktu, ze ciepło i praca nie są funkcjami stanu, bowiem jak zobaczymy, zależą od drogi przejścia pomiędzy stanami. Mówimy, że są '''funkcjami procesu'''. Symbol <math>dU\ | '''UWAGA:''' Symbolami <math>\delta Q</math> i <math>\delta W</math> oznaczamy różniczkowe porcje (a nie skończone przyrosty) wymienianego przez układ ciepła i wykonanej pracy przy nieskończenie małych (infinitezymalnych) zmianach parametrów stanu układu. Wynika, to z faktu, ze ciepło i praca nie są funkcjami stanu, bowiem jak zobaczymy, zależą od drogi przejścia pomiędzy stanami. Mówimy, że są '''funkcjami procesu'''. Symbol <math>dU\ </math>, oznacza zmianę energii wewnętrznej, która jest funkcją stanu. W przemianie kołowej, kiedy układ powraca do stanu początkowego, jego energia wewnętrzna mieć będzie taką samą wartość jak w stanie początkowym, co zapisujemy w postaci | ||
: <math> | : <math>\oint dU=0</math> | ||
Nieskończenie mały przyrost, dla którego spełniony jest powyższy warunek nazywamy '''różniczką zupełną'''. Kiedy warunek ten nie jest spełniony, mamy do czynienia z '''wyrażeniem różniczkowym'''. Różniczkami zupełnymi są nieskończenie małe przyrosty funkcji stanu, ale nie są nimi infinitezymalne ilości wymienianego ciepła, lub wykonanej pracy. Bilans ilości ciepła pobranego i oddanego przez układ w przemianie kołowej lub wykonanej przez układ pracy nie musi być równy zeru. | Nieskończenie mały przyrost, dla którego spełniony jest powyższy warunek nazywamy '''różniczką zupełną'''. Kiedy warunek ten nie jest spełniony, mamy do czynienia z '''wyrażeniem różniczkowym'''. Różniczkami zupełnymi są nieskończenie małe przyrosty funkcji stanu, ale nie są nimi infinitezymalne ilości wymienianego ciepła, lub wykonanej pracy. Bilans ilości ciepła pobranego i oddanego przez układ w przemianie kołowej lub wykonanej przez układ pracy nie musi być równy zeru. | ||
| Linia 75: | Linia 75: | ||
|valign="top"|'''Przemiana izochoryczna''' to proces, w którym objętość układu pozostaje stała, czyli <math>V=const</math>. W przemianie tej '''nie jest wykonywana praca'''. W oparciu o pierwszą zasadę termodynamiki mamy dla przemiany izochorycznej relację | |valign="top"|'''Przemiana izochoryczna''' to proces, w którym objętość układu pozostaje stała, czyli <math>V=const</math>. W przemianie tej '''nie jest wykonywana praca'''. W oparciu o pierwszą zasadę termodynamiki mamy dla przemiany izochorycznej relację | ||
: <math> | : <math>\delta Q_v=dU</math>, | ||
co oznacza, że w przemianie izochorycznej możemy zmienić energię wewnętrzną układu jedynie na drodze wymiany ciepła. | co oznacza, że w przemianie izochorycznej możemy zmienić energię wewnętrzną układu jedynie na drodze wymiany ciepła. | ||
Pojemność cieplna jednego mola, tzw. ciepło molowe substancji w procesie przebiegającym bez zmiany objętości wyraża się wzorem | Pojemność cieplna jednego mola, tzw. ciepło molowe substancji w procesie przebiegającym bez zmiany objętości wyraża się wzorem | ||
: <math> | : <math>C_v=({\partial U \over \partial T})_v</math>, | ||
gdzie indeks '''v''' przy znaku pochodnej cząstkowej oznacza, że proces zachodzi w stałej objętości. | gdzie indeks '''v''' przy znaku pochodnej cząstkowej oznacza, że proces zachodzi w stałej objętości. | ||
Energia wewnętrzna danej masy gazu doskonałego zależy jednak wyłącznie od temperatury. Przekonuje nas o tym doświadczenie J.P. Joule'a z rozprężaniem rozrzedzonego gazu do próżni, gdy układ jest w osłonie izolacyjnej uniemożliwiającej wymianę ciepła z otoczeniem. Możemy wiec dla gazu doskonałego napisać, że | Energia wewnętrzna danej masy gazu doskonałego zależy jednak wyłącznie od temperatury. Przekonuje nas o tym doświadczenie J.P. Joule'a z rozprężaniem rozrzedzonego gazu do próżni, gdy układ jest w osłonie izolacyjnej uniemożliwiającej wymianę ciepła z otoczeniem. Możemy wiec dla gazu doskonałego napisać, że | ||
: <math> | : <math>C_v={dU \over dT}</math>. | ||
W dowolnym procesie kwazistatycznym, odwracalnym, niezależnie, która z wielkości jest stała zmiana energii wewnętrznej <math>n_M</math> moli gazu doskonałego jest określona wzorem: | W dowolnym procesie kwazistatycznym, odwracalnym, niezależnie, która z wielkości jest stała zmiana energii wewnętrznej <math>n_M</math> moli gazu doskonałego jest określona wzorem: | ||
: <math> | : <math>dU=n_M \cdot C_v \cdot dT</math>. | ||
Bardziej szczegółowe uzasadnienie tego wzoru, w oparciu o analizę doświadczenia Joule'a, można znaleźć w literaturze. Zapamiętajmy, że powyższy wzór, określający zmianę energii wewnętrznej, ma charakter uniwersalny. Mimo że został sformułowany dla przypadku przemiany izochorycznej i występuje w nim ciepło molowe <math>C_v</math>, może być stosowany przy opisie innych przemian gazowych, gdyż energia wewnętrzna jest funkcją stanu. Informacja ta jest bardzo użyteczna przy rozwiązywaniu zadań. | Bardziej szczegółowe uzasadnienie tego wzoru, w oparciu o analizę doświadczenia Joule'a, można znaleźć w literaturze. Zapamiętajmy, że powyższy wzór, określający zmianę energii wewnętrznej, ma charakter uniwersalny. Mimo że został sformułowany dla przypadku przemiany izochorycznej i występuje w nim ciepło molowe <math>C_v</math>, może być stosowany przy opisie innych przemian gazowych, gdyż energia wewnętrzna jest funkcją stanu. Informacja ta jest bardzo użyteczna przy rozwiązywaniu zadań. | ||
| Linia 101: | Linia 101: | ||
|valign="top"|Jeśli proces zachodzi pod stałym ciśnieniem, czyli <math>p=const</math>, to mówimy, że zachodzi '''przemiana izobaryczna'''. Z równania stanu wynika, że w tym przypadku objętość jest liniową funkcją temperatury. Przy wzroście objętości praca jest wykonywana przez gaz <math>(W<0, W'>0)</math>, a przy zmniejszeniu objętości, przez otoczenie, <math>(W>0, W'<0)</math> Ciśnienie zachowuje stałą wartość, więc '''praca''' wykonana nad układem w przemianie izobarycznej wynosi | |valign="top"|Jeśli proces zachodzi pod stałym ciśnieniem, czyli <math>p=const</math>, to mówimy, że zachodzi '''przemiana izobaryczna'''. Z równania stanu wynika, że w tym przypadku objętość jest liniową funkcją temperatury. Przy wzroście objętości praca jest wykonywana przez gaz <math>(W<0, W'>0)</math>, a przy zmniejszeniu objętości, przez otoczenie, <math>(W>0, W'<0)</math> Ciśnienie zachowuje stałą wartość, więc '''praca''' wykonana nad układem w przemianie izobarycznej wynosi | ||
: <math> | : <math>W=-\int_{V_1}^{V_2} p \cdot dV=-p \cdot \int_{V_1}^{V_2} dV=p \cdot (V_1-V_2)</math>. | ||
Podwyższenie temperatury o jeden kelwin wymaga więcej ciepła niż w przypadku ogrzewania bez zmiany objętości, bowiem część ciepła zużywana jest na wykonanie pracy. | Podwyższenie temperatury o jeden kelwin wymaga więcej ciepła niż w przypadku ogrzewania bez zmiany objętości, bowiem część ciepła zużywana jest na wykonanie pracy. | ||
W procesie izobarycznym energię wewnętrzną możemy zmienić zarówno na drodze wykonania pracy jak i wymiany ciepła | W procesie izobarycznym energię wewnętrzną możemy zmienić zarówno na drodze wykonania pracy jak i wymiany ciepła | ||
: <math> | : <math>dU=\delta Q_p-p \cdot dV</math>. | ||
Wyrażenie to możemy przepisać dla <math>n_M</math> moli w innej postaci wykorzystując poznane wzory: | Wyrażenie to możemy przepisać dla <math>n_M</math> moli w innej postaci wykorzystując poznane wzory: | ||
: <math> | : <math>n_M \cdot C_v \cdot dT=n_M \cdot C_p \cdot dT - p \cdot dV</math> | ||
gdzie wprowadziliśmy pojęcie '''ciepła molowego przy stałym ciśnieniu''' | gdzie wprowadziliśmy pojęcie '''ciepła molowego przy stałym ciśnieniu''' | ||
: <math> | : <math>C_p={\delta Q_p \over dT}</math>. | ||
Różniczkując równanie stanu dla procesu izobarycznego, w którym <math>p=const</math> mamy | Różniczkując równanie stanu dla procesu izobarycznego, w którym <math>p=const</math> mamy | ||
: <math> | : <math>p \cdot dV=n_M \cdot R \cdot dT</math> | ||
Wykorzystując ten związek możemy napisać, że | Wykorzystując ten związek możemy napisać, że | ||
: <math> | : <math>n_M \cdot C_v \cdot dT = n_M \cdot C_p \cdot dT - n_M \cdot R \cdot dT</math> | ||
skąd otrzymujemy równanie Mayera | skąd otrzymujemy równanie Mayera | ||
| Linia 129: | Linia 129: | ||
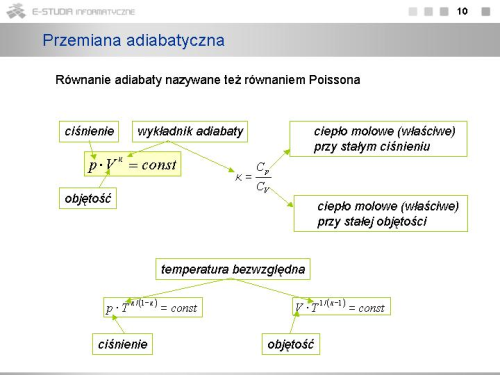
Stosunek ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości jest parametrem określającym rodzaj gazu i oznaczany jest zwykle symbolem <math>\kappa</math> (kappa). | Stosunek ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy stałej objętości jest parametrem określającym rodzaj gazu i oznaczany jest zwykle symbolem <math>\kappa</math> (kappa). | ||
: <math> | : <math>\kappa = {C_p \over C_v}</math>. | ||
Wykorzystując równanie Mayera można ciepła molowe <math>C_p</math> i <math>C_v</math> wyrazić za pomocą współczynnika <math>\kappa</math>. | Wykorzystując równanie Mayera można ciepła molowe <math>C_p</math> i <math>C_v</math> wyrazić za pomocą współczynnika <math>\kappa</math>. | ||
: <math> | : <math>\kappa = {C_v + R \over C_v}=1+{R \over C_v}</math> lub <math>C_v={R \over \kappa-1}</math>, <math>C_p={\kappa \cdot R \over \kappa - 1}</math>. | ||
Ze związków tych widzimy, że <math>\kappa > 1</math>. | Ze związków tych widzimy, że <math>\kappa > 1</math>. | ||
| Linia 143: | Linia 143: | ||
|valign="top"|Jeśli dany proces zachodzi w stałej temperaturze, czyli <math>T=const</math>, to mówimy, że zachodzi '''przemiana izotermiczna'''. Z równania stanu gazu wynika natychmiast, że w przemianie tej ciśnienie gazu jest odwrotnie proporcjonalne do jego objętości, bowiem dla danej masy gazu wyrażonej w molach mamy | |valign="top"|Jeśli dany proces zachodzi w stałej temperaturze, czyli <math>T=const</math>, to mówimy, że zachodzi '''przemiana izotermiczna'''. Z równania stanu gazu wynika natychmiast, że w przemianie tej ciśnienie gazu jest odwrotnie proporcjonalne do jego objętości, bowiem dla danej masy gazu wyrażonej w molach mamy | ||
: <math> | : <math>p \cdot V = n_M \cdot R \cdot T</math>, czyli <math>p={const \over V}</math>. | ||
Związek ten zwany jest '''prawem Boyle'a Mariotte'a'''. | Związek ten zwany jest '''prawem Boyle'a Mariotte'a'''. | ||
'''Pracę''' wykonaną nad układem przy przemianie izotermicznej wyznaczamy z jej definicji oraz korzystając z równania stanu dla przemiany izotermicznej. | '''Pracę''' wykonaną nad układem przy przemianie izotermicznej wyznaczamy z jej definicji oraz korzystając z równania stanu dla przemiany izotermicznej. | ||
: <math> | : <math>W=-\int_{V_1}^{V_2} p \cdot dV=-n_M \cdot R \cdot T \cdot \int_{V_1}^{V_2} {dV \over V}=</math> | ||
: <math> | : <math>-n_M \cdot R \cdot T (lnV_2-lnV_1)=n_M \cdot R \cdot T \cdot ln({V_1 \over V_2})</math> | ||
Zapiszmy pierwsza zasadę termodynamiki dla przemiany izotermicznej w postaci różniczkowej, | Zapiszmy pierwsza zasadę termodynamiki dla przemiany izotermicznej w postaci różniczkowej, | ||
: <math> | : <math>dU=\delta Q_T-p \cdot dV</math>. | ||
W przemianie izotermicznej <math>T = const</math>, więc <math>dU = 0</math>. Oznacza to, że '''w przemianie izotermicznej energia wewnętrzna układu nie zmienia się'''. Widzimy dalej, że temperatura układu jest stała, ale jest wymieniane ciepło między układem i otoczeniem. Ilość tego ciepła możemy określić | W przemianie izotermicznej <math>T = const</math>, więc <math>dU = 0</math>. Oznacza to, że '''w przemianie izotermicznej energia wewnętrzna układu nie zmienia się'''. Widzimy dalej, że temperatura układu jest stała, ale jest wymieniane ciepło między układem i otoczeniem. Ilość tego ciepła możemy określić | ||
: <math> | : <math>0=\delta Q_T - p \cdot dV</math>, czyli <math>\delta Q_T=p \cdot dV</math>. | ||
Wymiana ciepła następuje, na skutek wykonanej pracy. Jeśli praca jest wykonywana nad układem <math>(\delta W>0)</math>, to ciepło w równej ilości musi być oddawane do otoczenia <math>(\delta Q<0)</math> i vice versa. | Wymiana ciepła następuje, na skutek wykonanej pracy. Jeśli praca jest wykonywana nad układem <math>(\delta W>0)</math>, to ciepło w równej ilości musi być oddawane do otoczenia <math>(\delta Q<0)</math> i vice versa. | ||
| Linia 173: | Linia 173: | ||
W takim przypadku pierwsza zasada termodynamiki przyjmie postać | W takim przypadku pierwsza zasada termodynamiki przyjmie postać | ||
: <math> | : <math>dU=-p \cdot dV</math>, | ||
co oznacza, że w przemianie tej energię wewnętrzną można zmienić jedynie poprzez wykonanie pracy. Zapiszmy to bardziej szczegółowo | co oznacza, że w przemianie tej energię wewnętrzną można zmienić jedynie poprzez wykonanie pracy. Zapiszmy to bardziej szczegółowo | ||
: <math> | : <math>dU=-p \cdot dV</math>, czyli <math>n_M \cdot C_v \cdot dT + {n_M \cdot R \cdot T \over V} \cdot dV = 0</math>. | ||
Można to zapisać nieco inaczej dzieląc obustronnie ostatnie równanie przez <math>n_M \cdot C_v \cdot T</math> | Można to zapisać nieco inaczej dzieląc obustronnie ostatnie równanie przez <math>n_M \cdot C_v \cdot T</math> | ||
: <math> | : <math>{dT \over T}+{R \over C_v} \cdot {dV \over V}=0</math>. | ||
Pamiętając z matematyki, że <math>d(lnx)=dx/x</math> oraz, że różniczka sumy równa jest sumie różniczek, możemy to równanie przepisać w postaci | Pamiętając z matematyki, że <math>d(lnx)=dx/x</math> oraz, że różniczka sumy równa jest sumie różniczek, możemy to równanie przepisać w postaci | ||
: <math> | : <math>d(lnT+{R \over C_v} \cdot lnV)=0</math>. | ||
Jeśli różniczka funkcji równa jest zeru, to funkcja równa jest stałej, czyli | Jeśli różniczka funkcji równa jest zeru, to funkcja równa jest stałej, czyli | ||
: <math> | : <math>lnT+{R \over C_v} \cdot lnV=const</math>. | ||
Pamiętając, że <math> | Pamiętając, że <math>R/C_v=\kappa -1</math> mamy | ||
: <math> | : <math>lnT+(\kappa -1) \cdot lnV=const</math>, lub <math>ln(T \cdot V^{\kappa -1})=const</math>. | ||
Jeśli logarytm funkcji równy jest stałej, to i sama funkcja pozostaje stała. Możemy wiec napisać | Jeśli logarytm funkcji równy jest stałej, to i sama funkcja pozostaje stała. Możemy wiec napisać | ||
: <math> | : <math>T \cdot V^{\kappa -1}=const</math>. | ||
Wykorzystując równanie stanu gazu doskonałego '''pV = RT''' dostajemy | Wykorzystując równanie stanu gazu doskonałego '''pV = RT''' dostajemy | ||
: <math> | : <math>{p \cdot V \over R} \cdot V^{\kappa -1}=const</math> lub <math>{p \cdot V^\kappa \over R}=const</math>. | ||
Powyższe wzory pozostaną w mocy, jeśli stałą gazową <math>R\ | Powyższe wzory pozostaną w mocy, jeśli stałą gazową <math>R\ </math>, włączymy do stałej po prawej stronie. Otrzymamy wtedy | ||
: <math> | : <math>p \cdot V^\kappa=const</math>. | ||
|} | |} | ||
| Linia 214: | Linia 214: | ||
|valign="top"|Związek ten jest równaniem adiabaty i nosi nazwę '''równania Poissona'''. Postępując podobnie można otrzymać równania określające zależności między innymi parametrami stanu dla przemiany adiabatycznej | |valign="top"|Związek ten jest równaniem adiabaty i nosi nazwę '''równania Poissona'''. Postępując podobnie można otrzymać równania określające zależności między innymi parametrami stanu dla przemiany adiabatycznej | ||
: <math> | : <math>p \cdot T^{\kappa / (1-\kappa)}=const, \ V \cdot T^{1/(\kappa -1)}=const</math>. | ||
Realizacja przemiany adiabatycznej jest trudna, gdyż wymaga idealnej izolacji cieplnej gazu od otoczenia. Warto jednak zauważyć, że gdy sprężanie lub rozprężanie gazu zachodzi bardzo szybko, to nawet mimo nie najlepszej izolacji cieplnej przemiana taka ma charakter bardzo zbliżony do przemiany adiabatycznej. Właściwość tę wykorzystuje się w pracy silników cieplnych. | Realizacja przemiany adiabatycznej jest trudna, gdyż wymaga idealnej izolacji cieplnej gazu od otoczenia. Warto jednak zauważyć, że gdy sprężanie lub rozprężanie gazu zachodzi bardzo szybko, to nawet mimo nie najlepszej izolacji cieplnej przemiana taka ma charakter bardzo zbliżony do przemiany adiabatycznej. Właściwość tę wykorzystuje się w pracy silników cieplnych. | ||
| Linia 228: | Linia 228: | ||
Zapiszmy pierwszą zasadę termodynamiki dla gazu doskonałego w postaci różniczkowej, wzór pamiętając przy tym, że <math>\delta Q =C \cdot dT</math> oraz, że <math>dU=C_v \cdot dT</math> | Zapiszmy pierwszą zasadę termodynamiki dla gazu doskonałego w postaci różniczkowej, wzór pamiętając przy tym, że <math>\delta Q =C \cdot dT</math> oraz, że <math>dU=C_v \cdot dT</math> | ||
: <math> | : <math>n_M \cdot C_v \cdot dT = n_M \cdot C \cdot dT - p \cdot dV</math>. | ||
Wzór ten można też zapisać inaczej | Wzór ten można też zapisać inaczej | ||
: <math> | : <math>n_M \cdot (C-C_v) \cdot dT=p \cdot dV</math> lub <math>dT={p \cdot dV \over n_M \cdot (C-C_v)}</math>. | ||
Wykorzystamy także równanie stanu gazu doskonałego, różniczkując je mamy | Wykorzystamy także równanie stanu gazu doskonałego, różniczkując je mamy | ||
: <math> | : <math>p \cdot dV \cdot + V \cdot dp=n_M \cdot R \cdot dT</math>. | ||
Teraz wstawiając wyrażenie na <math>dT\ | Teraz wstawiając wyrażenie na <math>dT\ </math>, do ostatniego równania otrzymujemy po prostych przekształceniach | ||
: <math> | : <math>(C-C_v-R) \cdot p \cdot dV + (C-C_v) \cdot V \cdot dp = 0</math>. | ||
Pamiętając, że <math>C_v+R=C_p</math> i dzieląc stronami równanie przez <math>p \cdot V</math> otrzymujemy równanie różniczkowe, w którym zauważamy wyrażenia będące różniczkami logarytmu | Pamiętając, że <math>C_v+R=C_p</math> i dzieląc stronami równanie przez <math>p \cdot V</math> otrzymujemy równanie różniczkowe, w którym zauważamy wyrażenia będące różniczkami logarytmu | ||
: <math> | : <math>(C-C_p) \cdot {dV \over V} + (C-C_v) \cdot {dp \over p}=0</math>. | ||
Całkowanie tego równania daje w wyniku | Całkowanie tego równania daje w wyniku | ||
: <math> | : <math>(C-C_p) \cdot lnV + (C-C_v) \cdot lnp=const</math>. | ||
Dzieląc obie strony tego równania przez <math>(C-C_v)</math>, co jest możliwe tylko, jeżeli <math>(C \ne C_v)</math>, otrzymujemy po skorzystaniu z własności wyrażeń logarytmicznych | Dzieląc obie strony tego równania przez <math>(C-C_v)</math>, co jest możliwe tylko, jeżeli <math>(C \ne C_v)</math>, otrzymujemy po skorzystaniu z własności wyrażeń logarytmicznych | ||
: <math> | : <math>p \cdot V^n=const</math>. | ||
Powyższy wzór jest '''równaniem politropy''' gazu doskonałego obejmującym przypadki, dla których <math>(C \ne C_v)</math>. Wyrażenie | Powyższy wzór jest '''równaniem politropy''' gazu doskonałego obejmującym przypadki, dla których <math>(C \ne C_v)</math>. Wyrażenie | ||
: <math> | : <math>n={C-C_p \over C-C_v}</math>, | ||
nazywa się wykładnikiem politropy. (Pamiętajmy by nie mylić tego oznaczenia z oznaczeniem, także literą '''"n"''', liczby cząsteczek w jednostce objętości. Nie wprowadzamy tu nowych oznaczeń, by pozostać w zgodności z ogólnie przyjętym nazewnictwem.) | nazywa się wykładnikiem politropy. (Pamiętajmy by nie mylić tego oznaczenia z oznaczeniem, także literą '''"n"''', liczby cząsteczek w jednostce objętości. Nie wprowadzamy tu nowych oznaczeń, by pozostać w zgodności z ogólnie przyjętym nazewnictwem.) | ||
| Linia 268: | Linia 268: | ||
|valign="top"|Można teraz obliczyć ciepło molowe '''C''' w zależności od wykładnika '''n''' | |valign="top"|Można teraz obliczyć ciepło molowe '''C''' w zależności od wykładnika '''n''' | ||
: <math> | : <math>C={n \cdot C_v - C_p \over n-1}</math>. | ||
Kiedy zaś <math>(C = C_v)</math> to otrzymujemy, że | Kiedy zaś <math>(C = C_v)</math> to otrzymujemy, że | ||
: <math> | : <math>(C-C_p) \cdot lnV=const</math>. | ||
Przemiana taka zachodzi przy stałej objętości; jest to '''przemiana izochoryczna'''. Widzimy, że w tym przypadku wykładnik politropy <math>n \rightarrow \infty</math>. | Przemiana taka zachodzi przy stałej objętości; jest to '''przemiana izochoryczna'''. Widzimy, że w tym przypadku wykładnik politropy <math>n \rightarrow \infty</math>. | ||
| Linia 332: | Linia 332: | ||
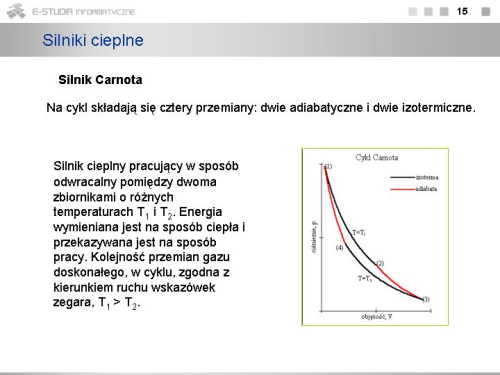
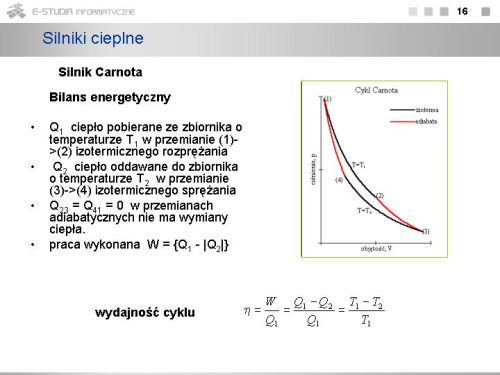
|valign="top"|W przemianie (1)->(2) izotermicznego rozprężania gaz pobiera ciepło <math>Q_1</math> ze zbiornika o temperaturze <math>T_1</math>. Przemiana zachodzi przy stałej temperaturze, więc energia wewnętrzna gazu nie ulega zmianie oraz | |valign="top"|W przemianie (1)->(2) izotermicznego rozprężania gaz pobiera ciepło <math>Q_1</math> ze zbiornika o temperaturze <math>T_1</math>. Przemiana zachodzi przy stałej temperaturze, więc energia wewnętrzna gazu nie ulega zmianie oraz | ||
: <math> | : <math>W'_1=Q_1=\int_{V_1}^{V_2} p \cdot dV=R \cdot T_1 \cdot \int_{V_1}^{V_2} {dV \over V}=R \cdot T_1 \cdot ln {V_2 \over V_1} > 0</math>. | ||
W przemianie drugiej, zachodzącej pomiędzy punktami '''2''' i '''3''', gaz ulega rozprężeniu adiabatycznemu. Oznacza to, że odcięty został zarówno dopływ ciepła, jak i możliwość przekazania ciepła otoczeniu, ale rozprężanie odbywało się nadal do objętości <math>V_3</math>.<br> | W przemianie drugiej, zachodzącej pomiędzy punktami '''2''' i '''3''', gaz ulega rozprężeniu adiabatycznemu. Oznacza to, że odcięty został zarówno dopływ ciepła, jak i możliwość przekazania ciepła otoczeniu, ale rozprężanie odbywało się nadal do objętości <math>V_3</math>.<br> | ||
Trzeci etap jest znów przemianą izotermiczną, w której gaz zostaje sprężony od objętości <math>V_3</math> do <math>V_4</math>. Gaz '''oddaje''' ciepło do chłodnicy o wielkiej pojemności cieplnej, wiec temperatura <math>T_2</math> pozostaje niezmieniona, ale wskutek rozprężania adiabatycznego od objętości <math>V_2</math> do <math>V_3</math>, które zaszło wcześniej, jest niższa od temperatury <math>T_1</math>. Praca wykonana przez gaz w tym procesie wynosi | Trzeci etap jest znów przemianą izotermiczną, w której gaz zostaje sprężony od objętości <math>V_3</math> do <math>V_4</math>. Gaz '''oddaje''' ciepło do chłodnicy o wielkiej pojemności cieplnej, wiec temperatura <math>T_2</math> pozostaje niezmieniona, ale wskutek rozprężania adiabatycznego od objętości <math>V_2</math> do <math>V_3</math>, które zaszło wcześniej, jest niższa od temperatury <math>T_1</math>. Praca wykonana przez gaz w tym procesie wynosi | ||
: <math> | : <math>W'_2=Q_2=\int_{V_3}^{V_4} p \cdot dV=R \cdot T_2 \cdot \int_{V_3}^{V_4} {dV \over V}=-R \cdot T_2 \cdot ln {V_3 \over V_4} < 0</math>. | ||
Zauważmy, że w tym przypadku obie wielkości: wykonana praca i ciepło "pobrane" z chłodnicy są ujemne. Ciepło oddane, któremu przypisujemy wartość dodatnią, oznacza się zwykle symbolem <math>\bar Q</math>. Mamy więc | Zauważmy, że w tym przypadku obie wielkości: wykonana praca i ciepło "pobrane" z chłodnicy są ujemne. Ciepło oddane, któremu przypisujemy wartość dodatnią, oznacza się zwykle symbolem <math>\bar Q</math>. Mamy więc | ||
: <math> | : <math>\bar Q_2=-Q_2</math>. | ||
Czwarty proces jest znów adiabatyczny i przeprowadza układ od punktu '''4''' do początkowego punktu '''1'''. W ten sposób cykl zostaje zamknięty, a energia wewnętrzna po wykonaniu całego cyklu ma swą pierwotną wartość. Przyrost energii wewnętrznej układu równy jest zeru, a sumaryczna wykonana praca równa jest pobranemu przez układ ciepłu | Czwarty proces jest znów adiabatyczny i przeprowadza układ od punktu '''4''' do początkowego punktu '''1'''. W ten sposób cykl zostaje zamknięty, a energia wewnętrzna po wykonaniu całego cyklu ma swą pierwotną wartość. Przyrost energii wewnętrznej układu równy jest zeru, a sumaryczna wykonana praca równa jest pobranemu przez układ ciepłu | ||
: <math> | : <math>W'=W'_1+W'_2=Q_1-\bar Q_2</math>. | ||
Stosunek pracy wykonanej przez układ w jednym cyklu do pobranego w tym cyklu ciepła nazywamy sprawnością lub wydajnością silnika cieplnego (maszyny cieplnej). W naszym przypadku mamy | Stosunek pracy wykonanej przez układ w jednym cyklu do pobranego w tym cyklu ciepła nazywamy sprawnością lub wydajnością silnika cieplnego (maszyny cieplnej). W naszym przypadku mamy | ||
: <math> | : <math>\eta = {W' \over Q_1}={Q_1- \bar Q_2 \over Q_1}=1-{\bar Q_2 \over Q_1}</math>. | ||
Widzimy, że sprawność byłaby równa jedności gdyby całe ciepło zostało zamienione na pracę. Układ musiałby wyłącznie pobierać ciepło. Część ciepła musi być jednak oddawana otoczeniu i w rezultacie sprawność jest zawsze mniejsza od jedności.<br> | Widzimy, że sprawność byłaby równa jedności gdyby całe ciepło zostało zamienione na pracę. Układ musiałby wyłącznie pobierać ciepło. Część ciepła musi być jednak oddawana otoczeniu i w rezultacie sprawność jest zawsze mniejsza od jedności.<br> | ||
Wykorzystując własności przemiany adiabatycznej, mamy w naszym przypadku związki | Wykorzystując własności przemiany adiabatycznej, mamy w naszym przypadku związki | ||
: <math> | : <math>T_1 \cdot V_2^{\kappa -1}=T_2 \cdot V_2^{\kappa -1}</math> oraz <math>T_1 \cdot V_1^{\kappa -1}=T_2 \cdot V_4^{\kappa -1}</math>. | ||
Dzieląc stronami pierwsze z powyższych równań przez drugie otrzymujemy | Dzieląc stronami pierwsze z powyższych równań przez drugie otrzymujemy | ||
: <math> | : <math>({V_2 \over V_1})^{\kappa -1}=({V_3 \over V_4})^{\kappa -1}</math> czyli <math>{V_2 \over V_1}={V_3 \over V_4}</math>. | ||
Wykorzystując ten związek mamy | Wykorzystując ten związek mamy | ||
: <math> | : <math>{\bar Q_2 \over Q_1}={T_2 \over T_1}</math> lub <math>{Q_1 \over T_1}={\bar Q_2 \over T_2}</math>. | ||
|} | |} | ||
| Linia 372: | Linia 372: | ||
|valign="top"|Wynika z tego, że '''sprawność silnika Carnota''' może być przedstawiona w postaci | |valign="top"|Wynika z tego, że '''sprawność silnika Carnota''' może być przedstawiona w postaci | ||
: <math> | : <math>\eta = 1-{T_2 \over T_1}={T_1-T_2 \over T_1}</math>. | ||
Otrzymaliśmy ważny związek, który mówi, że sprawność silnika Carnota określona jest wyłącznie stosunkiem temperatur; mniejszej do większej, i że rośnie wraz ze zmniejszaniem się tego stosunku. Widzimy też, że sprawność ta jest mniejsza od jedności, co oznacza, że nie całe pobrane ciepło zamienia się na pracę. Część ciepła oddawana jest chłodnicy, ale jest to konieczne dla przeprowadzenia cyklu kołowego.<br> | Otrzymaliśmy ważny związek, który mówi, że sprawność silnika Carnota określona jest wyłącznie stosunkiem temperatur; mniejszej do większej, i że rośnie wraz ze zmniejszaniem się tego stosunku. Widzimy też, że sprawność ta jest mniejsza od jedności, co oznacza, że nie całe pobrane ciepło zamienia się na pracę. Część ciepła oddawana jest chłodnicy, ale jest to konieczne dla przeprowadzenia cyklu kołowego.<br> | ||
Jeśli cykl jest nieodwracalny, co może być wynikiem niedoskonałej izolacji cieplnej lub tego, że przemiany nie są kwazistatyczne, to sprawność silnika jest mniejsza niż w przypadku cyklu odwracalnego | Jeśli cykl jest nieodwracalny, co może być wynikiem niedoskonałej izolacji cieplnej lub tego, że przemiany nie są kwazistatyczne, to sprawność silnika jest mniejsza niż w przypadku cyklu odwracalnego | ||
: <math> | : <math>\eta = 1-{\bar Q_2 \over Q_1}<1- {T_2 \over T_1}</math>. | ||
Wniosek, że sprawność silnika Carnota zależy wyłącznie od stosunku temperatur znany jest pod nazwą pierwszego twierdzenia Carnota. | Wniosek, że sprawność silnika Carnota zależy wyłącznie od stosunku temperatur znany jest pod nazwą pierwszego twierdzenia Carnota. | ||
| Linia 391: | Linia 391: | ||
Zwróćmy uwagę, że możliwe jest także przeprowadzenie cyklu w kierunku odwrotnym. Oznacza to, że nad układem wykonywana jest praca, zaś ciepło odbierane jest z chłodnicy i przekazywane nagrzewnicy. Układ taki działa jak maszyna chłodząca, czyli może stanowić lodówkę. Ciepło odbierane jest wtedy od ciała o temperaturze niższej i przekazywane ciału o temperaturze wyższej poprzez wykonanie pracy. Odpowiednikiem sprawności jest tutaj skuteczność chłodzenia określona jako | Zwróćmy uwagę, że możliwe jest także przeprowadzenie cyklu w kierunku odwrotnym. Oznacza to, że nad układem wykonywana jest praca, zaś ciepło odbierane jest z chłodnicy i przekazywane nagrzewnicy. Układ taki działa jak maszyna chłodząca, czyli może stanowić lodówkę. Ciepło odbierane jest wtedy od ciała o temperaturze niższej i przekazywane ciału o temperaturze wyższej poprzez wykonanie pracy. Odpowiednikiem sprawności jest tutaj skuteczność chłodzenia określona jako | ||
: <math> | : <math>\xi={Q \over W'}={\bar Q_2 \over Q_1-\bar Q_2}</math>. | ||
|} | |} | ||
| Linia 417: | Linia 417: | ||
W procesie (2) -> (3) izochorycznego ogrzewania gaz pobiera ciepło | W procesie (2) -> (3) izochorycznego ogrzewania gaz pobiera ciepło | ||
: <math> | : <math>Q_3=\Delta U_3=nC_v\Delta T=nC_v(T_3-T_2)</math>. | ||
W procesie (4) -> (1) izochorycznego ochładzania gaz oddaje ciepło | W procesie (4) -> (1) izochorycznego ochładzania gaz oddaje ciepło | ||
: <math> | : <math>Q_4=\Delta U_4=nC_v\Delta T=nC_v(T_1-T_4)</math>, | ||
ale <math>T_1<T_4</math>, więc ciepło oddane przez gaz wyniesie | ale <math>T_1<T_4</math>, więc ciepło oddane przez gaz wyniesie | ||
: <math> | : <math>|Q_4|=nC_v(T_4-T_1)</math>. | ||
Sprawność cyklu Otta obliczamy ze wzoru: <math> | Sprawność cyklu Otta obliczamy ze wzoru: <math>\eta={Q_3 - \bar Q_4 \over Q_3}</math>. Po podstawieniu, otrzymujemy <math>\eta = {T_3-T_2-T_4+T_1 \over T_3-T_2}</math>. | ||
Aby wyrazić tę sprawność za pomocą stopnia sprężenia wykorzystamy równania adiabat w postaci <math> | Aby wyrazić tę sprawność za pomocą stopnia sprężenia wykorzystamy równania adiabat w postaci <math>TV^{\kappa -1}=const</math>. Wykładnik w równaniu adiabaty (Poissona) <math>\kappa = {C_p \over C_v}</math>. | ||
Dla procesu (1) -> (2) mamy: <math> | Dla procesu (1) -> (2) mamy: <math>T_1V_1^{\kappa -1}=T_2V_2^{\kappa -1}</math>, dla procesu (3) -> (4) mamy: <math>T_3V_2^{\kappa -1}=T_4V_1^{\kappa -1}</math>. | ||
Z powyższych równań obliczamy temperatury i podstawiamy do wzoru na sprawność. Otrzymujemy, że <math> | Z powyższych równań obliczamy temperatury i podstawiamy do wzoru na sprawność. Otrzymujemy, że <math>\eta = 1-({V_2 \over V_1})^{\kappa -1}</math>. Wzór ten pokazuje łatwy, na pozór, sposób na zwiększenie wydajności silnika spalinowego poprzez zwiększenie stopnia sprężenia mieszanki w konsekwencji zwiększenia stosunku <math>V_1/V_2</math>. | ||
|} | |} | ||
| Linia 459: | Linia 459: | ||
W procesie (2) -> (3) izobarycznego ogrzewania gaz pobiera ciepło | W procesie (2) -> (3) izobarycznego ogrzewania gaz pobiera ciepło | ||
: <math> | : <math>Q_3=nC_p\Delta T=nC_p(T_3-T_2)</math>. | ||
W procesie (4) -> (1) izochorycznego ochładzania gaz oddaje ciepło | W procesie (4) -> (1) izochorycznego ochładzania gaz oddaje ciepło | ||
: <math> | : <math>Q_4=\Delta U_4=nC_v\Delta T=nC_v(T_1-T_4)</math>, | ||
ale <math>T_1<T_4</math>, więc ciepło oddane przez gaz wyniesie | ale <math>T_1<T_4</math>, więc ciepło oddane przez gaz wyniesie | ||
: <math> | : <math>|Q_4|=nC_v(T_4-T_1)</math>. | ||
Sprawność cyklu Diesla obliczamy ze wzoru: <math> | Sprawność cyklu Diesla obliczamy ze wzoru: <math>\eta = {Q_3 - |Q_4| \over Q_3}</math>.<br> | ||
Po podstawieniu, otrzymujemy: | Po podstawieniu, otrzymujemy: | ||
: <math> | : <math>\eta = 1-{C_v(T_4-T_1) \over C_p(T_3-T_2)}</math>. | ||
Korzystając z równania adiabaty i równania stanu gazu doskonałego możemy tę sprawność wyrazić za pomocą stopnia sprężenia. Wykładnik w równaniu adiabaty (Poissona) <math>\kappa = {C_p \over C_v}</math>. | Korzystając z równania adiabaty i równania stanu gazu doskonałego możemy tę sprawność wyrazić za pomocą stopnia sprężenia. Wykładnik w równaniu adiabaty (Poissona) <math>\kappa = {C_p \over C_v}</math>. | ||
Dla procesu (1) -> (2) mamy: <math> | Dla procesu (1) -> (2) mamy: <math>T_1V_1^{\kappa -1}=T_2V_2^{\kappa -1}</math>, dla procesu (3) -> (4) mamy: <math>T_3V_3^{\kappa -1}=T_4V_1^{\kappa -1}</math>. | ||
Dla osób zainteresowanych, zachęta do samodzielnego dokończenia obliczeń zależności wydajności od objętości gazu w tym cyklu, bo | Dla osób zainteresowanych, zachęta do samodzielnego dokończenia obliczeń zależności wydajności od objętości gazu w tym cyklu, bo | ||
: <math> | : <math>\eta = 1-{C_v \over C_p}({V_3 \over V_1})^{\kappa -1}{1-({V_2 \over V_3})^\kappa \over 1-{V_2 \over V_3}}</math> | ||
Jak widać, wydajność silnika Diesla zależy również od przebiegu procesu spalania, który ma charakter izobarycznego ogrzewania przy zmianie objętości od <math>V_2</math> do <math>V_3</math>. Warto zauważyć, że w obu przypadkach właściwą substancją pracującą jest powietrze, a proces spalania mieszanki paliwowej rozpatrujemy jako izochoryczne (cykl Otta), bądź izobaryczne (cykl Diesla) jego ogrzewanie. | Jak widać, wydajność silnika Diesla zależy również od przebiegu procesu spalania, który ma charakter izobarycznego ogrzewania przy zmianie objętości od <math>V_2</math> do <math>V_3</math>. Warto zauważyć, że w obu przypadkach właściwą substancją pracującą jest powietrze, a proces spalania mieszanki paliwowej rozpatrujemy jako izochoryczne (cykl Otta), bądź izobaryczne (cykl Diesla) jego ogrzewanie. | ||
| Linia 496: | Linia 496: | ||
Ponieważ <math>dS={\delta Q \over T}</math>, to dla kołowego procesu odwracalnego mamy <math>\oint_{C}{\delta Q \over T}=\oint_{C}dS=0</math>. Dla przemiany przeprowadzającej w sposób odwracalny układ ze stanu '''A''' do stanu '''B''' | Ponieważ <math>dS={\delta Q \over T}</math>, to dla kołowego procesu odwracalnego mamy <math>\oint_{C}{\delta Q \over T}=\oint_{C}dS=0</math>. Dla przemiany przeprowadzającej w sposób odwracalny układ ze stanu '''A''' do stanu '''B''' | ||
: <math> | : <math>\int_A^B{\delta Q \over T}=\int_A^B dS=S_B-S_A</math>. | ||
Podana tu definicja nie pozwala na wyznaczenie bezwzględnej wartości entropii, bowiem z powyższej zależności widać, że | Podana tu definicja nie pozwala na wyznaczenie bezwzględnej wartości entropii, bowiem z powyższej zależności widać, że | ||
: <math> | : <math>S_B=\int_A^B{\delta Q \over T}+S_A</math>. | ||
Dla wyznaczenia entropii układu w danym stanie musielibyśmy znać wartość bezwzględną entropii stanu początkowego. Możemy jednak wyznaczyć przyrost entropii w danym procesie i to (jak zobaczymy) ma zasadnicze znaczenie dotyczące określenia możliwości zachodzenia oraz kierunku przebiegu procesów w przyrodzie. Ważną cechą entropii jest także jej '''addytywność''', co oznacza, że entropia układu jest sumą entropii podukładów. Warto też zwrócić uwagę, że ponieważ w przemianie adiabatycznej, odwracalnej mamy <math>\delta Q=0</math>, to wartość entropii jest dla tej przemiany stała; <math>S=const, dS=0</math>. Proces adiabatyczny, odwracalny nazywa się, dlatego '''procesem izoentropowym'''. | Dla wyznaczenia entropii układu w danym stanie musielibyśmy znać wartość bezwzględną entropii stanu początkowego. Możemy jednak wyznaczyć przyrost entropii w danym procesie i to (jak zobaczymy) ma zasadnicze znaczenie dotyczące określenia możliwości zachodzenia oraz kierunku przebiegu procesów w przyrodzie. Ważną cechą entropii jest także jej '''addytywność''', co oznacza, że entropia układu jest sumą entropii podukładów. Warto też zwrócić uwagę, że ponieważ w przemianie adiabatycznej, odwracalnej mamy <math>\delta Q=0</math>, to wartość entropii jest dla tej przemiany stała; <math>S=const, dS=0</math>. Proces adiabatyczny, odwracalny nazywa się, dlatego '''procesem izoentropowym'''. | ||
| Linia 515: | Linia 515: | ||
Przy opisie mikroskopowych własności gazu doskonałego zakłada się, że cząsteczki gazu zajmują znikomą objętość, a ich oddziaływania sprowadzają się do zderzeń sprężystych. W rzeczywistości, objętość dostępna dla ruchu cząsteczek jest pomniejszona, bowiem nie mogą one zbliżać się do siebie na odległość mniejszą niż wynosi średnica cząsteczki i nie mogą zbliżyć się do ścianek na odległość mniejszą od ich promienia. Ciśnienie także jest wynikiem nie tylko sprężystych i natychmiastowych zderzeń cząsteczek, ale również rezultatem ich wzajemnych oddziaływań poza momentami zderzeń. Objętość dostępna dla ruchu cząsteczek jest, zatem pomniejszona w stosunku do objętości gazu doskonałego, a ciśnienie - powiększone. Efekty te zostały uwzględnione w równaniu van der Waalsa w postaci dodatkowych członów, które dodaje się do ciśnienia i odejmuje od objętości. | Przy opisie mikroskopowych własności gazu doskonałego zakłada się, że cząsteczki gazu zajmują znikomą objętość, a ich oddziaływania sprowadzają się do zderzeń sprężystych. W rzeczywistości, objętość dostępna dla ruchu cząsteczek jest pomniejszona, bowiem nie mogą one zbliżać się do siebie na odległość mniejszą niż wynosi średnica cząsteczki i nie mogą zbliżyć się do ścianek na odległość mniejszą od ich promienia. Ciśnienie także jest wynikiem nie tylko sprężystych i natychmiastowych zderzeń cząsteczek, ale również rezultatem ich wzajemnych oddziaływań poza momentami zderzeń. Objętość dostępna dla ruchu cząsteczek jest, zatem pomniejszona w stosunku do objętości gazu doskonałego, a ciśnienie - powiększone. Efekty te zostały uwzględnione w równaniu van der Waalsa w postaci dodatkowych członów, które dodaje się do ciśnienia i odejmuje od objętości. | ||
: <math> | : <math>(p+p')\cdot (V-V')=R\cdot T</math> | ||
Jeśli wartości <math>p'</math> i <math>V'</math> są równe zeru, otrzymujemy znane nam równanie stanu gazu doskonałego dla jednego mola gazu. Ciśnienie <math>p'</math> zwane jest ciśnieniem kohezyjnym. Ciśnienie to proporcjonalne jest do gęstości gazu <math>\rho</math> i sił wzajemnego oddziaływania cząsteczek. Siły te także wzrastają proporcjonalnie do gęstości gazu, a gęstość jest odwrotnie proporcjonalna do objętości. Mamy, więc | Jeśli wartości <math>p'</math> i <math>V'</math> są równe zeru, otrzymujemy znane nam równanie stanu gazu doskonałego dla jednego mola gazu. Ciśnienie <math>p'</math> zwane jest ciśnieniem kohezyjnym. Ciśnienie to proporcjonalne jest do gęstości gazu <math>\rho</math> i sił wzajemnego oddziaływania cząsteczek. Siły te także wzrastają proporcjonalnie do gęstości gazu, a gęstość jest odwrotnie proporcjonalna do objętości. Mamy, więc | ||
: <math> | : <math>p'\sim \rho \cdot F\sim \rho^2\sim 1/V^2</math>. | ||
Zmniejszenie objętości proporcjonalne jest do liczby cząsteczek, a liczba ta, przy danym ciśnieniu, jest proporcjonalna do objętości naczynia. Objętość <math>V'</math> stanowi, tę część objętości, która jest efektywnie zajęta przez cząsteczki gazu.<br> | Zmniejszenie objętości proporcjonalne jest do liczby cząsteczek, a liczba ta, przy danym ciśnieniu, jest proporcjonalna do objętości naczynia. Objętość <math>V'</math> stanowi, tę część objętości, która jest efektywnie zajęta przez cząsteczki gazu.<br> | ||
Wprowadzając oznaczenia: <math> | Wprowadzając oznaczenia: <math>p'=a/V^2</math> oraz <math>V'=b</math>, otrzymujemy równanie stanu gazu znane jako '''równanie van der Waalsa'''. | ||
: <math> | : <math>(p+{a \over V^2}) \cdot (V-b)=R \cdot T</math> | ||
Stałe '''a''' i '''b''' charakteryzują własności jednego mola danego gazu rzeczywistego. | Stałe '''a''' i '''b''' charakteryzują własności jednego mola danego gazu rzeczywistego. | ||
| Linia 535: | Linia 535: | ||
|valign="top"|Zależność ciśnienia od objętości przy stałej temperaturze dla jednego mola gazu wynikająca z równania van der Waalsa ma postać | |valign="top"|Zależność ciśnienia od objętości przy stałej temperaturze dla jednego mola gazu wynikająca z równania van der Waalsa ma postać | ||
: <math> | : <math>p={R\cdot T \over V-b}-{a \over V_2}</math>. | ||
Przykładowe izotermy van der Waalsa dla dwutlenku węgla, <math>CO_2</math> pokazane są na wykresie. Temperatury: 264 K, 284 K, 304 K, 334 K, 364 K, 404 K. | Przykładowe izotermy van der Waalsa dla dwutlenku węgla, <math>CO_2</math> pokazane są na wykresie. Temperatury: 264 K, 284 K, 304 K, 334 K, 364 K, 404 K. | ||
| Linia 541: | Linia 541: | ||
Naturalnym wnioskiem z analizy izoterm van der Waalsa jest to, że dla określonej temperatury (izoterma krytyczna) nie pojawia się minimum, ale jedynie punkt przegięcia na krzywej. Punkt ten zwany jest '''punktem krytycznym''' i na rysunku oznaczony jest literą '''K'''. Odpowiadające temu punktowi wartości ciśnienia, objętości i gęstości gazu noszą nazwę '''wartości krytycznych'''. Parametry krytyczne można wyznaczyć, zauważając, że dla izotermy krytycznej pierwiastki równania van der Waalsa są sobie równe: <math>V_1 = V_2 = V_3 = V_{kr}</math>. Można też analitycznie zbadać przebieg zmienności funkcji <math>p (V) \ dla T = const</math>. W punkcie krytycznym styczna do izotermy jest pozioma, co oznacza zerowanie się pierwszej pochodnej ciśnienia względem objętości. Punkt ten jest też punktem przegięcia, co oznacza zerowanie się drugiej pochodnej. Mamy, zatem dla <math>T = const</math> | Naturalnym wnioskiem z analizy izoterm van der Waalsa jest to, że dla określonej temperatury (izoterma krytyczna) nie pojawia się minimum, ale jedynie punkt przegięcia na krzywej. Punkt ten zwany jest '''punktem krytycznym''' i na rysunku oznaczony jest literą '''K'''. Odpowiadające temu punktowi wartości ciśnienia, objętości i gęstości gazu noszą nazwę '''wartości krytycznych'''. Parametry krytyczne można wyznaczyć, zauważając, że dla izotermy krytycznej pierwiastki równania van der Waalsa są sobie równe: <math>V_1 = V_2 = V_3 = V_{kr}</math>. Można też analitycznie zbadać przebieg zmienności funkcji <math>p (V) \ dla T = const</math>. W punkcie krytycznym styczna do izotermy jest pozioma, co oznacza zerowanie się pierwszej pochodnej ciśnienia względem objętości. Punkt ten jest też punktem przegięcia, co oznacza zerowanie się drugiej pochodnej. Mamy, zatem dla <math>T = const</math> | ||
: <math> | : <math>{dp \over dV}=-{RT \over (V-b)^2}+{2a \over V^3}=0</math> oraz | ||
: <math> | : <math>{d^2p \over dV^2}={2RT \over (V-b)^3}-{6a \over V^4}=0 \ (przy T=const)</math> | ||
Z równań tych wyznaczamy <math> | Z równań tych wyznaczamy <math>T_{kr}={8 \cdot a \over 27 \cdot b \cdot R}</math>, <math>p_{kr}={a \over 27 \cdot b^2}</math>, <math>V_{kr}=3 \cdot b</math>. | ||
Współczynniki równania van der Waalsa wyrażone przez wartości krytyczne wynoszą | Współczynniki równania van der Waalsa wyrażone przez wartości krytyczne wynoszą | ||
: <math> | : <math>a={27 \cdot (R \cdot T_{kr})^2 \over 64 \cdot p_{kr}}</math>, <math>b={R \cdot T_{kr} \over 8 \cdot p_{kr}}</math>. | ||
Tak wyznaczone współczynniki zostały użyte do naszych wykresów izoterm van der Waalsa dla dwutlenku węgla, gdzie <math>T_{kr} = 304 K</math>, <math>p_{kr} = 7,38 MPa</math>. | Tak wyznaczone współczynniki zostały użyte do naszych wykresów izoterm van der Waalsa dla dwutlenku węgla, gdzie <math>T_{kr} = 304 K</math>, <math>p_{kr} = 7,38 MPa</math>. | ||
Na koniec warto zaznaczyć, że nasze dotychczasowe rozważania w tej lekcji odnosiły się do jednego mola gazu. Kiedy rozważamy <math>n_M</math> moli, wówczas dodatkowe człony równania van der Waalsa są: <math> | Na koniec warto zaznaczyć, że nasze dotychczasowe rozważania w tej lekcji odnosiły się do jednego mola gazu. Kiedy rozważamy <math>n_M</math> moli, wówczas dodatkowe człony równania van der Waalsa są: <math>p'={n_M^2 \cdot a \over V^2}</math>, <math>V'=n_M \cdot b</math>, a równanie ma postać | ||
: <math> | : <math>(p+{n_M^2 \cdot a \over V^2})\cdot (V - n_M \cdot b)=n_M \cdot R \cdot T</math>. | ||
Należy dodać, że równanie van der Waalsa ma charakter empiryczny i jest jednym z kilku różnych równań stanu gazu rzeczywistego, najbardziej popularnym. | Należy dodać, że równanie van der Waalsa ma charakter empiryczny i jest jednym z kilku różnych równań stanu gazu rzeczywistego, najbardziej popularnym. | ||
| Linia 606: | Linia 606: | ||
W której z przemian, podczas rozszerzania, gaz ten ogrzewa się a w której oziębia? | W której z przemian, podczas rozszerzania, gaz ten ogrzewa się a w której oziębia? | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | |||
#<math>C = C_v - R</math>, oziębianie, | |||
#<math>C = C_p + R</math>, ogrzewanie. | |||
</div></div> | |||
---- | |||
'''Zadanie 8.3''' | '''Zadanie 8.3''' | ||
| Linia 616: | Linia 620: | ||
Silnik cieplny pracuje według cyklu składającego się z izotermy, izobary i izochory. Objętość gazu w czasie cyklu zmienia się dziesięciokrotnie, a temperatura przemiany izotermicznej jest równa 400 K. Gazem roboczym jest 1 kmol gazu doskonałego o cząsteczkach jednoatomowych. Oblicz sprawność cyklu. | Silnik cieplny pracuje według cyklu składającego się z izotermy, izobary i izochory. Objętość gazu w czasie cyklu zmienia się dziesięciokrotnie, a temperatura przemiany izotermicznej jest równa 400 K. Gazem roboczym jest 1 kmol gazu doskonałego o cząsteczkach jednoatomowych. Oblicz sprawność cyklu. | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | |||
<math>\eta = 0,38</math> | <math>\eta = 0,38</math> | ||
</div></div> | |||
---- | |||
'''Zadanie 8.4''' | '''Zadanie 8.4''' | ||
| Linia 625: | Linia 633: | ||
Oblicz zmianę entropii w cyklu Carnota. | Oblicz zmianę entropii w cyklu Carnota. | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | |||
Entropia jest funkcją stanu, <math>\Delta S = 0</math> | Entropia jest funkcją stanu, <math>\Delta S = 0</math> | ||
</div></div> | |||
---- | |||
'''Zadanie 8.5''' | '''Zadanie 8.5''' | ||
| Linia 637: | Linia 649: | ||
*Odpowiedz też na powyższe pytania zakładając, że jest to gaz doskonały | *Odpowiedz też na powyższe pytania zakładając, że jest to gaz doskonały | ||
<math> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | ||
<math>p={nR(273+t) \over V-nb}-{n^2 a \over V^2}</math>, <math>\Delta p={nRt \over V-nb}</math>, dla gazu doskonałego a = 0 i b = 0 | |||
</div></div> | |||
<hr width="100%"> | <hr width="100%"> | ||
Aktualna wersja na dzień 12:04, 5 wrz 2023
Wykład

|
Wprowadzenie
Omówione są tu ogólne prawa makroskopowe opisujące prawidłowo zjawiska cieplne i pozwalające ilościowo przewidywać skutki różnych procesów. |
Materiały do ćwiczeń
Zadanie 8.2
Oblicz ciepło molowe gazu doskonałego w przemianie politropowej o równaniu
- ,
- .
W której z przemian, podczas rozszerzania, gaz ten ogrzewa się a w której oziębia?
Zadanie 8.3
Silnik cieplny pracuje według cyklu składającego się z izotermy, izobary i izochory. Objętość gazu w czasie cyklu zmienia się dziesięciokrotnie, a temperatura przemiany izotermicznej jest równa 400 K. Gazem roboczym jest 1 kmol gazu doskonałego o cząsteczkach jednoatomowych. Oblicz sprawność cyklu.
Zadanie 8.4
Oblicz zmianę entropii w cyklu Carnota.
Zadanie 8.5
W naczyniu o objętości , w temperaturze , znajduje się n moli gazu rzeczywistego spełniającego równanie van der Waalsa, o znanych parametrach a, b.
- Jakie jest jego ciśnienie?
- O ile zmieni się to ciśnienie, jeśli temperatura tego gazu wzrośnie dwukrotnie przy stałej objętości?
- Odpowiedz też na powyższe pytania zakładając, że jest to gaz doskonały
Słowniczek
- pierwsza zasada termodynamiki - Przyrost energii wewnętrznej układu równy jest sumie dostarczonej do układu energii cieplnej, wykonanej nad układem pracy oraz energii uzyskanej wskutek wymiany materii z otoczeniem. Przyrost ten w procesach kwazistatycznych i odwracalnych nie zależy od sposobu, w jaki dokonuje się przejście, a określony jest całkowicie przez początkowy i końcowy stan układu
- pojemność cieplna - ilość ciepła potrzebna do podwyższenia temperatury ciała o jeden kelwin
- molowe ciepło właściwe - ilość ciepła potrzebna do podwyższenia temperatury jednego mola substancji o jeden kelwin
- przemiana izotermiczna - proces, który zachodzi w stałej temperaturze; T = const
- prawo Boyle'a Mariotte'a - odnosi się do przemiany izotermicznej: pV = const. W stałej temperaturze iloczyn ciśnienia i objętości jest stały lub - ciśnienie zmienia się odwrotnie proporcjonalnie do objętości.
- przemiana izochoryczna - proces, który zachodzi przy stałej objętości; V = const
- przemiana izobaryczna - proces, który zachodzi przy stałym ciśnieniu; p = const
- przemiana adiabatyczna - przemiana, która zachodzi bez wymiany ciepła z otoczeniem
- przemiana politropowa - przemiana, w czasie której pojemność cieplna ciała pozostaje stała
- cykl Carnota - cykl odwracalny składający się z dwóch przemian izotermicznych oraz dwóch adiabatycznych
- twierdzenia Carnota - 1. Wszystkie silniki pracujące w odwracalnym cyklu Carnota pomiędzy tymi samymi temperaturami mają tę samą sprawność.
2. Sprawność cyklu nieodwracalnego jest zawsze mniejsza od sprawności cyklu odwracalnego. - ciepło zredukowane - stosunek ilości ciepła pobranego z danego źródła do jego temperatury bezwzględnej
- entropia - 1. funkcja stanu której przyrost w przemianie odwracalnej równy jest przyrostowi ciepła zredukowanego
2. wielkość proporcjonalna do logarytmu prawdopodobieństwa termodynamicznego stanu układu - proces izoentropowy - proces, w którym entropia zachowuje wartość stałą. Procesem takim jest każdy proces adiabatyczny, odwracalny.
- nierówność Clausiusa - suma wartości ciepeł zredukowanych w każdej przemianie zamkniętej jest nie większa od zera
- prawo wzrostu entropii - Entropia układu izolowanego, w którym zachodzą procesy nieodwracalne może tylko rosnąć.
- druga zasada termodynamiki - 1. Niemożliwe jest przekazywanie ciepła przez ciało o temperaturze niższej ciału o temperaturze wyższej bez wprowadzenia innych zmian w obu ciałach i w otoczeniu
2. Niemożliwe jest pobieranie ciepła z jednego termostatu i zamiana go na pracę bez wprowadzania innych zmian w układzie i w otoczeniu.
3. Skonstruowanie perpetuum mobile drugiego rodzaju jest niemożliwe
4. Entropia układu izolowanego nie może maleć. - cykl Otta - cykl termodynamiczny składający się z dwóch adiabat i dwóch izochor. Do cyklu Otta zbliżony jest cykl pracy silnika benzynowego.
- cykl Diesla - cykl termodynamiczny składający się z dwóch adiabat izochory i izobary. Opisuje pracę silnika Diesla.
- równanie van der Waalsa - równanie stanu gazu rzeczywistego biorące pod uwagę objętość cząsteczek gazu i siły ich wzajemnych oddziaływań
- stan (punkt) krytyczny - stan, w którym znikają różnice pomiędzy własnościami cieczy, pary nasyconej i gazu. Gęstości substancji w tych trzech stanach są jednakowe.
- wartości krytyczne - wartości ciśnienia, temperatury i gęstości w punkcie krytycznym
- faza substancji - stan substancji charakteryzujący się jednoznacznie określonymi własnościami
- przejście fazowe - proces w rezultacie którego zmienia się faza substancji
- parowanie - proces polegający na przejściu z fazy ciekłej do gazowej
- skraplanie - proces polegający na przejściu z fazy gazowej do fazy ciekłej
- sublimacja - proces polegający na przejściu z fazy gazowej do fazy stałej
- stan równowagi dynamicznej - stan którego własności makroskopowe nie zmieniają się w czasie pomimo zachodzących procesów w skali mikroskopowej
- anizotropia - zależność własności fizycznych ciała od kierunku
- stan metastabilny - stan układu, który może być zmieniony wskutek bardzo niewielkiego zaburzenia warunków w jakich układ się znajduje
- para nasycona - para o maksymalnej możliwej gęstości w danej temperaturze
- para przesycona - metastabilny stan pary, w warunkach ciśnienia i temperatury odpowiadających stanowi ciekłemu danej substancji
- ciecz przegrzana - metastabilny stan cieczy, w warunkach ciśnienia i temperatury odpowiadających stanowi gazowemu danej substancji
- punkt potrójny - punkt określający warunki ciśnienia i temperatury, w których mogą istnieć w równowadze trzy stany skupienia danej substancji: stała, ciekła i gazowa
- wykres stanu - wykres we współrzędnych temperatury i ciśnienia określający warunki współistnienia faz danej substancji