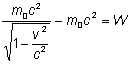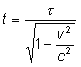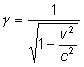PF Moduł 6: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 12 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
__TOC__ | |||
= Wykład = | |||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M6_Slajd1.png|thumbs|500px|]] | |width="450px" valign="top"|[[Grafika:PF_M6_Slajd1.png|thumbs|500px|]] | ||
| Linia 55: | Linia 58: | ||
|valign="top"|'''Transformacja Lorentza''' | |valign="top"|'''Transformacja Lorentza''' | ||
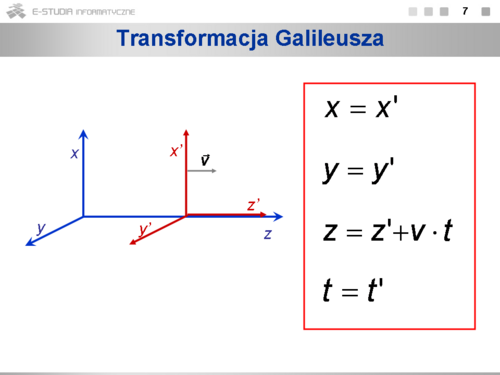
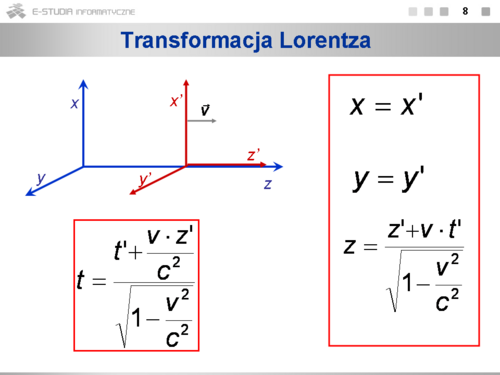
Transformacja to przepis, jak od współrzędnych w jednym układzie odniesienia przejść do współrzędnych w innym układzie. Klasyczna transformacja Galileusza zakłada istnienie absolutnego czasu jednakowego we wszystkich układach inercjalnych <math>(t = | Transformacja to przepis, jak od współrzędnych w jednym układzie odniesienia przejść do współrzędnych w innym układzie. Klasyczna transformacja Galileusza zakłada istnienie absolutnego czasu jednakowego we wszystkich układach inercjalnych <math>(t = t')</math>. Jeśli ciało porusza się w układzie <math>O'\ </math>, z prędkością <math>\vec {u'}</math> , to zgodnie z tą transformacją jego prędkość w układzie O jest równa <math>\vec u=\vec {u'}+\vec v</math> Jeśli w układzie <math>O'\ </math>, będzie wysłany impuls światła z prędkością c, to jego prędkość w układzie <math>O'\ </math>, byłaby większa od c, a to jest sprzeczne z doświadczeniem. Stałość prędkości światła w każdym układzie wymaga zmiany transformacji. Nowa transformacja musi zapewnić stałość prędkości światła niezależnie od tego, w którym układzie odniesienia prędkość ta jest rozpatrywana. Powinna też przechodzić w transformację Galileusza dla małych prędkości. | ||
|} | |} | ||
| Linia 69: | Linia 72: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M6_Slajd9.png|thumbs|500px|]] | |width="450px" valign="top"|[[Grafika:PF_M6_Slajd9.png|thumbs|500px|]] | ||
|valign="top"|Zdefiniujmy wielkość <math>\gamma\ | |valign="top"|Zdefiniujmy wielkość <math>\gamma\ </math>, zwaną czynnikiem Lorentza. Czynnik ten jest zawsze większy od jedności, bo jak niebawem się przekonamy <math>v < c</math>. Wzory transformacji Lorentza mają prostszą postać. | ||
|} | |} | ||
| Linia 76: | Linia 79: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M6_Slajd10.png|thumbs|500px|]] | |width="450px" valign="top"|[[Grafika:PF_M6_Slajd10.png|thumbs|500px|]] | ||
|valign="top"|Odwrotną transformację otrzymamy, jeśli zauważymy, że układ O porusza się względem układu <math>O'\ | |valign="top"|Odwrotną transformację otrzymamy, jeśli zauważymy, że układ O porusza się względem układu <math>O'\ </math>, z prędkością <math>-\vec {v'}</math> . Nietrudno zauważyć, że transformacja Lorentza przechodzi w transformację Galileusza, kiedy v dąży do 0, czyli dla prędkości małych w porównaniu z c. | ||
|} | |} | ||
| Linia 83: | Linia 86: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M6_Slajd11.png|thumbs|500px|]] | |width="450px" valign="top"|[[Grafika:PF_M6_Slajd11.png|thumbs|500px|]] | ||
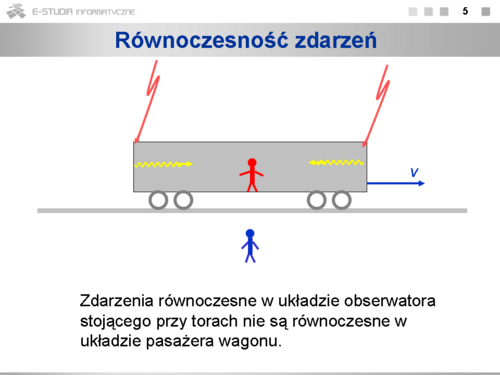
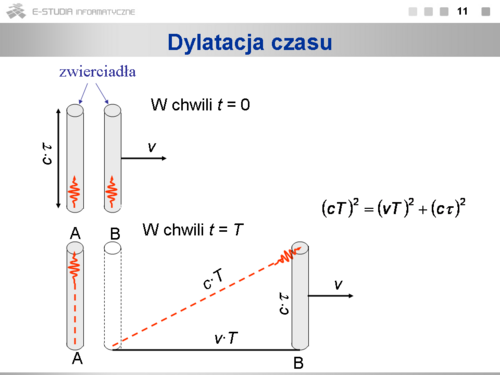
|valign="top"|Zasada względności i zasada stałości prędkości światła rewolucjonizuje nasze pojmowanie czasu. Zastosujmy te zasady do prostego „zegara świetlnego”. Jest to rurka z dwoma doskonale odbijającymi zwierciadłami na obu końcach. Wewnątrz porusza się impuls świetlny, który odbija się od zwierciadeł i biegnie tam i z powrotem. Tyknięciem zegara, czyli zmierzonym odstępem czasu, będzie czas, w jakim impuls przejdzie od zwierciadła dolnego do górnego. Początkowo (t = 0) dwa takie zegary tykają synchronicznie. Czas między kolejnymi odbiciami wynosi <math>\tau\ | |valign="top"|Zasada względności i zasada stałości prędkości światła rewolucjonizuje nasze pojmowanie czasu. Zastosujmy te zasady do prostego „zegara świetlnego”. Jest to rurka z dwoma doskonale odbijającymi zwierciadłami na obu końcach. Wewnątrz porusza się impuls świetlny, który odbija się od zwierciadeł i biegnie tam i z powrotem. Tyknięciem zegara, czyli zmierzonym odstępem czasu, będzie czas, w jakim impuls przejdzie od zwierciadła dolnego do górnego. Początkowo (t = 0) dwa takie zegary tykają synchronicznie. Czas między kolejnymi odbiciami wynosi <math>\tau\ </math>,, a więc długość zegara równa jest <math>c\tau\ </math>,. Zegar B porusza się w prawo z prędkością v. Czy obserwatorowi A będzie wydawało się, że poruszający względem niego zegar B będzie krótszy lub dłuższy? Wyobraźmy sobie, że na końcu zegara B przymocowaliśmy pędzelek, który przy mijaniu zegara A namaluje na nim kreskę. Jeśli by ta kreska wypadła poniżej krawędzi, to obserwator A będzie widział poruszający względem niego zegar B jako skrócony, natomiast obserwator B zobaczy poruszający się zegar A wydłużony. Taka obserwacja jest sprzeczna z zasadą względności – efekty obserwowane w obu układach powinny być takie same. Wnioskujemy stąd, że długości zegarów ( i wszystkich odcinków prostopadłych do prędkości) powinny być równe. | ||
Po upływie czasu <math>\tau\ | Po upływie czasu <math>\tau\ </math>, obserwator A (spoczywający) stwierdzi, że impuls świetlny w zegarze B przebył dłuższą drogę niż <math>c\tau\ </math>,, bo musi biec po przekątnej. Ponieważ jednak prędkość światła jest stała, zajęło mu to więcej czasu. Czas między tyknięciami zegara B wynosi <math>T>\tau\ </math>,. Stosując twierdzenie Pitagorasa do trójkąta widocznego na rysunku dostaniemy: | ||
<math>(cT)^2=(vT)^2+(c\tau)^2</math> , stąd [[Grafika:PF_M6_Wzor1.png]] | <math>(cT)^2=(vT)^2+(c\tau)^2</math> , stąd [[Grafika:PF_M6_Wzor1.png]] | ||
| Linia 94: | Linia 97: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M6_Slajd12.png|thumbs|500px|]] | |width="450px" valign="top"|[[Grafika:PF_M6_Slajd12.png|thumbs|500px|]] | ||
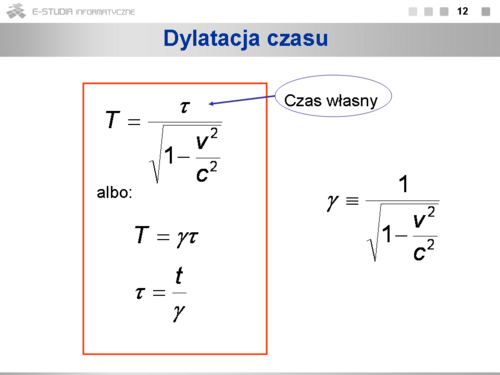
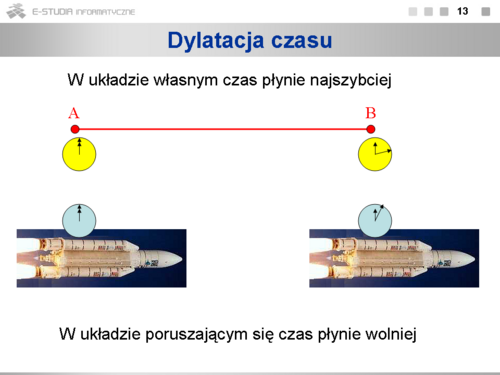
|valign="top"|Według spoczywającego obserwatora czas między dwoma tyknięciami zegara jest dłuższy, gdy zegar się porusza. Każdy obserwator widzi, że poruszający się względem niego zegar tyka <math>\gamma\ | |valign="top"|Według spoczywającego obserwatora czas między dwoma tyknięciami zegara jest dłuższy, gdy zegar się porusza. Każdy obserwator widzi, że poruszający się względem niego zegar tyka <math>\gamma\ </math>, razy wolniej. Odstęp czasu między dwoma zdarzeniami, które obserwator widzi w tym samym punkcie przestrzeni, nazywamy czasem własnym. To najkrótszy czas jaki można zaobserwować między danymi zdarzeniami. | ||
Opisane zjawisko to dylatacja czasu wynikająca z równań transformacji Lorentza. | Opisane zjawisko to dylatacja czasu wynikająca z równań transformacji Lorentza. | ||
Efekt ten możemy opisać następująco: w określonym miejscu (ustalone współrzędne przestrzenne) jednego układu, na przykład B, zachodzi pewne zjawisko, którego czas trwania wynosi | Efekt ten możemy opisać następująco: w określonym miejscu (ustalone współrzędne przestrzenne) jednego układu, na przykład B, zachodzi pewne zjawisko, którego czas trwania wynosi <math>\tau\ </math>,. W układzie A, względem którego układ B porusza się z prędkością v, zjawisko to zachodzi w różnych miejscach (różne współrzędne przestrzenne początku i końca zjawiska) i stąd wynika inny czas trwania tego zjawiska. | ||
Należy podkreślić, że spowolnienie upływu czasu w układzie poruszającym się względem obserwatora jest jak najbardziej realne. Zjawisko to jest obserwowane przez fizyków, którzy mierzą czas życia rozpadających się cząstek, na przykład mezonów <math>\pi\ | Należy podkreślić, że spowolnienie upływu czasu w układzie poruszającym się względem obserwatora jest jak najbardziej realne. Zjawisko to jest obserwowane przez fizyków, którzy mierzą czas życia rozpadających się cząstek, na przykład mezonów <math>\pi\ </math>,. Kiedy cząstka porusza się w układzie laboratoryjnym z prędkością bliską prędkości światła, jej czas życia ulega wydłużeniu, co bez trudu można sprawdzić doświadczalnie. | ||
|} | |} | ||
| Linia 114: | Linia 117: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M6_Slajd14.png|thumbs|500px|]] | |width="450px" valign="top"|[[Grafika:PF_M6_Slajd14.png|thumbs|500px|]] | ||
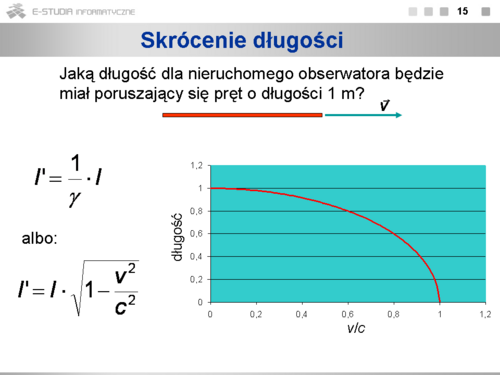
|valign="top"|Pręt o długości l spoczywa w układzie O. Jaka jest długość <math>l'\ | |valign="top"|Pręt o długości l spoczywa w układzie O. Jaka jest długość <math>l'\ </math>, tego pręta zmierzona w układzie <math>O'\ </math>,, który porusza się z prędkością <math>\vec {v}</math> ? Aby dowiedzieć się, jaka jest długość poruszającego się pręta, obserwator z układu <math>O'\ </math>, powinien zmierzyć odległość między jego końcami w tym samym momencie. Wyrażamy <math>l'\ </math>, jako różnicę współrzędnych <math>{z_2}'\ </math>, i <math>{z_1}'\ </math>, zmierzonych w tej samej chwili czasu <math>t'\ </math>, i korzystamy z transformacji Lorentza, podstawiając tę samą wartość <math>t'\ </math>, dla obu końców pręta. Otrzymany wynik oznacza, że pręt poruszający się względem obserwatora ma mniejszą długość niż w układzie, w którym ten pręt spoczywa. Kontrakcja (skrócenie) długości zachodzi tylko w kierunku ruchu. | ||
Kontrakcja długości jest w pewnym sensie skutkiem istnienia „nierównoczesności czasowej” zdarzeń. Jeśli pomiary położenia końców pręta w jednym układzie są równoczesne, to w drugim układzie są nierównoczesne i odwrotnie. | Kontrakcja długości jest w pewnym sensie skutkiem istnienia „nierównoczesności czasowej” zdarzeń. Jeśli pomiary położenia końców pręta w jednym układzie są równoczesne, to w drugim układzie są nierównoczesne i odwrotnie. | ||
| Linia 143: | Linia 146: | ||
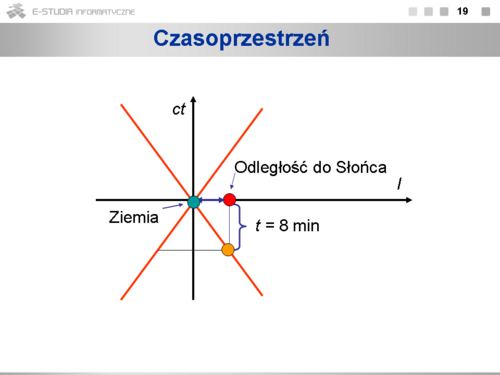
W zakresie prędkości nierelatywistycznych (transformacja Galileusza) długość odcinka i przedział czasowy są jednakowe w każdym układzie odniesienia. Mówimy, że te wielkości są niezmiennikami transformacji Galileusza. Jednak dla prędkości porównywalnych z prędkością światła ani długość, ani przedział czasu nie są jednakowe w różnych układach odniesienia. Współrzędne przestrzenne i czasowe są od siebie zależne – tworzą czterowymiarową czasoprzestrzeń (trzy wymiary przestrzenne, czwartym wymiarem jest czas pomnożony przez c). Każdemu punktowi w czasoprzestrzeni odpowiada określone zdarzenie. | W zakresie prędkości nierelatywistycznych (transformacja Galileusza) długość odcinka i przedział czasowy są jednakowe w każdym układzie odniesienia. Mówimy, że te wielkości są niezmiennikami transformacji Galileusza. Jednak dla prędkości porównywalnych z prędkością światła ani długość, ani przedział czasu nie są jednakowe w różnych układach odniesienia. Współrzędne przestrzenne i czasowe są od siebie zależne – tworzą czterowymiarową czasoprzestrzeń (trzy wymiary przestrzenne, czwartym wymiarem jest czas pomnożony przez c). Każdemu punktowi w czasoprzestrzeni odpowiada określone zdarzenie. | ||
Odpowiednikiem odległości między dwoma punktami w trójwymiarowej przestrzeni <math>\Delta l\ | Odpowiednikiem odległości między dwoma punktami w trójwymiarowej przestrzeni <math>\Delta l\ </math>, jest interwał czasoprzestrzenny <math>\Delta s\ </math>, - odległość między dwoma punktami w czasoprzestrzeni. Zauważmy, że odległość ta jest niezerowa nawet wtedy, gdy zdarzenia zachodzą w tym samym punkcie przestrzeni trójwymiarowej. Interwał czasoprzestrzenny jest niezmiennikiem transformacji Lorentza. | ||
|} | |} | ||
| Linia 166: | Linia 169: | ||
|valign="top"|'''Transformacja prędkości''' | |valign="top"|'''Transformacja prędkości''' | ||
Zapiszmy współrzędne wektora prędkości w spoczywającym układzie odniesienia O i zadanej w tym układzie chwili czasu t. Podobnie czynimy dla drugiego układu, poruszającego się względem pierwszego z prędkością <math>v_0\ | Zapiszmy współrzędne wektora prędkości w spoczywającym układzie odniesienia O i zadanej w tym układzie chwili czasu t. Podobnie czynimy dla drugiego układu, poruszającego się względem pierwszego z prędkością <math>v_0\ </math>,. Wszystkie wielkości odnoszące się do drugiego układu będziemy oznaczać symbolem (‘),"prim", | ||
|} | |} | ||
| Linia 180: | Linia 183: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M6_Slajd22.png|thumbs|500px|]] | |width="450px" valign="top"|[[Grafika:PF_M6_Slajd22.png|thumbs|500px|]] | ||
|valign="top"|Możemy teraz wyznaczyć składowe prędkości dzieląc pierwsze trzy równania określające transformacje przyrostów współrzędnych przez czwarte, określające przyrost czasu. Gdy prędkość <math>v_0\ | |valign="top"|Możemy teraz wyznaczyć składowe prędkości dzieląc pierwsze trzy równania określające transformacje przyrostów współrzędnych przez czwarte, określające przyrost czasu. Gdy prędkość <math>v_0\ </math>, będzie mała w stosunku do prędkości światła, to wzory przechodzą we wzory otrzymane za pomocą transformacji Galileusza. | ||
|} | |} | ||
| Linia 194: | Linia 197: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M6_Slajd24.png|thumbs|500px|]] | |width="450px" valign="top"|[[Grafika:PF_M6_Slajd24.png|thumbs|500px|]] | ||
|valign="top"|Sprawdźmy jaka będzie prędkość światła zmierzona przez obserwatora w układzie O, jeśli źródło światła porusza się względem obserwatora z prędkością <math>v_0\ | |valign="top"|Sprawdźmy jaka będzie prędkość światła zmierzona przez obserwatora w układzie O, jeśli źródło światła porusza się względem obserwatora z prędkością <math>v_0\ </math>,. Oczywiście prędkość światła w obu układach jest taka sama i wynosi c. Nie jest to niespodzianką, ponieważ wzory na transformację prędkości wyprowadziliśmy z transformacji Lorentza, a te zostały tak sformułowane, aby zapewnić stałość prędkości światła w każdym układzie odniesienia. | ||
|} | |} | ||
| Linia 205: | Linia 208: | ||
: II zasada dynamiki | : II zasada dynamiki | ||
Ważną wielkością w fizyce jest pęd zdefiniowany: <math>\vec{p}=m\cdot \vec{v}</math> . Szczególną rolę odgrywa zasada zachowania pędu, przy czym zasada ta jest spełniona niezależnie od tego w jakim układzie odniesienia znajduje się obserwator. Aby zapewnić niezależność zasady zachowania pędu od układu odniesienia, należy zmodyfikować definicję pędu. Masa nie może być stała – powinna rosnąć wraz z prędkością. Wielkość <math>m_0\ | Ważną wielkością w fizyce jest pęd zdefiniowany: <math>\vec{p}=m\cdot \vec{v}</math> . Szczególną rolę odgrywa zasada zachowania pędu, przy czym zasada ta jest spełniona niezależnie od tego w jakim układzie odniesienia znajduje się obserwator. Aby zapewnić niezależność zasady zachowania pędu od układu odniesienia, należy zmodyfikować definicję pędu. Masa nie może być stała – powinna rosnąć wraz z prędkością. Wielkość <math>m_0\ </math>, nazywamy masą spoczynkową. Pęd relatywistyczny nie jest wprost proporcjonalny do prędkości – rośnie szybciej z prędkością. | ||
|} | |} | ||
| Linia 228: | Linia 231: | ||
|valign="top"|'''Energia kinetyczna''' | |valign="top"|'''Energia kinetyczna''' | ||
Aby obliczyć relatywistyczną energię kinetyczną, rozważmy cząstkę o masie spoczynkowej <math>m_0\ | Aby obliczyć relatywistyczną energię kinetyczną, rozważmy cząstkę o masie spoczynkowej <math>m_0\ </math>,, będącą początkowo w spoczynku, przyspieszaną przez siłę o wartości F skierowaną wzdłuż osi x. Energia kinetyczna jest równa pracy wykonanej na drodze od <math>x=0\ </math>, do <math>x=x_k</math>, czyli całce z Fdx w granicach od zera do <math>x_k\ </math>,. Podstawiamy wzór na siłę F i otrzymujemy całkę, którą łatwo obliczyć przez części. | ||
|} | |} | ||
| Linia 256: | Linia 259: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M6_Slajd32.png|thumbs|500px|]] | |width="450px" valign="top"|[[Grafika:PF_M6_Slajd32.png|thumbs|500px|]] | ||
|valign="top"|Otrzymaliśmy słynny wzór Einsteina wyrażający równoważność masy i energii. Zwróćmy uwagę, że czynnik <math>c^2\ | |valign="top"|Otrzymaliśmy słynny wzór Einsteina wyrażający równoważność masy i energii. Zwróćmy uwagę, że czynnik <math>c^2\ </math>,, przez który mnożymy masę jest wielką liczbą – dlatego niewielki nawet ubytek masy spoczynkowej powoduje wyzwolenie ogromnej energii. Dzieje się tak na przykład podczas rozszczepienia ciężkich jąder w reaktorze atomowym lub, w sposób niekontrolowany, w bombie atomowej. Możliwy jest też proces odwrotny - zamiana energii na masę. Gdy zderzają się cząstki pędzące z prędkościami bliskimi prędkości światła, ich energia kinetyczna ulega zamianie na masę nowych cząstek rodzących się w zderzeniu. | ||
|} | |} | ||
| Linia 263: | Linia 266: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M6_Slajd33.png|thumbs|500px|]] | |width="450px" valign="top"|[[Grafika:PF_M6_Slajd33.png|thumbs|500px|]] | ||
|valign="top"|Dowodem słuszności związku wyrażającego równoważność masy i energii może być zdjęcie przedstawiające ponad 1000 cząstek wyprodukowanych w wyniku zderzenia dwóch jąder złota, których sumaryczna energia w układzie środka masy wynosiła 130 GeV (gigaelektronowoltów). Jądra przyspieszone były w specjalnym akceleratorze tzw. zderzaczu RHIC (Relativistic Heavy Ion Collider) w Brookhaven National Laboratory, w USA. Przed zderzeniem biegły w kierunku prostopadłym do płaszczyzny rysunku. | |valign="top"|Dowodem słuszności związku wyrażającego równoważność masy i energii może być zdjęcie przedstawiające tory ponad 1000 cząstek wyprodukowanych w wyniku zderzenia dwóch jąder złota, których sumaryczna energia w układzie środka masy wynosiła 130 GeV (gigaelektronowoltów). Jądra przyspieszone były w specjalnym akceleratorze tzw. zderzaczu RHIC (Relativistic Heavy Ion Collider) w Brookhaven National Laboratory, w USA. Przed zderzeniem biegły w kierunku prostopadłym do płaszczyzny rysunku. | ||
W momencie zderzenia energia kinetyczna jąder zamienia się w masy tysięcy cząstek powstałych w zderzeniu, zgodnie ze wzorem: <math>E=mc^2\ | W momencie zderzenia energia kinetyczna jąder zamienia się w masy tysięcy cząstek powstałych w zderzeniu, zgodnie ze wzorem: <math>E=mc^2\ </math>,. | ||
| Linia 294: | Linia 297: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M6_Slajd37.png|thumbs|500px|]] | |width="450px" valign="top"|[[Grafika:PF_M6_Slajd37.png|thumbs|500px|]] | ||
|valign="top"|Jeśli pęd wyrazimy przez współrzędne <math>p_x, p_y, p_z\ | |valign="top"|Jeśli pęd wyrazimy przez współrzędne <math>p_x, p_y, p_z\ </math>, otrzymamy wyrażenie, które oznacza stałość w różnych układach odniesienia długości czterowektora o składowych określonych przez energię i składowe pędu. Czterowektor ten nazywa się czterowektorem energii-pędu. | ||
|} | |} | ||
| Linia 303: | Linia 306: | ||
|valign="top"|'''Transformacja Lorentza pędu i energii''' | |valign="top"|'''Transformacja Lorentza pędu i energii''' | ||
Analogicznie do czterowektora czasoprzestrzennego konstruujemy czterowektor energii-pędu. Trzy współrzędne to składowe pędu <math>p_x, p_y, p_z\ | Analogicznie do czterowektora czasoprzestrzennego konstruujemy czterowektor energii-pędu. Trzy współrzędne to składowe pędu <math>p_x, p_y, p_z\ </math>, , a czwarta współrzędna to energia podzielona przez prędkość światła E/c. Zwróćmy uwagę, że zarówno pęd jak i energia nie są niezmiennikami transformacji Lorentza, to znaczy, nie są jednakowe w każdym inercjalnym układzie odniesienia. To samo ciało może spoczywać w jednym układzie, a w innym poruszać się z wielką prędkością. Oczywiście w pierwszym układzie pęd będzie równy zeru, a energia równa energii spoczynkowej, a w drugim pęd różny od zera a energia równa sumie energii spoczynkowej i kinetycznej. Natomiast długość czterowektora energii- pędu jest jednakowa we wszystkich układach inercjalnych. | ||
|} | |} | ||
| Linia 316: | Linia 319: | ||
---- | ---- | ||
= Podsumowanie = | |||
Wszystkie prawa relatywistyczne wynikają z dwóch postulatów Einsteina, które mówią, że | Wszystkie prawa relatywistyczne wynikają z dwóch postulatów Einsteina, które mówią, że | ||
po pierwsze prawa przyrody są takie same we wszystkich inercjalnych układach odniesienia, a po drugie, że prędkość światła w próżni jest jednakowa we wszystkich inercjalnych układach odniesienia i nie zależy od ruchu źródeł i odbiorników światła.Aby postulaty te były spełnione, trzeba transformację Galileusza zastąpić transformacją Lorentza. Jej konsekwencją jest dylatacja czasu, czyli spowolnienie wszelkich procesów w układzie poruszającym się względem obserwatora, a także kontrakcja długości, czyli skrócenie poruszającego się względem obserwatora pręta. Zdarzenia jednoczesne w jednym układzie nie muszą być jednoczesne w innym. | po pierwsze prawa przyrody są takie same we wszystkich inercjalnych układach odniesienia, a po drugie, że prędkość światła w próżni jest jednakowa we wszystkich inercjalnych układach odniesienia i nie zależy od ruchu źródeł i odbiorników światła.Aby postulaty te były spełnione, trzeba transformację Galileusza zastąpić transformacją Lorentza. Jej konsekwencją jest dylatacja czasu, czyli spowolnienie wszelkich procesów w układzie poruszającym się względem obserwatora, a także kontrakcja długości, czyli skrócenie poruszającego się względem obserwatora pręta. Zdarzenia jednoczesne w jednym układzie nie muszą być jednoczesne w innym. | ||
Jeśli pęd zdefiniujemy jako <math>\vec{p}=m\cdot \gamma \vec{v}</math> i energię jako <math>E=m\cdot \gamma \cdot c^2</math> ,gdzie <math>\gamma=\left(1-v^2/c^2 \right)^{-1/2}</math> to pęd i energia są zachowane we wszystkich układach inercjalnych, jeśli są zachowane w jakimkolwiek układzie. Ciało pozostające w spoczynku ma energię spoczynkową <math>E=m\cdot c^2\ | Jeśli pęd zdefiniujemy jako <math>\vec{p}=m\cdot \gamma \vec{v}</math> i energię jako <math>E=m\cdot \gamma \cdot c^2</math> ,gdzie <math>\gamma=\left(1-v^2/c^2 \right)^{-1/2}</math> to pęd i energia są zachowane we wszystkich układach inercjalnych, jeśli są zachowane w jakimkolwiek układzie. Ciało pozostające w spoczynku ma energię spoczynkową <math>E=m\cdot c^2\ </math>, i w pewnych procesach energia ta może być zamieniona na inne formy energii, na przykład na energię kinetyczną. Masa relatywistyczna ciała o prędkości v wyraża się wzorem: | ||
[[Grafika:PF_M6_Wzor3.png]] Prędkość światła jest graniczną prędkością: żadne ciało o różnej od zera masie spoczynkowej nie osiągnie tej prędkości. Związek między energią całkowitą, pędem i masą ma postać: <math>E^2=p^2c^2+(mc^2)^2</math> . | [[Grafika:PF_M6_Wzor3.png]] Prędkość światła jest graniczną prędkością: żadne ciało o różnej od zera masie spoczynkowej nie osiągnie tej prędkości. Związek między energią całkowitą E, pędem p i masą spoczynkową m ma postać: <math>E^2=p^2c^2+(mc^2)^2</math> . | ||
---- | ---- | ||
= Materiały do ćwiczeń = | |||
'''Zadanie 1''' | |||
Na spoczywającą cząstkę o masie <math>m_0\ </math>, zaczyna działać stała siła. Jaką prędkość uzyska cząstka, gdy siła wykona pracę W? Czy cząstka porusza się ruchem jednostajnie zmiennym? Jaki interesujący wniosek wynika z porównania rozwiązania klasycznego i relatywistycznego? | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
Energia kinetyczna cząstki jest równa pracy wykonanej przez siłę. | Energia kinetyczna cząstki jest równa pracy wykonanej przez siłę. | ||
| Linia 378: | Linia 350: | ||
:<math>mc^2-m_0 c^2=W</math> | :<math>mc^2-m_0 c^2=W</math> | ||
:[[Grafika:PF_M6_Wzor4.png]] <math>\Longrightarrow | :[[Grafika:PF_M6_Wzor4.png]] <math>\Longrightarrow</math> [[Grafika:PF_M6_Wzor5.png]] | ||
Z porównania rozwiązań wynika, że wzór relatywistyczny przechodzi we wzór klasyczny, gdy spełniony jest warunek <math>W<<m_0 c^2\ | Z porównania rozwiązań wynika, że wzór relatywistyczny przechodzi we wzór klasyczny, gdy spełniony jest warunek <math>W<<m_0 c^2\ </math>, , a zatem gdy praca wykonywana przez siłę przyspieszającą jest znacznie mniejsza od energii spoczynkowej przyspieszanej cząstki. Wynika stąd, że obok znanego kryterium stosowania mechaniki relatywistycznej, gdy prędkość ciała jest bliska prędkości światła w próżni c, można sformułować drugie kryterium, które mówi, że mechanikę relatywistyczną stosujemy wtedy, gdy energia dostarczona ciału jest, co najmniej bliska jego energii spoczynkowej. | ||
Odpowiedź: <math>v_{klas}=\sqrt{\frac{2W}{m_0}}</math> | Odpowiedź: <math>v_{klas}=\sqrt{\frac{2W}{m_0}}</math> | ||
:<math>v_{rel.}=\sqrt{\frac{2W}{m_0}}\cdot \frac{\sqrt{1+(W/2m_0c^2)}}{1+(W/m_0 c^2)}=v_{klas}\cdot \frac{\sqrt{1+(W/2m_0c^2)}}{1+(W/m_0 c^2)} </math> | :<math>v_{rel.}=\sqrt{\frac{2W}{m_0}}\cdot \frac{\sqrt{1+(W/2m_0c^2)}}{1+(W/m_0 c^2)}=v_{klas}\cdot \frac{\sqrt{1+(W/2m_0c^2)}}{1+(W/m_0 c^2)}</math> | ||
Mimo działania stałej siły cząstka porusza się ruchem zmiennym niejednostajnie. Przyspieszenie cząstki maleje, gdyż ze wzrostem prędkości rośnie masa cząstki. | Mimo działania stałej siły cząstka porusza się ruchem zmiennym niejednostajnie. Przyspieszenie cząstki maleje, gdyż ze wzrostem prędkości rośnie masa cząstki. | ||
| Linia 395: | Linia 367: | ||
Wskutek przebycia drogi, dla której różnica potencjałów wynosi U elektron uzyskuje energię kinetyczną równą pracy wykonanej przez pole elektryczne W = eU. Rozważmy dwa przypadki: | Wskutek przebycia drogi, dla której różnica potencjałów wynosi U elektron uzyskuje energię kinetyczną równą pracy wykonanej przez pole elektryczne W = eU. Rozważmy dwa przypadki: | ||
a) elektron przyspieszany w lampie kineskopowej w różnicy potencjałów <math>U_1 = 25 kV\ | a) elektron przyspieszany w lampie kineskopowej w różnicy potencjałów <math>U_1 = 25 kV\ </math>, uzyskuje energię | ||
: <math>W_1 =eU_1= 25 keV\ | : <math>W_1 =eU_1= 25 keV\ </math>, | ||
: zatem <math>\frac{W_1}{m_0 c^2} \approx 0,05</math> , <math>v_1=(v_{klas.})_1\cdot \frac{\sqrt{1+0,025}}{1+0,05}\approx (v_{klas.})_1\cdot 0,96</math> , gdzie <math>(v_{klas.})_1\approx 0,31c</math> | : zatem <math>\frac{W_1}{m_0 c^2} \approx 0,05</math> , <math>v_1=(v_{klas.})_1\cdot \frac{\sqrt{1+0,025}}{1+0,05}\approx (v_{klas.})_1\cdot 0,96</math> , gdzie <math>(v_{klas.})_1\approx 0,31c</math> | ||
| Linia 403: | Linia 375: | ||
czyli różnica między wartością prędkości końcowej obliczoną klasycznie i relatywistycznie jest niewielka | czyli różnica między wartością prędkości końcowej obliczoną klasycznie i relatywistycznie jest niewielka | ||
b) elektron przyspieszany w akceleratorze van de Graaffa w różnicy potencjałów <math>U_2 = 25 MV\ | b) elektron przyspieszany w akceleratorze van de Graaffa w różnicy potencjałów <math>U_2 = 25 MV\ </math>, uzyskuje energię | ||
: <math>W_1 =eU_2= 25 MeV\ | : <math>W_1 =eU_2= 25 MeV\ </math>, | ||
: zatem <math>\frac{W_1}{m_0 c^2} \approx 50</math> , <math>v_2=(v_{klas.})_2\cdot \frac{\sqrt{1+250}}{1+5}\approx (v_{klas.})_2\cdot 0,1</math> , gdzie <math>(v_{klas.})_2\approx 0,99c</math> | : zatem <math>\frac{W_1}{m_0 c^2} \approx 50</math> , <math>v_2=(v_{klas.})_2\cdot \frac{\sqrt{1+250}}{1+5}\approx (v_{klas.})_2\cdot 0,1</math> , gdzie <math>(v_{klas.})_2\approx 0,99c</math> | ||
W tym przypadku wartość prędkości końcowej obliczona ze wzoru klasycznego jest oczywiście nonsensowna. | W tym przypadku wartość prędkości końcowej obliczona ze wzoru klasycznego jest oczywiście nonsensowna. | ||
Odpowiedź: <math>T=2\pi \sqrt{\frac{m}{k_1+k_2}}</math> | |||
</div></div> | |||
---- | ---- | ||
| Linia 415: | Linia 391: | ||
'''Zadanie 2.''' | '''Zadanie 2.''' | ||
Cząstka o masie spoczynkowej <math>m_0\ | Cząstka o masie spoczynkowej <math>m_0\ </math>, porusza się z taką prędkością, że jej czas życia obserwowany w układzie laboratorium jest trzy razy dłuższy niż średni czas życia tej cząstki zmierzony wtedy, gdy cząstka jest w spoczynku. Oblicz energię kinetyczną tej cząstki i jej pęd. | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
[[Grafika:PF_M6_Wzor6.png]] podstawiamy [[Grafika:PF_M6_Wzor7.png]] , więc <math>t=\tau \gamma\ | [[Grafika:PF_M6_Wzor6.png]] podstawiamy [[Grafika:PF_M6_Wzor7.png]] , więc <math>t=\tau \gamma\ </math>, , <math>\gamma=3\ </math>, | ||
Energia kinetyczna: | Energia kinetyczna: | ||
| Linia 430: | Linia 407: | ||
<math>p=2\sqrt{2}m_0 c</math> | <math>p=2\sqrt{2}m_0 c</math> | ||
</div></div> | |||
---- | ---- | ||
| Linia 435: | Linia 414: | ||
'''Zadanie 3''' | '''Zadanie 3''' | ||
Jaka jest prędkość protonu, którego całkowita energia <math>E=100\cdot m_p c^2\ | Jaka jest prędkość protonu, którego całkowita energia <math>E=100\cdot m_p c^2\ </math>, ? <math>m_p\ </math>, – masa spoczynkowa protonu. | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | |||
:<math>v = 0,9999995c\ </math>, | |||
</div></div> | |||
---- | ---- | ||
| Linia 445: | Linia 429: | ||
Dwie cząstki lecą naprzeciwko siebie każda z prędkością 0,8c w układzie laboratorium. Jaka jest prędkość pierwszej cząstki obserwowana w układzie związanym z drugą cząstką? | Dwie cząstki lecą naprzeciwko siebie każda z prędkością 0,8c w układzie laboratorium. Jaka jest prędkość pierwszej cząstki obserwowana w układzie związanym z drugą cząstką? | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | |||
:<math>v_1' = 0,976c\ </math>, | |||
</div></div> | |||
---- | ---- | ||
| Linia 453: | Linia 442: | ||
Jeśli zdefiniujemy gęstość jako masę relatywistyczną podzieloną przez objętość, to ile razy wzrośnie gęstość ciała, gdy porusza się ono z prędkością v? | Jeśli zdefiniujemy gęstość jako masę relatywistyczną podzieloną przez objętość, to ile razy wzrośnie gęstość ciała, gdy porusza się ono z prędkością v? | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | |||
Gęstość wzrośnie n razy, gdzie: <math>n=\frac{1}{1-\frac{v^2}{c^2}}</math> | |||
</div></div> | |||
---- | |||
= Słowa kluczowe = | |||
: Inercjalny układ odniesienia | |||
: Prędkość światła | |||
: Postulaty Einsteina | |||
: Transformacja Galileusza | |||
: Transformacja Lorentza | |||
: Kontrakcja (skrócenie) długości | |||
: Dylatacja czasu | |||
: Czasoprzestrzeń | |||
: Interwał czasoprzestrzenny | |||
: Stożek świetlny | |||
: Linia świata | |||
: Czterowektor czasoprzestrzenny | |||
: Transformacja prędkości | |||
: Masa relatywistyczna | |||
: Pęd relatywistyczny | |||
: Energia całkowita | |||
: Energia spoczynkowa | |||
: Czterowektor energii-pędu | |||
---- | |||
= Bibliografia = | |||
#J. Orear, Fizyka, WNT, Warszawa (1998); | |||
#R. Resnick, D. Halliday, Fizyka 1, PWN, Warszawa (1994); | |||
#I.W. Sawieliew, Wykłady z fizyki, PWN, Warszawa (1994). | |||
---- | ---- | ||
Aktualna wersja na dzień 12:01, 5 wrz 2023
Wykład

|

|
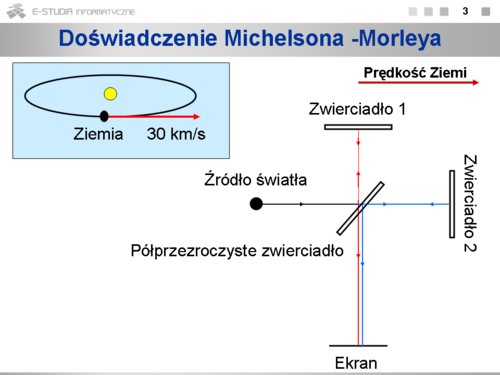
Wniosek: prędkość światła jest stała dla każdego obserwatora! |

|
Zdefiniujmy wielkość , zwaną czynnikiem Lorentza. Czynnik ten jest zawsze większy od jedności, bo jak niebawem się przekonamy . Wzory transformacji Lorentza mają prostszą postać. |
|
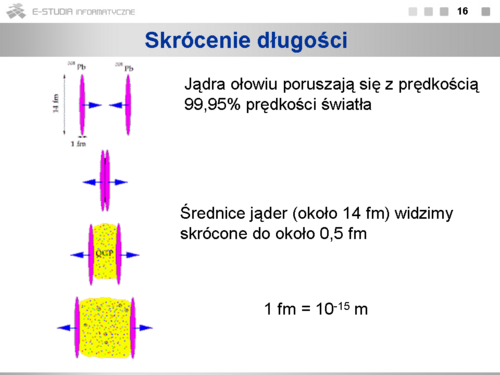
Poglądowa ilustracja zderzenia jąder ołowiu przyspieszonych do energii rzędu kilkudziesięciu tysięcy megaelektronowoltów. W wyniku skrócenia Lorentza kształt ich ze zbliżonego do kuli przekształcił się w formę dysków. Zauważmy bowiem, ze wymiary ciał skracają się tylko w kierunku ruchu. Środkowy obszar pokazany kolorem żółtym, to poszukiwany obecnie nowy stan materii zwany plazmą kwarkowo-gluonową. Zainteresowanych tymi zagadnieniami odsyłamy do strony internetowej Europejskiego Laboratorium Fizyki Cząstek CERN (http://www.cern.ch). |

|
Korzystając z transformacji Lorentza obliczamy różniczki dx, dy, dz i dt oraz dx’, dy’, dz’, i dt’. |

|
Podobnie możemy wyrazić składowe prędkości w układzie O’ przez składowe prędkości w układzie O. |

|
Podstawiamy wzór na pęd, a iloczyn prędkości i jej pochodnej vdv przedstawiamy jako pochodną kwadratu prędkości. |

|
Po scałkowaniu porządkujemy otrzymane wyrażenie. |
|
Związek energii, pędu i masy
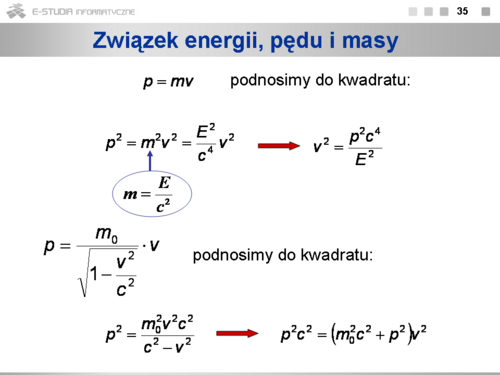
Aby znaleźć związek między pędem i energią, podnosimy stronami do kwadratu dwa równania wyrażające pęd oraz |

|
Czterowektor energii-pędu jest analogiczny do czterowektora czasoprzestrzennego. Dlatego transformacja Lorentza pędu i energii ma podobną postać do transformacji współrzędnych i czasu. |
Podsumowanie
Wszystkie prawa relatywistyczne wynikają z dwóch postulatów Einsteina, które mówią, że po pierwsze prawa przyrody są takie same we wszystkich inercjalnych układach odniesienia, a po drugie, że prędkość światła w próżni jest jednakowa we wszystkich inercjalnych układach odniesienia i nie zależy od ruchu źródeł i odbiorników światła.Aby postulaty te były spełnione, trzeba transformację Galileusza zastąpić transformacją Lorentza. Jej konsekwencją jest dylatacja czasu, czyli spowolnienie wszelkich procesów w układzie poruszającym się względem obserwatora, a także kontrakcja długości, czyli skrócenie poruszającego się względem obserwatora pręta. Zdarzenia jednoczesne w jednym układzie nie muszą być jednoczesne w innym.
Jeśli pęd zdefiniujemy jako i energię jako ,gdzie to pęd i energia są zachowane we wszystkich układach inercjalnych, jeśli są zachowane w jakimkolwiek układzie. Ciało pozostające w spoczynku ma energię spoczynkową , i w pewnych procesach energia ta może być zamieniona na inne formy energii, na przykład na energię kinetyczną. Masa relatywistyczna ciała o prędkości v wyraża się wzorem:
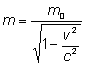 Prędkość światła jest graniczną prędkością: żadne ciało o różnej od zera masie spoczynkowej nie osiągnie tej prędkości. Związek między energią całkowitą E, pędem p i masą spoczynkową m ma postać: .
Prędkość światła jest graniczną prędkością: żadne ciało o różnej od zera masie spoczynkowej nie osiągnie tej prędkości. Związek między energią całkowitą E, pędem p i masą spoczynkową m ma postać: .
Materiały do ćwiczeń
Zadanie 1
Na spoczywającą cząstkę o masie , zaczyna działać stała siła. Jaką prędkość uzyska cząstka, gdy siła wykona pracę W? Czy cząstka porusza się ruchem jednostajnie zmiennym? Jaki interesujący wniosek wynika z porównania rozwiązania klasycznego i relatywistycznego?
Zadanie 2.
Cząstka o masie spoczynkowej , porusza się z taką prędkością, że jej czas życia obserwowany w układzie laboratorium jest trzy razy dłuższy niż średni czas życia tej cząstki zmierzony wtedy, gdy cząstka jest w spoczynku. Oblicz energię kinetyczną tej cząstki i jej pęd.
Zadanie 3
Jaka jest prędkość protonu, którego całkowita energia , ? , – masa spoczynkowa protonu.
Zadanie 4
Dwie cząstki lecą naprzeciwko siebie każda z prędkością 0,8c w układzie laboratorium. Jaka jest prędkość pierwszej cząstki obserwowana w układzie związanym z drugą cząstką?
Zadanie 5
Jeśli zdefiniujemy gęstość jako masę relatywistyczną podzieloną przez objętość, to ile razy wzrośnie gęstość ciała, gdy porusza się ono z prędkością v?
Słowa kluczowe
- Inercjalny układ odniesienia
- Prędkość światła
- Postulaty Einsteina
- Transformacja Galileusza
- Transformacja Lorentza
- Kontrakcja (skrócenie) długości
- Dylatacja czasu
- Czasoprzestrzeń
- Interwał czasoprzestrzenny
- Stożek świetlny
- Linia świata
- Czterowektor czasoprzestrzenny
- Transformacja prędkości
- Masa relatywistyczna
- Pęd relatywistyczny
- Energia całkowita
- Energia spoczynkowa
- Czterowektor energii-pędu
Bibliografia
- J. Orear, Fizyka, WNT, Warszawa (1998);
- R. Resnick, D. Halliday, Fizyka 1, PWN, Warszawa (1994);
- I.W. Sawieliew, Wykłady z fizyki, PWN, Warszawa (1994).