PF Moduł 5: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „,...,” na „,\ldots,” |
||
| (Nie pokazano 15 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
__TOC__ | |||
= Wykład = | |||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd1.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd1.png]] | ||
| Linia 26: | Linia 29: | ||
|valign="top"|'''5.1. Równanie ruchu harmonicznego''' | |valign="top"|'''5.1. Równanie ruchu harmonicznego''' | ||
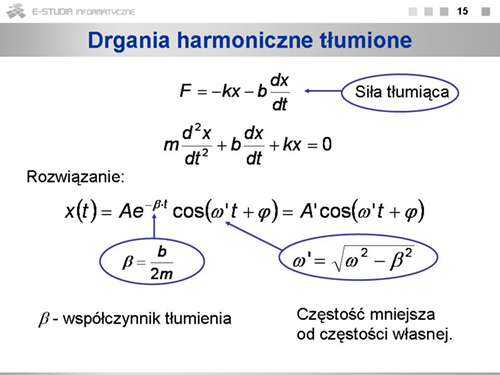
Ruch punktu materialnego nazywamy harmonicznym, jeśli porusza się on pod wpływem siły <math>F\ | Ruch punktu materialnego nazywamy harmonicznym, jeśli porusza się on pod wpływem siły <math>F\ </math>, o wartości wprost proporcjonalnej do wychylenia z położenia równowagi <math>x\ </math>, i skierowanej przeciwnie do wychylenia. O zwrocie siły mówi znak minus we wzorze <math>F = -kx</math>, gdzie <math>k\ </math>, jest współczynnikiem proporcjonalności. | ||
|} | |} | ||
| Linia 42: | Linia 45: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd5.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd5.png]] | ||
|valign="top"|Sprawdźmy, czy nasze równanie będzie spełnione przez funkcję <math>x(t)=A cos(\omega \cdot t +\varphi)</math> , gdzie <math>A\ | |valign="top"|Sprawdźmy, czy nasze równanie będzie spełnione przez funkcję <math>x(t)=A cos(\omega \cdot t +\varphi)</math> , gdzie <math>A\ </math>,, <math>\omega\ </math>, i <math>\varphi\ </math>, są dowolnymi parametrami. Obliczamy pierwszą i drugą pochodną wychylenia <math>x\ </math>, po czasie <math>t\ </math>, i podstawiamy do równania. | ||
|} | |} | ||
| Linia 50: | Linia 53: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd6.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd6.png]] | ||
|valign="top"|Funkcja <math>x(t)=A cos(\omega \cdot t +\varphi)</math> spełnia równanie ruchu pod warunkiem, że stała <math>\omega\ | |valign="top"|Funkcja <math>x(t)=A cos(\omega \cdot t +\varphi)</math> spełnia równanie ruchu pod warunkiem, że stała <math>\omega\ </math>, spełnia związek: <math>\omega^2=k/m</math>. Stałą <math>\omega\ </math>, nazywamy częstością drgań własnych. Argument funkcji ''cosinus'' <math>(\omega \cdot t +\varphi)\ </math>, to faza ruchu, <math>\varphi\ </math>, stanowi fazę początkową w chwili <math>t=0</math>. Największe wychylenie z położenia równowagi nazywamy amplitudą drgań. Wynosi ona <math>A\ </math>,, bowiem największa i najmniejsza wartość funkcji ''cosinus'' to 1 i -1. | ||
|} | |} | ||
| Linia 68: | Linia 71: | ||
|valign="top"|Odwrotność okresu, czyli liczbę drgań w jednostce czasu nazywamy częstotliwością. Jednostką częstotliwości jest hertz <math>(1Hz=1s^{-1})</math>. | |valign="top"|Odwrotność okresu, czyli liczbę drgań w jednostce czasu nazywamy częstotliwością. Jednostką częstotliwości jest hertz <math>(1Hz=1s^{-1})</math>. | ||
Jeśli czas będziemy mierzyć od takiego momentu, że faza początkowa <math>\varphi=-\pi/2\ | Jeśli czas będziemy mierzyć od takiego momentu, że faza początkowa <math>\varphi=-\pi/2\ </math>, , to ruch harmoniczny będzie opisany funkcją sinus. Jak widać wybór funkcji sinus czy cosinus jest w istocie wyborem fazy początkowej. | ||
|} | |} | ||
| Linia 77: | Linia 80: | ||
|valign="top"|'''Prędkość i przyspieszenie''' | |valign="top"|'''Prędkość i przyspieszenie''' | ||
Prędkość i przyspieszenie w ruchu harmonicznym obliczamy jako pierwszą i drugą pochodną wychylenia <math>x\ | Prędkość i przyspieszenie w ruchu harmonicznym obliczamy jako pierwszą i drugą pochodną wychylenia <math>x\ </math>, po czasie. | ||
|} | |} | ||
| Linia 93: | Linia 96: | ||
|valign="top"|'''Energia w ruchu harmonicznym''' | |valign="top"|'''Energia w ruchu harmonicznym''' | ||
Ciało wychylone z położenia równowagi, na które działa siła harmoniczna, ma pewną energię potencjalną. Energię tę można wyznaczyć, obliczając pracę jaką musimy wykonać, aby przesunąć ciało z położenia równowagi, <math>x=0\ | Ciało wychylone z położenia równowagi, na które działa siła harmoniczna, ma pewną energię potencjalną. Energię tę można wyznaczyć, obliczając pracę jaką musimy wykonać, aby przesunąć ciało z położenia równowagi, <math>x=0\ </math>,, do punktu o danym <math>x\ </math>,. | ||
Zmiana energii potencjalnej <math>dE_p\ | Zmiana energii potencjalnej <math>dE_p\ </math>, równa jest pracy, jaką wykonuje siła równoważąca siłę harmoniczną na drodze <math>dx\ </math>,. Po obliczeniu całki w granicach od zera do <math>x\ </math>,, otrzymujemy wzór na energię potencjalną ciała wychylonego z położenia równowagi o <math>x\ </math>,: <math>E_p(x)=kx^2/2</math> . | ||
|} | |} | ||
| Linia 117: | Linia 120: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd14.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd14.png]] | ||
|valign="top"|Pierwszy rysunek przedstawia zależność od położenia energii kinetycznej i potencjalnej oraz będącej ich sumą energii całkowitej. Widać, że energia kinetyczna jest największa w położeniu równowagi <math>(x=0)</math>, a energia potencjalna jest równa wtedy zeru. Gdy ciało jest maksymalnie wychylone <math>(x=\pm A)\ | |valign="top"|Pierwszy rysunek przedstawia zależność od położenia energii kinetycznej i potencjalnej oraz będącej ich sumą energii całkowitej. Widać, że energia kinetyczna jest największa w położeniu równowagi <math>(x=0)</math>, a energia potencjalna jest równa wtedy zeru. Gdy ciało jest maksymalnie wychylone <math>(x=\pm A)\ </math>,, energia kinetyczna jest równa zeru, a potencjalna maksymalna. | ||
Drugi rysunek pokazuje, jak zależy od czasu energia kinetyczna i potencjalna. Dla porównania przedstawiono również zależność od czasu położenia i prędkości. Zwróćmy uwagę, że zarówno energia kinetyczna, jak i potencjalna przyjmują tylko dodatnie wartości, a okres ich zmian jest dwa razy mniejszy niż okres zmian położenia i prędkości. | Drugi rysunek pokazuje, jak zależy od czasu energia kinetyczna i potencjalna. Dla porównania przedstawiono również zależność od czasu położenia i prędkości. Zwróćmy uwagę, że zarówno energia kinetyczna, jak i potencjalna przyjmują tylko dodatnie wartości, a okres ich zmian jest dwa razy mniejszy niż okres zmian położenia i prędkości. | ||
| Linia 162: | Linia 165: | ||
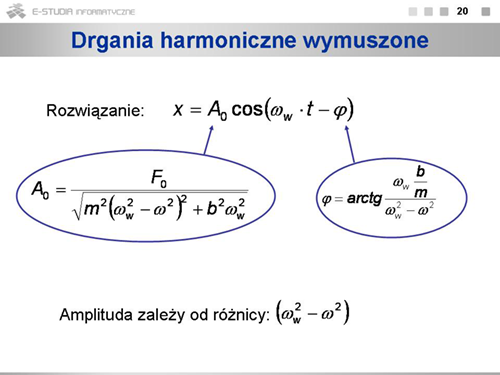
|valign="top"|'''Drgania harmoniczne wymuszone''' | |valign="top"|'''Drgania harmoniczne wymuszone''' | ||
Dobrze wiemy, że aby długo huśtać się na huśtawce tak, jak dama na tym pięknym obrazie, potrzebny jest ktoś, kto będzie huśtawkę popychał w odpowiednich momentach. W ogólności siłę podtrzymującą drganie, zwaną też siłą wymuszającą, przedstawiamy jako siłę zależną sinusoidalnie od czasu. Na przykład może ona mieć postać: <math>F_w=F_0(cos_w \cdot t)</math> . Równanie ruchu uwzględnia zarówno siłę wymuszającą, jak i tłumiącą drgania. Zwróćmy uwagę, że częstość siły wymuszającej <math>\omega_w\ | Dobrze wiemy, że aby długo huśtać się na huśtawce tak, jak dama na tym pięknym obrazie, potrzebny jest ktoś, kto będzie huśtawkę popychał w odpowiednich momentach. W ogólności siłę podtrzymującą drganie, zwaną też siłą wymuszającą, przedstawiamy jako siłę zależną sinusoidalnie od czasu. Na przykład może ona mieć postać: <math>F_w=F_0(cos_w \cdot t)</math> . Równanie ruchu uwzględnia zarówno siłę wymuszającą, jak i tłumiącą drgania. Zwróćmy uwagę, że częstość siły wymuszającej <math>\omega_w\ </math>, jest w ogólnym przypadku inna niż częstość drgań własnych <math>\omega\ </math>, . | ||
|} | |} | ||
| Linia 187: | Linia 190: | ||
Dla wartości współczynników tłumienia różnych od zera amplituda osiąga największą wartość (czyli występuje rezonans) dla częstości określonych wzorem: <math>\omega_w=\sqrt{\omega^2-b^2 /2m^2}</math> , a więc mniejszych od częstości drgań własnych. | Dla wartości współczynników tłumienia różnych od zera amplituda osiąga największą wartość (czyli występuje rezonans) dla częstości określonych wzorem: <math>\omega_w=\sqrt{\omega^2-b^2 /2m^2}</math> , a więc mniejszych od częstości drgań własnych. | ||
Rysunek przedstawia kilka krzywych rezonansowych, czyli zależności amplitudy drgań od częstości siły wymuszającej dla kilku wartości współczynników tłumienia <math>\beta\ | Rysunek przedstawia kilka krzywych rezonansowych, czyli zależności amplitudy drgań od częstości siły wymuszającej dla kilku wartości współczynników tłumienia <math>\beta\ </math>, . Widać, że im większy współczynnik tłumienia, tym niższą wartość osiąga amplituda i tym bardziej częstość rezonansowa różni się od częstości drgań własnych, która tu wynosi <math>1s^{-1}\ </math>, . | ||
|} | |} | ||
| Linia 196: | Linia 199: | ||
|valign="top"|'''Składanie drgań równoległych''' | |valign="top"|'''Składanie drgań równoległych''' | ||
Jaki będzie wynik nałożenia się dwóch drgań harmonicznych o kierunkach równoległych, ale różnych częstościach, amplitudach i fazach? Wychylenie wypadkowe będzie sumą obu wychyleń. Intuicyjnie przewidujemy, że w chwili, gdy oba wychylenia są w tym samym kierunku - otrzymamy wzmocnienie, kiedy w przeciwnym - osłabienie sumarycznego wychylenia, <math>x\ | Jaki będzie wynik nałożenia się dwóch drgań harmonicznych o kierunkach równoległych, ale różnych częstościach, amplitudach i fazach? Wychylenie wypadkowe będzie sumą obu wychyleń. Intuicyjnie przewidujemy, że w chwili, gdy oba wychylenia są w tym samym kierunku - otrzymamy wzmocnienie, kiedy w przeciwnym - osłabienie sumarycznego wychylenia, <math>x\ </math>,. | ||
Szczególnie ciekawy jest przypadek, kiedy obie częstości mają zbliżone wartości. Dla uproszczenia przyjmiemy, że amplitudy i fazy są takie same, a różnica ich częstości <math>\Delta \omega\ | Szczególnie ciekawy jest przypadek, kiedy obie częstości mają zbliżone wartości. Dla uproszczenia przyjmiemy, że amplitudy i fazy są takie same, a różnica ich częstości <math>\Delta \omega\ </math>, jest niewielka. Po wykonaniu przekształceń trygonometrycznych otrzymujemy wzór przestawiający drganie harmoniczne, ale z amplitudą, która zmienia się periodycznie z częstością znacznie mniejszą od <math>\omega\ </math>, . Zjawisko to nazywamy dudnieniem. | ||
|} | |} | ||
| Linia 205: | Linia 208: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd23.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd23.png]] | ||
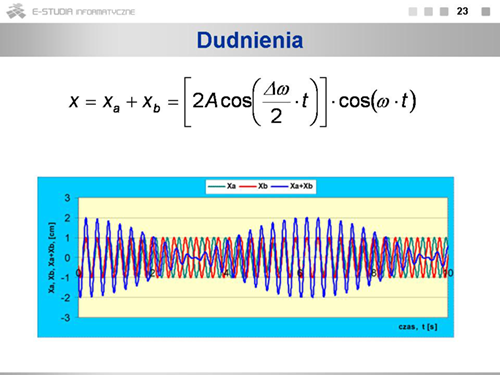
|valign="top"|Wykres przedstawia zależność wychyleń drgań składowych <math>x_a\ | |valign="top"|Wykres przedstawia zależność wychyleń drgań składowych <math>x_a\ </math>, i <math>x_b\ </math>, oraz ich sumy <math>x_a+x_b</math> . | ||
Amplitudy drgań składowych są jednakowe i mają wartość 1 cm, natomiast amplituda drgań wypadkowych wolno oscyluje od zera do wartości 2 cm. | Amplitudy drgań składowych są jednakowe i mają wartość 1 cm, natomiast amplituda drgań wypadkowych wolno oscyluje od zera do wartości 2 cm. | ||
| Linia 216: | Linia 219: | ||
|valign="top"|'''Składanie drgań prostopadłych''' | |valign="top"|'''Składanie drgań prostopadłych''' | ||
Kiedy drgania punktu materialnego odbywają się równocześnie w dwóch prostopadłych do siebie kierunkach, na przykład wzdłuż osi <math>x\ | Kiedy drgania punktu materialnego odbywają się równocześnie w dwóch prostopadłych do siebie kierunkach, na przykład wzdłuż osi <math>x\ </math>, i <math>y\ </math>, prostokątnego układu współrzędnych, to wypadkowy ruch tego punktu na płaszczyźnie można opisać z pomocą równań: <math>x=A_x cos(\omega_x t)</math> oraz <math>y=A_y cos(\omega_y t+\varphi)</math> . Jeśli częstości drgań są jednakowe i różnica faz wynosi zero, to ruch wypadkowy będzie odbywał się wzdłuż prostej o równaniu <math>y=(A_y/A_x)\cdot x</math> . Będzie to również drgania harmoniczne. | ||
|} | |} | ||
| Linia 224: | Linia 227: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd25.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd25.png]] | ||
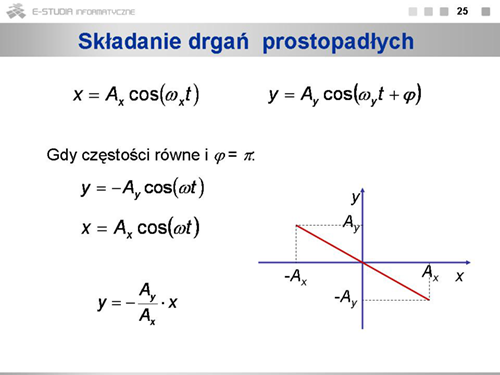
|valign="top"|Jeśli częstości drgań są jednakowe i różnica faz wynosi <math>\pi\ | |valign="top"|Jeśli częstości drgań są jednakowe i różnica faz wynosi <math>\pi\ </math>, , to ruch będzie ruchem harmonicznym wzdłuż prostej o równaniu <math>y=-(A_y/A_x)\cdot x</math> . | ||
|} | |} | ||
| Linia 232: | Linia 235: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd26.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd26.png]] | ||
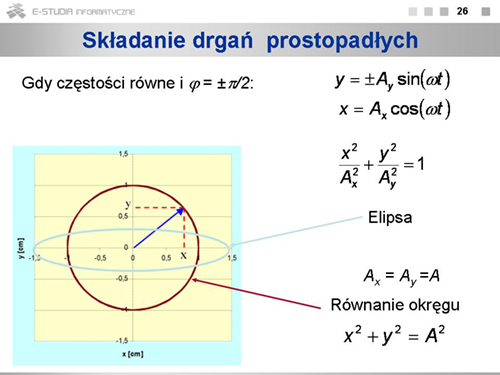
|valign="top"|Ciekawa jest sytuacja, gdy częstości są równe, a fazy różnią się o <math>\pi/2\ | |valign="top"|Ciekawa jest sytuacja, gdy częstości są równe, a fazy różnią się o <math>\pi/2\ </math>, . Podnosząc do kwadratu wyrażenia na <math>x\ </math>, i <math>y\ </math>, i dodając równania stronami, otrzymujemy równanie elipsy. Po takim właśnie torze porusza się punkt. W przypadku, gdy amplitudy są równe, elipsa przechodzi w okrąg. | ||
Widzimy, że jeśli punkt materialny porusza się ruchem jednostajnym po okręgu w płaszczyźnie <math>(x, y)\ | Widzimy, że jeśli punkt materialny porusza się ruchem jednostajnym po okręgu w płaszczyźnie <math>(x, y)\ </math>,, to ruch jego rzutu na osie układu współrzędnych jest ruchem harmonicznym. | ||
To interesujące stwierdzenie łączy ruch harmoniczny z ruchem jednostajnym po okręgu. | To interesujące stwierdzenie łączy ruch harmoniczny z ruchem jednostajnym po okręgu. | ||
| Linia 244: | Linia 247: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd27.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd27.png]] | ||
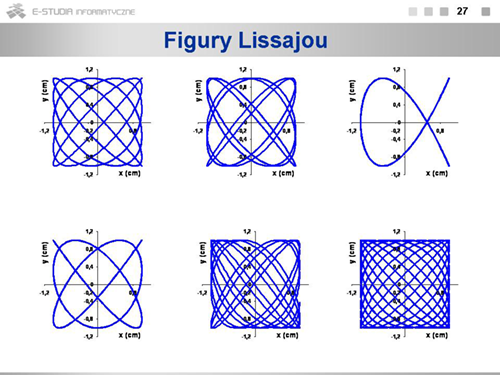
|valign="top"|Podana wyżej relacja pomiędzy ruchem harmonicznym i ruchem po okręgu jest jednak tylko przypadkiem szczególnym składania harmonicznych drgań prostopadłych. Kiedy częstości drgań w obu kierunkach różnią się, to tor punktu tworzy skomplikowane figury zwane figurami Lissajou. Figury te mieszczą się w prostokącie o wymiarach <math>2A_x\ | |valign="top"|Podana wyżej relacja pomiędzy ruchem harmonicznym i ruchem po okręgu jest jednak tylko przypadkiem szczególnym składania harmonicznych drgań prostopadłych. Kiedy częstości drgań w obu kierunkach różnią się, to tor punktu tworzy skomplikowane figury zwane figurami Lissajou. Figury te mieszczą się w prostokącie o wymiarach <math>2A_x\ </math>,, i <math>2A_y\ </math>,. | ||
Stosunek liczby punktów stycznych do obu boków prostokąta wyznacza stosunek częstości obu ruchów składowych: <math>\omega_x/{\omega_y}\ | Stosunek liczby punktów stycznych do obu boków prostokąta wyznacza stosunek częstości obu ruchów składowych: <math>\omega_x/{\omega_y}\ </math>, Rysunek pokazuje przykłady takich figur. | ||
|} | |} | ||
| Linia 256: | Linia 259: | ||
|valign="top"|'''Rozchodzenie się fal w ośrodku sprężystym''' | |valign="top"|'''Rozchodzenie się fal w ośrodku sprężystym''' | ||
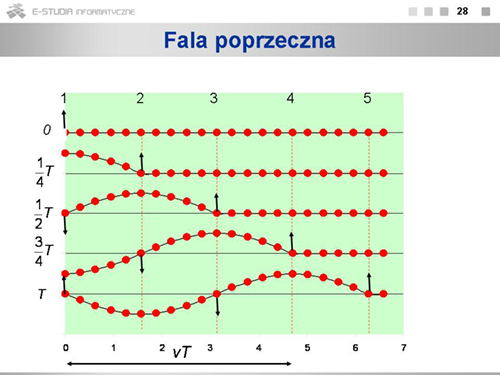
Jeśli jakimś miejscu ośrodka sprężystego wywołamy drganie, to drgająca cząstka pociągnie za sobą kolejne cząstki i ruch drgający będzie się przenosić od cząstki do cząstki z pewną prędkością <math>v\ | Jeśli jakimś miejscu ośrodka sprężystego wywołamy drganie, to drgająca cząstka pociągnie za sobą kolejne cząstki i ruch drgający będzie się przenosić od cząstki do cząstki z pewną prędkością <math>v\ </math>,. Takie rozchodzenie się drgań w ośrodku nazywamy falą. Należy podkreślić, że poszczególne cząstki ośrodka nie przemieszczają się, wykonują tylko drgania wokół swoich położeń równowagi. Jeśli drgania zachodzą w kierunku prostopadłym do kierunku rozchodzenia się fali, falę nazywamy falą poprzeczną. | ||
Rysunek pokazuje ruch cząsteczek podczas rozchodzenia się fali poprzecznej. Numerami <math>1, 2, | Rysunek pokazuje ruch cząsteczek podczas rozchodzenia się fali poprzecznej. Numerami <math>1, 2, \dots</math> oznaczone są cząstki odległe od siebie o <math>\frac{1}{4} vT\ </math>,, czyli odległość, jaką fala przebywa w czasie <math>\frac{1}{4}\ </math>, okresu drgań. W chwili <math>t=0\ </math>, fala biegnąca w prawo dochodzi do cząstki <math>1</math>,. Cząstka ta rozpoczyna ruch ku górze, pociągając za sobą kolejne cząstki. Po upływie <math>\frac{1}{4}\ </math>, okresu cząstka 1 osiąga maksymalne wychylenie, a ruch ku górze rozpoczyna cząstka <math>2</math>,. Po następnej ćwiartce okresu cząstka 1 wraca do położenia równowagi i rozpoczyna ruch w dół, cząstka <math>2</math>, osiąga maksymalne wychylenie, a cząstka <math>3</math>, zaczyna przemieszczać się do góry. Po upływie pełnego okresu w chwili <math>t=T\ </math>, pierwsza cząstka wraca do stanu, w jakim była w chwili <math>t=0\ </math>,, a fala, przebywając drogę <math>vT\ </math>,, dociera do cząstki <math>5</math>.. | ||
|} | |} | ||
| Linia 268: | Linia 271: | ||
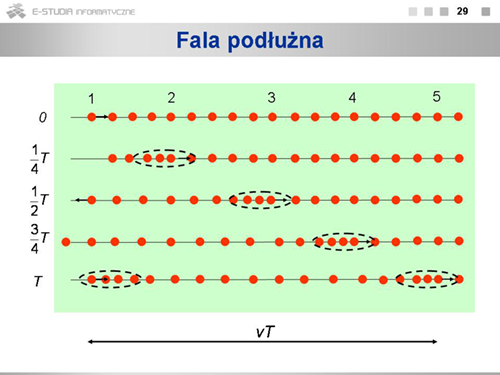
|valign="top"|Falą podłużną nazywamy falę, której kierunek rozchodzenia się jest równoległy do kierunku drgań cząstek. | |valign="top"|Falą podłużną nazywamy falę, której kierunek rozchodzenia się jest równoległy do kierunku drgań cząstek. | ||
Rysunek pokazuje ruch cząstek podczas rozchodzenia się w ośrodku fali podłużnej. Widać, że rozchodzenie się fali podłużnej związane jest z powstawaniem w ośrodku postępujących po sobie zagęszczeń i rozrzedzeń cząstek. Zagęszczenia i rozrzedzenia przesuwają się w ośrodku z prędkością <math>v\ | Rysunek pokazuje ruch cząstek podczas rozchodzenia się w ośrodku fali podłużnej. Widać, że rozchodzenie się fali podłużnej związane jest z powstawaniem w ośrodku postępujących po sobie zagęszczeń i rozrzedzeń cząstek. Zagęszczenia i rozrzedzenia przesuwają się w ośrodku z prędkością <math>v\ </math>,. | ||
|} | |} | ||
| Linia 276: | Linia 279: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd30.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd30.png]] | ||
|valign="top"|Podczas rozchodzenia się fali w drganiach biorą udział nie tylko cząstki leżące na osi <math>x\ | |valign="top"|Podczas rozchodzenia się fali w drganiach biorą udział nie tylko cząstki leżące na osi <math>x\ </math>,, jak na poprzednich rysunkach, lecz układ cząstek znajdujących się w pewnej objętości. Zbiór punktów, do których fala dochodzi w danej chwili nazywamy czołem fali. Zbiór punktów drgających w tej samej fazie nazywamy powierzchnią falową. Przez każdy punkt biorący udział w ruchu falowym można przeprowadzić powierzchnię falową. Powierzchni falowych jest więc nieskończenie wiele, ale czoło fali jest tylko jedno. Spośród wszystkich możliwych kształtów powierzchni falowych wyróżniamy takie, które są płaszczyznami i powierzchniami kulistymi. Fale takie nazywamy odpowiednio falą płaską i falą kulistą. | ||
|} | |} | ||
| Linia 284: | Linia 287: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd31.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd31.png]] | ||
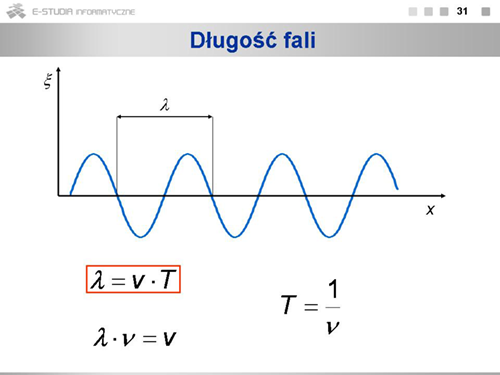
|valign="top"|Rysunek przedstawia wychylenia cząstek z położenia równowagi <math>\xi(x)\ | |valign="top"|Rysunek przedstawia wychylenia cząstek z położenia równowagi <math>\xi(x)\ </math>, dla cząstek o różnych wartościach <math>x\ </math>,. Zauważmy, że wykres ten może dotyczyć zarówno fali poprzecznej, jak i podłużnej. Długością fali nazywamy odległość, na jaką rozchodzi się fala w czasie równym okresowi drgań ośrodka. Można też powiedzieć, że długość fali to najmniejsza odległość między cząstkami drgającymi w jednakowej fazie. Długość fali związana jest okresem drgań prostym wzorem: <math>\lambda=v\cdot T\ </math>, . | ||
|} | |} | ||
| Linia 292: | Linia 295: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd32.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd32.png]] | ||
|valign="top"|Równaniem fali nazywamy zależność wychylenia <math>\xi\ | |valign="top"|Równaniem fali nazywamy zależność wychylenia <math>\xi\ </math>, drgającej cząstki od czasu <math>t\ </math>, i od współrzędnych tej cząstki <math>(x, y, z)\ </math>,: <math>\xi=\xi(x, y, z, t)\ </math>, . Określimy to wyrażenie dla fali płaskiej biegnącej w kierunku osi <math>x\ </math>,. Powierzchnie falowe są płaszczyznami prostopadłymi do osi <math>x\ </math>,, więc wychylenie zależy tylko od <math>x\ </math>, i <math>t\ </math>,: <math>\xi=\xi(x, t)\ </math>, . Drgania punktów leżących w płaszczyźnie <math>x=0\ </math>, można opisać wzorem: <math>\xi(0, t)=a cos(\omega t +\varphi)\ </math>, . Jak będą drgały punkty w płaszczyźnie odpowiadającej dowolnej wartości <math>x\ </math>,? Drogę <math>x\ </math>, fala przebędzie w czasie <math>\tau=x/v</math> . O taki czas będą opóźnione drgania w punkcie <math>x\ </math>, w stosunku do <math>x=0\ </math>,: | ||
<math>\xi(x, t)=a cos[\omega (t-\tau) +\varphi]=a cos \left[\omega\left(t-\frac{x}{v} \right) | <math>\xi(x, t)=a cos[\omega (t-\tau) +\varphi]=a cos \left[\omega\left(t-\frac{x}{v} \right) +\varphi \right]</math> | ||
|} | |} | ||
| Linia 302: | Linia 305: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd33.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd33.png]] | ||
|valign="top"|Argument funkcji cosinus nazywamy fazą. Z jaką prędkością przesuwa się dana wartość fazy? Wyrażenie: <math>\omega\left(t-\frac{x}{v} \right) +\varphi=const</math> wiąże wartości <math>x\ | |valign="top"|Argument funkcji cosinus nazywamy fazą. Z jaką prędkością przesuwa się dana wartość fazy? Wyrażenie: <math>\omega\left(t-\frac{x}{v} \right) +\varphi=const</math> wiąże wartości <math>x\ </math>, i <math>t\ </math>,, dla których faza ma daną wartość. Po zróżniczkowaniu tego wyrażenia otrzymujemy: <math>v=\frac{dx}{dt}</math> . Prędkość v nazywamy prędkością fazową, bo jest to prędkość przemieszczania się fazy. | ||
|} | |} | ||
| Linia 310: | Linia 313: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd34.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd34.png]] | ||
|valign="top"|Równanie fali jest funkcją periodyczną zarówno ze względu na czas <math>t\ | |valign="top"|Równanie fali jest funkcją periodyczną zarówno ze względu na czas <math>t\ </math>,, jak i na współrzędną przestrzenną <math>x\ </math>,. Symetria funkcji względem <math>x\ </math>, i <math>t\ </math>, będzie lepiej widoczna, jeśli wprowadzimy wielkość <math>k\ </math>,, zwaną liczbą falową: <math>k=\frac{2\pi}{\lambda}</math> . Zauważmy, że związek liczby falowej z długością fali jest podobny do związku częstości kołowej i okresu: <math>\omega=2\pi/T</math> . Otrzymujemy równanie fali płaskiej: <math>\xi(x, t)=a cos [\omega t -kx+\varphi]</math> | ||
|} | |} | ||
| Linia 318: | Linia 321: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd35.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd35.png]] | ||
|valign="top"|Oczywiście równanie fali płaskiej rozchodzącej się w kierunku malejących wartości <math>x\ | |valign="top"|Oczywiście równanie fali płaskiej rozchodzącej się w kierunku malejących wartości <math>x\ </math>,, otrzymamy zmieniając znak przy <math>x\ </math>,. W przypadku, gdy ośrodek pochłania energię fali, amplituda drgań maleje wykładniczo: <math>a=a_0 e^{-\beta x}</math> . Drgania w miarę wzrostu <math>x\ </math>, odbywają się z coraz mniejszą amplitudą, aż fala praktycznie zaniknie. | ||
|} | |} | ||
| Linia 326: | Linia 329: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd36.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd36.png]] | ||
|valign="top"|Jeśli fala rozchodzi się w ośrodku jednorodnym i izotropowym, a źródło fali jest punktowe, to rozchodząca się fala jest falą kulistą. Równanie fali kulistej jest podobne do równania fali płaskiej – musimy współrzędną <math>x\ | |valign="top"|Jeśli fala rozchodzi się w ośrodku jednorodnym i izotropowym, a źródło fali jest punktowe, to rozchodząca się fala jest falą kulistą. Równanie fali kulistej jest podobne do równania fali płaskiej – musimy współrzędną <math>x\ </math>, zastąpić odległością od źródła fali <math>r\ </math>,. Jest jednak pewna różnica. Amplituda fali kulistej, nawet w przypadku braku tłumienia, maleje wraz z odległością <math>r\ </math>, i wynosi <math>a/r\ </math>, , gdzie <math>a\ </math>, to amplituda drgań źródła fali. Jest to związane z faktem, że powierzchnie falowe fali kulistej są coraz większe w miarę rozchodzenia się fali. Energia drgającego punktu, źródła fali, musi być rozłożona na coraz więcej drgających punktów na powierzchniach falowych, a więc amplitudy drgań muszą maleć z <math>r\ </math>,. | ||
|} | |} | ||
| Linia 336: | Linia 339: | ||
|valign="top"|'''Równanie falowe''' | |valign="top"|'''Równanie falowe''' | ||
Równanie ruchu harmonicznego <math>x(t)=A cos(\omega t+\varphi)</math> otrzymaliśmy rozwiązując równanie różniczkowe wyrażające II zasadę dynamiki: <math>\frac{d^2 x}{dt^2}=-\frac{k}{m}x</math> . Jaka jest postać równania, którego rozwiązaniem jest równanie fali płaskiej? Domyślamy się, że powinno to być również równanie różniczkowe drugiego rzędu, symetryczne względem <math>x\ | Równanie ruchu harmonicznego <math>x(t)=A cos(\omega t+\varphi)</math> otrzymaliśmy rozwiązując równanie różniczkowe wyrażające II zasadę dynamiki: <math>\frac{d^2 x}{dt^2}=-\frac{k}{m}x</math> . Jaka jest postać równania, którego rozwiązaniem jest równanie fali płaskiej? Domyślamy się, że powinno to być również równanie różniczkowe drugiego rzędu, symetryczne względem <math>x\ </math>, i <math>t\ </math>,. | ||
|} | |} | ||
| Linia 344: | Linia 347: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd38.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd38.png]] | ||
|valign="top"|Aby znaleźć równanie falowe, obliczmy drugie pochodne cząstkowe po współrzędnej <math>x\ | |valign="top"|Aby znaleźć równanie falowe, obliczmy drugie pochodne cząstkowe po współrzędnej <math>x\ </math>, i po czasie <math>t\ </math>,. Dzieląc otrzymane wyrażenia odpowiednio przez <math>-\omega^2\ </math>, i <math>-k^2\ </math>, , otrzymujemy po prawej stronie identyczną wielkość <math>\xi\ </math>, . Wobec tego możemy przyrównać lewe strony do siebie i otrzymujemy poszukiwane równanie falowe. | ||
|} | |} | ||
| Linia 362: | Linia 365: | ||
|valign="top"|Jeśli w ośrodku rozchodzi się kilka fal, to zgodnie z zasadą superpozycji (nakładania się) fal drganie każdego punktu jest sumą drgań pochodzących od każdej z fal. | |valign="top"|Jeśli w ośrodku rozchodzi się kilka fal, to zgodnie z zasadą superpozycji (nakładania się) fal drganie każdego punktu jest sumą drgań pochodzących od każdej z fal. | ||
Szczególnym przypadkiem jest nakładanie się fali biegnącej i fali odbitej od jakiejś przeszkody. Powstaje wtedy fala stojąca. Niech <math>\xi_1=a cos (\omega t -kx)</math> oznacza falę biegnącą w prawo, a <math>\xi_1=a cos (\omega t +kx)</math> falę odbitą rozchodzącą się w lewo. Wybraliśmy tu taką chwilę początkową <math>(t=0)</math>, aby faza początkowa była równa zeru <math>(\varphi=0)</math>. Wychylenie dowolnego punktu z położenie równowagi <math>\xi\ | Szczególnym przypadkiem jest nakładanie się fali biegnącej i fali odbitej od jakiejś przeszkody. Powstaje wtedy fala stojąca. Niech <math>\xi_1=a cos (\omega t -kx)</math> oznacza falę biegnącą w prawo, a <math>\xi_1=a cos (\omega t +kx)</math> falę odbitą rozchodzącą się w lewo. Wybraliśmy tu taką chwilę początkową <math>(t=0)</math>, aby faza początkowa była równa zeru <math>(\varphi=0)</math>. Wychylenie dowolnego punktu z położenie równowagi <math>\xi\ </math>, jest sumą wychyleń <math>\xi_1+\xi_2</math> . | ||
|} | |} | ||
| Linia 370: | Linia 373: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd41.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd41.png]] | ||
|valign="top"|Po skorzystaniu ze wzoru na sumę cosinusów, otrzymujemy wyrażenie opisujące drgania z częstością kołową równą częstości drgań składowych <math>\omega\ | |valign="top"|Po skorzystaniu ze wzoru na sumę cosinusów, otrzymujemy wyrażenie opisujące drgania z częstością kołową równą częstości drgań składowych <math>\omega\ </math>,. Amplituda tych drgań jest zależna od położenia <math>x\ </math>,, zmienia się sinusoidalnie od zera do maksymalnej wartości <math>2a\ </math>, . W punktach, których współrzędna <math>x\ </math>, spełnia warunek: <math>kx=\pm \left(n+\frac{1}{2} \right)\pi</math> , gdzie <math>n =0, 1, 2,\ldots,\ </math>, amplituda wynosi zero. Oznacza to, że te punkty cały czas pozostają w spoczynku. Miejsca takie nazywamy węzłami fali stojącej. Współrzędne węzłów wynoszą: <math>x_w=\pm \left(n+\frac{1}{2} \right)\frac{\lambda}{2}</math> . Natomiast punkty, dla których <math>kx=\pm n\pi</math> , drgają z maksymalną amplitudą. To są strzałki fali. Współrzędne strzałek mają wartości: <math>x_{strz}=\pm n\frac{\lambda}{2}</math> | ||
|} | |} | ||
| Linia 378: | Linia 381: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M5_Slajd42.png]] | |width="450px" valign="top"|[[Grafika:PF_M5_Slajd42.png]] | ||
|valign="top"|Rysunek przedstawia wychylenia cząstek (niebieska linia) w określonych momentach. W chwili <math>t\ | |valign="top"|Rysunek przedstawia wychylenia cząstek (niebieska linia) w określonych momentach. W chwili <math>t\ </math>, wszystkie cząstki mają maksymalne wychylenie. Po upływie <math>\frac{1}{4}\ </math>, okresu w chwili <math>(t + T/4)</math> cząstki przechodzą przez położenie równowagi. Strzałki pokazują prędkości cząstek. Po kolejnej <math>\frac{1}{4}\ </math>, okresu w chwili <math>(t + T/2)</math> cząstki znów są w maksymalnym wychyleniu. Zwróćmy uwagę, że wszystkie cząstki między dwoma węzłami drgają w jednakowej fazie, natomiast faza drgań po dwóch stronach węzła różni się o <math>\pi\ </math>,. | ||
|} | |} | ||
---- | ---- | ||
| Linia 394: | Linia 390: | ||
|valign="top"|Jeśli fala stojąca powstaje w strunie umocowanej na obu końcach, w miejscach zamocowania muszą powstać węzły. Narzuca to warunek na długość fali stojącej w strunie, mianowicie w długości struny musi mieścić się całkowita liczba połówek długości fali: <math>l=n\frac{\lambda}{2}</math> . | |valign="top"|Jeśli fala stojąca powstaje w strunie umocowanej na obu końcach, w miejscach zamocowania muszą powstać węzły. Narzuca to warunek na długość fali stojącej w strunie, mianowicie w długości struny musi mieścić się całkowita liczba połówek długości fali: <math>l=n\frac{\lambda}{2}</math> . | ||
Fale o innej długości szybko ulegną wygaszeniu. Kolejne długości fali stojącej w strunie o długości <math>l\ | Fale o innej długości szybko ulegną wygaszeniu. Kolejne długości fali stojącej w strunie o długości <math>l\ </math>, wynoszą: <math>\lambda_n=\frac{2l}{n}</math> , a odpowiadające im częstotliwości: <math>\nu_n=\frac{v}{\lambda_n}=\frac{v}{2l}n</math> , gdzie <math>v\ </math>, jest prędkością fazową fali zależną między innymi od naciągu struny. Częstotliwości te nazywamy częstotliwościami własnymi struny. Częstotliwość <math>\nu_1=\frac{v}{2l}</math> to częstotliwość podstawowa, zwana też pierwszą harmoniczną, a wszystkie inne częstotliwości własne są jej wielokrotnością. Na rysunku pokazane są drgania harmoniczne struny dla n = 1, 2 i 3. W ogólnym przypadku drgania struny są złożeniem wielu drgań harmonicznych. | ||
|} | |} | ||
| Linia 400: | Linia 396: | ||
---- | ---- | ||
= Podsumowanie = | |||
Pod wpływem siły harmonicznej <math>F = -kx</math> ciało porusza się ruchem harmonicznym, w którym wychylenie ciała z położenia równowagi zależy sinusoidalnie od czasu: <math>x(t)=A cos(\omega \cdot t +\varphi)</math> , gdzie <math>\omega=\frac{2\pi}{T}=\sqrt{\frac{k}{m}}</math> . Energia całkowita drgań, będąca sumą energii kinetycznej i potencjalnej, jest zachowana. Jeśli drgania są tłumione przez siłę oporu, amplituda drgań <math>A\ | Pod wpływem siły harmonicznej <math>F = -kx</math> ciało porusza się ruchem harmonicznym, w którym wychylenie ciała z położenia równowagi zależy sinusoidalnie od czasu: <math>x(t)=A cos(\omega \cdot t +\varphi)</math> , gdzie <math>\omega=\frac{2\pi}{T}=\sqrt{\frac{k}{m}}</math> . Energia całkowita drgań, będąca sumą energii kinetycznej i potencjalnej, jest zachowana. Jeśli drgania są tłumione przez siłę oporu, amplituda drgań <math>A\ </math>, maleje wykładniczo z czasem, a okres drgań jest dłuższy niż dla drgań swobodnych. Jeśli ruch harmoniczny odbywa się pod wpływem siły wymuszającej: <math>F=F_0 cos(\omega_w t)</math> , to częstość drgań jest równa częstości siły wymuszającej <math>\omega_w\ </math>,. Amplituda drgań zależna jest wtedy od różnicy kwadratów częstości własnej i częstości siły wymuszającej: <math>({\omega^2}_w-\omega^2)</math> , a dla częstości siły wymuszającej <math>\omega_w=\sqrt{\omega^2-2\beta^2}</math> , gdzie <math>\beta\ </math>, to współczynnik tłumienia, amplituda jest największa, czyli występuje rezonans. | ||
Jeśli ciało bierze udział w kilku ruchach harmonicznych, wychylenie wypadkowe jest sumą geometryczną składowych wychyleń. W szczególności, wynikiem złożenia dwóch równoległych drgań harmonicznych o niewielkiej różnicy częstości jest dudnienie, czyli drganie, w którym amplituda wolno oscyluje od zera do wartości maksymalnej. Złożenie drgań prostopadłych o równych częstościach daje ruch po prostej, elipsie lub okręgu w zależności od różnicy faz i relacji między amplitudami drgań składowych. Jeśli częstości prostopadłych drgań składowych są różne, to punkt zakreśla skomplikowane krzywe zwane krzywymi Lissajou. | Jeśli ciało bierze udział w kilku ruchach harmonicznych, wychylenie wypadkowe jest sumą geometryczną składowych wychyleń. W szczególności, wynikiem złożenia dwóch równoległych drgań harmonicznych o niewielkiej różnicy częstości jest dudnienie, czyli drganie, w którym amplituda wolno oscyluje od zera do wartości maksymalnej. Złożenie drgań prostopadłych o równych częstościach daje ruch po prostej, elipsie lub okręgu w zależności od różnicy faz i relacji między amplitudami drgań składowych. Jeśli częstości prostopadłych drgań składowych są różne, to punkt zakreśla skomplikowane krzywe zwane krzywymi Lissajou. | ||
| Linia 416: | Linia 404: | ||
Fala to rozchodzenie się w ośrodku drgań cząsteczek. Rozróżniamy fale poprzeczne, w których drgania cząstek ośrodka są prostopadłe do kierunku rozchodzenia się fali i fale podłużne, gdzie cząstki drgają w kierunku równoległym do kierunku rozchodzenia się fali. | Fala to rozchodzenie się w ośrodku drgań cząsteczek. Rozróżniamy fale poprzeczne, w których drgania cząstek ośrodka są prostopadłe do kierunku rozchodzenia się fali i fale podłużne, gdzie cząstki drgają w kierunku równoległym do kierunku rozchodzenia się fali. | ||
Wychylenie <math>\xi\ | Wychylenie <math>\xi\ </math>, z położenia równowagi cząstek biorących udział w ruchu falowym, opisuje wzór: <math>\xi(x, t)=a cos \left(\omega t -kx+\varphi \right)</math> , gdzie <math>k=\frac{2\pi}{\lambda}</math> jest liczbą falową, <math>\omega=\frac{2\pi}{T}</math> częstością, a <math>\varphi\ </math>, - fazą początkową. Funkcja <math>\xi(x, t)=a cos \left(\omega t -kx+\varphi \right)</math> jest rozwiązaniem równania falowego: | ||
: <math>\frac{\partial^2\xi}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \xi}{\partial t^2}</math> | : <math>\frac{\partial^2\xi}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \xi}{\partial t^2}</math> | ||
Jeśli nałożą się fale o jednakowej częstości biegnące w przeciwne strony, to powstaje fala stojąca: <math>\xi=2acos(kx)cos(\omega t)</math> , w której wszystkie cząstki drgają ze stałą częstością <math>\omega\ | Jeśli nałożą się fale o jednakowej częstości biegnące w przeciwne strony, to powstaje fala stojąca: <math>\xi=2acos(kx)cos(\omega t)</math> , w której wszystkie cząstki drgają ze stałą częstością <math>\omega\ </math>,, ale amplituda tych zmian <math>2acos(kx)\ </math>, zależna jest od samego położenia punktu <math>x\ </math>,. Punkty, gdzie amplituda drgań jest maksymalna to strzałki fali stojącej. Węzłami nazywamy punkty, które pozostają w spoczynku (amplituda równa zeru). Odległość między kolejnymi węzłami (i strzałkami) wynosi <math>\lambda/2\ </math>,. | ||
---- | ---- | ||
= Materiały do ćwiczeń = | |||
'''Zadanie 1''' | '''Zadanie 1''' | ||
| Linia 450: | Linia 418: | ||
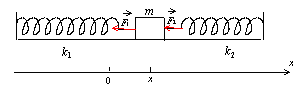
Obliczyć okres drgań układu składającego się z ciała o masie m i przyczepionych po obu jego stronach sprężyn o współczynnikach sprężystości k1 i k2. Zaniedbać opór powietrza i tarcie. | Obliczyć okres drgań układu składającego się z ciała o masie m i przyczepionych po obu jego stronach sprężyn o współczynnikach sprężystości k1 i k2. Zaniedbać opór powietrza i tarcie. | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
[[Grafika:PF_M5_Rys1.png]] | [[Grafika:PF_M5_Rys1.png]] | ||
| Linia 468: | Linia 437: | ||
Odpowiedź: <math>T=2\pi \sqrt{\frac{m}{k_1+k_2}}</math> | Odpowiedź: <math>T=2\pi \sqrt{\frac{m}{k_1+k_2}}</math> | ||
</div></div> | |||
---- | ---- | ||
| Linia 473: | Linia 444: | ||
'''Zadanie 2''' | '''Zadanie 2''' | ||
Na powierzchni wody pływa drewniany sześcian o krawędzi <math>a\ | Na powierzchni wody pływa drewniany sześcian o krawędzi <math>a\ </math>,. Gdy wepchnięto go głębiej i puszczono, sześcian zaczął wykonywać drgania w górę i w dół. Wykazać, że są to drgania harmoniczne i obliczyć okres drgań, jeśli gęstość wody wynosi <math>\rho_1\ </math>,, gęstość sześcianu <math>\rho_1\ </math>,, przyspieszenie ziemskie <math>g\ </math>,. | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
Ruch sześcianu odbywa się pod wpływem siły ciężkości i siły wyporu. Jeśli wykażemy, że siła wypadkowa jest wprost proporcjonalna do wychylenia z położenia równowagi i przeciwnie skierowana, to udowodnimy, że ruch jest harmoniczny. | Ruch sześcianu odbywa się pod wpływem siły ciężkości i siły wyporu. Jeśli wykażemy, że siła wypadkowa jest wprost proporcjonalna do wychylenia z położenia równowagi i przeciwnie skierowana, to udowodnimy, że ruch jest harmoniczny. | ||
W położeniu równowagi (1) siły wyporu i ciężkości równoważą się. Kiedy wepchniemy sześcian o x głębiej, do położenia (2), na część zakreskowaną sześcianu działa dodatkowa, niezrównoważona siła wyporu skierowana do góry: <math>F=-xa^2\cdot \rho_2 \cdot g</math> . Jeśli sześcian przesunie się z położenia równowagi w górę o <math>x\ | W położeniu równowagi (1) siły wyporu i ciężkości równoważą się. Kiedy wepchniemy sześcian o x głębiej, do położenia (2), na część zakreskowaną sześcianu działa dodatkowa, niezrównoważona siła wyporu skierowana do góry: <math>F=-xa^2\cdot \rho_2 \cdot g</math> . Jeśli sześcian przesunie się z położenia równowagi w górę o <math>x\ </math>, (położenie (3)), siła wyporu zmniejszy o wartość <math>\Delta F=xa^2\cdot \rho_2 \cdot g</math> , więc siła wypadkowa będzie działać w dół, a jej wartość będzie równa <math>F=-\Delta F=-xa^2\cdot \rho_2 \cdot g</math> | ||
Widzimy, że siła jest zawsze wprost proporcjonalna do wychylenia <math>x\ | Widzimy, że siła jest zawsze wprost proporcjonalna do wychylenia <math>x\ </math>, i przeciwnie skierowana. Jest to więc ruch harmoniczny o współczynniku <math>k=a^2\cdot \rho_2 \cdot g</math> . Okres obliczamy ze wzoru: <math>T=2\pi \sqrt{\frac{m}{k}}</math>, gdzie <math>m=a^3\cdot \rho_1</math> | ||
Okres wynosi: <math>T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{\rho_1 a}{\rho_2 g}}</math> | Okres wynosi: <math>T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{\rho_1 a}{\rho_2 g}}</math> | ||
</div></div> | |||
---- | ---- | ||
| Linia 495: | Linia 469: | ||
: c) Ile wynosi największe wychylenie kulki? | : c) Ile wynosi największe wychylenie kulki? | ||
: d) Oblicz największą energię kinetyczną, jaką osiąga kulka, jaka wtedy będzie energia potencjalna siły sprężystości? | : d) Oblicz największą energię kinetyczną, jaką osiąga kulka, jaka wtedy będzie energia potencjalna siły sprężystości? | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
a) Ze związku: <math>\omega^2=\frac{k}{m}</math> wyznaczamy k: <math>k=m\omega^2=0,1kg\cdot 0,81s^{-1}=0,081 kgs^{-1}</math> | a) Ze związku: <math>\omega^2=\frac{k}{m}</math> wyznaczamy k: <math>k=m\omega^2=0,1kg\cdot 0,81s^{-1}=0,081 kgs^{-1}</math> | ||
| Linia 504: | Linia 481: | ||
c) Amplituda wynosi <math>A=\frac{v_0}{\omega}=\frac{2ms^{-1}}{0,9s^{-1}}=2,22m</math> | c) Amplituda wynosi <math>A=\frac{v_0}{\omega}=\frac{2ms^{-1}}{0,9s^{-1}}=2,22m</math> | ||
d) Energia kinetyczna wyraża się wzorem: <math>E_k=\frac{mv^2}{2}=\frac{m{v^2}_0 cos^2 (\omega t)}{2}</math> . Największą wartość będzie miała, gdy <math>cos^2(\omega t)\ | d) Energia kinetyczna wyraża się wzorem: <math>E_k=\frac{mv^2}{2}=\frac{m{v^2}_0 cos^2 (\omega t)}{2}</math> . Największą wartość będzie miała, gdy <math>cos^2(\omega t)\ </math>, , czyli na przykład w chwili t = 0. | ||
: <math>E_{kmax}=\frac{m{v^2}_0}{2}=\frac{0,1kg \cdot 4m^2 s^{-2}}{2}=2J</math> | : <math>E_{kmax}=\frac{m{v^2}_0}{2}=\frac{0,1kg \cdot 4m^2 s^{-2}}{2}=2J</math> | ||
Energia potencjalna to: <math>E_p=\frac{mx^2}{2}=\frac{kv_0 sin\omega t}{2\omega}</math>, w chwili t=0 energia potencjalna równa jest zeru: <math>E_p(0)=0</math> | Energia potencjalna to: <math>E_p=\frac{mx^2}{2}=\frac{kv_0 sin\omega t}{2\omega}</math>, w chwili t=0 energia potencjalna równa jest zeru: <math>E_p(0)=0</math> | ||
</div></div> | |||
---- | ---- | ||
| Linia 514: | Linia 493: | ||
'''Zadanie 4''' | '''Zadanie 4''' | ||
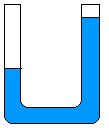
W rurce o przekroju <math>S\ | W rurce o przekroju <math>S\ </math>, zgiętej w kształcie litery U znajduje się słup wody o całkowitej długości <math>l\ </math>,, przy czym w chwili początkowej poziom wody w jednym ramieniu rurki jest wyższy niż w drugim. Jaki będzie okres drgań słupa wody? Pominąć siły lepkości. | ||
Załóżmy, że gęstość wody wynosi <math>\rho\ | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Załóżmy, że gęstość wody wynosi <math>\rho\ </math>,. Zatem masa słupa wody o długości <math>l\ </math>,, i przekroju <math>S\ </math>, wynosi: <math>m=\rho l S</math> . Zastanówmy się, jaka siła działa na słup wody. | |||
: [[Grafika:PF_M5_Rys2.png]] | : [[Grafika:PF_M5_Rys2.png]] | ||
Oznaczmy przez <math>x\ | Oznaczmy przez <math>x\ </math>, wychylenie słupa wody z położenia równowagi w jednym z ramion. Oczywiście niezrównoważony słup wody ma wysokość <math>2x\ </math>,, bo jeśli w jednym ramieniu poziom wody podniósł się o <math>x\ </math>,, to w drugim opadł o <math>x\ </math>,. Ciężar niezrównoważonego słupa wody wynosi: <math>F(x)=-2xS\rho g</math> . Znak minus oznacza, że siła jest skierowana przeciwnie do wychylenia <math>x\ </math>,, czyli w dół. Wartość siły jest wprost proporcjonalna do wychylenia ze współczynnikiem proporcjonalności <math>k=2S\rho g</math> , a więc ruch cieczy w rurce jest ruchem harmonicznym. Częstość drgań wyraża się wzorem: <math>\omega=\sqrt{\frac{k}{m}}</math> , a więc okres drgań: | ||
: <math>T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{\rho lS}{2S\rho g}}=2\pi \sqrt{\frac{l}{g}}</math> | : <math>T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{\rho lS}{2S\rho g}}=2\pi \sqrt{\frac{l}{g}}</math> | ||
</div></div> | |||
---- | ---- | ||
| Linia 532: | Linia 514: | ||
Najniższe i najwyższe częstotliwości odbierane przez ucho ludzkie wynoszą odpowiednio około 20 i 15000 Hz. Jakie odpowiadają temu długości fal? Prędkość dźwięku w powietrzu wynosi 330 m/s. | Najniższe i najwyższe częstotliwości odbierane przez ucho ludzkie wynoszą odpowiednio około 20 i 15000 Hz. Jakie odpowiadają temu długości fal? Prędkość dźwięku w powietrzu wynosi 330 m/s. | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | |||
Szukane długości fal wynoszą: 16,5 m oraz 0,022 m, czyli 2,2 cm. | |||
</div></div> | |||
---- | |||
= Słowa kluczowe = | |||
: amplituda drgań | |||
: okres drgań | |||
: częstotliwość drgań własnych | |||
: faza początkowa | |||
: drgania tłumione | |||
: współczynnik tłumienia | |||
: drgania wymuszone | |||
: rezonans | |||
: figury Lissajou | |||
: zasada superpozycji | |||
: równanie falowe | |||
: fala stojąca | |||
: fala płaska | |||
: fala kulista | |||
---- | |||
= Bibliografia = | |||
#J. Orear, Fizyka, WNT, Warszawa (1998); | |||
#R. Resnick, D. Halliday, Fizyka 1, PWN, Warszawa (1994); | |||
#I.W. Sawieliew, Wykłady z fizyki, PWN, Warszawa (1994). | |||
---- | ---- | ||
Aktualna wersja na dzień 21:56, 15 wrz 2023
Wykład

|

|
Sprawdźmy, czy nasze równanie będzie spełnione przez funkcję , gdzie ,, , i , są dowolnymi parametrami. Obliczamy pierwszą i drugą pochodną wychylenia , po czasie , i podstawiamy do równania. |

|
Okres i częstotliwość drgań
Okresem nazywamy czas jednego pełnego drgania. Po upływie okresu drgające ciało jest znów w takiej samej fazie. Okres powiązany jest z częstością wzorem: |

|
Prędkość i przyspieszenie
Prędkość i przyspieszenie w ruchu harmonicznym obliczamy jako pierwszą i drugą pochodną wychylenia , po czasie. |

|
Energię kinetyczną w ruchu harmonicznym obliczamy, podstawiając do wzoru na energię kinetyczną prędkość w postaci . |
|
Jeśli częstości drgań są jednakowe i różnica faz wynosi , , to ruch będzie ruchem harmonicznym wzdłuż prostej o równaniu . |

|
Po uwzględnieniu, że równanie falowe przybiera postać: |
Podsumowanie
Pod wpływem siły harmonicznej ciało porusza się ruchem harmonicznym, w którym wychylenie ciała z położenia równowagi zależy sinusoidalnie od czasu: , gdzie . Energia całkowita drgań, będąca sumą energii kinetycznej i potencjalnej, jest zachowana. Jeśli drgania są tłumione przez siłę oporu, amplituda drgań , maleje wykładniczo z czasem, a okres drgań jest dłuższy niż dla drgań swobodnych. Jeśli ruch harmoniczny odbywa się pod wpływem siły wymuszającej: , to częstość drgań jest równa częstości siły wymuszającej ,. Amplituda drgań zależna jest wtedy od różnicy kwadratów częstości własnej i częstości siły wymuszającej: , a dla częstości siły wymuszającej , gdzie , to współczynnik tłumienia, amplituda jest największa, czyli występuje rezonans.
Jeśli ciało bierze udział w kilku ruchach harmonicznych, wychylenie wypadkowe jest sumą geometryczną składowych wychyleń. W szczególności, wynikiem złożenia dwóch równoległych drgań harmonicznych o niewielkiej różnicy częstości jest dudnienie, czyli drganie, w którym amplituda wolno oscyluje od zera do wartości maksymalnej. Złożenie drgań prostopadłych o równych częstościach daje ruch po prostej, elipsie lub okręgu w zależności od różnicy faz i relacji między amplitudami drgań składowych. Jeśli częstości prostopadłych drgań składowych są różne, to punkt zakreśla skomplikowane krzywe zwane krzywymi Lissajou.
Fala to rozchodzenie się w ośrodku drgań cząsteczek. Rozróżniamy fale poprzeczne, w których drgania cząstek ośrodka są prostopadłe do kierunku rozchodzenia się fali i fale podłużne, gdzie cząstki drgają w kierunku równoległym do kierunku rozchodzenia się fali.
Wychylenie , z położenia równowagi cząstek biorących udział w ruchu falowym, opisuje wzór: , gdzie jest liczbą falową, częstością, a , - fazą początkową. Funkcja jest rozwiązaniem równania falowego:
Jeśli nałożą się fale o jednakowej częstości biegnące w przeciwne strony, to powstaje fala stojąca: , w której wszystkie cząstki drgają ze stałą częstością ,, ale amplituda tych zmian , zależna jest od samego położenia punktu ,. Punkty, gdzie amplituda drgań jest maksymalna to strzałki fali stojącej. Węzłami nazywamy punkty, które pozostają w spoczynku (amplituda równa zeru). Odległość między kolejnymi węzłami (i strzałkami) wynosi ,.
Materiały do ćwiczeń
Zadanie 1
Obliczyć okres drgań układu składającego się z ciała o masie m i przyczepionych po obu jego stronach sprężyn o współczynnikach sprężystości k1 i k2. Zaniedbać opór powietrza i tarcie.
Zadanie 2
Na powierzchni wody pływa drewniany sześcian o krawędzi ,. Gdy wepchnięto go głębiej i puszczono, sześcian zaczął wykonywać drgania w górę i w dół. Wykazać, że są to drgania harmoniczne i obliczyć okres drgań, jeśli gęstość wody wynosi ,, gęstość sześcianu ,, przyspieszenie ziemskie ,.
Zadanie 3
Kulka o masie m = 0,1 kg zaczepiona na sprężynie wykonuje drgania harmoniczne. Zależność jej prędkości od czasu opisuje wzór: , gdzie ,
- a) Jaki jest współczynnik sprężystości sprężyny?
- b) Jakie jest wychylenie kulki w chwili t, jeśli x(0)=0 ?
- c) Ile wynosi największe wychylenie kulki?
- d) Oblicz największą energię kinetyczną, jaką osiąga kulka, jaka wtedy będzie energia potencjalna siły sprężystości?
Zadanie 4
W rurce o przekroju , zgiętej w kształcie litery U znajduje się słup wody o całkowitej długości ,, przy czym w chwili początkowej poziom wody w jednym ramieniu rurki jest wyższy niż w drugim. Jaki będzie okres drgań słupa wody? Pominąć siły lepkości.
Zadanie 5
Najniższe i najwyższe częstotliwości odbierane przez ucho ludzkie wynoszą odpowiednio około 20 i 15000 Hz. Jakie odpowiadają temu długości fal? Prędkość dźwięku w powietrzu wynosi 330 m/s.
Słowa kluczowe
- amplituda drgań
- okres drgań
- częstotliwość drgań własnych
- faza początkowa
- drgania tłumione
- współczynnik tłumienia
- drgania wymuszone
- rezonans
- figury Lissajou
- zasada superpozycji
- równanie falowe
- fala stojąca
- fala płaska
- fala kulista
Bibliografia
- J. Orear, Fizyka, WNT, Warszawa (1998);
- R. Resnick, D. Halliday, Fizyka 1, PWN, Warszawa (1994);
- I.W. Sawieliew, Wykłady z fizyki, PWN, Warszawa (1994).