MN02: Różnice pomiędzy wersjami
Nie podano opisu zmian |
|||
| (Nie pokazano 22 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
<!-- | |||
Konwertowane z pliku LaTeX przez latex2mediawiki, zob. http://www.ii.uj.edu.pl/ pawlik1/latex2mediawiki.php. | |||
Niezb�dne rozszerzenia i modyfikacje oryginalnego latex2mediawiki | |||
wprowadzi� przykry@mimuw.edu.pl | |||
--> | |||
=Równania nieliniowe= | =Równania nieliniowe= | ||
W wielu zadaniach, m.in. | {{powrot |Metody numeryczne | do strony głównej | ||
rozwiązania skalarnego równania nieliniowego postaci <math> | przedmiotu <strong>Metody numeryczne</strong>}} | ||
W wielu zadaniach, m.in. matematyki stosowanej, spotykamy się z problemem | |||
rozwiązania skalarnego równania nieliniowego postaci <math>f(x) = 0</math>. Oto kilka przykładów: | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | |||
<span style="font-variant:small-caps;">Przykład</span> | |||
<div class="solution" style="margin-left,margin-right:3em;"> | |||
Równanie Keplera | |||
<center><math>f(x) \equiv x - \epsilon \sin(x) - M = 0 | |||
</math></center> | |||
jest bardzo ważne w astronomii, jego rozwiązanie pozwala wyznaczyć przyszłe położenie planety. Parametr <math>\epsilon</math> odpowiada ekscentryczności orbity i przyjmuje wartości z przedziału <math>[0,1]</math>. Poza paru prostymi przypadkami, w ogólności równanie Keplera nie daje się rozwiązać w terminach funkcji elementarnych. | |||
< | [[grafika:Kepler.jpg|thumb|right||Johann Kepler<br> [[Biografia Kepler|Zobacz biografię]]]] | ||
</div></div> | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | |||
<span style="font-variant:small-caps;">Przykład</span> | |||
<div class="solution" style="margin-left,margin-right:3em;"> | |||
Znajdowanie miejsc zerowych wielomianu | |||
<center><math>f(x) \equiv a_nx^n + \ldots + a_1x + a_0 = 0</math></center> | |||
Bardzo wiele modeli matematycznych wymaga rozwiązania równania z wielomianową nieliniowością. Piękne [[MN14|kwadratury]] (Gaussa) opierają się na węzłach będących zerami pewnego wielomianu. Wielomiany są bardzo szczególnymi funkcjami i dla nich istnieje szereg wyspecjalizowanych metod znajdowania ich pierwiastków, m.in. metoda Laguerre'a, metoda Bairstow'a (o nich tu nie będziemy mówić), a także zaskakujące metody sprowadzające zadanie poszukiwania miejsc zerowych wielomianu do zupełnie innego zadania matematycznego --- o nich jednak będzie mowa dopiero w wykładzie dotyczącym [[MN13|znajdowania wartości własnych macierzy]]. | |||
</div></div> | |||
</ | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | |||
<span style="font-variant:small-caps;">Przykład</span> | |||
<div class="solution" style="margin-left,margin-right:3em;"> | |||
Obliczanie pierwiastka kwadratowego z zadanej liczby <math>a</math>, czyli sposób na implementację funkcji "<code>sqrt()</code>". Można to zadanie wyrazić, jako rozwiązywanie równania | |||
<center><math>f(x) \equiv x^2 - a = 0</math></center> | |||
Szybkie algorytmy wyznaczania pierwiastka kwadratowego były znane już starożytnym. W wykładzie zrozumiemy, dlaczego <strong>metoda Herona</strong>, | |||
<center><math> | <center><math> | ||
x_{k+1} = \frac{1}{2}\left(x_k + \frac{a}{x_k}\right) | x_{k+1} = \frac{1}{2}\left(x_k + \frac{a}{x_k}\right) | ||
</math></center> | </math></center> | ||
daje bardzo dobre przybliżenie <math>\sqrt{a}</math> już po kilku iteracjach. | |||
</div></div> | |||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | |||
<span style="font-variant:small-caps;">Przykład</span> | |||
<div class="solution" style="margin-left,margin-right:3em;"> | |||
Implementacja wyznaczania odwrotności liczby <math>a</math> (<strong>bez</strong> dzielenia!) jest możliwa, gdy odpowiednią metodą będziemy poszukiwać rozwiązania równania | |||
<center><math> | <center><math>f(x) \equiv \frac{1}{x} - a = 0</math></center> | ||
\frac{1}{x} - a = 0</math></center> | |||
To zadanie jest ważne praktycznie, np. tak można poprawić precyzję | |||
[http://www.amd.com/us-en/assets/content_type/white_papers_and_tech_docs/21928.pdf funkcji | [http://www.amd.com/us-en/assets/content_type/white_papers_and_tech_docs/21928.pdf funkcji wektorowych stosowanych w niektórych procesorach AMD]. Okazuje się, że instrukcja procesora służąca do równoległego obliczania odwrotności sekwencji liczb umieszczonych w 128-bitowym rejestrze wektorowym daje wynik z małą precyzją (oczywiście po to, by wykonywała się szybciej!). Jeśli taka dokładność wyniku nie odpowiada nam, możemy ją --- zgodnie z manualem procesora --- poprawić, rozwiązując właśnie takie równanie jak powyżej, metodą korzystającą wyłącznie z (wektorowych) operacji mnożenia i dodawania. | ||
wektorowych stosowanych w niektórych procesorach AMD]. | </div></div> | ||
odwrotności sekwencji liczb umieszczonych w 128-bitowym rejestrze wektorowym | |||
daje wynik z małą precyzją (oczywiście po to, by wykonywała się szybciej!). | |||
Jeśli taka dokładność wyniku nie odpowiada nam, możemy ją --- zgodnie z manualem | |||
procesora --- poprawić, rozwiązując właśnie takie równanie jak powyżej, metodą | |||
korzystającą wyłącznie z (wektorowych) operacji mnożenia i dodawania. | |||
==Bisekcja== | ==Bisekcja== | ||
| Linia 67: | Linia 74: | ||
działach informatyki, jest dość | działach informatyki, jest dość | ||
naturalną metodą obliczania zer skalarnych funkcji | naturalną metodą obliczania zer skalarnych funkcji | ||
ciągłych określonych na danym przedziale <math> | ciągłych określonych na danym przedziale <math>[a,b]</math> | ||
i zmieniających znak. Dokładniej, rozpatrzmy klasę | i zmieniających znak. Dokładniej, rozpatrzmy klasę | ||
funkcji | funkcji | ||
<center><math> | <center><math> | ||
F\,=\,\{\,f\in C([a,b])\,:\;f(a)\cdot f(b) < 0\,\} | F\,=\,\{\,f\in C([a,b])\,:\;f(a)\cdot f(b) < 0\,\}</math>,</center> | ||
</math></center> | |||
Oczywiście, każda funkcja <math> | to znaczy <math>f \in F</math> przyjmują w krańcach przedziału wartości przeciwnego znaku. | ||
zero w <math> | Oczywiście, każda funkcja <math>f\in F</math> ma, na mocy twierdzenia Darboux, co najmniej jedno zero w <math>[a,b]</math>. Startując z przedziału <math>[a,b]</math>, w kolejnych krokach metody bisekcji obliczamy informację o wartości <math>f</math> w środku przedziału, co pozwala nam w następnym kroku zmniejszyć o połowę przedział, w którym na pewno znajduje się zero funkcji. | ||
kolejnych krokach metody bisekcji obliczamy informację | |||
o wartości <math> | |||
w | |||
o połowę przedział, w którym na pewno znajduje się | |||
zero funkcji. | |||
Bisekcję realizuje następujący ciąg | Bisekcję realizuje następujący ciąg | ||
poleceń, po wykonaniu którego <math> | poleceń, po wykonaniu którego <math>x</math> jest przybliżeniem | ||
zera funkcji <math> | zera funkcji <math>f</math> z zadaną dokładnością <math>\epsilon</math>. | ||
{{algorytm|Metoda bisekcji|| | {{algorytm|Metoda bisekcji|Metoda bisekcji| | ||
< | <Source> | ||
lewy = a; prawy = b; | |||
flewy = f(lewy); fprawy = f(prawy); | |||
x | x = (a+b)/2; /* przybliżenie rozwiązania */ | ||
while (e > <math> | e = (b-a)/2; /* przedział lokalizujący rozwiązanie dokładne */ | ||
while (e > <math>\epsilon</math>) | |||
{ | { | ||
if (f( | fx = f(x); /* reszta */ | ||
if ( abs(fx) == 0 ) /* trafiliśmy dokładnie w miejsce zerowe */ | |||
return(x); | |||
if ( sign(fx) != sign(flewy) ) /* tzn. f(lewy)*f(x) < 0 */ | |||
{ | |||
prawy = x; | |||
fprawy = fx; | |||
} | |||
else | else | ||
{ | |||
x | lewy = x; | ||
} | flewy = fx; | ||
</ | } | ||
x = (lewy+prawy)/2; /* najlepsze przybliżenie rozwiązania przy danym przedziale */ | |||
e = e/2; | |||
} | |||
return(x); | |||
</Source>}} | |||
Z konstrukcji metody | Z konstrukcji metody łatwo wynika, że po wykonaniu | ||
<math> | <math>k</math> obrotów pętli <code>while</code> (czyli po obliczeniu <math>k+2</math> wartości funkcji) | ||
otrzymujemy <math> | otrzymujemy <math>x</math>, które odległe jest od pewnego rozwiązania <math>x^*</math> o co najwyżej | ||
rozwiązania <math> | |||
<center><math> | <center><math> | ||
|x-x^*|\,\le\,\Big(\frac 12\Big)^k | |x-x^*|\,\le\,\Big(\frac 12\Big)^k | ||
\Big(\frac{b-a}{2}\Big) | \Big(\frac{b-a}{2}\Big)</math></center> | ||
</math></center> | |||
Metoda bisekcji jest więc zbieżna <strong>liniowo</strong> z | Metoda bisekcji jest więc zbieżna <strong>liniowo</strong> z | ||
ilorazem <math> | ilorazem <math>1/2</math>. Choć ta zbieżność nie jest | ||
imponująca, bisekcja ma kilka istotnych zalet. Oprócz | imponująca, bisekcja ma kilka istotnych zalet. Oprócz | ||
jej prostoty, należy podkreślić fakt, że bisekcja jest | jej prostoty, należy podkreślić fakt, że bisekcja jest | ||
w pewnym sensie uniwersalna. Jeśli tylko dysponujemy dwoma punktami <math> | w pewnym sensie uniwersalna. Jeśli tylko dysponujemy dwoma punktami <math>a</math> i <math>b</math> | ||
takimi, że <math> | takimi, że <math>f</math> przyjmuje w nich wartości przeciwnych znaków, to metoda bisekcji | ||
z pewnością znajdzie miejsce zerowe funkcji, choćby początkowa długość | z pewnością znajdzie miejsce zerowe funkcji, choćby początkowa długość | ||
przedziału <math> | przedziału <math>|b-a|</math> była bardzo duża: zbieżność metody bisekcji jest <strong>globalna</strong>. Co ważniejsze, dla zbieżności metody bisekcji | ||
wystarcza jedynie <strong>ciągłość</strong> funkcji. Poza tym | wystarcza jedynie <strong>ciągłość</strong> funkcji. Poza tym | ||
możemy łatwo kontrolować <strong>błąd bezwzględny aproksymacji miejsca zerowego</strong>. Konsekwencją | możemy łatwo kontrolować <strong>błąd bezwzględny aproksymacji miejsca zerowego</strong>. Konsekwencją | ||
| Linia 125: | Linia 136: | ||
{{wniosek||| | {{wniosek||| | ||
Dla znalezienia zera <math> | Dla znalezienia zera <math>x^*</math> z dokładnością | ||
<math> | <math>\epsilon>0</math>, wystarczy obliczyć w metodzie bisekcji | ||
<center><math> | <center><math>k\,=\,k(\epsilon)\,=\, | ||
\Big\lceil{\log_2\frac{(b-a)}{\epsilon}}\Big\rceil - 1 | \Big\lceil{\log_2\frac{(b-a)}{\epsilon}}\Big\rceil - 1 | ||
</math></center> | </math></center> | ||
| Linia 138: | Linia 149: | ||
Zupełnie inne, i jak się okaże --- przy odrobinie sprytu bardzo skuteczne --- | Zupełnie inne, i jak się okaże --- przy odrobinie sprytu bardzo skuteczne --- | ||
podejście do wyznaczania miejsca zerowego jest oparte na <strong>metodzie Banacha</strong>. | podejście do wyznaczania miejsca zerowego jest oparte na <strong>metodzie Banacha</strong>. Dla większej ogólności, będziemy zakładać teraz, że <math>f: D\rightarrow R^N</math> i <math>D</math> jest otwartym, niepustym podzbiorem <math>R^N</math>. | ||
Najpierw nasze równanie nieliniowe | Najpierw nasze równanie nieliniowe | ||
<center><math> | <center><math> | ||
f(x) = 0 | f(x) = 0 | ||
</math></center> | </math></center> | ||
przekształcamy (dobierając odpowiednią funkcję <math> | przekształcamy (dobierając odpowiednią funkcję <math>\phi</math>) do równania równoważnego | ||
(tzn. mającego te same rozwiązania) | (tzn. mającego te same rozwiązania) | ||
<center><math> | <center><math> | ||
x\,=\,\phi( x) | x\,=\,\phi( x) | ||
</math></center> | </math></center> | ||
Taki <math>x</math>, dla którego zachodzi powyższa równość, nazywamy <strong>punktem stałym</strong> odwzorowania <math>\phi</math>. | |||
<center><math> | Następnie, startując z pewnego przybliżenia | ||
</math></center> | początkowego <math>x_0 \in D</math>, konstruujemy ciąg kolejnych | ||
przybliżeń <math>x_k</math> według wzoru | |||
<center><math>x_k\,=\,\phi( x_{k-1}),\qquad k\ge 1</math></center> | |||
[[grafika:Banach.jpg|thumb|right||Stefan Banach<br> [[Biografia Banach|Zobacz biografię]]]] | [[grafika:Banach.jpg|thumb|right||Stefan Banach<br> [[Biografia Banach|Zobacz biografię]]]] | ||
{{twierdzenie|Banacha, o | {{twierdzenie|Banacha, o kontrakcji|Banacha, o kontrakcji| | ||
Niech <math> | Niech <math>D_0</math> będzie domkniętym | ||
podzbiorem dziedziny <math> | podzbiorem dziedziny <math>D</math>, | ||
<center><math> | <center><math>\overline D_0\,=\,D_0\subset D | ||
</math></center> | </math></center> | ||
w którym <math> | w którym <math>\phi</math> jest odwzorowaniem zwężającym. | ||
To znaczy, <math> | To znaczy, <math>\phi(D_0)\subset D_0</math>, oraz istnieje stała | ||
<math> | <math>0\le L<1</math> taka, że | ||
<center><math> | <center><math>\|\phi( x)-\phi( y)\|\,\le\,L\,\| x- y\|, | ||
\qquad\forall x, y\in D_0 | |||
</math></center> | </math></center> | ||
Wtedy równanie | Wtedy równanie | ||
<center><math> | <center><math> | ||
x\,=\,\phi( x) | |||
</math></center> | </math></center> | ||
ma dokładnie jedno | ma dokładnie jedno | ||
rozwiązanie <math> | rozwiązanie <math>x^*</math>, oraz | ||
<center><math> | <center><math>x^*\,=\,\lim_{k\to\infty} x_k | ||
</math></center> | </math></center> | ||
dla dowolnego przybliżenia początkowego | dla dowolnego przybliżenia początkowego | ||
<math> | <math>x_0\in D_0</math>. | ||
}} | }} | ||
| Linia 197: | Linia 209: | ||
Wobec | Wobec | ||
<center><math>\ | <center><math>\begin{align} \| x_k- x_{k-1}\| &= \|\phi( x_{k-1})-\phi( x_{k-2})\| \,\le\,L\,\| x_{k-1}- x_{k-2}\| \\ | ||
&\le &\cdots\;\le\;L^{k-1}\| x_1- x_0\|, | |||
\end{align}</math></center> | |||
\ | |||
dla <math> | dla <math>k\ge s</math> mamy | ||
<center><math>\ | <center><math>\begin{align} \| x_k- x_s\| &&\le \sum_{j=s+1}^k\| x_j- x_{j-1}\| \,\le\,\sum_{j=s+1}^k L^{j-1}\| x_1- x_0\| \\ | ||
&&= L^s(1+L+\cdots+L^{k-s-1})\| x_1- x_0\| \,\le\,\frac{L^s}{1-L}\| x_1- x_0\|. | |||
\end{align}</math></center> | |||
\ | |||
Ciąg <math> | Ciąg <math>\{ x_k\}_k</math> jest więc ciągiem Cauchy'ego. | ||
Stąd istnieje granica | Stąd istnieje granica | ||
<math> | <math>\alpha=\lim_{k\to\infty} x_k</math>, która należy do | ||
<math> | <math>D_0</math>, wobec domkniętości tego zbioru. Ponieważ | ||
lipschitzowskość <math>\phi</math> implikuje jej ciągłość, | |||
mamy też | mamy też | ||
<center><math> | <center><math>\phi(\alpha)\,=\,\phi\Big(\lim_{k\to\infty} x_k\Big) | ||
\,=\,\lim_{k\to\infty}\phi( x_k) | \,=\,\lim_{k\to\infty}\phi( x_k) | ||
\,=\,\lim_{k\to\infty} x_k\,=\,\alpha | \,=\,\lim_{k\to\infty} x_k\,=\,\alpha</math>,</center> | ||
</math></center> | |||
tzn. <math> | tzn. <math>\alpha</math> jest punktem stałym odwzorowania <math>\phi</math>. | ||
Dla jednoznaczności zauważmy, że jeśliby istniał | Dla jednoznaczności zauważmy, że jeśliby istniał | ||
drugi, różny od <math> | drugi, różny od <math>\alpha</math>, punkt stały <math>\beta</math>, | ||
to mielibyśmy | to mielibyśmy | ||
<center><math> | <center><math>\|\alpha-\beta\|\,=\, | ||
\|\phi(\alpha)-\phi(\beta)\| | \|\phi(\alpha)-\phi(\beta)\| | ||
\,\le\,L\,\|\alpha-\beta\| | \,\le\,L\,\|\alpha-\beta\| | ||
</math></center> | </math></center> | ||
Stąd <math> | Stąd <math>1<L</math>, co jest sprzeczne z założeniem, że | ||
<math> | <math>\phi</math> jest zwężająca. }} | ||
Z powyższych rozważań otrzymujemy natychmiastowy | Z powyższych rozważań otrzymujemy natychmiastowy | ||
| Linia 241: | Linia 247: | ||
{{wniosek||| | {{wniosek||| | ||
Przy założeniach [[ | Przy założeniach [[#Banacha, o kontrakcji|twierdzenia Banacha]], | ||
metoda iteracji prostych jest zbieżna co | metoda iteracji prostych jest zbieżna co | ||
najmniej liniowo z ilorazem <math> | najmniej liniowo z ilorazem <math>L</math>, tzn. | ||
<center><math> | <center><math>\| x_k- x^*\|\,\le\,L^k\,\| x_0- x^*\|</math></center> | ||
</math></center> | |||
}} | }} | ||
| Linia 252: | Linia 257: | ||
<div style="margin-top:1em; padding-top,padding-bottom:1em;"> | <div style="margin-top:1em; padding-top,padding-bottom:1em;"> | ||
<span style="font-variant:small-caps;">Przykład</span> | <span style="font-variant:small-caps;">Przykład</span> | ||
<div class="solution"> | <div class="solution" style="margin-left,margin-right:3em;"> | ||
Dla ilustracji, rozpatrzmy | Dla ilustracji, rozpatrzmy | ||
równanie | równanie Keplera, gdy <math>0 < \epsilon < 1</math>: | ||
<center><math> | <center><math> | ||
x\,=\,\ | x\,=\,M+\epsilon\sin(x), \qquad \mbox{dla} \qquad x\in R | ||
</math></center> | </math></center> | ||
W tym przypadku <math> | [[Image:MNrownaniekeplera.png|thumb|550px|center|Graficzna ilustracja równania Keplera dla <math>M=1</math> i <math>\epsilon = \frac{1}{4}</math>.]] | ||
stałą | W tym przypadku <math>\phi(x)=M+\epsilon\,\sin(x)</math>. Zauważmy, że w | ||
funkcja <math>\phi</math> jest zwężająca ze stałą | |||
<center><math> | <center><math>L \leq \max_{x} |\phi'(x)| \leq \epsilon < 1</math></center> | ||
</math></center> | |||
Ponieważ obrazem prostej przy przekształceniu <math>\phi</math> jest odcinek <math>D = [M-\epsilon, M+\epsilon]</math>, to znaczy, że <math>\phi</math> --- ograniczona do <math>D</math> --- spełnia założenia [[#Banacha, o kontrakcji|twierdzenia Banacha o kontrakcji]]. | |||
Stąd istnieje dokładnie jedno rozwiązanie naszego równania | Stąd istnieje dokładnie jedno rozwiązanie naszego równania | ||
w przedziale <math> | w przedziale <math>D</math>. Rozwiązanie to może | ||
być aproksymowane z dowolnie małym błędem przy pomocy | być aproksymowane z dowolnie małym błędem przy pomocy | ||
iteracji prostych, startując z dowolnego przybliżenia | iteracji prostych, startując z dowolnego przybliżenia | ||
początkowego <math> | początkowego <math>x_0\in D</math>. Jednak, gdy <math>\epsilon \approx 1</math>, zbieżność może być bardzo powolna... (Wkrótce przekonasz się, że są szybsze metody). | ||
</div></div> | </div></div> | ||
Zaletą iteracji prostych jest fakt, że zbieżność | Zaletą iteracji prostych jest fakt, że zbieżność | ||
nie zależy od wymiaru <math> | nie zależy od wymiaru <math>n</math> zadania, ale tylko od stałej | ||
Lipschitza <math> | Lipschitza <math>L</math> (jednak w praktyce czasem sama stała Lipschitza może zależeć od | ||
wymiaru zadania...). Metoda Banacha ma szczególne zastosowanie w | wymiaru zadania...). Metoda Banacha ma szczególne zastosowanie w | ||
przypadku, gdy funkcja <math> | przypadku, gdy funkcja <math>\phi</math> jest zwężająca na całym | ||
zbiorze <math> | zbiorze <math>D</math>, tzn. <math>D_0=D</math>. Jeśli ponadto <math>D</math> ma | ||
skończoną średnicę <math> | skończoną średnicę, <math>\mbox{diam} (D) < +\infty</math>, to dla | ||
osiągnięcia <math> | osiągnięcia <math>\epsilon</math>-aproksymacji zera funkcji <math>f</math> | ||
wystarczy wykonać | wystarczy wykonać | ||
<center><math> | <center><math>k\,=\,k(\epsilon)\,=\,\Big\lceil\frac | ||
{\log(\| x_0- x^*\|/\epsilon)}{\log(1/L)}\Big\rceil | {\log(\| x_0- x^*\|/\epsilon)}{\log(1/L)}\Big\rceil | ||
\,=\,\Big\lceil\frac | \,=\,\Big\lceil\frac | ||
| Linia 291: | Linia 297: | ||
</math></center> | </math></center> | ||
iteracji, niezależnie od <math> | iteracji, niezależnie od <math>x_0</math>. Metody zbieżne dla | ||
dowolnego przybliżenia początkowego nazywamy | dowolnego przybliżenia początkowego nazywamy | ||
<strong>zbieżnymi globalnie</strong>. Obie przedstawione dotychczas metody: bisekcji i | <strong>zbieżnymi globalnie</strong>. Obie przedstawione dotychczas metody: bisekcji i | ||
Banacha przy rozsądnych | Banacha, przy rozsądnych | ||
założeniach są zbieżne globalnie. | założeniach, są zbieżne globalnie. | ||
Okazuje się, że metoda iteracji prostej może być --- w bardzo szczególnych | Okazuje się, że metoda iteracji prostej może być --- w bardzo szczególnych | ||
przypadkach --- zbieżna szybciej niż liniowo. Z taką sytuacją będziemy mieli do czynienia, | przypadkach --- zbieżna szybciej niż liniowo. Z taką sytuacją będziemy mieli do czynienia, gdy rozpatrzymy metodę Newtona. | ||
gdy | |||
==Metoda Newtona== | ==Metoda Newtona== | ||
Zarówno metoda Banacha, jak i bisekcja są zbieżnie liniowo, co w praktyce może | Zarówno metoda Banacha, jak i bisekcja, są zbieżnie liniowo, co w praktyce może | ||
okazać się zbieżnością dość powolną (np. dla metody zbieżnej liniowo z ilorazem | okazać się zbieżnością dość powolną (np. dla metody zbieżnej liniowo z ilorazem | ||
<math> | <math>1/2</math> dopiero po piątej iteracji dostajemy kolejną | ||
dokładną cyfrę wyniku). Wykorzystując więcej informacji o funkcji <math> | dokładną cyfrę wyniku). Wykorzystując więcej informacji o funkcji <math>f</math>, której | ||
miejsca zerowego poszukujemy, możemy istotnie przyspieszyć zbieżność metody. | miejsca zerowego poszukujemy, możemy istotnie przyspieszyć zbieżność metody. | ||
Ceną, jaką przyjdzie nam zapłacić, będzie utrata globalnej zbieżności. | Ceną, jaką przyjdzie nam zapłacić, będzie utrata globalnej zbieżności. | ||
[[grafika:Newton.jpg|thumb|right||Isaac Newton<br> [[Biografia Newton|Zobacz biografię]]]] | |||
W dalszych rozważaniach będziemy zakładać dla | W dalszych rozważaniach będziemy zakładać dla | ||
uproszczenia, że dziedzina <math> | uproszczenia, że dziedzina <math>D=R</math>. | ||
Idea metody Newtona opiera się na popularnym wśród inżynierów pomyśle <strong>linearyzacji</strong>: zamiast szukać miejsca zerowego skomplikowanej <math> | Idea <strong>metody Newtona</strong> opiera się na popularnym wśród inżynierów pomyśle <strong>linearyzacji</strong>: zamiast szukać miejsca zerowego skomplikowanej <math>f</math>, przybliżmy ją | ||
linią prostą, a dla niej już umiemy znaleźć miejsce zerowe! | linią prostą, a dla niej już umiemy znaleźć miejsce zerowe! | ||
<!-- | |||
Przypisywanie metody | |||
stycznych Newtonowi jest pewną przesadą. Metodę Newtona taką, jaką znamy (z | stycznych Newtonowi jest pewną przesadą. Metodę Newtona taką, jaką znamy (z | ||
pochodną w mianowniku), zaproponował w 1740 roku Simpson (ten od kwadratury), kilknaście lat po śmierci Newtona. Żeby było jeszcze zabawniej, odkrywcą | pochodną w mianowniku), zaproponował w 1740 roku Simpson (ten od kwadratury), kilknaście lat po śmierci Newtona. Żeby było jeszcze zabawniej, odkrywcą | ||
metody siecznych zdaje się być... Newton! Więcej na ten temat przeczytasz w | metody siecznych zdaje się być... Newton! Więcej na ten temat przeczytasz w | ||
artykule T.Ypma w SIAM Review 37, 1995. | artykule T.Ypma w SIAM Review 37, 1995. | ||
--> | |||
Startując z pewnego przybliżenia | Startując z pewnego przybliżenia | ||
początkowego <math> | początkowego <math>x_0</math>, w kolejnych krokach metody, <math>k</math>-te | ||
przybliżenie <math> | przybliżenie <math>x_k</math> jest punktem przecięcia stycznej do | ||
wykresu <math> | wykresu <math>f</math> w punkcie <math>x_{k-1}</math>. Ponieważ równanie | ||
stycznej wynosi <math> | stycznej wynosi <math>y(x)=f(x_{k-1})+f'(x_{k-1})(x-x_{k-1})</math>, | ||
otrzymujemy wzór | otrzymujemy wzór | ||
< | {{algorytm|Metoda Newtona (stycznych)|Metoda Newtona (stycznych)| | ||
</math></ | <pre>for k = 1,2,... | ||
<math>x_k\,=\,x_{k-1}\,-\,\frac{f(x_{k-1})}{f'(x_{k-1})}</math>; | |||
</pre>}} | |||
Oczywiście, aby metoda Newtona była dobrze zdefiniowana, | Oczywiście, aby metoda Newtona była dobrze zdefiniowana, | ||
musimy założyć, że <math> | musimy założyć, że <math>f'(x_{k-1})</math> istnieje i nie | ||
jest zerem. | jest zerem. | ||
<div class="thumb | <!-- | ||
[[Image:MNnewtononestep.png|thumb|550px|center|Metoda Newtona: pierwszy krok]] | |||
--> | |||
<div class="center"><div class="thumb tnone"><div style="width:552px;"><flash>file=Newtononestep.swf|width=550|height=300</flash> <div class="thumbcaption">Postęp iteracji Newtona</div></div></div></div> | |||
Zauważmy, że metodę Newtona można traktować jako | Zauważmy, że metodę Newtona można traktować jako | ||
szczególny przypadek iteracji prostych, gdzie | szczególny przypadek iteracji prostych, gdzie | ||
<center><math> | <center><math>\phi(x)\,=\,x-\frac{f(x)}{f'(x)}. | ||
</math></center> | </math></center> | ||
Widać też, że nie jest ona zbieżna globalnie. | Widać też, że nie jest ona zbieżna globalnie. | ||
Nawet jeśli pochodna w <math> | Metoda Newtona i jej podobne należą do | ||
ciąg <math> | grupy metod <strong>zbieżnych lokalnie</strong>. Znaczy to, że | ||
zbieżność ciągu <math>\{x_k\}_k</math> do zera danej funkcji <math>f</math> | |||
jest zapewniona jedynie wtedy, gdy przybliżenia początkowe | |||
zostały wybrane dostatecznie blisko <math>x^*</math>. | |||
Nawet jeśli pochodna w <math>x_{k-1}</math> się nie zeruje, | |||
ciąg <math>\{x_k\}_k</math> może nie zbiegać do zera funkcji <math>f</math>. | |||
Okazuje się jednak, że jeśli | Okazuje się jednak, że jeśli | ||
wystartujemy dostatecznie blisko rozwiązania <math> | wystartujemy dostatecznie blisko rozwiązania <math>x^*</math>, to | ||
metoda Newtona jest zbieżna. | metoda Newtona jest zbieżna. Dokładniej, załóżmy | ||
najpierw, że | najpierw, że | ||
<center><math>\ | <center><math>f(x^*)=0\quad \mbox{ oraz } \quad f'(x^*)\,\ne\,0. | ||
</math></center> | </math></center> | ||
Ponadto załóżmy, że <math> | Ponadto załóżmy, że <math>f</math> jest dwukrotnie | ||
różniczkowalna w sposób ciągły, <math> | różniczkowalna w sposób ciągły, <math>f\in C^2(D)</math>. | ||
Rozwijając <math> | Rozwijając <math>\phi</math> w szereg Taylora w punkcie <math>x^*</math>, | ||
otrzymujemy | otrzymujemy | ||
<center><math> | <center><math>x_k-x^*\,=\,\phi(x_{k-1})-\phi(x^*)\,=\, | ||
(x_{k-1}-x^*)\phi'(x^*)+(x_{k-1}-x^*)^2\phi''(\xi_k)/2, | (x_{k-1}-x^*)\phi'(x^*)+(x_{k-1}-x^*)^2\phi''(\xi_k)/2, | ||
</math></center> | </math></center> | ||
gdzie <math> | gdzie <math>\min(x^*,x_{k-1})\le\xi_k\le\max(x^*,x_{k-1})</math>. | ||
Wobec tego, że <math> | Wobec tego, że <math>\phi'(x^*)=f(x)f''(x)/(f'(x))^2=0</math> i | ||
<math> | <math>\phi''(\xi_k)=f''(\xi_k)/f'(\xi_k)</math>, mamy | ||
<center><math> | <center><math> | ||
x_k-x^*\,=\,(x_{k-1}-x^*)^2\frac{f''(\xi_k)}{2f'(\xi_k)} | x_k-x^*\,=\,(x_{k-1}-x^*)^2\frac{f''(\xi_k)}{2f'(\xi_k)}</math></center> | ||
</math></center> | |||
Zdefiniujmy liczbę | Zdefiniujmy liczbę | ||
<center><math> | <center><math>R_f\,=\,\sup_{r\ge 0}\sup_{\{x:|x-x^*|\le r\}} | ||
\Big|\frac{2(x-x^*)f''(x)}{f'(x)}\Big|\,<\,1. | \Big|\frac{2(x-x^*)f''(x)}{f'(x)}\Big|\,<\,1. | ||
</math></center> | </math></center> | ||
Oczywiście <math> | Oczywiście <math>R_f>0</math>. Dla <math>x_{k-1}</math> spełniającego | ||
<math> | <math>|x_{k-1}-x^*|\le R<R_f</math>, mamy z poprzedniej równości | ||
<center><math> | <center><math>|x_k-x^*|\,\le\,q\,|x_{k-1}-x^*|</math>,</center> | ||
</math></center> | |||
gdzie <math> | gdzie <math>q<1</math> i <math>q</math> zależy tylko od <math>R</math>. | ||
Niech teraz <math> | Niech teraz <math>x^*</math> będzie zerem <math>m</math>-krotnym, | ||
<center><math> | <center><math>f(x^*)=f'(x^*)=\cdots =f^{(m-1)}(x^*)=0\ne f^{(m)}(x^*)</math>,</center> | ||
</math></center> | |||
gdzie <math> | gdzie <math>m\ge 2</math>, oraz niech <math>f</math> będzie <math>m</math>-krotnie | ||
różniczkowalna w sposób ciągły. Wtedy | różniczkowalna w sposób ciągły. Wtedy | ||
<center><math>\ | <center><math>\begin{align} x_k-x^* &= (x_{k-1}-x^*)\,-\,\frac{(x_{k-1}-x^*)^m | ||
\frac{f^{(m)} (\eta_k^{(1)})}{m!}}{(x_{k-1}-x^*)^{m-1} | \frac{f^{(m)} (\eta_k^{(1)})}{m!}}{(x_{k-1}-x^*)^{m-1} | ||
\frac{f^{(m-1)}(\eta_k^{(2)})}{(m-1)!}} | \frac{f^{(m-1)}(\eta_k^{(2)})}{(m-1)!}} \\ | ||
&= (x_{k-1}-x^*)\left(1-\frac 1m\frac | &= (x_{k-1}-x^*)\left(1-\frac 1m\frac | ||
{f^{(m)}(\eta_k^{(1)})}{f^{(m)}(\eta_k^{(2)})} | {f^{(m)}(\eta_k^{(1)})}{f^{(m)}(\eta_k^{(2)})}\right) \\ | ||
&\approx & (x_{k-1}-x^*)\Big( 1-\frac 1m\Big), | |||
\end{align}</math></center> | |||
\ | |||
o ile <math>x_{k-1}</math> jest "blisko" <math>x^*</math>. | |||
Metoda Newtona jest więc zbieżna lokalnie. Gdy <math>x_0</math> jest zbyt daleko od rozwiązania może zdarzyć się, że iteracja Newtona zacznie nas oddalać od miejsca zerowego, co ilustruje poniższy przykład: | |||
<!-- | |||
[[Image:MNnewtononestepdiv.png|thumb|550px|center|Metoda Newtona: jeśli startujemy zbyt daleko od miejsca zerowego <math>f</math>, zamiast przybliżać się do niego, zaczynamy się oddalać! (gdzie będzie <math>x_3</math>?...)]] | |||
--> | |||
<div class="center"><div class="thumb tnone"><div style="width:552px;"><flash>file=Newtononestepdiv.swf|width=550|height=300</flash> <div class="thumbcaption">Metoda Newtona: jeśli startujemy zbyt daleko od miejsca zerowego <math>f</math>, zamiast przybliżać się do niego, zaczynamy się oddalać! (gdzie będzie <math>x_3</math>?...)</div></div></div></div> | |||
Z powyższego można też wywnioskować, | Z powyższego można też wywnioskować, | ||
jaki jest charakter zbieżności metody Newtona. Dla zera | jaki jest charakter zbieżności metody Newtona. Dla zera | ||
jednokrotnego <math> | jednokrotnego <math>x^*</math> oraz <math>f''(x^*)\ne 0</math> mamy bowiem | ||
<center><math> | <center><math>|x_k-x^*|\, \approx \,|x-x_{k-1}|^2 \frac{|f''(x^*)|}{2|f'(x^*)|}</math></center> | ||
</math></center> | |||
Mówimy, że zbieżność metody Newtona, gdy <math> | Mówimy, że zbieżność metody Newtona, gdy <math>f'(x^*)\neq 0</math> jest <strong>kwadratowa</strong>. | ||
{{stwierdzenie||| | {{stwierdzenie||| | ||
Jeśli <math> | Jeśli <math>f'(x^*)\neq 0</math> oraz | ||
<math> | <math>f''(x^*)=0</math> to zbieżność jest nawet szybsza. Z kolei dla | ||
zera <math> | zera <math>m</math>-krotnego (tzn. <math>f(x^*) = f'(x^*)= \ldots f^{(m)}(x^*)= 0</math>, <math>m>1</math>) | ||
zbieżność jest liniowa z ilorazem <math> | zbieżność jest liniowa z ilorazem <math>(1-\frac{1}{m})</math>. | ||
}} | }} | ||
| Linia 435: | Linia 452: | ||
zdefiniowany następująco. | zdefiniowany następująco. | ||
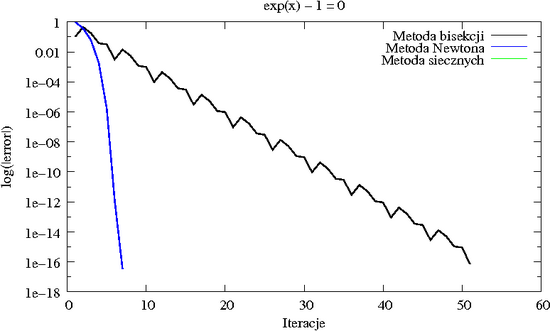
[[Image:MNstycznebisekcja.png|thumb| | [[Image:MNstycznebisekcja.png|thumb|550px|center|Porównanie zbieżności metody bisekcji i stycznych | ||
dla równania <math> | dla równania <math>e^x - 1 = 0</math>. Błąd kolejnych przybliżeń wyświetlany jest w skali | ||
logarytmicznej, dzięki czemu lepiej widać różnicę między zbieżnością liniową a | logarytmicznej, dzięki czemu lepiej widać różnicę między zbieżnością liniową a | ||
kwadratową.]] | kwadratową.]] | ||
Powiemy, że metoda iteracyjna <math> | Powiemy, że metoda iteracyjna <math>\phi</math> jest w klasie funkcji <math>F</math> | ||
rzędu co najmniej <math> | <strong>rzędu co najmniej <math>p\ge 1</math></strong>, gdy spełniony jest następujący | ||
warunek. Niech <math> | warunek. Niech <math>f\in F</math> i <math>f(x^*)=0</math>. Wtedy istnieje stała | ||
<math> | <math>C<\infty</math> taka, że dla dowolnych przybliżeń początkowych | ||
<math> | <math>x_0,\ldots,x_{s-1}</math> dostatecznie bliskich <math>x^*</math>, kolejne | ||
przybliżenia <math> | przybliżenia <math>x_k=\phi(x_{k-1},\ldots,x_{k-s})</math> generowane | ||
tą metodą spełniają | tą metodą spełniają | ||
<center><math> | <center><math>|x_k-x^*|\,\le\,C\,|x_{k-1}-x^*|^p</math></center> | ||
</math></center> | |||
Ponadto, jeśli <math> | Ponadto, jeśli <math>p=1</math> to dodatkowo żąda się, aby <math>C<1</math>. | ||
{{definicja||| | {{definicja||| | ||
Wykładnikiem zbieżności metody | <strong>Wykładnikiem zbieżności</strong> metody | ||
iteracyjnej <math> | iteracyjnej <math>\phi</math> w klasie <math>F</math> nazywamy liczbę <math>p^*</math> | ||
zdefiniowaną równością | zdefiniowaną równością | ||
<center><math> | <center><math>p^*\,=\,\sup\,\{\,p\ge 1:\,\phi | ||
\mbox{ jest rzędu co najmniej } p\,\} | \mbox{ jest rzędu co najmniej } p\,\}</math></center> | ||
</math></center> | |||
}} | }} | ||
| Linia 467: | Linia 482: | ||
które natychmiast wynika z poprzednich rozważań. | które natychmiast wynika z poprzednich rozważań. | ||
{{twierdzenie||| | {{twierdzenie|O rzędzie zbieżności metody Newtona|O rzędzie zbieżności metody Newtona| | ||
Wykładnik zbieżności metody Newtona | Wykładnik zbieżności metody Newtona | ||
(stycznych) wynosi <math> | (stycznych) wynosi <math>p^*=2</math> w klasie funkcji o zerach | ||
jednokrotnych, oraz <math> | jednokrotnych, oraz <math>p^*=1</math> w klasie funkcji o zerach | ||
wielokrotnych. | wielokrotnych. | ||
}} | }} | ||
[[Image:MNmultiplezeros.png|thumb| | [[Image:MNmultiplezeros.png|thumb|550px|center|Zbieżność metody Newtona dla zer wielokrotnych <math>f(x) | ||
= (x-1)^5</math> jest liniowa z ilorazem <math> | = (x-1)^5</math> jest liniowa z ilorazem <math>\frac{4}{5}</math> (końcowe załamanie wykresu | ||
spowodowane jest przypadkowym trafieniem w dokładne miejsce zerowe). Metoda bisekcji nie jest na to czuła i dalej zbiega z ilorazem | spowodowane jest przypadkowym trafieniem w dokładne miejsce zerowe). Metoda bisekcji nie jest na to czuła i dalej zbiega z ilorazem | ||
<math> | <math>\frac{1}{2}</math>.]] | ||
==Metoda siecznych== | ==Metoda siecznych== | ||
Inną znaną i często używaną metodą iteracyjną opartą na podobnym pomyśle | Inną znaną i często używaną metodą iteracyjną, opartą na podobnym pomyśle | ||
linearyzacyjnym co metoda Newtona, | |||
jest <strong>metoda siecznych</strong>, w której zamiast przybliżenia wykresu <math> | jest <strong>metoda siecznych</strong>, w której zamiast przybliżenia wykresu <math>f</math> przez | ||
styczną, stosuje się przybliżenie sieczną. | styczną, stosuje się przybliżenie sieczną. | ||
Metoda ta | Metoda ta | ||
wykorzystuje więc do konstrukcji <math> | wykorzystuje więc do konstrukcji <math>x_k</math> przybliżenia | ||
<math> | <math>x_{k-1}</math> i <math>x_{k-2}</math>. Musimy również wybrać dwa różne | ||
punkty startowe <math> | punkty startowe <math>x_0</math> i <math>x_1</math>. Ponieważ sieczna dla | ||
<math> | <math>f</math> w punktach <math>x_{k-1}</math> i <math>x_{k-2}</math> ma wzór | ||
<center><math> | <center><math>y(x)\,=\,\frac{x-x_{k-2}}{x_{k-1}-x_{k-2}}f(x_{k-1})+ | ||
\frac{x-x_{k-1}}{x_{k-2}-x_{k-1}}f(x_{k-2}) | \frac{x-x_{k-1}}{x_{k-2}-x_{k-1}}f(x_{k-2})</math>,</center> | ||
</math></center> | |||
otrzymujemy | otrzymujemy | ||
< | {{algorytm|Metoda siecznych|Metoda siecznych| | ||
<pre>for k = 1,2,... | |||
</math></ | <math>x_k\,=\,x_{k-1}\,-\,\frac{x_{k-1}-x_{k-2}} {f(x_{k-1})-f(x_{k-2})}\,f(x_{k-1})</math>; | ||
end | |||
</pre>}} | |||
Zauważmy, że jeśli <math> | Zauważmy, że jeśli <math>x_{k-1}</math> i <math>x_{k-2}</math> są blisko | ||
siebie, to <math> | siebie, to <math>x_k</math> jest podobny do tego z metody Newtona, | ||
bowiem wtedy iloraz różnicowy | bowiem wtedy iloraz różnicowy [[MN14#Różniczkowanie|przybliża pochodną]] <math>f</math>, | ||
<center><math> | <center><math> | ||
\frac{f(x_{k-1})-f(x_{k-2})}{x_{k-1}-x_{k-2}} \approx f'(x_{k-1}) | \frac{f(x_{k-1})-f(x_{k-2})}{x_{k-1}-x_{k-2}} \approx f'(x_{k-1})</math></center> | ||
</math></center> | |||
Nie wystarcza to | Nie wystarcza to jednak, aby osiągnąć zbieżność z wykładnikiem | ||
jednak, aby osiągnąć zbieżność z wykładnikiem | <math>2</math>. Można pokazać, że przy podobnych założeniach o funkcji, wykładnik zbieżności metody siecznych dla zer jednokrotnych i dostatecznie gładkich funkcji wynosi <math>p^*=\frac{1+\sqrt{5}}{2}=1.618\ldots</math>. Jako wariant metody Newtona, metoda siecznych jest również zbieżna lokalnie. | ||
<math> | |||
zbieżności metody siecznych dla zer jednokrotnych dostatecznie gładkich funkcji | [[Image:MNstycznesiecznebisekcja.png|thumb|550px|center|Porównanie zbieżności metody bisekcji, | ||
wynosi <math> | stycznych i siecznych | ||
siecznych jest również zbieżna lokalnie. | dla równania <math>e^x - 1 = 0</math>. Błąd kolejnych przybliżeń wyświetlany jest w skali | ||
logarytmicznej.]] | |||
Niewątpliwą zaletą metody siecznych jest jednak to, | Niewątpliwą zaletą metody siecznych jest jednak to, że <strong>nie wymaga obliczania pochodnej funkcji</strong> (bywa, że dokładne wyznaczenie pochodnej jest niemożliwe, gdy np. funkcja jest zadana zewnętrzną procedurą, do której kodu źródłowego nie mamy dostępu; zwykle też koszt obliczenia wartości pochodnej jest wyższy od kosztu obliczenia wartości funkcji). Jest to również istotne w pakietach numerycznych, gdzie czasem nie chcemy wymagać od użytkownika czegokolwiek, oprócz podania wzoru na funkcję i przybliżonej lokalizacji miejsca zerowego. | ||
że nie wymaga | |||
numerycznych, gdzie czasem nie chcemy wymagać od użytkownika czegokolwiek | |||
Ponadto, często zdarza się, że wyznaczenie wartości pochodnej, <math> | Ponadto, często zdarza się, że wyznaczenie wartości pochodnej, <math>f'(x_k)</math>, jest | ||
tak samo, albo i bardziej kosztowne od wyznaczenia wartości <math> | tak samo, albo i bardziej kosztowne od wyznaczenia wartości <math>f(x_k)</math>. W takim | ||
wypadku okazuje się, że metoda | wypadku okazuje się, że metoda siecznych --- choć wolniej zbieżna niż metoda | ||
Newtona --- dzięki temu, że jej iteracja wymaga jedynie wyznaczenia jednej wartości <math>f</math>, jest <strong>bardziej efektywna</strong> od metody Newtona: koszt osiągnięcia zadanej dokładności jest w takim przypadku mniejszy od analogicznego kosztu dla metody Newtona. | |||
jej iteracja wymaga jedynie wyznaczenia jednej wartości <math> | |||
efektywna</strong> od metody Newtona: koszt osiągnięcia zadanej dokładności jest w | |||
takim przypadku mniejszy od analogicznego kosztu dla metody Newtona. | |||
Jednak | Jednak gdy żądane przez użytkownika dokładności są bardzo wielkie, a sama | ||
funkcja "złośliwa", metoda siecznych może cierpieć z powodu redukcji cyfr | funkcja "złośliwa", metoda siecznych może cierpieć z powodu redukcji cyfr | ||
przy odejmowaniu. | przy odejmowaniu. | ||
==Metoda Brenta== | ==Metoda Brenta== | ||
| Linia 545: | Linia 549: | ||
sposób połączyć globalnej zbieżności metody bisekcji z szybką zbieżnością | sposób połączyć globalnej zbieżności metody bisekcji z szybką zbieżnością | ||
metody siecznych tak, by uzyskać metodę zbieżną globalnie, a jednocześnie | metody siecznych tak, by uzyskać metodę zbieżną globalnie, a jednocześnie | ||
istotnie szybciej niż liniowo | istotnie szybciej niż liniowo. | ||
Okazuje się, że można to zrobić, wprowadzając metodę opartą na <strong>trzech</strong> punktach lokalizujących miejsce zerowe: dwóch odcinających zero tak jak | Okazuje się, że można to zrobić, wprowadzając metodę opartą na <strong>trzech</strong> punktach lokalizujących miejsce zerowe: dwóch odcinających zero tak jak | ||
w metodzie bisekcji i trzecim, konstruowanym | w metodzie bisekcji i trzecim, konstruowanym np. jak w metodzie stycznych. W | ||
kolejnej iteracji | kolejnej iteracji wymieniamy jeden z punktów albo wedle metody | ||
siecznych (i wtedy zapewne szybciej zbliżamy się do zera), albo | siecznych (i wtedy zapewne szybciej zbliżamy się do zera), albo wykonując bisekcję (aby zagwarantować sobie, że w wiadomym przedziale miejsce zerowe rzeczywiście się znajduje). | ||
(aby zagwarantować sobie, że w wiadomym przedziale miejsce zerowe rzeczywiście | |||
się znajduje). | Ten prosty pomysł <strong>metody hybrydowej</strong> wymaga jednak subtelnego dopracowania. Zostało to zrobione w 1973 roku przez [http://www.rpbrent.com Richarda Brenta]. Funkcja MATLABa (i Octave'a) <code style="color: #006">fzero</code> implementują właśnie metodę Brenta. | ||
Autorem implementacji w Octave jest ówczesny student [http://www.mimuw.edu.pl matematyki] na Uniwersytecie Warszawskim, Łukasz Bodzon. Fortranowski kod metody Brenta można znaleźć także w [http://www.netlib.org/go/zeroin.f Netlibie]. Inną funkcją Octave'a służącą rozwiązywaniu równań nieliniowych jest <code style="color: #006">fsolve</code>: | |||
<div style="font-family: monospace; white-space: pre; border-style: dashed; border-width: thin; border-color: black; margin: 1em; padding:1em; color: #444; background-color:#fdfdfd;"><nowiki>octave:1> [X, MSG, INFO] = fsolve ('cos', 1) | |||
X = 1.5708 | |||
MSG = 1 | |||
INFO = solution converged within specified tolerance | |||
octave:2> cos(X) | |||
ans = 6.1230e-17 | |||
</nowiki></div> | |||
==Metody dla układów równań nieliniowych== | |||
Niektóre z poznanych metod można łatwo rozszerzyć na przypadek układu <math>N</math> równań z <math>N</math> niewiadomymi, to znaczy | |||
<center><math>F(x) = 0</math>,</center> | |||
== | gdzie <math>F: R^N \rightarrow R^N</math>. | ||
===Metoda Banacha=== | |||
Jak pamiętamy, [[#Banacha, o kontrakcji|metodę Banacha]] sformułowaliśmy od razu dla zagadnienia wielowymiarowego. Analiza i własności metody są zatem już [[#Banacha, o kontrakcji|omówione]]. | |||
===Wielowymiarowa metoda Newtona=== | |||
Okazuje się, że metodę Newtona można uogólnić na przypadek układu <math>N</math> równań nieliniowych z <math>N</math> niewiadomymi. Zapiszmy wzór na skalarną metodę Newtona odrobinę inaczej: | |||
<center><math>x_{k+1} = x_k - [F'(x_k)]^{-1}\, F(x_k)</math></center> | |||
Niezwykłe jest, że taki wzór nie tylko ma sens w przypadku, gdy <math>F: R^N \rightarrow R^N</math> (wtedy <math>F'(x_k)</math> jest macierzą Jakobianu <math>F</math> w punkcie <math>x_k</math>), ale dodatkowo ta metoda zachowuje wszystkie własności metody stycznych dla przypadku skalarnego: | |||
{{twierdzenie|O zbieżności wielowymiarowej metody Newtona|O zbieżności wielowymiarowej metody Newtona| | |||
Załóżmy, że <math>F: R^N \rightarrow R^N</math> i istnieje <math>x^* \in R^N</math> taki, że | |||
<center><math>F(x^*) = 0</math></center> | |||
Załóżmy ponadto, że <math>F</math> jest różniczkowalna, a jej pochodna <math>F': R^N \rightarrow R^{N\times N}</math> jest lipschitzowska i dodatkowo | |||
<center><math>F'(x^*) \mbox{ jest nieosobliwa} </math></center> | |||
Wówczas, jeśli tylko <math>x_0</math> jest dostatecznie blisko rozwiązania <math>x^*</math>, to ciąg kolejnych przybliżeń <math>x_k</math>, generowany wielowymiarową metodą Newtona, jest zbieżny do <math>x^*</math>. Co więcej, szybkość zbieżności jest kwadratowa. | |||
}} | |||
===Implementacja wielowymiarowej metody Newtona=== | |||
Implementując wielowymiarową metodę Newtona, musimy dysponować nie tylko funkcją obliczającą <math>N</math> współrzędnych wektora wartości <math>F</math>, ale także funkcją wyznaczającą <math>N^2</math> elementów macierzy pochodnej <math>F</math> w zadanym punkcie <math>x \in R^N</math>. Zwróćmy uwagę na to, że w implementacji metody nie trzeba wyznaczać <math>F'(x_k)^{-1}</math>, tylko rozwiązać układ równań: | |||
{{algorytm|Wielowymiarowa metoda Newtona|Wielowymiarowa metoda Newtona| | |||
<Source>while (!stop) | |||
{ | |||
rozwiąż (względem <math>s</math>) układ równań liniowych <math>F'(x_k)\, s = -F(x_k)</math>; | |||
<math>x_{k+1}</math> = <math>x_k</math> + <math>s</math>; | |||
} | |||
</Source>}} | |||
O tym, [[MN05|jak skutecznie rozwiązywać układy równań liniowych]], dowiesz się z kolejnych wykładów. Dowiesz się także, dlaczego ''nie należy'' w implementacji korzystać z wyznaczonej ''explicite'' macierzy odwrotnej do macierzy Jakobianu. | |||
==Literatura== | |||
W celu dogłębnego zapoznania się z omawianym na wykładzie materiałem, przeczytaj <b>rozdział 3</b> w | |||
* D. Kincaid, W. Cheney <cite>Analiza numeryczna</cite>, Wydawnictwa Naukowo-Techniczne, Warszawa 2006, ISBN 83-204-3078-X. | |||
Rozdziały 3.5 i 3.6 nie są obowiązkowe. | |||
Wiele wariantów metod rozwiązywania <strong>układów</strong> równań nieliniowych jest przedstawionych w znakomitej monografii | |||
* <span style="font-variant:small-caps">C.T.Kelley</span>, <cite>Iterative Solution of Systems of Linear and Nonlinear Equations</cite>, SIAM, 1995. | |||
Opis metody Brenta znajdziesz w książce | |||
* <span style="font-variant:small-caps">R. Brent</span>, <cite>Algorithms for Minimization Without Derivatives</cite>, Prentice-Hall, 1973. | |||
Aktualna wersja na dzień 11:13, 12 wrz 2023
Równania nieliniowe
<<< Powrót do strony głównej przedmiotu Metody numeryczne
W wielu zadaniach, m.in. matematyki stosowanej, spotykamy się z problemem rozwiązania skalarnego równania nieliniowego postaci . Oto kilka przykładów:
Przykład
Równanie Keplera
jest bardzo ważne w astronomii, jego rozwiązanie pozwala wyznaczyć przyszłe położenie planety. Parametr odpowiada ekscentryczności orbity i przyjmuje wartości z przedziału . Poza paru prostymi przypadkami, w ogólności równanie Keplera nie daje się rozwiązać w terminach funkcji elementarnych.

Zobacz biografię
Przykład
Znajdowanie miejsc zerowych wielomianu
Bardzo wiele modeli matematycznych wymaga rozwiązania równania z wielomianową nieliniowością. Piękne kwadratury (Gaussa) opierają się na węzłach będących zerami pewnego wielomianu. Wielomiany są bardzo szczególnymi funkcjami i dla nich istnieje szereg wyspecjalizowanych metod znajdowania ich pierwiastków, m.in. metoda Laguerre'a, metoda Bairstow'a (o nich tu nie będziemy mówić), a także zaskakujące metody sprowadzające zadanie poszukiwania miejsc zerowych wielomianu do zupełnie innego zadania matematycznego --- o nich jednak będzie mowa dopiero w wykładzie dotyczącym znajdowania wartości własnych macierzy.
Przykład
Obliczanie pierwiastka kwadratowego z zadanej liczby , czyli sposób na implementację funkcji "sqrt()". Można to zadanie wyrazić, jako rozwiązywanie równania
Szybkie algorytmy wyznaczania pierwiastka kwadratowego były znane już starożytnym. W wykładzie zrozumiemy, dlaczego metoda Herona,
daje bardzo dobre przybliżenie już po kilku iteracjach.
Przykład
Implementacja wyznaczania odwrotności liczby (bez dzielenia!) jest możliwa, gdy odpowiednią metodą będziemy poszukiwać rozwiązania równania
To zadanie jest ważne praktycznie, np. tak można poprawić precyzję funkcji wektorowych stosowanych w niektórych procesorach AMD. Okazuje się, że instrukcja procesora służąca do równoległego obliczania odwrotności sekwencji liczb umieszczonych w 128-bitowym rejestrze wektorowym daje wynik z małą precyzją (oczywiście po to, by wykonywała się szybciej!). Jeśli taka dokładność wyniku nie odpowiada nam, możemy ją --- zgodnie z manualem procesora --- poprawić, rozwiązując właśnie takie równanie jak powyżej, metodą korzystającą wyłącznie z (wektorowych) operacji mnożenia i dodawania.
Bisekcja
Metoda bisekcji, czyli połowienia, często stosowana w innych działach informatyki, jest dość naturalną metodą obliczania zer skalarnych funkcji ciągłych określonych na danym przedziale i zmieniających znak. Dokładniej, rozpatrzmy klasę funkcji
to znaczy przyjmują w krańcach przedziału wartości przeciwnego znaku. Oczywiście, każda funkcja ma, na mocy twierdzenia Darboux, co najmniej jedno zero w . Startując z przedziału , w kolejnych krokach metody bisekcji obliczamy informację o wartości w środku przedziału, co pozwala nam w następnym kroku zmniejszyć o połowę przedział, w którym na pewno znajduje się zero funkcji.
Bisekcję realizuje następujący ciąg poleceń, po wykonaniu którego jest przybliżeniem zera funkcji z zadaną dokładnością .
Algorytm Metoda bisekcji
lewy = a; prawy = b;
flewy = f(lewy); fprawy = f(prawy);
x = (a+b)/2; /* przybliżenie rozwiązania */
e = (b-a)/2; /* przedział lokalizujący rozwiązanie dokładne */
while (e > <math>\epsilon</math>)
{
fx = f(x); /* reszta */
if ( abs(fx) == 0 ) /* trafiliśmy dokładnie w miejsce zerowe */
return(x);
if ( sign(fx) != sign(flewy) ) /* tzn. f(lewy)*f(x) < 0 */
{
prawy = x;
fprawy = fx;
}
else
{
lewy = x;
flewy = fx;
}
x = (lewy+prawy)/2; /* najlepsze przybliżenie rozwiązania przy danym przedziale */
e = e/2;
}
return(x);Z konstrukcji metody łatwo wynika, że po wykonaniu
obrotów pętli while (czyli po obliczeniu wartości funkcji)
otrzymujemy , które odległe jest od pewnego rozwiązania o co najwyżej
Metoda bisekcji jest więc zbieżna liniowo z ilorazem . Choć ta zbieżność nie jest imponująca, bisekcja ma kilka istotnych zalet. Oprócz jej prostoty, należy podkreślić fakt, że bisekcja jest w pewnym sensie uniwersalna. Jeśli tylko dysponujemy dwoma punktami i takimi, że przyjmuje w nich wartości przeciwnych znaków, to metoda bisekcji z pewnością znajdzie miejsce zerowe funkcji, choćby początkowa długość przedziału była bardzo duża: zbieżność metody bisekcji jest globalna. Co ważniejsze, dla zbieżności metody bisekcji wystarcza jedynie ciągłość funkcji. Poza tym możemy łatwo kontrolować błąd bezwzględny aproksymacji miejsca zerowego. Konsekwencją powyższego oszacowania błędu jest bowiem następujący wniosek.
Wniosek
Dla znalezienia zera z dokładnością , wystarczy obliczyć w metodzie bisekcji
wartości funkcji.
Iteracja prosta Banacha
Zupełnie inne, i jak się okaże --- przy odrobinie sprytu bardzo skuteczne --- podejście do wyznaczania miejsca zerowego jest oparte na metodzie Banacha. Dla większej ogólności, będziemy zakładać teraz, że i jest otwartym, niepustym podzbiorem .
Najpierw nasze równanie nieliniowe
przekształcamy (dobierając odpowiednią funkcję ) do równania równoważnego (tzn. mającego te same rozwiązania)
Taki , dla którego zachodzi powyższa równość, nazywamy punktem stałym odwzorowania .
Następnie, startując z pewnego przybliżenia początkowego , konstruujemy ciąg kolejnych przybliżeń według wzoru

Zobacz biografię
Twierdzenie Banacha, o kontrakcji
Niech będzie domkniętym podzbiorem dziedziny ,
w którym jest odwzorowaniem zwężającym. To znaczy, , oraz istnieje stała taka, że
Wtedy równanie
ma dokładnie jedno rozwiązanie , oraz
dla dowolnego przybliżenia początkowego .
Dowód
Wobec
dla mamy
Ciąg jest więc ciągiem Cauchy'ego. Stąd istnieje granica , która należy do , wobec domkniętości tego zbioru. Ponieważ lipschitzowskość implikuje jej ciągłość, mamy też
tzn. jest punktem stałym odwzorowania . Dla jednoznaczności zauważmy, że jeśliby istniał drugi, różny od , punkt stały , to mielibyśmy
Stąd , co jest sprzeczne z założeniem, że
jest zwężająca.Z powyższych rozważań otrzymujemy natychmiastowy wniosek dotyczący zbieżności iteracji prostych.
Wniosek
Przy założeniach twierdzenia Banacha, metoda iteracji prostych jest zbieżna co najmniej liniowo z ilorazem , tzn.
Przykład
Dla ilustracji, rozpatrzmy równanie Keplera, gdy :

W tym przypadku . Zauważmy, że w funkcja jest zwężająca ze stałą
Ponieważ obrazem prostej przy przekształceniu jest odcinek , to znaczy, że --- ograniczona do --- spełnia założenia twierdzenia Banacha o kontrakcji. Stąd istnieje dokładnie jedno rozwiązanie naszego równania w przedziale . Rozwiązanie to może być aproksymowane z dowolnie małym błędem przy pomocy iteracji prostych, startując z dowolnego przybliżenia początkowego . Jednak, gdy , zbieżność może być bardzo powolna... (Wkrótce przekonasz się, że są szybsze metody).
Zaletą iteracji prostych jest fakt, że zbieżność nie zależy od wymiaru zadania, ale tylko od stałej Lipschitza (jednak w praktyce czasem sama stała Lipschitza może zależeć od wymiaru zadania...). Metoda Banacha ma szczególne zastosowanie w przypadku, gdy funkcja jest zwężająca na całym zbiorze , tzn. . Jeśli ponadto ma skończoną średnicę, , to dla osiągnięcia -aproksymacji zera funkcji wystarczy wykonać
iteracji, niezależnie od . Metody zbieżne dla dowolnego przybliżenia początkowego nazywamy zbieżnymi globalnie. Obie przedstawione dotychczas metody: bisekcji i Banacha, przy rozsądnych założeniach, są zbieżne globalnie.
Okazuje się, że metoda iteracji prostej może być --- w bardzo szczególnych przypadkach --- zbieżna szybciej niż liniowo. Z taką sytuacją będziemy mieli do czynienia, gdy rozpatrzymy metodę Newtona.
Metoda Newtona
Zarówno metoda Banacha, jak i bisekcja, są zbieżnie liniowo, co w praktyce może okazać się zbieżnością dość powolną (np. dla metody zbieżnej liniowo z ilorazem dopiero po piątej iteracji dostajemy kolejną dokładną cyfrę wyniku). Wykorzystując więcej informacji o funkcji , której miejsca zerowego poszukujemy, możemy istotnie przyspieszyć zbieżność metody. Ceną, jaką przyjdzie nam zapłacić, będzie utrata globalnej zbieżności.
Zobacz biografię
W dalszych rozważaniach będziemy zakładać dla uproszczenia, że dziedzina .
Idea metody Newtona opiera się na popularnym wśród inżynierów pomyśle linearyzacji: zamiast szukać miejsca zerowego skomplikowanej , przybliżmy ją linią prostą, a dla niej już umiemy znaleźć miejsce zerowe!
Startując z pewnego przybliżenia
początkowego , w kolejnych krokach metody, -te
przybliżenie jest punktem przecięcia stycznej do
wykresu w punkcie . Ponieważ równanie
stycznej wynosi ,
otrzymujemy wzór
Algorytm Metoda Newtona (stycznych)
for k = 1,2,...
<math>x_k\,=\,x_{k-1}\,-\,\frac{f(x_{k-1})}{f'(x_{k-1})}</math>;
Oczywiście, aby metoda Newtona była dobrze zdefiniowana, musimy założyć, że istnieje i nie jest zerem.
Zauważmy, że metodę Newtona można traktować jako szczególny przypadek iteracji prostych, gdzie
Widać też, że nie jest ona zbieżna globalnie.
Metoda Newtona i jej podobne należą do grupy metod zbieżnych lokalnie. Znaczy to, że zbieżność ciągu do zera danej funkcji jest zapewniona jedynie wtedy, gdy przybliżenia początkowe zostały wybrane dostatecznie blisko .
Nawet jeśli pochodna w się nie zeruje, ciąg może nie zbiegać do zera funkcji . Okazuje się jednak, że jeśli wystartujemy dostatecznie blisko rozwiązania , to metoda Newtona jest zbieżna. Dokładniej, załóżmy najpierw, że
Ponadto załóżmy, że jest dwukrotnie różniczkowalna w sposób ciągły, . Rozwijając w szereg Taylora w punkcie , otrzymujemy
gdzie . Wobec tego, że i , mamy
Zdefiniujmy liczbę
Oczywiście . Dla spełniającego , mamy z poprzedniej równości
gdzie i zależy tylko od .
Niech teraz będzie zerem -krotnym,
gdzie , oraz niech będzie -krotnie różniczkowalna w sposób ciągły. Wtedy
o ile jest "blisko" .
Metoda Newtona jest więc zbieżna lokalnie. Gdy jest zbyt daleko od rozwiązania może zdarzyć się, że iteracja Newtona zacznie nas oddalać od miejsca zerowego, co ilustruje poniższy przykład:
Z powyższego można też wywnioskować, jaki jest charakter zbieżności metody Newtona. Dla zera jednokrotnego oraz mamy bowiem
Mówimy, że zbieżność metody Newtona, gdy jest kwadratowa.
Stwierdzenie
Jeśli oraz to zbieżność jest nawet szybsza. Z kolei dla zera -krotnego (tzn. , ) zbieżność jest liniowa z ilorazem .
Metoda Newtona jest pierwszą poznaną tutaj metodą iteracyjną, która jest (dla zer jednokrotnych) zbieżna szybciej niż liniowo. Dla takich metod wprowadza się pojęcie wykładnika zbieżności, który jest zdefiniowany następująco.
Powiemy, że metoda iteracyjna jest w klasie funkcji rzędu co najmniej , gdy spełniony jest następujący warunek. Niech i . Wtedy istnieje stała taka, że dla dowolnych przybliżeń początkowych dostatecznie bliskich , kolejne przybliżenia generowane tą metodą spełniają
Ponadto, jeśli to dodatkowo żąda się, aby .
Definicja
Wykładnikiem zbieżności metody iteracyjnej w klasie nazywamy liczbę zdefiniowaną równością
Możemy teraz sformułować następujące twierdzenie, które natychmiast wynika z poprzednich rozważań.
Twierdzenie O rzędzie zbieżności metody Newtona
Wykładnik zbieżności metody Newtona (stycznych) wynosi w klasie funkcji o zerach jednokrotnych, oraz w klasie funkcji o zerach wielokrotnych.

Metoda siecznych
Inną znaną i często używaną metodą iteracyjną, opartą na podobnym pomyśle linearyzacyjnym co metoda Newtona, jest metoda siecznych, w której zamiast przybliżenia wykresu przez styczną, stosuje się przybliżenie sieczną.
Metoda ta wykorzystuje więc do konstrukcji przybliżenia i . Musimy również wybrać dwa różne punkty startowe i . Ponieważ sieczna dla w punktach i ma wzór
otrzymujemy
Algorytm Metoda siecznych
for k = 1,2,...
<math>x_k\,=\,x_{k-1}\,-\,\frac{x_{k-1}-x_{k-2}} {f(x_{k-1})-f(x_{k-2})}\,f(x_{k-1})</math>;
end
Zauważmy, że jeśli i są blisko siebie, to jest podobny do tego z metody Newtona, bowiem wtedy iloraz różnicowy przybliża pochodną ,
Nie wystarcza to jednak, aby osiągnąć zbieżność z wykładnikiem . Można pokazać, że przy podobnych założeniach o funkcji, wykładnik zbieżności metody siecznych dla zer jednokrotnych i dostatecznie gładkich funkcji wynosi . Jako wariant metody Newtona, metoda siecznych jest również zbieżna lokalnie.

Niewątpliwą zaletą metody siecznych jest jednak to, że nie wymaga obliczania pochodnej funkcji (bywa, że dokładne wyznaczenie pochodnej jest niemożliwe, gdy np. funkcja jest zadana zewnętrzną procedurą, do której kodu źródłowego nie mamy dostępu; zwykle też koszt obliczenia wartości pochodnej jest wyższy od kosztu obliczenia wartości funkcji). Jest to również istotne w pakietach numerycznych, gdzie czasem nie chcemy wymagać od użytkownika czegokolwiek, oprócz podania wzoru na funkcję i przybliżonej lokalizacji miejsca zerowego.
Ponadto, często zdarza się, że wyznaczenie wartości pochodnej, , jest tak samo, albo i bardziej kosztowne od wyznaczenia wartości . W takim wypadku okazuje się, że metoda siecznych --- choć wolniej zbieżna niż metoda Newtona --- dzięki temu, że jej iteracja wymaga jedynie wyznaczenia jednej wartości , jest bardziej efektywna od metody Newtona: koszt osiągnięcia zadanej dokładności jest w takim przypadku mniejszy od analogicznego kosztu dla metody Newtona.
Jednak gdy żądane przez użytkownika dokładności są bardzo wielkie, a sama funkcja "złośliwa", metoda siecznych może cierpieć z powodu redukcji cyfr przy odejmowaniu.
Metoda Brenta
Naturalnie, uważny student zaczyna zadawać sobie pytanie, czy nie można w jakiś sposób połączyć globalnej zbieżności metody bisekcji z szybką zbieżnością metody siecznych tak, by uzyskać metodę zbieżną globalnie, a jednocześnie istotnie szybciej niż liniowo.
Okazuje się, że można to zrobić, wprowadzając metodę opartą na trzech punktach lokalizujących miejsce zerowe: dwóch odcinających zero tak jak w metodzie bisekcji i trzecim, konstruowanym np. jak w metodzie stycznych. W kolejnej iteracji wymieniamy jeden z punktów albo wedle metody siecznych (i wtedy zapewne szybciej zbliżamy się do zera), albo wykonując bisekcję (aby zagwarantować sobie, że w wiadomym przedziale miejsce zerowe rzeczywiście się znajduje).
Ten prosty pomysł metody hybrydowej wymaga jednak subtelnego dopracowania. Zostało to zrobione w 1973 roku przez Richarda Brenta. Funkcja MATLABa (i Octave'a) fzero implementują właśnie metodę Brenta.
Autorem implementacji w Octave jest ówczesny student matematyki na Uniwersytecie Warszawskim, Łukasz Bodzon. Fortranowski kod metody Brenta można znaleźć także w Netlibie. Inną funkcją Octave'a służącą rozwiązywaniu równań nieliniowych jest fsolve:
Metody dla układów równań nieliniowych
Niektóre z poznanych metod można łatwo rozszerzyć na przypadek układu równań z niewiadomymi, to znaczy
gdzie .
Metoda Banacha
Jak pamiętamy, metodę Banacha sformułowaliśmy od razu dla zagadnienia wielowymiarowego. Analiza i własności metody są zatem już omówione.
Wielowymiarowa metoda Newtona
Okazuje się, że metodę Newtona można uogólnić na przypadek układu równań nieliniowych z niewiadomymi. Zapiszmy wzór na skalarną metodę Newtona odrobinę inaczej:
Niezwykłe jest, że taki wzór nie tylko ma sens w przypadku, gdy (wtedy jest macierzą Jakobianu w punkcie ), ale dodatkowo ta metoda zachowuje wszystkie własności metody stycznych dla przypadku skalarnego:
Twierdzenie O zbieżności wielowymiarowej metody Newtona
Załóżmy, że i istnieje taki, że
Załóżmy ponadto, że jest różniczkowalna, a jej pochodna jest lipschitzowska i dodatkowo
Wówczas, jeśli tylko jest dostatecznie blisko rozwiązania , to ciąg kolejnych przybliżeń , generowany wielowymiarową metodą Newtona, jest zbieżny do . Co więcej, szybkość zbieżności jest kwadratowa.
Implementacja wielowymiarowej metody Newtona
Implementując wielowymiarową metodę Newtona, musimy dysponować nie tylko funkcją obliczającą współrzędnych wektora wartości , ale także funkcją wyznaczającą elementów macierzy pochodnej w zadanym punkcie . Zwróćmy uwagę na to, że w implementacji metody nie trzeba wyznaczać , tylko rozwiązać układ równań:
Algorytm Wielowymiarowa metoda Newtona
while (!stop)
{
rozwiąż (względem <math>s</math>) układ równań liniowych <math>F'(x_k)\, s = -F(x_k)</math>;
<math>x_{k+1}</math> = <math>x_k</math> + <math>s</math>;
}O tym, jak skutecznie rozwiązywać układy równań liniowych, dowiesz się z kolejnych wykładów. Dowiesz się także, dlaczego nie należy w implementacji korzystać z wyznaczonej explicite macierzy odwrotnej do macierzy Jakobianu.
Literatura
W celu dogłębnego zapoznania się z omawianym na wykładzie materiałem, przeczytaj rozdział 3 w
- D. Kincaid, W. Cheney Analiza numeryczna, Wydawnictwa Naukowo-Techniczne, Warszawa 2006, ISBN 83-204-3078-X.
Rozdziały 3.5 i 3.6 nie są obowiązkowe.
Wiele wariantów metod rozwiązywania układów równań nieliniowych jest przedstawionych w znakomitej monografii
- C.T.Kelley, Iterative Solution of Systems of Linear and Nonlinear Equations, SIAM, 1995.
Opis metody Brenta znajdziesz w książce
- R. Brent, Algorithms for Minimization Without Derivatives, Prentice-Hall, 1973.