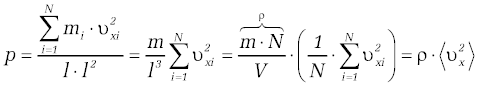PF Moduł 9: Różnice pomiędzy wersjami
mNie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 7 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
__TOC__ | |||
= Wykład = | |||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd1.png]] | |width="450px" valign="top"|[[Grafika:PF_M9_Slajd1.png]] | ||
|valign="top"|'''Wprowadzenie''' | |valign="top"|'''Wprowadzenie''' | ||
Z mikroskopowego punktu widzenia substancje mają budowę "ziarnistą". Składnikami ich są atomy bądź cząsteczki, których wzajemne oddziaływania określają własności makroskopowe substancji jak ciśnienie lub temperatura oraz stan skupienia: stały, ciekły lub gazowy. Ogromna liczba cząsteczek, z jaką zwykle mamy do czynienia uniemożliwia stosowanie do opisu ich ruchu równań Newtona w takim sensie, jak się to czyni w mechanice. W jednym centymetrze sześciennym gazu mieści się w warunkach normalnych około <math>10^{19}\ | Z mikroskopowego punktu widzenia substancje mają budowę "ziarnistą". Składnikami ich są atomy bądź cząsteczki, których wzajemne oddziaływania określają własności makroskopowe substancji jak ciśnienie lub temperatura oraz stan skupienia: stały, ciekły lub gazowy. Ogromna liczba cząsteczek, z jaką zwykle mamy do czynienia uniemożliwia stosowanie do opisu ich ruchu równań Newtona w takim sensie, jak się to czyni w mechanice. W jednym centymetrze sześciennym gazu mieści się w warunkach normalnych około <math>10^{19}\ </math>, cząsteczek, które zderzają się ze sobą oraz ze ściankami naczynia. Do opisu ich ruchu stosuje się metody statystyczne, a wielkości makroskopowe charakteryzuje się poprzez uśrednione wartości wielkości mikroskopowych takich jak prędkości cząsteczek czy energie ich wzajemnego oddziaływania. | ||
|} | |} | ||
| Linia 13: | Linia 16: | ||
|valign="top"|'''Czym jest ciśnienie gazu z mikroskopowego punktu widzenia?''' | |valign="top"|'''Czym jest ciśnienie gazu z mikroskopowego punktu widzenia?''' | ||
Ścianki naczynia zawierającego pewną porcję gazu uderzane są ustawicznie przez cząsteczki będące w chaotycznym ruchu. Wyznaczmy przekaz pędu przy takich zderzeniach. Dla uproszczenia przyjmijmy, że naczynie ma kształt sześcianu o długości ścianek równej <math>l\ | Ścianki naczynia zawierającego pewną porcję gazu uderzane są ustawicznie przez cząsteczki będące w chaotycznym ruchu. Wyznaczmy przekaz pędu przy takich zderzeniach. Dla uproszczenia przyjmijmy, że naczynie ma kształt sześcianu o długości ścianek równej <math>l\ </math>, . | ||
|} | |} | ||
| Linia 21: | Linia 24: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd3.png]] | |width="450px" valign="top"|[[Grafika:PF_M9_Slajd3.png]] | ||
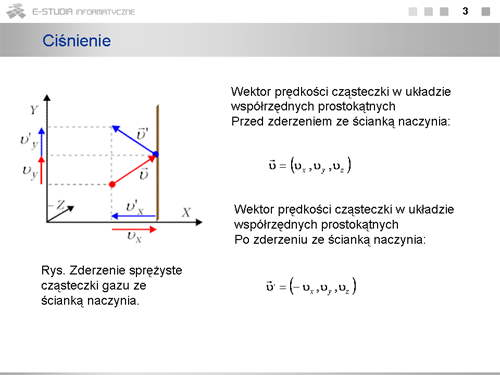
|valign="top"|W układzie współrzędnych prostokątnych rozważamy sprężyste zderzenie cząsteczki gazu, o wektorze prędkości <math>v\ | |valign="top"|W układzie współrzędnych prostokątnych rozważamy sprężyste zderzenie cząsteczki gazu, o wektorze prędkości <math>v\ </math>,, ze ścianką naczynia prostopadłą do osi <math>X\ </math>,. Prędkość cząsteczki zapiszemy w postaci wektora | ||
: <math>\vec{v}=(v_x, v_y, v_z)</math> | : <math>\vec{v}=(v_x, v_y, v_z)</math> | ||
Po odbiciu się od ścianki naczynia cząsteczka porusza się z prędkością <math>v'\ | Po odbiciu się od ścianki naczynia cząsteczka porusza się z prędkością <math>v'\ </math>,. W wyniku sprężystego zderzenia cząsteczki ze ścianką prostopadłą do osi <math>X\ </math>, zmieni znak tylko składowa prędkości wzdłuż tej osi, czyli będzie | ||
: <math>{v'}_x=-v_x</math> , <math>{v'}_y=v_y</math> , <math>{v'}_z=v_z</math> | : <math>{v'}_x=-v_x</math> , <math>{v'}_y=v_y</math> , <math>{v'}_z=v_z</math> | ||
Dalsze nasze rozważania dotyczyć będą tylko kierunku <math>X\ | Dalsze nasze rozważania dotyczyć będą tylko kierunku <math>X\ </math>, , stosować będziemy zapis skalarny. | ||
|} | |} | ||
| Linia 37: | Linia 40: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd4.png]] | |width="450px" valign="top"|[[Grafika:PF_M9_Slajd4.png]] | ||
|valign="top"|Zmiana składowej pędu wzdłuż osi <math>X\ | |valign="top"|Zmiana składowej pędu wzdłuż osi <math>X\ </math>, będzie różnicą pomiędzy pędem po i przed zderzeniem (Pęd oznaczamy tu dużą literą <math>P\ </math>, , bowiem małą litera oznaczać będziemy ciśnienie.) | ||
<math>\Delta P_x=-m\cdot v_x-(m\cdot v_x)=-2m\cdot v_x</math> | <math>\Delta P_x=-m\cdot v_x-(m\cdot v_x)=-2m\cdot v_x</math> | ||
Pęd przekazany ściance będzie odwrotnego znaku, a więc wyniesie <math>2m\cdot v_x\ | Pęd przekazany ściance będzie odwrotnego znaku, a więc wyniesie <math>2m\cdot v_x\ </math>, . | ||
|} | |} | ||
| Linia 49: | Linia 52: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd5.png]] | |width="450px" valign="top"|[[Grafika:PF_M9_Slajd5.png]] | ||
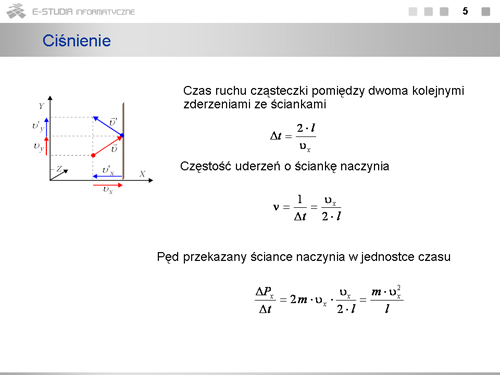
|valign="top"|Czas przelotu cząsteczki przez kostkę wynosi <math>t=l/v_x\ | |valign="top"|Czas przelotu cząsteczki przez kostkę wynosi <math>t=l/v_x\ </math>, , zaś przelot w obie strony trwać będzie dwa razy dłużej; <math>\Delta t=2\cdot l/v_x\ </math>, . Częstość <math>\nu\ </math>, uderzeń o ściankę, czyli liczba uderzeń w jednostce czasu będzie odwrotnością czasu przelotu cząsteczki w dwie strony, czyli <math>\nu=1/{\Delta t}=v_x/(2\cdot l)</math> . Pęd przekazany ściance w jednostce czasu równy będzie pędowi przekazanemu w jednym uderzeniu pomnożonemu przez liczbę uderzeń w jednostce czasu. | ||
<math>\frac{\Delta P_x}{\Delta t}=\frac{v_x}{2\cdot l}\cdot 2\cdot m\cdot v_x=\frac{m\cdot {v^2}_x}{l}</math> | <math>\frac{\Delta P_x}{\Delta t}=\frac{v_x}{2\cdot l}\cdot 2\cdot m\cdot v_x=\frac{m\cdot {v^2}_x}{l}</math> | ||
| Linia 59: | Linia 62: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd6.png]] | |width="450px" valign="top"|[[Grafika:PF_M9_Slajd6.png]] | ||
|valign="top"|Z drugiej zasady dynamiki wiemy, że <math>\Delta P/{\Delta t}=F\ | |valign="top"|Z drugiej zasady dynamiki wiemy, że <math>\Delta P/{\Delta t}=F\ </math>, . Pamiętamy też, że ciśnienie jest stosunkiem siły do powierzchni, na którą siła działa. Powierzchnia ta jest w naszym przypadku równa kwadratowi boku ścianki. Ciśnienie będące skutkiem uderzeń jednej cząsteczki w ściankę wynosi, więc <math>p=F/S=F/l^2</math> . Sumując przyczynki od wszystkich uderzających w ściankę cząsteczek otrzymujemy wyrażenie na '''ciśnienie gazu działające na ściankę''' | ||
[[Grafika:PF_M9_Wzor1.png]] | [[Grafika:PF_M9_Wzor1.png]] | ||
Założyliśmy tu, że wszystkie cząsteczki w liczbie <math>N\ | Założyliśmy tu, że wszystkie cząsteczki w liczbie <math>N\ </math>, mają tę samą masę <math>m\ </math>, . Długość ścianki w trzeciej potędze zamieniliśmy objętością sześcianu <math>V\ </math>, . Iloczyn masy cząsteczki m przez liczbę cząsteczek <math>N\ </math>, jest masą gazu w naczyniu, zaś podzielony przez objętość <math>V\ </math>, jest gęstością gazu, którą oznaczyliśmy symbolem <math>\rho\ </math>, . Symbol <math>\left \langle {v^2}_x\right \rangle\ </math>, oznacza wartość średnią kwadratu składowej wektora prędkości wzdłuż osi <math>X\ </math>, . | ||
|} | |} | ||
| Linia 87: | Linia 90: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd8.png]] | |width="450px" valign="top"|[[Grafika:PF_M9_Slajd8.png]] | ||
|valign="top"|Dla znalezienia związku pomiędzy makroskopową i mikroskopową interpretacją temperatury pomnóżmy lewą i prawą stronę równania opisującego ciśnienie gazu przez objętość naczynia <math>V\ | |valign="top"|Dla znalezienia związku pomiędzy makroskopową i mikroskopową interpretacją temperatury pomnóżmy lewą i prawą stronę równania opisującego ciśnienie gazu przez objętość naczynia <math>V\ </math>, i porównajmy to wyrażenie z równaniem stanu gazu doskonałego | ||
<math>p\cdot V=\frac{1}{3}\cdot\rho\left\langle v^2\right\rangle\cdot V=\frac{1}{3}\cdot \begin{matrix} n_M\cdot M \\ \overbrace{ \rho\cdot V} \end{matrix}\cdot \left\langle v^2\right\rangle </math> | <math>p\cdot V=\frac{1}{3}\cdot\rho\left\langle v^2\right\rangle\cdot V=\frac{1}{3}\cdot \begin{matrix} n_M\cdot M \\ \overbrace{ \rho\cdot V} \end{matrix}\cdot \left\langle v^2\right\rangle</math> | ||
We wzorze tym iloczyn gęstości i objętości jest po prostu masą gazu, którą następnie wyraziliśmy w molach oznaczając przez <math>M\ | We wzorze tym iloczyn gęstości i objętości jest po prostu masą gazu, którą następnie wyraziliśmy w molach oznaczając przez <math>M\ </math>, jego masę molową. | ||
|} | |} | ||
| Linia 99: | Linia 102: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd9.png]] | |width="450px" valign="top"|[[Grafika:PF_M9_Slajd9.png]] | ||
|valign="top"|Teraz masę gazu wyraziliśmy w molach, oznaczając przez <math>M\ | |valign="top"|Teraz masę gazu wyraziliśmy w molach, oznaczając przez <math>M\ </math>, jego masę molową. Mnożąc stronami przez <math>3/2\ </math>, i dzieląc przez liczbę Avogadro otrzymujemy | ||
:<math>\frac{1}{2}\cdot \begin{matrix} m_0 \\ \overbrace{ \frac{M}{N_A} } \end{matrix} \cdot \left\langle v^2\right\rangle=\frac{3}{2}\cdot \begin{matrix} k \\ \overbrace{ \frac{R}{N_A} } \end{matrix}\cdot T</math> | :<math>\frac{1}{2}\cdot \begin{matrix} m_0 \\ \overbrace{ \frac{M}{N_A} } \end{matrix} \cdot \left\langle v^2\right\rangle=\frac{3}{2}\cdot \begin{matrix} k \\ \overbrace{ \frac{R}{N_A} } \end{matrix}\cdot T</math> | ||
Zauważamy przy tym, że masa molowa podzielona przez liczbę Avogadro to po prostu masa jednej cząsteczki <math>m_0\ | Zauważamy przy tym, że masa molowa podzielona przez liczbę Avogadro to po prostu masa jednej cząsteczki <math>m_0\ </math>, . Iloraz stałej gazowej i liczby Avogadro, to stała Boltzmanna <math>k\ </math>, . Stała ta ma sens stałej gazowej odniesionej do jednej cząsteczki. Jak zobaczymy, stała ta odgrywa fundamentalna rolę w fizyce. | ||
Wykorzystując wprowadzone oznaczenia możemy przepisać ostatnie równanie w postaci | Wykorzystując wprowadzone oznaczenia możemy przepisać ostatnie równanie w postaci | ||
| Linia 119: | Linia 122: | ||
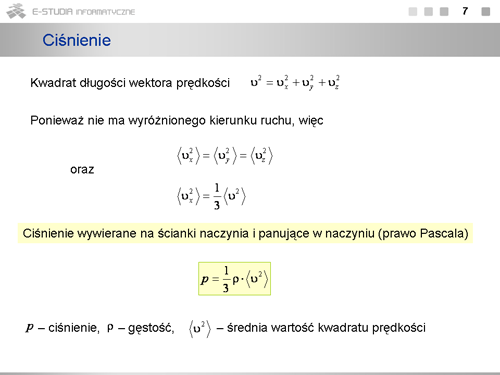
Średnia wartość kwadratu prędkości wynosi | Średnia wartość kwadratu prędkości wynosi | ||
: <math>\left\langle v^2\right\rangle=\frac{3\cdot k\cdot T}{m_0}</math> | : <math>\left\langle v^2 \right \rangle = \frac{3\cdot k\cdot T}{m_0}</math> | ||
Na tej podstawie możemy określić tzw. średnią prędkość kwadratową definiując ją jako | Na tej podstawie możemy określić tzw. średnią prędkość kwadratową definiując ją jako | ||
: <math>v_{ | : <math>v_{sr. kw.}=\sqrt{\left\langle v^2\right\rangle}=\sqrt{\frac{3\cdot k\cdot T}{m_0}}</math> | ||
Zauważmy, że możemy średnią prędkość kwadratową wyrazić poprzez wielkości makroskopowe: ciśnienie <math>p\ | Zauważmy, że możemy średnią prędkość kwadratową wyrazić poprzez wielkości makroskopowe: ciśnienie <math>p\ </math>, i gęstość gazu <math>\rho\ </math>, , bowiem również <math>v_{sr. kw.}=\sqrt{\frac{3\cdot p}{\rho}}</math> . Mamy, więc ideę prostego eksperymentu, za pomocą, którego określając łatwo mierzalne wielkości makroskopowe: <math>p\ </math>, (manometr) oraz objętość i masę gazu w celu wyznaczenia jego gęstości <math>\rho\ </math>, , możemy wyznaczyć statystycznie uśrednioną wielkość mikroskopową, jaką jest <math>v_{sr. kw.}\ </math>, . | ||
|} | |} | ||
| Linia 146: | Linia 149: | ||
Na każdy stopień swobody cząsteczki przypada średnio ta sama energia. | Na każdy stopień swobody cząsteczki przypada średnio ta sama energia. | ||
Jej wartość możemy określić na przykładzie ruchu postępowego cząsteczek punktowych. W tym przypadku liczba stopni swobody wynosi 3, a średnia energia kinetyczna cząsteczki, jest równa <math>3/2\cdot k\cdot T</math> . Możemy uzupełnić ilościowo treść zasady ekwipartycji energii. | Jej wartość możemy określić na przykładzie ruchu postępowego cząsteczek punktowych. W tym przypadku liczba stopni swobody wynosi 3, a średnia energia kinetyczna cząsteczki, jest równa <math>3/2\cdot k\cdot T</math> . Możemy uzupełnić ilościowo treść zasady ekwipartycji energii. | ||
Na każdy stopień swobody cząsteczki przypada średnio energia równa <math>kT/2 | Na każdy stopień swobody cząsteczki przypada średnio energia równa <math>kT/2</math>. | ||
W oparciu o nasze rozważania widzimy, że energia ruchu cząsteczek w gazach wieloatomowych jest większa niż w gazach jednoatomowych. | W oparciu o nasze rozważania widzimy, że energia ruchu cząsteczek w gazach wieloatomowych jest większa niż w gazach jednoatomowych. | ||
| Linia 155: | Linia 158: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd13.png]] | |width="450px" valign="top"|[[Grafika:PF_M9_Slajd13.png]] | ||
|valign="top"|Średnia energia cząsteczki o danej liczbie stopni swobody <math>i\ | |valign="top"|Średnia energia cząsteczki o danej liczbie stopni swobody <math>i\ </math>, wynosi | ||
:<math>\left\langle E\right\rangle=\frac{i}{2}\cdot k\cdot T</math> | :<math>\left\langle E\right\rangle=\frac{i}{2}\cdot k\cdot T</math> | ||
Dla <math>N\ | Dla <math>N\ </math>, cząsteczek gazu doskonałego, kiedy zaniedbuje się energię potencjalną wynikającą z sił wzajemnego oddziaływania cząsteczek, iloczyn <math>N\left\langle E\right\rangle\ </math>, jest po prostu energią wewnętrzną gazu równą | ||
:<math>U=N\cdot \left\langle E\right\rangle=N\cdot\frac{i}{2}\cdot k\cdot T</math> | :<math>U=N\cdot \left\langle E\right\rangle=N\cdot\frac{i}{2}\cdot k\cdot T</math> | ||
Dla <math>n_M\ | Dla <math>n_M\ </math>, moli gazu doskonałego | ||
:<math>U=n_M\cdot N_A\cdot\frac{i}{2}\cdot k\cdot T=n_M\cdot\frac{i}{2}\cdot k\cdot T</math> | :<math>U=n_M\cdot N_A\cdot\frac{i}{2}\cdot k\cdot T=n_M\cdot\frac{i}{2}\cdot k\cdot T</math> | ||
Energię wewnętrzną układu <math>U\ | Energię wewnętrzną układu <math>U\ </math>, utożsamiamy z całkowitą energia wszystkich cząsteczek. | ||
Ponieważ dla <math>n_M\ | Ponieważ dla <math>n_M\ </math>, moli gazu doskonałego | ||
:<math>dU=n_M\cdot C_V\cdot dT</math> | :<math>dU=n_M\cdot C_V\cdot dT</math> | ||
| Linia 175: | Linia 178: | ||
więc, otrzymujemy | więc, otrzymujemy | ||
:<math>C_V=\frac{1}{n_M}\cdot \frac{dU}{dT}=\frac{i}{2}\cdot R </math> | :<math>C_V=\frac{1}{n_M}\cdot \frac{dU}{dT}=\frac{i}{2}\cdot R</math> | ||
Wykorzystując wzór Mayera, <math>C_p-C_V=R\ | Wykorzystując wzór Mayera, <math>C_p-C_V=R\ </math>, | ||
: <math>C_p=\frac{i+2}{2}\cdot R</math> | : <math>C_p=\frac{i+2}{2}\cdot R</math> | ||
| Linia 197: | Linia 200: | ||
: <math>\sigma=\pi\cdot d^2</math> | : <math>\sigma=\pi\cdot d^2</math> | ||
Średnia długość drogi, jaką przebywa cząsteczka w ciągu jednej sekundy równa jest, co do wartości, średniej prędkości cząsteczki <math>\left\langle v\right\rangle</math> . Jeśli w tym czasie cząsteczka zderzyła się <math>\nu\ | Średnia długość drogi, jaką przebywa cząsteczka w ciągu jednej sekundy równa jest, co do wartości, średniej prędkości cząsteczki <math>\left\langle v\right\rangle</math> . Jeśli w tym czasie cząsteczka zderzyła się <math>\nu\ </math>, razy, to jej średnia droga pomiędzy zderzeniami wynosi | ||
: <math>\lambda=\frac{\left\langle v\right\rangle}{\nu}</math> | : <math>\lambda=\frac{\left\langle v\right\rangle}{\nu}</math> | ||
Droga ta nosi nazwę '''średniej drogi swobodnej'''. Dla wyznaczenia średniej liczby zderzeń załóżmy chwilowo, że porusza się tylko jedna cząsteczka, zaś wszystkie pozostałe są nieruchome. Zderzenie z inną cząsteczką nastąpi wtedy, kiedy ta znajdzie się w obrębie walca, jaki wyznacza poruszająca się cząsteczka. Jest to swego rodzaju "rurka" o przekroju równym przekrojowi czynnemu i długości równej długości przebiegu cząsteczki w ciągu sekundy. Objętość tej rurki wynosi <math>\pi\cdot d^2\cdot \left\langle v\right\rangle\ | Droga ta nosi nazwę '''średniej drogi swobodnej'''. Dla wyznaczenia średniej liczby zderzeń załóżmy chwilowo, że porusza się tylko jedna cząsteczka, zaś wszystkie pozostałe są nieruchome. Zderzenie z inną cząsteczką nastąpi wtedy, kiedy ta znajdzie się w obrębie walca, jaki wyznacza poruszająca się cząsteczka. Jest to swego rodzaju "rurka" o przekroju równym przekrojowi czynnemu i długości równej długości przebiegu cząsteczki w ciągu sekundy. Objętość tej rurki wynosi <math>\pi\cdot d^2\cdot \left\langle v\right\rangle\ </math>, . Liczbę cząsteczek w obrębie rurki uzyskamy mnożąc jej objętość przez liczbę cząsteczek w jednostce objętości <math>n\ </math>, . Liczba zderzeń z nieruchomymi cząsteczkami wyniosłaby wiec <math>\nu'=\pi\cdot d^2\cdot \left\langle v\right\rangle\cdot n</math> . | ||
Cząsteczki poruszają się jednak, a względna prędkość dwu cząsteczek równa jest <math>{\vec{v}}_{wzgl}={\vec{v}}_2-{\vec{v}}_1</math> . Kwadrat tej prędkości względnej wynosi <math>{v^2}_{wzgl}=({\vec{v}}_2-{\vec{v}}_1)^2={v^2}_2+{v^2}_1-2\cdot {\vec{v}}_1\cdot {\vec{v}}_2</math> . | Cząsteczki poruszają się jednak, a względna prędkość dwu cząsteczek równa jest <math>{\vec{v}}_{wzgl}={\vec{v}}_2-{\vec{v}}_1</math> . Kwadrat tej prędkości względnej wynosi <math>{v^2}_{wzgl}=({\vec{v}}_2-{\vec{v}}_1)^2={v^2}_2+{v^2}_1-2\cdot {\vec{v}}_1\cdot {\vec{v}}_2</math> . | ||
| Linia 239: | Linia 242: | ||
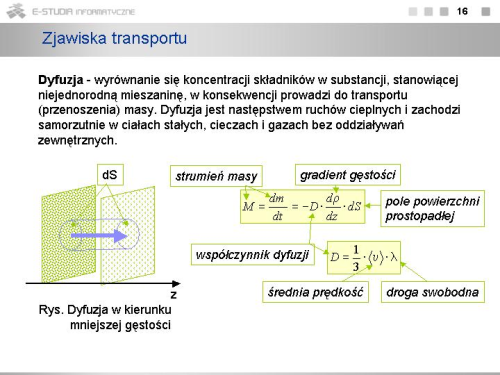
|valign="top"|'''Dyfuzja''' - to proces proces zmierzający do wyrównania się koncentracji składników w substancji, stanowiącej niejednorodną mieszaninę, prowadzący w konsekwencji do transportu (przenoszenia) masy. Dyfuzja jest następstwem ruchów cieplnych i zachodzi samorzutnie w ciałach stałych, cieczach i gazach bez oddziaływań zewnętrznych. | |valign="top"|'''Dyfuzja''' - to proces proces zmierzający do wyrównania się koncentracji składników w substancji, stanowiącej niejednorodną mieszaninę, prowadzący w konsekwencji do transportu (przenoszenia) masy. Dyfuzja jest następstwem ruchów cieplnych i zachodzi samorzutnie w ciałach stałych, cieczach i gazach bez oddziaływań zewnętrznych. | ||
Weźmy pod uwagę dwuskładnikową mieszaninę. '''Koncentrację''' składników niech określa liczba cząsteczek danego rodzaju w jednostce objętości, <math>n_1\ | Weźmy pod uwagę dwuskładnikową mieszaninę. '''Koncentrację''' składników niech określa liczba cząsteczek danego rodzaju w jednostce objętości, <math>n_1\ </math>, i <math>n_2\ </math>, , przy czym <math>n_1+n_2=n\ </math>, , gdzie <math>n\ </math>, jest całkowitą liczbą cząsteczek w jednostce objętości. | ||
Względną koncentrację cząsteczek danego rodzaju określimy jako <math>c_i=n_i/n\ | Względną koncentrację cząsteczek danego rodzaju określimy jako <math>c_i=n_i/n\ </math>, . Koncentracja ta nie jest jednak stała w całej objętości. Przyjmijmy, że zmiany koncentracji zachodzą wzdłuż osi <math>z\ </math>, i charakteryzowane są przez wielkości <math>dc_1/dz\ </math>, oraz <math>dc_2/dz\ </math>, , przy czym <math>dc_1/dz=-dc_2/dz</math> . | ||
Wyrażenie określające strumień cząsteczek danego rodzaju przez powierzchnię prostopadłą do osi <math>z\ | Wyrażenie określające strumień cząsteczek danego rodzaju przez powierzchnię prostopadłą do osi <math>z\ </math>, może być zapisane w postaci | ||
: <math>N_i=-D\cdot \frac{dn_i}{dz}\cdot S</math> | : <math>N_i=-D\cdot \frac{dn_i}{dz}\cdot S</math> | ||
gdzie <math>D\ | gdzie <math>D\ </math>, zwane jest współczynnikiem dyfuzji. Występujący tu znak minus jest konsekwencją faktu, że jeśli <math>dn_i/dz>0\ </math>, , czyli koncentracja składnika <math>i\ </math>, zwiększa się w kierunku większych wartości <math>z\ </math>, , to strumień związany z dyfuzją ma kierunek przeciwny zmierzając do wyrównania się koncentracji składników. Zwróćmy uwagę, że "siłą motoryczną" zjawiska dyfuzji jest zależność koncentracji od współrzędnej <math>z\ </math>, : <math>n_i = n_i(z)\ </math>,. Jeśli <math>dn_i/dz = 0\ </math>,, to znika dyfuzja, <math>N_i = 0\ </math>,. Wielkość <math>dn_i/dz\ </math>, nazywamy gradientem koncentracji w kierunku osi <math>Z\ </math>,. | ||
Mnożąc obustronnie wyrażenie na strumień cząsteczek danego rodzaju przez masę cząsteczki <math>m_i\ | Mnożąc obustronnie wyrażenie na strumień cząsteczek danego rodzaju przez masę cząsteczki <math>m_i\ </math>, otrzymujemy wyrażenie określające strumień masy składnika <math>i\ </math>,, | ||
: <math>M_i=-D\cdot \frac{d{\rho}_i}{dz}\cdot S</math> | : <math>M_i=-D\cdot \frac{d{\rho}_i}{dz}\cdot S</math> | ||
gdzie <math>\rho_i=n_i\cdot m_i</math> jest gęstością składnika <math>i\ | gdzie <math>\rho_i=n_i\cdot m_i</math> jest gęstością składnika <math>i\ </math>, w mieszaninie w punkcie, w którym koncentracja tego składnika wynosi <math>n_i(z)\ </math>,. Zależność stanowi empiryczne równanie dyfuzji. Sformułowana została w 1855 roku przez niemieckiego fizjologa A. Ficka i nosi nazwę '''prawa Ficka'''. Prawo to można wyrazić następująco. | ||
'''Prawo Ficka''' | '''Prawo Ficka''' | ||
| Linia 267: | Linia 270: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd17.png]] | |width="450px" valign="top"|[[Grafika:PF_M9_Slajd17.png]] | ||
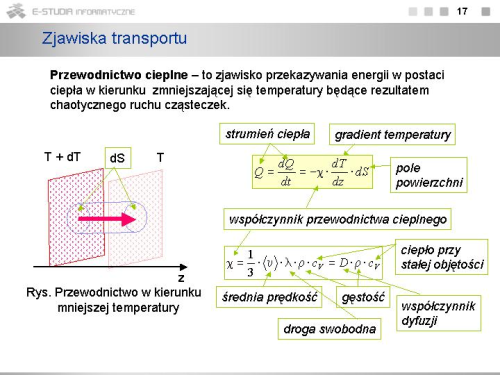
|valign="top"|W podobny sposób jak to zostało przedstawione dla transportu masy możemy rozważać zagadnienie '''przewodnictwa cieplnego'''. Jeśli w ośrodku występują różnice temperatur wzdłuż (umownego) kierunku <math>Z\ | |valign="top"|W podobny sposób jak to zostało przedstawione dla transportu masy możemy rozważać zagadnienie '''przewodnictwa cieplnego'''. Jeśli w ośrodku występują różnice temperatur wzdłuż (umownego) kierunku <math>Z\ </math>, , to pojawia się strumień ciepła określony wzorem | ||
:<math>Q_z=-\chi \cdot \frac{dT}{dz}\cdot S</math> | :<math>Q_z=-\chi \cdot \frac{dT}{dz}\cdot S</math> | ||
Strumień ciepła jest proporcjonalny do szybkości zmian temperatury wzdłuż osi <math>Z\ | Strumień ciepła jest proporcjonalny do szybkości zmian temperatury wzdłuż osi <math>Z\ </math>, i do powierzchni <math>S\ </math>, . Wielkość <math>\chi\ </math>, zwana jest współczynnikiem przewodnictwa cieplnego lub przewodnością cieplną ośrodka. Znak minus ma taki sam sens jak w poprzednio. Zależność ta, którą sformułował w 1822 roku francuski fizyk i matematyk Jean Baptiste Joseph Fourier, nosi nazwę '''prawa Fouriera'''. | ||
Prawo to można wyrazić następująco. | Prawo to można wyrazić następująco. | ||
| Linia 279: | Linia 282: | ||
''Strumień ciepła przez daną powierzchnię jest wprost proporcjonalny do pola tej powierzchni i do szybkości zmiany temperatury w kierunku do powierzchni tej prostopadłym.'' | ''Strumień ciepła przez daną powierzchnię jest wprost proporcjonalny do pola tej powierzchni i do szybkości zmiany temperatury w kierunku do powierzchni tej prostopadłym.'' | ||
Przez analogię do zjawiska dyfuzji warto podkreślić, że czynnikiem "motorycznym" przewodnictwa cieplnego, polegającego na transporcie energii kinetycznej chaotycznych ruchów cząsteczek, jest istnienie różnicy temperatury. Zjawisko to, czyli przenoszenie ciepła, zanika, jeśli temperatura w każdym punkcie ośrodka jest jednakowa. Wielkość <math>dT/dz\ | Przez analogię do zjawiska dyfuzji warto podkreślić, że czynnikiem "motorycznym" przewodnictwa cieplnego, polegającego na transporcie energii kinetycznej chaotycznych ruchów cząsteczek, jest istnienie różnicy temperatury. Zjawisko to, czyli przenoszenie ciepła, zanika, jeśli temperatura w każdym punkcie ośrodka jest jednakowa. Wielkość <math>dT/dz\ </math>, nazywamy gradientem temperatury w kierunku osi <math>Z\ </math>,. | ||
|} | |} | ||
| Linia 287: | Linia 290: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="450px" valign="top"|[[Grafika:PF_M9_Slajd18.png]] | |width="450px" valign="top"|[[Grafika:PF_M9_Slajd18.png]] | ||
|valign="top"|Kolejnym przykładem zjawiska transportu jest '''przekaz pędu''' pomiędzy cząsteczkami ośrodka prowadzący do '''zjawiska tarcia wewnętrznego'''. Siłę tarcia poznaliśmy np. na lekcjach z mechaniki cieczy. Siła ta okazała się być proporcjonalna do szybkości zmian prędkości warstw cieczy w jej ruchu laminarnym (warstwowym). Pamiętając, że drugie prawo dynamiki wyraża związek pomiędzy siłą a pędem przekazanym w jednostce czasu <math>F=dp/dt\ | |valign="top"|Kolejnym przykładem zjawiska transportu jest '''przekaz pędu''' pomiędzy cząsteczkami ośrodka prowadzący do '''zjawiska tarcia wewnętrznego'''. Siłę tarcia poznaliśmy np. na lekcjach z mechaniki cieczy. Siła ta okazała się być proporcjonalna do szybkości zmian prędkości warstw cieczy w jej ruchu laminarnym (warstwowym). Pamiętając, że drugie prawo dynamiki wyraża związek pomiędzy siłą a pędem przekazanym w jednostce czasu <math>F=dp/dt\ </math>, możemy zamienić siłę tarcia wewnętrznego pędem <math>P\ </math>, , przekazywanym w jednostce czasu pomiędzy trącymi się warstwami płynącej cieczy. Uzyskujemy wtedy wyrażenie | ||
: <math>P=-\eta \cdot\frac{du}{dz}\cdot S</math> | : <math>P=-\eta \cdot\frac{du}{dz}\cdot S</math> | ||
gdzie <math>du/dz\ | gdzie <math>du/dz\ </math>, wyraża szybkość zmian prędkości (gradient) warstw cieczy, a <math>S\ </math>, jest powierzchnią warstw tworzących strumień w kierunku prostopadłym do kierunku osi <math>Z\ </math>,. Współczynnik proporcjonalności <math>\eta\ </math>, jest współczynnikiem lepkości. Znak minus po prawej stronie wzoru oznacza, że pęd przekazywany jest w kierunku malenia prędkości. Zauważmy, że wyrażenie to jest podobne do wyrażeń dla rozważanych wcześniej zjawisk: dyfuzji i przewodnictwa cieplnego. | ||
W przypadku tarcia wewnętrznego pęd przekazywany między warstwami strumienia cząstek, o kierunku zgodnym z kierunkiem ruchu warstw, jest zależny od tego jak szybko zmienia się prędkość warstw w kierunku <math>Z\ | W przypadku tarcia wewnętrznego pęd przekazywany między warstwami strumienia cząstek, o kierunku zgodnym z kierunkiem ruchu warstw, jest zależny od tego jak szybko zmienia się prędkość warstw w kierunku <math>Z\ </math>, - prostopadłym do kierunku prędkości warstw <math>u\ </math>,. Ta zmiana prędkości jest czynnikiem "motorycznym" przekazywania pędu prowadzącym do wystąpienia zjawiska lepkości. Wielkość <math>du/dz\ </math>, nazywamy gradientem prędkości warstw cieczy w kierunku <math>Z\ </math>,. | ||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
= Materiały do ćwiczeń = | |||
'''Zadanie 9.1''' | '''Zadanie 9.1''' | ||
W zamkniętym zbiorniku jest <math>m = 1 g\ | W zamkniętym zbiorniku jest <math>m = 1 g\ </math>, argonu. Oblicz zmianę średniej energii kinetycznej atomów po dostarczeniu ciepła <math>Q = 4185 J\ </math>, | ||
Odpowiedź | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | ||
:<math>\left\langle\Delta E\right\rangle \approx 2,77\cdot 10^{-21}J</math> | :<math>\left\langle\Delta E\right\rangle \approx 2,77\cdot 10^{-21}J</math> | ||
</div></div> | |||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 313: | Linia 321: | ||
Oblicz ciepło właściwe przy stałej objętości dla atomów argonu i cząsteczek azotu | Oblicz ciepło właściwe przy stałej objętości dla atomów argonu i cząsteczek azotu | ||
Dla argonu <math>C_V = 311 J kg^{-1}K^{-1}\ | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | ||
Dla argonu <math>C_V = 311 J kg^{-1}K^{-1}\ </math>, , dla azotu <math>C_V = 742 J kg^{-1}K^{-1}\ </math>,. | |||
</div></div> | |||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 321: | Linia 332: | ||
'''Zadanie 9.3''' | '''Zadanie 9.3''' | ||
Masa <math>m = 1kg\ | Masa <math>m = 1kg\ </math>, azotu pod ciśnieniem <math>p = 10^5 N/m^2\ </math>, ma gęstość <math>\rho = 4 kg/m^3\ </math>,. Średnica każdej z cząsteczek wynosi <math>d = 3,1\cdot 10^{-10} m\ </math>,. Oblicz, jaką średnią drogę swobodną pokonują cząsteczki. | ||
Odpowiedź | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | ||
:<math>\lambda=2,7\cdot 10^{-8}m</math> . | :<math>\lambda=2,7\cdot 10^{-8}m</math> . | ||
</div></div> | |||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 331: | Linia 345: | ||
'''Zadanie 9.4''' | '''Zadanie 9.4''' | ||
Oblicz, jaka część cząsteczek gazu ma prędkości różniące się od prędkości najbardziej prawdopodobnej nie więcej niż o <math>1\%\,</ | Oblicz, jaka część cząsteczek gazu ma prędkości różniące się od prędkości najbardziej prawdopodobnej nie więcej niż o <math>1\%\ </math>, | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | |||
:<math>2\Delta N/N = 0,0166\ </math>, | |||
</div></div> | |||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 343: | Linia 360: | ||
:[[Grafika:PF_M9_Rys1.png]] | :[[Grafika:PF_M9_Rys1.png]] | ||
Podgrzewamy jeden koniec stalowego pręta o długości <math>L = 20\, cm\ | Podgrzewamy jeden koniec stalowego pręta o długości <math>L = 20\, cm\ </math>, i przekroju poprzecznym <math>S = 3cm^2\ </math>, do temperatury <math>T_2 = 573\, K\ </math>,, a drugi jego koniec umieszczamy w naczyniu z mieszaniną wody z lodem (o temperaturze <math>T_1 = 273\, K\ </math>,). Oblicz masę lodu stopionego w czasie <math>t = 10\, minut\ </math>,, zakładając że ciepło rozchodzi się wzdłuż pręta bez strat. Znane są też: współczynnik przewodnictwa cieplnego dla stali <math>c = 0,66 J / K \,sek\, cm\ </math>, oraz ciepło właściwe topnienia lodu <math>C = 330\, J / g\ </math>,. | ||
Odpowiedź | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowiedź </span><div class="mw-collapsible-content" style="display:none"> | |||
Stopią się 54 g lodu. | Stopią się 54 g lodu. | ||
</div></div> | |||
<hr width="100%"> | <hr width="100%"> | ||
= Słowniczek = | |||
{| border="1" | {| border="1" | ||
| Linia 358: | Linia 378: | ||
| '''liczba stopni swobody''' || (dla układu mechanicznego) liczba niezależnych wielkości za pomocą, których może być opisane położenie układu. | | '''liczba stopni swobody''' || (dla układu mechanicznego) liczba niezależnych wielkości za pomocą, których może być opisane położenie układu. | ||
|- | |- | ||
| '''zasada ekwipartycji energii'''|| na każdy stopień swobody cząsteczki przypada średnio ta sama energia równa <math>kT/2\ | | '''zasada ekwipartycji energii'''|| na każdy stopień swobody cząsteczki przypada średnio ta sama energia równa <math>kT/2\ </math>,. | ||
|- | |- | ||
| '''strumień''' || wielkość określająca jaka wartość danej wielkości fizycznej przenoszona jest przez określoną powierzchnię (często przyjmuje się powierzchnię jednostkową) w jednostce czasu. | | '''strumień''' || wielkość określająca jaka wartość danej wielkości fizycznej przenoszona jest przez określoną powierzchnię (często przyjmuje się powierzchnię jednostkową) w jednostce czasu. | ||
Aktualna wersja na dzień 12:03, 5 wrz 2023
Wykład
Materiały do ćwiczeń
Zadanie 9.1
W zamkniętym zbiorniku jest , argonu. Oblicz zmianę średniej energii kinetycznej atomów po dostarczeniu ciepła ,
Zadanie 9.2
Oblicz ciepło właściwe przy stałej objętości dla atomów argonu i cząsteczek azotu
Zadanie 9.3
Masa , azotu pod ciśnieniem , ma gęstość ,. Średnica każdej z cząsteczek wynosi ,. Oblicz, jaką średnią drogę swobodną pokonują cząsteczki.
Zadanie 9.4
Oblicz, jaka część cząsteczek gazu ma prędkości różniące się od prędkości najbardziej prawdopodobnej nie więcej niż o ,
Zadanie 9.5
Podgrzewamy jeden koniec stalowego pręta o długości , i przekroju poprzecznym , do temperatury ,, a drugi jego koniec umieszczamy w naczyniu z mieszaniną wody z lodem (o temperaturze ,). Oblicz masę lodu stopionego w czasie ,, zakładając że ciepło rozchodzi się wzdłuż pręta bez strat. Znane są też: współczynnik przewodnictwa cieplnego dla stali , oraz ciepło właściwe topnienia lodu ,.
Słowniczek
| statystyczna interpretacja temperatury | temperatura jest miarą średniej energii kinetycznej chaotycznego ruchu cząsteczek. |
| liczba stopni swobody | (dla układu mechanicznego) liczba niezależnych wielkości za pomocą, których może być opisane położenie układu. |
| zasada ekwipartycji energii | na każdy stopień swobody cząsteczki przypada średnio ta sama energia równa ,. |
| strumień | wielkość określająca jaka wartość danej wielkości fizycznej przenoszona jest przez określoną powierzchnię (często przyjmuje się powierzchnię jednostkową) w jednostce czasu. |
| koncentracja | liczba cząsteczek danego rodzaju w jednostce objętości |
| gęstość strumienia | strumień odniesiony do jednostkowej powierzchni prostopadłej do kierunku przepływu. |
| gradient pola | wektor wyrażający szybkość zmian w przestrzeni danej wielkości charakteryzującej pole w określonym punkcie pola i w określonym kierunku. |
| dyfuzja | proces przenoszenia masy zmierzający do wyrównania się koncentracji składników w substancji, stanowiącej niejednorodną mieszaninę. Dyfuzja jest następstwem ruchów cieplnych i zachodzi samorzutnie w ciałach stałych, cieczach i gazach. |
| prawo Ficka | Strumień substancji dyfundującej przez daną powierzchnię (ustawioną prostopadle do kierunku dyfuzji) jest proporcjonalny do pola tej powierzchni i szybkości zmiany (gradientu) koncentracji cząsteczek w kierunku prostopadłym do powierzchni. |
| konwekcja | proces w którym masa lub/i ciepło przenoszone są poprzez przemieszczające się masy gazu lub cieczy pod wpływem czynników zewnętrznych. |
| przewodnictwo cieplne | zjawisko przenoszenia w ośrodku energii kinetycznej chaotycznych ruchów cieplnych cząsteczek, pojawiające się w ośrodku, kiedy występują różnice temperatur. |
| tarcie wewnętrzne (lepkość) | przekaz pędu pomiędzy przemieszczającymi się względem siebie warstwami ośrodka. |
| prawo Fouriera | Strumień ciepła przez daną powierzchnię jest wprost proporcjonalny do pola tej powierzchni i do szybkości zmiany temperatury cząsteczek w kierunku prostopadłym do tej powierzchni. |
| efektywna średnica cząsteczki | odległość między środkami cząsteczek przy ich największym zbliżeniu. |
| przekrój czynny na zderzenie | efektywne pole powierzchni, jakie cząsteczka stanowi w procesie wzajemnych zderzeń. |
| średnia droga swobodna | średnia droga pomiędzy zderzeniami w chaotycznym ruchu cząsteczek. |