TTS Moduł 2: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
|||
| (Nie pokazano 9 wersji utworzonych przez 2 użytkowników) | |||
| Linia 4: | Linia 4: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd1.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M2_Slajd1.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Fala elektromagnetyczna rozchodząca się w wolnej przestrzeni służy do transmisji sygnału w systemach radiokomunikacyjnych (radiofonia, telewizja naziemna i satelitarna, radiotelefonia). Fala wypromieniowana przez antenę nadawczą rozchodzi się we wszystkich kierunkach, choć oczywiście pewne kierunki są uprzywilejowane, o czym mówi charakterystyka anteny. Z punktu widzenia anteny odbiorczej oddalonej odpowiednio daleko, o wiele kilometrów, fala dochodząca do niej jest ''falą płaską''. Wartości chwilowe wektorów pól elektrycznego i magnetycznego tej fali są takie same w każdym punkcie płaszczyzny prostopadłej do kierunku rozchodzenia się fali. Fala płaska jest najprostszym typem fali elektromagnetycznej. | ||
Celem wykładu jest przedstawienie matematycznego opisu, własności i parametrów fali płaskiej rozchodzącej się w przestrzeni nieograniczonej wypełnionej stratnym dielektrykiem. | |||
Propagacja fali płaskiej w bezstratnej wolnej przestrzeni jest przypadkiem szczególnym, a jej własności wynikają z rozwiązania dla przypadku bardzej ogólnego, z uwzglenieniem strat ośrodka. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd2.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:TTS_M2_Slajd2.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|Na wstępie przypomnimy, znany z kursu fizyki, układ równań Maxwella w dziedzinie czasu. Równania te opisują tak pola statyczne (elektryczne albo magnetyczne) jak i zmienne w czasie pola elektromagnetyczne o dowolnej, ale zdeterminowanej zależności od czasu. | ||
Przedmiotem wykładu jest monochromatyczna fala elektromagnetyczna, czyli fala o ustalonej częstotliwości harmonicznych (cosinusoidalnych) zmian pól w czasie. W zagadnieniach dotyczących takich pól stosujemy rachunek symboliczny wykorzystujący operacje na funkcjach zespolonych w dziedzinie częstotliwości. | |||
Wprowadzimy wektory zespolone dla wielkości związanych z polem elektromagnetycznym, oraz sformułujemy równania Maxwella w postaci zespolonej. | |||
Przeprowadzimy uproszczoną klasyfikację ośrodków materialnych w oparciu o ich cechy elektryczne oraz poznamy zachowanie się dielektryków w obecności zewnętrznego pola elektrycznego cosinusoidalnie zmieniającego się w czasie. | |||
Z równań Maxwella w postaci zespolonej wyprowadzimy równania Helmholtza (odpowiednik równania falowego) dla pola elektrycznego i magnetycznego fali płaskiej rozchodzącej się w nieograniczonym ośrodku dielektrycznym. | |||
Na podstawie wyprowadzonych równań Helmholtza, wspomagając się równaniami Maxwella, znajdziemy matematyczny opis fali płaskiej rozchodzącej się w nieograniczonej przestrzeni, określimy jej własności i parametry. | |||
Omówimy również rodzaje polaryzacji płaskiej fali elektromagnetycznej. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd3.png|thumb|500px]] | |||
|valign="top"|Przypomnijmy podstawowe wielkości charakteryzujące pole elektromagnetyczne będące kompozycją pól elektrycznego i magnetycznego: | |||
*Natężenie pola elektrycznego <math>\overrightarrow{E}\,</math> jest wektorem (ma swoją wartość i kierunek), funkcją miejsca i czasu. Natężenie pola elektrycznego mierzymy w woltach na metr <math>[V/m]\,</math>. | |||
*Natężenie pola magnetycznego <math>\overrightarrow{H}\,</math> jest także wektorem, mierzymy jego wartość w amperach na metr <math>[A/m]\,</math>. | |||
*Indukcja elektryczna <math>\overrightarrow{D}\,</math> jest wektorem, mierzymy jej wartość w amperach razy sekunda na metr kwadratowy <math>[As/m^2]\,</math>, czyli kulombach na <math>m^2\,</math> <math>[C/m^2]\,</math>. | |||
*Indukcja magnetyczna <math>\overrightarrow{B}\,</math> jest wektorem, mierzymy jej wartość w voltach razy sekunda na metr kwadratowy <math>[Vs/m^2]\,</math>. | |||
Ładunek elektryczny jest skalarnym źrodłem pola elektrycznego. W punkcie przestrzeni miarą ładunku jest jego gęstość objętościowa <math>\rho\,</math>, której jednostką jest kulomb na metr sześcienny <math>[C/m^3]\,</math>. | |||
Prądy elektryczne są wektorowymi źródłami pola magnetycznego. Wektor gęstości prądu <math>\overrightarrow{J}\,</math> opisuje prąd w punkcie przestrzeni. Wartość <math>\overrightarrow{J}\,</math> mierzymy w amperach na metr kwadratowy <math>[A/m^2]\,</math>. | |||
Wymienione powyżej pięć pól wektorowych i skalarne pole gęstości ładunku są funkcjami położenia (w prostokątnym układzie współrzędnych zależą od <math>(x, y, z)\,</math> oraz czasu <math>t\,</math>. Wzajemne relacje między tymi polami określają równania Maxwella. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd4.png|thumb|500px]] | |||
|valign="top"|Pierwsze równanie Maxwella w postaci różniczkowej stwierdza, że rotacja wektora natężenia pola elektrycznego jest równa co do wartości szybkości zmian w czasie wektora indukcji magnetycznej. Zatem, zmiany indukcji magnetycznej powodują powstanie wirowego (niepotencjalnego) pola elektrycznego. | |||
| width=" | |||
| | |||
| | |||
| | |||
Równanie to opisuje zjawisko indukcji elektromagnetycznej, której istotą jest indukowanie przez zmienne w czasie pole indukcji magnetycznej zmiennego pola elektrycznego, przy czym wektor natężenia pola elektrycznego jest w każdym punkcie przestrzeni prostopadły do wektora indukcji magnetycznej. | |||
Drugie równanie Maxwella stanowi, że rotacja wektora natężenia pola magnetycznego w punkcie przestrzeni jest równa wektorowi gęstości całkowitego prądu występującego w tym punkcie. Prawa strona równania zawiera dwa składniki: | |||
*wektor gęstości prądu elektrycznego <math>\overrightarrow{J}\,</math> , który jest sumą wektora gęstości prądu przewodzenia wynikającego z ruchu ładunków w materiale i wektora gęstości prądu unoszenia polegającego na ruchu naładowanych ciał; | |||
*wprowadzony przez Maxwella prąd przesunięcia związany ze zmianami indukcji elektrycznej w czasie, którego wektor gęstości to <math>\partial \overrightarrow{D}/{\partial t}</math> . Miarą gęstości prądu przesunięcia jest amper na metr kwadratowy <math>[A/m^2]\,</math>. | |||
Pomijając prąd przesunięcia stwierdzimy, że przepływ prądu elektrycznego powoduje powstanie wirowego pola magnetycznego o rotacji równej gęstości tego prądu. Prąd elektryczny jest więc źródłem wektorowym pola magnetycznego. | |||
Gdy występuje tylko prąd przesunięcia to drugie równanie Maxwella wyraża zjawisko indukcji magnetoelektrycznej polegające na indukowaniu przez zmienne pole indukcji elektrycznej zmiennego pola magnetycznego, przy czym wektor natężenia pola magnetycznego jest w każdym punkcie przestrzeni prostopadły do wektora indukcji elektrycznej. | |||
Z pierwszych dwóch równań Maxwella wynika, że zmiany w czasie indukcji magnetycznej powodują powstanie wirowego (niepotencjalnego) pola elektrycznego, a zmienna w czasie indukcja elektryczna wytwarza wirowe pole magnetyczne. Nie można odseparować od siebie pól elektrycznego i magnetycznego. Mówimy więc o polu elektromagnetycznym. | |||
Pola te mogą występować niezależnie tylko wtedy gdy nie zmieniają się w czasie. | |||
Dodatkowo, z omawianych równań wynika, że pola zmienne w czasie muszą być zmienne w przestrzeni (w przeciwnym razie rotacja jest równa zero). | |||
W trzech ostatnich równaniach Maxwella z lewej strony występuje dywergencja. Gdy dywergencja pola wektorowego nie jest równa zeru to pole nazywamy źródłowym, występują skalarne źródła tego pola. W przeciwnym przypadku pole jest bezźródłowe. | |||
Prawo Gaussa dla pola elektrycznego mówi, że dywergencja wektora indukcji elektrycznej równa jest objętościowej gęstość ładunku elektrycznego. Skalarnym źródłem pola indukcji elektrycznej są ładunki elektryczne. | |||
Prawo Gaussa dla indukcji magnetycznej informuje, że nie ma swobodnych ładunków magnetycznych. Pole indukcji magnetycznej jest bezźródłowe. | |||
Prawo zachowania ładunku mówi, że dywergencja gęstości prądu przewodzenia w określonym punkcie przestrzeni równa jest szybkości zmian w czasie gęstości objętościowej niezrównoważonego ładunku swobodnego. Skalarnym źródłem pola gęstości prądu przewodzenia jest zmiana ładunku w czasie. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd5.png|thumb|500px]] | |||
|valign="top"|Rozwiązanie szeregu zagadnień elektrodynamiki upraszcza się gdy zastosuje się rachunek symboliczny wykorzystujący operacje na funkcjach zespolonych. | |||
| width=" | |||
| | |||
| | |||
<math>\ | Wektorem zespolonym <math>\overrightarrow{E}\,</math> nazywamy wektor, którego trzy składowe mogą być liczbami zespolonymi. Taki wektor jest jednoznacznie określony przez podanie sześciu uporządkowanych liczb lub dwóch wektorów rzeczywistych: <math>Re(\overrightarrow{E})\,</math> oraz <math>Im(\overrightarrow{E})\,</math> ; <math>\overrightarrow{E}= Re(\overrightarrow{E})+jIm(\overrightarrow{E})</math> . | ||
Działania na wektorach zespolonych wykonujemy tak jak na wektorach rzeczywistych, przy czym należy pamiętać, że kwadrat jednostki urojonej należy zastąpić przez minus jeden. | |||
Przyjęto regułę, że wektory zespolone oznaczanę są kursywą, a wektory rzeczywiste literami prostymi. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd6.png|thumb|500px]] | |||
|valign="top"|Układ zespolonych równań Maxwella jest analogiczny do układu dla wektorów rzeczywistych, przy czym różniczkowanie po czasie <math>\partial /{\partial t}</math> zastąpiono mnożeniem przez <math>j\omega\,</math> . | |||
| width=" | |||
Rozwiązaniem układu równań są amplitudy zespolone zależne od zmiennych przestrzeni, na podstawie których wyznacza się pola rzeczywiste. | |||
<math>\ | Przykładowo, znamy amplitudę zespoloną <math>\overrightarrow{E}(x,y,z)=\overrightarrow{i}_x|E_x(x,y,z)|exp(jArgE_x)</math> | ||
<math>\ | Mnożymy ją przez <math>exp(j\omega t)\,</math> i wyznaczamy część rzeczywistą, która jest poszukiwanym wektorem rzeczywistym, czyli | ||
<math>\overrightarrow{E}(x,y,z,t)=Re[\overrightarrow{E}(x,y,z)e^{j\omega t}=\overrightarrow{i}_x|E_x(x,y,z)|cos(\omega t+ArgE_x)</math> | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd7.png|thumb|500px]] | |||
|valign="top"|Dotychczas mówilismy o wektorach <math>\overrightarrow{E},\overrightarrow{D},\overrightarrow{H},\overrightarrow{B}\,</math> określających pole elektromagnetyczne w taki sposób, jakby były one niezależne od siebie. Pierwsze dwa równania materiałowe wiążą ze sobą wymienione wektory w szekokiej klasie ośrodków (istnieją ośrodki, np. bianizotropowe, dla których związki między wektorami natężeń i indukcji pól są bardziej skomplikowane). | |||
Trzecie równanie materiałowe, nazywane wektorowym prawem Ohma, wiąże wektor gęstości prądu przewodzenia z wektorem natężeniam pola elektrycznego. | |||
Przenikalność elektryczna i konduktywność charakteryzują dielektryki, a przenikalność magnetyczna - magnetyki | |||
Przenikalność elektryczna <math>\varepsilon\,</math> to miara zdolności dielektryka do osłabiania zewnętrznego pola elektrycznego, ale również miara zdolności do koncentracji energii pola elektrycznego; | |||
Przenikalność elektryczną mierzymy w faradach na metr. | |||
Często posługujemy się bezwymiarowym pojęciem względnej przenikalności elektrycznej <math>\varepsilon_w\,</math>, która jest <math>\varepsilon\,</math> unormowaną do przenikalności elektrycznej próżni <math>\varepsilon_0\,</math>. | |||
Analogicznie można opisać przenikalność magnetyczną w stosunku do magnetyka, której miarą jest henr na metr. Normalizując <math>\mu\,</math> do przenikalności magnetycznej próżni <math>\mu_0\,</math> uzyskujemy względną przenikalność magnetyczną <math>\mu_w\,</math> ośrodka. W niniejszym wykładzie będziemy zajmować się ośrodkami niemagnetycznymi, dla których <math>\mu_w=1</math>. | |||
Konduktywność <math>\sigma\,</math> to miara zdolności środowiska do przepływu prądu przewodzenia, mierzona w siemensach na metr, a pośrednio miara liczby swobodnych nośników ładunku w jednostce objętości dielektryka. | |||
Gdy wektory występujące w równaniach materiałowych są rzeczywiste to parametry materiałowe są wielkościami rzeczywistymi. | |||
Dla pól cosinusoidalnie zmiennych w czasie parametry materiałowe w ogólności są wielkościami zespolonymi. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd8.png|thumb|500px]] | |||
|valign="top"|Ośrodki dzielimy na materialne i próżnię. | |||
Podano szereg przymiotników opisujących własności próżni, które należy zdefiniować. | |||
W tym celu dokonajmy pewnej uproszczonej klasyfikacji ośrodków materialnych ze względu na ich cechy elektryczne, a więc postać parametrów i równań materiałowych. | |||
Równania materiałowe wskazują na liniową zależność wektorów indukcji oraz gęstości prądu od natężeń pól. Oznacza to, że wielkości <math>\varepsilon, \mu, \sigma\,</math> nie zależą od natężeń pól i taki ośrodek nazywamy ''liniowym''. Jeżeli przynajmniej jeden z parametrów ośrodka zależy od natężeń pól to ośrodek nazywa się ''nieliniowym''. | |||
Ośrodek o zerowej konduktywności określmy, dla potrzeb czynionej klasyfikacji przyjmijmy, jako ''bezstratne''. Takie materiały charakteryzują tylko dwa pozostałe parametry materiałowe. | |||
Materialny ośrodek jest ''jednorodny'' gdy jego parametry nie zależą od współrzędnych punktu. W przeciwnym przypadku mówimy o ośrodku ''niejednorodnym''. | |||
Istnieją ośrodki, których parametry <math>\varepsilon, \mu, \sigma\,</math> zależą od częstotliwości. Ośrodki takie nazywamy ''dyspersyjnymi''. Równania materiałowe w prezentowanej formie mają sens dla ośrodków dyspersyjnych tylko w przypadku sinusoidalnej zależności pól od czasu. | |||
Jeżeli wielkości <math>\varepsilon, \mu, \sigma\,</math> są niezależne od kierunku pól to ośrodek nazywamy ''izotropowym''. Odpowiednie wektory występujące w poszczególnych równaniach materiałowych są do siebie równoległe. | |||
Gdy parametry ośrodka zależą od kierunku pól, to mówimy o ośrodku ''anizotropowym'', którego własności nie mogą być opisane przez skalarne wielkości <math>\varepsilon, \mu, \sigma\,</math>. Równania materiałowe mogą być prawdziwe dla ośrodka anizotropowego, ale wtedy parametry materiałowe są reprezentowane przez tensory. | |||
Zauważmy, że prędkość światła w próżni związana jest z jej parametrami materiałowymi. | |||
Pierwiastek ze stosunku przenikalności magnetycznej i elektrycznej ma wymiar ohm i wielkość tę nazywamy impedancją właściwą próżni. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd9.png|thumb|500px]] | |||
|valign="top"|Podział ośrodków na próżnię i ośrodki materialne nie jest przypadkowy. Jedynie próżnia jest ośrodkiem bezstratnym. | |||
Konduktywność ośrodków występujących w przyrodzie zawiera się w bardzo szerokich granicach od <math>\sim 10^{-17} S/m\,</math> dla kwarcu do <math>6,1\cdot 10^7 S/m\,</math> dla srebra. Należy zadać pytanie, które ośrodki można uznać za bezstratne. | |||
Konduktywność ośrodka jest właściwym kryterium jego bezstratności tylko dla niskich częstotliwości. Dla wyższych częstotliwości poza stratami przewodzenia mamy do czynienia z tzw. stratami polaryzacji, które omówimy w dalszej części wykładu. | |||
Przyjmijmy arbitralnie, że ośrodek, w którym wartość prądu przesunięcia jest co najmniej trzy rzędy większy od prądu przewodzenia można uznać za bezstratny dielektryk. Przykładem takiego dielektryka jest suche czyste powietrze. | |||
Dla bezstratnych dielektryków, podobnie jak dla próżni, znając przenikalność elektryczną (przenikalność magnetyczna jest taka jak dla próżni) można obliczyć prędkość rozchodzenia się światła oraz impedancję właściwą. Obie wielkości maleją z pierwiastkiem przenikalności elektrycznej materiału. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd10.png|thumb|500px]] | |||
|valign="top"|Materiały dielektryczne powszechnie występują w technice mikrofalowej w konstrukcji tak linii transmisyjnych jak i elementów oraz podzespołów. Z tego względu ważne jest poznanie zachowania izotropowego dielektryka w zewnętrznym polu elektrycznym o sinusoidalnej zależności od czasu, stosując wektory zespolone. | |||
| width=" | |||
| | |||
W przypadku braku zewnętrznego pola elektrycznego dielektryk można traktować jako elektrycznie obojętny. W momencie pojawienia się pola zewnętrznego dielektryk polaryzuje się, czyli następuje nieznaczne przemieszczenie się ładunków związanych z atomami i (lub) cząsteczkami. Wytwarzają one pole skierowane tak, aby przeciwdziałać polu zewnętrznemu i dlatego wypadkowe natężenie pola elektrycznego jest mniejsze niż natężenie pola zewnętrznego. | |||
Współczynnikiem proporcjonalności między zespolonymi wektorami indukcji i natężenia jest zespolona przenikalność elektryczna. | |||
W przypadku statycznym lub przy wolnych zmianach pola wektor indukcji elektrycznej jest w przybliżeniu w fazie z wektorem natężenia pola elektrycznego i część urojoną przenikalności elektrycznej można pominąć. | |||
Dla pól szybkozmiennych opóźnienie wektora indukcji względem wektora natężenia nie jest pomijalnie małe, wymienione wektory mają różne fazy. Część urojona przenikalności elektrycznej, która opisuje straty w ośrodku (grzanie) wywołane tłumieniem wibracji dipoli i tym samym opóźnienie wektora indukcji elektrycznej względem wektora pola elektrycznego, musi być ujemna (<math>\varepsilon''\,</math> jest dodatnie). | |||
Wprowadzenie zespolonej przenikalności elektrycznej pozwala w prosty sposób uwzględnić w opisie ośrodka skomplikowane procesy polaryzacji występujące w otaczających nas materiałach. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd11.png|thumb|500px]] | |||
|valign="top"|Źródłem strat przewodzenia w dielektryku jest prąd przewodzenia o gęstości określonej przez tzw. wektorowe prawo Ohma: <math>\overrightarrow{J}=\sigma \overrightarrow{E}</math>. | |||
W oparciu o drugie prawo Maxwella wyznaczamy gęstość całkowitego prądu w dielektryku jako sumę prądów przewodzenia i przesunięcia. Z zapisu tego prądu widać, że straty związane z tłumienia oscylacji dipoli <math>(\omega \varepsilon'')\,</math> i straty wynikające z istnienia prądu przewodzenia <math>(\sigma)\,</math> są nierozróżnialne. Wielkość <math>(\sigma+\omega \varepsilon'')\,</math> nazywamy zastępczą konduktywnością ośrodka i mówi ona o całkowitych stratach cieplnych. | |||
Przy niskich częstotliwościach, kiedy można zaniedbać zjawiska polaryzacji, o stratach decyduje konduktywność ośrodka. Zjawisko tłumienia drgań dipoli ma dominujący udział w stratach ośrodka dielektrycznego przy wysokich częstotliwościach. | |||
Zauważmy, że prąd wywołujący straty mocy fali elektromagnetycznej w ośrodku jest w fazie z polem elektrycznym. Natomiast faza prądu odpowiedzialnego za magazynowanie energii pola elektrycznego jest przesunięta o 90º względem natężenia tego pola. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd12.png|thumb|500px]] | |||
|valign="top"|Dla potrzeb analizy fali płaskiej w przestrzeni wypełnionej dielektrykiem stratnym przyjmujemy, że ośrodek ten charakteryzują: | |||
| width=" | |||
| | |||
*zastępcza konduktywność <math>\sigma\,</math>, która uwzględnia tak konduktywność ośrodka jak i urojoną część przenikalności elektrycznej. Dla uproszczenia zapisu użyjemy symbolu konduktywności; | |||
*przenikalność elektryczna <math>\varepsilon\,</math>, która w istocie jest częścią rzeczywistą przenikalności zapisaną z pominięciem górnego indeksu. Można przyjąć taki uproszczony zapis gdyż część urojona przenikalności elektrycznej włączono do zastępczej konduktywności; | |||
*przenikalność magnetyczna próżni <math>\mu_0\,</math>. | |||
Parametry dielektryka stratnego są liczbami rzeczywistymi gdy jest to ośrodek liniowy, izotropowy, niedyspersyjny, jednorodny i stacjonarny (parametry nie zależą od czasu). | |||
Powszechnie przyjętym parametrem charakteryzującym straty w dielektryku jest tangens kąta stratności. W przyjętym modelu opisu dielektryka, tangens kąta stratności jest stosunkiem prądu strat cieplnych, który jest proporcjonalny do zastępczej konduktywności <math>\sigma\,</math>, do wartości prądu związanego z magazynowaniem energii pola elektrycznego i proporcjonalnego do <math>\omega \varepsilon\,</math>. W oparciu o wartość tangensa kąta stratności można wyróżnić dwie grupy materiałów. Gdy <math>tg\delta\,</math> jest znacznie mniejszy od jedności (np. nie większy niż 0.1) to ośrodek nazywamy małostratnym dielektrykiem. Tego typu materiały stosujemy w technice mikrofalowej. Ośrodek, którego tangens kąta stratności jest znacznie większy od jedności (np. większy od 10) określamy mianem przewodnika rzeczywistego. | |||
Należy pamiętać, że tangens kąta stratności jest funkcją częstotliwości i o tym czy dany ośrodek uważamy za małostratny dielektryk bądź rzeczywisty przewodnik zależy od wartości częstotliwości. Według takiego modelu, gdy częstotliwość jest odpowiednio wielka to nawet metale można uważać za małostratne dielektryki. Przykładowo, dla miedzi, której konduktywność wynosi <math>5,7\cdot 10^7 S/m</math>, tangens kąta stratności jest znacznie mniejszy od jedności począwszy od częstotliwości ok. 3000 THz, czyli częstotliwości kilkukrotnie wiekszej niż częstotliwości światła widzialnego. | |||
W | W oparciu o parametry dielektryka stratnego definiujemy jego impedancję właściwą <math>Z\,</math>. | ||
Impedancja ta jest wielkością zespoloną. Pomimo założenia, że ośrodek jest niedyspersyjny jego impedancja właściwa zmienia się z częstotliwością. | |||
Przypomnijmy, że dla bezstratnego dielektryka, znając jego przenikalność elektryczną, można obliczyć prędkość światła. Nie możemy tak postąpić dla stratnego dielektryka bo uzyskalibyśmy wielkość zespoloną. W dalszej części wykładu podane zostanie rozwiązanie tego problemu. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
| width=" | |width="500px" valign="top"|[[Grafika:TTS_M2_Slajd13.png|thumb|500px]] | ||
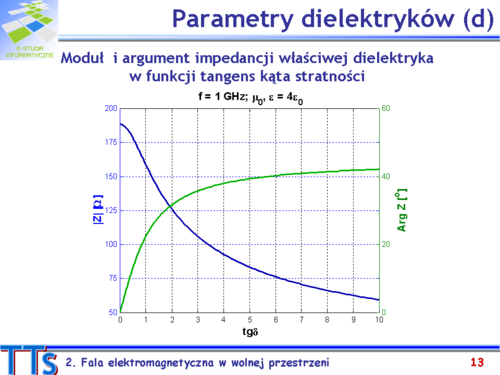
|valign="top"|Na wykresie pokazano zachowanie modułu i argumentu impedancji właściwej przykładowego ośrodka ze wzrostem jego strat. Przebiegi wyznaczono dla określonej częstotliwości i przenikalności elektrycznej, a więc pokazują one zmianę impedancji właściwej ze wzrostem konduktywności. | |||
Argument impedancji właściwej rośnie liniowo ze stratami w zakresie tangensa kąta stratności odpowiadającego małostratnym dielektrykom. Dla <math>tg\delta\,</math> większych od czterech obserwujemy wyraźne osłabienie wzrostu <math>Arg\, Z\,</math>. Dąży on asymptotycznie do <math>45^\circ\,</math> i taką jego wartość przyjmujemy dla przewodników rzeczywistych. | |||
Moduł impedancji właściwej monotonicznie maleje i dla idealnego przewodnika wynosi zero. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
| width=" | |width="500px" valign="top"|[[Grafika:TTS_M2_Slajd14.png|thumb|500px]] | ||
|valign="top"|Rozważamy przestrzeń nieograniczoną wypełnioną dielektrykiem stratnym o parametrach <math>\varepsilon, \mu_0, \sigma\,</math>. Zakładamy, że w dielektryku nie ma niezrównoważonych ładunków elektrycznych, tzn. <math>\rho = 0</math>. Podany wcześniej układ zespolonych równań Maxwella dla dielektryka stratnego przybiera formę przedstawioną na slajdzie. | |||
Przypomnijmy, że dla fali płaskiej wartości wektorów pól elektrycznego i magnetycznego tej fali są takie same w każdym punkcie płaszczyzny prostopadłej do kierunku rozchodzenia się fali. | |||
Oznacza to, że pola fali rozchodzącej się w wzdłuż osi z nie mogą być funkcjami współrzędnych x i y. Wektory zespolone natężeń pól elektrycznego i magnetycznego są tylko funkcjami z i ich pochodne cząstkowe po x i y są równe zeru. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd15.png|thumb|500px]] | |||
|valign="top"|Pole elektromagnetyczne fali płaskiej rozchodzącej się w dielektryku musi spełniać wszystkie równania Maxwella. | |||
Z trzeciego równania Maxwella wynika, że wektor natężenia pole elektrycznego fali nie może mieć składowej równoległej do kierunku rozchodzenia się fali. | |||
Analogiczny wniosek dla wektora natężenia pola magnetycznego wynika z czwartego równania Maxwella. | |||
Fala płaska w nieograniczonym dielektryku stratnym jest falą poprzeczną, czyli falą, w której drgania są prostopadłe do kierunku propagacji. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd16.png|thumb|500px]] | |||
|valign="top"|Aby zmniejszyć komplikacje matematyczne przyjmiemy, że zespolony wektor natężenia pola elektrycznego fali ma tylko składową x. | |||
| width=" | |||
Rotacja wektora mającego tylko składową x, która jest funkcją z, jest wektorem posiadającym jedynie składową y. Zatem pierwsze równanie Maxwella wskazuje, że zespolony wektor natężenia pola magnetycznego fali ma tylko składową y. | |||
Dla takiego pola elektromagnetycznego pierwsze dwa równania Maxwella stanowią układ skalarnych równań różniczkowymi pierwszego rzędu z zespolonymi funkcjami niewiadomymi. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd17.png|thumb|500px]] | |||
|valign="top"|Na slajdzie przedstawiono sposób, w który eliminując z układu pierwszych równań natężenie pola magnetycznego uzyskuje się równanie Helmholtza względem natężenia pola elektrycznego. | |||
Postępując podobnie, eliminując z układu równań Maxwella pole elektryczne, otrzymujemy równanie Helmholtza spełniane przez natężenie pola magnetycznego. | |||
Zagadnienie rozwiązania układu zespolonych równań Maxwella sprowadzono do rozwiązania układu dwóch równań Helmholtza. | |||
Występujący w równaniach Helmholtza współczynnik propagacji <math>\gamma\,</math> jest ważnym parametrem dla opisu procesu rozchodzenia się fali płaskiej w ośrodku nieograniczonym. Współczynnik ten jest funkcją parametrów ośrodka i pulsacji. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd18.png|thumb|500px]] | |||
|valign="top"|Znane z matematyki rozwiązanie równania Helmholtza jest sumą dwóch składników, z których jeden zawiera czynnik <math>exp(-\gamma z)\,</math>, a drugi <math>exp(\gamma z) \,</math>. Dla rozważanego przypadku fali płaskiej rozwiązanie ogólne jest superpozycją dwóch fal rozchodzących się wzdłuż osi z, z których pierwsza propagowana jest zgodnie ze zwrotem osi 0z o czym informuje czynnik <math>exp(-\gamma z)\,</math>, a druga fala rozchodzi się w kierunku przeciwnym i zachowanie jej pól zespolonych wzdłuż osi z opisuje czynnik <math>exp(\gamma z) \,</math>. | |||
Do określenia parametrów fali płaskiej wystarczy rozpatrywać jedną z tych fal. Przyjęto, że fala płaska rozchodzi się zgodnie z kierunkiem osi z i dla tej fali przedstawiono zespolone amplitudy natężenia pól elektrycznego i magnetycznego. | |||
Wstawiając uzyskane rozwiązania do pierwszego albo drugiego równania Maxwella otrzymujemy prosty związek między wartościami natężeń pól elektrycznego i magnetycznego. | |||
Mówi on, że gdy dane jest natężenie pola magnetycznego to mnożąc je przez impedancję właściwą ośrodka otrzymujemy wartość natężenia pola elektrycznego. Podkreślmy, że wymienione wielkości są zespolone. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd19.png|thumb|500px]] | |||
|valign="top"|Dotychczas stwierdziliśmy, że fala płaska rozchodząca się zgodnie z kierunkiem osi z ma składową x wektora natężenia pola elektrycznego i składową y wektora natężenia pola magnetycznego. Oznacza to, że wektory natężenia pól elektrycznego i magnetycznego są do siebie prostopadłe oraz prostopadłe do kierunku rozchodzenia się fali. | |||
| width=" | |||
| | |||
i | |||
Falę, która ma wymienione własności, nazywamy falą typu TEM (ang. Transverse Electro-Magnetic). Z falami typu TEM mamy do czynienia w ośrodkach nieograniczonych i izotropowych oraz w pewnych prowadnicach falowych. | |||
Dla fal elektromagnetycznych rozchodzących się w przestrzeni albo w prowadnicach falowych wprowadza się pojęcie impedancji falowej. | |||
Impedancją falową <math>Z_f\,</math> nazywamy stosunek wartości wzajemnie prostopadłych składowych pola elektrycznego i magnetycznego, przy czym składowe te są również prostopadłe do kierunku rozchodzenia się fali. | |||
Dla fali płaskiej w nieograniczonym dielektryku stratnym impedancja falowa jest równa impedancji właściwej materiału. Szerzej, równość tych impedancji dotyczy fal typu TEM i tylko fal tego typu. Przykładowo, nie jest spełniona dla fal rozchodzących się falowodach, o których będzie mowa w kolejnym wykładzie. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd20.png|thumb|500px]] | |||
|valign="top"|Zajmijmy się teraz współczynnikiem propagacji γ, który dla fali rozchodzącej się w dielektryku stratnym jest wielkością zespoloną. Współczynnik ten zapisujemy zwykle w postaci algebraicznej. | |||
Część rzeczywistą <math>\gamma\,</math> nazywamy współczynnikiem tłumienia <math>\alpha\,</math>, mierzymy jego wartość w Neperach na metr. Neper jest logarytmiczną miarą analogiczną do decybela. Definiuje się go jako logarytm naturalny ze stosunku dwóch wartości tej samej wielkości, np. prądu, napięcia czy amplitudy fali elektromagnetycznej. Współczynnik tłumienia o wartości 1 Np/m oznacza, że amplituda fali zmaleje e-krotnie na drodze jednego metra. | |||
Część urojoną <math>\gamma\,</math> nazywamy współczynnikiem fazy <math>\beta\,</math> i jego miarą jest radian na metr. | |||
Wartość współczynnika fazy określa o ile radianów zmieni się faza fali na drodze jednego metra. | |||
Korzystając z algebraicznej postaci współczynnika propagacji zapisujemy zespolone wektory natężeń pola elektromagnetycznego fali w formie przydatnej do wyznaczenia wektorów rzeczywistych. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd21.png|thumb|500px]] | |||
|valign="top"|Wektor zespolony mnożymy przez czynnik <math>exp(j\omega t)\,</math> i wyznaczamy część rzeczywistą wypadkowego wektora, która jest poszukiwanym wektorem rzeczywistym. | |||
Patrząc na postać rzeczywistych wektorów pola elektromagnetycznego fali płaskiej czytelne stają się role współczynników fazy i tłumienia. | |||
Współczynnik fazy występuje przy zmiennej z w argumencie funkcji cosinus. Jego wartość informuje o tempie zmiany fazy wzdłuż osi z. | |||
Czynnik <math>E_0exp(-\alpha z)\,</math>, który jest amplitudą natężenia pola elektrycznego maleje eksponencjalnie wzdłuż kierunku rozchodzenia się fali i to tym szybciej im większy jest współczynnik tłumienia. W tym samym tempie tłumiona jest amplituda natężenia pola magnetycznego. | |||
Tłumienie fali płaskiej nie jest jedynym efektem wywołanym przez stratność dielektryka. Wiemy, że impedancja właściwa dielektryka stratnego jest zespolona, ma moduł i argument. | |||
Moduł impedancji właściwej określa stosunek amplitud natężeń pola elektrycznego i magnetycznego. Argument tej impedancji opisuje opóźnienie fazy wektora natężenia pola magnetycznego w stosunku do fazy wektora natężenia pola elektrycznego. Zatem w dielektryku stratnym przebiegi pól są rozsunięte. Obserwując falę w ustalonej płaszczyźnie z = const. stwierdzimy, że w pewnych momentach natężenie pola elektrycznego jest równe zero przy niezerowym natężeniu pola magnetycznego. Zauważmy, że zmiana znaku wartości wektora oznacza zmianę jego zwrotu. Przesunięcie fazy między wektorami pól fali powoduje, że zmiany zwrotów wektorów tych pól nie odbywają się równocześnie. | |||
Gdy fala płaska rozchodzi się w próżni lub bezstratnym dielektryku to nie ma tłumienia fali, współczynnik tłumienia jest równy zeru oraz pola elektryczne i magnetyczne drgają synchronicznie, impedancja właściwa jest liczbą rzeczywistą. | |||
Należy zapamiętać, że w ośrodku bezstratnym współczynnik fazy jest liniową funkcją pulsacji. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd22.png|thumb|500px]] | |||
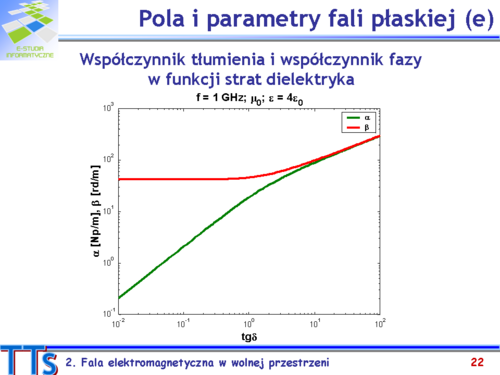
|valign="top"|Przedstawione na wykresie charakterystyki ilustrują wpływ strat dielektryka na wartości współczynników tłumienia i fazy. | |||
| width=" | |||
| | |||
Z przebiegu współczynnika fazy wynika, że dla małostratnych dielektryków wartość <math>\beta\,</math> jest z dobrym przybliżeniem taka jak dla dielektryka bezstratnego. Wartość tego współczynnika jest wielokrotnie większa od wartości współczynnika tłumienia. | |||
Fala płaska ma podobne cechy w dielektrykach małostratnych i bezstratnych. Istotną różnicą jest tłumienie fali w małostratnym materiale. | |||
<math>\ | W przypadku przewodników rzeczywitych wartości <math>\alpha\,</math> i <math>\beta\,</math> są w przybliżeniu równe i tym większe im większy jest tangens kąta stratności ośrodka. Fala płaska w przewodniku ulega bardzo silnemu tłumieniu, w związku z czym wnika na niewielką głębokość. Prąd przewodzenia zanika tak jak natężenie pola elektrycznego i występuje tylko w cienkiej warstwie przy powierzchni przewodnika. Zjawisko to nosi nazwę naskórkowości i bardzo istotne dla mikrofalowych prowadnic falowych. | ||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd23.png|thumb|500px]] | |||
|valign="top"|Wyrażenie <math>\omega t – \beta z\,</math> określające fazę natężenia pola elektrycznego jest prostym matematycznym opisem ruchu fazy fali. Widzimy, że faza tego pola zależy od dwóch zmiennych, czasu t i współrzędnej z. Nie mamy wpływu na czas i zasadne jest stwierdzenie, że wartość t rośnie. Aby śledzić określoną wartość fazy musimy przesuwać się odpowiednią prędkością zgodnie z kierunkiem osi z. Prędkość przesuwania się płaszczyzny stałej fazy nazywamy prędkością fazową, której wartość określa stosunek pulsacji do współczynnika fazy. | |||
Ruch płaszczyzny stałej fazy jest pojęciem matematycznym i nie oznacza przesuwania się żadnego obiektu materialnego, a tym samym przenoszenia energii. Z tego względu prędkość fazowa może przyjmować dowolne wartości dodatnie, może być większa od prędkości światła. | |||
Zwróćmy uwagę, że prędkość fazowa fali płaskiej rozchodzącej się w dielektryku stratnym zmienia się z częstotliwością ponieważ współczynnik fazy tej fali nie jest liniową funkcją pulsacji. Mówimy o dyspersji fali, która w tym wypadku wynika ze strat ośrodka. | |||
Dyspersja fali jest zjawiskiem bardzo niekorzystnym z punktu widzenia systemów transmisji sygnałów. W celu przesłania informacji za pomocą fali elektromagnetycznej, trzeba przebieg o pulsacji nośnej ω zmodulować odpowiednim sygnałem. W wyniku modulacji z sygnału monochromatycznego otrzymujemy widmo częstotliwości. Gdy wysyłamy sygnał falą dyspersyjną to każda z częstotliwości porusza się z inną prędkością fazową, i w trakcie propagacji fali informacja ulega zniekształcaniu. | |||
Dla fali płaskiej | Dla próżni lub dielektryka bezstratnego prędkość fazowa fali płaskiej nie zależy od częstotliwości i jest równa prędkości światła w tym ośrodku. | ||
Kolejnym parametrem fali jest jej długość, czyli droga, którą przebędzie płaszczyzna stałej fazy w czasie okresu fali. Długość fali jest powiązana z współczynnikem fazy bardzo prostym związkiem. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd24.png|thumb|500px]] | |||
|valign="top"|Do poprawnej interpretacji zjawisk związanych z propagacją fal elektromagnetycznych należy wprowadzić dwie prędkości. Jedną z nich jest prędkość fazowa, a drugą prędkość grupowa. Przypomnijmy, że w procesie modulacji „nakładamy” informację na falę nośną. W najprostszym przypadku modulacji amplitudowej jedną częstotliwością otrzymujemy dwie częstotliwości prążków bocznych, różniące się od nośnej o <math>\Delta \omega\,</math>. Superpozycję kilku fal o zbliżonych częstotliwościach, <math>\Delta \omega \to 0\,</math>, i współczynnikach fazowych, <math>\Delta \beta \to 0\,</math>, zwana jest fizyce grupą fal. Obserwując ruch płaszczyzny stałej fazy obwiedni (np. płaszczyzny, w której superpozycja dwóch fal osiąga maksimum) można zapisać warunek <math>\Delta \omega t- \Delta \beta z=const.\,</math> , z którego wynika, podana na slajdzie, zależność opisująca prędkość grupową. | |||
Dla omawianego przypadku, prędkość grupową interpretujemy jako prędkość poruszania się obwiedni grupy fal, a więc jest to również prędkość przesyłania informacji zawartych w tej obwiedni. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd25.png|thumb|500px]] | |||
|valign="top"|Obecności pola elektrycznego, jak i magnetycznego, towarzyszy magazynowanie energii w ośrodku. Rozchodząca się fala niesie ze sobą energie pochodzącą od obydwu pól. | |||
Na slajdzie przedstawiono zależności opisujące gęstości energii pól elektrycznego i magnetycznego fali płaskiej rozchodzącej się w dielektryku stratnym. | |||
Widzimy, że jedynie w bezstratnej nieograniczonej przestrzeni dla fali płaskiej energia pola elektrycznego jest równa energii pola magnetycznego. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd26.png|thumb|500px]] | |||
|valign="top"|Pola fali są funkcjami czasu co oznacza, że mamy do czynienia ze zmianami w czasie energii elektrycznej i magnetycznej magazynowanymi w danym obszarze. Szybkość tych zmian określa moc dostarczaną bądź pobieraną z tego obszaru. Zatem rozchodzeniu się fali towarzyszy przepływ mocy. | |||
{| border=" | |||
| | |||
Miarą powierzchniowej gęstości mocy niesionej przez falę elektromagnetyczną jest wektorowy iloczyn rzeczywistych wektorów natężeń pól elektrycznego i magnetycznego, który nazywamy wektorem Poyntinga, ma wymiar wat na metr kwadratowy. Wektor ten wskazuje kierunek przepływu mocy fali elektromagnetycznej. | |||
i magnetycznego fali | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:TTS_M2_Slajd27.png|thumb|500px]] | |||
|valign="top"|Przytoczmy standardową definicję polaryzacji fali: | |||
polaryzacja fali definiowana jest jako własność rozchodzącej się fali elektromagnetycznej opisująca zmianę w czasie kierunku i względnej amplitudy wektora pola elektrycznego; szczególnie, krzywa rysowana w funkcji czasu przez koniec wektora w ustalonym położeniu w przestrzeni, a sposób w jaki jest śledzony jest taki jakby go obserwować wzdłuż kierunku rozchodzenia się fali. | |||
Innymi słowy, rodzaj polaryzacji fali identyfikując krzywą zakreślaną przez koniec wektora chwilowego pola elektrycznego fali płaskiej w płaszczyźnie <math>z = z_0</math>. Obserwację zachowania tego wektora prowadzimy „patrząc” w tę stronę, w którą rozchodzi się fali. | |||
: | Wyróżniamy trzy rodzaje polaryzacji fali: liniową, kołową i eliptyczną. | ||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
| width=" | |width="500px" valign="top"|[[Grafika:TTS_M2_Slajd28.png|thumb|500px]] | ||
|valign="top"|Dotychczas zajmowaliśmy się falą płaską, której wektror natężenia pola elektrycznego ma tylko składową x. Polaryzacja takiej fali jest liniowa. | |||
Chcąc określić warunki dla pola elektrycznego fali, których spełnienie determinuje określony rodzaj polaryzacji, należy rozważać bardziej złożoną falę. | |||
Utrzymując w mocy założenie, że fala rozchodzi się w kierunku zgodnym z osią 0z, przedstawiono ogólną postać rzeczywistego wektora natężenia pola elektrycznego fali płaskiej w płaszczyźnie z = 0. Amplitudy <math>E_{x0}\,</math> i <math>E_{y0}\,</math> oraz fazy początkowe <math>\varphi_{x0}\,</math> i <math>\varphi_{y0}\,</math> obu składowych wektora mogą przyjmość dowolne wartości. | |||
Polaryzacja liniowa fali występuje dla trzech przedstawionych przypadków. | |||
Dwa pierwsze są oczywiste i wymagają zniknięcia jednej ze składowych wektora pola elektrycznego. | |||
Trzeci przypadek ma miejsce gdy różnica między fazami początkowymi składowych wektora jest równa zeru albo <math>\pi\,</math>, co oznacza że składowe identycznie zmieniają się w czasie, niezależnie od wartości ich amplitud. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
| width=" | |width="500px" valign="top"|[[Grafika:TTS_M2_Slajd29.png|thumb|500px]] | ||
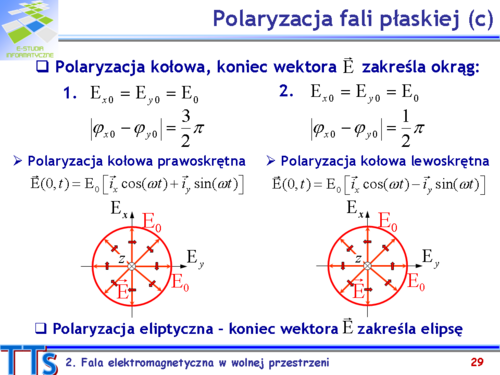
|valign="top"|Polaryzację kołową uzyskujemy gdy amplitudy składowych mają taką samą wartość i przesunięcie fazy między składowymi jest nieparzystą wielokrotnością <math>90^\circ\,</math>, czyli gdy zmiany w czasie jednej składowej opisuje funkcja sinus to drugiej cosinus. | |||
Przy różnicy faz składowych x i y wynoszącej <math>270^\circ\,</math> wektor natężenia pola elektrycznego wiruje zgodnie z ruchem wskazówek zegara i wtedy mówimy o kołowej polaryzacji prawoskrętnej. Polaryzacja kołowa lewoskrętna występuje gdy różnica faz składowych jest równa <math>90^\circ\,</math>. | |||
Zauważmy, że gdy sumujemy dwie fale spolaryzawane kołowo, z których jedna ma polaryzację prawoskrętną, a druga lewoskrętną, to wypadkowa fala jest spolaryzowana liniowo. | |||
Przykładem systemu radiokomunikacyjnego stosującym falę płaską o polaryzacji kołowej jest telewizja satelitarna. Wykorzystuje się fakt, że kołowo spolaryzowana monochromatyczna fala jest superpozycją dwóch fal o polaryzacji liniowej ortogonalnych w czasie i przestrzeni. Dzieki temu każda z fal składowych jest zmodulowana innym kanałem telewizyjnym, które nie zakłócają się wzajemnie. W ten prosty sposób podwaja się pojemność informacyjną systemu. | |||
|} | |} | ||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
| width=" | |width="500px" valign="top"|[[Grafika:TTS_M2_Slajd30.png|thumb|500px]] | ||
|valign="top"| | |||
|} | |} | ||
---- | |||
= Słownik = | = Słownik = | ||
| Linia 824: | Linia 488: | ||
*'''Warunki brzegowe na granicy dielektryk idealny przewodnik:''' W idealnym przewodniku pole elektryczne jest równe 0 i z tego wynikają następujące jego właściwości: | *'''Warunki brzegowe na granicy dielektryk idealny przewodnik:''' W idealnym przewodniku pole elektryczne jest równe 0 i z tego wynikają następujące jego właściwości: | ||
**Pole elektryczne musi być prostopadłe do przewodnika. | **Pole elektryczne musi być prostopadłe do przewodnika. | ||
**Ta prostopadła (normalna) składowa pola indukuje na powierzchni przewodnika ładunek o gęstości <math>\rho\,\</math> równej indukcji elektrycznej <math>D\,</math>. | **Ta prostopadła (normalna) składowa pola indukuje na powierzchni przewodnika ładunek o gęstości <math>\rho\,\ </math> równej indukcji elektrycznej <math>D\,</math>. | ||
**Pole magnetyczne musi być styczne do przewodnika. | **Pole magnetyczne musi być styczne do przewodnika. | ||
**Pole magnetyczne wywołuję na powierzchni przewodnika prąd o gęstości powierzchniowej <math>j\,</math> równej <math>H\,</math>. | **Pole magnetyczne wywołuję na powierzchni przewodnika prąd o gęstości powierzchniowej <math>j\,</math> równej <math>H\,</math>. | ||
Aktualna wersja na dzień 12:03, 5 wrz 2023
Wykład
 |
Słownik
- Częstotliwość graniczna - częstotliwość powyżej której może się propagować fala w falowodzie. Poniżej tej częstotliwości fala jest silnie tłumiona.
- Mikrofale - zakres częstotliwości fal elektromagnetycznych od 300 MHz do 1000 GHz.
- Równania Maxwella - fundamentalne równania techniki mikrofalowej opisujące pole elektromagnetyczne w czasie i przestrzeni.
- Przenikalność dielektryczna i magnetyczna -Podstawowe parametry opisujące właściwości przestrzeni odpowiednio dla pola elektrycznego i magnetycznego.
- Podstawowe parametry pola elektromagnetycznego:
- Natężenie pola elektrycznego .
- Natężenie pola magnetycznego .
- Indukcja pola elektrycznego - wielkość wektorowa proporcjonalna do natężenia pola elektrycznego i przenikalności dielektrycznej.
- Indukcja pola magnetycznego - wielkość wektorowa proporcjonalna do natężenia pola magnetycznego i przenikalności magnetycznej.
- I prawo Maxwella - z pierwszego równania Maxwella widać że zmienne pole magnetyczne jest źródłem zmiennego pola elektrycznego
- W postaci całkowej jest zapisem prawa Faradaya i wiąże ze sobą zmianę strumienia indukcji magnetycznej przenikającego powierzchnię z polem elektrycznym całkowanym wzdłuż zamkniętego konturu otaczającego tą powierzchnię (zal. 2-1).
- W postaci różniczkowej I prawo Maxwella mówi, że rotacja pola elektrycznego jest równa pochodnej indukcji magnetycznej po czasie (zal.2-6).
- II prawo Maxwella - z drugiego równania Maxwella widać że źródłem zmiennego pola magnetycznego jest zmienny w czasie prąd lub zmienne pole elektryczne.
- W postaci całkowej jest zapisem prawa Ampera i wiąże ze sobą zmianę strumienia indukcji elektrycznej i prąd przenikający powierzchnię z polem magnetycznym całkowanym wzdłuż zamkniętego konturu otaczającego tą powierzchnię (zal. 2-2).
- W postaci różniczkowej II prawo Maxwella mówi nam że rotacja pola magnetycznego jest równa pochodnej indukcji elektrycznej i prądu po czasie (zal.2-6).
- III prawo Maxwella - jest zapisem prawa Gaussa dla pola elektrycznego i mówi, że źródłem pola indukcji elektrycznej są ładunki elektryczne.
- W postaci całkowej prawo to mówi że strumień wektora indukcji pola elektrycznego wypływający z objętości przez zamkniętą powierzchnię równy jest zgromadzonemu w tej objętości ładunkowi (zal 2-3).
- W postaci różniczkowej prawo to mówi że divergencja (rozbieżność) wektora indukcji elektrycznej jest równa gęstości ładunku elektrycznego (zal.2-6).
- IV prawo Maxwella - jest zapisem prawa Gaussa dla pola magnetycznego i mówi, że pole magnetyczne jest bezźródłowe.
- W postaci całkowej prawo to mówi że strumień wektora indukcji pola magnetycznego wypływający z objętości przez zamkniętą powierzchnię jest równy 0 co znaczy że pole magnetyczne jest bezźródłowe (zal. 2-4).
- W postaci różniczkowej prawo to mówi, że divergencja (rozbieżność) wektora indukcji magnetycznej jest równa 0, co również znaczy że pola magnetyczne jest bezźródłowe (zal1-6).
- Równanie ciągłości prądu - opisuje relacje między prądem i ładunkiem elektrycznym.
- W postaci całkowej prawo to mówi nam, że prąd przewodzenia wypływający przez powierzchnię zamkniętej objętości V równy jest szybkości zmian ładunku w tej objętości (zal.2-5).
- W postaci różniczkowej prawo to mówi nam, że źródłem pola gęstości prądów jest zmiana gęstości ładunku w czasie (zal 2-6).
- Parametry materiałowe ośrodka dla pola elektromagnetycznego:
- Przenikalność dielektryczna - określa relację między natężeniem pola elektrycznego a jego indukcją (zal. 2-11)
- Przenikalność magnetyczna - określa relację między natężeniem pola magnetycznego a jego indukcją (zal. 2-11)
- Konduktywność - określa relację między natężeniem pola elektrycznego a gęstością prądu przewodzenia ( zal 2-11).
- Rodzaje ośrodków pod katem właściwości dla pola elektromagnetycznego:
- Ośrodki liniowe i nieliniowe.
- Ośrodki jednorodne i niejednorodne.
- Ośrodki dyspersyjne i niedyspersyjne. Parametry materiałowe ośrodka dyspersyjnego zależą a ośrodka niedyspersyjnego nie zależą od częstotliwości.
- Ośrodki izotropowe i anizotropowe. Parametry materiałowe ośrodka izotropowego nie zależą zaś ośrodka anizotropowego zależą od kierunku pola
- Warunki brzegowe na granicy dwóch dielektryków:
- Nie ma prądów i ładunków powierzchniowych.
- Składowe normalne wektorów indukcji i oraz składowe styczne wektorów natężenia pól i są ciągłe.
- Warunki brzegowe na granicy dielektryk idealny przewodnik: W idealnym przewodniku pole elektryczne jest równe 0 i z tego wynikają następujące jego właściwości:
- Pole elektryczne musi być prostopadłe do przewodnika.
- Ta prostopadła (normalna) składowa pola indukuje na powierzchni przewodnika ładunek o gęstości równej indukcji elektrycznej .
- Pole magnetyczne musi być styczne do przewodnika.
- Pole magnetyczne wywołuję na powierzchni przewodnika prąd o gęstości powierzchniowej równej .
- Równania Helmholtza - równania falowe dla pól harmonicznych w zapisie zespolonym.
- Stała propagacji – funkcja parametrów materiałowych ośrodka (zal 2-38). Wartość decyduje o szybkości zmian parametrów fali wzdłuż kierunku propagacji.
- Stała tłumienia część rzeczywista stałej propagacji, decyduje o szybkości strat mocy fali wzdłuż kierunku jej propagacji (zal. 2-51a)
- Stała fazowa część urojona stałej propagacji, decyduje o szybkości zmian fazy fali ( zal. 2-51b, 2-52b).
- Prędkość fazowa fali - prędkość z jaką przesuwa się płaszczyzna stałej fazy fali.
- Prędkość grupowa fali - jest prędkością przepływu energii.
- Fala płaska - Wartości chwilowe wektorów pól elektrycznego i magnetycznego tej fali są takie same w każdym punkcie płaszczyzny prostopadłej do kierunku rozchodzenia się fali. Powierzchnia ekwifazowa fali płaskiej jest płaszczyzna prostopadłą do kierunku propagacji.
- Właściwości fali płaskiej - fala płaska jest falą typu TEM (Transverse Electro-Magnetic)
- Wektory i fali TEM leżą w płaszczyźnie prostopadłej do kierunku propagacji i są prostopadłe względem siebie.
- Zwrot iloczynu wektorowego pola razy pole wyznacza kierunek propagacji a jego moduł gęstość mocy fali.
- Impedancja falowa (stosunek wartości wzajemnie prostopadłych składowych pola i ) fali płaskiej jest równy impedancji właściwej ośrodka.
Bibliografia
- Bogdan Galwas. Miernictwo mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1985, Rozdział 1, 2 i 3.
- Tadeusz Morawski, Wojciech Gwarek. Pola i fale elektromagnetyczne, Wydawnictwa Naukowo-Techniczne, Warszawa, 1998, Rozdział 1 do 8.
- Janusz Dobrowolski. Technika wielkich częstotliwości, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa, 1998 Rozdział 1 i 3.
- Stanisław Rosłoniec. Liniowe obwody mikrofalowe, Wydawnictwa Komunikacji i Łączności, Warszawa, 1999, Rozdział 2.