Zaawansowane algorytmy i struktury danych/Ćwiczenia 7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „ </math>” na „</math>” |
||
| (Nie pokazano 14 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
== Zadanie 1 == | == Zadanie 1 == | ||
{{kotwica|zadanie 1|}} | {{kotwica|zadanie 1|}} | ||
Masz dany graf <math>G=(V, E)</math> wraz z dwoma wybranymi wierzchołkami <math>s,t \in V</math>. Pokaż, jak używając algorytmu Hopcrofta-Karpa wyznaczyć maksymalną liczbę wierzchołkowo rozłącznych ścieżek z <math>s</math> do <math>t</math>. Wierzchołki <math>s</math> i <math>t</math> będą oczywiście wspólne dla tych ścieżek. | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Rozwiązanie''' | |||
<div class="mw-collapsible-content" style="display:none"> | |||
Na podstawie grafu <math>G=(V,E)</math> konstruujemy graf dwudzielny <math>G^k_{in,out} = (V^k_{in} \cup V^k_{out}, E^k_{in,out})</math> w następujący sposób: | |||
{{wzor2|1= | |||
<math> | |||
\begin{array}{r@{}c@{}l} | |||
V^k_{out} &:=& \{v_{out} : v \in V\, \ v\neq s\} \cup \{s_{out}^{i} : | |||
1\le i \le k\},\\ | |||
V^k_{in} &:=& \{v_{in} : v \in V\, \ v\neq t\} \cup \{t_{in}^{i} : 1\le | |||
i \le k\},\\ | |||
E^k_{out,in} &:=& \{v_{out} u_{in} : (v,u) \in V, \ v \neq s,\ u\neq t\} \cup\\ | |||
&\cup& \{v_{out}v_{in} : v \in V\}\cup\\ | |||
&\cup& \{s_{out}^i u_{in} : (s,u) \in V, \ 1\le i \le k\}\cup\\ | |||
&\cup& \{v_{out} t_{in}^i : (v,t) \in V, \ 1\le i \le k\}.\\ | |||
\end{array} | |||
</math> | |||
}} | |||
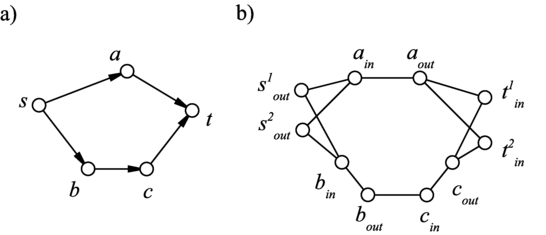
Konstrukcja ta jest przedstawiona na poniższym rysunku a) przykładowy graf <math>G</math> b) graf <math>G^2_{in,out}</math> skonstruowany na podstawie grafu <math>G</math>. | |||
[[Grafika:Zasd_path-transformation.png|546px|center]] | |||
< | Zauważ, że jeżeli w grafie <math>G^{k}_{in,out}</math> istnieje doskonałe skojarzenie, to w grafie <math>G</math> istnieje <math>k</math> rozłącznych wierzchołkowo ścieżek z <math>s</math> do <math>t</math>. Jest tak, ponieważ każde doskonałe skojarzenie w <math>G^k_{in,out}</math> koduje zbiór wierzchołkowo rozłącznych ścieżek z <math>s</math> do <math>t</math>. Krawędzie wybrane do doskonałego skojarzenia <math>M</math> kodują krawędzie wchodzące do i wychodzące z wierzchołka <math>v</math>. Krawędź wchodząca z <math>v</math> jest kodowana przez krawędź <math>M</math> kojarzącą wierzchołek <math>v_{in}</math>, a krawędź wychodząca kodowana jest przez krawędź kojarzącą <math>v_{out}</math>. Odczytując skojarzenie <math>M</math> w ten sposób dostajemy zbiór ścieżek, zaczynających się w <math>s</math> i kończących w <math>t</math>, oraz ewentualnie pewien zbiór cykli. W drugą stronę łatwo zauważyć, że z każdego zbioru <math>k</math> rozłącznych ścieżek możemy skonstruować doskonałe skojarzenie w grafie <math>G</math>. | ||
< | |||
W celu wyznaczenia liczby wierzchołkowo rozłącznych ścieżek w <math>G</math>, możemy przy pomocy binarnego wyszukiwania znaleźć największe <math>k</math>, dla którego <math>G^k_{in,out}</math> zawiera doskonałe skojarzenie. Liczbę <math>k</math> można też wyznaczyć, nie używając wyszukiwania binarnego. Rozważmy graf <math>G^{|V|}_{in,out}</math>, oraz załóżmy, że w <math>G</math> jest w nim <math>k</math> wierzchołkowo rozłącznych ścieżek. Używając kodowania opisanego powyżej możemy skonstruować w <math>G^{|V|}_{in,out}</math> skojarzenie o liczności <math>|V| - k</math>. Weźmy teraz maksymalne skojarzenie w <math>G^{|V|}_{in,out}</math> i przyjrzyjmy się zbiorowi ścieżek, jaki ono koduje w <math>G</math>. Zauważmy, że jeżeli ścieżka wychodząca z wierzchołka <math>s</math> urywa się nagle, to można ja usunąć nie zmieniając liczności skojarzenie <math>M</math>, te same wierzchołki można skojarzyć krawędziami postaci <math>v_{out}v_{in}</math>, które odpowiadają jednoelementowym cyklom. | |||
</div> | </div> | ||
</div> | </div> | ||
| Linia 12: | Linia 33: | ||
== Zadanie 2 == | == Zadanie 2 == | ||
{{kotwica|zadanie 2|}} | {{kotwica|zadanie 2|}} | ||
Masz daną sieć przepływową <math>G=(V, E)</math> wraz z dwoma wybranymi wierzchołkami <math>s,t \in V</math>, w której wszystkie przepustowości krawędzi wynoszą 1. Pokaż, jak używając algorytmu Hopcrofta-Karpa wyznaczyć maksymalny przepływ z <math>s</math> do <math>t</math> w sieci <math>G</math>. | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Rozwiązanie''' | <div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Rozwiązanie''' | ||
<div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible-content" style="display:none"> | ||
Graf krawędziowy dla grafu <math>G=(V,E)</math> to graf <math>G_L=(E,E_L)</math>, w którym wierzchołkami są krawędzie grafu <math>G</math>. Natomiast zbiór krawędzi w grafie <math>G_L</math> to zbiór par krawędzi sąsiednich w <math>G</math>. Dodajmy do grafu <math>G</math> dwie nowe krawędzie: krawędź <math>e_s</math> wchodzącą do <math>s</math> i krawędź | |||
<math>e_t</math> wychodzącą z <math>t</math>. Skonstruujemy teraz z <math>G</math> graf <math>G_L</math>. Łatwo zauważyć teraz, że maksymalna liczba wierzchołkowo rozłącznych ścieżek w <math>G</math> odpowiada maksymalnemu przepływowi w sieci <math>G</math>. | |||
</div> | </div> | ||
</div> | </div> | ||
| Linia 24: | Linia 45: | ||
== Zadanie 3 == | == Zadanie 3 == | ||
{{kotwica|zadanie 3|}} | {{kotwica|zadanie 3|}} | ||
Masz daną planarną sieć przepływową <math>G=(V, E)</math> wraz z dwoma wybranymi wierzchołkami <math>s,t \in V</math>, w której wszystkie przepustowości krawędzi wynoszą <math>1</math>. Pokaż, jak rozwiązać problem wyznaczenia maksymalnego przepływu w sieci <math>G</math> poprzez znalezienie maksymalnego skojarzenia w planarnym grafie dwudzielnym, tzn. pokaż konstrukcję taką, jak ta przedstawiona w Zadaniu 1 i 2, ale zachowującą planarność grafu. | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Rozwiązanie''' | |||
<div class="mw-collapsible-content" style="display:none"> | |||
Dla każdego wierzchołka trzeba wykonać transformację przedstawioną na poniższym rysunku a) transformowany wierzchołek b) podgraf skonstruowany na podstawie tego wierzchołka, który łączy się z tymi samymi krawędziami. | |||
[[Grafika:zasd_planar-path-transformation.png|500px|center]] | |||
W transformacji tej zamieniamy wierzchołek o stopniu <math>d</math> na <math>\lfloor \frac{d}{2} \rfloor</math> skierowanych cykli zawierających <math>d</math> wierzchołków, po jednym dla każdej krawędzi. Następnie wierzchołki odpowiadające wchodzącej krawędzi łączymy skierowaną ścieżką, skierowanie tej ścieżki jest zgodne z kierunkiem tej krawędzi. Zauważ, że w tak skonstruowanym grafie <math>G'</math> liczba wierzchołkowo rozłącznych ścieżek jest równa maksymalnemu przepływowi w oryginalnym grafie. Co więcej, graf <math>G'</math> jest planarny. Pozostaje nam wykonać teraz na <math>G'</math> transformację z [[#zadanie 1|Zadania 1]]. Zauważmy, że także po jej wykonaniu graf pozostanie planarny. | |||
</div> | |||
</div> | |||
== Zadanie 4 == | |||
{{kotwica|zadanie 4|}} | |||
Masz dany graf <math>G=(V_1 \cup V_2, E)</math> dwudzielny. Pokaż, jak używając algorytmu Hopcrofta-Karpa wyznaczyć minimalne pokrycie wierzchołkowe tego grafu. | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Rozwiązanie''' | <div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Rozwiązanie''' | ||
<div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible-content" style="display:none"> | ||
Znajdźmy maksymalne skojarzenie <math>M</math> w grafie <math>G</math> przy pomocy algorytmu Hopcrofta-Karpa. Liczność skojarzenia <math>M</math> na pewno jest nie większa niż liczność minimalnego pokrycia wierzchołkowego, ponieważ co najmniej jeden koniec każdej krawędzi skojarzenia musi być wzięty do minimalnego pokrycia wierzchołkowego. Pokażemy teraz, że zachodzi równość, tzn. liczność maksymalnego skojarzenia w grafie dwudzielnym jest równa liczności minimalnego pokrycia wierzchołkowego tego grafu. Dowód ten będzie konstrukcyjny, więc automatycznie dostaniemy algorytm wyznaczający minimalne pokrycie wierzchołkowe. | |||
Skierujmy krawędzie skojarzenia od <math>V_2</math> do <math>V_1</math>, a wszystkie pozostałe krawędzie od <math>V_1</math> do <math>V_2</math>. Niech <math>R_1</math> i <math>R_2</math> będą zbiorami wierzchołków wolnych odpowiednio w <math>V_1</math> i <math>V_2</math>. Niech <math>Z</math> oznacza zbiór wierzchołków osiągalnych w tym grafie z <math>R_1</math>. Zauważmy, że <math>Z \cap R_2 = \emptyset</math>, ponieważ w innym wypadku ścieżka z <math>R_1</math> do <math>R_2</math> stanowiłaby ścieżkę powiększającą względem maksymalnego skojarzenia <math>M</math>. Niech <math>L:= (V_2 \cap Z) \cup (V_1 - Z)</math>. Łatwo zauważyć, że liczność <math>L</math> jest równa liczności zbioru <math>M</math> oraz że <math>L</math> jest pokryciem wierzchołkowym. | |||
</div> | |||
</div> | |||
== Zadanie 5 == | |||
{{kotwica|zadanie 5|}} | |||
Niech <math>G = (V_1 \cup V_2,E)</math> będzie grafem dwudzielnym. O krawędzi <math>e\in E</math> mówimy, że jest dozwolona w <math>G</math> jeżeli istnieje doskonałe skojarzenie <math>M</math> zawierające <math>e</math>. Dwudzielny graf <math>G</math> nazywamy natomiast ''elementarnym'' jeżeli wszystkie krawędzie są dozwolone. Zaproponuj, jak wykorzystując algorytm Hopcrofta-Karpa sprawdzić, czy <math>G</math> jest elementarny? | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed">'''Wskazówka''' | |||
<div class="mw-collapsible-content" style="display:none"> | |||
Znajdźmy doskonałe skojarzenie <math>M</math> w grafie <math>G</math> przy pomocy algorytmu Hopcrofta-Karpa. Jeżeli <math>G</math> nie zawiera doskonałego skojarzenia, to na pewno nie jest elementarny. Skonstruujmy graf <math>G'</math> z <math>G</math> poprzez skierowanie krawędzi skojarzenia od <math>V_2</math> do <math>V_1</math>, a wszystkich pozostałych krawędzi od <math>V_1</math> do <math>V_2</math>. Łatwo jest pokazać, że graf <math>G</math> jest elementarny wtedy i tylko wtedy, gdy graf <math>G'</math> jest silnie spójny. | |||
</div> | </div> | ||
</div> | </div> | ||
Aktualna wersja na dzień 11:01, 5 wrz 2023
Zadanie 1
Masz dany graf wraz z dwoma wybranymi wierzchołkami . Pokaż, jak używając algorytmu Hopcrofta-Karpa wyznaczyć maksymalną liczbę wierzchołkowo rozłącznych ścieżek z do . Wierzchołki i będą oczywiście wspólne dla tych ścieżek.
Zadanie 2
Masz daną sieć przepływową wraz z dwoma wybranymi wierzchołkami , w której wszystkie przepustowości krawędzi wynoszą 1. Pokaż, jak używając algorytmu Hopcrofta-Karpa wyznaczyć maksymalny przepływ z do w sieci .
Zadanie 3
Masz daną planarną sieć przepływową wraz z dwoma wybranymi wierzchołkami , w której wszystkie przepustowości krawędzi wynoszą . Pokaż, jak rozwiązać problem wyznaczenia maksymalnego przepływu w sieci poprzez znalezienie maksymalnego skojarzenia w planarnym grafie dwudzielnym, tzn. pokaż konstrukcję taką, jak ta przedstawiona w Zadaniu 1 i 2, ale zachowującą planarność grafu.
Zadanie 4
Masz dany graf dwudzielny. Pokaż, jak używając algorytmu Hopcrofta-Karpa wyznaczyć minimalne pokrycie wierzchołkowe tego grafu.
Zadanie 5
Niech będzie grafem dwudzielnym. O krawędzi mówimy, że jest dozwolona w jeżeli istnieje doskonałe skojarzenie zawierające . Dwudzielny graf nazywamy natomiast elementarnym jeżeli wszystkie krawędzie są dozwolone. Zaproponuj, jak wykorzystując algorytm Hopcrofta-Karpa sprawdzić, czy jest elementarny?