Matematyka dyskretna 1/Wykład 13: Grafy II

Grafy eulerowskie

Leonhard Euler stanął przed następującym problemem. W Królewcu (wówczas Konigsbergu) na rzece Pregole, na której są dwie wyspy wybudowano siedem mostów łączące wyspy ze sobą, oraz z oboma brzegami rzeki. Układ mostów został przedstawiony na rysunku:

Mapa mostów w Królewcu

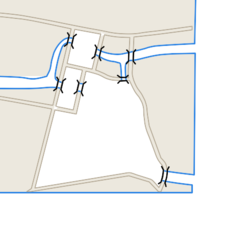
Pytanie, jakie zostało postawione Eulerowi, to czy można tak ułożyć spacer po wszystkich mostach Królewca, by po każdym przejść tylko raz i wrócić do punktu startowego. Euler oczywiście odpowiedział na zadane mu pytanie. Postaramy się rozwiązać Zagadnienie Mostów Królewieckich. Zacznijmy od przedstawienia powyższego problemu w języku grafów. Niech każdy spójny kawałek lądu w Królewcu odpowiada wierzchołkowi. Otrzymamy w ten sposób dwa wierzchołki odpowiadające wyspom oraz dwa obu brzegom Pregoły. Most pomiędzy dwoma kawałkami lądu będziemy interpretować jako krawędź łączącą wierzchołki odpowiadające tym skrawkom lądu. W ten sposób otrzymamy następujący graf (nie będący grafem prostym):

Mapa mostów w Królewcu

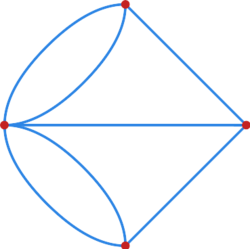
Naszym celem jest skonstruowanie specjalnego cyklu w grafie z rysunku Mapa mostów w Królewcu.

Przykład grafu eulerowskiego (a) i nieeulerowskiego (b)

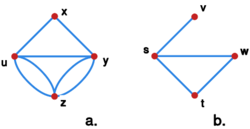
Cykl Eulera to zamknięta marszruta przechodząca przez każdą krawędź grafu dokładnie raz.

Graf eulerowski to graf posiadający cykl Eulera.

Graf na rysunku Grafy eulerowskie posiada cykl Eulera $x\to u\to z\to y\to u\to z\to y\to x$, zaś graf w części b. nie jest eulerowski, bo jeżeli wejdzie się do wierzchołka $v$, to już nie będzie można z niego wyjść; jeśli zaś rozpoczęlibyśmy naszą marszrutę z wierzchołka $v$ to nie będzie można doń powrócić.

Grafy eulerowskie posiadają ładną charakterystykę umożliwiającą prostą i szybką weryfikację omawianej własności.

Twierdzenie 13.1

Graf $\mathbf{𝐆}=(V,E)$ jest eulerowski wtedy i tylko wtedy, gdy jest spójny i stopień każdego wierzchołka jest parzysty.

Dowód

Załóżmy najpierw, że $\mathbf{𝐆}$ jest eulerowski i niech $E$ jakimś jego cyklem Eulera. Poruszając się po $\mathbf{𝐆}$ wzdłuż cyklu $E$ zliczajmy stopniowo używane krawędzie incydentne do poszczególnych wierzchołków. Zawsze po wejściu i wyjściu z danego wierzchołka $v$ liczba policzonych krawędzi incydentnych z $v$ zwiększy się o $2$. Tak więc, jeśli $v$ nie jest początkiem cyklu, to zawsze będzie miał parzystą liczbę aktualnie policzonych krawędzi incydentnych. Początek cyklu zaś, dopóki nie przeszliśmy ostatnią krawędzią grafu (która oczywiście prowadzi do niego) będzie miał nieparzystą liczbę policzonych krawędzi. Po użyciu jednak tej ostatniej krawędzi okaże się, że i on ma parzysty stopień. Żadna krawędź nie zostanie pominięta, ani policzona wielokrotnie, bo przeczyłoby to eulerowskości cyklu $E$ lub spójności grafu $\mathbf{𝐆}$.

Dla dowodu implikacji odwrotnej, pokażmy najpierw, że jeżeli w skończonym grafie $\mathbf{𝐆}$ dowolny wierzchołek ma parzysty stopień, to $\mathbf{𝐆}$ posiada cykl. Istnienie takiego cyklu pokażemy wskazując jego kolejne krawędzie. Zaczynamy od dowolnie wybranej krawędzi $v_0{v}_1$. Następnie przechodzimy do jakiejkolwiek innej krawędzi wychodzącej z wierzchołka $v_1$. Załóżmy, że była to krawędź $v_1{v}_2$. Wybieramy następnie dowolną różną od $v_1{v}_2$ krawędź wychodzącą z $v_2$. Czynność tę powtarzamy tak długo, aż dojdziemy do jakiegoś wierzchołka $v_i$, który został już wcześniej odwiedzony. W ten sposób otrzymamy cykl $v_i\to v_{i+1}\to \dots \to v_k\to v_i$. Jedynym problemem mógłby, w jakimś momencie, być brak możliwości kontynuowania marszu zanim dojdziemy do odwiedzonego wcześniej punktu $v_i$. Sytuacja taka nie jest jednak możliwa, gdyż oznaczałoby to istnienie wierzchołka o incydentnego z jedną tylko krawędzią (wejściową), co stoi w sprzeczności z parzystością jego stopnia.

Teraz możemy przejść do dowodu Twierdzenia, który przeprowadzimy indukcyjnie ze względu na liczbę krawędzi w grafie $\mathbf{𝐆}$. Jak już zauważyliśmy powyżej, graf $\mathbf{𝐆}$ posiada jakiś cykl $C$. Usuńmy z grafu $\mathbf{𝐆}$ krawędzie i wierzchołki cyklu $C$ otrzymując w ten sposób mniejszy graf ${\mathbf{𝐆}}^{\prime }$. Graf ${\mathbf{𝐆}}^{\prime }$ może już nie być spójny, ale nadal będzie posiadał jedynie wierzchołki parzystego stopnia. Jeżeli ${\mathbf{𝐆}}^{\prime }$ jest pusty, to cykl $C$ jest cyklem Eulera, co kończyłoby dowód. W przeciwnym razie, w każdej spójnej składowej grafu ${\mathbf{𝐆}}^{\prime }$ nie będącej punktem izolowanym, korzystając z założenia indukcyjnego, znajdujemy cykle Eulera $E_1,\dots E_l$. Ponieważ graf $\mathbf{𝐆}$ był spójny, to cykl $C$ musi przechodzić przez jakiś wierzchołek każdego cyklu $E_1,\dots E_l$. Tak więc cykl Eulera dla grafu $\mathbf{𝐆}$ możemy wyznaczyć w ten sposób, że przechodząc przez cykl $C$, za każdym razem gdy napotkamy nieodwiedzony jeszcze cykl $E_i$, zbaczamy z cyklu $C$ i przechodzimy w całości $E_i$, a później kontynuujemy wędrówkę po cyklu $C$. W konsekwencji przejdziemy po wszystkich krawędziach, każdą odwiedzając jedynie raz.

Bogatsi o nowo zdobytą wiedzę możemy już negatywnie odpowiedzieć na pytanie postawione Leonhardowi Euler'owi.

Analizując dowód Twierdzenia 13.1 dostajemy następujący wniosek.

Wniosek 13.2

Graf spójny jest eulerowski wtedy i tylko wtedy, gdy rodzinę jego krawędzi da się podzielić na rozłączne krawędziowo cykle.

Z grafami eulerowskimi ściśle związane są grafy, które można narysować bez odrywania ołówka i rysując każdą krawędź dokładnie raz.

Graf jednokreślny to graf posiadający marszrutę przechodzącą dokładnie raz przez każdą krawędź.

Wniosek 13.3

Graf $\mathbf{𝐆}=(V,E)$ jest jednokreślny wtedy i tylko wtedy, gdy jest spójny i jego wszystkie, poza co najwyżej dwoma wierzchołkami, mają parzysty stopień.

Dowód

Jeśli $\mathbf{𝐆}$ jest jednokreślny, i marszruta przechodząca przez każda krawędź jest cyklem, to $\mathbf{𝐆}$ jest eulerowski i wobec Twierdzenia 13.1 ma jedynie wierzchołki o parzystym stopniu. Jeśli zaś marszruta ta nie jest cyklem, to oczywiście wszystkie wierzchołki poza początkowym i końcowym mają parzysty stopień.

Na odwrót, jeśli w grafie $\mathbf{𝐆}$ wszystkie wierzchołki mają parzysty stopień, to $\mathbf{𝐆}$ jest eulerowski, a zatem jednokreślny. Jeśli zaś $\mathbf{𝐆}$ ma wierzchołki o nieparzystym stopniu, to - wobec naszego założenia, może ich mieć dokładnie dwa, bo może mieć jedynie parzyście wiele wierzchołków o nieparzystym stopniu. Łącząc teraz te dwa wierzchołki nową krawędzią, dostajemy graf ${\mathbf{𝐆}}^{\prime }$, w którym już wszystkie wierzchołki mają parzysty stopień. A zatem ${\mathbf{𝐆}}^{\prime }$ posiada cykl Eulera $E$. Cykl ten przechodzi oczywiście przez nowo dodana krawędź. Usuwając ją z cyklu $E$ dostajemy marszrutę w grafie $\mathbf{𝐆}$, świadcząca o jego jednokreślności.

Grafy hamiltonowskie

Graf połączeń między klientami firmy kurierskiej

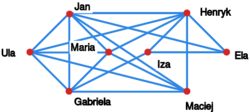
Inny, ciekawy problem można przedstawić na przykadzie firmy rozwożącej przesyłki. Dotyczy on pracy kuriera mającego rozwieść przesyłki do odbiorców, w ten sposób by odwiedzić każdego klienta jedynie raz, a na końcu wrócić do siedziby firmy. Załóżmy, że na przesyłki czeka następujący zbiór osób: Henryk, Elżbieta, Maciej, Jan, Ula, Izabela, Gabriela, oraz Maria. Niestety, jak widać z rysunku, nie ma połączeń umożliwiających przejazd między dowolnymi dwoma klientami.

Zachodzi pytanie, czy kurier mimo to jest w stanie wykonać swoje zadanie. Jeśli prześledzimy warunki nałożone na trasę swojej wędrówki okaże się, że szukamy tzw. cyklu Hamiltona.

Cykl Hamiltona to cykl przechodzący przez wszystkie wierzchołki grafu (czyli marszruta zamknięta odwiedzająca każdy wierzchołek dokładnie raz).

Graf hamiltonowski to graf posiadający cykl Hamiltona.

Ścieżka Hamiltona to ścieżka przechodząca przez wszystkie wierzchołki, każdy odwiedzając jedynie jeden raz.

W odróżnieniu od grafów eulerowskich, grafy hamiltonowskie nie posiadają prostej i szybkiej w użyciu charakteryzacji. Nie znana jest żadna metoda, pozwalająca szybko (tzn. w czasie wielomianowym) stwierdzić czy dany graf jest hamiltonowski. Są natomiast znane pewne warunki wystarczające na to, by graf był hamiltonowski. Jednym z ciekawszych takich warunków wystarczających jest warunek wykorzystujący jedynie stopnie wierzchołków. Przedstawiony jest w postaci następującego twierdzenia.

Twierdzenie 13.4 [Ore 1960]

Jeśli w grafie prostym $\mathbf{𝐆}=(V,E)$ o co najmniej $3$ wierzchołkach dowolne dwa niesąsiednie wierzchołki $v$ i $w$ spełniają $\mathrm{deg}v+\mathrm{deg}w\ge \left|V\right|$, to graf $\mathbf{𝐆}$ jest hamiltonowski.

Cykl Hamiltona w grafie $\mathbf{𝐆}$

Dowód

Dla dowodu niewprost załóżmy, że pewien niehamiltonowski graf $\mathbf{𝐆}$ o $n$ wierzchołkach spełnia

(*) $\mathrm{deg}v+\mathrm{deg}w\ge n$, dla niesąsiednich wierzchołków $v,w$.

Dodawanie krawędzi do $\mathbf{𝐆}$ nie psuje warunku (*), więc do grafu $\mathbf{𝐆}$ można dokładać krawędzie tak długo, jak długo jest on niehamiltonowski. Możemy więc dodatkowo założyć, że $\mathbf{𝐆}$ ma tę własność, że po dodaniu jakiejkolwiek krawędzi otrzymamy już cykl Hamiltona. Tak więc w $\mathbf{𝐆}$ musi istnieć ścieżka Hamiltona $v_0\to v_1\to \dots \to v_{n-1}\to v_n$.

Wierzchołek $v_0$ ma, poza wierzchołkiem $v_1$, dodatkowo $\mathrm{deg}{v}_0-1$ sąsiadów. Oznaczmy ich przez $v_{i_1},\dots ,v_{i_{\mathrm{deg}{v}_0-1}}$. Z kolei, na mocy (*), wierzchołek $v_n$ w zbiorze $\{v_2,\dots ,v_{n-2}\}$ ma $\mathrm{deg}{v}_n-1>(n-3)-(\mathrm{deg}{v}_0-1)$ sąsiadów. To gwarantuje, że $v_n$ jest sąsiadem któregoś z $\mathrm{deg}{v}_0-1$ wierzchołków $v_{i_1-1},\dots ,v_{i_{\mathrm{deg}{v}_1-1}-1}$. Istnieje więc takie miejsce $j$ w ścieżce $v_0\to v_1\to \dots \to v_{n-1}\to v_n$, że $v_1$ jest incydentny z $v_j$, zaś $v_n$ z $v_{j-1}$.

Tak więc cykl $v_1\to v_j\to v_{j+1}\to \dots \to v_n\to v_{j-1}\to v_{j-2}\to \dots \to v_1$ jest cyklem Hamiltona w grafie $\mathbf{𝐆}$, co w konsekwencji daje sprzeczność z faktem, że $\mathbf{𝐆}$ miał nie być hamiltonowski.

Twierdzenie Ore'a jest uogólnieniem silniejszego warunku znalezionego parę lat wcześniej przez Dirac'a.

Wniosek 13.5 [G. A. Dirac 1952]

Graf prosty $\mathbf{𝐆}=(V,E)$, w którym każdy wierzchołek ma stopień co najmniej $\left|V\right|/2$ jest hamiltonowski.

Wróćmy teraz do przykładu o kurierze. Licząc stopnie wierzchołków w grafie z rysunku i używając Twierdzenia Ore'a możemy stwierdzić, że graf ten ma cykl Hamiltona. Tak więc kurier, nie bojąc się utraty pracy, może spokojnie spełnić swoje zadanie.

Grafy dwudzielne i skojarzenia

Przypomnijmy, że:

Graf dwudzielny to graf $\mathbf{𝐆}=(V,E)$, w którym zbiór wierzchołków $V$ da się podzielić na dwa rozłączne podzbiory $V_1$ oraz $V_2$ tak, by żadne dwa wierzchołki w obrębie tego samego podzbioru $V_i$ nie były sąsiadami. Czasem, dla podkreślenia takiego podziału, graf dwudzielny będziemy oznaczać przez $(V_1\cup V_2,E)$. Zauważmy jednak, że podział taki nie jest jednoznaczny - np. w antyklice ${{𝒜}}_n$ dowolny podział zbioru wierzchołków na dwa podzbiory jest podziałem dwudzielnym.

Twierdzenie 13.6

Graf jest dwudzielny wtedy i tylko wtedy, gdy każdy jego cykl ma parzystą długość.

Dowód

Załóżmy najpierw, że graf $\mathbf{𝐆}=(V,E)$ jest dwudzielny czyli, że $V$ można podzielić na dwa rozłączne zbiory wierzchołków $V_1$ oraz $V_2$, w ten sposób, że podgrafy indukowane $\mathbf{𝐆}{|}_{V_i}$ są antyklikami. Rozważmy cykl $v_1\to v_2\to \dots \to v_{k-1}\to v_k\to v_1$ o $k$ elementach. Bez straty ogólności możemy załóżyć, że $v_1\in V_1$. Ponieważ pomiędzy wierzchołkami z $V_1$ nie ma krawędzi, to $v_2\in V_2$. Z kolei $v_3\in V_1$, a $v_4\in V_2$ i tak dalej. Tak więc każdy $v_i$ o nieparzystym indeksie $i$ należy do $V_1$. W konsekwencji $v_k$ musi mieć parzysty indeks $k$, aby mógł być połączony z $v_1$. W rezultacie otrzymujemy, że cykle muszą być parzystej długości.

Dowód odwrotnej implikacji przeprowadzimy najpierw przy założeniu, że graf $\mathbf{𝐆}$ jest spójny. Naszym celem jest takie podzielenie $V$ na dwa zbiory wierzchołków $V_1,V_2$, by, dla $i=1,2$, żadne dwa wierzchołki z $V_i$ nie były ze sobą połączone. Wybierzmy z $V$ dowolny wierzchołek $v$. Niech $V_1$ będzie zbiorem, do którego należy $v$ oraz wszystkie wierzchołki, do których można dojść z $v$ ścieżką parzystej długości, zaś $V_2$ niech składa się z pozostałych wierzchołków. Załóżmy, że $u_1,u_2\in V_1$. Wtedy oczywiście istnieją ścieżki $v\to \dots \to u_1$ oraz $u_2\to \dots \to v$ o parzystej długości. Gdyby $u_1,u_2$ były połączone krawędzią, to dostalibyśmy cykl $v\to \dots \to u_1\to u_2\to \dots \to v$ o nieparzystej długości. A zatem $\mathbf{𝐆}{|}_{V_1}$ jest antykliką. Aby zobaczyć, że również $\mathbf{𝐆}{|}_{V_2}$ jest antykliką, wystarczy zauważyć że $V_2$ składa się z tych wierzchołków grafu $\mathbf{𝐆}$, do których z początkowo wybranego wierzchołka $v$ można dojść jedynie ścieżkami nieparzystej długości. Teraz uzasadnienie, że także $V_2$ indukuje antyklikę jest analogiczne jak dla $V_1$.

Niech teraz graf $\mathbf{𝐆}$ ma $l>1$ spójnych składowych $C_1,\dots ,C_l$. Wtedy każdą spójną składową $C_i$ możemy podzielić na zbiory $C_i^1,C_i^2$ świadczące o dwudzielności grafu indukowanego ${\mathbf{𝐆}}_{C_i}$. W konsekwencji daje to podział $V$ na $C_1^1\cup \dots \cup C_l^1$ oraz $C_1^2\cup \dots \cup C_l^2$ świadczący o dwudzielności całego grafu $\mathbf{𝐆}$.

Z grafami dwudzielnymi związany jest problem biura matrymonialnego. Do biura matrymonialnego zgłaszają się mężczyźni i kobiety poszukujący swojej drugiej połowy. Niestety nie każdemu mężczyźnie odpowiada każda kobieta i na odwrót. A więc każdy zgłaszający podaje swój opis, jak i wymagania stawiane potencjalnemu partnerowi. Interpretując mężczyzn i kobiety jako wierzchołki grafu, w którym krawędzie łączą "mężczyznę" z "kobietą", jeśli nawzajem sobie odpowiadają, otrzymujemy dwudzielny graf ${\mathbf{𝐆}}_z(M,K)$ odpowiadający potencjalnym związkom. Biuro matrymonialne ku uciesze klientów (i maksymalizacji swojego zysku) chciałoby stworzyć jak najwięcej par. Optymalnie by było, gdyby nikt nie został samotny. Wtedy jednak musimy oczywiście założyć, że mężczyzn jest tyle samo co kobiet.

Skojarzenie w grafie dwudzielnym $\mathbf{𝐆}=(V_1\cup V_2,E)$ to podzbiór krawędzi $M\subseteq \mathsf{E}\left(\mathbf{𝐆}\right)$, w którym żadne dwie $v_1{v}_2,u_1{u}_2\in M$ nie wychodzą z tego samego wierzchołka.
Powiemy ponadto, że $v\in V_i$ jest skojarzony, jeśli istnieje $w\in V_{3-i}$ taki, że krawędź $vw$ należy do skojarzenia.

Pełne skojarzenie $V_1$ z $V_2$ w grafie dwudzielnym $\mathbf{𝐆}=(V_1\cup V_2,E)$ to skojarzenie, w którym każdy wierzchołek z $V_1$ jest skojarzony.

Naturalnym jest pytanie, kiedy istnieje pełne skojarzenie $V_1$ z $V_2$ w grafie dwudzielnym $\mathbf{𝐆}=(V_1\cup V_2,E)$. Odpowiedział na nie P. Hall. Użył do tego funkcji $\mathrm{\Phi }\left(A\right)$ zwracającej dla $A\subseteq V_1$ zbiór tych wierzchołków $V_2$, które są sąsiednie z przynajmniej jednym wierzchołkiem w $A$.

Twierdzenie 13.7 [O Skojarzeniach w Grafie Dwudzielnym, P. Hall 1935]

Niech $\mathbf{𝐆}=(V_1\cup V_2,E)$ będzie grafem dwudzielnym. Wówczas pełne skojarzenie $V_1$ z $V_2$ istnieje wtedy i tylko wtedy, gdy $\left|A\right|\le \left|\mathrm{\Phi }\left(A\right)\right|$ dla każdego podzbioru $A$ zbioru $V_1$.

Dowód

Dla dowodu nierówności $\left|A\right|\le \left|\mathrm{\Phi }\left(A\right)\right|$ załóżmy, że $M$ jest pełnym skojarzeniem. Elementy skojarzone z elementami zbioru $A$ muszą być oczywiście w $\mathrm{\Phi }\left(A\right)$. Z drugiej strony skojarzenie $M$ determinuje injekcję $A⟶\mathrm{\Phi }\left(A\right)$, skąd natychmiast $\left|A\right|\le \left|\mathrm{\Phi }\left(A\right)\right|$.

Dowód implikacji odwrotnej jest nieco trudniejszy. Przeprowadzimy go indukcyjnie ze względu na liczbę wierzchołków $n_1=\left|V_1\right|$. Dla $n_1=1$ nierówność $\left|V_1\right|\le \left|\mathrm{\Phi }\left(V_1\right)\right|$ gwarantuje, że jest co kojarzyć z jedynym wierzchołkiem w $V_1$. Załóżmy więc, że $n_1>1$ i rozważmy dwa przypadki:

1. Dowolny właściwy podzbiór $W$ zbioru wierzchołków $V_1$ posiada więcej sąsiadów niż jego moc, tzn. $\left|\mathrm{\Phi }\left(W\right)\right|>\left|W\right|$. Wtedy wybieramy dowolne wierzchołki $v_1\in V_1$ oraz $v_2\in V_2$ i je kojarzymy. Dla $W\subseteq V_1-\left\{v_1\right\}$ zbiór sąsiadów w zbiorze $V_2$ pomniejszonym o wybrany już $v_2$ jest nadal nie liczniejszy niż liczność $\left|W\right|$. Założenie indukcyjne gwarantuje nam więc jakieś skojarzenie pełne $M$ zbioru $V_1-\left\{v_1\right\}$ z $V_2-\left\{v_2\right\}$ w grafie pozostałych wierzchołków $\mathbf{𝐆}{|}_{(V_1-\left\{v_1\right\})\cup (V_2-\left\{v_2\right\})}$. Oczywiście $M\cup v_1{v}_2$ jest poszukiwanym skojarzeniem pełnym w $\mathbf{𝐆}$.

2. Istnieje właściwy podzbiór $W$ zbioru $V_1$, taki że $\left|\mathrm{\Phi }\left(W\right)\right|=\left|W\right|$.

Ponieważ dla $A\subseteq W$ mamy $\mathrm{\Phi }\left(A\right)\subseteq \mathrm{\Phi }\left(W\right)$, to

$\left|A\right|\le \left|\mathrm{\Phi }\left(A\right)\right|=|\mathrm{\Phi }\left(A\right)\cap \mathrm{\Phi }\left(W\right)|$

Ta nierówność pozwala użyć założenia indukcyjnego do skojarzenia wszystkich elementów ze zbioru $W$ z elementami należącymi do $\mathrm{\Phi }\left(W\right)$.

Wystarczy więc znaleźć skojarzenie pozostałych elementów, czyli skojarzenie zbioru $V_1-W$ ze zbiorem $V_2-\mathrm{\Phi }\left(W\right)$. Skojarzenie takie dostaniemy również indukcyjnie, o ile pokażemy, że dla dowolnego $A\subseteq V_1-W$, zbiór jego sąsiadów w $V_2-\mathrm{\Phi }\left(W\right)$ jest liczniejszy od $A$, tzn.

$\left|A\right|\le |\mathrm{\Phi }\left(A\right)-\mathrm{\Phi }\left(W\right)|$

Załóżmy, że jakiś zbiór $A\subseteq V_1-W$ nie spełnia powyższej nierówności. Wtedy

$|A\cup W|=\left|A\right|\cup \left|W\right|>|\mathrm{\Phi }\left(A\right)-\mathrm{\Phi }\left(W\right)|+\left|\mathrm{\Phi }\left(W\right)\right|\ge \left|\mathrm{\Phi }(A\cup W)\right|$,

co przeczy założeniu twierdzenia, przy którym pracujemy.

Wielospójność

Zarówno drzewo, jak i klika są grafami spójnymi. W drzewie jednak, usunięcie jakiegokolwiek wierzchołka nie będącego liściem rozspaja go. Z drugiej strony, klika pozostaje spójna po usunięciu dowolnej liczby wierzchołków. Aby rozróżnić te różne rodzaje spójności rozważa się następujące uogólnienia spójności.

Graf $k$-spójny to graf, który po usunięciu dowolnie wybranych $k-1$ wierzchołków (i incydentnych z nimi krawędzi) pozostaje spójny.

Graf $k$-spójny krawędziowo to graf, który po usunięcie dowolnie wybranych $k-1$ krawędzi (bez usuwania wierzchołków) pozostaje spójny.

Przykład

• Grafy $1$-spójne lub $1$-spójne krawędziowo to po prostu grafy spójne.

• Drzewa są spójne, ale nie $2$-spójne i nie $2$-spójne krawędziowo.

• Klika ${{𝒦}}_n$ jest $n$-spójna i $n-1$-spójna krawędziowo.

Z pojęciami wielospójności związane są następujące pojęcia:

Zbiór rozdzielający wierzchołki $u,v$ to zbiór wierzchołków $S\subseteq V-\{u,v\}$ taki, że każda droga z $u$ do $v$ przechodzi przez któryś element ze zbioru $S$.

Ponadto powiemy, że $S$ jest zbiorem rozdzielającym, jeśli $S$ jest zbiorem rozdzielającym jakichś dwu wierzchołków $u,v$.

Zbiór rozspajający wierzchołki $u,v$ to zbiór krawędzi $F\subseteq E$ taki, że każda droga z $u$ do $v$ zawiera jakąś krawędź z $F$.

Rozcięcie wierzchołków $u,v$ to zbiór rozspajający wierzchołki $u,v$, którego żaden podzbiór właściwy nie rozspaja $u$ z $v$.
Zbiór krawędzi $F$ będziemy nazywać rozcięciem, jeśli $F$ jest rozcięciem jakichś dwu wierzchołków $u,v$

Most to taka krawędź $e$, że zbiór $\left\{e\right\}$ tworzy rozcięcie.

Uwaga

Jeżeli graf jest $k$-spójny, to każdy jego zbiór rozdzielający musi mieć co najmniej $k$ wierzchołków. Analogicznie jeśli $\mathbf{𝐆}$ jest $k$-spójny krawędziowo, to każde jego rozcięcie musi mieć co najmniej $k$ krawędzi.

Grafy menger

W grafie z rysunku Grafy menger odpowiednim rozspajającym zbiorem $X$ z przypadku 1, może być zbiór $\{xs,xy,uy,zt\}$ zaznaczonych liniami przerywanymi

Load video

Local File

Local File might collect personal data.

Continue Dismiss

Kontynuacja przykładu z rysunku Grafy menger i rysunku z liniami przerywanymi. Pokazane są grafy ${\mathbf{𝐔}}^{\prime }$ (a) oraz ${\mathbf{𝐖}}^{\prime }$ (b)

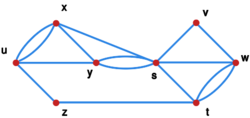
Przykład

Przykładowymi zbiorami rozdzielającymi wierzchołki $u,w$ w grafie z rysunku Grafy menger są zbiory $\{x,y,z\}$ i $\{s,t\}$. Zbiory $\{xs,xy,ys,ys,zt\}$ jest rozspajający, a zbiór $\{xs,xy,uy,uz\}$ jest rozcięciem. Graf ten jest $2$-spójny oraz $2$-spójny krawędziowo.

Okazuje się, że dla dwu różnych wierzchołków istnieje powiązanie - między wielkością rozcięcia, a liczbą dróg pomiędzy nimi - silniejsze niż to wynikające z definicji.

Twierdzenie 13.8 [Menger 1927]

Największa możliwa liczba krawędziowo rozłącznych dróg łączących dwa różne niesąsiednie wierzchołki grafu spójnego, jest równa najmniejszej liczbie krawędzi w zbiorze rozspajającym te wierzchołki.

Dowód

Niech $w,u$ będą dwoma różnymi i niesąsiednimi wierzchołkami grafu spójnego $\mathbf{𝐆}=(V,E)$. Przez $k$ oznaczmy najmniejszą możliwą liczność zbioru krawędzi rozspajającego $w,u$. Oczywiście każda droga łącząca $w$ z $u$ musi przejść przez każdy zbiór rozspajający. A zatem dróg krawędziowo rozłącznych łączących $w$ z $u$ nie może być więcej niż $k$. Tak więc wystarczy pokazać, że istnieje $k$ rozłącznych krawędziowo dróg z $w$ do $u$.

Dowód przeprowadzimy indukcyjnie ze względu na liczbę krawędzi w grafie $\mathbf{𝐆}$ rozważając dwa przypadki.

1. Pewien zbiór rozspajający $X$ mocy $k$ ma krawędź nie incydentną z $w$ oraz ma krawędź (być może inną) nie incydentną z $u$.

Graf $G$, po usunięciu wszystkich krawędzi z $X$, podzieli się na dwie spójne składowe $W$ oraz $U$, do których odpowiednio należą $w$ i $u$.

Przez ${\mathbf{𝐖}}^{\prime }$ oznaczmy graf powstały z grafu $\mathbf{𝐆}$ poprzez ściągnięcie $U$ w jeden wierzchołek $u^{\prime }$. Wtedy $u^{\prime }$ jest połączony z tymi wierzchołkami $t\in W$, z którymi połączony był jakiś wierzchołek $s\in U$. Warto zauważyć, że wtedy musiało być $st\in X$. Krawędzie łączące wierzchołki wewnątrz $W$ pozostały niezmienione. Graf ${\mathbf{𝐔}}^{\prime }$ definiujemy analogicznie, poprzez ściągnięcie zbioru $W$ do wierzchołka $w^{\prime }$.

W grafie ${\mathbf{𝐖}}^{\prime }$ zbiór krawędzi incydentnych z $u^{\prime }$, których jest $k$, tworzy minimalny zbiór rozspajający wierzchołki $w,u^{\prime }$. Ponieważ założyliśmy, że w $X$ istnieje krawędź nieincydentna z $u$, to $U$ ma co najmniej dwa wierzchołki, a zatem graf ${\mathbf{𝐖}}^{\prime }$ ma mniej krawędzi niż $\mathbf{𝐆}$. Tak więc możemy skorzystać z założenia indukcyjnego otrzymując $k$ rozłącznych krawędziowo dróg łączących $w$ z $u^{\prime }$. Analogicznie w grafie ${\mathbf{𝐔}}^{\prime }$ otrzymujemy $k$ rozłącznych krawędziowo dróg łączących $w^{\prime }$ z $u$. Sklejając obie te rodziny dróg otrzymujemy $k$ rozłącznych ścieżek łączących $w$ z $u$ w grafie $\mathbf{𝐆}$.

2. W każdym zbiorze rozspajającym $X$ o mocy $k$ każda krawędź jest incydentna do $w$ lub do $u$.

Możemy wtedy założyć, że $\mathbf{𝐆}$ zawiera jedynie krawędzie należące do któregoś zbioru rozspajającego $w,u$ o liczności $k$. Gdyby tak nie było i istniałaby jakaś inna krawędź $e$, to moglibyśmy $e$ usunąć i, na mocy założenia indukcyjnego, otrzymać natychmiast $k$ rozłącznych dróg łączących $w,u$. Tak więc pozostały nam jedynie te krawędzie, które są w minimalnych zbiorach rozspajających $w,u$. To zaś, zgodnie z założeniem przypadku 2 oznacza, że każda krawędź jest incydentna z $w$ lub z $u$. W ten sposób drugi przypadek sprowadziliśmy do sytuacji, w której każda ścieżka z $w$ do $u$ ma co najwyżej dwie krawędzie. Wśród takich ścieżek nietrudno jest już wskazać $k$ rozłącznych krawędziowo.

Jako ćwiczenie 9 pozostawiamy dowód twierdzenia analogicznego do Twierdzenia 13.8, a wiążącego tym razem zbiory rozdzielające z drogami rozłącznymi wierzchołkowo.

Twierdzenie 13.9

Największa możliwa liczba wierzchołkowo rozłącznych dróg łączących dwa różne niesąsiednie wierzchołki grafu spójnego, jest równa najmniejszej liczbie wierzchołków w zbiorze rozdzielającym te wierzchołki.

Z Twierdzenia 13.9, można w łatwy sposób wywnioskować Twierdzenia 13.7, o skojarzeniach w grafach dwudzielnych. Wyprowadzenie to pozostawiamy jako ćwiczenie 10.

W grafie $k$-spójnym usunięcie jakichś $k-1$ punktów nie rozspaja go. A zatem zbiór rozdzielający jakieś dwa wierzchołki $w,u$ ma co najmniej $k$ wierzchołków. Tym samym między $u$ a $w$ musi istnieć co najmniej $k$ dróg. Pisząc zwięźlej możemy powiedzieć, że:

Wniosek 13.10

Graf z co najmniej $k+1$ wierzchołkami jest $k$-spójny wtedy i tylko wtedy, gdy dowolne dwa wierzchołki są połączone przynajmniej $k$ drogami wierzchołkowo rozłącznymi.

Analogiczne rozumowanie przeprowadzone dla ścieżek rozłącznych krawędziowo prowadzi do następującego wniosku.

Wniosek 13.11

Graf z co najmniej $k-1$ krawędziami jest $k$-spójny krawędziowo wtedy i tylko wtedy, gdy dowolne dwa wierzchołki są połączone przynajmniej $k$ drogami krawędziowo rozłącznymi.

Przepływy i przekroje

Wyobraźmy sobie sieć wodociągową, składającą się z rur o zadanej przepustowości, przystosowanych do przesyłania wody w określonym z góry kierunku oraz ze zbiorników połączonych tymi rurami. W przedstawionej sieci dwa zbiorniki są wyróżnione. Jeden z nich to źródło, w którym jest umieszczona pompa wpompowująca wodę, oraz ujście, czyli klient firmy wodociągowej lubiący nad wyraz zużywać wodę. Zadaniem firmy wodociągowej jest dostarczanie jak największej ilości wody klientowi. Ilość przesyłanej wody konkretną rurą nie może oczywiście przekraczać jej przepustowości. Pytanie, na które chciałby sobie odpowiedzieć właściciel firmy doprowadzającej wodę, to ile maksymalnie wody jest w stanie przesyłać w każdej chwili do klienta. Formalnym modelem dla tego typu zagadnień są sieci.

Przykładowa sieć

Przepływ w sieci z rysunku Przykładowa sieć

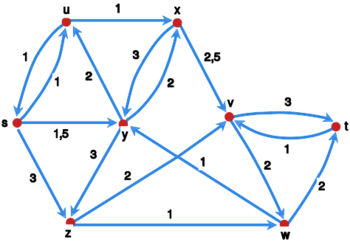
Sieć to trójka $\mathbf{𝐍}=(V,A,\mathsf{c})$, w której:

• $(V,A)$ jest pełnym digrafem (czyli $A=V\times V$),

• funkcja $\mathsf{c}:E⟶[0,+\mathrm{\infty })$, zwana przepustowością sieci, każdej krawędzi $vw$ przypisuje nieujemną liczbę rzeczywistą $\mathsf{c}\left(vw\right)$.

• Ponadto wyróżnia się dwa wierzchołki $s,t\in V$, które są odpowiednio źródłem oraz ujściem sieci.

Przepustowość $\mathsf{c}(vw)$ krawędzi $vw$ może być interpretowana jako wartość potencjalnie maksymalnego przepływu z wierzchołka $v$ do $w$. Jeśli przepustowość jakiejś krawędzi $e$ wynosi $0$, to krawędź $e$ jest pomijana w graficznym przedstawieniu sieci.

Przepływ w sieci $\mathbf{𝐍}=(V,A,\mathsf{c})$ to funkcja $\mathsf{f}:E⟶[0,+\mathrm{\infty })$ spełniająca warunki:

• $0\le \mathsf{f}\left(vw\right)\le \mathsf{c}\left(vw\right)$ dla każdej krawędzi $vw$. Wartość przepływu daną krawędzią nie może przekroczyć przepustowości tej krawędzi.

• $\sum _{x\in V}\mathsf{f}\left(xv\right)=\sum _{x\in V}\mathsf{f}\left(vx\right)$ dla każdego wierzchołka $v$ poza źródłem $s$ i ujściem $t$. Równość ta oznacza, że sumaryczna wartość tego, co wpływa do wierzchołka jest równa sumarycznej wartości tego, co zeń wypływa.

• $\sum _{x\in V}(\mathsf{f}\left(sx\right)-\mathsf{f}\left(xs\right))=\sum _{x\in V}(\mathsf{f}\left(xt\right)-\mathsf{f}\left(tx\right))$, tzn. sumaryczna wartość tego, co wypływa ze źródła musi być równa sumarycznej wartości tego, co wpływa do ujścia. Wartość ta będzie określana wartością przepływu $\mathsf{f}$.

Do analizy przepływów przydatne okazuje się pojęcie przekroju sieci. Można go sobie wyobrażać jako zbiór krawędzi $X\subseteq A$, usunięcie których z sieci $\mathbf{𝐍}=(V,A,\mathsf{c})$ rozspaja sieć na dwie części $S$ oraz $T$, przy czym $S$ zawiera źródło, a $T$ ujście. Warto zauważyć, że $X$ tworzy zbiór rozspajający w grafie szkieletowym digrafu $(V,A)$. Formalnie przekrój zdefiniujemy jako parę powstałych zbiorów wierzchołków. Taka definicja okaże się bardziej użyteczna w praktyce.

Przekrój sieci to para podzbiorów $(S,T)$ zbioru wierzchołków $V$, taka że:

• $S,T$ tworzą podział $V$, tzn. są rozłączne i w sumie dają cały zbiór $V$,

• źródło $s$ należy do $S$, a ujście $t$ należy do zbioru $T$.

Przepustowość przekroju $(S,T)$ to suma

$\mathsf{c}(S,T)=\sum _{v\in S,w\in T}\mathsf{c}\left(vw\right)$

Zależność między przepływem a przekrojem została podana w następującym Twierdzeniu o maksymalnym przepływie i minimalnym przekroju.

Twierdzenie 13.12 [Ford i Fulkerson 1956]

W dowolnej sieci wartość maksymalnego przepływu jest równa przepustowości minimalnego przekroju.

Dowód

Niech $\mathbf{𝐍}=(V,A,\mathsf{c})$ będzie siecią o źródle $s$ i ujściu $t$. Oczywiście wartość maksymalnego przepływu nie może przekraczać przepustowości minimalnego przekroju. Wystarczy więc wskazać przekrój, którego przepustowość równa się wartości maksymalnego przepływu $\mathsf{f}$ w sieci $\mathbf{𝐍}$.

Niech $S\subseteq V$ będzie zbiorem zawierającym źródło $s$ oraz te wierzchołki $w$, które w grafie szkieletowym digrafu $(V,A)$ połączone są ze źródłem pewną ścieżką $s=v_1\to \dots \to v_k=w$, w której łuk $v_i{v}_{i+1}$ ma niepełny przepływ (tzn. $\mathsf{f}\left(v_i{v}_{i+1}\right)<\mathsf{c}\left(v_i{v}_{i+1}\right)$) lub też łuk $v_{i+1}{v}_i$ ma niezerowy przepływ $\mathsf{f}\left(v_{i+1}{v}_i\right)>0$. W języku firmy wodociągowej $S$ jest zbiorem wierzchołków, do których można jeszcze przepchnąć choć trochę wody.

Załóżmy przez chwilę, że $t\in S$. Istnieje wtedy ścieżka $s=v_0\to \dots \to v_k=t$, w której dla każdej pary kolejnych wierzchołków $v_i,v_{i+1}$ można byłoby zwiększyć przepływ na łuku $v_i{v}_{i+1}$ lub zmniejszyć na łuku $v_{i+1}{v}_i$. Niech $\epsilon >0$ będzie jakąś wartością zmian przepływu możliwych do wykonania na każdej parze $v_i,v_{i+1}$ kolejnych wierzchołków ścieżki. Wtedy, modyfikując odpowiednio łuki pomiędzy wierzchołkami $v_i,v_{i+1}$ uzyskalibyśmy przepływ o wartości $\mathsf{f}+ϵ$, co przeczy maksymalności przepływu $\mathsf{f}$.

Udowodniliśmy właśnie, że $S,T$ tworzy przekrój sieci $\mathbf{𝐍}$, gdzie $T=V-S$. Pokażmy, że przepustowość tego przekroju równa się wartości przepływu $\mathsf{f}$. Z definicji $S$ wynika, że jeżeli rozważymy dwa elementy $v\in S$ oraz $w\in T$, to przepływ $\mathsf{f}\left(vw\right)=\mathsf{c}\left(vw\right)$ oraz $\mathsf{f}\left(wv\right)=0$.Tak więc przepustowość przekroju równa jest

$\sum _{v\in S,w\in T}\mathsf{c}\left(vw\right)=\sum _{v\in S,w\in T}(\mathsf{f}\left(vw\right)-\mathsf{f}\left(wv\right)).(1)$

Z faktu, że dla $u\in S-\left\{s\right\}$ wartość tego co wpływa jest równa temu co wypływa, czyli innymi słowy

$\sum _{x\in V}(\mathsf{f}\left(ux\right)-\mathsf{f}\left(xu\right))=0$,

otrzymujemy następującą równość:

$\sum _{x\in T}(\mathsf{f}\left(ux\right)-\mathsf{f}\left(xu\right))=\sum _{x\in S-\left\{u\right\}}(\mathsf{f}\left(xu\right)-\mathsf{f}\left(ux\right))$

Prawą stronę równości (1) można więc przekształcić w następujący sposób:

$\begin{array}{rl}\sum _{v\in S}\sum _{w\in T}(\mathsf{f}\left(vw\right)-\mathsf{f}\left(wv\right))& =\sum _{v\in S-\left\{u\right\}}\sum _{w\in T}(\mathsf{f}\left(vw\right)-\mathsf{f}\left(wv\right))+\sum _{x\in T}(\mathsf{f}\left(ux\right)-\mathsf{f}\left(xu\right))\\ & =\sum _{v\in S-\left\{u\right\}}\sum _{w\in T}(\mathsf{f}\left(vw\right)-\mathsf{f}\left(wv\right))+\sum _{x\in S-\left\{u\right\}}(\mathsf{f}\left(xu\right)-\mathsf{f}\left(ux\right))\\ & =\sum _{v\in S-\left\{u\right\}}\sum _{w\in T\cup \left\{u\right\}}(\mathsf{f}\left(vw\right)-\mathsf{f}\left(wv\right))\end{array}$

Powtarzając wielokrotnie przekładanie kolejnych punktów $u$ z $S$ do $T$ otrzymamy w konsekwencji

$\sum _{v\in S}\sum _{w\in T}(\mathsf{f}\left(vw\right)-\mathsf{f}\left(wv\right))=\sum _{w\in V-\left\{v\right\}}(\mathsf{f}\left(sw\right)-\mathsf{f}\left(ws\right))$,

co na mocy (1) oznacza, że wartość przepływu z wierzchołka $s$ do wierzchołka $t$ jest równa przepustowości przekroju wyznaczonego przez zbiory $S,T$.