Zaawansowane CPP/Wykład 9: Szablony wyrażeń: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „<math> ” na „<math>” |
|||
| (Nie pokazano 88 wersji utworzonych przez 6 użytkowników) | |||
| Linia 10: | Linia 10: | ||
return integral*ds; | return integral*ds; | ||
} | } | ||
([[media:Integrate.cpp | Źródło: integrate.cpp]]) | |||
Pomijając prostotę zaimplementowanego algorytmu numerycznego możemy | Pomijając prostotę zaimplementowanego algorytmu numerycznego, możemy | ||
jej używać następująco: | jej używać następująco: | ||
std::cout<< ::integrate(sin,0,3.1415926,0.01)<<std::endl; | std::cout<< ::integrate(sin,0,3.1415926,0.01)<<std::endl; | ||
Jest to standardowy sposób implementowania takich | Jest to standardowy sposób implementowania takich zagadnień w C czy w | ||
Fortranie. W C++ szablony dają nam większe możliwości. Funkcja | Fortranie. W C++ szablony dają nam większe możliwości. Funkcja | ||
<tt>integrate</tt> przyjmuje jako swój pierwszy argument wskaźnik do | <tt>integrate</tt> przyjmuje jako swój pierwszy argument wskaźnik do | ||
jednoargumentowej funkcji zwracającej <tt>double</tt>, ale to co jest | jednoargumentowej funkcji zwracającej <tt>double</tt>, ale to co jest | ||
naprawdę istotne to to że można użyć w stosunku do niego notacji | naprawdę istotne to to, że można użyć w stosunku do niego notacji | ||
wywołania funkcji: <tt>f(x)</tt>. W C++ możemy wyposażyć w tę możliwość | wywołania funkcji: <tt>f(x)</tt>. W C++ możemy wyposażyć w tę możliwość | ||
każdą klasę poprzez zdefiniowanie w niej metody <tt>operator()</tt>. Jeśli | każdą klasę poprzez zdefiniowanie w niej metody <tt>operator()</tt>. Jeśli | ||
zdefiniujemy funkcję <tt>integrate</tt> jako szablon, to będziemy mieli | zdefiniujemy funkcję <tt>integrate</tt> jako szablon, to będziemy mieli | ||
możliwość przekazywania również takich obiektów nazywanych | możliwość przekazywania również takich obiektów nazywanych | ||
obiektami funkcyjnymi lub funktorami. | obiektami funkcyjnymi lub funktorami. | ||
template<typename F> double integrate(F f,double min,double max,double ds) { | template<typename F> double integrate(F f,double min,double max,double ds) { | ||
double integral<nowiki>=</nowiki>.0; | double integral<nowiki>=</nowiki>.0; | ||
| Linia 34: | Linia 34: | ||
return integral*ds; | return integral*ds; | ||
} | } | ||
([[media:Integrate_temp.cpp | Źródło: integrate_temp.cpp]]) | |||
Wywołanie | |||
std::cout<< ::integrate(sin,0,3.1415926,0.01)<<std::endl; | std::cout<< ::integrate(sin,0,3.1415926,0.01)<<std::endl; | ||
dalej zadziała, ale można używać również | dalej zadziała, ale można używać również: | ||
class sina { | class sina { | ||
| Linia 46: | Linia 47: | ||
sina(double a): _a(a) {}; | sina(double a): _a(a) {}; | ||
double operator()(double x) {return sin(_a*x);} | double operator()(double x) {return sin(_a*x);} | ||
}; | }; | ||
std::cout<< ::integrate(sina(0),0,3.1415926,0.01)<<std::endl; | std::cout<< ::integrate(sina(0),0,3.1415926,0.01)<<std::endl; | ||
std::cout<< ::integrate(sina(1),0,3.1415926,0.01)<<std::endl; | std::cout<< ::integrate(sina(1),0,3.1415926,0.01)<<std::endl; | ||
std::cout<< ::integrate(sina(2),0,3.1415926,0.01)<<std::endl; | std::cout<< ::integrate(sina(2),0,3.1415926,0.01)<<std::endl; | ||
([[media:Integrate_temp.cpp | Źródło: integrate_temp.cpp]]) | |||
Widać tu już pierwszą zaletę funktorów: jako obiekty mogą one posiadać | Widać tu już pierwszą zaletę funktorów: jako obiekty mogą one posiadać | ||
| Linia 64: | Linia 66: | ||
integrate(1.0/(1.0+x),...) | integrate(1.0/(1.0+x),...) | ||
Okazuje się że można i technika która to umożliwia nosi nazwę | Okazuje się, że można i technika, która to umożliwia, nosi nazwę | ||
"szablonów wyrażeń". Z pozoru wydaje się | "szablonów wyrażeń". Z pozoru wydaje się to być tylko ciekawostką, | ||
ale w następnej części tego wykładu pokażemy jak za pomocą tej | ale w następnej części tego wykładu pokażemy jak za pomocą tej | ||
techniki można istotnie przyspieszyć program. | techniki można istotnie przyspieszyć program. | ||
Naszym celem jest napisane kodu który będzie generował funktory | Naszym celem jest napisane kodu, który będzie generował funktory | ||
automatycznie z "normalnych" wyrażeń typu <math> | automatycznie z "normalnych" wyrażeń typu <math>1/(1+x)</math> i umożliwi pisanie wyrażeń w rodzaju: | ||
pisanie wyrażeń w rodzaju: | |||
integrate(1/(1+x),0,1,0.01); | integrate(1/(1+x),0,1,0.01); | ||
<math> | <math>x</math> oznacza tu zmienną, po której całkujemy. Oznacza to, że kompilator musi wyrażenie <math>1/(1+x)</math> przekształcić na funktor | ||
musi wyrażenie <math> | |||
class _some_functor_ { | class _some_functor_ { | ||
| Linia 92: | Linia 92: | ||
integrate(x,...); | integrate(x,...); | ||
Żeby to działało | Żeby to działało prawidłowo, <tt>x</tt> musi być funktorem który zwraca | ||
własny argument: | własny argument: | ||
| Linia 101: | Linia 101: | ||
} | } | ||
}; | }; | ||
([[media:Expr_templates.h | Źródło: expr_templates.h]]) | |||
Możemy więc już wykonać całkę <math> | Możemy więc już wykonać całkę <math>\int_0^1x\;</math> d <math>x</math> | ||
Variable x; | Variable x; | ||
integrate(x,0,1,0.001); | integrate(x,0,1,0.001); | ||
co nie jest jakimś porywającym wyczynem :) | co nie jest jakimś porywającym wyczynem :). | ||
Żeby się posunąć dalej potrzebujemy kolejnych elementów. | Żeby się posunąć dalej potrzebujemy kolejnych elementów. | ||
===Stałe=== | ===Stałe=== | ||
Ewidentnie potrzebujemy stałych (literałów). Stała to funktor który | Ewidentnie potrzebujemy stałych (literałów). Stała to funktor, który | ||
zwraca wartość niezależną od swojego argumentu: | zwraca wartość niezależną od swojego argumentu: | ||
| Linia 121: | Linia 122: | ||
double operator()(double x) {return _c;} | double operator()(double x) {return _c;} | ||
}; | }; | ||
([[media:Expr_templates.h | Źródło: expr_templates.h]]) | |||
Niestety literałów nie możemy używać bezpośrednio w naszym wyrażeniu: | Niestety literałów nie możemy używać bezpośrednio w naszym wyrażeniu: | ||
| Linia 130: | Linia 132: | ||
integrate(Constant(1.0),0,1,0.001); | integrate(Constant(1.0),0,1,0.001); | ||
Można by wprawdzie | Można by wprawdzie przeładować definicje <tt>integrate</tt> dla argumentów typu | ||
<tt>double</tt> ale chyba nie warto, zważywszy na to że całkowanie stałej | <tt>double</tt> ale chyba nie warto, zważywszy na to, że całkowanie stałej | ||
nie jest zbyt kłopotliwe. | nie jest zbyt kłopotliwe. | ||
Następnym krokiem będzie dodanie wyrażeń arytmetycznych. | Następnym krokiem będzie dodanie wyrażeń arytmetycznych. | ||
===Dodawanie=== | ===Dodawanie=== | ||
Zaczniemy od dodawania. Potrzebne będą dwa elementy: klasa funktor która | Zaczniemy od dodawania. Potrzebne będą dwa elementy: klasa funktor, która | ||
symbolizuje dodawanie oraz | symbolizuje dodawanie oraz odpowiednio zdefiniowany operator dodawania. | ||
Funktor symbolizujący dodawanie musi mieć dwie składowe odpowiadające | Funktor symbolizujący dodawanie musi mieć dwie składowe odpowiadające | ||
dwu składnikom tej operacji. Przypominamy że każdy z tych | dwu składnikom tej operacji. Przypominamy, że każdy z tych składników | ||
też jest funktorem a więc posiada jednoargmentowy | też jest funktorem, a więc posiada jednoargmentowy <tt>operator()(double)</tt>. Operacja dodawania polegać więc bedzie na dodaniu wyników obu funktorów składowych: | ||
<tt>operator()(double)</tt>. Operacja dodawania polegać więc bedzie na | |||
dodaniu wyników obu funktorów składowych: | |||
template<typename LHS,typename RHS > class AddExpr { | template<typename LHS,typename RHS > class AddExpr { | ||
| Linia 156: | Linia 156: | ||
} | } | ||
}; | }; | ||
([[media:Expr_templates.h | Źródło: expr_templates.h]]) | |||
Pozostaje nam tylko zdefiniować operator dodawania, który z dwu składników | Pozostaje nam tylko zdefiniować operator dodawania, który z dwu składników | ||
utworzy nam obiekt | utworzy nam obiekt typu <tt>AddExpr</tt>. Ponieważ możemy dodawać cokolwiek, to | ||
operator dodawania będzie szablonem: | operator dodawania będzie szablonem: | ||
| Linia 166: | Linia 167: | ||
return Add<LHS,RHS>(l,r); | return Add<LHS,RHS>(l,r); | ||
}; | }; | ||
([[media:Expr_templates.h | Źródło: expr_templates.h]]) | |||
Żeby móc dodawać stałe potrzebujemy jeszcze specjalizacji szablonu dla | Żeby móc dodawać stałe potrzebujemy jeszcze specjalizacji szablonu dla | ||
przypadku, w którym jeden z argumentów jest typu <tt>double</tt>: | przypadku, w którym jeden z argumentów jest typu <tt>double</tt>): | ||
template<typename LHS > | template<typename LHS > | ||
| Linia 174: | Linia 176: | ||
double r) { | double r) { | ||
return Add<LHS,Constant>(l,Constant(r)); | return Add<LHS,Constant>(l,Constant(r)); | ||
}; | }; | ||
template<typename RHS > | template<typename RHS > | ||
Add<Constant,RHS> operator+(double l, | Add<Constant,RHS> operator+(double l, | ||
| Linia 180: | Linia 182: | ||
return Add<Constant,RHS>(Constant(l),r); | return Add<Constant,RHS>(Constant(l),r); | ||
}; | }; | ||
([[media:Expr_templates.h | Źródło: expr_templates.h]]) | |||
Widać że w identyczny sposób możemy zaimplementować pozostałe trzy | Widać, że w identyczny sposób możemy zaimplementować pozostałe trzy | ||
działania. Odpowiadające im klasy nazwiemy odpowiednio <tt>SubsExpr</tt>, | działania. Odpowiadające im klasy nazwiemy odpowiednio <tt>SubsExpr</tt>, | ||
<tt>MultExpr</tt> i <tt>DivExpr</tt> (pominąłem jednoargumentowy | <tt>MultExpr</tt> i <tt>DivExpr</tt> (pominąłem jednoargumentowy | ||
<tt>operator-()</tt>). Ich kod można zaobaczyć w [ | <tt>operator-()</tt>). Ich kod można zaobaczyć w [[media:Expr_templates.h | Źródło: expr_templates.h]]. | ||
===Funkcje=== | ===Funkcje=== | ||
| Linia 199: | Linia 202: | ||
return SinExpr<Arg>(a);} | return SinExpr<Arg>(a);} | ||
i operatory unarne (jednoargumentowe) takie jak operator negacji: | i operatory unarne (jednoargumentowe), takie jak operator negacji: | ||
template<typename LHS> class NegativeExpr { | template<typename LHS> class NegativeExpr { | ||
| Linia 212: | Linia 215: | ||
NegativeExpr<LHS> operator-(const LHS &l) { | NegativeExpr<LHS> operator-(const LHS &l) { | ||
return NegativeExpr<LHS>(l); | return NegativeExpr<LHS>(l); | ||
}; | }; | ||
([[media:Expr_templates.h | Źródło: expr_templates.h]]) | |||
===Jak to działa?=== | ===Jak to działa?=== | ||
Mam nadzieję że zasada działania szablonów wyrażeń jest już jasna, ale | Mam nadzieję, że zasada działania szablonów wyrażeń jest już jasna, ale | ||
prześledźmy jeszcze raz przykład wyrażenia | prześledźmy jeszcze raz przykład wyrażenia: | ||
\Variable x; | \Variable x; | ||
| Linia 226: | Linia 230: | ||
operator/(1.0,operator+(1,x)) | operator/(1.0,operator+(1,x)) | ||
Wiedząc że <tt>x</tt> jest typu <tt>Variable</tt> kompilator stara się znaleźć | Wiedząc, że <tt>x</tt> jest typu <tt>Variable</tt>, kompilator stara się znaleźć | ||
odpowiednie szablony operatorów. Najpierw dopasuje | odpowiednie szablony operatorów. Najpierw dopasuje wewnętrzny | ||
<tt>operator+<Variable>(double, Variable)</tt> | <tt>operator+<Variable>(double, Variable)</tt> | ||
operator/(double,operator+<Variable>(double 1.0 , Variable x)) | operator/(double,operator+<Variable>(double 1.0 , Variable x)) | ||
a potem wiedząć, że typ zwracany przez ten | a potem wiedząć, że typ zwracany przez ten operator | ||
to <tt>AddExpr<Constant,Variable></tt> skonkretyzuje odpowiedni | to <tt>AddExpr<Constant,Variable></tt>, skonkretyzuje odpowiedni | ||
szablon operatora dzielenia: | szablon operatora dzielenia: | ||
| Linia 243: | Linia 247: | ||
) | ) | ||
Po zastąpieniu skonkretyzowanych operatorów ich definicjami powstanie kod | Po zastąpieniu skonkretyzowanych operatorów ich definicjami powstanie kod, | ||
który generuje tymczasowy obiekt: | który generuje tymczasowy obiekt: | ||
{{kotwica|rys.9.1|}}[[File:cpp-8-expr1.svg|350x250px|thumb|right|Rysunek 9.1. Funktor wygenerowany z wyrażenia <math>1.0/(1.0+x)</math>.]] | |||
expr<nowiki>=</nowiki>DivExpression<Constant, | expr<nowiki>=</nowiki>DivExpression<Constant, | ||
AddExpr<Constant,Variable> >(Constant(1.0), | AddExpr<Constant,Variable> >(Constant(1.0), | ||
AddExpr<Constant,Variable>(Constant(1.0),Variable() ); | AddExpr<Constant,Variable>(Constant(1.0),Variable() ); | ||
Przedstawienie tego obiektu zamieszczone jest na rys 9.1 | Przedstawienie tego obiektu zamieszczone jest na [[#rys.9.1|rysunku 9.1]]. | ||
Widać że obiekt <tt>expr</tt> reprezentuje drzewo rozkładu wyrażenia | Widać, że obiekt <tt>expr</tt> reprezentuje drzewo rozkładu wyrażenia | ||
<math> | <math>1.0/(1.0+x)</math>. Wywołanie operatora nawiasów spowoduje rekurencyjne wywoływanie operatorów nawiasów wyrażeń składowych i w konsekwencji | ||
wywoływanie operatorów nawiasów wyrażeń składowych i w konsekwencji | |||
obliczenie tego wyrażenia. | obliczenie tego wyrażenia. | ||
Proszę zwrócić uwagę że opisana technika szablonów wyrażeń składa się | Proszę zwrócić uwagę, że opisana technika szablonów wyrażeń składa się | ||
z | z dwóch części. Pierwsza to klasy reprezentujące wyrażenia: | ||
<tt>Constant,Variable,AddExpr</tt>, itd. | <tt>Constant,Variable,AddExpr</tt>, itd., za pomocą których budujemy | ||
drzewo rozkładu gramatycznego. Druga to przeciążone operatory i | drzewo rozkładu gramatycznego. Druga - to przeciążone operatory i | ||
funkcje, które to drzewo generują. | funkcje, które to drzewo generują. | ||
| Linia 274: | Linia 270: | ||
W przedstawionym przykładzie ograniczyliśmy się do wyrażeń typu | W przedstawionym przykładzie ograniczyliśmy się do wyrażeń typu | ||
<tt>double</tt>. W duchu programowania uogólnionego postaramy się zmienić | <tt>double</tt>. W duchu programowania uogólnionego postaramy się zmienić | ||
nasz kod tak aby można było wybierać typ wyrażenia poprzez parametr | nasz kod tak, aby można było wybierać typ wyrażenia poprzez parametr | ||
szablonu. | szablonu. | ||
Okazuje się to jednak nie tak proste. Łatwo jest dodać dodatkowy | Okazuje się to jednak nie tak proste. Łatwo jest dodać dodatkowy | ||
parametr do klas | parametr do klas reprezentujących wyrażenia: | ||
template<typename T> class Variable { | template<typename T> class Variable { | ||
| Linia 285: | Linia 281: | ||
return x; | return x; | ||
} | } | ||
}; | }; | ||
template<typename T> class Constant { | template<typename T> class Constant { | ||
T _c; | T _c; | ||
| Linia 291: | Linia 287: | ||
Constant(T c) :_c(c){}; | Constant(T c) :_c(c){}; | ||
T operator()(T x) {return _c;} | T operator()(T x) {return _c;} | ||
}; | }; | ||
template<typename T, typename LHS,typename RHS > class AddExpr { | template<typename T, typename LHS,typename RHS > class AddExpr { | ||
LHS _lhs; | LHS _lhs; | ||
| Linia 303: | Linia 299: | ||
ale niestety operatory arytmetyczne nie będą miały jak automatycznie | ale niestety operatory arytmetyczne nie będą miały jak automatycznie | ||
wydedukować | wydedukować typu <tt>T</tt>. | ||
template<typename T,typename LHS,typename RHS > | template<typename T,typename LHS,typename RHS > | ||
| Linia 314: | Linia 310: | ||
wydedukowany. Mamy więć kłopot. | wydedukowany. Mamy więć kłopot. | ||
Rozwiązaniem może być dodanie dodatkowej klasy <tt>Expr</tt> " | Rozwiązaniem może być dodanie dodatkowej klasy <tt>Expr</tt> "opakowującej" | ||
wyrażenia która będzie przenosiła informację o typie: | wyrażenia, która będzie przenosiła informację o typie: | ||
template<typename T,typename R <nowiki>=</nowiki> Variable<T> > class Expr { | template<typename T,typename R <nowiki>=</nowiki> Variable<T> > class Expr { | ||
| Linia 325: | Linia 321: | ||
R rep() const {return _rep;}; | R rep() const {return _rep;}; | ||
}; | }; | ||
([[media:Expr_templates_T.h | Źródło: expr_templates_T.h]]) | |||
Odpowiednie operatory dodawania będą teraz wyglądały następująco: | Odpowiednie operatory dodawania będą teraz wyglądały następująco: | ||
| Linia 343: | Linia 340: | ||
Ponieważ teraz typ <tt>T</tt> pojawia się w argumentach wywołania, jest | Ponieważ teraz typ <tt>T</tt> pojawia się w argumentach wywołania, jest | ||
możliwa jego dedukcja. Pełna implementacja wszystkich operatorów znajduje się | możliwa jego dedukcja. Pełna implementacja wszystkich operatorów znajduje się | ||
w [ | w [[media:Expr_templates_T.h | Źródło: expr_templates_T.h]]. | ||
W porównaniu z poprzednią implementacją jedyna zmiana to taka, że | W porównaniu z poprzednią implementacją jedyna zmiana to taka, że | ||
| Linia 359: | Linia 356: | ||
Expr<int> i; | Expr<int> i; | ||
Niestety to ciągle nie jest koniec naszych kłopotów, nie możemy bowiem | Niestety, to ciągle nie jest koniec naszych kłopotów, nie możemy bowiem | ||
mieszać wyrażeń różnych typów. Jeśli np. zdefiniujemy: | mieszać wyrażeń różnych typów. Jeśli np. zdefiniujemy: | ||
| Linia 370: | Linia 367: | ||
x+i; | x+i; | ||
nieskompilują się. Oczywiście możemy pisać: | |||
x+1.0; | x+1.0; | ||
x+(double)i; | x+(double)i; | ||
ale jest to niewygodne zwłaszcza | ale jest to niewygodne; zwłaszcza jeśli będziemy chcieli użyć zmiennych | ||
zespolonych | zespolonych | ||
Expr<std::complex<double> > c; | Expr<std::complex<double> > c; | ||
| Linia 383: | Linia 380: | ||
wydaje się trochę skomplikowane. Można jednak, używając cech promocji, | wydaje się trochę skomplikowane. Można jednak, używając cech promocji, | ||
tak zmodyfikować nasz kod aby potrafił automatycznie konwertować typy. | tak zmodyfikować nasz kod, aby potrafił automatycznie konwertować typy. | ||
Jest to przedmiotem jednego z ćwiczeń do tego wykładu. | Jest to przedmiotem jednego z ćwiczeń do tego wykładu. | ||
| Linia 391: | Linia 388: | ||
technika daje się łatwo zastosować również do funktorów dwuargumentowych. | technika daje się łatwo zastosować również do funktorów dwuargumentowych. | ||
W tym celu musimy mieć możność rozróżnienia pierwszego i drugiego argumentu. | W tym celu musimy mieć możność rozróżnienia pierwszego i drugiego argumentu. | ||
Dlatego wprawadzamy dwie klasy, które | Dlatego wprawadzamy dwie klasy, które zastąpią klasę <tt>Variable</tt>. Klasa | ||
class First { | class First { | ||
| Linia 397: | Linia 394: | ||
double operator()(double x) { | double operator()(double x) { | ||
return x; | return x; | ||
} | } | ||
double operator()(double x,double) { | double operator()(double x,double) { | ||
return x; | return x; | ||
| Linia 403: | Linia 400: | ||
}; | }; | ||
reprezentuje pierwszy argument i może występować w funktorach jedno lub | reprezentuje pierwszy argument i może występować w funktorach jedno- lub | ||
dwuargumentowych, więc ma dwa operatory nawiasów. Klasa | |||
class Second { | class Second { | ||
| Linia 413: | Linia 410: | ||
}; | }; | ||
reprezentuje drugi argument funktora więc może występować tylko jako | reprezentuje drugi argument funktora, więc może występować tylko jako | ||
funkcja dwuargumentowa, stąd tylko jeden dwuargumentowy operator | funkcja dwuargumentowa, stąd tylko jeden dwuargumentowy operator | ||
nawiasów. Podobnie klasa | nawiasów. Podobnie klasa | ||
| Linia 425: | Linia 422: | ||
}; | }; | ||
dorobiła się drugiego | dorobiła się drugiego operatora nawiasów. | ||
Ostatnia zmiana to dodanie dwuargumentowego operatora nawiasów dla klasy | Ostatnia zmiana to dodanie dwuargumentowego operatora nawiasów dla klasy | ||
| Linia 446: | Linia 443: | ||
Jako przykład zastosowania opisanych (lub podobnych) technik może | Jako przykład zastosowania opisanych (lub podobnych) technik może | ||
służyć biblioteka | służyć biblioteka [http://www.boost.org/doc/html/lambda.html <tt>lambda</tt>] z | ||
repozytorium <tt>boost</tt>. Korzystając z tej biblioteki możemy używać | repozytorium <tt>boost</tt>. Korzystając z tej biblioteki możemy używać | ||
predefiniowanych zmiennych <tt>_1</tt>, <tt>_2</tt> i <tt>_3</tt>, które oznaczają | predefiniowanych zmiennych <tt>_1</tt>, <tt>_2</tt> i <tt>_3</tt>, które oznaczają | ||
odpowiednio pierwszy, drugi i trzeci argument. Korzystając z nich | odpowiednio pierwszy, drugi i trzeci argument. Korzystając z nich | ||
możemy przyklad z | możemy przyklad z [http://osilek.mimuw.edu.pl/index.php?title=Zaawansowane_CPP/Wyk%C5%82ad_2:_Programowanie_uog%C3%B3lnione#prz.2.6.3 wykładu 2.6.3] zapisać następująco: | ||
std::generate_n(v.begin(),n,SequenceGen<int>(1,2)); | std::generate_n(v.begin(),n,SequenceGen<int>(1,2)); | ||
| Linia 458: | Linia 455: | ||
==Szablony wyrażeń wektorowych== | ==Szablony wyrażeń wektorowych== | ||
Wszystko to | Wszystko to piękne, ale po co? Używając wyrażeń szablonowych zyskujemy | ||
być może na wygodzie, ale dzieje się to kosztem znacznego | być może na wygodzie, ale dzieje się to kosztem znacznego | ||
skomplikowania kodu, a co za tym idzie czasu kompilacji. Kod | skomplikowania kodu, a co za tym idzie - czasu kompilacji. Kod jest | ||
również dużo trudniejszy do zdebugowania. Powyższy przykład | również dużo trudniejszy do zdebugowania. Powyższy przykład | ||
ma | ma głównie walor edukacyjny. Teraz pokażę jak tę technikę można | ||
zastosować do problemu w którym daje ona istotne korzyści. | zastosować do problemu, w którym daje ona istotne korzyści. | ||
Rozważmy w tym celu kolejny typowy przykład wykorzystania C++. | Rozważmy w tym celu kolejny typowy przykład wykorzystania C++. | ||
Przeładowywanie operatorów pozwala nam prosto rozszerzyć język o | Przeładowywanie operatorów pozwala nam prosto rozszerzyć język o | ||
operacje wektorowe. Implementacja np. operatora dodawania dla | operacje wektorowe. Implementacja np. operatora dodawania dla dwóch wektorów | ||
mogłaby | mogłaby wyglądać następująco: | ||
template<typename T> vector<T> operator+(const vector<T> &lhs, | template<typename T> vector<T> operator+(const vector<T> &lhs, | ||
| Linia 479: | Linia 476: | ||
Potrzebne są jeszcze przeładowane wersje tego operatora, w których | Potrzebne są jeszcze przeładowane wersje tego operatora, w których | ||
jeden z argumentów jest <tt>double</tt>-em. Zakładając, że | jeden z argumentów jest <tt>double</tt>-em. Zakładając, że zdefiniujemy | ||
pozostałe potrzebne operatory, możemy teraz pisać kod tak jakby typy | pozostałe potrzebne operatory, możemy teraz pisać kod tak jakby typy | ||
wektorowe i operacje na nich były wbudowane w język (to | wektorowe i operacje na nich były wbudowane w język (to | ||
| Linia 486: | Linia 483: | ||
vector<double> v1(100,1); | vector<double> v1(100,1); | ||
vector<double> v2(100,2); | vector<double> v2(100,2); | ||
vector<double> res(100); | vector<double> res(100); | ||
res=1.2*v1+v1*v2+v2*0.5; | res=1.2*v1+v1*v2+v2*0.5; | ||
Niestety powyższy kod traci wiele przy bliższej analizie. Jeśli | Niestety, powyższy kod traci wiele przy bliższej analizie. Jeśli | ||
popatrzymy na definicję operatorów to zauważymy że ta linijka w | popatrzymy na definicję operatorów, to zauważymy, że ta linijka w | ||
rzeczywistości generuje coś takiego: | rzeczywistości generuje coś takiego: | ||
| Linia 505: | Linia 502: | ||
res=tmp5 | res=tmp5 | ||
Tworzymy pięć(!) tymczasowych wektorów (przydzielając na nie | Tworzymy pięć(!) tymczasowych wektorów (przydzielając na nie pamięć!) | ||
i sześć razy kopiujemy wektory!! | i sześć razy kopiujemy wektory!! | ||
Pisząc ten sam kod ręcznie napisalibyśmy: | Pisząc ten sam kod ręcznie napisalibyśmy: | ||
| Linia 512: | Linia 509: | ||
res[i]=1.2*v1[i]+v1[i]*v2[i]+v2[i]*.5; | res[i]=1.2*v1[i]+v1[i]*v2[i]+v2[i]*.5; | ||
Niepotrzebny jest żaden obiekt tymczasowy i tylko jedno kopiowanie. | |||
Ponadto można liczyć że kompilator lepiej zoptymalizuje tak prosty | Ponadto można liczyć, że kompilator lepiej zoptymalizuje tak prosty | ||
kod np. eliminując | kod np. eliminując jedno mnożenie: | ||
for(int i=0;i<100;i++) | for(int i=0;i<100;i++) | ||
| Linia 524: | Linia 521: | ||
wcześniej szablony wyrażeń. Jak widzieliśmy w poprzednim wykładzie, | wcześniej szablony wyrażeń. Jak widzieliśmy w poprzednim wykładzie, | ||
korzystając z tej techniki najpierw tworzymy reprezentację wyrażenia, | korzystając z tej techniki najpierw tworzymy reprezentację wyrażenia, | ||
a dopiero potem | a dopiero potem ją wykonujemy. Postaramy się więc napisać kod, który | ||
będzie tworzył reprezentację wyrażeń wektorowych a dopiero potem | będzie tworzył reprezentację wyrażeń wektorowych, a dopiero potem | ||
obliczał je w jednej ostatniej pętli generowanej przez operator | obliczał je w jednej ostatniej pętli, generowanej przez operator | ||
przypisania. Podobnie jak w poprzednim przykładzie kod będzie prostszy | przypisania. Podobnie jak w poprzednim przykładzie kod będzie prostszy | ||
jeśli ograniczymy się do wektorów jednego | jeśli ograniczymy się do wektorów jednego typu (<tt>double</tt>). | ||
Zaczynamy więc od zdefiniowania nowej klasy <tt>Vector</tt>. Nie możemy | Zaczynamy więc od zdefiniowania nowej klasy <tt>Vector</tt>. Nie możemy | ||
użyć <tt>std::vector</tt> bezpośrednio, bo potrzebujemy przeładować | |||
operator przypisania, ale możemy wykorzystać <tt>std::vector</tt> do | operator przypisania, ale możemy wykorzystać <tt>std::vector</tt> do | ||
implementacji naszej klasy, np. korzystając z dziedziczenia: | |||
class Vector : public vector<double> { | class Vector : public vector<double> { | ||
| Linia 541: | Linia 538: | ||
Vector(int n,double x):vector<double>(n,x){}; | Vector(int n,double x):vector<double>(n,x){}; | ||
Vector(const Vector& v):vector<double>(static_cast<vector<double> >(v)){}; | Vector(const Vector& v):vector<double>(static_cast<vector<double> >(v)){}; | ||
Vector(const vector<double>& v):vector<double>(v) {}; | Vector(const vector<double>& v):vector<double>(v) {}; | ||
Vector &operator=(const Vector& rhs) { | Vector &operator=(const Vector& rhs) { | ||
vector<double>::operator=(static_cast<vector<double> >(rhs)); | vector<double>::operator=(static_cast<vector<double> >(rhs)); | ||
| Linia 547: | Linia 544: | ||
template<typename V> Vector &operator=(const V &rhs) { | template<typename V> Vector &operator=(const V &rhs) { | ||
for(size_t i =0 ;i<vector<double>::size();++i) | for(size_t i =0 ;i<vector<double>::size();++i) | ||
(*this)[i]=rhs[i]; | (*this)[i]=rhs[i]; | ||
return *this; | return *this; | ||
} | } | ||
}; | }; | ||
| Linia 555: | Linia 552: | ||
własne konstruktory. Definiujemy też nowy operator przypisania. | własne konstruktory. Definiujemy też nowy operator przypisania. | ||
Korzystając z szablonów możemy uczynić argumentem operatora | Korzystając z szablonów możemy uczynić argumentem operatora | ||
przypisania jakiekolwiek wyrażenie które posiada operator | przypisania jakiekolwiek wyrażenie, które posiada operator | ||
indeksowania. Implementacja klasy <tt>Vector</tt> nie jest istotna jak długo | indeksowania. Implementacja klasy <tt>Vector</tt> nie jest istotna jak długo | ||
posiada operator indeksowania i szablon operatora przypisania. | posiada operator indeksowania i szablon operatora przypisania. | ||
Podobnie jak poprzednio potrzebne jeszcze będzie wyrażenie | Podobnie jak poprzednio, potrzebne jeszcze będzie wyrażenie | ||
reprezentujące skalar, który zachowuje sie jak | reprezentujące skalar, który zachowuje sie jak wektor o wszystkich | ||
polach takich samych: | polach takich samych: | ||
| Linia 570: | Linia 567: | ||
}; | }; | ||
Następnie definiujemy wyrażenie reprezentujace sumę dwóch wektorów: | |||
Następnie definiujemy wyrażenie reprezentujace sumę | |||
template<typename LHS,typename RHS> class AddVectors { | template<typename LHS,typename RHS> class AddVectors { | ||
| Linia 577: | Linia 573: | ||
const RHS &_rhs; /* bład ! */ | const RHS &_rhs; /* bład ! */ | ||
public: | public: | ||
AddVectors(const LHS &lhs,const RHS &rhs): _lhs(lhs),_rhs(rhs){}; | AddVectors(const LHS &lhs,const RHS &rhs): _lhs(lhs),_rhs(rhs){}; | ||
double operator[](int i) const {return _lhs[i]+_rhs[i];} | double operator[](int i) const {return _lhs[i]+_rhs[i];} | ||
}; | }; | ||
Proszę zwrócić uwagę że pola <tt>_lhs</tt> i <tt>_rhs</tt> są referencjami. | Proszę zwrócić uwagę, że pola <tt>_lhs</tt> i <tt>_rhs</tt> są referencjami. | ||
Gdyby tak nie było inicjalizacja klasy wymagałaby kopiowania i | Gdyby tak nie było inicjalizacja klasy wymagałaby kopiowania i | ||
stracilibyśmy cały zysk. Niestety to nie jest jeszcze poprawna implementacja. | stracilibyśmy cały zysk. Niestety, to nie jest jeszcze poprawna implementacja. | ||
Żeby to zauważyć przyjrzyjmy sie | Żeby to zauważyć przyjrzyjmy sie operatorowi dodawania: | ||
template<typename LHS,typename RHS> inline AddVectors<LHS,RHS> | template<typename LHS,typename RHS> inline AddVectors<LHS,RHS> | ||
| Linia 591: | Linia 587: | ||
} | } | ||
a dokładniej tej jego wersji, w której jeden z argmentów jest typu | a dokładniej - tej jego wersji, w której jeden z argmentów jest typu | ||
<tt>double</tt>: | <tt>double</tt>: | ||
| Linia 598: | Linia 594: | ||
return AddVectors<LHS,Const_vector>(lhs,Const_vector(rhs) ); | return AddVectors<LHS,Const_vector>(lhs,Const_vector(rhs) ); | ||
} | } | ||
W takim przypadku <tt>operator+(...)</tt> tworzy tymczasowy obiekt | i symetryczny. | ||
<tt>Const_vector</tt> który przekazuje do konstruktora | W takim przypadku <tt>operator+(...)</tt> tworzy tymczasowy obiekt typu | ||
<tt>Const_vector</tt>, który przekazuje do konstruktora | |||
<tt>AddVectors<LHS,Const_vector></tt>. Taki obiekt nie może być | <tt>AddVectors<LHS,Const_vector></tt>. Taki obiekt nie może być | ||
przechowywany przez referencję, bo przestaje istnieć poza zakresem | przechowywany przez referencję, bo przestaje istnieć poza zakresem | ||
| Linia 614: | Linia 610: | ||
} ; | } ; | ||
za | za pomocą której definiujemy pola składowe <tt>AddVectors</tt> jako: | ||
typename V_expr_traits<LHS>::op_type _lhs; | typename V_expr_traits<LHS>::op_type _lhs; | ||
typename V_expr_traits<RHS>::op_type _rhs; | typename V_expr_traits<RHS>::op_type _rhs; | ||
Pomijając te aspekty, widać więc że implementacja jest całkowicie | {{kotwica|rys.9.2|}}[[File:cpp-8-vec_expr1.svg|350x250px|thumb|right|Rysunek 9.2. Obiekt wygenerowany z wyrażenia <tt>v1*(1.2+v2)+v2*.5</tt>.]] | ||
analogiczna do przykładu z funktorami tyle że operator nawiasów został | Pomijając te aspekty, widać więc, że implementacja jest całkowicie | ||
zastąpiony operatorem indeksowania. Zakładając że zaimplementujemy | analogiczna do przykładu z funktorami, tyle że operator nawiasów został | ||
zastąpiony operatorem indeksowania. Zakładając, że zaimplementujemy | |||
pozostałe klasy i operatory to kompilator z wyrażenia | pozostałe klasy i operatory to kompilator z wyrażenia | ||
v1*(1.2+v2)+v2*.5; | v1*(1.2+v2)+v2*.5; | ||
stworzy nam obiekt przestawiony na rys 9.2 | stworzy nam obiekt przestawiony na [[#rys.9.2|rysunku 9.2]]. | ||
Dopiero próba przypisania tego obiektu do wektora <tt>res</tt> | Dopiero próba przypisania tego obiektu do wektora <tt>res</tt> spowoduje wywołanie w pętli operatora indeksowania dla tego obiektu, co pociągnie za sobą efektywnie obliczenie wyrażenia | ||
for(int i=0;i<n;++i) | for(int i=0;i<n;++i) | ||
| Linia 648: | Linia 638: | ||
v1*(1.2+v2)+v2*.5; | v1*(1.2+v2)+v2*.5; | ||
korzystając ze "zwykłej" implementacji operatorów arytmetycznych i z | |||
szablonów wyrażeń. Pomiaru dokonywałem poprzez umieszczenie tego | szablonów wyrażeń. Pomiaru dokonywałem poprzez umieszczenie tego | ||
wyrażenia w | wyrażenia w pętli: | ||
Vector v1(100,1); | Vector v1(100,1); | ||
Vector v2(100,2); | Vector v2(100,2); | ||
Vector res(100); | Vector res(100); | ||
for(size_t j = 0 ;j< 10000000;++j){ | for(size_t j = 0 ;j< 10000000;++j){ | ||
res=1.2*v1+v1*v2+v2*0.5; | res=1.2*v1+v1*v2+v2*0.5; | ||
| Linia 660: | Linia 650: | ||
} | } | ||
Czas wykonania | Czas wykonania programu mierzyłem poleceniem | ||
systemowym <tt>time</tt>. Wyniki są | systemowym <tt>time</tt>. Wyniki są następujace (w sekundach): | ||
<div align=center> | <div align=center> | ||
| Linia 688: | Linia 678: | ||
</div> | </div> | ||
Proszę zauważyć że znów włączanie optymalizacji daje dramatyczny 20-50 | Proszę zauważyć, że znów włączanie optymalizacji daje dramatyczny 20 - 50-krotny wzrost szybkości programu. Podkreślam raz jeszcze, że opcja | ||
krotny wzrost szybkości programu. Podkreślam raz jeszcze że opcja | <tt>-O0</tt>, czyli brak optymalizacji, jest domyślną opcją dla kompilatora | ||
<tt>-O0</tt> czyli brak optymalizacji jest domyślną opcją dla kompilatora | g++. Widać też, że używanie szablonów wyrażeń daje pięciokrotny wzrost | ||
g++. Widać też że używanie szablonów wyrażeń daje pięciokrotny wzrost | |||
szybkości programu. Oczywiście ten wynik będzie silnie zależał od | szybkości programu. Oczywiście ten wynik będzie silnie zależał od | ||
konkretnych | konkretnych zastosowań. Jak zwykle gorąco zachęcam do własnych eksperymentów. | ||
Aktualna wersja na dzień 22:13, 11 wrz 2023
Wprowadzenie
Rozważmy implementację funkcji całkującej inne funkcje:
double integrate(double (*f)(double ),double min,double max,double ds) {
double integral=.0;
for(double x=min;x<max;x+=ds) {
integral+=f(x);
}
return integral*ds;
}
Pomijając prostotę zaimplementowanego algorytmu numerycznego, możemy jej używać następująco:
std::cout<< ::integrate(sin,0,3.1415926,0.01)<<std::endl;
Jest to standardowy sposób implementowania takich zagadnień w C czy w Fortranie. W C++ szablony dają nam większe możliwości. Funkcja integrate przyjmuje jako swój pierwszy argument wskaźnik do jednoargumentowej funkcji zwracającej double, ale to co jest naprawdę istotne to to, że można użyć w stosunku do niego notacji wywołania funkcji: f(x). W C++ możemy wyposażyć w tę możliwość każdą klasę poprzez zdefiniowanie w niej metody operator(). Jeśli zdefiniujemy funkcję integrate jako szablon, to będziemy mieli możliwość przekazywania również takich obiektów nazywanych obiektami funkcyjnymi lub funktorami.
template<typename F> double integrate(F f,double min,double max,double ds) {
double integral=.0;
for(double x=min;x<max;x+=ds) {
integral+=f(x);
}
return integral*ds;
}
Wywołanie
std::cout<< ::integrate(sin,0,3.1415926,0.01)<<std::endl;
dalej zadziała, ale można używać również:
class sina {
double _a;
public:
sina(double a): _a(a) {};
double operator()(double x) {return sin(_a*x);}
};
std::cout<< ::integrate(sina(0),0,3.1415926,0.01)<<std::endl;
std::cout<< ::integrate(sina(1),0,3.1415926,0.01)<<std::endl;
std::cout<< ::integrate(sina(2),0,3.1415926,0.01)<<std::endl;
Widać tu już pierwszą zaletę funktorów: jako obiekty mogą one posiadać stan. W przypadku funkcji do takich celów musielibyśmy używać zmiennych globalnych. Ale żeby móc funktora używać musimy go najpierw zdefiniować. Pytanie na które bedę się starał odpowiedzieć na tym wykładzie brzmi: czy możemy definicję funktora uprościć? Np. czy nie moglibyśmy pisać
integrate(sin(2*x),...)
lub
integrate(1.0/(1.0+x),...)
Okazuje się, że można i technika, która to umożliwia, nosi nazwę "szablonów wyrażeń". Z pozoru wydaje się to być tylko ciekawostką, ale w następnej części tego wykładu pokażemy jak za pomocą tej techniki można istotnie przyspieszyć program.
Naszym celem jest napisane kodu, który będzie generował funktory
automatycznie z "normalnych" wyrażeń typu i umożliwi pisanie wyrażeń w rodzaju:
integrate(1/(1+x),0,1,0.01);
oznacza tu zmienną, po której całkujemy. Oznacza to, że kompilator musi wyrażenie przekształcić na funktor
class _some_functor_ {
public:
double operator()(double x) return {1/(1+x);}
}
Zmienne
Chińczycy mówią, że podróż stumilową zaczyna się od pierwszego kroku. Zróbmy więc pierwszy krok i spróbujmy doprowadzić do prawidłowej kompilacji i wykonania wyrażenie:
integrate(x,...);
Żeby to działało prawidłowo, x musi być funktorem który zwraca własny argument:
class Variable {
public:
double operator()(double x) {
return x;
}
};
Możemy więc już wykonać całkę d
Variable x; integrate(x,0,1,0.001);
co nie jest jakimś porywającym wyczynem :). Żeby się posunąć dalej potrzebujemy kolejnych elementów.
Stałe
Ewidentnie potrzebujemy stałych (literałów). Stała to funktor, który zwraca wartość niezależną od swojego argumentu:
class Constant {
double _c;
public:
Constant(double c) :_c(c){};
double operator()(double x) {return _c;}
};
Niestety literałów nie możemy używać bezpośrednio w naszym wyrażeniu:
integrate(1.0,0,1,0.001);
nie zadziała. Musimy pisać
integrate(Constant(1.0),0,1,0.001);
Można by wprawdzie przeładować definicje integrate dla argumentów typu double ale chyba nie warto, zważywszy na to, że całkowanie stałej nie jest zbyt kłopotliwe.
Następnym krokiem będzie dodanie wyrażeń arytmetycznych.
Dodawanie
Zaczniemy od dodawania. Potrzebne będą dwa elementy: klasa funktor, która symbolizuje dodawanie oraz odpowiednio zdefiniowany operator dodawania.
Funktor symbolizujący dodawanie musi mieć dwie składowe odpowiadające dwu składnikom tej operacji. Przypominamy, że każdy z tych składników też jest funktorem, a więc posiada jednoargmentowy operator()(double). Operacja dodawania polegać więc bedzie na dodaniu wyników obu funktorów składowych:
template<typename LHS,typename RHS > class AddExpr {
LHS _lhs;
RHS _rhs;
public:
AddExpr(const LHS &l,const RHS &r) :_lhs(l),_rhs(r) {};
double operator()(double x) {
return _lhs(x)+_rhs(x);
}
};
Pozostaje nam tylko zdefiniować operator dodawania, który z dwu składników utworzy nam obiekt typu AddExpr. Ponieważ możemy dodawać cokolwiek, to operator dodawania będzie szablonem:
template<typename LHS,typename RHS >
Add<LHS,RHS> operator+(const LHS &l,
const RHS &r) {
return Add<LHS,RHS>(l,r);
};
Żeby móc dodawać stałe potrzebujemy jeszcze specjalizacji szablonu dla przypadku, w którym jeden z argumentów jest typu double):
template<typename LHS >
Add<LHS,Constant> operator+(const LHS &l,
double r) {
return Add<LHS,Constant>(l,Constant(r));
};
template<typename RHS >
Add<Constant,RHS> operator+(double l,
const RHS &r) {
return Add<Constant,RHS>(Constant(l),r);
};
Widać, że w identyczny sposób możemy zaimplementować pozostałe trzy działania. Odpowiadające im klasy nazwiemy odpowiednio SubsExpr, MultExpr i DivExpr (pominąłem jednoargumentowy operator-()). Ich kod można zaobaczyć w Źródło: expr_templates.h.
Funkcje
Analogicznie implementujemy funkcje np.:
template<typename Arg> class SinExpr{
Arg _arg;
public:
SinExpr(const Arg& arg) :_arg(arg) {};
double operator()(double x) {return sin(_arg(x));}
};
template<typename Arg> SinExpr<Arg> sin(const Arg&a) {
return SinExpr<Arg>(a);}
i operatory unarne (jednoargumentowe), takie jak operator negacji:
template<typename LHS> class NegativeExpr {
LHS _lhs;
public:
NegativeExpr(const LHS &l) :_lhs(l) {};
double operator()(double x) {
return - _lhs(x);
}
};
template<typename LHS>
NegativeExpr<LHS> operator-(const LHS &l) {
return NegativeExpr<LHS>(l);
};
Jak to działa?
Mam nadzieję, że zasada działania szablonów wyrażeń jest już jasna, ale prześledźmy jeszcze raz przykład wyrażenia:
\Variable x; 1.0/(1.0+x)
Kompilator dokonuje rozkładu gramatycznego i interpretuje to wyrażenia jako:
operator/(1.0,operator+(1,x))
Wiedząc, że x jest typu Variable, kompilator stara się znaleźć odpowiednie szablony operatorów. Najpierw dopasuje wewnętrzny operator+<Variable>(double, Variable)
operator/(double,operator+<Variable>(double 1.0 , Variable x))
a potem wiedząć, że typ zwracany przez ten operator to AddExpr<Constant,Variable>, skonkretyzuje odpowiedni szablon operatora dzielenia:
operator/<AddExpr<Constant,Variable> >
(double 1.0,
AddExpr<Constant,Variable>
operator+<Variable>(double 1.0 ,
Variable x)
)
Po zastąpieniu skonkretyzowanych operatorów ich definicjami powstanie kod, który generuje tymczasowy obiekt:
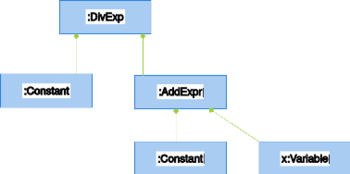
expr=DivExpression<Constant, AddExpr<Constant,Variable> >(Constant(1.0), AddExpr<Constant,Variable>(Constant(1.0),Variable() );
Przedstawienie tego obiektu zamieszczone jest na rysunku 9.1.
Widać, że obiekt expr reprezentuje drzewo rozkładu wyrażenia . Wywołanie operatora nawiasów spowoduje rekurencyjne wywoływanie operatorów nawiasów wyrażeń składowych i w konsekwencji obliczenie tego wyrażenia.
Proszę zwrócić uwagę, że opisana technika szablonów wyrażeń składa się z dwóch części. Pierwsza to klasy reprezentujące wyrażenia: Constant,Variable,AddExpr, itd., za pomocą których budujemy drzewo rozkładu gramatycznego. Druga - to przeciążone operatory i funkcje, które to drzewo generują.
Zmienne różnych typów
W przedstawionym przykładzie ograniczyliśmy się do wyrażeń typu double. W duchu programowania uogólnionego postaramy się zmienić nasz kod tak, aby można było wybierać typ wyrażenia poprzez parametr szablonu.
Okazuje się to jednak nie tak proste. Łatwo jest dodać dodatkowy parametr do klas reprezentujących wyrażenia:
template<typename T> class Variable {
public:
T operator()(T x) {
return x;
}
};
template<typename T> class Constant {
T _c;
public:
Constant(T c) :_c(c){};
T operator()(T x) {return _c;}
};
template<typename T, typename LHS,typename RHS > class AddExpr {
LHS _lhs;
RHS _rhs;
public:
AddExpr(const LHS &l,const RHS &r) :_lhs(l),_rhs(r) {};
T operator()(T x) {
return _lhs(x)+_rhs(x);
}
};
ale niestety operatory arytmetyczne nie będą miały jak automatycznie wydedukować typu T.
template<typename T,typename LHS,typename RHS >
Add<T,LHS,RHS> operator+(const LHS &l,
const RHS &r) {
return Add<T,LHS,RHS>(l,r);
};
Typ T nie pojawia się w argumentach wywołania, a więc nie może być wydedukowany. Mamy więć kłopot.
Rozwiązaniem może być dodanie dodatkowej klasy Expr "opakowującej" wyrażenia, która będzie przenosiła informację o typie:
template<typename T,typename R = Variable<T> > class Expr {
R _rep;
public:
Expr() {};
Expr(R rep):_rep(rep) {};
T operator()(T x) {return _rep(x);}
R rep() const {return _rep;};
};
Odpowiednie operatory dodawania będą teraz wyglądały następująco:
template<typename T,typename LHS,typename RHS >
Expr<T,AddExpr<T,LHS,RHS> > operator+(const Expr<T,LHS> &l,
const Expr<T,RHS> &r) {
return Expr<T,AddExpr<T,LHS,RHS> >(AddExpr<T,LHS,RHS>(l.rep(),r.rep()));
};
template<typename T,typename LHS >
Expr<T,AddExpr<T,LHS,Constant<T> > >
operator+(const Expr<T,LHS> &l,
T r) {
return Expr<T,AddExpr<T,LHS,Constant<T> > >
(AddExpr<T,LHS,Constant<T> >(l.rep(),Constant<T>(r)));
};
Ponieważ teraz typ T pojawia się w argumentach wywołania, jest możliwa jego dedukcja. Pełna implementacja wszystkich operatorów znajduje się w Źródło: expr_templates_T.h.
W porównaniu z poprzednią implementacją jedyna zmiana to taka, że zmienne musimy teraz deklarować jako:
Expr<double> x;
lub równoważnie
Expr<double,Variable<double> > x;
Teraz możemy również definiować zmienne innych typów:
Expr<complex<double> > z; Expr<int> i;
Niestety, to ciągle nie jest koniec naszych kłopotów, nie możemy bowiem mieszać wyrażeń różnych typów. Jeśli np. zdefiniujemy:
Expr<double> x; int i;
to wyrażenia
x+1; x+i;
nieskompilują się. Oczywiście możemy pisać:
x+1.0; x+(double)i;
ale jest to niewygodne; zwłaszcza jeśli będziemy chcieli użyć zmiennych zespolonych
Expr<std::complex<double> > c; double x; std::complex<double>(x)+c
wydaje się trochę skomplikowane. Można jednak, używając cech promocji, tak zmodyfikować nasz kod, aby potrafił automatycznie konwertować typy. Jest to przedmiotem jednego z ćwiczeń do tego wykładu.
Więcej zmiennych
Jak na razie generowaliśmy funktory jednoargumentowe. Powyższa technika daje się łatwo zastosować również do funktorów dwuargumentowych. W tym celu musimy mieć możność rozróżnienia pierwszego i drugiego argumentu. Dlatego wprawadzamy dwie klasy, które zastąpią klasę Variable. Klasa
class First {
public:
double operator()(double x) {
return x;
}
double operator()(double x,double) {
return x;
}
};
reprezentuje pierwszy argument i może występować w funktorach jedno- lub dwuargumentowych, więc ma dwa operatory nawiasów. Klasa
class Second {
public:
double operator()(double,double y) {
return y;
}
};
reprezentuje drugi argument funktora, więc może występować tylko jako funkcja dwuargumentowa, stąd tylko jeden dwuargumentowy operator nawiasów. Podobnie klasa
class Constant {
double _c;
public:
Constant(double c) :_c(c){};
double operator()(double) {return _c;}
double operator()(double,double) {return _c;}
};
dorobiła się drugiego operatora nawiasów. Ostatnia zmiana to dodanie dwuargumentowego operatora nawiasów dla klasy
template<typename LHS,typename RHS > class AddExpr {
LHS _lhs;
RHS _rhs;
public:
AddExpr(const LHS &l,const RHS &r) :_lhs(l),_rhs(r) {};
double operator()(double x) {
return _lhs(x)+_rhs(x);
}
double operator()(double x,double y) {
return _lhs(x,y)+_rhs(x,y);
}
};
I podobnie dla reszty działań. Operatory pozostają bez zmian.
Biblioteka lambda
Jako przykład zastosowania opisanych (lub podobnych) technik może służyć biblioteka lambda z repozytorium boost. Korzystając z tej biblioteki możemy używać predefiniowanych zmiennych _1, _2 i _3, które oznaczają odpowiednio pierwszy, drugi i trzeci argument. Korzystając z nich możemy przyklad z wykładu 2.6.3 zapisać następująco:
std::generate_n(v.begin(),n,SequenceGen<int>(1,2)); std::vector<int>::iterator it=find_if(v.begin(),v.end(),_1>4); std::cout<<*it<<std::endl;
Szablony wyrażeń wektorowych
Wszystko to piękne, ale po co? Używając wyrażeń szablonowych zyskujemy być może na wygodzie, ale dzieje się to kosztem znacznego skomplikowania kodu, a co za tym idzie - czasu kompilacji. Kod jest również dużo trudniejszy do zdebugowania. Powyższy przykład ma głównie walor edukacyjny. Teraz pokażę jak tę technikę można zastosować do problemu, w którym daje ona istotne korzyści.
Rozważmy w tym celu kolejny typowy przykład wykorzystania C++. Przeładowywanie operatorów pozwala nam prosto rozszerzyć język o operacje wektorowe. Implementacja np. operatora dodawania dla dwóch wektorów mogłaby wyglądać następująco:
template<typename T> vector<T> operator+(const vector<T> &lhs,
const vector<T> &rhs) {
vector<T> res(lhs) ;
for(size_t i=0;i<rhs.size();++i)
res[i]+=rhs[i];
return res;
}
Potrzebne są jeszcze przeładowane wersje tego operatora, w których jeden z argumentów jest double-em. Zakładając, że zdefiniujemy pozostałe potrzebne operatory, możemy teraz pisać kod tak jakby typy wektorowe i operacje na nich były wbudowane w język (to zresztą było jednym z kryteriów przy projektowaniu C++):
vector<double> v1(100,1); vector<double> v2(100,2); vector<double> res(100); res=1.2*v1+v1*v2+v2*0.5;
Niestety, powyższy kod traci wiele przy bliższej analizie. Jeśli popatrzymy na definicję operatorów, to zauważymy, że ta linijka w rzeczywistości generuje coś takiego:
vector<double> tmp1(100); tmp1=0.5*v2; vector<double> tmp2(100); tmp2=v1*v2; vector<double> tmp3(100); tmp3=tmp1+tmp2 vector<double> tmp4(100); tmp4=1.2*v1; vector<double> tmp5(100); tmp5=tmp3+tmp4; res=tmp5
Tworzymy pięć(!) tymczasowych wektorów (przydzielając na nie pamięć!) i sześć razy kopiujemy wektory!! Pisząc ten sam kod ręcznie napisalibyśmy:
for(int i=0;i<100;i++)
res[i]=1.2*v1[i]+v1[i]*v2[i]+v2[i]*.5;
Niepotrzebny jest żaden obiekt tymczasowy i tylko jedno kopiowanie. Ponadto można liczyć, że kompilator lepiej zoptymalizuje tak prosty kod np. eliminując jedno mnożenie:
for(int i=0;i<100;i++)
res[i]=v1[i]*(1.2+v2[i])+v2[i]*.5;
Te dodatkowe niepotrzebne kopiowania i tymczasowe obiekty stanowią duży narzut, a co za tym idzie mocno ograniczją użyteczność tego typu bibliotek, a to wielka szkoda. Na ratunek przychodzą nam opisane wcześniej szablony wyrażeń. Jak widzieliśmy w poprzednim wykładzie, korzystając z tej techniki najpierw tworzymy reprezentację wyrażenia, a dopiero potem ją wykonujemy. Postaramy się więc napisać kod, który będzie tworzył reprezentację wyrażeń wektorowych, a dopiero potem obliczał je w jednej ostatniej pętli, generowanej przez operator przypisania. Podobnie jak w poprzednim przykładzie kod będzie prostszy jeśli ograniczymy się do wektorów jednego typu (double).
Zaczynamy więc od zdefiniowania nowej klasy Vector. Nie możemy użyć std::vector bezpośrednio, bo potrzebujemy przeładować operator przypisania, ale możemy wykorzystać std::vector do implementacji naszej klasy, np. korzystając z dziedziczenia:
class Vector : public vector<double> {
public:
Vector():vector<double>(){};
Vector(int n):vector<double>(n){};
Vector(int n,double x):vector<double>(n,x){};
Vector(const Vector& v):vector<double>(static_cast<vector<double> >(v)){};
Vector(const vector<double>& v):vector<double>(v) {};
Vector &operator=(const Vector& rhs) {
vector<double>::operator=(static_cast<vector<double> >(rhs));
}
template<typename V> Vector &operator=(const V &rhs) {
for(size_t i =0 ;i<vector<double>::size();++i)
(*this)[i]=rhs[i];
return *this;
}
};
Dziedziczymy cały interfejs z std::vector ale musimy zdefiniować własne konstruktory. Definiujemy też nowy operator przypisania. Korzystając z szablonów możemy uczynić argumentem operatora przypisania jakiekolwiek wyrażenie, które posiada operator indeksowania. Implementacja klasy Vector nie jest istotna jak długo posiada operator indeksowania i szablon operatora przypisania.
Podobnie jak poprzednio, potrzebne jeszcze będzie wyrażenie reprezentujące skalar, który zachowuje sie jak wektor o wszystkich polach takich samych:
class Const_vector {
double _c;
public:
Const_vector(double c):_c(c) {};
double operator[](int i) const {return _c;}
};
Następnie definiujemy wyrażenie reprezentujace sumę dwóch wektorów:
template<typename LHS,typename RHS> class AddVectors {
const LHS &_lhs; /* bład ! */
const RHS &_rhs; /* bład ! */
public:
AddVectors(const LHS &lhs,const RHS &rhs): _lhs(lhs),_rhs(rhs){};
double operator[](int i) const {return _lhs[i]+_rhs[i];}
};
Proszę zwrócić uwagę, że pola _lhs i _rhs są referencjami. Gdyby tak nie było inicjalizacja klasy wymagałaby kopiowania i stracilibyśmy cały zysk. Niestety, to nie jest jeszcze poprawna implementacja. Żeby to zauważyć przyjrzyjmy sie operatorowi dodawania:
template<typename LHS,typename RHS> inline AddVectors<LHS,RHS>
operator+(const LHS &lhs,const RHS &rhs) {
return AddVectors<LHS,RHS>(lhs,rhs);
}
a dokładniej - tej jego wersji, w której jeden z argmentów jest typu double:
template<typename LHS> inline AddVectors<LHS,Const_vector>
operator+(const LHS &lhs,double rhs) {
return AddVectors<LHS,Const_vector>(lhs,Const_vector(rhs) );
}
i symetryczny. W takim przypadku operator+(...) tworzy tymczasowy obiekt typu Const_vector, który przekazuje do konstruktora AddVectors<LHS,Const_vector>. Taki obiekt nie może być przechowywany przez referencję, bo przestaje istnieć poza zakresem operatora dodawania. Obiekty tego typu muszą wiec być przechowywane jako kopie. Można to łatwo zaimplementować za pomocą klasy cech:
template<typename T> struct V_expr_traits {
typedef T const & op_type;
} ;
template<> struct V_expr_traits<Const_vector> {
typedef Const_vector op_type;
} ;
za pomocą której definiujemy pola składowe AddVectors jako:
typename V_expr_traits<LHS>::op_type _lhs; typename V_expr_traits<RHS>::op_type _rhs;
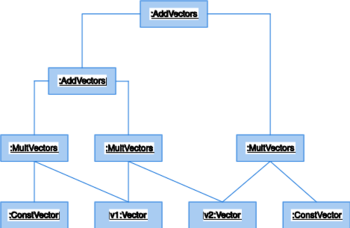
Pomijając te aspekty, widać więc, że implementacja jest całkowicie analogiczna do przykładu z funktorami, tyle że operator nawiasów został zastąpiony operatorem indeksowania. Zakładając, że zaimplementujemy pozostałe klasy i operatory to kompilator z wyrażenia
v1*(1.2+v2)+v2*.5;
stworzy nam obiekt przestawiony na rysunku 9.2.
Dopiero próba przypisania tego obiektu do wektora res spowoduje wywołanie w pętli operatora indeksowania dla tego obiektu, co pociągnie za sobą efektywnie obliczenie wyrażenia
for(int i=0;i<n;++i) res[i]=v1[i]*(1.2+v2[i])+v2[i]*.5;
zgodnie z naszymi zamiarami.
Efektywność kodu
Aby sprawdzić jak działa to w praktyce, porównałem czas wykonania wyrażenia
v1*(1.2+v2)+v2*.5;
korzystając ze "zwykłej" implementacji operatorów arytmetycznych i z szablonów wyrażeń. Pomiaru dokonywałem poprzez umieszczenie tego wyrażenia w pętli:
Vector v1(100,1);
Vector v2(100,2);
Vector res(100);
for(size_t j = 0 ;j< 10000000;++j){
res=1.2*v1+v1*v2+v2*0.5;
f(res);
}
Czas wykonania programu mierzyłem poleceniem systemowym time. Wyniki są następujace (w sekundach):
| zwykłe | szablony | |
| -O0 | 720 | 311 |
| -O1 | 36 | 6.3 |
| -O2 | 30 | 5.5 |
| -O3 | 30 | 5.5 |
Proszę zauważyć, że znów włączanie optymalizacji daje dramatyczny 20 - 50-krotny wzrost szybkości programu. Podkreślam raz jeszcze, że opcja -O0, czyli brak optymalizacji, jest domyślną opcją dla kompilatora g++. Widać też, że używanie szablonów wyrażeń daje pięciokrotny wzrost szybkości programu. Oczywiście ten wynik będzie silnie zależał od konkretnych zastosowań. Jak zwykle gorąco zachęcam do własnych eksperymentów.