PEE Moduł 11: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 22 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd1.png|thumb|500px]] | |width="500px" valign="top"|[[Grafika:PEE_M11_Slajd1.png|thumb|500px]] | ||
|valign="top"| | |valign="top"|'''Podstawy fizyczne działania elementów półprzewodnikowych.''' | ||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd2.png|thumb|500px]] | |||
|valign="top"|'''Wprowadzenie''' | |||
Większość materiałów stosowanych w elektronice to materiały krystaliczne, które ze względu na zdolność przewodzenia prądu elektrycznego można zakwalifikować do jednej z grup: izolatory, półprzewodniki i przewodniki. Izolatory praktycznie nie przewodzą prądu elektrycznego. Półprzewodniki i przewodniki przewodzą. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd3.png|thumb|500px]] | |||
|valign="top"|W przewodnikach zjawisko przewodzenia prądu jest wyłącznie wynikiem ruchu ładunku ujemnego. W półprzewodnikach przewodzenie prądu odbywa się wskutek działania dwóch różnych i niezależnych od siebie mechanizmów poruszania się elektronów. Jeden z tych mechanizmów może być opisany jako ruch ładunku ujemnego, a drugi należy rozpatrywać jako ruch ładunku dodatniego | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd4.png|thumb|500px]] | |||
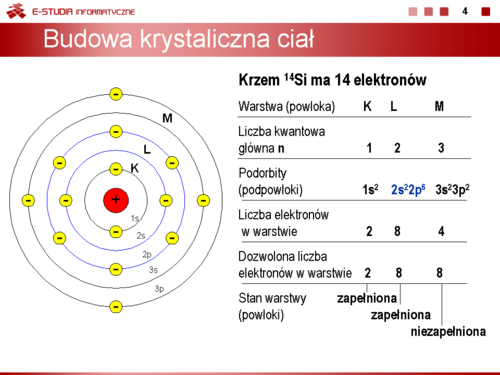
|valign="top"|'''Budowa krystaliczna ciał, swobodne elektrony, dziury''' | |||
Podstawowym materiałem do produkcji współczesnych przyrządów półprzewodnikowych jest krzem. Każdy atom krzemu ma 14 elektronów. Na pierwszej orbicie jest 2 elektrony, na drugiej 8 elektronów. Orbita pierwsza i druga są w pełni obsadzone. Na orbicie trzeciej jest tylko 4 elektrony na 8 możliwych do obsadzenia miejsc. Te cztery elektrony nazywane są elektronami walencyjnymi. Decydują one o aktywności chemicznej i właściwościach elektrycznych krzemu. W tym stanie atom jest obojętny elektrycznie. Aby zmienić ten stan należy do atomu doprowadzić z zewnątrz energię, przy czym najłatwiej jest oderwać od atomu elektrony walencyjne, a najtrudniej te położone blisko jądra. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd5.png|thumb|500px]] | |||
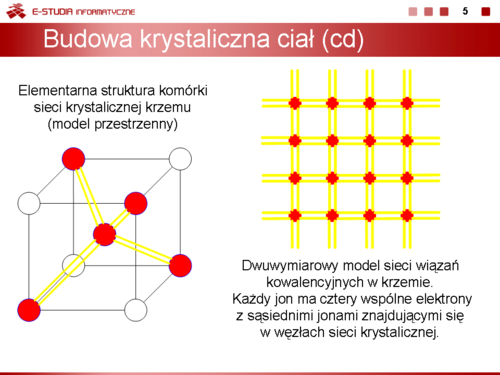
|valign="top"|W elektronice stosuje się krzem o strukturze krystalicznej, w której wszystkie atomy w całej objętości materiału są uporządkowane i związane ze sobą siłami wiązań atomowych tzw. kowalencyjnych i tworzą tzw. siatkę krystaliczną. Strukturę krystaliczną krzemu, którą często nazywamy strukturą diamentu przedstawiono na slajdzie 5. Dla temperatury zera bezwzględnego, kiedy siatka krystaliczna nie wykonuje żadnych ruchów w każdym narożniku sześcianu o boku około <math>5,4 angstrem (1 angstrem = 10^{-10 }m)</math> są umieszczone nieruchome jądra atomów. Pomiędzy sąsiadującymi ze sobą jądrami krążą pary elektronów tworząc bardzo trwałe wiązanie atomowe przy czym, ponieważ w każdej chwili czasowej z każdym jądrem są związane cztery elektrony walencyjne struktura ta jest elektrycznie obojętna. Aby rozerwać wiązanie atomowe utworzone przez cztery elektrony walencyjne należy dostarczyć do siatki krystalicznej znacznej energii tzw. energii jonizacji. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd6.png|thumb|500px]] | |||
|valign="top"|Są trzy podstawowe mechanizmy jonizacji: | |||
*podgrzanie (promieniowanie cieplne) – generacja termiczna, | |||
*naświetlenie (promieniowanie świetlne w zakresie fal widzialnych i niewidzialne) – fotogeneracja, | |||
*przyspieszenie nośników ładunku w polu elektrycznym i nadanie im takiej energii, że są one w stanie wybić z siatki krystalicznej kolejne elektrony, a te następne itd. tak, że proces ten rozwija się lawinowo – jonizacja zderzeniowa. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd7.png|thumb|500px]] | |||
|valign="top"|Elementy półprzewodnikowe na ogół pracują w temperaturze otoczenia około 300 K. Zatem do siatki krystalicznej w sposób naturalny jest dostarczana energia cieplna. Energia ta powoduje, że zarówno jądra atomów, jak i elektrony drgają wokół swoich położeń spoczynkowych (dla T = 0 K) co jest źródłem dodatkowych naprężeń mechanicznych w siatce krystalicznej. Jeżeli doprowadzona energia jonizacji (np. energia cieplna) jest dostatecznie duża to powstające siły zrywają wiązania atomowe i uwolnione w ten sposób elektrony mogą się swobodnie poruszać w krysztale. Te elektrony nazywamy elektronami swobodnymi. Po każdym uwolnionym elektronie pozostaje w siatce krystalicznej dodatnio naładowany jon związany z jądrem atomu. Nazywamy go dziurą. Dziura może przemieszczać się, podobnie jak elektrony swobodne w całej objętości kryształu. Ponieważ uzupełnienie brakującego na orbicie elektronu może odbywać się kosztem wolnych elektronów lub elektronów walencyjnych związanych z sąsiednimi atomami ruch ten jest niezależny od ruch elektronów swobodnych. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd8.png|thumb|500px]] | |||
|valign="top"|Można zatem w półprzewodniku wyróżnić prąd elektronowy związany z poruszającym się ładunkiem ujemnym wytworzony przez swobodne elektrony i prąd dziurowy związany z ładunkiem dodatnim wytworzonym przez poruszające się dziury. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd9.png|thumb|500px]] | |||
|valign="top"|Zgodnie z teorią Nielsa Bohra elektrony krążące po orbicie kołowej wokół jądra atomu | |||
o ściśle określonym promieniu mają określoną energię. Mówimy, że odpowiada im określony stan energetyczny. W przypadku atomu odosobnionego energia całkowita elektronu wyraża się zależnością: | |||
<math>W=\frac{Z\cdot e^4 \cdot m_e}{8n^2\cdot h^2 \cdot \epsilon^2_0}</math> | |||
gdzie: | |||
*<math>W</math> – całkowita energia elektronu | |||
*<math>Z</math> – liczba atomowa pierwiastka <math>(dla krzemu Z = 14)</math> | |||
*<math>e</math> – ładunek elementarny <math>(1,6•10^{-19} C)</math> | |||
*<math>m_e</math> – masa elektronu <math>(1,78•10^{-31} kg)</math> | |||
*<math>n</math> – numer orbity | |||
*<math>h</math> – stała Plancka <math>(6,625•10^{-34} J•s)</math> | |||
*<math>\epsilon_0</math> – przenikalność elektryczna próżni <math>(8,854•10^{-12} F/m)</math> | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd10.png|thumb|500px]] | |||
|valign="top"|Z równania 11.1 wynika, że elektron poruszający się po n – tej orbicie ma określoną energię. Przejście z orbity na orbitę związane jest ze zmiana energii i może odbywać się tylko w sposób skokowy. Mówimy w tym wypadku o zjawisku kwantowania orbit. Jeżeli atom nie jest odosobniony i wchodzi w skład siatki krystalicznej to ruch elektronów jest bardziej złożony i energia całkowita każdego z nich na poszczególnych orbitach nieznacznie różni się od energii podanej zależnością 11.1. Mówimy w tym wypadku | |||
o rozszczepieniu dyskretnego poziomu energetycznego. Rozszczepione poziomy energetyczne tworzą tzw. pasma energetyczne, a elektrony będące na określonej orbicie mogą przyjmować każdą wartość energii, która mieści się wewnątrz pasma. Takie pasma nazywamy dozwolonymi w odróżnieniu od pasm zabronionych, które zawierają takie poziomy energetyczne, których żaden elektron nie może obsadzić. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd11.png|thumb|500px]] | |||
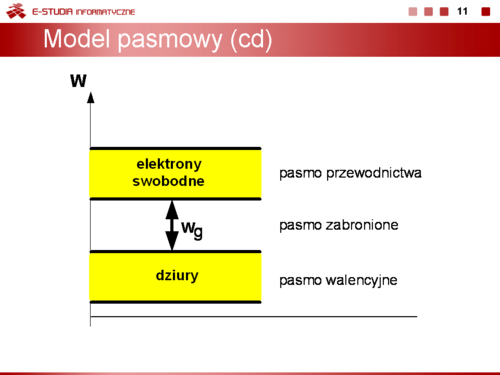
|valign="top"|W temperaturze zera bezwzględnego (T = 0 K) wszystkie elektrony walencyjne są związane z jądrem atomu i zajmują w modelu pasmowym półprzewodnika tzw. pasmo walencyjne. Po dostarczeniu odpowiednio dużej energii jonizacji elektrony te są wyrywane z siatki krystalicznej, ich energia całkowita rośnie i przechodzą one do pasma przewodnictwa. Te swobodne elektrony są nośnikami ujemnego ładunku elektrycznego | |||
i tworzą w materiale półprzewodnika prąd elektronowy. | |||
Różnica pomiędzy poziomem energii pasma walencyjnego i przewodnictwa Wg wyznacza szerokość pasma zabronionego. Wartość Wg określa minimalną energię, jaka musi być dostarczona do elektronu walencyjnego, aby został on wyrwany z wiązań siatki krystalicznej. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd12.png|thumb|500px]] | |||
|valign="top"|'''Rodzaje materiałów krystalicznych''' | |||
Analizując wzajemne usytuowanie pasma walencyjnego i przewodnictwa w modelu pasmowym ciał można wyróżnić trzy podstawowe grupy materiałów krystalicznych: izolatory, półprzewodniki i przewodniki. | |||
W izolatorach szerokość pasma zabronionego jest bardzo duża rzędu 10 eV i więcej, | |||
a zatem przeskok elektronu z pasma walencyjnego do pasma przewodnictwa jest bardzo trudny w realizacji ponieważ wymaga dostarczenia do elektronu dużej energii. | |||
W izolatorach tylko znikoma ilość elektronów przechodzi do pasma przewodnictwa i tworzy prąd elektryczny dlatego rezystywność izolatorów jest bardzo wielka | |||
rzędu <math>10^{10} - 10^{20} \Omega\cdot m</math>. | |||
Półprzewodniki, które w temperaturze T = 0 K są izolatorami, w temperaturze otoczenia 300 K wykazują właściwości przewodzące, ponieważ w tej temperaturze niektóre elektrony walencyjne przeskakują do pasma przewodzenia i tworzą prąd elektryczny. Ponieważ koncentracja atomów w ciałach stałych jest mniej więcej stała i porównywalna z liczbą Avogadra tzn. w <math>1\, m^3</math> jest około <math>5\cdot 10^{28}</math> atomów, to w temperaturze 300 K, dla <math>n_i = 10^{13}</math> tylko jeden na <math>5\cdot 10^{15}</math> atomów półprzewodnika jest zjonizowany. Oznacza to, że w paśmie przewodnictwa jest w <math>1\, m^3</math> około <math>10^{13}\ </math>, elektronów swobodnych, które tworzą prąd elektryczny. Rezystywność ma w tym wypadku wartość około <math>10 - 10^5 \Omega \cdot m</math> i silnie zależy od temperatury. | |||
Na slajdzie w tabeli podano energię pasma zabronionego dla różnych materiałów półprzewodnikowych. | |||
Półprzewodniki, które w temperaturze T = 0 K są izolatorami, w temperaturze otoczenia 300 K wykazują właściwości przewodzące, ponieważ w tej temperaturze niektóre elektrony walencyjne przeskakują do pasma przewodzenia i tworzą prąd elektryczny. Ponieważ koncentracja atomów w ciałach stałych jest mniej więcej stała i porównywalna z liczbą Avogadra tzn. w <math>1 cm^3</math> jest około <math>6\cdot 10^2^3</math> atomów, to w temperaturze 300 K tylko jeden na <math>6\cdot 10^1^2</math> atomów półprzewodnika jest zjonizowany. Oznacza to, że w paśmie przewodnictwa jest w <math>1 cm^3</math> około <math>10^1^4</math> elektronów swobodnych, które tworzą prąd elektryczny. Rezystywność ma w tym wypadku wartość około <math>10-10^5 \Omega\cdot m</math> i silnie zależy od temperatury. | |||
W metalach pasmo walencyjne i przewodnictwa nakładają się na siebie. Oznacza to, | |||
że w metalu nawet bez dostarczania energii z zewnątrz istnieją elektrony swobodne. Ponieważ koncentracja atomów w przewodnikach jest podobnie jak w półprzewodnikach rzędu <math>6\cdot 10^2^3</math>, a z jednego atomu jeden lub dwa elektrony walencyjne znajdują się | |||
w paśmie przewodnictwa to ładunek swobodny tworzący prąd elektryczny w przewodniku jest związany z ruchem bardzo wielkiej rzędu <math>10^2^4</math> w <math>1 cm^3</math> ilości elektronów. W tym wypadku rezystywność jest bardzo mała rzędu <math>10^{-8} \Omega \cdot m</math>. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd13.png|thumb|500px]] | |||
|valign="top"|Półprzewodniki samoistne | |||
Sieć krystaliczna półprzewodnika w temperaturze różnej od temperatury zera bezwzględnego drga. Te drgania cieplne są źródłem generacji termicznej par nośników elektron-dziura. szybkość generacji nośników zależy od temperatury oraz rodzaju materiału półprzewodnikowego. Ilość nośników ładunku w jednostce objętości nazywa się koncentracją: n <math>[m^-^3]</math> elektronów oraz p <math>[m^-^3]</math> dziur. Zjawisku generacji termicznej par elektron – dziura towarzyszy zawsze zjawisko przechwytywania elektronów przez dziury, które nazywamy rekombinacją nośników. W stanie równowagi termiczne oba procesy zachodzą z jednakową szybkością tzn. w tym samym czasie taka sama ilość par nośników jest generowana co rekombinuje. Podczas rekombinacji powracający z pasma przewodzenia do pasma walencyjnego elektron oddaje do otoczenia energię. W przypadku rekombinacji pośredniej (typowej dla Si i Ge) nadwyżka energii w postaci fononu jest zamieniona na drgania siatki krystalicznej, a w przypadku rekombinacji bezpośredniej (typowa dla GaAs) zostaje wypromieniowana w postaci fotonu | |||
(o odpowiedniej długości fali). | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd14.png|thumb|500px]] | |||
|valign="top"|W idealnym krysztale półprzewodnika samoistnego (ang. intrinsic), np. krzemu każdy elektron swobodny pozostawia w siatce krystalicznej dziurę, dlatego w danej temperaturze spełniony jest warunek <math>n_i</math> = <math>p_i</math> co oznacza, że , dla T=const | |||
W warunkach równowagi termicznej koncentrację nośników można obliczyć korzystając | |||
ze statystyki Boltzmana: | |||
<math>n_i=p_i=Ae^{\frac{-W_g}{2kT}}</math> | |||
gdzie: | |||
*A – stała materiałowa | |||
*k – stała Boltzmana | |||
*T – temperatura bezwzględna | |||
lub jeżeli jest znana koncentracja ładunku w temperaturze <math>T_1</math> ze statystyki | |||
Fermiego-Diracka: | |||
<math>n_i^2=n_i_1^2(\frac{T}{T_1})^3\cdot e ^{\frac{W_g(T-T_1)}{k\cdot T\cdot T_1}}</math> | |||
gdzie <math>n_i_1 – n_i</math> w temperaturze <math>T_1</math> | |||
Mała w porównaniu z metalami i zależna silnie od temperatury koncentracja nośników | |||
w półprzewodnikach samoistnych powoduje, że nie są one szeroko stosowane w technice. Do budowy elementów i przyrządów półprzewodnikowych stosuje się powszechnie półprzewodniki niesamoistne inaczej domieszkowane. | |||
'''Przykład 1''' | |||
Przyjmując, że liczba atomów krzemu w <math>1\, m^3</math> jest rzędu <math>4,99\cdot 10^{28}</math>, szerokość pasma zabronionego 1,12 eV, koncentracja elektronów w paśmie przewodnictwa w temperaturze 300 K <math>n_{i1} = 1,5\cdot 10^{16}</math>, oszacować temperaturę w której koncentracja swobodnych elektronów osiągnie wartość <math>n_i = 10^{20}</math>, <math>k = 1,38\cdot 10^{-23} J/K</math>. | |||
Rozwiązanie: | |||
Zależności | |||
<math>n_i^2=n_i_1^2(\frac{T}{T_1})^3\cdot e ^{\frac{W_g(T-T_1)}{k\cdot T\cdot T_1}}</math> | |||
ma postać uwikłaną i nie można z niej wyznaczyć prostymi metodami temperatury T. Jeżeli jednak zauważymy, że dla temperatur <math>T > T_1</math> dominującym czynnikiem w równaniu jest czynnik ekspotencjalny to upraszczając w/w zależność otrzymujemy: | |||
<math>n_i^2\cong n_i_1^2\cdot e ^{\frac{W_g(T-T_1)}{k\cdot T\cdot T_1}}</math> | |||
<math>T\cong \frac{T_1}{1-\frac{kT_1}{W_g}ln\frac{n_i^2}{n_{i1}^2}}=506K</math> | |||
Odp: T = 506 K <math>(233^\circ C)</math> | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd15.png|thumb|500px]] | |||
|valign="top"|Tabela. Podstawowe materiały półprzewodnikowe | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd16.png|thumb|500px]] | |||
|valign="top"|'''Defekty sieci krystalicznej''' | |||
W warunkach rzeczywistych, na skutek defektów sieci krystalicznej powstają lokalne zmiany koncentracji nośników powodujące, że jeden rodzaj nośników przeważa. Do najczęściej występujących defektów sieci krystalicznej zaliczamy: | |||
*zanieczyszczenia – wtrącenie pomiędzy atomy w węzłach siatki krystalicznej atomów innych pierwiastków, | |||
*brak atomów w niektórych węzłach siatki – luki | |||
*zastąpienie w niektórych węzłach siatki krystalicznej atomów półprzewodnika atomami innego pierwiastka – domieszki | |||
*przesunięci płaszczyzny krystalograficznej całej grupy atomów względem siebie – dyslokacje | |||
Wszystkie wymienione defekty siatki krystalicznej powodują, że w danym obszarze materiału półprzewodnikowego może przeważać ładunek dodatni i ten obszar półprzewodnika będziemy nazywać półprzewodnikiem typu p lub ujemny i wtedy powstanie półprzewodnik typu n. Wszystkie wymienione defekty powstają w trakcie wytwarzania monokryształów półprzewodnika lub podczas obróbki cieplnej, jakiej wymaga proces technologiczny przy produkcji elementów i przyrządów półprzewodnikowych. Wtrącenia obcych pierwiastków wprowadzane przypadkowo podczas procesu technologicznego w sposób nie kontrolowany i nie pożądany nazywamy zanieczyszczeniami. Wtrącenia wprowadzane celowo nazywamy domieszkami | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd17.png|thumb|500px]] | |||
|valign="top"|'''Przykłady defektów sieci krystalicznej''' | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd18.png|thumb|500px]] | |||
|valign="top"|'''Półprzewodniki niesamoistne''' | |||
Jeżeli do siatki krystalicznej półprzewodnika samoistnego (np. krzemu <math>S_i</math>) wprowadzimy przez domieszkowanie małe ilości pierwiastka pięciowartościowego, np.: antymonu <math>S_b</math>, arsenu <math>A_s</math> lub fosforu <math>P\ </math>, to w niektórych węzłach atomy półprzewodnika zostaną zamienione atomami domieszki. Nazywamy je donorami. Koncentrację domieszki donorowej oznaczmy przez <math>N_d\ </math>,. Piąty elektron walencyjny donorów nie bierze udziału w wiązaniach kowalentnych sieci i staje się elektronem swobodnym. | |||
Na wykresie pasmowym półprzewodnika pojawia się dodatkowy poziom energetyczny tzw. poziom donorowy. W temperaturze otoczenia około 300 K wszystkie atomy domieszki są zjonizowane tzn. elektrony z pasma donorowego przeskoczyły do pasma przewodnictwa. | |||
Powstał półprzewodnik typu n. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd19.png|thumb|500px]] | |||
|valign="top"|W tej sytuacji liczba elektronów swobodnych w paśmie przewodnictwa jest większa niż dziur w paśmie walencyjnym. Można zatem napisać: | |||
<math>N_n-N_d+n</math> | |||
gdzie | |||
*<math>N_n</math> – koncentracja elektronów swobodnych w półprzewodniku typu n | |||
*<math>n\ </math>, – koncentracja elektronów na skutek generacji termicznej | |||
oraz | |||
*<math>P_n</math> = p | |||
gdzie | |||
*<math>P_n</math> – koncentracja dziur w półprzewodniku typu n | |||
*<math>p\ </math>, – koncentracja dziur na skutek generacji termicznej | |||
<math>N_n >> P_n</math> | |||
Wprowadzenie domieszki donorowej spowodowało wielokrotny wzrost koncentracji elektronów swobodnych (donorowych) w paśmie przewodnictwa w stosunku do elektronów samoistnych powstających w procesie generacji termicznej par elektron-dziura. Jednocześnie zmniejszyła się koncentracja dziur w paśmie walencyjnym. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd20.png|thumb|500px]] | |||
|valign="top"|Jeżeli do siatki krystalicznej półprzewodnika samoistnego (np. krzemu Si) wprowadzimy przez domieszkowanie małe ilości pierwiastka trójwartościowego, np.: glinu Al, indu In lub galu Ga to w niektórych węzłach atomy półprzewodnika zostaną zamienione atomami domieszki. Nazywamy je akceptorami. Koncentrację domieszki akceptorowej oznaczmy przez <math>P_a\ </math>,. Brak czwartego elektronu walencyjnego dekompletuje jedno z wiązań kowalentnych w siatce krystalicznej. Występujący tu brak elektronu może być uzupełniony elektronem z sąsiedniego wiązania. Powstaje w ten sposób dziura, która może przemieszczać się w krysztale podobnie jak elektron walencyjny, ale w zasadzie niezależnie od niego. W tym wypadku w pobliżu pasma walencyjnego powstaje poziom energetyczny zwany poziomem akceptorowym. W temperaturze otoczenia około 300 K wszystkie atomy domieszki akceptorowej są zjonizowane. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd21.png|thumb|500px]] | |||
|valign="top"|W tym przypadku można napisać: | |||
<math>P_p = P_a +p </math> | |||
<math>N_p = n </math> | |||
gdzie | |||
*<math>P_p</math> – koncentracja dziur w półprzewodniku typu p | |||
*<math>p\ </math>, – koncentracja dziur na skutek generacji termicznej | |||
<math>P_p >> N_p </math> | |||
W półprzewodniku typu p liczba dziur w paśmie walencyjnym jest znacznie większa od liczby elektronów w paśmie przewodnictwa. | |||
'''Przykład 2''' | |||
Płytka krzemu jest domieszkowana atomami akceptorowymi. Koncentracja domieszki <math>P_a = 3\cdot 10^{22} m^{-3}</math>. Jaka jest koncentracja dziur i elektronów swobodnych w temperaturze pokojowej <math>27^\circ C</math>, jeżeli koncentracja nośników samoistnych jest równa <math>n_i = 1,5\cdot 10^{16} m^{-3}</math>. | |||
Rozwiązanie: | |||
<math>P_P=P_a+p\approx P_a=3\cdot 10^{22}m^{-3}</math> | |||
<math>N_P=\frac{n_i^2}{P_a}=7,5\cdot 10^{22}m^{-3}</math> | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd22.png|thumb|500px]] | |||
|valign="top"|Obszar, w którym zachodzi bardzo silna (o kilka rzędów wielkości) zmiana koncentracji ładunku nazywa się złączem. | |||
Szerokość złącza ma na ogół wymiar rzędu <math>10^{-7}-10^{-6} m</math>. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd23.png|thumb|500px]] | |||
|valign="top"|'''Generacja i rekombinacja''' | |||
W stanie równowagi termicznej niezależnie od koncentracji domieszek w każdym półprzewodniku spełniony jest tzw. warunek neutralności, który mówi, że w każdym punkcie obszaru półprzewodnika wypadkowy ładunek elektryczny jest równy zeru, | |||
a wszelkie zaburzenia warunku neutralności powodują powstanie pola elektrycznego przywracającego stan równowagi | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd24.png|thumb|500px]] | |||
|valign="top"|Odpowiedni poziom koncentracji nośników zapewnia proces rekombinacji. | |||
W półprzewodniku samoistnym polega on na bezpośrednim przejściu elektronu z pasma przewodnictwa do pasma walencyjnego W półprzewodniku niesamoistnym proces ten jest bardziej złożony i odbywa się etapowo. Podczas przeskoku elektronu z pasma przewodnictwa do pasma walencyjnego przyjmuje on dodatkowe położenia, którym odpowiadają w modelu pasmowym poziomy energetyczne wewnątrz pasma zabronionego. Są to tzw. centra rekombinacji lub inaczej centra pułapkowe, które | |||
w czystych półprzewodnikach samoistnych stanowią defekty sieci krystalicznej, a w półprzewodnikach niesamoistnych dodatkowo także atomy międzywęzłowe szczególnych domieszek np. złota lub miedzi. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd25.png|thumb|500px]] | |||
|valign="top"|Proces rekombinacji jest opóźniony względem procesu generacji o krótki rzędu mikrosekund czas τ nazywany czasem życia nośników. Wartość tego czasu mówi o jakości struktury krystalicznej półprzewodnika oraz o stopniu jej uporządkowania. Obróbka termiczna w wysokich temperaturach skraca o rząd wielkości czas życia nośników. W czasie τ nośniki ładunku przebywają pewien odcinek drogi L nazywany drogą dyfuzji. Droga dyfuzji jest związana z czasem życia nośników równaniem: | |||
<math>L=\sqrt D\tau</math> | |||
gdzie D – stała dyfuzji | |||
W temperaturze pokojowej 300 K <math>D_n = 35\cdot 10^{-4} m^2s^{-1}</math>, <math>D_p = 12,5\cdot 10^{-4} m^2s^{-1}</math> | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd26.png|thumb|500px]] | |||
|valign="top"|'''Oddziaływanie pola elektrycznego na nośniki ładunku. Konduktywność półprzewodników.''' | |||
W warunkach równowagi termicznej ładunki swobodne w półprzewodniku jak w każdy ciele stałym poruszają się w sposób nie porządkowany, chaotycznie we wszystkich kierunkach. W tym wypadku trudno jest wyróżnić jeden uprzywilejowany kierunek w którym poruszałaby się przynajmniej większość ładunków, a zatem nie ma przepływu prądu. Jeżeli jednak w półprzewodniku zostanie wytworzone pole elektryczne np. wzdłuż osi x o natężeniu Ex to będzie ono oddziaływało na elektrony z siłą <math>F = -e\cdot E_x</math>. Pod wpływem tej siły wszystkie elektrony i dziury zaczną dryfować w kierunku pola, tzn. na ruch chaotyczny nałoży się ruch uporządkowany w kierunku osi x. Pomimo działania stałej siły powodującej przyspieszanie elektronów i dziur ruch ich jest ciągle hamowany przez siły oddziaływania atomów siatki krystalicznej (mówimy w tym przypadku o zderzeniach | |||
z atomami półprzewodnika i domieszki, które tkwią w węzłach siatki krystalicznej) z tego powodu przyjmujemy, że prędkości unoszenia vxn i vxp są stałe i równe średniej wartości prędkości elektronu i dziury pomiędzy kolejnymi zderzeniami. warto zauważyć, że wartości prędkości <math>v_x_n i v_x_p</math> są bardzo mała rzędu <math>10^-^4-10^-^3 m/s</math>. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd27.png|thumb|500px]] | |||
|valign="top"|Zgodnie z definicją prądu | |||
<math>i=\frac{dQ}{dt}</math> | |||
gdzie dQ – ładunek przepływający w czasie dt przez przekrój S półprzewodnika | |||
<math>dQ=nev_x_ndtS+pe v_x_pdtS</math> | |||
Zatem gęstość prądu | |||
<math>j_xnev_x_n+pev_x_p</math> | |||
Ponieważ prawo Ohma w postaci różniczkowej ma postać | |||
<math>j_x=\gamma E_x</math> | |||
to przyrównując do siebie i przekształcając prawe strony równań otrzymujemy zależność na konduktywność półprzewodnika | |||
<math>\gamma =e(n\frac{v_x_n}{E_x}+\frac{v_x_p}{E_x})</math> | |||
Parametry <math>\frac{v_x_n}{E_x}\mu_n</math> oraz <math>\frac{v_x_n}{E_x}\mu_n</math> nazywamy ruchliwością nośników, odpowiednio elektronów i dziur. Ich wartość leży w zakresie <math>10^-^3 \div 10^-^2 m^2/V\cdot s</math> dla metali, | |||
<math>4\cdot10^-^2 \div 4\cdot 10^-^1 m^2/V\cdot s</math> dla krzemu i germanu oraz około <math>7 m^2/V\cdot s</math> dla innych półprzewodników typu III – V i zmienia się w funkcji temperatury. Dla krzemu obowiązuje zależność <math>µ_n = 3µ_p</math>. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd28.png|thumb|500px]] | |||
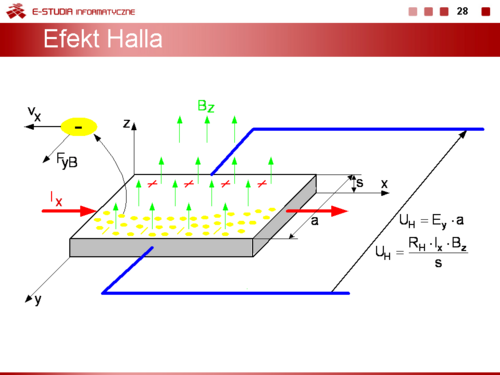
|valign="top"|'''Oddziaływanie pola magnetycznego na nośniki ładunku w półprzewodniku. Efekt Halla.''' | |||
Weźmy pod uwagę płytkę prostopadłościenną wykonaną z półprzewodnika typu n. | |||
W kierunku osi x poruszają się z prędkością <math>v_x</math> ładunki swobodne tworząc prąd <math>I_x</math> W kierunku prostopadłym do osi x, wzdłuż osi z, wytworzone zostało stałe pole magnetyczne | |||
o indukcji Bz. Pod wpływem tego pola tor ruchu poruszających się elektronów zostaje zakrzywiony w kierunku osi y. Żeby zrównoważyć siłę <math>F_y_B = - v_x•B_z</math> powodującą dryfowanie elektronów w kierunku tej siły, wewnątrz płytki półprzewodnikowej powstaje pole elektryczne <math>E_y</math> o zwrocie zgodnym z kierunkiem osi y. Kiedy siła <math>F_y_E = e•E_y</math> jest równa co do wartości sile F_y_B ustala się stan równowagi i elektrony mogą nadal przemieszczać się | |||
w płytce wzdłuż osi x. Powstawanie pola elektrycznego Ey nosi nazwę efektu Halla, a napięcie <math>U_H = E_y</math> a - napięciem Halla. Jeżeli płytka półprzewodnikowa będzie typu p zmienią się zwroty sił <math>F_y_B, F_y_E</math> oraz natężenia pola elektrycznego <math>E_y</math> i napięcia Halla <math>U_H</math>. Zjawisko Halla praktycznie zastosowano do badania przewodnictwa materiałów (w tym również metali) oraz do konstrukcji półprzewodnikowych czujników pola magnetycznego. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd29.png|thumb|500px]] | |||
|valign="top"|'''Transport nośników nadmiarowych w półprzewodniku niesamoistnym. Dyfuzja.''' | |||
W półprzewodniku typu n nośnikami nadmiarowymi są elektrony, a w półprzewodniku typu p dziury. Jeżeli w pewnej objętości półprzewodnika znajdzie się więcej nośników nadmiarowych niż w innym oznacza to, że ich koncentracje w różnych obszarach materiału są różne. W tym wypadku nośniki z obszaru o większej koncentracji będą się przesuwały do obszaru o koncentracji mniejszej. Ten proces nazywamy dyfuzją. Dyfuzja jest naturalnym efektem przypadkowych ruchów poszczególnych nośników i występuje bez działania żadnej konwencjonalnej siły. Dyfuzja i unoszenie w polu elektrycznym to dwa podstawowe procesy transportu nośników w półprzewodnikach. W wyniku nierównomiernego rozkładu nośników w materiale półprzewodnika płynie prąd, który składa się z dwóch składników: prądu unoszenia pochodzącego od pola elektrycznego powstającego w wyniku rozsunięcia się ładunków w przestrzeni oraz prądu dyfuzji. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd30.png|thumb|500px]] | |||
|valign="top"|W stanie równowagi termicznej suma prądu unoszenia i dyfuzji jest równa zeru. Dokładniejsze badanie warunków równowagi pozwala wyznaczyć tzw. zależność Einsteina wiążącą ruchliwość ładunku ze współczynnikiem dyfuzji: | |||
<math>\frac{D_n}{\mu_n}=\frac{D_p}{\mu_p}=\frac{kT}{e}=U_T</math> | |||
gdzie UT potencjał elektrokinetyczny. | |||
W temperaturze pokojowej <math>U_T</math> jest równe około 25 mV | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd31.png|thumb|500px]] | |||
|valign="top"|Przy niewielkich odchyleniach koncentracji nośników od stanu równowagi wypadkowa gęstość prądu elektronów i dziur jest równa: | |||
<math>J_n(X)=J_u_n+J_d_n=e\mu_n n(X)E_x+eD_n\frac{dn(X)}{dx}</math> | |||
<math>J_p(X)=J_u_p+J_d_p=e\mu_p p(X)E_x+eD_n\frac{dp(X)}{dx}</math> | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd32.png|thumb|500px]] | |||
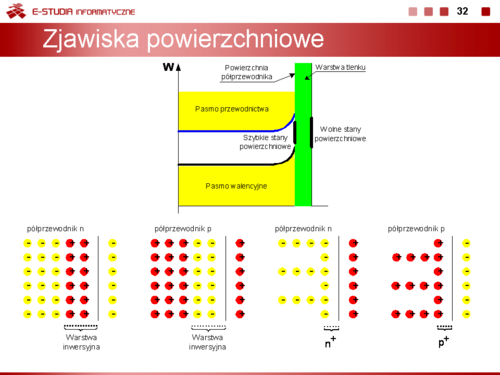
|valign="top"|'''Zjawiska powierzchniowe''' | |||
Na powierzchni półprzewodnika występuje w sposób naturalny nieciągłość sieci krystalicznej. W modelu pasmowym oznacza to, że pojawiają się na granicy materiału tzw. energetyczne stany powierzchniowe, które mogą być obsadzone przez elektrony. Stany te są usytuowane w pobliżu środka pasma zabronionego. Wyróżnia się tzw. stany szybkie, powstające na powierzchni czystego półprzewodnika i stany wolne, w przypadku, gdy powierzchnia półprzewodnika pokryta jest warstwą tlenku. Stany powierzchniowe mogą być donorowe lub akceptorowe. Powodują one, że na powierzchni półprzewodnika w cienkiej warstwie o grubości od kilku do kilkudziesięciu angstremów <math>(1 \overset{\circ}{A} = 10^-^{10} m)</math> gromadzi się ładunek ujemny (elektrony) lub dodatni (dziury). W wyniku oddziaływania tej warstwy na ładunki znajdujące się wewnątrz półprzewodnika w pobliżu jego powierzchni powstaje tzw. warstwa inwersyjna ładunku przeciwnego znaku | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd33.png|thumb|500px]] | |||
|valign="top"|Grubość warstwy inwersyjnej jest funkcją wnikania pola elektrycznego w półprzewodnik, a ta jest określona wzorem Debeya | |||
<math>L_D=\sqrt \frac{2\epsilon \cdot \epsilon_0 \cdot k\cdot T}{n\cdot e^2}</math> | |||
gdzie | |||
<math>\epsilon</math> – względna przenikalność elektryczna krzemu | |||
<math>\epsilon_0</math> – przenikalność elektryczna próżni | |||
<math>N</math> – koncentracja domieszki: donorowej Nd lub akceptorowe Np. | |||
Wartość LD zawiera się w przedziale wartości <math>10^{-10}-10^{-8} m</math>. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd34.png|thumb|500px]] | |||
|valign="top"|'''Szumy w półprzewodnikach''' | |||
Trzy zjawiska fizyczne są źródłem niezdeterminowanych, chaotycznych i niepożądanych sygnały występujących w materiałach, a w szczególności w półprzewodnikach stosowanych w elektronice, do budowy elementów elektronicznych: | |||
#Szumy cieplne. | |||
#Szumy śrutowe. | |||
#Szumy strukturalne. | |||
|} | |} | ||
---- | ---- | ||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd35.png|thumb|500px]] | |||
|valign="top"|Szumy cieplne są spowodowane ciągłym, bezładnym ruchem swobodnych elektronów i dziur w materiale półprzewodnikowym. Wartość skuteczna napięcia, jakie w związku z tym ruchem powstaje, w zakresie częstotliwości <math>\Delta f</math> jest równa: | |||
<math>U_s_z=\sqrt {kTR\Delta f}</math> | |||
gdzie R – rezystancja próbki materiału | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd36.png|thumb|500px]] | |||
|valign="top"|Szumy śrutowe spowodowane są występowaniem statystycznych fluktuacji procesów związanych z generacją, rekombinacją i dyfuzją nośników ładunków w półprzewodniku podczas przepływu prądu. Wartość skuteczna zastępczego źródła prądu reprezentującego te szumy w zakresie częstotliwości <math>\Delta f</math> jest równa: | |||
<math>I_s_z=\sqrt{ 2e\Delta fi_0}</math> | |||
gdzie <math>I_0</math> – składowa stała przepływającego przez próbkę prądu. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd37.png|thumb|500px]] | |||
|valign="top"|Szumy strukturalne, czasami nazywane modulacyjnymi, wywołane są zjawiskami powierzchniowymi. Wartość skuteczna zastępczego źródła prądu reprezentującego te szumy w zakresie częstotliwości <math>\Delta f</math> maleje ze wzrostem częstotliwości i jest równa: | |||
<math>I_s_z=AI_0\frac{\Delta f}{f}</math> | |||
gdzie A – stała zależna od wymiarów i parametrów materiału półprzewodnikowego. | |||
|} | |||
---- | |||
{| border="0" cellpadding="4" width="100%" | |||
|width="500px" valign="top"|[[Grafika:PEE_M11_Slajd38.png|thumb|500px]] | |||
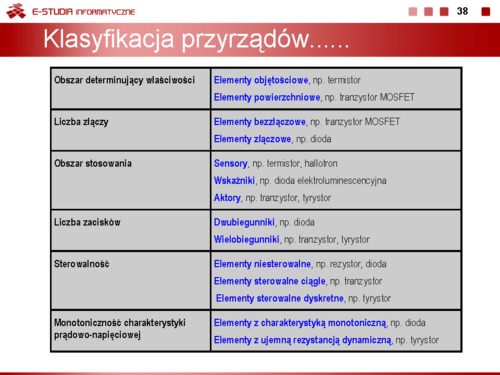
|valign="top"|'''Klasyfikacja przyrządów półprzewodnikowych''' | |||
Przyrządy półprzewodnikowe klasyfikujemy przyjmując różne kryteria podziału. Przyjmując jako kryterium liczbę złącz półprzewodnikowych dzielimy przyrządy półprzewodnikowe na bezzłączowe, jednozłączowe i wielozłączowe, a ze względu na liczbę wyprowadzeń na dwu-, trój- i wielozaciskowe. | |||
Ze względu na obszar, w którym zachodzą zjawiska fizyczne decydujące | |||
o właściwościach elektrycznych dzielimy przyrządy półprzewodnikowe na takie, w których występują efekty objętościowe (decydują zjawiska zachodzące w całej objętości materiału półprzewodnikowego) i takie, w których występują efekty powierzchniowe (decydują zjawiska zachodzące na powierzchni materiału półprzewodnikowego). | |||
Przyjmując jako kryterium możliwość wzmacniania sygnałów dzielimy przyrządy półprzewodnikowe na pasywne (tłumią sygnały) i aktywne (umożliwiają wzmacnianie sygnałów). | |||
Ze względu na możliwość zmiany stanu pracy elementu dzielimy przyrządy półprzewodnikowe na sterowalne i niesterowalne, a z punktu widzenia energetycznego na przyrządy małej mocy (sygnałowe) i przyrządy mocy (do pracy w układach energoelektronicznych). | |||
|} | |||
---- | |||
{| | |||
|'''Literatura''' | |||
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, | |||
Oficyna Wydawnicza PW, Warszawa 2005 | |||
J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, | |||
WNT, Warszawa 1981 | |||
P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976 | |||
|} | |||
Aktualna wersja na dzień 12:02, 5 wrz 2023
 |
Podstawy fizyczne działania elementów półprzewodnikowych. |
 |
Tabela. Podstawowe materiały półprzewodnikowe |
 |
Przykłady defektów sieci krystalicznej |
 |
Obszar, w którym zachodzi bardzo silna (o kilka rzędów wielkości) zmiana koncentracji ładunku nazywa się złączem.
Szerokość złącza ma na ogół wymiar rzędu .
|
 |
Przy niewielkich odchyleniach koncentracji nośników od stanu równowagi wypadkowa gęstość prądu elektronów i dziur jest równa:
|
| Literatura
M. P. Kaźmierkowski, J. T. Matysik: Wprowadzenie do elektroniki i energoelektroniki, Oficyna Wydawnicza PW, Warszawa 2005 J. Jaczewski, A. Opolski, J. Stolz: Podstawy elektroniki i energoelektroniki, WNT, Warszawa 1981 P. E. Gray, C. L. Searle: Podstawy elektroniki, PWN, Warszawa 1976 |