|
|
| (Nie pokazano 2 wersji utworzonych przez 2 użytkowników) |
| Linia 1: |
Linia 1: |
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |valign="top" width="500px"|[[Grafika:PEE_M10_Slajd1.png|500px]] | | |valign="top" width="500px"|[[Grafika:PEE_M10_Slajd1.png|500px]] |
| |valign="top"|'''Wykład10. Czwórniki''' | | |valign="top"| |
| |} | | |} |
|
| |
|
| Linia 17: |
Linia 17: |
| jak to zaznaczono na rysunku. Sygnały prądu i napięcia po stronie wejściowej oznaczać będziemy ze wskaźnikiem 1, a po stronie wyjściowej – ze wskaźnikiem 2. Przyjmiemy umownie, że oba prądy: na wejściu i wyjściu są zwrócone do prostokąta oznaczającego czwórnik. | | jak to zaznaczono na rysunku. Sygnały prądu i napięcia po stronie wejściowej oznaczać będziemy ze wskaźnikiem 1, a po stronie wyjściowej – ze wskaźnikiem 2. Przyjmiemy umownie, że oba prądy: na wejściu i wyjściu są zwrócone do prostokąta oznaczającego czwórnik. |
|
| |
|
| W zależności od elementów tworzących obwód, czwórnik może być liniowy (gdy wszystkie elementy obwodu są liniowe) lub nieliniowy. W dalszych rozważaniach ograniczymy się wyłącznie do czwórników liniowych. Czwórnik nazywać będziemy pasywnym, jeśli nie wytwarza energii a jedynie pobiera ją ze źródła zasilającego i przetwarza w określony sposób. Czwórnik złożony z samych elementów pasywnych <math>R</math>, <math>L</math>, <math>C</math> i <math>M</math> jest zawsze czwórnikiem pasywnym. Czwórnik pasywny jest zdolny do gromadzenia i rozpraszania energii pobranej ze źródła, może ją również oddawać na zewnątrz, jednak w dowolnej chwili czasowej <math>t\,</math> energia ta nie może przewyższać energii pobranej. Czwórnik, który nie spełnia powyższych warunków jest czwórnikiem aktywnym (generatorem energii). | | W zależności od elementów tworzących obwód, czwórnik może być liniowy (gdy wszystkie elementy obwodu są liniowe) lub nieliniowy. W dalszych rozważaniach ograniczymy się wyłącznie do czwórników liniowych. Czwórnik nazywać będziemy pasywnym, jeśli nie wytwarza energii a jedynie pobiera ją ze źródła zasilającego i przetwarza w określony sposób. Czwórnik złożony z samych elementów pasywnych <math>R</math>, <math>L</math>, <math>C</math> i <math>M</math> jest zawsze czwórnikiem pasywnym. Czwórnik pasywny jest zdolny do gromadzenia i rozpraszania energii pobranej ze źródła, może ją również oddawać na zewnątrz, jednak w dowolnej chwili czasowej <math>t\ </math>, energia ta nie może przewyższać energii pobranej. Czwórnik, który nie spełnia powyższych warunków jest czwórnikiem aktywnym (generatorem energii). |
|
| |
|
| |} | | |} |
| Linia 66: |
Linia 66: |
| </math> | | </math> |
|
| |
|
| Macierz <math>\mathbf{Y}\,</math> jest nazywana macierzą admitancyjną a parametry tej macierzy mają interpretację admitancji operatorowych. | | Macierz <math>\mathbf{Y}\ </math>, jest nazywana macierzą admitancyjną a parametry tej macierzy mają interpretację admitancji operatorowych. |
|
| |
|
|
| |
|
| Linia 94: |
Linia 94: |
| </math> | | </math> |
|
| |
|
| Macierz <math>\mathbf{Z}\,</math> jest nazywana macierzą impedancyjną a parametry tej macierzy mają interpretację impedancji operatorowych. Łatwo jest udowodnić, że macierze impedancyjna i admitancyjna są powiązane relacją | | Macierz <math>\mathbf{Z}\ </math>, jest nazywana macierzą impedancyjną a parametry tej macierzy mają interpretację impedancji operatorowych. Łatwo jest udowodnić, że macierze impedancyjna i admitancyjna są powiązane relacją |
|
| |
|
| : <math>\mathbf{Y}=\mathbf{Z}^{-1}</math> | | : <math>\mathbf{Y}=\mathbf{Z}^{-1}</math> |
| Linia 156: |
Linia 156: |
| </math> | | </math> |
|
| |
|
| w której <math>\mathbf{H}\,</math> jest '''macierzą hybrydową'''. Jak widać z opisu hybrydowego parametr <math>H_{11}</math> ma interpretację impedancji a <math>H_{22}</math> admitancji. Parametry <math>H_{12}</math> i <math>H_{21}</math> są bezwymiarowe i wyrażają stosunek odpowiednio dwu napięć i dwu prądów w obwodzie. | | w której <math>\mathbf{H}\ </math>, jest '''macierzą hybrydową'''. Jak widać z opisu hybrydowego parametr <math>H_{11}</math> ma interpretację impedancji a <math>H_{22}</math> admitancji. Parametry <math>H_{12}</math> i <math>H_{21}</math> są bezwymiarowe i wyrażają stosunek odpowiednio dwu napięć i dwu prądów w obwodzie. |
|
| |
|
|
| |
|
| Linia 182: |
Linia 182: |
| </math> | | </math> |
|
| |
|
| Stanowi on odwrotność opisu hybrydowego macierzą <math>\mathbf{H}\,</math>. Obie macierze powiązane są następująca relacją | | Stanowi on odwrotność opisu hybrydowego macierzą <math>\mathbf{H}\ </math>,. Obie macierze powiązane są następująca relacją |
|
| |
|
| : <math>\mathbf{G}=\mathbf{H}^{-1}</math> | | : <math>\mathbf{G}=\mathbf{H}^{-1}</math> |
|
| |
|
| Duża liczba stosowanych opisów macierzowych czwórnika wynika również z faktu, że dla niektórych czwórników pewne opisy mogą nie istnieć. Najbardziej uniwersalne pod tym względem są opisy hybrydowe wykorzystujące macierz <math>\mathbf{H}\,</math> lub <math>\mathbf{G}\,</math>, które można otrzymać dla większości obwodów elektrycznych. | | Duża liczba stosowanych opisów macierzowych czwórnika wynika również z faktu, że dla niektórych czwórników pewne opisy mogą nie istnieć. Najbardziej uniwersalne pod tym względem są opisy hybrydowe wykorzystujące macierz <math>\mathbf{H}\ </math>, lub <math>\mathbf{G}\ </math>,, które można otrzymać dla większości obwodów elektrycznych. |
|
| |
|
| |} | | |} |
| Linia 194: |
Linia 194: |
| {| border="0" cellpadding="4" width="100%" | | {| border="0" cellpadding="4" width="100%" |
| |valign="top" width="500px"|[[Grafika:PEE_M10_Slajd6.png|500px]] | | |valign="top" width="500px"|[[Grafika:PEE_M10_Slajd6.png|500px]] |
| |valign="top"|Jako przykład wyznaczymy opis czwórnika przedstawionego na rysunku na slajdzie 6. Czwórnik ten nosi nazwę czwórnika typu <math>T\,</math> i jest jedną z najpopularniejszych struktur czwórnikowych. | | |valign="top"|Jako przykład wyznaczymy opis czwórnika przedstawionego na rysunku na slajdzie 6. Czwórnik ten nosi nazwę czwórnika typu <math>T\ </math>, i jest jedną z najpopularniejszych struktur czwórnikowych. |
|
| |
|
|
| |
|
| Linia 226: |
Linia 226: |
| </math> | | </math> |
|
| |
|
| Macierz łańcuchowa <math>\mathbf{A}\,</math> dana jest więc wzorem | | Macierz łańcuchowa <math>\mathbf{A}\ </math>, dana jest więc wzorem |
|
| |
|
| : <math> | | : <math> |
| Linia 347: |
Linia 347: |
| : <math>T_u(s)={U_2(s) \over U_1(s)}={1 \over A_{11}}={1 \over 1+Z_1Y}={Z \over Z+Z_1}</math> | | : <math>T_u(s)={U_2(s) \over U_1(s)}={1 \over A_{11}}={1 \over 1+Z_1Y}={Z \over Z+Z_1}</math> |
|
| |
|
| Wobec braku obciążenia czwórnika przez impedancję <math>Z_2</math> nie przepływa prąd, stąd całe napięcie wyjściowe pochodzi z impedancji poprzecznej <math>Z\,</math> (dzielnik impedancyjny). | | Wobec braku obciążenia czwórnika przez impedancję <math>Z_2</math> nie przepływa prąd, stąd całe napięcie wyjściowe pochodzi z impedancji poprzecznej <math>Z\ </math>, (dzielnik impedancyjny). |
|
| |
|
| Impedancja wejściowa czwórnika przy obciążeniu bramy wyjściowej impedancją <math>Z_0</math> na podstawie wzoru jest równa | | Impedancja wejściowa czwórnika przy obciążeniu bramy wyjściowej impedancją <math>Z_0</math> na podstawie wzoru jest równa |
| Linia 362: |
Linia 362: |
| |valign="top"|'''Połączenie łańcuchowe''', zwane również kaskadowym czwórników to takie połączenie , w którym zaciski wejściowe jednego czwórnika są przyłączone do zacisków wyjściowych poprzedniego. Przykład połączenia łańcuchowego dwu czwórników przedstawiony jest na rysunku obok. | | |valign="top"|'''Połączenie łańcuchowe''', zwane również kaskadowym czwórników to takie połączenie , w którym zaciski wejściowe jednego czwórnika są przyłączone do zacisków wyjściowych poprzedniego. Przykład połączenia łańcuchowego dwu czwórników przedstawiony jest na rysunku obok. |
|
| |
|
| Łatwo jest pokazać, że macierz łańcuchowa <math>\mathbf{A}\,</math> czwórników połączonych kaskadowo jest równa iloczynowi macierzy łańcuchowych poszczególnych czwórników tworzących to połączenie | | Łatwo jest pokazać, że macierz łańcuchowa <math>\mathbf{A}\ </math>, czwórników połączonych kaskadowo jest równa iloczynowi macierzy łańcuchowych poszczególnych czwórników tworzących to połączenie |
|
| |
|
| : <math>\mathbf{A}=\mathbf{A}_1 \cdot \mathbf{A}_2</math> | | : <math>\mathbf{A}=\mathbf{A}_1 \cdot \mathbf{A}_2</math> |
| Linia 384: |
Linia 384: |
| Na rysunku obok przedstawiono układ dwu czwórników połączonych szeregowo, spełniający powyższe warunki. | | Na rysunku obok przedstawiono układ dwu czwórników połączonych szeregowo, spełniający powyższe warunki. |
|
| |
|
| Łatwo jest pokazać, że w połączeniu szeregowym czwórników macierz impedancyjna <math>\mathbf{Z}\,</math> połączenia jest równa sumie macierzy impedancyjnych każdego czwórnika. Oznacza to, że | | Łatwo jest pokazać, że w połączeniu szeregowym czwórników macierz impedancyjna <math>\mathbf{Z}\ </math>, połączenia jest równa sumie macierzy impedancyjnych każdego czwórnika. Oznacza to, że |
|
| |
|
| : <math>\mathbf{Z}=\mathbf{Z}_1+\mathbf{Z}_2</math> | | : <math>\mathbf{Z}=\mathbf{Z}_1+\mathbf{Z}_2</math> |
| Linia 408: |
Linia 408: |
| Na rysunku obok przedstawiono układ dwu czwórników połączonych równolegle, spełniający powyższe warunki. | | Na rysunku obok przedstawiono układ dwu czwórników połączonych równolegle, spełniający powyższe warunki. |
|
| |
|
| Łatwo jest pokazać, że w połączeniu równoległym czwórników macierz admitancyjna <math>\mathbf{Y}\,</math> połączenia jest równa sumie macierzy admitancyjnych każdego czwórnika. Oznacza to, że | | Łatwo jest pokazać, że w połączeniu równoległym czwórników macierz admitancyjna <math>\mathbf{Y}\ </math>, połączenia jest równa sumie macierzy admitancyjnych każdego czwórnika. Oznacza to, że |
|
| |
|
| : <math>\mathbf{Y}=\mathbf{Y}_1+\mathbf{Y}_2</math> | | : <math>\mathbf{Y}=\mathbf{Y}_1+\mathbf{Y}_2</math> |
| Linia 432: |
Linia 432: |
| Na rysunku obok przedstawiono układ dwu czwórników połączonych szeregowo-równolegle (szeregowo po stronie zacisków wejściowych i równolegle po stronie zacisków wyjściowych), spełniający powyższe warunki. | | Na rysunku obok przedstawiono układ dwu czwórników połączonych szeregowo-równolegle (szeregowo po stronie zacisków wejściowych i równolegle po stronie zacisków wyjściowych), spełniający powyższe warunki. |
|
| |
|
| Łatwo jest pokazać, że w połączeniu szeregowo-równoległym czwórników macierz hybrydowa <math>H\,</math> połączenia jest równa sumie macierzy hybrydowych <math>\mathbf{H}\,</math> każdego czwórnika. Oznacza to, że | | Łatwo jest pokazać, że w połączeniu szeregowo-równoległym czwórników macierz hybrydowa <math>H\ </math>, połączenia jest równa sumie macierzy hybrydowych <math>\mathbf{H}\ </math>, każdego czwórnika. Oznacza to, że |
|
| |
|
| : <math>\mathbf{H}=\mathbf{H}_1+\mathbf{H}_2</math> | | : <math>\mathbf{H}=\mathbf{H}_1+\mathbf{H}_2</math> |
|
| |
|
| Przy większej liczbie czwórników połączonych szeregowo-równolegle macierz hybrydowa <math>\mathbf{H}\,</math>, wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych <math>\mathbf{H}\,</math> wszystkich czwórników występujących w połączeniu. | | Przy większej liczbie czwórników połączonych szeregowo-równolegle macierz hybrydowa <math>\mathbf{H}\ </math>,, wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych <math>\mathbf{H}\ </math>, wszystkich czwórników występujących w połączeniu. |
|
| |
|
| : <math>\mathbf{H}=\sum_{i=1}^n \mathbf{H}_i</math> | | : <math>\mathbf{H}=\sum_{i=1}^n \mathbf{H}_i</math> |
| Linia 456: |
Linia 456: |
| Na rysunku obok przedstawiono układ dwu czwórników połączonych równolegle-szeregowo (równolegle po stronie zacisków wejściowych i szeregowo po stronie zacisków wyjściowych), spełniający powyższe warunki. | | Na rysunku obok przedstawiono układ dwu czwórników połączonych równolegle-szeregowo (równolegle po stronie zacisków wejściowych i szeregowo po stronie zacisków wyjściowych), spełniający powyższe warunki. |
|
| |
|
| Łatwo jest pokazać, że w połączeniu równolegle-szeregowym czwórników macierz hybrydowa odwrotna <math>\mathbf{G}\,</math> połączenia jest równa sumie macierzy hybrydowych <math>G\,</math> każdego czwórnika. Oznacza to, że | | Łatwo jest pokazać, że w połączeniu równolegle-szeregowym czwórników macierz hybrydowa odwrotna <math>\mathbf{G}\ </math>, połączenia jest równa sumie macierzy hybrydowych <math>G\ </math>, każdego czwórnika. Oznacza to, że |
|
| |
|
| : <math>\mathbf{G}=\mathbf{G}_1+\mathbf{G}_2</math> | | : <math>\mathbf{G}=\mathbf{G}_1+\mathbf{G}_2</math> |
|
| |
|
| Przy większej liczbie czwórników połączonych równolegle-szeregowo macierz hybrydowa odwrotna <math>\mathbf{G}\,</math>, wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych <math>\mathbf{G}\,</math> wszystkich czwórników występujących w połączeniu. | | Przy większej liczbie czwórników połączonych równolegle-szeregowo macierz hybrydowa odwrotna <math>\mathbf{G}\ </math>,, wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych <math>\mathbf{G}\ </math>, wszystkich czwórników występujących w połączeniu. |
|
| |
|
| : <math>\mathbf{G}=\sum_{i=1}^n \mathbf{G}_i</math> | | : <math>\mathbf{G}=\sum_{i=1}^n \mathbf{G}_i</math> |
| Linia 530: |
Linia 530: |
| : <math>Z_{we}=sR_z^2C</math> | | : <math>Z_{we}=sR_z^2C</math> |
|
| |
|
| Jest to postać odpowiadająca ogólnemu opisowi impedancji operatorowej cewki <math>Z_L=sL</math>. Zatem układ żyratora obciążonego pojemnością <math>C\,</math> przedstawia sobą cewkę o indukcyjności <math>L\,</math> | | Jest to postać odpowiadająca ogólnemu opisowi impedancji operatorowej cewki <math>Z_L=sL</math>. Zatem układ żyratora obciążonego pojemnością <math>C\ </math>, przedstawia sobą cewkę o indukcyjności <math>L\ </math>, |
|
| |
|
| : <math>L=R_z^2C</math> | | : <math>L=R_z^2C</math> |
| Linia 583: |
Linia 583: |
|
| |
|
|
| |
|
| Parametr <math>K\,</math> (<math>K_i</math> dla konwertera ujemno-impedancyjnego prądu oraz <math>K_u</math> dla konwertera ujemno-impedancyjnego napięcia) jest współczynnikiem przetwarzania bądź prądu bądź napięcia. W konwerterze INIC prąd wejściowy jest proporcjonalny do prądu wyjściowego z ujemnym współczynnikiem proporcjonalności <math>–K_i</math> przy niezmienionej wartości napięcia wejściowego. W konwerterze VNIC napięcie wejściowe jest proporcjonalne do napięcia wyjściowego z ujemnym współczynnikiem proporcjonalności <math>–K_u</math> przy niezmienionym prądzie wejściowym. | | Parametr <math>K\ </math>, (<math>K_i</math> dla konwertera ujemno-impedancyjnego prądu oraz <math>K_u</math> dla konwertera ujemno-impedancyjnego napięcia) jest współczynnikiem przetwarzania bądź prądu bądź napięcia. W konwerterze INIC prąd wejściowy jest proporcjonalny do prądu wyjściowego z ujemnym współczynnikiem proporcjonalności <math>–K_i</math> przy niezmienionej wartości napięcia wejściowego. W konwerterze VNIC napięcie wejściowe jest proporcjonalne do napięcia wyjściowego z ujemnym współczynnikiem proporcjonalności <math>–K_u</math> przy niezmienionym prądzie wejściowym. |
| |} | | |} |
|
| |
|

|
|

|
Definicja czwórnika
Czwórnik jest elementem czterozaciskowym, mającym dwie pary uporządkowanych zacisków, z których jedna para jest wejściem a druga para wyjściem Oznaczenie czwórnika z zaznaczonymi zwrotami prądów i napięć końcówkowych jest przedstawione na rysunku na slajdzie obok. W odniesieniu do wejścia i wyjścia czwórnika musi być spełniony warunek równości prądów:
jak to zaznaczono na rysunku. Sygnały prądu i napięcia po stronie wejściowej oznaczać będziemy ze wskaźnikiem 1, a po stronie wyjściowej – ze wskaźnikiem 2. Przyjmiemy umownie, że oba prądy: na wejściu i wyjściu są zwrócone do prostokąta oznaczającego czwórnik.
W zależności od elementów tworzących obwód, czwórnik może być liniowy (gdy wszystkie elementy obwodu są liniowe) lub nieliniowy. W dalszych rozważaniach ograniczymy się wyłącznie do czwórników liniowych. Czwórnik nazywać będziemy pasywnym, jeśli nie wytwarza energii a jedynie pobiera ją ze źródła zasilającego i przetwarza w określony sposób. Czwórnik złożony z samych elementów pasywnych , , i jest zawsze czwórnikiem pasywnym. Czwórnik pasywny jest zdolny do gromadzenia i rozpraszania energii pobranej ze źródła, może ją również oddawać na zewnątrz, jednak w dowolnej chwili czasowej , energia ta nie może przewyższać energii pobranej. Czwórnik, który nie spełnia powyższych warunków jest czwórnikiem aktywnym (generatorem energii).
|

|
Równania czwórnika
Czwórnik może być scharakteryzowany za pomocą równań liniowych wiążących ze sobą dwie wielkości prądowe i dwie napięciowe dotyczące bramy wejściowej i wyjściowej: , , oraz . W zależności od wyboru zmiennych można wyróżnić 6 podstawowych postaci równań czwórnika. Są to
- postać admitancyjna, w której prądy wejściowy i wyjściowy () są wyrażone w zależności od napięć zewnętrznych ()
- postać impedancyjna, w której napięcia wejściowe i wyjściowe () są wyrażone w zależności od prądów końcówkowych ()
- postać hybrydowa w której para wielkości () jest wyrażona jako funkcja drugiej pary ()
- postać hybrydowa odwrotna w której para wielkości () jest wyrażona jako funkcja drugiej pary ()
- postać łańcuchowa w której para wielkości () dotycząca zacisków wejściowych jest wyrażona jako funkcja drugiej pary () związanej z zaciskami wyjściowymi
- postać łańcuchowa odwrotna w której para wielkości () dotycząca zacisków wyjściowych jest wyrażona jako funkcja drugiej pary () związanej z zaciskami wejściowymi.
|

|
Równanie admitancyjne
Jeżeli za zmienne niezależne przyjmie się napięcia obu bram oraz czwórnik przyjmie opis admitancyjny, który można wyrazić w postaci
Macierz , jest nazywana macierzą admitancyjną a parametry tej macierzy mają interpretację admitancji operatorowych.
Równanie impedancyjne
Jeżeli za zmienne niezależne przyjmie się prądy obu bram oraz , czwórnik przyjmie opis impedancyjny, który można wyrazić w postaci
Macierz , jest nazywana macierzą impedancyjną a parametry tej macierzy mają interpretację impedancji operatorowych. Łatwo jest udowodnić, że macierze impedancyjna i admitancyjna są powiązane relacją
Równanie łańcuchowe
Równanie łańcuchowe czwórnika uzależnia prąd i napięcie na wejściu czwórnika od prądu i napięcia na jego wyjściu
W równaniu tym, inaczej niż w pozostałych opisach, przyjmuje się prąd wypływający z czwórnika, w związku z czym przy założonym na wstępie zwrocie prądu do czwórnika w opisie pojawia się prąd wyjściowy ze znakiem minus. Elementy macierzy łańcuchowej A nazywane są parametrami łańcuchowymi czwórnika.
|

|
Równania hybrydowe
Przy opisie hybrydowym za zmienne niezależne wybiera się prąd wejściowy i napięcie wyjściowe czwórnika. Równanie hybrydowe przyjmuje się w postaci
w której , jest macierzą hybrydową. Jak widać z opisu hybrydowego parametr ma interpretację impedancji a admitancji. Parametry i są bezwymiarowe i wyrażają stosunek odpowiednio dwu napięć i dwu prądów w obwodzie.
Zamieniając zmienne wejściowe i wyjściowe otrzymuje się opis hybrydowy odwrotny czwórnika w postaci
Stanowi on odwrotność opisu hybrydowego macierzą ,. Obie macierze powiązane są następująca relacją
Duża liczba stosowanych opisów macierzowych czwórnika wynika również z faktu, że dla niektórych czwórników pewne opisy mogą nie istnieć. Najbardziej uniwersalne pod tym względem są opisy hybrydowe wykorzystujące macierz , lub ,, które można otrzymać dla większości obwodów elektrycznych.
|

|
Jako przykład wyznaczymy opis czwórnika przedstawionego na rysunku na slajdzie 6. Czwórnik ten nosi nazwę czwórnika typu , i jest jedną z najpopularniejszych struktur czwórnikowych.
Rozwiązanie
Z prawa napięciowego i prądowego Kirchhoffa zastosowanego do obwodu z rysunku można napisać następujące równania
Po podstawieniu równania pierwszego do drugiego otrzymuje się
Jeśli jako opis macierzowy przyjmiemy równanie łańcuchowe to zależności określające prąd wejściowy i napięcie wejściowe w funkcji prądu i napięcia wyjściowego można zapisać w postaci
Macierz łańcuchowa , dana jest więc wzorem
Jeśli jako opis macierzowy przyjmiemy równanie impedancyjne, wówczas z przetworzenia równania łańcuchowego otrzymujemy
Macierz impedancyjna dana jest więc w postaci
Jest to macierz symetryczna, która jest równa macierzy oczkowej obwodu tworzącego analizowany czwórnik.
|

|
Pokażemy związek opisu transmitancyjnego z parametrami macierzowymi czwórnika.
Transmitancja napięciowa
Weźmy pod uwagę transmitancję napięciową, jako stosunek napięcia wyjściowego do napięcia wejściowego w dziedzinie operatorowej przy założeniu zerowego prądu obciążenia czwórnika ()
Z równania łańcuchowego, wobec otrzymujemy
Stąd
O transmitancji napięciowej decyduje jeden parametr łańcuchowy czwórnika. W identyczny sposób uzyskać można relację wiążącą transmitancję napięciową z parametrami dowolnego opisu czwórnikowego. Przykładowo na podstawie opisu admitancyjnego z równania drugiego czwórnika, wobec , wynika
Stąd
|

|
Impedancja wejściowa
Określenie funkcji impedancji wejściowej układu czwórnika wymaga ustalenia przy jakiej impedancji obciążenia badany jest czwórnik. Załóżmy w ogólności obciążenie czwórnika impedancją Zo. Z równań łańcuchowych czwórnika otrzymuje się
gdzie oznacza admitancję obciążenia (odwrotność impedacji , ). Z powyższych równań otrzymuje się
Impedancja wejściowa czwórnika obciążonego jest funkcją wszystkich parametrów łańcuchowych tego czwórnika. Pewne uproszczenia powstają w stanach szczególnych obciążeń. Na przykład w stanie jałowym na zaciskach wyjściowych ()
oraz w stanie zwarcia na wyjściu ()
impedancja wejściowa zależy wyłącznie od dwóch parametrów łańcuchowych. Identyczne zależności określające impedancje wejściową otrzymać można na podstawie dowolnego opisu czwórnikowego.
|

|
Wyznaczyć wyrażenie na transmitancję napięciową i impedancję wejściową czwórnika z poprzedniego przykładu.
Rozwiązanie
Macierz łańcuchowa czwórnika ma postać
Transmitancja napięciowa w stanie jałowym na wyjściu jest więc równa
Wobec braku obciążenia czwórnika przez impedancję nie przepływa prąd, stąd całe napięcie wyjściowe pochodzi z impedancji poprzecznej , (dzielnik impedancyjny).
Impedancja wejściowa czwórnika przy obciążeniu bramy wyjściowej impedancją na podstawie wzoru jest równa
Jest ona funkcją wszystkich parametrów układu oraz impedancji obciążenia.
|

|
Połączenie łańcuchowe, zwane również kaskadowym czwórników to takie połączenie , w którym zaciski wejściowe jednego czwórnika są przyłączone do zacisków wyjściowych poprzedniego. Przykład połączenia łańcuchowego dwu czwórników przedstawiony jest na rysunku obok.
Łatwo jest pokazać, że macierz łańcuchowa , czwórników połączonych kaskadowo jest równa iloczynowi macierzy łańcuchowych poszczególnych czwórników tworzących to połączenie
Przy większej liczbie czwórników połączonych kaskadowo macierz łańcuchowa wypadkowa jest równa iloczynowi macierzy łańcuchowych wszystkich czwórników branych w kolejności ich występowania w łańcuchu.
Należy zwrócić uwagę, że przy mnożeniu macierzy istotna jest kolejność tych macierzy, gdyż w ogólności
|
|
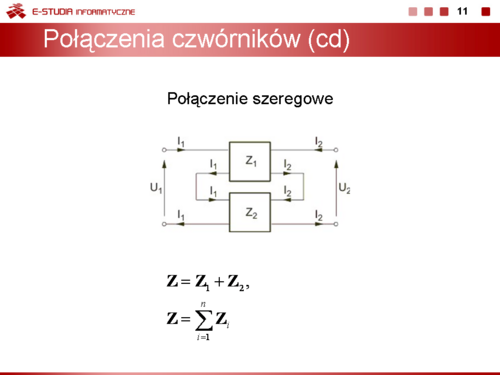
Dwa czwórniki są połączone szeregowo, jeśli spełnione są warunki:
- prąd wejściowy jednego czwórnika jest równy prądowi wejściowemu drugiego a prąd wyjściowy jednego czwórnika jest równy prądowi wyjściowemu drugiego
- napięcie wejściowe (wyjściowe) połączenia jest równe sumie napięć wejściowych (wyjściowych) każdego czwórnika.
Na rysunku obok przedstawiono układ dwu czwórników połączonych szeregowo, spełniający powyższe warunki.
Łatwo jest pokazać, że w połączeniu szeregowym czwórników macierz impedancyjna , połączenia jest równa sumie macierzy impedancyjnych każdego czwórnika. Oznacza to, że
Przy większej liczbie czwórników połączonych szeregowo macierz impedancyjna wypadkowa jest równa sumie macierzy impedancyjnych wszystkich czwórników występujących w połączeniu.
Kolejność sumowania macierzy impedancyjnych nie odgrywa żadnej roli.
|

|
Dwa czwórniki są połączone równolegle, jeśli spełnione są warunki:
- napięcie wejściowe każdego czwórnika jest takie samo, podobnie napięcie wyjściowe
- prąd wejściowy (wyjściowy) połączenia jest równy sumie prądów wejściowych (wyjściowych) każdego czwórnika.
Ponadto w tym przypadku należy zapewnić spełnienie warunków regularności połączenia zdefiniowanych odpowiednią równością prądów.
Na rysunku obok przedstawiono układ dwu czwórników połączonych równolegle, spełniający powyższe warunki.
Łatwo jest pokazać, że w połączeniu równoległym czwórników macierz admitancyjna , połączenia jest równa sumie macierzy admitancyjnych każdego czwórnika. Oznacza to, że
Przy większej liczbie czwórników połączonych równolegle macierz admitancyjna wypadkowa jest równa sumie macierzy admitancyjnych wszystkich czwórników występujących w połączeniu.
Kolejność sumowania macierzy admitancyjnych nie odgrywa żadnej roli.
|
|
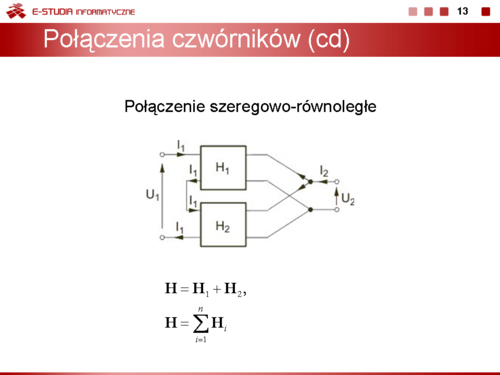
Dwa czwórniki są połączone szeregowo-równolegle, jeśli spełnione są warunki:
- prąd wejściowy każdego czwórnika jest taki sam a napięcie wejściowe połączenia jest równe sumie napięć wejściowych każdego czwórnika
- prąd wyjściowy połączenia jest równy sumie prądów wyjściowych każdego czwórnika a napięcie wyjściowe obu czwórników jest takie samo.
Ponadto w tym przypadku należy zapewnić spełnienie warunku regularności połączenia zdefiniowanego odpowiednią równością prądów.
Na rysunku obok przedstawiono układ dwu czwórników połączonych szeregowo-równolegle (szeregowo po stronie zacisków wejściowych i równolegle po stronie zacisków wyjściowych), spełniający powyższe warunki.
Łatwo jest pokazać, że w połączeniu szeregowo-równoległym czwórników macierz hybrydowa , połączenia jest równa sumie macierzy hybrydowych , każdego czwórnika. Oznacza to, że
Przy większej liczbie czwórników połączonych szeregowo-równolegle macierz hybrydowa ,, wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych , wszystkich czwórników występujących w połączeniu.
Kolejność sumowania macierzy hybrydowych nie odgrywa żadnej roli.
|
|
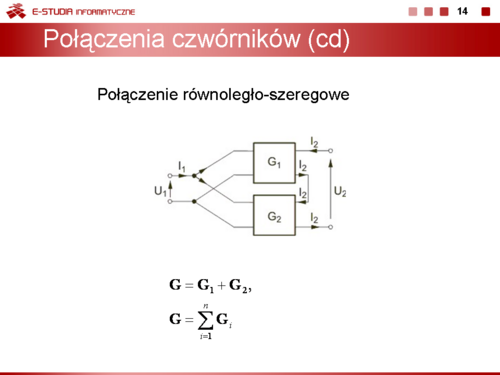
Dwa czwórniki są połączone równolegle-szeregowo, jeśli spełnione są warunki:
- napięcie wejściowe każdego czwórnika jest takie samo a prąd wejściowy połączenia jest równy sumie prądów wejściowych każdego czwórnika
- prąd wyjściowy każdego czwórnika jest taki sam a napięcie wyjściowe połączenia jest równe sumie napięć wyjściowych każdego z nich.
Ponadto w tym przypadku należy zapewnić spełnienie warunku regularności połączenia zdefiniowanego odpowiednią równością prądów.
Na rysunku obok przedstawiono układ dwu czwórników połączonych równolegle-szeregowo (równolegle po stronie zacisków wejściowych i szeregowo po stronie zacisków wyjściowych), spełniający powyższe warunki.
Łatwo jest pokazać, że w połączeniu równolegle-szeregowym czwórników macierz hybrydowa odwrotna , połączenia jest równa sumie macierzy hybrydowych , każdego czwórnika. Oznacza to, że
Przy większej liczbie czwórników połączonych równolegle-szeregowo macierz hybrydowa odwrotna ,, wypadkowa dla całego połączenia jest równa sumie macierzy hybrydowych , wszystkich czwórników występujących w połączeniu.
Kolejność sumowania macierzy nie odgrywa żadnej roli.
|

|
Żyrator
Żyrator jest czwórnikiem opisanym następującą macierzą łańcuchową
Parametr jest nazywany konduktancją żyracji a rezystancją. Oznaczenia graficzne żyratora przedstawione są na rysunku obok.
Znak minus występujący przy prądzie wyjściowym wynika z przyjętego zwrotu prądu wyjściowego (do pudełka). Równaniu łańcuchowemu żyratora odpowiada opis admitancyjny o postaci
Najważniejszą własnością żyratora jest przetwarzanie impedancji obciążenia w impedancję odwrotnie proporcjonalną do niej. Rozważmy układ żyratora obciążonego impedancją .
Impedancja wejściowa takiego układu zdefiniowana w postaci
, , , , więc
|
|
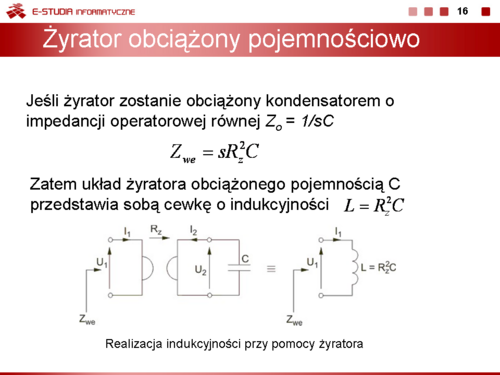
Impedancja układu żyratora obciążonego impedancją jest odwrotnie proporcjonalna do impedancji obciążenia ze współczynnikiem proporcjonalności równym . Jeśli żyrator zostanie obciążony kondensatorem o impedancji operatorowej równej to impedancja wejściowa układu jest równa
Jest to postać odpowiadająca ogólnemu opisowi impedancji operatorowej cewki . Zatem układ żyratora obciążonego pojemnością , przedstawia sobą cewkę o indukcyjności ,
Powyższej zależności matematycznej można przyporządkować transformację układową zilustrowaną na rysunku obok.
Żyrator jako czwórnik jest bardzo łatwo realizowalny w praktyce przy wykorzystaniu układów tranzystorowych lub wzmacniaczy operacyjnych. Z tego względu układy wykorzystujące żyratory są powszechnie stosowane w układach elektronicznych (np. filtrach) eliminując z nich cewki, trudno realizowalne w technologii scalonej.
|

|
Konwerter ujemno-impedancyjny (NIC)
Konwerter ujemno-impedancyjny (NIC) jest czwórnikiem aktywnym (wytwarzającym energię) posiadającym własność przetwarzania prądu bądź napięcia z ujemnym znakiem. Wyróżnia się dwa rodzaje konwerterów ujemno-impedancyjnych
- NIC z inwersją prądu (INIC)
- NIC z inwersją napięcia (VNIC)
Parametr , ( dla konwertera ujemno-impedancyjnego prądu oraz dla konwertera ujemno-impedancyjnego napięcia) jest współczynnikiem przetwarzania bądź prądu bądź napięcia. W konwerterze INIC prąd wejściowy jest proporcjonalny do prądu wyjściowego z ujemnym współczynnikiem proporcjonalności Parser nie mógł rozpoznać (błąd składni): {\displaystyle –K_i}
przy niezmienionej wartości napięcia wejściowego. W konwerterze VNIC napięcie wejściowe jest proporcjonalne do napięcia wyjściowego z ujemnym współczynnikiem proporcjonalności Parser nie mógł rozpoznać (błąd składni): {\displaystyle –K_u}
przy niezmienionym prądzie wejściowym.
|

|
Konwerter impedancyjny przetwarza impedancję obciążenia w impedancję wejściową z ujemnym znakiem. Rozważmy układ konwertera INIC obciążonego impedancją , przedstawiony na rysunku obok.
Wykorzystując równania konwertera i uwzględniając równanie opisujące obciążenie impedancja wejściowa układu dana jest zależnością
Jak z powyższego równania wynika konwerter ujemno-impedancyjny obciążony impedancją reprezentuje sobą (z punktu widzenia wejścia) impedancję ujemną . Podobną własność ma konwerter ujemno-impedancyjny napięcia (VNIC).
Cecha ta może być wykorzystana do realizacji rezystancji ujemnej. Mianowicie przyjmując obciążenie konwertera rezystancją otrzymuje się impedancję wejściową równą . Należy pamiętać, że ujemna rezystancja zastosowana samodzielnie prowadzi do niestabilności układu (wobec ujemnych wartości rezystancji bieguny układu znajdą się w prawej półpłaszczyźnie). Z tego względu stosuje się ją zwykle w specjalnych połączeniach z innymi elementami obwodowymi zapewniającymi stabilne działanie układu.
|
Zadania sprawdzjące
Zadanie 10.1
Wyznaczyć macierzowy opis czwórnikowy czwórnika typu o strukturze podanej na rysunku poniżej.

Rozwiązanie
Układ równań Kirchhoffa opisujących obwód
Równania czwórnikowe
Macierz admitancyjna
Zadanie 10.2
Wyznaczyć macierz łańcuchową czwórnika odpowiadającego obwodowi z rysunku poniżej. Określić na tej podstawie transmitancję napięciową układu.

Rozwiązanie
Z równań Kirchhoffa dla obwodu otrzymuje się
Opis łańcuchowy czwórnika
Transmitancja napięciowa określana przy założeniu jest równa



















