Pr-1st-1.1-m07-Slajd09: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „<math> ” na „<math>” |
||
| (Nie pokazano 1 pośredniej wersji utworzonej przez tego samego użytkownika) | |||
| Linia 6: | Linia 6: | ||
'''Odcięcie''' <math>\mathit{\Psi}</math> zbioru zdarzeń <math>\Lambda</math>' nazwiemy '''odcięciem spójnym''', gdy: | '''Odcięcie''' <math>\mathit{\Psi}</math> zbioru zdarzeń <math>\Lambda</math>' nazwiemy '''odcięciem spójnym''', gdy: | ||
:<math>(E' \in \mathit{\Psi} \land E \mapsto E') \Rightarrow (E \in \mathit{\Psi}) </math> | :<math>(E' \in \mathit{\Psi} \land E \mapsto E') \Rightarrow (E \in \mathit{\Psi})</math> | ||
Definicja ta mówi, że jeżeli jakieś zdarzenie | Definicja ta mówi, że jeżeli jakieś zdarzenie | ||
| Linia 12: | Linia 12: | ||
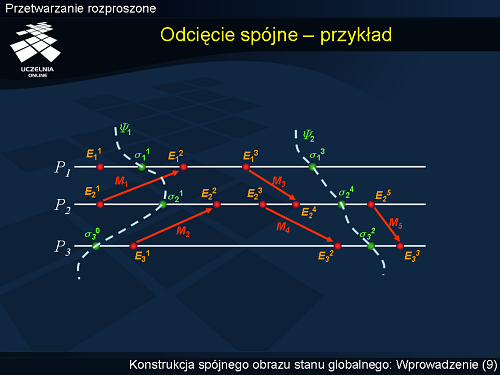
Na rysunku widzimy dwa odcięcia spójne, <math>\mathit{\Psi} _1</math> oraz <math>\mathit{\Psi} _2</math>. Pierwsze z nich obejmuje dwa zdarzenia | Na rysunku widzimy dwa odcięcia spójne, <math>\mathit{\Psi} _1</math> oraz <math>\mathit{\Psi} _2</math>. Pierwsze z nich obejmuje dwa zdarzenia | ||
<math>E_1^1</math> oraz <math>E_2^1</math>. Reprezentuje ono konfigurację, w której wiadomość <math>M1</math> jest w kanale. Drugie jest późniejsze od <math>\mathit{\Psi} _1 </math> | <math>E_1^1</math> oraz <math>E_2^1</math>. Reprezentuje ono konfigurację, w której wiadomość <math>M1</math> jest w kanale. Drugie jest późniejsze od <math>\mathit{\Psi} _1</math> | ||
(<math> \mathit{\Psi} _1 \subseteq \mathit{\Psi} _2</math> – wszystkie zdarzenia należące do <math>\Psi _1</math> należą także do <math>\mathit{\Psi} _2</math>) i obejmuje dodatkowo zdarzenia | (<math>\mathit{\Psi} _1 \subseteq \mathit{\Psi} _2</math> – wszystkie zdarzenia należące do <math>\Psi _1</math> należą także do <math>\mathit{\Psi} _2</math>) i obejmuje dodatkowo zdarzenia | ||
<math>E_1^2 , E_1^3, E_2^2, E_2^3, E_2^4, E_3^1</math> oraz <math>E_3^2</math>. Odcięcie to reprezentuje sytuację, w której wszystkie kanały są puste. Gdyby odcięcie <math>\mathit{\Psi} _1</math> obejmowało dodatkowo zdarzenie <math>E_2^2</math>, nie byłoby odcięciem spójnym, gdyż istniałoby takie zdarzenie (<math>E_3^1</math> ), od którego <math>E_2^2</math> byłoby przyczynowe zależne, które równocześnie nie należałoby do odcięcia | <math>E_1^2 , E_1^3, E_2^2, E_2^3, E_2^4, E_3^1</math> oraz <math>E_3^2</math>. Odcięcie to reprezentuje sytuację, w której wszystkie kanały są puste. Gdyby odcięcie <math>\mathit{\Psi} _1</math> obejmowało dodatkowo zdarzenie <math>E_2^2</math>, nie byłoby odcięciem spójnym, gdyż istniałoby takie zdarzenie (<math>E_3^1</math> ), od którego <math>E_2^2</math> byłoby przyczynowe zależne, które równocześnie nie należałoby do odcięcia | ||
<math>\Psi _1</math> | <math>\Psi _1</math> | ||
Aktualna wersja na dzień 22:16, 11 wrz 2023
Odcięcie spójne (1)
Odcięcie zbioru zdarzeń ' nazwiemy odcięciem spójnym, gdy:
Definicja ta mówi, że jeżeli jakieś zdarzenie ' należy do odcięcia, to także wszystkie zdarzenia od których jest zależne przyczynowo, należą do tego odcięcia.
Na rysunku widzimy dwa odcięcia spójne, oraz . Pierwsze z nich obejmuje dwa zdarzenia oraz . Reprezentuje ono konfigurację, w której wiadomość jest w kanale. Drugie jest późniejsze od ( – wszystkie zdarzenia należące do należą także do ) i obejmuje dodatkowo zdarzenia oraz . Odcięcie to reprezentuje sytuację, w której wszystkie kanały są puste. Gdyby odcięcie obejmowało dodatkowo zdarzenie , nie byłoby odcięciem spójnym, gdyż istniałoby takie zdarzenie ( ), od którego byłoby przyczynowe zależne, które równocześnie nie należałoby do odcięcia
Natomiast rozszerzenie o zdarzenie również byłoby odcięciem spójnym.