PEE Moduł 7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „,...,” na „,\ldots,” |
||
| (Nie pokazano 9 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd1.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd1.png|500px]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 29: | Linia 29: | ||
'''Prawo komutacji dotyczące kondensatorów''' | '''Prawo komutacji dotyczące kondensatorów''' | ||
Suma ładunków kondensatorów dołączonych do danego węzła nie może zmienić się w sposób skokowy na skutek komutacji, co można zapisać w postaci (w równaniu przyjęto, że komutacja zachodzi w chwili <math>t_0=0\ | Suma ładunków kondensatorów dołączonych do danego węzła nie może zmienić się w sposób skokowy na skutek komutacji, co można zapisać w postaci (w równaniu przyjęto, że komutacja zachodzi w chwili <math>t_0=0\ </math>,) | ||
: <math>\Sigma_iq_i(0^-)=\Sigma_iq_i(0^+)</math> | : <math>\Sigma_iq_i(0^-)=\Sigma_iq_i(0^+)</math> | ||
| Linia 41: | Linia 41: | ||
'''Prawo komutacji dotyczące cewek''' | '''Prawo komutacji dotyczące cewek''' | ||
Suma strumieni skojarzonych cewek należących do danego oczka nie może ulec skokowej zmianie na skutek przełączenia w obwodzie, co można zapisać w postaci (w równaniu przyjęto, że komutacja zachodzi w chwili <math>t_0=0\ | Suma strumieni skojarzonych cewek należących do danego oczka nie może ulec skokowej zmianie na skutek przełączenia w obwodzie, co można zapisać w postaci (w równaniu przyjęto, że komutacja zachodzi w chwili <math>t_0=0\ </math>,) | ||
: <math>\Sigma_i\psi_i(0^-)=\Sigma_i\psi_i(0^+)</math> | : <math>\Sigma_i\psi_i(0^-)=\Sigma_i\psi_i(0^+)</math> | ||
| Linia 77: | Linia 77: | ||
: <math>\frac{dx_2}{dt}=a_2_1x_1+a_2_2 x_2+ ...+ a_2_n x_n + f_2(t)</math> | : <math>\frac{dx_2}{dt}=a_2_1x_1+a_2_2 x_2+ ...+ a_2_n x_n + f_2(t)</math> | ||
: <math>\cdots | : <math>\cdots</math> | ||
: <math>\frac{dx_n}{dt}=a_n_1x_1+a_n_2 x_2+ ...+ a_n_n x_n + f_n(t)</math> | : <math>\frac{dx_n}{dt}=a_n_1x_1+a_n_2 x_2+ ...+ a_n_n x_n + f_n(t)</math> | ||
Zmienne <math>x_1, x_2, \cdots, x_n</math> występujące w równaniach oznaczają prądy cewek lub napięcia kondensatorów (tzw. '''zmienne stanu'''). W opisie obwodu operuje się zwykle minimalnym zbiorem zmiennych stanu, które są niezbędne dla wyznaczenia pozostałych wielkości w obwodzie. Liczba zmiennych stanu n zależy od liczby reaktancji w obwodzie i jest najczęściej równa (w szczególnych przypadkach mniejsza) sumie liczby kondensatorów i cewek włączonych w obwodzie. Stałe współczynniki <math>a_i_j\ | Zmienne <math>x_1, x_2, \cdots, x_n</math> występujące w równaniach oznaczają prądy cewek lub napięcia kondensatorów (tzw. '''zmienne stanu'''). W opisie obwodu operuje się zwykle minimalnym zbiorem zmiennych stanu, które są niezbędne dla wyznaczenia pozostałych wielkości w obwodzie. Liczba zmiennych stanu n zależy od liczby reaktancji w obwodzie i jest najczęściej równa (w szczególnych przypadkach mniejsza) sumie liczby kondensatorów i cewek włączonych w obwodzie. Stałe współczynniki <math>a_i_j\ </math>, występujące w równaniu stanowią kombinacje wartości parametrów R, L, C, M elementów pasywnych obwodu oraz parametrów źródeł sterowanych. Funkcje czasu <math>f_1(t), f_2(t), ..., f_n(t)</math> związane są z wymuszeniami napięciowymi i prądowymi w obwodzie. | ||
|} | |} | ||
| Linia 89: | Linia 89: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd5.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd5.png|500px]] | ||
|valign="top"|W przypadku obwodów liniowych funkcje <math>f_i(t)</math> występujące po prawej stronie wzoru są liniowymi funkcjami wymuszeń prądowych i napięciowych. Oznaczając wymuszenia prądowe bądź napięciowe w ogólności przez <math>u_i (i=1, 2, | |valign="top"|W przypadku obwodów liniowych funkcje <math>f_i(t)</math> występujące po prawej stronie wzoru są liniowymi funkcjami wymuszeń prądowych i napięciowych. Oznaczając wymuszenia prądowe bądź napięciowe w ogólności przez <math>u_i (i=1, 2,\ldots,m)</math> można opis stanowy obwodu przedstawić w postaci | ||
: <math>\frac{d\mathbf{x}(t)}{dt}=\mathbf{Ax}(t)+\mathbf{Bu}(t)</math> | : <math>\frac{d\mathbf{x}(t)}{dt}=\mathbf{Ax}(t)+\mathbf{Bu}(t)</math> | ||
gdzie <math>\mathbf{A}\ </math>, jest macierzą stanu o wymiarach <math>n×n\ </math>, zawierającą elementy <math>a_i_j\ </math>,, a macierz <math>\mathbf{B}\ </math>, o wymiarach <math>n×m\ </math>, składa się ze współczynników uzależniających pochodną zmiennych stanu od wektora wymuszeń <math>\mathbf{u}\ </math>,. | |||
gdzie <math>\mathbf{A}\ | |||
Jest to ogólna postać opisu stanowego obwodu liniowego RLC. Reprezentuje ona układ <math>n</math> równań różniczkowych liniowych rzędu pierwszego. Elementy macierzy <math>\mathbf{A}</math> i <math>\mathbf{B}</math> zależą wyłącznie od wartości parametrów obwodu. Elementy wektora u stanowią źródła niezależne prądu i napięcia w obwodzie. Zmienne stanu to niezależne napięcia na kondensatorach i prądy cewek. | Jest to ogólna postać opisu stanowego obwodu liniowego RLC. Reprezentuje ona układ <math>n</math> równań różniczkowych liniowych rzędu pierwszego. Elementy macierzy <math>\mathbf{A}</math> i <math>\mathbf{B}</math> zależą wyłącznie od wartości parametrów obwodu. Elementy wektora u stanowią źródła niezależne prądu i napięcia w obwodzie. Zmienne stanu to niezależne napięcia na kondensatorach i prądy cewek. | ||
Równanie nazywane jest macierzowym równaniem stanu obwodu elektrycznego. Rozwiązanie tego równania pozwala wyznaczyć przebiegi czasowe zmiennych stanu tworzących wektor <math>\mathbf{x}(t)\ | Równanie nazywane jest macierzowym równaniem stanu obwodu elektrycznego. Rozwiązanie tego równania pozwala wyznaczyć przebiegi czasowe zmiennych stanu tworzących wektor <math>\mathbf{x}(t)\ </math>,. Jeśli dodatkowo interesują nas inne zmienne w obwodzie, na przykład prądy i napięcia rezystorów, prądy kondensatorów czy napięcia na cewkach to należy sformułować drugie równanie, tzw. równanie odpowiedzi <math>\mathbf{y}(t)\ </math>,, które uzależnia poszukiwane wielkości od zmiennych stanu i wymuszeń. Równanie to zapiszemy w postaci | ||
: <math>\mathbf{y}(t)=\mathbf{Cx}(t)+\mathbf{Du}(t)</math> | : <math>\mathbf{y}(t)=\mathbf{Cx}(t)+\mathbf{Du}(t)</math> | ||
Równania tworzą parę równań stanu | Równania tworzą parę równań stanu | ||
| Linia 113: | Linia 109: | ||
która w pełni opisuje stan obwodu przy założeniu, że znane są warunki początkowe <math>\mathbf{x}_0=\mathbf{x}(t0)</math>, gdzie <math>t_0\ | która w pełni opisuje stan obwodu przy założeniu, że znane są warunki początkowe <math>\mathbf{x}_0=\mathbf{x}(t0)</math>, gdzie <math>t_0\ </math>, oznacza chwilę przełączenia. W przypadku ogólnym rozwiązanie równania stanu przyjmuje postać | ||
: <math>\mathbf{x}(t)=e^{\mathbf{A}(t-t_0)}\mathbf{x}(t_0)+\int_{t_0}^t e^{\mathbf{A}(t-\tau)}\mathbf{Bu}(\tau)d\tau</math> | : <math>\mathbf{x}(t)=e^{\mathbf{A}(t-t_0)}\mathbf{x}(t_0)+\int_{t_0}^t e^{\mathbf{A}(t-\tau)}\mathbf{Bu}(\tau)d\tau</math> | ||
Zależność powyższa stanowi rozwiązanie ogólne, które dla konkretnych wartości funkcji wymuszających zadanych wektorem u wyznacza rozwiązanie czasowe dla zmiennych stanu. We współczesnych metodach numerycznych równania stanu stanowią punkt wyjścia w określaniu dokładnego rozwiązania równań liniowych lub przybliżonego dla zlinearyzowanych równań stanu. | Zależność powyższa stanowi rozwiązanie ogólne, które dla konkretnych wartości funkcji wymuszających zadanych wektorem u wyznacza rozwiązanie czasowe dla zmiennych stanu. We współczesnych metodach numerycznych równania stanu stanowią punkt wyjścia w określaniu dokładnego rozwiązania równań liniowych lub przybliżonego dla zlinearyzowanych równań stanu. | ||
| Linia 126: | Linia 120: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd6.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd6.png|500px]] | ||
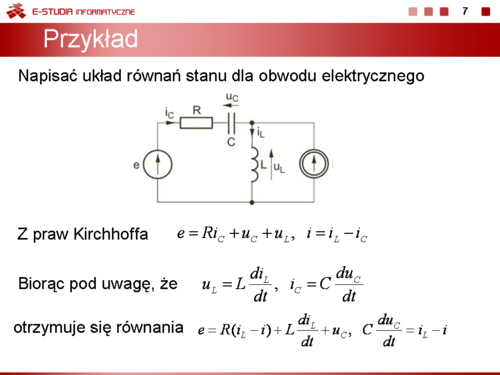
|valign="top"|Kolejny przykład pokazuje jak napisać układ równań stanu dla obwodu elektrycznego. | |valign="top"|Kolejny przykład pokazuje jak napisać układ równań stanu dla obwodu elektrycznego. Z praw Kirchhoffa napisanych dla obwodu z rysunku obok wynikają następujące równania | ||
Z praw Kirchhoffa napisanych dla obwodu z rysunku obok wynikają następujące równania | |||
: <math>e=Ri_C+u_C+u_L</math> | : <math>e=Ri_C+u_C+u_L</math> | ||
: <math>i=i_L=L-i_C</math> | : <math>i=i_L=L-i_C</math> | ||
Biorąc pod uwagę, że | Biorąc pod uwagę, że | ||
: <math>u_L=L\frac{di_L}{dt}</math>, <math>i_C=C\frac{du_C}{dt}</math> | : <math>u_L=L\frac{di_L}{dt}</math>, <math>i_C=C\frac{du_C}{dt}</math> | ||
równania Kirchhoffa można przekształcić do równoważnej postaci równań różniczkowych | równania Kirchhoffa można przekształcić do równoważnej postaci równań różniczkowych | ||
| Linia 146: | Linia 135: | ||
: <math>C\frac{du_C}{dt}=i_L-i</math> | : <math>C\frac{du_C}{dt}=i_L-i</math> | ||
które przyjmują uporządkowaną formę odpowiadającą postaci | które przyjmują uporządkowaną formę odpowiadającą postaci | ||
| Linia 160: | Linia 148: | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd7.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd7.png|500px]] | ||
|valign="top"|Równania powyższe można zapisać w postaci zależności macierzowej równania stanu, w której zmiennymi stanu są prąd cewki i napięcie kondensatora | |valign="top"|Równania powyższe można zapisać w postaci zależności macierzowej równania stanu, w której zmiennymi stanu są prąd cewki i napięcie kondensatora | ||
: <math>\begin{bmatrix}\frac{di_L}{dt}\\ \frac{du_C}{dt}\end{bmatrix}=\begin{bmatrix}\frac{-R}{L}&\frac{-1}{L} \\ \frac{1}{C}& 0\end{bmatrix}\begin{bmatrix}i_L\\u_C\end{bmatrix}+\begin{bmatrix}\frac{1}{L}&\frac{R}{L}\\ 0& \frac{-1}{C}\end{bmatrix}\begin{bmatrix}e\\i\end{bmatrix}</math> | : <math>\begin{bmatrix}\frac{di_L}{dt}\\ \frac{du_C}{dt}\end{bmatrix}=\begin{bmatrix}\frac{-R}{L}&\frac{-1}{L} \\ \frac{1}{C}& 0\end{bmatrix}\begin{bmatrix}i_L\\u_C\end{bmatrix}+\begin{bmatrix}\frac{1}{L}&\frac{R}{L}\\ 0& \frac{-1}{C}\end{bmatrix}\begin{bmatrix}e\\i\end{bmatrix}</math> | ||
Wektor stanu <math>\mathbf{x}</math> oraz wektor wymuszeń <math>\mathbf{u}</math> są równe | Wektor stanu <math>\mathbf{x}</math> oraz wektor wymuszeń <math>\mathbf{u}</math> są równe | ||
: <math>\mathbf{x}=\begin{bmatrix}i_l\\u_C\end{bmatrix}</math>, <math>\mathbf{u}=\begin{bmatrix}e\\i\end{bmatrix}</math> | : <math>\mathbf{x}=\begin{bmatrix}i_l\\u_C\end{bmatrix}</math>, <math>\mathbf{u}=\begin{bmatrix}e\\i\end{bmatrix}</math> | ||
Obwód liniowy zawierający dwa elementy reaktancyjne (cewka i kondensator) opisuje się więc macierzowym równaniem stanu drugiego rzędu. Macierz stanu <math>\mathbf{A}</math> jest macierzą również drugiego rzędu o współczynnikach uzależnionych od wartości rezystancji, pojemności oraz indukcyjności. Macierz <math>\mathbf{B}</math> zawiera dwa wiersze (liczba zmiennych stanu) oraz dwie kolumny (liczba wymuszeń w obwodzie). Przyjmując w analizie wartości liczbowe obwodu: <math>R=2\Omega, L=1H, C=1F</math> otrzymuje się macierz stanu <math>\mathbf{A}</math> o postaci | Obwód liniowy zawierający dwa elementy reaktancyjne (cewka i kondensator) opisuje się więc macierzowym równaniem stanu drugiego rzędu. Macierz stanu <math>\mathbf{A}</math> jest macierzą również drugiego rzędu o współczynnikach uzależnionych od wartości rezystancji, pojemności oraz indukcyjności. Macierz <math>\mathbf{B}</math> zawiera dwa wiersze (liczba zmiennych stanu) oraz dwie kolumny (liczba wymuszeń w obwodzie). Przyjmując w analizie wartości liczbowe obwodu: <math>R=2\Omega, L=1H, C=1F</math> otrzymuje się macierz stanu <math>\mathbf{A}</math> o postaci | ||
: <math>\mathbf{A}=\begin{bmatrix}-2&-1\\1&0\end{bmatrix}</math> | : <math>\mathbf{A}=\begin{bmatrix}-2&-1\\1&0\end{bmatrix}</math> | ||
| Linia 196: | Linia 180: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd9.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd9.png|500px]] | ||
|valign="top"|Składowa przejściowa zależy jedynie od warunków początkowych odniesionych do tej składowej (napięć początkowych kondensatorów i prądów początkowych cewek), struktury obwodu i wartości parametrów tego obwodu. Dla obwodów elektrycznych zawierających elementy rozpraszające energię (rezystancje) składowa przejściowa, jak zostanie pokazane później, zanika z biegiem czasu do zera. Równanie składowej przejściowej otrzymuje się zakładając wymuszenie <math>f(t)\ | |valign="top"|Składowa przejściowa zależy jedynie od warunków początkowych odniesionych do tej składowej (napięć początkowych kondensatorów i prądów początkowych cewek), struktury obwodu i wartości parametrów tego obwodu. Dla obwodów elektrycznych zawierających elementy rozpraszające energię (rezystancje) składowa przejściowa, jak zostanie pokazane później, zanika z biegiem czasu do zera. Równanie składowej przejściowej otrzymuje się zakładając wymuszenie <math>f(t)\ </math>, we wzorze równe zeru i zastępując zmienną <math>x(t)\ </math>, poprzez jej składową przejściową <math>x_p(t)\ </math>, . Otrzymuje się wówczas równanie różniczkowe jednorodne o postaci | ||
| Linia 205: | Linia 189: | ||
: <math>a_ns^n+a_{n-1}s^{n-1}+a_{n-2}s^{n-2}+...+a_1s | : <math>a_ns^n+a_{n-1}s^{n-1}+a_{n-2}s^{n-2}+...+a_1s+a_0=0</math> | ||
Jest to wielomian n-tego rzędu zmiennej zespolonej s o współczynnikach rzeczywistych <math>a_i\ | Jest to wielomian n-tego rzędu zmiennej zespolonej s o współczynnikach rzeczywistych <math>a_i\ </math>, Pierwiastki <math>s_i (i=1, 2,\ldots, n)</math> tego wielomianu stanowią '''bieguny układu'''. | ||
|} | |} | ||
| Linia 219: | Linia 203: | ||
: <math>x_p(t)=\Sigma_{i=1}^n A_i e^{s_it}</math> | : <math>x_p(t)=\Sigma_{i=1}^n A_i e^{s_it}</math> | ||
W rozwiązaniu tym współczynniki <math>A_i\ | W rozwiązaniu tym współczynniki <math>A_i\ </math>, są stałymi całkowania, które należy wyznaczyć wykorzystując znajomość warunków początkowych w obwodzie (napięć kondensatorów i prądów cewek w chwili komutacji <math>t=0\ </math>,). Z ciągłości prądów cewek i napięć kondensatorów wynika następująca zależność | ||
: <math>x(0^-)=x(0^+)</math> | : <math>x(0^-)=x(0^+)</math> | ||
Pisząc tę równość dla wszystkich n zmiennych stanu otrzymuje się n równań algebraicznych z n nieznanymi współczynnikami . Z rozwiązania tego układu wyznacza się wszystkie współczynniki <math>A_i\ | Pisząc tę równość dla wszystkich n zmiennych stanu otrzymuje się n równań algebraicznych z n nieznanymi współczynnikami . Z rozwiązania tego układu wyznacza się wszystkie współczynniki <math>A_i\ </math>, i podstawia do wzoru ogólnego . Po wyznaczeniu rozwiązania obwodu dla składowej ustalonej i przejściowej rozwiązanie całkowite jest sumą obu rozwiązań cząstkowych, to znaczy | ||
<math>x(t)=x_u(t)+x_p(t)</math> | <math>x(t)=x_u(t)+x_p(t)</math> | ||
| Linia 290: | Linia 274: | ||
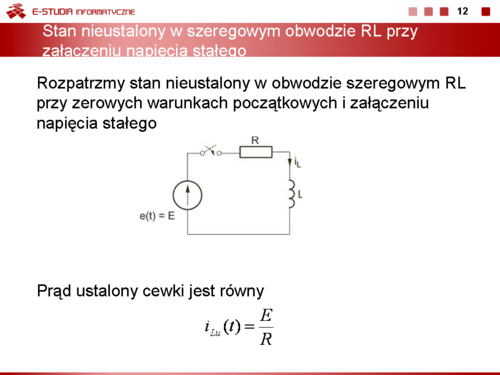
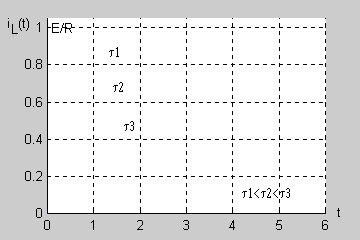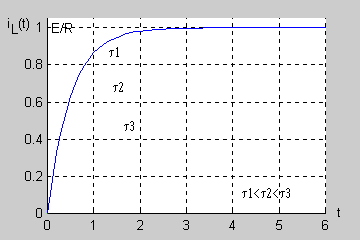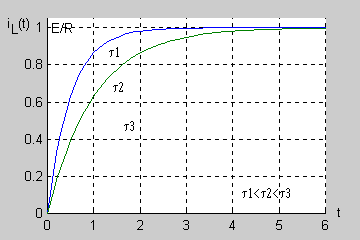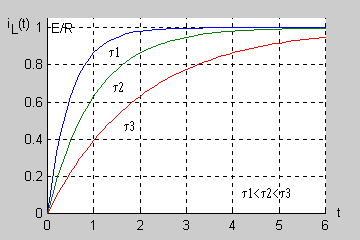
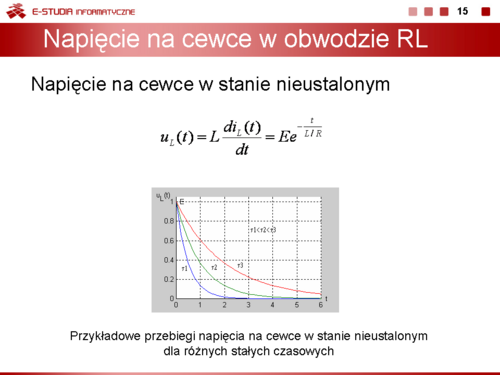
: <math>i_L(t)=\frac{E}{R}(1-e^{-\frac{t}{L/R}})</math> | : <math>i_L(t)=\frac{E}{R}(1-e^{-\frac{t}{L/R}})</math> | ||
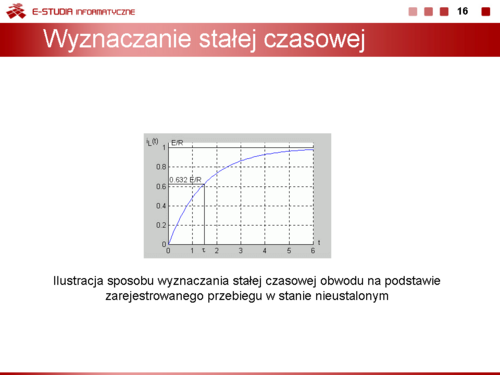
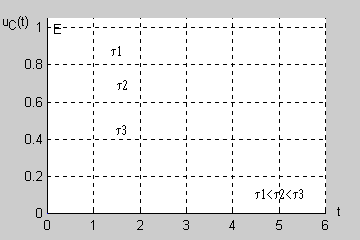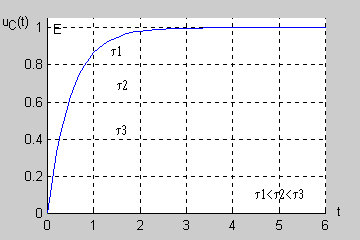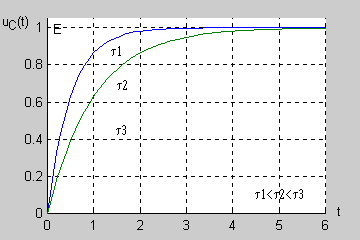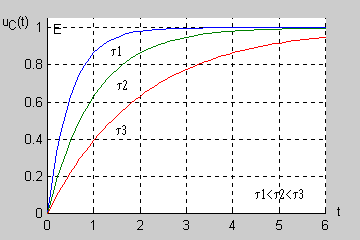
Wprowadzając pojęcie stałej czasowej <math>\tau\ | Wprowadzając pojęcie stałej czasowej <math>\tau\ </math>, obwodu RL | ||
: <math>\tau=\frac{L}{R}</math> | : <math>\tau=\frac{L}{R}</math> | ||
| Linia 320: | Linia 304: | ||
[[Grafika: | [[Grafika:PEE_M7_anim_14xx.gif]] | ||
| Linia 376: | Linia 360: | ||
: <math>u_{Cp}=A_1e^{s_1t}=A_1e^{-\frac{t}{RC}}</math> | : <math>u_{Cp}=A_1e^{s_1t}=A_1e^{-\frac{t}{RC}}</math> | ||
W rozwiązaniu tym współczynnik <math>A_1\ | W rozwiązaniu tym współczynnik <math>A_1\ </math>, jest stałą całkowania, którą należy wyznaczyć korzystając z prawa komutacji. Rozwiązanie całkowite będące sumą składowej ustalonej i przejściowej przybiera więc postać | ||
: <math>u_C(t)=u_{Cu}(t)+u_{Cp}=E+A_1e^{-\frac{t}{RC}}</math> | : <math>u_C(t)=u_{Cu}(t)+u_{Cp}=E+A_1e^{-\frac{t}{RC}}</math> | ||
| Linia 437: | Linia 421: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd19.png|500px]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd19.png|500px]] | ||
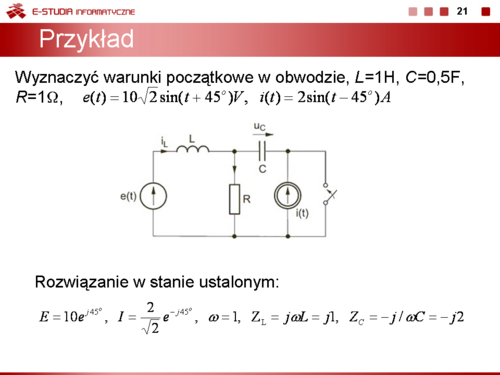
|valign="top"|Wyznaczyć warunki początkowe w obwodzie przedstawionym na rysunku. Parametry elementów obwodu są następujące: <math>L=1H, C=0,5F, R=1\Omega, e(t)=10\sqrt 2 sin( | |valign="top"|Wyznaczyć warunki początkowe w obwodzie przedstawionym na rysunku. Parametry elementów obwodu są następujące: <math>L=1H, C=0,5F, R=1\Omega, e(t)=10\sqrt 2 sin(t+45^o)V, i(t)=2sin(t-45^o)A</math> | ||
| Linia 444: | Linia 428: | ||
: <math>E=10e^{j45^o}</math> | : <math>E=10e^{j45^o}</math> | ||
: <math>I=\frac{2}{\sqrt 2}e^{- | : <math>I=\frac{2}{\sqrt 2}e^{-j45^o}</math> | ||
: <math>\omega=1</math> | : <math>\omega=1</math> | ||
| Linia 463: | Linia 447: | ||
: <math>I_L=\frac{E-RI}{R+Z_L}=7,21e^{j11,31^o}</math> | : <math>I_L=\frac{E-RI}{R+Z_L}=7,21e^{j11,31^o}</math> | ||
: <math>U_C=Z_CI=\frac{4}{\sqrt 2}e^{-j135^ | : <math>U_C=Z_CI=\frac{4}{\sqrt 2}e^{-j135^o}</math> | ||
Aktualna wersja na dzień 21:56, 15 wrz 2023

|

|
Równania obwodu w stanie ustalonym
|
| Zadania sprawdzające
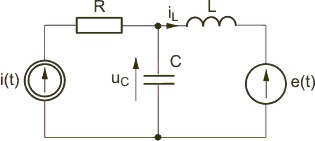
Napisać równanie stanu dla obwodu o strukturze przedstawionej na rysunku
Z praw Kirchhoffa napisanych dla obwodu z rysunku wynika
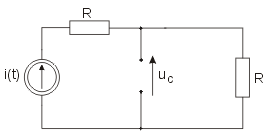
Zadanie 7.2 Określić przebieg czasowy napięcia na kondensatorze w stanie nieustalonym w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów: .
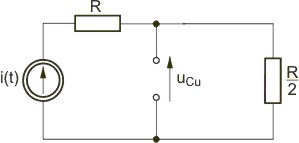
Warunki początkowe w obwodzie wynikają ze stanu ustalonego obwodu przed przełączeniem, który wobec wymuszenia stałego ma postać uproszczoną przedstawioną na rysunku Schemat obwodu w stanie ustalonym przed przełączeniem dla wymuszenia stałego
Schemat obwodu w stanie ustalonym po przełączeniu
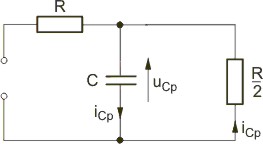
Schemat obwodu w stanie przejściowym po przełączeniu
Stała czasowa obwodu jest więc równa . |