Matematyka dyskretna 1/Ćwiczenia 13: Grafy II: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „,↵</math>” na „</math>,” |
|||
| (Nie pokazano 20 wersji utworzonych przez 3 użytkowników) | |||
| Linia 2: | Linia 2: | ||
{{cwiczenie|1|cw 1| | {{cwiczenie|1|cw 1| | ||
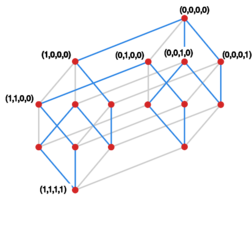
Kostka <math> | Kostka <math>k</math> -wymiarowa <math>\mathcal{Q}_{k}</math> jest grafem, | ||
którego wierzchołki to ciągi <math> | którego wierzchołki to ciągi <math>\left( a_1,a_2,\ldots,a_k \right)</math> , gdzie <math>a_i=0,1</math> , | ||
a krawędzie łączą te ciągi, które różnią się tylko na jednej pozycji. | a krawędzie łączą te ciągi, które różnią się tylko na jednej pozycji. | ||
Oblicz liczbę wierzchołków, krawędzi oraz rozmiar najdłuższego cyklu. | Oblicz liczbę wierzchołków, krawędzi oraz rozmiar najdłuższego cyklu. | ||
| Linia 10: | Linia 10: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Aby znaleźć liczbę wierzchołków policz liczbę <math> | Aby znaleźć liczbę wierzchołków policz liczbę <math>k</math> -elementowych ciągów złożonych | ||
z <math> | z <math>0</math> i <math>1</math> . | ||
Przy znalezieniu liczby krawędzi przydatna będzie znajomość stopnia wierzchołków. | Przy znalezieniu liczby krawędzi przydatna będzie znajomość stopnia wierzchołków. | ||
Najdłuższy cykl, to cykl przechodzący przez wszystkie wierzchołki. | Najdłuższy cykl, to cykl przechodzący przez wszystkie wierzchołki. | ||
Konstrukcję takiego cyklu przeprowadź indukcyjnie ze względu na <math> | Konstrukcję takiego cyklu przeprowadź indukcyjnie ze względu na <math>k</math> . | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
[[File:Cw grafy 4kostka.svg|350x250px|thumb|right" id="cw_grafy_4kostka|Cykl <math>16</math> -elementowy w kostce <math>\mathcal{Q}_{4}</math>]] | |||
* Wierzchołki <math>\mathsf{ V}\!\left(\mathcal{Q}_{k}\right)</math> odpowiadają ciągom <math>\left( a_1,a_2,\ldots,a_k \right)</math> , gdzie <math>a_i=0,1</math>. Liczba <math>k</math> -elementowych ciągów liczb z dwuelementowego zbioru wynosi <math>2^k</math> . | |||
* Z kolei krawędzie łączą te ciągi, które różnią się na jednej tylko pozycji. Ciąg ze względu na konkretną pozycję jest sąsiedni z dokładnie jednym ciągiem. Stopień dowolnego wierzchołka równy jest więc <math>k</math>. Ponieważ każda krawędź ma dwa końce, to liczba wszystkich krawędzi jest równa <math>\frac{k\cdot 2^k}{2}=k\cdot 2^{k-1}</math> . | |||
* Najdłuższy cykl w <math>\mathcal{Q}_{k}</math> jest cyklem przechodzącym przez wszystkie wierzchołki. Wykażemy jego istnienie indukcyjnie ze względu na <math>k</math> , pokazując ścieżkę z wierzchołka <math>\left( 0,0,\ldots,0 \right)</math> do <math>\left( 1,0,\ldots,0 \right)</math> , przechodzącą przez wszystkie wierzchołki. | |||
<center><math>\ | Kostkę <math>\mathcal{Q}_{k+1}</math> można rozłożyć na dwie kostki w ten sposób, że w pierwszej znajdą się wszystkie wierzchołki odpowiadające ciągom zaczynającym się od <math>0</math> , czyli <math>\left( 0,a_2,\ldots,a_{k+1} \right)</math> , | ||
a w drugiej wierzchołki odpowiadające ciągom zaczynającym się od <math>1</math> , czyli <math>\left( 1,a_2,\ldots,a_{k+1} \right)</math> . Na mocy założenia indukcyjnego otrzymujemy ścieżkę z wierzchołka <math>\left( 0,0,0,\ldots,0 \right)</math> do <math>\left( 0,1,0,\ldots,0 \right)</math> , przechodzącą przez wszystkie wierzchołki pierwszej kostki. Analogicznie otrzymujemy także ścieżkę z wierzchołka <math>\left( 1,0,0,\ldots,0 \right)</math> do <math>\left( 1,1,0,\ldots,0 \right)</math> , przechodzącą przez wszystkie wierzchołki drugiej kostki. Po złożeniu obu ścieżek w ścieżkę postaci | |||
<center><math>\begin{align} \left( 0,0,0,\ldots,0 \right)\to\ldots\to\left( 0,1,0,\ldots,0 \right)\to\left( 1,1,0,\ldots,0 \right)\to\ldots&&\\ | |||
\ldots\to\left( 1,0,0,\ldots,0 \right)&& | \ldots\to\left( 1,0,0,\ldots,0 \right)&& | ||
\ | \end{align}</math></center> | ||
otrzymujemy szukaną ścieżkę. W konsekwencji otrzymujemy, że najdłuższa ścieżka <math>\mathcal{Q}_{k}</math> | |||
składa się ze wszystkich <math>2^k</math> wierzchołków. | |||
</div></div> | </div></div> | ||
{{cwiczenie|2|cw 2| | {{cwiczenie|2|cw 2| | ||
Dla jakich wartości <math> | Dla jakich wartości <math>n</math> grafy <math>\mathcal{K}_{n}</math> , <math>\mathcal{K}_{n,m}</math> , <math>\mathcal{Q}_{n}</math> są eulerowskie. | ||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Skorzystaj z twierdzenia | Skorzystaj z twierdzenia [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.1|13.1]]. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Korzystając z twierdzenia | Korzystając z twierdzenia [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.1|13.1]] otrzymujemy warunek, że każdy graf eulerowski musi posiadać jedynie wierzchołki o stopniu parzystym. | ||
otrzymujemy warunek, że każdy graf eulerowski musi posiadać jedynie wierzchołki | * W klice <math>\mathcal{K}_{n}</math> , każdy wierzchołek ma stopień równy <math>n-1</math> , więc eulerowskimi są jedynie kliki <math>\mathcal{K}_{2k+1}</math> o <math>2k+1</math> wierzchołkach, gdzie <math>k=0,1,2,\ldots</math> . | ||
o stopniu parzystym. | * W pełnym grafie dwudzielnym <math>\mathcal{K}_{n,m}</math> wierzchołki mają stopnie równe <math>n</math> lub <math>m</math> . Wsród pełnych grafów dwudzielnych eulerowskie są jedynie grafy <math>\mathcal{K}_{2k,2l}</math> dla <math>k,l=0,1,2,\ldots</math> . | ||
* W klice <math> | * W kostce <math>\mathcal{Q}_{n}</math> każdy wierzchołek ma <math>n</math> sąsiadów, więc eulerowskie są kostki <math>\mathcal{Q}_{2k}</math> dla <math>k=0,1,2,\ldots</math> . | ||
każdy wierzchołek ma stopień równy <math> | |||
więc eulerowskimi są jedynie kliki <math> | |||
gdzie <math> | |||
* W pełnym grafie dwudzielnym <math> | |||
wierzchołki mają stopnie równe <math> | |||
Wsród pełnych grafów dwudzielnych eulerowskie są jedynie grafy | |||
dla <math> | |||
* W kostce <math> | |||
więc eulerowskie są kostki | |||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|3|cw 3| | ||
Przedstaw cztery pięciowierzchołkowe grafy -- kolejno graf który: | Przedstaw cztery pięciowierzchołkowe grafy -- kolejno graf który: | ||
* nie jest hamiltonowski i nie jest eulerowski | * nie jest hamiltonowski i nie jest eulerowski | ||
| Linia 83: | Linia 70: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
<div class="thumb tright" id="cw_grafy_eul_ham"><div style="width:250px;"> | |||
<flash>file=Cw grafy eul ham.swf|width=250|height=200</flash> | |||
<div.thumbcaption>Przykłady na: graf niehamiltonowski i nieeulerowski(a), | |||
graf niehamiltonowski ale eulerowskim (b), | graf niehamiltonowski ale eulerowskim (b), | ||
graf hamiltonowski lecz nieeulerowski (c), | graf hamiltonowski lecz nieeulerowski (c), | ||
oraz graf eulerowski będący zarazem hamiltonowskim (d) | oraz graf eulerowski będący zarazem hamiltonowskim (d)</div></div> | ||
</div> | |||
Rozwiązanie jest przedstawione na [[#cw grafy eul ham|rysunku]]. | |||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|4|cw 4| | ||
Dla jakich wartości <math>n</math> grafy <math>\mathcal{K}_{n}</math> , <math>\mathcal{K}_{n,m}</math> , <math>\mathcal{Q}_{n}</math> | |||
Dla jakich wartości <math> | |||
są hamiltonowskie. | są hamiltonowskie. | ||
| Linia 103: | Linia 90: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Wyciągnij wnioski o liczności <math> | Wyciągnij wnioski o liczności <math>V_1</math> oraz <math>V_2</math> z istnienia cyklu Hamiltona | ||
w grafie <math> | w grafie <math>\mathcal{K}_{n,m}=\left( V_1\cup V_2,E \right)</math> . | ||
W odpowiedzi na pytanie, które kostki posiadają cykl Hamiltona, | W odpowiedzi na pytanie, które kostki posiadają cykl Hamiltona, | ||
wróć do ćwiczenia [[# | wróć do ćwiczenia [[#cw_3|1]]. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
* Każda klika <math> | * Każda klika <math>n\geq 3</math> elementowa jest hamiltonowska, ponieważ w klice dowolne dwa elementy są połączone krawędzią, | ||
ponieważ w klice dowolne dwa elementy są połączone krawędzią, | dowolny ciąg wszystkich elementów tworzy więc cykl. | ||
* W pełnym grafie dwudzielnym <math>\mathbf{G}=\left( V_1\cup V_2,E \right)</math> dowolna ścieżka ma na przemian wierzchołki ze zbiorów <math>V_1</math> oraz <math>V_2</math>, tzn. ścieżka ma postać | |||
* W pełnym grafie dwudzielnym <math> | |||
dowolna ścieżka ma na przemian wierzchołki ze zbiorów <math> | |||
tzn. | <center><math>v_1\to v_2\to v_3\to \ldots v_k\to v_1</math>,</center> | ||
gdzie <math> | gdzie <math>v_1, v_3, v_5,\ldots\in V_1</math> , zaś <math>v_2, v_4, v_6,\ldots\in V_2</math> . | ||
Jeżeli skojarzymy wierzchołek <math> | Jeżeli skojarzymy wierzchołek <math>v_1</math> z wierzchołkiem <math>v_2</math> , | ||
wierzchołek <math> | wierzchołek <math>v_3</math> z wierzchołkiem <math>v_4</math> | ||
i w ogólności <math> | i w ogólności <math>v_{2j+1}</math> z <math>v_{2j+2}</math> , | ||
to wykorzystamy wszystkie wierzchołki grafu <math> | to wykorzystamy wszystkie wierzchołki grafu <math>\mathbf{G}</math> . | ||
Skonstruowane zostało skojarzenie wierzchołków z <math> | Skonstruowane zostało skojarzenie wierzchołków z <math>V_1</math> z wierzchołkami z <math>V_2</math> | ||
wykorzystujące wszystkie wierzchołki, więc <math> | wykorzystujące wszystkie wierzchołki, więc <math>\left\vert V_1 \right\vert=\left\vert V_2 \right\vert</math> . | ||
Pełny graf dwudzielny <math> | Pełny graf dwudzielny <math>\mathcal{K}_{n,m}</math> jest więc hamiltonowski | ||
wtedy i tylko wtedy, gdy <math> | wtedy i tylko wtedy, gdy <math>n=m</math> . | ||
* Ścieżka o maksymalnej długości znaleziona w ćwiczeniu [[# | * Ścieżka o maksymalnej długości znaleziona w ćwiczeniu [[#wc_1|1]] jest ścieżką Hamiltona. Otrzymujemy więc wniosek, że każda kostka jest grafem hamiltonowskim. | ||
jest ścieżką Hamiltona. | |||
Otrzymujemy więc wniosek, że każda kostka jest grafem hamiltonowskim. | |||
</div></div> | </div></div> | ||
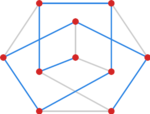
[[File:Cw grafy petersen.svg|150x150px|thumb|right" id="cw grafy petersen 2|Graf Petersena]] | |||
Czy graf Petersena (patrz | {{cwiczenie|5|cw 5| | ||
Czy graf Petersena (patrz [[#cw grafy petersen 2|rysunek]]) ma ścieżkę Hamiltona. | |||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | |||
[[File:Cw grafy petersen ham.svg|150x150px|thumb|right" id="cw_grafy_petersen_ham|Ścieżka Hamiltona w grafie Petersena]] | |||
Ścieżka Hamiltona w grafie Petersena została przedstawiona na | |||
[[#cw grafy petersen ham|rysunku]]. | |||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|6|cw 6| | ||
Podaj przykład grafu ilustrujący, że warunek <math>\deg{v}\geq n/2</math> | |||
Podaj przykład grafu ilustrujący, że warunek <math> | występujący w Twierdzeniu Diraca [[Matematyka dyskretna 1/Wykład 13: Grafy II#wn_13.5|13.5]] | ||
występujący w Twierdzeniu Diraca | nie może być zastąpiony warunkiem <math>\deg{v}\geq n/2-1</math> . | ||
nie może być zastąpiony warunkiem <math> | |||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Przeanalizuj dowód twierdzenia Ore'a (patrz tw. | Przeanalizuj dowód twierdzenia Ore'a (patrz tw. [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.4|13.4]]). | ||
W którym miejscu załamałby się ten dowód, | W którym miejscu załamałby się ten dowód, | ||
gdyby istniały wierzchołki <math> | gdyby istniały wierzchołki <math>v,w</math> takie, że <math>\deg{v}+\deg{w}= n-1</math> . | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
[[File:Cw grafy kontr dirac.svg|250x100px|thumb|right" id="cw_grafy_kontr_dirac|Kontrprzykład do zmodyfikowanego twierdzenia Diraca]] | |||
Jeżeli w wypowiedzi Twierdzenia Diraca, | Jeżeli w wypowiedzi Twierdzenia Diraca, | ||
warunek <math> | warunek <math>\deg{v}\geq n/2</math> zastąpimy warunkiem <math>\deg{v}\geq n/2-1</math> , | ||
to tak zmodyfikowane zdanie | to tak zmodyfikowane zdanie | ||
ma kontrprzykład przedstawiony na | ma kontrprzykład przedstawiony na [[#cw grafy kontr dirac|rysunku]]. | ||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|7|cw 7| | ||
Wykaż, że <math>n</math> elementowy <math>\mathbf{G}</math> jest hamiltonowski jeśli tylko | |||
Wykaż, że <math> | ma przynajmniej <math>\left( n-1 \right)\left( n-2 \right)/2+2</math> krawędzi. | ||
ma przynajmniej <math> | Podaj przykład grafu niehamiltonowskiego z <math>n</math> wierzchołkami | ||
Podaj przykład grafu niehamiltonowskiego z <math> | i <math>\left( n-1 \right)\left( n-2 \right)/2+1</math> krawędziami. | ||
i <math> | |||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Skorzystaj z Twierdzenia Ore'a (patrz tw. | Skorzystaj z Twierdzenia Ore'a (patrz tw. [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.4|13.4]]). | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
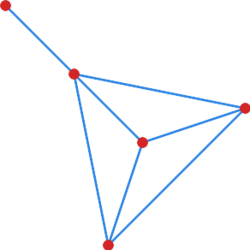
< | [[File:Cw grafy kontr moc v.svg|250x250px|thumb|right" id="cw_grafy_kontr_moc_v|Graf o <math>5</math> wierzchołkach i <math>7</math> krawędziach, ale bez cyklu Hamiltona]] | ||
< | |||
Niech <math>u</math> i <math>v</math> będą niesąsiednimi wierzchołkami grafu <math>\mathbf{G}</math> . | |||
Dopełnienie grafu <math>\mathbf{G}</math> posiada co najwyżej | |||
Dopełnienie grafu <math> | |||
<center><math>\ | <center> | ||
</math></center> | <math>\frac{n\left( n-1 \right)}{2}-\left( \frac{\left( n-1 \right)\left( n-2 \right)}{2}-2 \right)=n-3 | ||
</math> | |||
</center> | |||
krawędzi, więc <math>u</math> i <math>v</math> | |||
więc | mogą być incydentne w sumie z co najwyżej <math>n-3</math> krawędziami w <math>\overline{\mathbf{G}}</math> . | ||
Liczba krawędzi incydentnych z <math>u</math> lub <math>v</math> | |||
w grafie pełnym <math>\left( \mathsf{ V}\!\left(\mathbf{G}\right),\mathcal{P}_{2}\!\left( \mathsf{ V}\!\left(\mathbf{G}\right) \right) \right)</math> , | |||
jest równa <math>2n-3</math> . | |||
Dopełnienie grafu <math>\mathbf{G}</math> jest to graf postaci | |||
<math>\overline{\mathbf{G}}=\left( \mathsf{ V}\!\left(\mathbf{G}\right),\mathcal{P}_{2}\!\left( \mathsf{ V}\!\left(\mathbf{G}\right) \right)-\mathsf{ E}\!\left(\mathbf{G}\right) \right)</math> , | |||
więc liczba krawędzi incydentnych z <math>u</math> lub <math>v</math> to co najmniej | |||
<center><math>\ | <center> | ||
</math></center> | <math>\left( 2n-3 \right)-\left( n-3 \right)=n</math> | ||
</center> | |||
Wierzchołki <math>u</math> i <math>v</math> nie sąsiadują ze sobą, | |||
więc zbiory incydentnych krawędzi są rozłączne, co w konsekwencji daje że | |||
<center> | |||
<math>\mathsf{ deg}\ u+\mathsf{ deg}\ v\geq n</math> | |||
</center> | |||
[ | Na mocy więc Twierdzenia Ore'a (patrz tw. [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.4|13.4]]) otrzymujemy, że <math>\mathbf{G}</math> jest hamiltonowski. | ||
Wartość <math>\left( n-1 \right)\left( n-2 \right)/2+2</math> jest najmniejszą taką liczbą, że każdy graf o <math>n</math> wierzchołkach i co najmniej tylu krawędziach jest hamiltonowski. Graf o <math>n=5</math> wierzchołkach i <math>\left( n-1 \right)\left( n-2 \right)/2+1=7</math> krawędziach, który nie jest hamiltonowski jest przedstawiony na rysunku [[#cw grafy kontr moc v|6]]. | |||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|8|cw 8| | ||
Wykaż, że każde drzewo jest grafem dwudzielnym. | Wykaż, że każde drzewo jest grafem dwudzielnym. | ||
Które drzewa są pełnymi grafami dwudzielnymi? | Które drzewa są pełnymi grafami dwudzielnymi? | ||
| Linia 245: | Linia 215: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Dla drzewa <math> | Dla drzewa <math>T=\left( V,E \right)</math> wybierz dowolny wierzchołek <math>v\in V</math> | ||
i zdefiniuj odpowiedni podział <math> | i zdefiniuj odpowiedni podział <math>V=V_1\cup V_2</math> korzystając z parzystości | ||
odległości od <math> | odległości od <math>v</math> . | ||
Kiedy pełny graf dwudzielny nie ma cykli? | Kiedy pełny graf dwudzielny nie ma cykli? | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math> | Niech <math>T=\left( V,E \right)</math> będzie drzewem a | ||
<math> | <math>v\in V</math> dowolnie wybranym jego wierzchołkiem. | ||
Podzielimy zbiór <math> | Podzielimy zbiór <math>V</math> na wierzchołki, które: | ||
* są oddalone od <math> | * są oddalone od <math>v</math> o odległość będącą liczbą parzystą - wraz z <math>v</math> będą tworzyć zbiór <math>V_1</math> , | ||
wraz z <math> | * są oddalone od <math>v</math> o odległość będącą liczbą nieparzystą - te z kolei będą składać się na zbiór <math>V_2</math> . | ||
* są oddalone od <math> | |||
te z kolei będą składać się na zbiór <math> | |||
W drzewie pomiędzy dowolnymi wierzchołkami istnieje dokładnie jedna ścieżka, | W drzewie pomiędzy dowolnymi wierzchołkami istnieje dokładnie jedna ścieżka, | ||
tak więc ścieżka świadcząca o odległości wierzchołka <math> | tak więc ścieżka świadcząca o odległości wierzchołka <math>w</math> od wierzchołka <math>v</math> jest jedyną ścieżką pomiędzy <math>v</math> a <math>w</math> . Niech <math>ux\in E</math> dla wierzchołków <math>u,x\in V_i</math>. Ścieżka | ||
jest jedyną ścieżką pomiędzy <math> | |||
Niech <math> | |||
<center><math>v\to\ldots\to u\to x</math>,</center> | |||
ma długość innej parzystości niż ścieżka | ma długość innej parzystości niż ścieżka | ||
co przeczy temu, że <math> | <center><math>v\to\ldots\to u</math>,</center> | ||
co przeczy temu, że <math>u</math> oraz <math>v</math> są razem w jednym zbiorze <math>V_i</math> . | |||
''Drzewo jest pełnym grafem dwudzielnym wtedy i tylko wtedy gdy jest gwiazdą.'' | ''Drzewo jest pełnym grafem dwudzielnym wtedy i tylko wtedy gdy jest gwiazdą.'' | ||
Istotnie, gwiazda o <math> | Istotnie, gwiazda o <math>n</math> liściach jest pełnym grafem dwudzielnym <math>\mathcal{K}_{1,n}</math> . | ||
Z drugiej strony załóżmy, że drzewo <math> | Z drugiej strony załóżmy, że drzewo <math>\mathbf{T}=\left( V_1\cup V_2, E \right)</math> | ||
jest pełnym grafem dwudzielnym, ale nie jest gwiazdą, | jest pełnym grafem dwudzielnym, ale nie jest gwiazdą, | ||
czyli zawiera ścieżkę o długości <math> | czyli zawiera ścieżkę o długości <math>3</math> , np.: | ||
<center><math>u\to v\to w\to x</math></center> | |||
Bez straty ogólności załóżmy, że <math>u\in V_1</math> , | |||
tak więc <math>v,x\in V_2</math> oraz <math>w\in V_1</math> . | |||
W pełnym grafie dwudzielnym istnieje więc krawędź łącząca wierzchołek <math>x\in V_2</math> | |||
z wierzchołkiem <math>u\in V_1</math> . Mam więc cykl postaci: | |||
<center><math>u\to v\to w\to x\to u</math>,</center> | |||
co przeczy temu, że <math> | co przeczy temu, że <math>\mathbf{T}</math> jest drzewem. | ||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|9|cw 9| | ||
Udowodnij wierzchołkową wersję Twierdzenia Mengera. | Udowodnij wierzchołkową wersję Twierdzenia Mengera. | ||
| Linia 303: | Linia 271: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Naśladuj dowód Twierdzenia | Naśladuj dowód Twierdzenia [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.8|13.8]]. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math> | Niech <math>w</math> , <math>u</math> będą dwoma różnymi i niesąsiednimi wierzchołkami spójnego grafu | ||
<math> | <math>\mathbf{G} = \left( V,E \right)</math> . | ||
Przez <math> | Przez <math>k</math> oznaczmy najmniejszą możliwą | ||
liczność zbioru wierzchołków rozdzielających <math> | liczność zbioru wierzchołków rozdzielających <math>w</math> , <math>u</math> . | ||
Oczywiście każda droga łącząca <math> | Oczywiście każda droga łącząca <math>w</math> z <math>u</math> | ||
musi przejść przez każdy zbiór rozdzielający. | musi przejść przez każdy zbiór rozdzielający. | ||
A zatem dróg wierzchołkowo rozłącznych łączących <math> | A zatem dróg wierzchołkowo rozłącznych łączących <math>w</math> z <math>u</math> | ||
nie może być więcej niż <math> | nie może być więcej niż <math>k</math> . | ||
Tak więc wystarczy pokazać, | Tak więc wystarczy pokazać, | ||
że istnieje <math> | że istnieje <math>k</math> rozłącznych wierzchołkowo dróg z <math>w</math> do <math>u</math> . | ||
Dowód przeprowadzimy indukcyjnie ze względu na liczbę wierzchołków w grafie | Dowód przeprowadzimy indukcyjnie ze względu na liczbę wierzchołków w grafie <math>\mathbf{G}</math> rozważając dwa przypadki. | ||
<math> | ;1. Pewien zbiór rozdzielający <math>X</math> mocy <math>k</math> ma wierzchołek niesąsiedni z <math>w</math> oraz ma wierzchołek (być może inny) niesąsiedni z <math>u</math> . | ||
ma wierzchołek niesąsiedni z <math> | |||
oraz ma wierzchołek (być może inny) niesąsiedni z <math> | |||
Graf <math> | Graf <math>\mathbf{G}</math> , po usunięciu wszystkich wierzchołków z <math>X</math> , podzieli się na dwie spójne składowe <math>W</math> oraz <math>U</math> , | ||
podzieli się na dwie spójne składowe <math> | do których należą odpowiednio <math>w</math> i <math>u</math> . | ||
do których należą odpowiednio <math> | |||
Przez <math> | Przez <math>W'</math> oznaczmy graf powstały z grafu <math>\mathbf{G}</math> poprzez ściągnięcie <math>U</math> w jeden wierzchołek <math>u'</math> . Wtedy <math>u'</math> jest połączony z tymi wierzchołkami <math>t\in X</math> , z którymi połączony był jakiś wierzchołek <math>s\in U</math> . Krawędzie łączące wierzchołki wewnątrz <math>W</math> pozostały niezmienione. Graf <math>U'</math> definiujemy analogicznie, poprzez ściągnięcie zbioru <math>W</math> do wierzchołka <math>w'</math> . | ||
poprzez ściągnięcie <math> | |||
Wtedy <math> | |||
z którymi połączony był jakiś wierzchołek <math> | |||
Krawędzie łączące wierzchołki wewnątrz <math> | |||
Graf <math> | |||
ściągnięcie zbioru <math> | |||
W grafie <math> | W grafie <math>W'</math> minimalny zbiór rozdzielający wierzchołki <math>w, u'</math> posiada <math>k</math> wierzchołków. Ponieważ założyliśmy, ze w <math>X</math> istnieje wierzchołek niesąsiedni z <math>u</math> , to <math>U</math> ma co najmniej dwa wierzchołki, a zatem graf <math>W'</math> ma mniej wierzchołków niż <math>\mathbf{G}</math> . Tak wiec możemy skorzystać z założenia indukcyjnego otrzymując <math>k</math> rozłącznych wierzchołkowo dróg łączących <math>w</math> z <math>u'</math> w <math>W'</math> . Analogicznie w grafie <math>U</math> otrzymujemy <math>k</math> rozłącznych wierzchołkowo dróg łączących <math>w'</math> z <math>u</math> . Sklejając odpowiednio drogi z obu tych rodzin otrzymujemy <math>k</math> rozłącznych ścieżek łączących <math>w</math> z <math>u</math> w grafie <math>\mathbf{G}</math> . | ||
posiada <math> | ;2. W każdym zbiorze rozdzielającym <math>X</math> o mocy <math>k</math> , każdy wierzchołek jest sąsiedni do <math>w</math> lub do <math>u</math> . | ||
Ponieważ założyliśmy, ze w <math> | |||
to <math> | |||
a zatem graf <math> | |||
Tak wiec możemy skorzystać z założenia indukcyjnego | |||
otrzymując <math> | |||
Analogicznie w grafie <math> | |||
łączących <math> | |||
Sklejając odpowiednio drogi z obu tych rodzin otrzymujemy <math> | |||
łączących <math> | |||
każdy wierzchołek jest sąsiedni do <math> | |||
Możemy wtedy założyć, że <math> | Możemy wtedy założyć, że <math>\mathbf{G}</math> poza <math>w,u</math> zawiera jedynie wierzchołki należące do któregoś zbioru rozdzielającego <math>w, u</math> | ||
zawiera jedynie wierzchołki należące do któregoś zbioru rozdzielającego <math> | o liczności <math>k</math> . Gdyby tak nie było i istniałby jakiś inny wierzchołek <math>v</math> , to moglibyśmy <math>v</math> usunąć i, na mocy założenia indukcyjnego, | ||
o liczności <math> | otrzymać natychmiast <math>k</math> rozłącznych dróg łączących <math>w, u</math> . Tak wiec pozostały nam jedynie te wierzchołki, które są w minimalnych zbiorach rozdzielających <math>w, u</math> . To zaś, zgodnie z założeniem przypadku 2 oznacza, że każdy wierzchołek jest sąsiedni z <math>w</math> lub z <math>u</math> . W ten sposób drugi przypadek sprowadziliśmy do sytuacji, w której każda ścieżka z <math>w</math> do <math>u</math> ma co najwyżej dwie krawędzie. | ||
Gdyby tak nie było i istniałby jakiś inny wierzchołek <math> | Wśród takich ścieżek nietrudno jest już wskazać <math>k</math> rozłącznych wierzchołkowo. | ||
to moglibyśmy <math> | |||
otrzymać natychmiast <math> | |||
Tak wiec pozostały nam jedynie te wierzchołki, | |||
które są w minimalnych zbiorach rozdzielających <math> | |||
To zaś, zgodnie z założeniem przypadku 2 oznacza, | |||
że każdy wierzchołek jest sąsiedni z <math> | |||
W ten sposób drugi przypadek sprowadziliśmy do sytuacji, | |||
w której każda ścieżka z <math> | |||
Wśród takich ścieżek nietrudno jest już wskazać <math> | |||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|10|cw 10| | ||
Korzystając z Twierdzenia Mengera udowodnij Twierdzenie Halla | Korzystając z Twierdzenia Mengera udowodnij Twierdzenie Halla | ||
o skojarzeniach w grafach dwudzielnych. | o skojarzeniach w grafach dwudzielnych. | ||
| Linia 374: | Linia 311: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Dla grafu dwudzielnego <math> | Dla grafu dwudzielnego <math>\mathbf{G}=\left( V_1\cup V_2,E \right)</math> , | ||
oraz funkcji <math> | oraz funkcji <math>\Phi\!\left(A\right)</math> , | ||
która zwraca zbiór wierzchołków z <math> | która zwraca zbiór wierzchołków z <math>V_2</math> | ||
sąsiednich z przynajmniej jednym wierzchołkiem w <math> | sąsiednich z przynajmniej jednym wierzchołkiem w <math>A\subseteq V_1</math> | ||
twierdzenie Hall'a (patrz tw. | twierdzenie Hall'a (patrz tw. [[Matematyka dyskretna 1/Wykład 13: Grafy II#tw_13.7|13.7]]) mówi, że: | ||
''Pełne skojarzenie <math>V_1</math> z <math>V_2</math> istnieje wtedy i tylko wtedy, gdy <math>\left\vert A \right\vert \leq\left\vert \Phi\!\left(A\right) \right\vert</math> , dla każdego podzbioru <math>A</math> zbioru <math>V_1</math> .'' | |||
<math>\Rightarrow</math> Implikacja ta wynika natychmiast z faktu, że jeśli w pełnym skojarzeniu <math>V_1</math> z <math>V_2</math> , w <math>\Phi\!\left(A\right)</math> jest <math>\left\vert A \right\vert</math> wierzchołków skojarzonych z wierzchołkami z <math>A</math> , co w szczególności implikuje, że <math>\left\vert A \right\vert \leq\left\vert \Phi\!\left(A\right) \right\vert</math> . | |||
<math>\Leftarrow</math> Do grafu dwudzielnego <math>\mathbf{G}=\left( V_1\cup V_2,E \right)</math> | |||
dołóżmy dwa wierzchołki <math>v_1</math> oraz <math>v_2</math> łącząc <math>v_1</math> ze wszystkimi wierzchołkami z <math>V_1</math> , a <math>v_2</math> ze wszystkimi wierzchołkami z <math>V_2</math> . Rozważmy dowolny zbiór <math>S\subseteq V_1\cup V_2</math> o <math>\left\vert V_1 \right\vert-1</math> wierzchołkach. Na mocy założenia otrzymujemy, że zbiór wierzchołków z <math>V_2</math> sąsiadujących z wierzchołkami <math>V_1- S</math> jest co najmniej tak duży, jak <math>V_1- S</math> , czyli | |||
< | <center><math>\left\vert V_1- S \right\vert \leq\left\vert \Phi\!\left(V_1- S\right) \right\vert</math></center> | ||
Ponieważ <math> | Ponieważ <math>\left\vert S \right\vert<\left\vert V_1 \right\vert</math> , to | ||
<math> | <math>\left\vert V_2\cap S \right\vert < \left\vert V_1- S \right\vert \leq\left\vert \Phi\!\left(V_1- S\right) \right\vert</math> , | ||
a zatem | a zatem | ||
<math> | <math>\Phi\!\left(V_1- S\right)- S\neq\emptyset</math> , | ||
czyli <math> | czyli <math>\Phi\!\left(V_1- S\right)\not\subseteq S</math> . | ||
Istnieją więc sąsiednie wierzchołki <math> | Istnieją więc sąsiednie wierzchołki <math>u_1\in V_1- S</math> | ||
oraz <math> | oraz <math>u_2\in\Phi\!\left(V_1- S\right)- S</math> . | ||
Teraz, ścieżka postaci | Teraz, ścieżka postaci | ||
<center><math> | |||
<center><math>v_1\to u_1\to u_2\to v_2 | |||
</math></center> | </math></center> | ||
świadczy więc o tym, że <math> | |||
świadczy więc o tym, że <math>S</math> nie był w stanie rozdzielić wierzchołka <math>v_1</math> od <math>v_2</math> . | |||
Na mocy wierzchołkowej wersji twierdzenia Mangera | Na mocy wierzchołkowej wersji twierdzenia Mangera | ||
(patrz ćw. [[# | (patrz ćw. [[#cw_9|9]]), | ||
istnieje <math> | istnieje <math>\left\vert V_1 \right\vert</math> rozłącznych wierzchołkowo ścieżek łączących <math>v_1</math> z <math>v_2</math> . | ||
Każda taka ścieżka musi być postaci | Każda taka ścieżka musi być postaci | ||
gdzie <math> | <center><math>v_1\to w_1\to w_2\to v_2</math>,</center> | ||
Istotnie ścieżek tych jest dokładnie <math> | |||
więc każda z nich przechodzi dokładnie raz przez <math> | |||
przez <math> | gdzie <math>w_1\in V_1</math> oraz <math>w_2\in V_2</math> . | ||
Usuwając teraz z każdej takiej ścieżki wierzchołki <math> | Istotnie ścieżek tych jest dokładnie <math>\left\vert V_1 \right\vert</math> , | ||
otrzymujemy pełne skojarzenie <math> | więc każda z nich przechodzi dokładnie raz przez <math>V_1</math> i dokładnie raz | ||
przez <math>V_2</math> . | |||
Usuwając teraz z każdej takiej ścieżki wierzchołki <math>v_1,v_2</math> , | |||
otrzymujemy pełne skojarzenie <math>V_1</math> z <math>V_2</math> . | |||
</div></div> | </div></div> | ||
Aktualna wersja na dzień 21:49, 11 wrz 2023
Grafy II
Ćwiczenie 1
Kostka -wymiarowa jest grafem, którego wierzchołki to ciągi , gdzie , a krawędzie łączą te ciągi, które różnią się tylko na jednej pozycji. Oblicz liczbę wierzchołków, krawędzi oraz rozmiar najdłuższego cyklu.
Ćwiczenie 2
Dla jakich wartości grafy , , są eulerowskie.
Ćwiczenie 3
Przedstaw cztery pięciowierzchołkowe grafy -- kolejno graf który:
- nie jest hamiltonowski i nie jest eulerowski
- nie jest hamiltonowski, ale jest eulerowski
- jest hamiltonowski i nie jest eulerowski
- jest hamiltonowski i eulerowski.
Rozwiązanie jest przedstawione na rysunku.
Ćwiczenie 4
Dla jakich wartości grafy , , są hamiltonowskie.
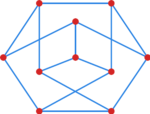
Ćwiczenie 5
Czy graf Petersena (patrz rysunek) ma ścieżkę Hamiltona.
Ćwiczenie 6
Podaj przykład grafu ilustrujący, że warunek występujący w Twierdzeniu Diraca 13.5 nie może być zastąpiony warunkiem .
Ćwiczenie 7
Wykaż, że elementowy jest hamiltonowski jeśli tylko ma przynajmniej krawędzi. Podaj przykład grafu niehamiltonowskiego z wierzchołkami i krawędziami.
Ćwiczenie 8
Wykaż, że każde drzewo jest grafem dwudzielnym. Które drzewa są pełnymi grafami dwudzielnymi?
Ćwiczenie 9
Udowodnij wierzchołkową wersję Twierdzenia Mengera.
Ćwiczenie 10
Korzystając z Twierdzenia Mengera udowodnij Twierdzenie Halla o skojarzeniach w grafach dwudzielnych.