Metody realizacji języków programowania/MRJP Wykład 8: Różnice pomiędzy wersjami

Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
← poprzednia edycja
WizualnieWikikod
Gorecki (dyskusja | edycje)
90 edycji
Gorecki (dyskusja | edycje)
90 edycji
 
(Nie pokazano 29 wersji utworzonych przez 3 użytkowników)
Linia 1: Linia 1:
= Wprowadzenie =
autor: Paweł Górecki (gorecki@mimuw.edu.pl)


Jeszcze nie ma...
= Optymalizacja kodu pośredniego w postaci SSA =
 
Optymalizacja kodu (tu pośredniego) jest procesem, którego celem
jest zmiana kodu przy zachowaniu obliczanej funkcji tak, by przyspieszyć
działanie docelowego programu i ewentualnie zmniejszyć jego rozmiar.
To drugie wymaganie w obecnych czasach ma mniejsze znaczenie.
Zwróćmy uwagę, że optymalizacja jest raczej "poprawianiem" programu, bo rzadko
otrzymany kod jest "optymalny".
Należy pamiętać, że w optymalizacji powinno uwzględniać się wiele ogólnych warunków:
 
* czas działania docelowego programu jest najbardziej istotny; złożony program może pewne fragmenty wykonywać częściej - te powinny być lepiej zoptymalizowane i odwrotnie nie warto optymalizować rzadko wykonywanych fragmentów programu,
* dane wejściowe mogą wpływać na to jak często wykonuje się określone fragmenty programu - dobry optymalizator powinien próbować zgadnąć istotne (czyli często wykonywane) dla optymalizacji fragmenty,
* rozmiar docelowego programu obecnie ma mniejsze znaczenie,
* rozsądny czas wykonywania optymalizacji.
 
Wykład przedstawia podstawowe techniki optymalizacji kodu pośredniego
w postaci SSA, choć niektóre z nich mogą być stosowane do innych postaci np. kodu czwórkowego (ang. three-address code).
Jak już wiemy z wykładu o
[[Metody realizacji języków programowania/MRJP Wykład 6| generowaniu kodu pośredniego]]
postać SSA jest szczególnie użyteczna w optymalizacji - istotnie upraszcza zapis i implementację algorytmów poprawiających kod. Jest stosowana w optymalizatorach ważnych kompilatorów np. GCC.


= Podstawowe przekształcenia poprawiające kod =
= Podstawowe przekształcenia poprawiające kod =
Poniższe przykłady nie są przedstawione w postaci SSA,
ale mogą być łatwo do niego przekształcone (w celu lepszej czytelności piszemy
''a'' zamiast ''a1'', ''x'' zamiast ''x1'', itd.).


== Propagacja kopii ==
== Propagacja kopii ==
 
{{kotwica|propagacjakopii|}}
Instrukcja postaci <math>X = Y</math> jest instrukcją kopiowania.
Instrukcja postaci ''X = Y'' jest instrukcją kopiowania.
Naturalne jest zastąpienie wystąpień zmiennej <math>X</math> przez <math>Y</math>.
Naturalne jest zastąpienie wystąpień zmiennej ''X'' przez ''Y''.


Przykład:
Przykład:
Linia 26: Linia 49:


== Eliminacja wspólnych podwyrażeń ==
== Eliminacja wspólnych podwyrażeń ==
Wyrażenie <math>E</math> postaci <math>X\;op\;Y</math> jest nazywane '''wspólnym podwyrażeniem''' jeśli występuje ono w kilku miejscach oraz
Wyrażenie ''E'' postaci ''X op Y'' jest nazywane '''wspólnym podwyrażeniem''', jeśli występuje ono w kilku miejscach, oraz jeśli
wartości zmiennych <math>X</math> i <math>Y</math> użytych w kolejnych wystąpieniach  <math>E</math> nie zmieniły się po poprzednim obliczeniu <math>E</math>. W takiej sytuacji można zastąpić
wartości zmiennych ''X'' i ''Y'' użytych w kolejnych wystąpieniach  ''E'' nie zmieniły się po poprzednim obliczeniu ''E''. W takiej sytuacji można zastąpić
kolejne wystąpienia <math>E</math> przez wartość wyliczoną za pierwszym razem.
kolejne wystąpienia ''E'' przez wartość wyliczoną za pierwszym razem.


Przykład:
Przykład:
Linia 35: Linia 58:
  c = a + b
  c = a + b


Drugie wyliczenie <math>4 * i</math> można zastąpić przez <math>b</math>. Przekształcony blok:
Drugie wyliczenie ''4 * i'' można zastąpić przez ''b''. Przekształcony blok:
  a = 4 * i
  a = 4 * i
  b = a
  b = a
Linia 48: Linia 71:
Zmienną nazywamy '''żywą''' w danym miejscu programu, jeżeli jej wartość może zostać użyta.
Zmienną nazywamy '''żywą''' w danym miejscu programu, jeżeli jej wartość może zostać użyta.
W pozostałych przypadkach nazywamy zmienną '''martwą''' w tym miejscu.
W pozostałych przypadkach nazywamy zmienną '''martwą''' w tym miejscu.
Analogicznie definiujemy '''kod martwy''', tzn. taki który oblicza wartości bezużyteczne.
Analogicznie definiujemy '''kod martwy''', tzn. taki, który oblicza wartości bezużyteczne.
Na przykład wyliczenie wartości dla zmiennej martwej lub instrukcja postaci  
Na przykład wyliczenie wartości dla zmiennej martwej lub instrukcja postaci  


Linia 55: Linia 78:
to kod martwy.
to kod martwy.


W oczywisty sposób kod martwy usuwamy.
Oczywiści kod martwy usuwamy.


Często kod martwy powstaje po  
Często kod martwy powstaje po  
Linia 63: Linia 86:


== Zwijanie stałych ==
== Zwijanie stałych ==
{{kotwica|zwijaniestalych|}}


Jest to proces upraszczania wyrażeń stałych. Przykład:
Jest to proces upraszczania wyrażeń stałych. Przykład:
Linia 73: Linia 97:


Zwijanie stałych czasem wykonuje się na wcześniejszych etapach kompilacji.
Zwijanie stałych czasem wykonuje się na wcześniejszych etapach kompilacji.


== Propagacja stałych ==
== Propagacja stałych ==
 
{{kotwica|propagacjastalych|}}
Jest to proces zastępowania wystąpień stałych przez ich wartości. Przykład
Jest to proces zastępowania wystąpień stałych przez ich wartości. Przykład


Linia 92: Linia 115:
  y = 180
  y = 180


W wyniku propagacji stałych instrukcja definiująca stałą staje się martwym kodem,  
W wyniku propagacji stałych instrukcja definiująca stałą staje się [[Metody realizacji języków programowania/MRJP Wykład 8#martwykod|martwym kodem]],  
który można usunąć w trakcie eliminacji martwego kodu.
który można usunąć w trakcie eliminacji martwego kodu.


= Optymalizacja pętli =
= Optymalizacja pętli =


Wstępniak!


== Przemieszczenie kodu ==


Polega na zmiejszeniu ilości kodu w pętli, przez przemieszczenie obliczeń niezmienniczych  
== Przemieszczanie kodu ==
 
Polega na zmiejszeniu ilości kodu w pętli, przez przemieszczenie '''obliczeń niezmienniczych'''
przed pętle.
przed pętle.


Linia 127: Linia 150:


W ogólnej sytuacji stosujemy schemat:
W ogólnej sytuacji stosujemy schemat:
jeśli <math>I</math> jest instrukcją <math>X = Y op Z</math>, oraz <math>Y</math>, <math>Z</math> nie odwołują się do <math>\phi</math>-węzła lub definicji wewnątrz pętli, wtedy
jeśli ''I'' jest instrukcją ''X = Y op Z'', oraz ''Y'', ''Z'' nie odwołują się do <math>\phi</math>-węzła lub definicji wewnątrz pętli, wtedy
* usuń instrukcję <math>I</math> (to jest instrukcja niezmiennicza dla tej pętli)
* usuń instrukcję ''I'' (to jest instrukcja niezmiennicza dla tej pętli),
* utwórz nową tymczasową zmienną <math>T</math>
* utwórz nową tymczasową zmienną ''T'',
* wstaw nową instrukcję <math>T = Y op Z</math> oraz <math>X = T</math> do (ewentualnie nowego) bloku przed tą pętlą.
* wstaw nową instrukcję ''T = Y op Z'' oraz ''X = T'' do (ewentualnie) nowego bloku przed tą pętlą.


Proces ten rozszerzamy wykonując iteracyjnie:
Proces ten rozszerzamy, wykonując iteracyjnie:
* jeśli argumenty operacji pewnej instrukcji są zdefiniowane przez instrukcje niezmiennicze (tzn. ta instrukcja jest również niezmiennicza w pętli), wykonuj analogiczne przenoszenie kodu do bloku przed pęltą.
* jeśli argumenty operacji pewnej instrukcji są zdefiniowane przez instrukcje niezmiennicze (tzn. ta instrukcja jest również niezmiennicza w pętli), wykonuj analogiczne przenoszenie kodu do bloku przed pęltą.


== Zmienne indukcyjne i redukcja mocy==
== Zmienne indukcyjne i redukcja mocy==


Identyfikacja zmiennych, które zmieniają się w regularny sposób w pętli ułatwia  optymalizacje pętli. Zmienne o takiej własności nazywany indukcyjnymi.
=== Wyszukanie zmiennych indukcyjnych ===
W połączeniu z redukcją mocy (czyli zastępowaniem drogich obliczeń przez tańsze, np. zamiast mnożenia dodawanie), można w najlepszym przypadku zostawić tylko jedną zmienną indukcyjną.


Zmienne indukcyjne w poniższym przykładzie to <math>i, j</math>:  
Identyfikacja zmiennych, które zmieniają się w regularny sposób w pętli ułatwia optymalizację pętli. Zmienne o takiej własności nazywany '''indukcyjnymi'''.
W połączeniu z '''redukcją mocy''' (czyli zastępowaniem drogich obliczeń przez tańsze, np. zamiast mnożenia dodawanie), można w najlepszym przypadku zostawić tylko jedną zmienną indukcyjną.
 
Zmienne indukcyjne w poniższym przykładzie to ''i, j'':  


  i = 0  
  i = 0  
Linia 148: Linia 173:
  } '''while''' (i < 20)
  } '''while''' (i < 20)


Identyfikowanie zmiennych indukcyjnych jest prostsze gdy program jest w postaci SSA.
Identyfikowanie zmiennych indukcyjnych jest prostsze, gdy program jest w postaci SSA.


Zaczniemy od obliczenia zbioru '''kandydatów na zmienne indukcyjne''':  
Zaczniemy od obliczenia zbioru '''kandydatów na zmienne indukcyjne''':  
Dla danej pętli <math>L</math>, zmienna <math>T</math> jest kandydatem na zmienną indukcyjną dla <math>L</math> (niżej będziemy pisać ''jest kandydatem'') wtedy i tylko wtedy gdy <math>T</math> jest obliczana w <math>L</math> i to obliczenie ma jedną następujących postaci:  
Dla danej pętli ''L'' zmienna ''T'' jest kandydatem na zmienną indukcyjną dla ''L'' (niżej będziemy pisać ''jest kandydatem'') wtedy i tylko wtedy, gdy ''T'' jest obliczana w ''L'' i to obliczenie ma jedną następujących postaci:  
* <math>T = T_i</math> ± <math>T_j</math>, gdzie jeden z argumentów jest kandydatem, a drugi jest niezmienniczy dla <math>L</math>.  
* ''T = X ± Y'', gdzie jeden z argumentów jest kandydatem, a drugi jest niezmienniczy dla ''L''.  
* <math>T = T_k</math>, gdzie <math>T_k</math> jest kandydatem lub niezmienniczy dla <math>L</math>.  
* ''T = X'', gdzie ''X'' jest kandydatem lub niezmienniczy dla ''L''.  
* <math>T = </math> ± <math> T_k</math>, gdzie <math>T_k</math> jest kandydatem dla <math>L</math>.  
* ''T = ± X'', gdzie ''X'' jest kandydatem dla ''L''.  
* <math>T = \phi(T_1, . . ., T_m)</math>, gdzie każdy z argumentów jest albo kandydatem albo niezmienniczy dla <math>L</math>.
* ''T = <math>\phi</math>(T1, . . ., Tm)'', gdzie każdy z argumentów jest albo kandydatem, albo jest niezmienniczy dla ''L''.


Zdefiniujemy teraz pojęcie '''zbioru indukcyjnego''' i '''zmiennych indukcyjnych'''.
Zdefiniujemy teraz pojęcie '''zbioru indukcyjnego''' i '''zmiennych indukcyjnych'''.
Rozważmy graf skierowany, którego wierzchołkami są kandydaci, a zbiór krawędzi  posiada krawędź z T do U jeśli T jest użyta do obliczenia wartości U. '''Zmienna indukcyjna''' jest kandydatem, który jest elementem silnie spójnej składowej tego grafu. Zbiór zmiennych w takiej silnie spójnej składowej nazywamy '''zbiorem indukcyjnym'''.
Rozważmy graf skierowany, którego wierzchołkami są kandydaci, a zbiór krawędzi  posiada krawędź z T do U, jeśli T jest użyta do obliczenia wartości U. '''Zmienna indukcyjna''' jest kandydatem, który jest elementem silnie spójnej składowej tego grafu. Zbiór zmiennych w takiej silnie spójnej składowej nazywamy '''zbiorem indukcyjnym'''.


Przykład:
Przykład:
Linia 170: Linia 195:
Zapisujemy w postaci SSA:
Zapisujemy w postaci SSA:


  (1) <math>m_0</math> = 0
  (1) m<math>{}_0</math> = 0
  (2) <math>m_1=\phi(m_0,m_2)</math>
  (2) m<math>{}_1</math>=<math>\phi</math>(m<math>{}_0</math>,m<math>{}_2</math>)
  (3) <math>l_1</math> = <math>m_1</math> + 1
  (3) l<math>{}_1</math> = m<math>{}_1</math> + 1
  (4) <math>t_1</math> = <math>l_1</math> + 2
  (4) t<math>{}_1</math> = l<math>{}_1</math> + 2
  (5) <math>m_2</math> = <math>t_1</math> - 4
  (5) m<math>{}_2</math> = t<math>{}_1</math> - 4
  (6) '''goto''' (2)
  (6) '''goto''' (2)


Graf skierowany dla kandydatów na zmienne indukcyjne jest przedstawiony poniżej:
Graf skierowany dla kandydatów na zmienne indukcyjne jest przedstawiony poniżej:


[[Grafika:Mrjp8cykl.png]]
[[Grafika:Mrjp8cykl.png|112px|center]]


Zbiorem indukcyjnym jest: <math>\{m_1,l_1,t_1,m_2\}</math>. Zaczynamy od zmiennej <math>m_1</math> definiowanej przez
Zbiorem indukcyjnym jest: ''{m<math>{}_1</math>,l<math>{}_1</math>,t<math>{}_1</math>,m<math>{}_2</math>}''. Zaczynamy od zmiennej ''m<math>{}_1</math>'' definiowanej przez
<math>\phi</math> i wartości pozostałych można przedstawić w postaci: <math>m_1 + C</math>, gdzie
<math>\phi</math> i wartości pozostałych można przedstawić w postaci:  
<math>C</math> jest stałą. Tu:
''m<math>{}_1</math> + C'', gdzie
''C'' jest stałą. Tu:


  (1) <math>m_0</math> = 0
  (1) m<math>{}_0</math> = 0
  (2) <math>m_1=\phi(m_0,m_2)</math>
  (2) m<math>{}_1</math>=<math>\phi</math>(m<math>{}_0</math>,m<math>{}_2</math>)
  (3) <math>l_1</math> = <math>m_1</math> + 1
  (3) l<math>{}_1</math> = m<math>{}_1</math> + 1
  (4) <math>t_1</math> = <math>m_1</math> + 3
  (4) t<math>{}_1</math> = m<math>{}_1</math> + 3
  (5) <math>m_2</math> = <math>m_1</math> - 1
  (5) m<math>{}_2</math> = m<math>{}_1</math> - 1
  (6) '''goto''' (2)
  (6) '''goto''' (2)


Po wykonaniu tej operacji zmienne <math>l_1</math>, <math>t_2</math> nie są używane do obliczania
Po wykonaniu tej operacji zmienne ''l<math>{}_1</math>'', ''t<math>{}_1</math>'' nie są używane do obliczania
<math>m_2</math>. Jest mniej zależności i być może część zmiennych będzie usunięta po zastosowaniu innych rodzajów optymaliazacji.
''m<math>{}_2</math>''. Jest mniej zależności i być może część zmiennych będzie usunięta po zastosowaniu innych rodzajów optymalizacji.


W przypadku gdy do wyliczania używamy mnożenia, można zastosować inne podejście.
=== Redukcja mocy w pętlach ===
Tu klasyfikujemy zmienne na kilka rodzajów:
* '''Zmienna indukcyjna podstawowa''' - jej definicja występuje dokładnie raz w pętli i jest postaci  <math>i = i + C</math>, gdzie <math>C</math> jest niezmiennicze w pętli.
* '''Zmienna indukcyjna wspólna''' - jej definicja występuje dokładnie raz w pętli i jej wartość jest funkcją liniową pewnej zmiennej indukcyjnej; czyli <math>i = j op C_1 + C_2</math>, gdzie <math>C_1</math> oraz <math>C_2</math> są niezmiennicze w pętli, <math>op</math> jest operatorem mnożenia lub dzieleniam, a <math>j</math> jest zmienną indukcyjną.
*


'''Algorytm redukcji mocy''': dla zmiennej indukcyjnej wspólnej <math>i</math> zdefiniowanej przez <math>i = j * C_1 + C_2</math>, gdzie <math>j</math> jest zmienną indukcyjną podstawową.
W przypadku, gdy do wyliczania używamy mnożenia, można zastosować inne podejście.
# Stwórz nową zmienną <math>k</math>.
Najpierw klasyfikujemy zmienne na kilka rodzajów:
# Dodaj przed pętlą <math>k = j * C_1 + C_2</math> (przekształć do SSA).
* '''Zmienna indukcyjna podstawowa''' - jej definicja występuje dokładnie raz w pętli i jest postaci  ''i = i + C'', gdzie ''C'' jest niezmiennicze w pętli.
# Za instrukcją <math>j = j + C_3</math> dodaj <math>k = k + C_1 * C_3</math> (przekształć do SSA).
* '''Zmienna indukcyjna wspólna''' - jej definicja występuje dokładnie raz w pętli i jej wartość jest funkcją liniową pewnej zmiennej indukcyjnej; czyli ''i = A op j + B'', gdzie ''A'' oraz ''B'' są niezmiennicze w pętli, ''op'' jest operatorem mnożenia lub dzielenia, a ''j'' jest zmienną indukcyjną.
# Zastąp definicję <math>i</math> przez <math>i = k</math>.
 
'''Algorytm redukcji mocy''': dla zmiennej indukcyjnej wspólnej ''i'' zdefiniowanej przez ''i = A * j + B'', gdzie ''j'' jest zmienną indukcyjną podstawową.
# Stwórz nową zmienną ''k''.
# Dodaj przed pętlą ''k = A * j + B'' (przekształć do SSA).
# Za instrukcją ''j = j + C'' dodaj ''k = k + B * C'' (przekształć do SSA).
# Zastąp definicję ''i'' przez ''i = k''.


Odniesione korzyści to  mniejsza liczba operacji mnożenia oraz wyniesione przed pętle obliczenia
Odniesione korzyści to  mniejsza liczba operacji mnożenia oraz wyniesione przed pętle obliczenia
na wartościach niezmienniczych <math>C_1</math>, <math>C_2</math> oraz <math>C_3</math>.
na wartościach niezmienniczych ''A'', ''B'' oraz ''C''.
*
 
W analogiczny sposób można redukować moc dla sytuacji, w których
zmienna indukcyjna jest wykorzystywana do przypisania z mnożeniem, tzn.
w pętli jest instrukcja ''k = j * A'',  gdzie ''A'' jest niezmiennicze,
a ''j'' jest zmienną indukcyjną podstawową, której inkrementacja w pętli jest postaci ''j = j + C''.
W tej sytuacji zastępujemy przypisanie na ''k'' instrukcją
''k = k + C * A'' oraz dodajemy przed pętlą odpowiednią inicjalizację wartości ''k''.

Aktualna wersja na dzień 20:59, 1 paź 2006

autor: Paweł Górecki (gorecki@mimuw.edu.pl)

Optymalizacja kodu pośredniego w postaci SSA

Optymalizacja kodu (tu pośredniego) jest procesem, którego celem jest zmiana kodu przy zachowaniu obliczanej funkcji tak, by przyspieszyć działanie docelowego programu i ewentualnie zmniejszyć jego rozmiar. To drugie wymaganie w obecnych czasach ma mniejsze znaczenie. Zwróćmy uwagę, że optymalizacja jest raczej "poprawianiem" programu, bo rzadko otrzymany kod jest "optymalny". Należy pamiętać, że w optymalizacji powinno uwzględniać się wiele ogólnych warunków:

  • czas działania docelowego programu jest najbardziej istotny; złożony program może pewne fragmenty wykonywać częściej - te powinny być lepiej zoptymalizowane i odwrotnie nie warto optymalizować rzadko wykonywanych fragmentów programu,
  • dane wejściowe mogą wpływać na to jak często wykonuje się określone fragmenty programu - dobry optymalizator powinien próbować zgadnąć istotne (czyli często wykonywane) dla optymalizacji fragmenty,
  • rozmiar docelowego programu obecnie ma mniejsze znaczenie,
  • rozsądny czas wykonywania optymalizacji.

Wykład przedstawia podstawowe techniki optymalizacji kodu pośredniego w postaci SSA, choć niektóre z nich mogą być stosowane do innych postaci np. kodu czwórkowego (ang. three-address code). Jak już wiemy z wykładu o generowaniu kodu pośredniego postać SSA jest szczególnie użyteczna w optymalizacji - istotnie upraszcza zapis i implementację algorytmów poprawiających kod. Jest stosowana w optymalizatorach ważnych kompilatorów np. GCC.

Podstawowe przekształcenia poprawiające kod

Poniższe przykłady nie są przedstawione w postaci SSA, ale mogą być łatwo do niego przekształcone (w celu lepszej czytelności piszemy a zamiast a1, x zamiast x1, itd.).

Propagacja kopii

Instrukcja postaci X = Y jest instrukcją kopiowania. Naturalne jest zastąpienie wystąpień zmiennej X przez Y.

Przykład: 

x = y
a = x + y
b = a + x

Zastępujemy przez: 

x = y
a = y + y
b = a + y

Po wykonaniu propagacji kopii, instrukcja kopiująca jest martwym kodem. Ostatecznie otrzymamy: 

a = y + y
b = a + y

Eliminacja wspólnych podwyrażeń

Wyrażenie E postaci X op Y jest nazywane wspólnym podwyrażeniem, jeśli występuje ono w kilku miejscach, oraz jeśli wartości zmiennych X i Y użytych w kolejnych wystąpieniach E nie zmieniły się po poprzednim obliczeniu E. W takiej sytuacji można zastąpić kolejne wystąpienia E przez wartość wyliczoną za pierwszym razem.

Przykład: 

a = 4 * i
b = 4 * i
c = a + b

Drugie wyliczenie 4 * i można zastąpić przez b. Przekształcony blok: 

a = 4 * i
b = a
c = a + b

Eliminację wspólnych podwyrażeń można stosować

  • lokalnie - gdy przeszukujemy jeden blok bazowy,
  • globalnie - dla całego grafu przepływu (trudniejsze z powodu pętli).

Usuwanie martwego kodu

Zmienną nazywamy żywą w danym miejscu programu, jeżeli jej wartość może zostać użyta. W pozostałych przypadkach nazywamy zmienną martwą w tym miejscu. Analogicznie definiujemy kod martwy, tzn. taki, który oblicza wartości bezużyteczne. Na przykład wyliczenie wartości dla zmiennej martwej lub instrukcja postaci 

if (false) ...

to kod martwy.

Oczywiści kod martwy usuwamy.

Często kod martwy powstaje po propagacji kopii lub po zwijaniu stałych .

Zwijanie stałych

Jest to proces upraszczania wyrażeń stałych. Przykład: 

x = 30 * 2

można zastąpić przez 

x = 60

Zwijanie stałych czasem wykonuje się na wcześniejszych etapach kompilacji.

Propagacja stałych

Jest to proces zastępowania wystąpień stałych przez ich wartości. Przykład 

x = 60
y = 3 * x

można zastąpić przez 

x = 60
y = 3 * 60

i dalej po zwinięciu wartości w drugim przypisaniu otrzymamy 

x = 60
y = 180

W wyniku propagacji stałych instrukcja definiująca stałą staje się martwym kodem, który można usunąć w trakcie eliminacji martwego kodu.

Optymalizacja pętli

Przemieszczanie kodu

Polega na zmiejszeniu ilości kodu w pętli, przez przemieszczenie obliczeń niezmienniczych przed pętle.

Prosty przykład: 

i = 0
do {
   a = 13
   i = i + 1
} while (i < 15)

przedstawiamy w postaci SSA: 

(0) i1 = 0
(1) i2 = ϕ(i1,i3)
(2) a = 13
(3) i3 = i2 + 1
(4) if (i3 < 15) goto (1)

Wyrażeniem niezmienniczym jest instrukcja przypisania w linii (2). Możemy ją przemieścić przed pętlę: 

(0) i1 = 0
(1) a = 13
(2) i2 = ϕ(i1,i3)
(3) i3 = i2 + 1
(4) if (i3 < 15) goto (2)

W ogólnej sytuacji stosujemy schemat: jeśli I jest instrukcją X = Y op Z, oraz Y, Z nie odwołują się do ϕ-węzła lub definicji wewnątrz pętli, wtedy

  • usuń instrukcję I (to jest instrukcja niezmiennicza dla tej pętli),
  • utwórz nową tymczasową zmienną T,
  • wstaw nową instrukcję T = Y op Z oraz X = T do (ewentualnie) nowego bloku przed tą pętlą.

Proces ten rozszerzamy, wykonując iteracyjnie:

  • jeśli argumenty operacji pewnej instrukcji są zdefiniowane przez instrukcje niezmiennicze (tzn. ta instrukcja jest również niezmiennicza w pętli), wykonuj analogiczne przenoszenie kodu do bloku przed pęltą.

Zmienne indukcyjne i redukcja mocy

Wyszukanie zmiennych indukcyjnych

Identyfikacja zmiennych, które zmieniają się w regularny sposób w pętli ułatwia optymalizację pętli. Zmienne o takiej własności nazywany indukcyjnymi. W połączeniu z redukcją mocy (czyli zastępowaniem drogich obliczeń przez tańsze, np. zamiast mnożenia dodawanie), można w najlepszym przypadku zostawić tylko jedną zmienną indukcyjną.

Zmienne indukcyjne w poniższym przykładzie to i, j: 

i = 0 
do { 
  j = 4 * i
  i = i + 1 
} while (i < 20)

Identyfikowanie zmiennych indukcyjnych jest prostsze, gdy program jest w postaci SSA.

Zaczniemy od obliczenia zbioru kandydatów na zmienne indukcyjne: Dla danej pętli L zmienna T jest kandydatem na zmienną indukcyjną dla L (niżej będziemy pisać jest kandydatem) wtedy i tylko wtedy, gdy T jest obliczana w L i to obliczenie ma jedną następujących postaci:

  • T = X ± Y, gdzie jeden z argumentów jest kandydatem, a drugi jest niezmienniczy dla L.
  • T = X, gdzie X jest kandydatem lub niezmienniczy dla L.
  • T = ± X, gdzie X jest kandydatem dla L.
  • T = ϕ(T1, . . ., Tm), gdzie każdy z argumentów jest albo kandydatem, albo jest niezmienniczy dla L.

Zdefiniujemy teraz pojęcie zbioru indukcyjnego i zmiennych indukcyjnych. Rozważmy graf skierowany, którego wierzchołkami są kandydaci, a zbiór krawędzi posiada krawędź z T do U, jeśli T jest użyta do obliczenia wartości U. Zmienna indukcyjna jest kandydatem, który jest elementem silnie spójnej składowej tego grafu. Zbiór zmiennych w takiej silnie spójnej składowej nazywamy zbiorem indukcyjnym.

Przykład: 

m = 0 
do 
   l = m + 1
   t = l + 2
   m = t - 4
while (true)

Zapisujemy w postaci SSA: 

(1) m0 = 0
(2) m1=ϕ(m0,m2)
(3) l1 = m1 + 1
(4) t1 = l1 + 2
(5) m2 = t1 - 4
(6) goto (2)

Graf skierowany dla kandydatów na zmienne indukcyjne jest przedstawiony poniżej:

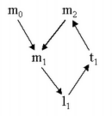
Zbiorem indukcyjnym jest: {m1,l1,t1,m2}. Zaczynamy od zmiennej m1 definiowanej przez ϕ i wartości pozostałych można przedstawić w postaci: m1 + C, gdzie C jest stałą. Tu: 

(1) m0 = 0
(2) m1=ϕ(m0,m2)
(3) l1 = m1 + 1
(4) t1 = m1 + 3
(5) m2 = m1 - 1
(6) goto (2)

Po wykonaniu tej operacji zmienne l1, t1 nie są używane do obliczania m2. Jest mniej zależności i być może część zmiennych będzie usunięta po zastosowaniu innych rodzajów optymalizacji.

Redukcja mocy w pętlach

W przypadku, gdy do wyliczania używamy mnożenia, można zastosować inne podejście. Najpierw klasyfikujemy zmienne na kilka rodzajów:

  • Zmienna indukcyjna podstawowa - jej definicja występuje dokładnie raz w pętli i jest postaci i = i + C, gdzie C jest niezmiennicze w pętli.
  • Zmienna indukcyjna wspólna - jej definicja występuje dokładnie raz w pętli i jej wartość jest funkcją liniową pewnej zmiennej indukcyjnej; czyli i = A op j + B, gdzie A oraz B są niezmiennicze w pętli, op jest operatorem mnożenia lub dzielenia, a j jest zmienną indukcyjną.

Algorytm redukcji mocy: dla zmiennej indukcyjnej wspólnej i zdefiniowanej przez i = A * j + B, gdzie j jest zmienną indukcyjną podstawową.

  1. Stwórz nową zmienną k.
  2. Dodaj przed pętlą k = A * j + B (przekształć do SSA).
  3. Za instrukcją j = j + C dodaj k = k + B * C (przekształć do SSA).
  4. Zastąp definicję i przez i = k.

Odniesione korzyści to mniejsza liczba operacji mnożenia oraz wyniesione przed pętle obliczenia na wartościach niezmienniczych A, B oraz C.

W analogiczny sposób można redukować moc dla sytuacji, w których zmienna indukcyjna jest wykorzystywana do przypisania z mnożeniem, tzn. w pętli jest instrukcja k = j * A, gdzie A jest niezmiennicze, a j jest zmienną indukcyjną podstawową, której inkrementacja w pętli jest postaci j = j + C. W tej sytuacji zastępujemy przypisanie na k instrukcją k = k + C * A oraz dodajemy przed pętlą odpowiednią inicjalizację wartości k.

Źródło: „https://wazniak.mimuw.edu.pl/index.php?title=Metody_realizacji_języków_programowania/MRJP_Wykład_8&oldid=61593”