Pr-1st-1.1-m03-Slajd22: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „<math> ” na „<math>” |
||
| Linia 6: | Linia 6: | ||
Na slajdzie przedstawiono przykładowy diagram przestrzenno-czasowy oraz odpowiadający mu graf stanów osiągalnych. Dla uproszczenia oznaczono tu stan | Na slajdzie przedstawiono przykładowy diagram przestrzenno-czasowy oraz odpowiadający mu graf stanów osiągalnych. Dla uproszczenia oznaczono tu stan | ||
<math> \left \langle S_1^i, S_2^j, S_3^k \right \rangle</math> przez <math>\mathit{\Sigma} ^{i,j,k}</math>. | <math>\left \langle S_1^i, S_2^j, S_3^k \right \rangle</math> przez <math>\mathit{\Sigma} ^{i,j,k}</math>. | ||
Ponieważ kolejność występowania zdarzeń współbieżnych jest dowolna, relacja poprzedzania określa (modeluje) wiele możliwych realizacji, z których każda odpowiada pewnej ścieżce w grafie stanów osiągalnych przetwarzania. Z drugiej strony, relacja ta określa jednoznacznie zależności przyczynowe między zdarzeniami lokalnymi, w tym oczywiście - między zdarzeniami odbioru przez określony proces wiadomości wysłanych w wyniku zdarzeń współbieżnych. Zauważmy jednak, że zdarzenia odbioru wiadomości <math>M_1</math> i <math>M_2</math> przedstawione na przykładowym diagramie, mogą w ogólności zajść w odwrotnej kolejności, jeżeli tylko zdarzenie odbioru w procesie docelowym jest <math>P_1</math> wynikiem operacji niedeterministycznego odbioru ''receive''(<math>\mathcal{P}_1^S, P_1, sInM</math>), gdzie <math>\mathcal{P}_1^S = \{P_2, P_3\}</math> i nadejście wiadomości <math>M_2</math> wyprzedzi nadejście wiadomości <math>M_1</math>. | Ponieważ kolejność występowania zdarzeń współbieżnych jest dowolna, relacja poprzedzania określa (modeluje) wiele możliwych realizacji, z których każda odpowiada pewnej ścieżce w grafie stanów osiągalnych przetwarzania. Z drugiej strony, relacja ta określa jednoznacznie zależności przyczynowe między zdarzeniami lokalnymi, w tym oczywiście - między zdarzeniami odbioru przez określony proces wiadomości wysłanych w wyniku zdarzeń współbieżnych. Zauważmy jednak, że zdarzenia odbioru wiadomości <math>M_1</math> i <math>M_2</math> przedstawione na przykładowym diagramie, mogą w ogólności zajść w odwrotnej kolejności, jeżeli tylko zdarzenie odbioru w procesie docelowym jest <math>P_1</math> wynikiem operacji niedeterministycznego odbioru ''receive''(<math>\mathcal{P}_1^S, P_1, sInM</math>), gdzie <math>\mathcal{P}_1^S = \{P_2, P_3\}</math> i nadejście wiadomości <math>M_2</math> wyprzedzi nadejście wiadomości <math>M_1</math>. | ||
Uwzględnienie takiej alternatywy w modelu przetwarzania rozproszonego, jakim jest zbiór częściowo uporządkowany <math> \left \langle \boldsymbol{\Lambda}, \mapsto \right \rangle</math>, jest oczywiście możliwe przez stosowną zmianę zbioru <math>\boldsymbol{\Lambda}</math> i definicji relacji poprzedzania. Dlatego też w literaturze zbiór uporządkowany <math> \left \langle \boldsymbol{\Lambda}, \mapsto \right \rangle</math> przyjmuje się często za ogólny model przetwarzania, reprezentujący wszystkie możliwe jego realizacje. | Uwzględnienie takiej alternatywy w modelu przetwarzania rozproszonego, jakim jest zbiór częściowo uporządkowany <math>\left \langle \boldsymbol{\Lambda}, \mapsto \right \rangle</math>, jest oczywiście możliwe przez stosowną zmianę zbioru <math>\boldsymbol{\Lambda}</math> i definicji relacji poprzedzania. Dlatego też w literaturze zbiór uporządkowany <math>\left \langle \boldsymbol{\Lambda}, \mapsto \right \rangle</math> przyjmuje się często za ogólny model przetwarzania, reprezentujący wszystkie możliwe jego realizacje. | ||
[[pr-1st-1.1-m03-Slajd21 | << Poprzedni slajd]] | [[pr-1st-1.1-m03-toc|Spis treści ]] | [[pr-1st-1.1-m03-Slajd23 | Następny slajd >>]] | [[pr-1st-1.1-m03-Slajd21 | << Poprzedni slajd]] | [[pr-1st-1.1-m03-toc|Spis treści ]] | [[pr-1st-1.1-m03-Slajd23 | Następny slajd >>]] | ||
Aktualna wersja na dzień 10:29, 5 wrz 2023
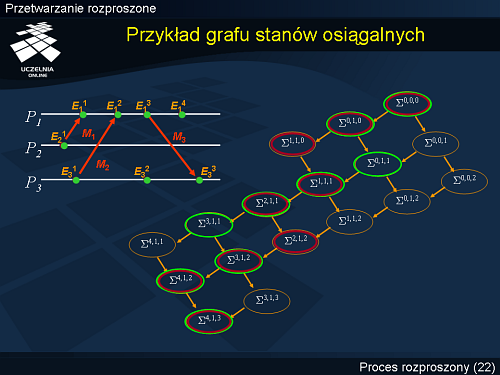
Przykład grafu stanów osiągalnych
Dla ilustracji tego zagadnienia, rozważmy graf stanów osiągalnych przetwarzania rozproszonego odpowiadający diagramowi przestrzenno-czasowemu, a więc określony w pełni przez relację poprzedzania między zdarzeniami wynikającą wyłącznie z diagramu, przyjmując jednak, że zdarzenia współbieżne mogą zachodzić w dowolnej kolejności względem siebie.
Na slajdzie przedstawiono przykładowy diagram przestrzenno-czasowy oraz odpowiadający mu graf stanów osiągalnych. Dla uproszczenia oznaczono tu stan przez .
Ponieważ kolejność występowania zdarzeń współbieżnych jest dowolna, relacja poprzedzania określa (modeluje) wiele możliwych realizacji, z których każda odpowiada pewnej ścieżce w grafie stanów osiągalnych przetwarzania. Z drugiej strony, relacja ta określa jednoznacznie zależności przyczynowe między zdarzeniami lokalnymi, w tym oczywiście - między zdarzeniami odbioru przez określony proces wiadomości wysłanych w wyniku zdarzeń współbieżnych. Zauważmy jednak, że zdarzenia odbioru wiadomości i przedstawione na przykładowym diagramie, mogą w ogólności zajść w odwrotnej kolejności, jeżeli tylko zdarzenie odbioru w procesie docelowym jest wynikiem operacji niedeterministycznego odbioru receive(), gdzie i nadejście wiadomości wyprzedzi nadejście wiadomości .
Uwzględnienie takiej alternatywy w modelu przetwarzania rozproszonego, jakim jest zbiór częściowo uporządkowany , jest oczywiście możliwe przez stosowną zmianę zbioru i definicji relacji poprzedzania. Dlatego też w literaturze zbiór uporządkowany przyjmuje się często za ogólny model przetwarzania, reprezentujący wszystkie możliwe jego realizacje.