PEE Moduł 7: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „,...,” na „,\ldots,” |
||
| (Nie pokazano 13 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd1.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd1.png|500px]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 7: | Linia 7: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd2.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd2.png|500px]] | ||
|valign="top"|'''Podstawowe pojęcia stanów nieustalonych ''' | |valign="top"|'''Podstawowe pojęcia stanów nieustalonych ''' | ||
| Linia 22: | Linia 22: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd3.png|500px]] | ||
|valign="top"|Z podstawowych praw rządzących obwodami elektrycznymi wynika, że w rezultacie przełączenia zachowana zostaje ciągłość sumy ładunków kondensatorów dołączonych do węzła. Oznacza to, że suma ładunków kondensatorów dołączonych do takiego węzła przed przełączeniem jest równa sumie ładunków kondensatorów dołączonych do tych węzłów po przełączeniu. Zasada ta wynika stąd, że do danego węzła nie może dopłynąć skończony ładunek w zerowym czasie. | |valign="top"|Z podstawowych praw rządzących obwodami elektrycznymi wynika, że w rezultacie przełączenia zachowana zostaje ciągłość sumy ładunków kondensatorów dołączonych do węzła. Oznacza to, że suma ładunków kondensatorów dołączonych do takiego węzła przed przełączeniem jest równa sumie ładunków kondensatorów dołączonych do tych węzłów po przełączeniu. Zasada ta wynika stąd, że do danego węzła nie może dopłynąć skończony ładunek w zerowym czasie. | ||
| Linia 29: | Linia 29: | ||
'''Prawo komutacji dotyczące kondensatorów''' | '''Prawo komutacji dotyczące kondensatorów''' | ||
Suma ładunków kondensatorów dołączonych do danego węzła nie może zmienić się w sposób skokowy na skutek komutacji, co można zapisać w postaci (w równaniu przyjęto, że komutacja zachodzi w chwili <math>t_0=0\ | Suma ładunków kondensatorów dołączonych do danego węzła nie może zmienić się w sposób skokowy na skutek komutacji, co można zapisać w postaci (w równaniu przyjęto, że komutacja zachodzi w chwili <math>t_0=0\ </math>,) | ||
: <math>\Sigma_iq_i(0^-)=\Sigma_iq_i(0^+)</math> | : <math>\Sigma_iq_i(0^-)=\Sigma_iq_i(0^+)</math> | ||
| Linia 41: | Linia 41: | ||
'''Prawo komutacji dotyczące cewek''' | '''Prawo komutacji dotyczące cewek''' | ||
Suma strumieni skojarzonych cewek należących do danego oczka nie może ulec skokowej zmianie na skutek przełączenia w obwodzie, co można zapisać w postaci (w równaniu przyjęto, że komutacja zachodzi w chwili <math>t_0=0\ | Suma strumieni skojarzonych cewek należących do danego oczka nie może ulec skokowej zmianie na skutek przełączenia w obwodzie, co można zapisać w postaci (w równaniu przyjęto, że komutacja zachodzi w chwili <math>t_0=0\ </math>,) | ||
: <math>\Sigma_i\psi_i(0^-)=\Sigma_i\psi_i(0^+)</math> | : <math>\Sigma_i\psi_i(0^-)=\Sigma_i\psi_i(0^+)</math> | ||
| Linia 55: | Linia 55: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd3a.png|500px]] | ||
|valign="top"|Przy założeniu, że chwilę komutacji uważać będziemy za chwilę początkową analizy obwodu w stanie nieustalonym <math>(t_0=0)</math> istotnym problemem w analizie obwodu jest wyznaczenie warunków początkowych procesu, czyli wartości napięć na kondensatorach i prądów cewek w chwili przełączenia (u nas <math>i_L(0^-)</math> oraz <math>u_C(0^-)</math> ). Zwykle przyjmuje się, że przełączenie następuje ze stanu ustalonego obwodu. Warunki początkowe wynikają wówczas z wartości ustalonych tych wielkości w chwili tuż przed przełączeniem <math>(t_0=0^-)</math> . Warunki początkowe mogą być przy tym zerowe, jeśli prądy wszystkich cewek i napięcia wszystkich kondensatorów w chwili przełączenia miały wartości zerowe. Znajomość warunków początkowych w obwodzie jest niezbędna przy wyznaczaniu rozwiązania obwodu w stanie nieustalonym. | |valign="top"|Przy założeniu, że chwilę komutacji uważać będziemy za chwilę początkową analizy obwodu w stanie nieustalonym <math>(t_0=0)</math> istotnym problemem w analizie obwodu jest wyznaczenie warunków początkowych procesu, czyli wartości napięć na kondensatorach i prądów cewek w chwili przełączenia (u nas <math>i_L(0^-)</math> oraz <math>u_C(0^-)</math> ). Zwykle przyjmuje się, że przełączenie następuje ze stanu ustalonego obwodu. Warunki początkowe wynikają wówczas z wartości ustalonych tych wielkości w chwili tuż przed przełączeniem <math>(t_0=0^-)</math> . Warunki początkowe mogą być przy tym zerowe, jeśli prądy wszystkich cewek i napięcia wszystkich kondensatorów w chwili przełączenia miały wartości zerowe. Znajomość warunków początkowych w obwodzie jest niezbędna przy wyznaczaniu rozwiązania obwodu w stanie nieustalonym. | ||
| Linia 67: | Linia 67: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd4.png|500px]] | ||
|valign="top"|'''Opis obwodu elektrycznego za pomocą równań stanu ''' | |valign="top"|'''Opis obwodu elektrycznego za pomocą równań stanu ''' | ||
| Linia 77: | Linia 77: | ||
: <math>\frac{dx_2}{dt}=a_2_1x_1+a_2_2 x_2+ ...+ a_2_n x_n + f_2(t)</math> | : <math>\frac{dx_2}{dt}=a_2_1x_1+a_2_2 x_2+ ...+ a_2_n x_n + f_2(t)</math> | ||
: <math>\cdots | : <math>\cdots</math> | ||
: <math>\frac{dx_n}{dt}=a_n_1x_1+a_n_2 x_2+ ...+ a_n_n x_n + f_n(t)</math> | : <math>\frac{dx_n}{dt}=a_n_1x_1+a_n_2 x_2+ ...+ a_n_n x_n + f_n(t)</math> | ||
Zmienne <math>x_1, x_2, \cdots, x_n</math> występujące w równaniach oznaczają prądy cewek lub napięcia kondensatorów (tzw. '''zmienne stanu'''). W opisie obwodu operuje się zwykle minimalnym zbiorem zmiennych stanu, które są niezbędne dla wyznaczenia pozostałych wielkości w obwodzie. Liczba zmiennych stanu n zależy od liczby reaktancji w obwodzie i jest najczęściej równa (w szczególnych przypadkach mniejsza) sumie liczby kondensatorów i cewek włączonych w obwodzie. Stałe współczynniki <math>a_i_j\ | Zmienne <math>x_1, x_2, \cdots, x_n</math> występujące w równaniach oznaczają prądy cewek lub napięcia kondensatorów (tzw. '''zmienne stanu'''). W opisie obwodu operuje się zwykle minimalnym zbiorem zmiennych stanu, które są niezbędne dla wyznaczenia pozostałych wielkości w obwodzie. Liczba zmiennych stanu n zależy od liczby reaktancji w obwodzie i jest najczęściej równa (w szczególnych przypadkach mniejsza) sumie liczby kondensatorów i cewek włączonych w obwodzie. Stałe współczynniki <math>a_i_j\ </math>, występujące w równaniu stanowią kombinacje wartości parametrów R, L, C, M elementów pasywnych obwodu oraz parametrów źródeł sterowanych. Funkcje czasu <math>f_1(t), f_2(t), ..., f_n(t)</math> związane są z wymuszeniami napięciowymi i prądowymi w obwodzie. | ||
|} | |} | ||
| Linia 88: | Linia 88: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd5.png|500px]] | ||
|valign="top"|W przypadku obwodów liniowych funkcje <math>f_i(t)</math> występujące po prawej stronie wzoru są liniowymi funkcjami wymuszeń prądowych i napięciowych. Oznaczając wymuszenia prądowe bądź napięciowe w ogólności przez <math>u_i (i=1, 2, | |valign="top"|W przypadku obwodów liniowych funkcje <math>f_i(t)</math> występujące po prawej stronie wzoru są liniowymi funkcjami wymuszeń prądowych i napięciowych. Oznaczając wymuszenia prądowe bądź napięciowe w ogólności przez <math>u_i (i=1, 2,\ldots,m)</math> można opis stanowy obwodu przedstawić w postaci | ||
: <math>\frac{d\mathbf{x}(t)}{dt}=\mathbf{Ax}(t)+\mathbf{Bu}(t)</math> | : <math>\frac{d\mathbf{x}(t)}{dt}=\mathbf{Ax}(t)+\mathbf{Bu}(t)</math> | ||
gdzie <math>\mathbf{A}\ </math>, jest macierzą stanu o wymiarach <math>n×n\ </math>, zawierającą elementy <math>a_i_j\ </math>,, a macierz <math>\mathbf{B}\ </math>, o wymiarach <math>n×m\ </math>, składa się ze współczynników uzależniających pochodną zmiennych stanu od wektora wymuszeń <math>\mathbf{u}\ </math>,. | |||
gdzie <math>\mathbf{A}\ | |||
Jest to ogólna postać opisu stanowego obwodu liniowego RLC. Reprezentuje ona układ <math>n</math> równań różniczkowych liniowych rzędu pierwszego. Elementy macierzy <math>\mathbf{A}</math> i <math>\mathbf{B}</math> zależą wyłącznie od wartości parametrów obwodu. Elementy wektora u stanowią źródła niezależne prądu i napięcia w obwodzie. Zmienne stanu to niezależne napięcia na kondensatorach i prądy cewek. | Jest to ogólna postać opisu stanowego obwodu liniowego RLC. Reprezentuje ona układ <math>n</math> równań różniczkowych liniowych rzędu pierwszego. Elementy macierzy <math>\mathbf{A}</math> i <math>\mathbf{B}</math> zależą wyłącznie od wartości parametrów obwodu. Elementy wektora u stanowią źródła niezależne prądu i napięcia w obwodzie. Zmienne stanu to niezależne napięcia na kondensatorach i prądy cewek. | ||
Równanie nazywane jest macierzowym równaniem stanu obwodu elektrycznego. Rozwiązanie tego równania pozwala wyznaczyć przebiegi czasowe zmiennych stanu tworzących wektor <math>\mathbf{x}(t)\ | Równanie nazywane jest macierzowym równaniem stanu obwodu elektrycznego. Rozwiązanie tego równania pozwala wyznaczyć przebiegi czasowe zmiennych stanu tworzących wektor <math>\mathbf{x}(t)\ </math>,. Jeśli dodatkowo interesują nas inne zmienne w obwodzie, na przykład prądy i napięcia rezystorów, prądy kondensatorów czy napięcia na cewkach to należy sformułować drugie równanie, tzw. równanie odpowiedzi <math>\mathbf{y}(t)\ </math>,, które uzależnia poszukiwane wielkości od zmiennych stanu i wymuszeń. Równanie to zapiszemy w postaci | ||
: <math>\mathbf{y}(t)=\mathbf{Cx}(t)+\mathbf{Du}(t)</math> | : <math>\mathbf{y}(t)=\mathbf{Cx}(t)+\mathbf{Du}(t)</math> | ||
Równania tworzą parę równań stanu | Równania tworzą parę równań stanu | ||
| Linia 113: | Linia 109: | ||
która w pełni opisuje stan obwodu przy założeniu, że znane są warunki początkowe <math>\mathbf{x}_0=\mathbf{x}(t0)</math>, gdzie <math>t_0\ | która w pełni opisuje stan obwodu przy założeniu, że znane są warunki początkowe <math>\mathbf{x}_0=\mathbf{x}(t0)</math>, gdzie <math>t_0\ </math>, oznacza chwilę przełączenia. W przypadku ogólnym rozwiązanie równania stanu przyjmuje postać | ||
: <math>\mathbf{x}(t)=e^{\mathbf{A}(t-t_0)}\mathbf{x}(t_0)+\int_{t_0}^t e^{\mathbf{A}(t-\tau)}\mathbf{Bu}(\tau)d\tau</math> | : <math>\mathbf{x}(t)=e^{\mathbf{A}(t-t_0)}\mathbf{x}(t_0)+\int_{t_0}^t e^{\mathbf{A}(t-\tau)}\mathbf{Bu}(\tau)d\tau</math> | ||
Zależność powyższa stanowi rozwiązanie ogólne, które dla konkretnych wartości funkcji wymuszających zadanych wektorem u wyznacza rozwiązanie czasowe dla zmiennych stanu. We współczesnych metodach numerycznych równania stanu stanowią punkt wyjścia w określaniu dokładnego rozwiązania równań liniowych lub przybliżonego dla zlinearyzowanych równań stanu. | Zależność powyższa stanowi rozwiązanie ogólne, które dla konkretnych wartości funkcji wymuszających zadanych wektorem u wyznacza rozwiązanie czasowe dla zmiennych stanu. We współczesnych metodach numerycznych równania stanu stanowią punkt wyjścia w określaniu dokładnego rozwiązania równań liniowych lub przybliżonego dla zlinearyzowanych równań stanu. | ||
| Linia 125: | Linia 119: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd6.png|500px]] | ||
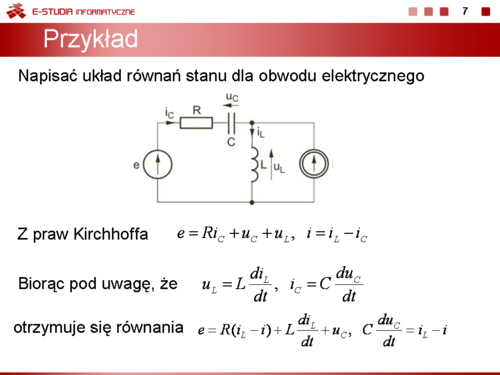
|valign="top"|Kolejny przykład pokazuje jak napisać układ równań stanu dla obwodu elektrycznego. | |valign="top"|Kolejny przykład pokazuje jak napisać układ równań stanu dla obwodu elektrycznego. Z praw Kirchhoffa napisanych dla obwodu z rysunku obok wynikają następujące równania | ||
Z praw Kirchhoffa napisanych dla obwodu z rysunku obok wynikają następujące równania | |||
: <math>e=Ri_C+u_C+u_L</math> | : <math>e=Ri_C+u_C+u_L</math> | ||
: <math>i=i_L=L-i_C</math> | : <math>i=i_L=L-i_C</math> | ||
Biorąc pod uwagę, że | Biorąc pod uwagę, że | ||
: <math>u_L=L\frac{di_L}{dt}</math>, <math>i_C=C\frac{du_C}{dt}</math> | : <math>u_L=L\frac{di_L}{dt}</math>, <math>i_C=C\frac{du_C}{dt}</math> | ||
równania Kirchhoffa można przekształcić do równoważnej postaci równań różniczkowych | równania Kirchhoffa można przekształcić do równoważnej postaci równań różniczkowych | ||
| Linia 146: | Linia 135: | ||
: <math>C\frac{du_C}{dt}=i_L-i</math> | : <math>C\frac{du_C}{dt}=i_L-i</math> | ||
które przyjmują uporządkowaną formę odpowiadającą postaci | które przyjmują uporządkowaną formę odpowiadającą postaci | ||
| Linia 158: | Linia 146: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd7.png|500px]] | ||
|valign="top"|Równania powyższe można zapisać w postaci zależności macierzowej równania stanu, w której zmiennymi stanu są prąd cewki i napięcie kondensatora | |valign="top"|Równania powyższe można zapisać w postaci zależności macierzowej równania stanu, w której zmiennymi stanu są prąd cewki i napięcie kondensatora | ||
: <math>\begin{bmatrix}\frac{di_L}{dt}\\ \frac{du_C}{dt}\end{bmatrix}=\begin{bmatrix}\frac{-R}{L}&\frac{-1}{L} \\ \frac{1}{C}& 0\end{bmatrix}\begin{bmatrix}i_L\\u_C\end{bmatrix}+\begin{bmatrix}\frac{1}{L}&\frac{R}{L}\\ 0& \frac{-1}{C}\end{bmatrix}\begin{bmatrix}e\\i\end{bmatrix}</math> | : <math>\begin{bmatrix}\frac{di_L}{dt}\\ \frac{du_C}{dt}\end{bmatrix}=\begin{bmatrix}\frac{-R}{L}&\frac{-1}{L} \\ \frac{1}{C}& 0\end{bmatrix}\begin{bmatrix}i_L\\u_C\end{bmatrix}+\begin{bmatrix}\frac{1}{L}&\frac{R}{L}\\ 0& \frac{-1}{C}\end{bmatrix}\begin{bmatrix}e\\i\end{bmatrix}</math> | ||
Wektor stanu <math>\mathbf{x}</math> oraz wektor wymuszeń <math>\mathbf{u}</math> są równe | Wektor stanu <math>\mathbf{x}</math> oraz wektor wymuszeń <math>\mathbf{u}</math> są równe | ||
: <math>\mathbf{x}=\begin{bmatrix}i_l\\u_C\end{bmatrix}</math>, <math>\mathbf{u}=\begin{bmatrix}e\\i\end{bmatrix}</math> | : <math>\mathbf{x}=\begin{bmatrix}i_l\\u_C\end{bmatrix}</math>, <math>\mathbf{u}=\begin{bmatrix}e\\i\end{bmatrix}</math> | ||
Obwód liniowy zawierający dwa elementy reaktancyjne (cewka i kondensator) opisuje się więc macierzowym równaniem stanu drugiego rzędu. Macierz stanu <math>\mathbf{A}</math> jest macierzą również drugiego rzędu o współczynnikach uzależnionych od wartości rezystancji, pojemności oraz indukcyjności. Macierz <math>\mathbf{B}</math> zawiera dwa wiersze (liczba zmiennych stanu) oraz dwie kolumny (liczba wymuszeń w obwodzie). Przyjmując w analizie wartości liczbowe obwodu: <math>R=2\Omega, L=1H, C=1F</math> otrzymuje się macierz stanu <math>\mathbf{A}</math> o postaci | Obwód liniowy zawierający dwa elementy reaktancyjne (cewka i kondensator) opisuje się więc macierzowym równaniem stanu drugiego rzędu. Macierz stanu <math>\mathbf{A}</math> jest macierzą również drugiego rzędu o współczynnikach uzależnionych od wartości rezystancji, pojemności oraz indukcyjności. Macierz <math>\mathbf{B}</math> zawiera dwa wiersze (liczba zmiennych stanu) oraz dwie kolumny (liczba wymuszeń w obwodzie). Przyjmując w analizie wartości liczbowe obwodu: <math>R=2\Omega, L=1H, C=1F</math> otrzymuje się macierz stanu <math>\mathbf{A}</math> o postaci | ||
: <math>\mathbf{A}=\begin{bmatrix}-2&-1\\1&0\end{bmatrix}</math> | : <math>\mathbf{A}=\begin{bmatrix}-2&-1\\1&0\end{bmatrix}</math> | ||
| Linia 179: | Linia 163: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd8.png|500px]] | ||
|valign="top"|'''Rozwiązanie równań różniczkowych metodą klasyczną ''' | |valign="top"|'''Rozwiązanie równań różniczkowych metodą klasyczną ''' | ||
| Linia 195: | Linia 179: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd9.png|500px]] | ||
|valign="top"|Składowa przejściowa zależy jedynie od warunków początkowych odniesionych do tej składowej (napięć początkowych kondensatorów i prądów początkowych cewek), struktury obwodu i wartości parametrów tego obwodu. Dla obwodów elektrycznych zawierających elementy rozpraszające energię (rezystancje) składowa przejściowa, jak zostanie pokazane później, zanika z biegiem czasu do zera. Równanie składowej przejściowej otrzymuje się zakładając wymuszenie <math>f(t)\ | |valign="top"|Składowa przejściowa zależy jedynie od warunków początkowych odniesionych do tej składowej (napięć początkowych kondensatorów i prądów początkowych cewek), struktury obwodu i wartości parametrów tego obwodu. Dla obwodów elektrycznych zawierających elementy rozpraszające energię (rezystancje) składowa przejściowa, jak zostanie pokazane później, zanika z biegiem czasu do zera. Równanie składowej przejściowej otrzymuje się zakładając wymuszenie <math>f(t)\ </math>, we wzorze równe zeru i zastępując zmienną <math>x(t)\ </math>, poprzez jej składową przejściową <math>x_p(t)\ </math>, . Otrzymuje się wówczas równanie różniczkowe jednorodne o postaci | ||
| Linia 205: | Linia 189: | ||
: <math>a_ns^n+a_{n-1}s^{n-1}+a_{n-2}s^{n-2}+...+a_1s | : <math>a_ns^n+a_{n-1}s^{n-1}+a_{n-2}s^{n-2}+...+a_1s+a_0=0</math> | ||
Jest to wielomian n-tego rzędu zmiennej zespolonej s o współczynnikach rzeczywistych <math>a_i\ | Jest to wielomian n-tego rzędu zmiennej zespolonej s o współczynnikach rzeczywistych <math>a_i\ </math>, Pierwiastki <math>s_i (i=1, 2,\ldots, n)</math> tego wielomianu stanowią '''bieguny układu'''. | ||
|} | |} | ||
| Linia 214: | Linia 198: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd10.png|500px]] | ||
|valign="top"|W tym punkcie ograniczymy się jedynie do przypadku biegunów pojedynczych. Przy takim założeniu rozwiązanie równania dla składowej przejściowej zapiszemy w postaci | |valign="top"|W tym punkcie ograniczymy się jedynie do przypadku biegunów pojedynczych. Przy takim założeniu rozwiązanie równania dla składowej przejściowej zapiszemy w postaci | ||
: <math>x_p(t)=\Sigma_{i=1}^n A_i e^{s_it}</math> | : <math>x_p(t)=\Sigma_{i=1}^n A_i e^{s_it}</math> | ||
W rozwiązaniu tym współczynniki <math>A_i\ | W rozwiązaniu tym współczynniki <math>A_i\ </math>, są stałymi całkowania, które należy wyznaczyć wykorzystując znajomość warunków początkowych w obwodzie (napięć kondensatorów i prądów cewek w chwili komutacji <math>t=0\ </math>,). Z ciągłości prądów cewek i napięć kondensatorów wynika następująca zależność | ||
: <math>x(0^-)=x(0^+)</math> | : <math>x(0^-)=x(0^+)</math> | ||
Pisząc tę równość dla wszystkich n zmiennych stanu otrzymuje się n równań algebraicznych z n nieznanymi współczynnikami . Z rozwiązania tego układu wyznacza się wszystkie współczynniki <math>A_i\ | Pisząc tę równość dla wszystkich n zmiennych stanu otrzymuje się n równań algebraicznych z n nieznanymi współczynnikami . Z rozwiązania tego układu wyznacza się wszystkie współczynniki <math>A_i\ </math>, i podstawia do wzoru ogólnego . Po wyznaczeniu rozwiązania obwodu dla składowej ustalonej i przejściowej rozwiązanie całkowite jest sumą obu rozwiązań cząstkowych, to znaczy | ||
<math>x(t)=x_u(t)+x_p(t)</math> | <math>x(t)=x_u(t)+x_p(t)</math> | ||
| Linia 233: | Linia 217: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd11.png|500px]] | ||
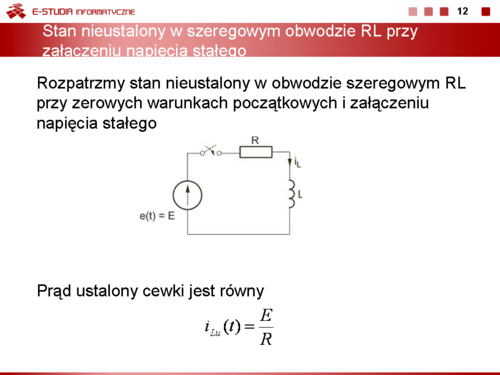
|valign="top"|'''Stan nieustalony w szeregowym obwodzie RL przy załączeniu napięcia stałego ''' | |valign="top"|'''Stan nieustalony w szeregowym obwodzie RL przy załączeniu napięcia stałego ''' | ||
| Linia 248: | Linia 232: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd12.png|500px]] | ||
|valign="top"|Przechodząc do obliczenia stanu przejściowego należy wyeliminować zewnętrzne źródło zasilające. Ponieważ jest to źródło napięciowe, należy go zewrzeć. Schemat obwodu dla stanu przejściowego po zwarciu źródła zasilającego, dla którego odpowiedź została właśnie obliczona, ma postać przedstawioną na rysunku. Stosując prawo napięciowe Kirchhoffa dla tego obwodu przy uwzględnieniu | |valign="top"|Przechodząc do obliczenia stanu przejściowego należy wyeliminować zewnętrzne źródło zasilające. Ponieważ jest to źródło napięciowe, należy go zewrzeć. Schemat obwodu dla stanu przejściowego po zwarciu źródła zasilającego, dla którego odpowiedź została właśnie obliczona, ma postać przedstawioną na rysunku. Stosując prawo napięciowe Kirchhoffa dla tego obwodu przy uwzględnieniu | ||
| Linia 277: | Linia 261: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd13.png|500px]] | ||
|valign="top"|Z prawa komutacji dla cewki wynika, że <math>i_L(0^-)=i_L(0^+)</math>, stąd wobec <math>i_L(0^-)=0</math> otrzymuje się | |valign="top"|Z prawa komutacji dla cewki wynika, że <math>i_L(0^-)=i_L(0^+)</math>, stąd wobec <math>i_L(0^-)=0</math> otrzymuje się | ||
| Linia 290: | Linia 274: | ||
: <math>i_L(t)=\frac{E}{R}(1-e^{-\frac{t}{L/R}})</math> | : <math>i_L(t)=\frac{E}{R}(1-e^{-\frac{t}{L/R}})</math> | ||
Wprowadzając pojęcie stałej czasowej <math>\tau\ | Wprowadzając pojęcie stałej czasowej <math>\tau\ </math>, obwodu RL | ||
: <math>\tau=\frac{L}{R}</math> | : <math>\tau=\frac{L}{R}</math> | ||
| Linia 312: | Linia 296: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd13a.png|500px]] | ||
|valign="top"| | |valign="top"|Wyznaczenie rozwiązania na prąd w stanie nieustalonym w obwodzie RL pozwala na określenie przebiegu czasowego pozostałych wielkości w obwodzie. Korzystając z zależności definicyjnej cewki otrzymuje się | ||
: <math>u_L(t)=L\frac{di_L(t)}{dt}=Ee^{-\frac{t}{L/R}}</math> | |||
Przebieg napięcia na cewce w stanie nieustalonym w obwodzie szeregowym RL przedstawiono na rysunku | |||
[[Grafika:PEE_M7_anim_14xx.gif]] | |||
Napięcie na rezystorze R, jak wynika z prawa Ohma, jest proporcjonalne do prądu | |||
: <math>u_R(t)=Ri_L(t)=E(1-e^{-\frac{t}{L/R}})</math> | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd14.png|500px]] | ||
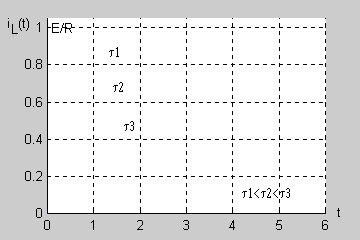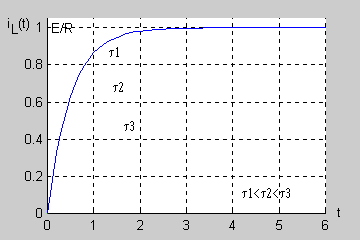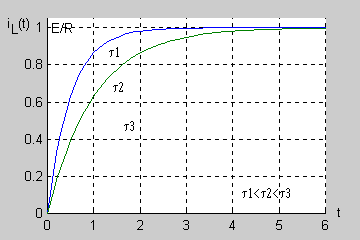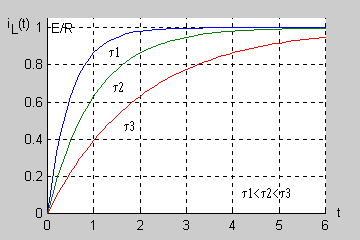
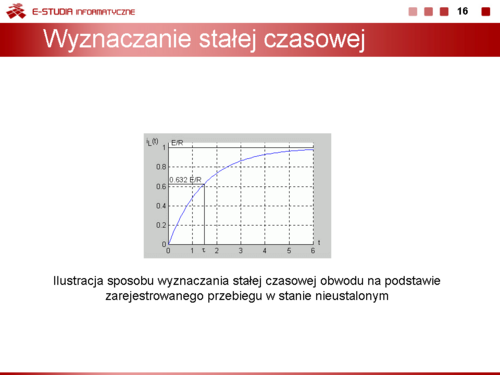
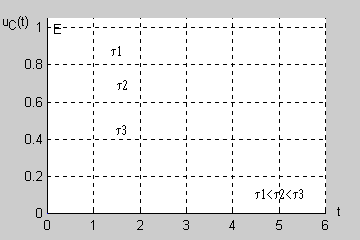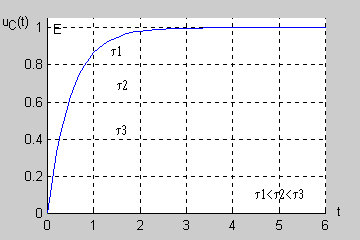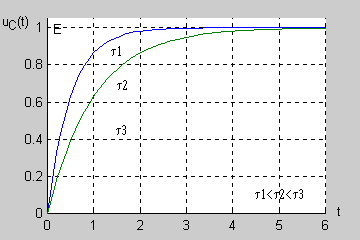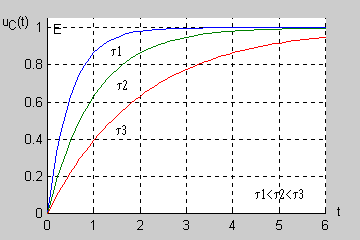
|valign="top"| | |valign="top"|Stałą czasową obwodu RL można wyznaczyć na podstawie zarejestrowanego przebiegu nieustalonego bez znajomości wartości rezystancji i indukcyjności. Zauważmy, że dla prąd cewki przyjmuje wartość | ||
: <math>i_L(\tau)=\frac{E}{R}(1-e^{-1})=0,632\frac{E}{R}</math> | |||
Oznacza to, że wartość prądu <math>i_L(t)|_{t=\tau}=0,632\frac{E}{R}</math> wyznacza na osi odciętych wartość stałej czasowej. Sposób wyznaczania stałej czasowej zilustrowany jest na rysunku | |||
: | [[Grafika:PEE_M7_anim_13_b.gif]] | ||
|} | |} | ||
| Linia 346: | Linia 330: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd15.png|500px]] | ||
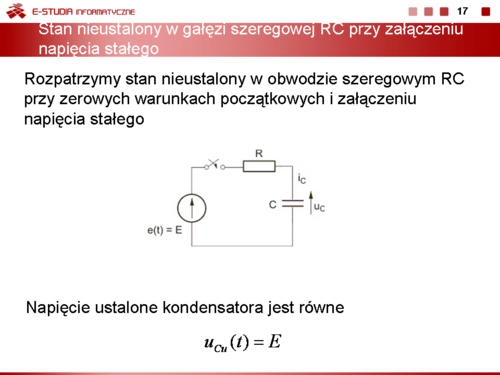
|valign="top"|'''Stan nieustalony w gałęzi szeregowej RC przy załączeniu napięcia stałego ''' | |valign="top"|'''Stan nieustalony w gałęzi szeregowej RC przy załączeniu napięcia stałego ''' | ||
| Linia 363: | Linia 347: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd16.png|500px]] | ||
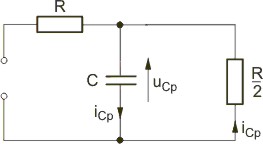
|valign="top"|Schemat obwodu dla stanu przejściowego (po zwarciu źródła zasilającego, dla którego odpowiedź została właśnie obliczona) ma postać przedstawioną na rysunku Stosując prawo napięciowe Kirchhoffa dla tego obwodu i uwzględniając, że <math>i_{Cp}=C\frac{du_{Cp}}{dt}</math>, otrzymuje się równanie różniczkowe jednorodne o postaci | |valign="top"|Schemat obwodu dla stanu przejściowego (po zwarciu źródła zasilającego, dla którego odpowiedź została właśnie obliczona) ma postać przedstawioną na rysunku Stosując prawo napięciowe Kirchhoffa dla tego obwodu i uwzględniając, że <math>i_{Cp}=C\frac{du_{Cp}}{dt}</math>, otrzymuje się równanie różniczkowe jednorodne o postaci | ||
| Linia 376: | Linia 360: | ||
: <math>u_{Cp}=A_1e^{s_1t}=A_1e^{-\frac{t}{RC}}</math> | : <math>u_{Cp}=A_1e^{s_1t}=A_1e^{-\frac{t}{RC}}</math> | ||
W rozwiązaniu tym współczynnik <math>A_1\ | W rozwiązaniu tym współczynnik <math>A_1\ </math>, jest stałą całkowania, którą należy wyznaczyć korzystając z prawa komutacji. Rozwiązanie całkowite będące sumą składowej ustalonej i przejściowej przybiera więc postać | ||
: <math>u_C(t)=u_{Cu}(t)+u_{Cp}=E+A_1e^{-\frac{t}{RC}}</math> | : <math>u_C(t)=u_{Cu}(t)+u_{Cp}=E+A_1e^{-\frac{t}{RC}}</math> | ||
| Linia 384: | Linia 368: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd17.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd17.png|500px]] | ||
|valign="top"|Z prawa komutacji dla kondensatora wynika, że <math>u_C(0^-)=u_C(0^+)</math> , stąd wobec <math>u_C(0^-)=0</math> otrzymuje się | |valign="top"|Z prawa komutacji dla kondensatora wynika, że <math>u_C(0^-)=u_C(0^+)</math> , stąd wobec <math>u_C(0^-)=0</math> otrzymuje się | ||
| Linia 417: | Linia 401: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd18.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd18.png|500px]] | ||
|valign="top"|Po określeniu funkcji opisującej przebieg napięcia na kondensatorze można określić przebieg czasowy prądu w obwodzie. Korzysta się przy tym z zależności definicyjnej kondensatora, zgodnie z którą | |valign="top"|Po określeniu funkcji opisującej przebieg napięcia na kondensatorze można określić przebieg czasowy prądu w obwodzie. Korzysta się przy tym z zależności definicyjnej kondensatora, zgodnie z którą | ||
| Linia 436: | Linia 420: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd19.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd19.png|500px]] | ||
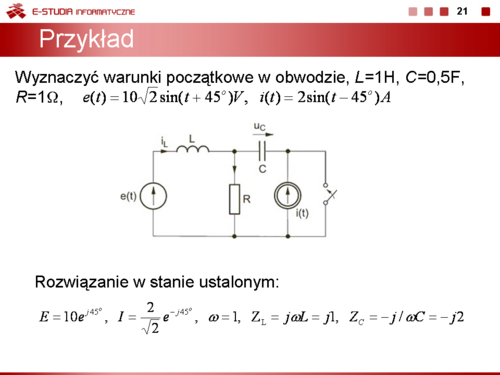
|valign="top"|Wyznaczyć warunki początkowe w obwodzie przedstawionym na rysunku. Parametry elementów obwodu są następujące: <math>L=1H, C=0,5F, R=1\Omega, e(t)=10\sqrt 2 sin( | |valign="top"|Wyznaczyć warunki początkowe w obwodzie przedstawionym na rysunku. Parametry elementów obwodu są następujące: <math>L=1H, C=0,5F, R=1\Omega, e(t)=10\sqrt 2 sin(t+45^o)V, i(t)=2sin(t-45^o)A</math> | ||
| Linia 444: | Linia 428: | ||
: <math>E=10e^{j45^o}</math> | : <math>E=10e^{j45^o}</math> | ||
: <math>I=\frac{2}{\sqrt 2}e^{- | : <math>I=\frac{2}{\sqrt 2}e^{-j45^o}</math> | ||
: <math>\omega=1</math> | : <math>\omega=1</math> | ||
| Linia 456: | Linia 440: | ||
<hr width="100%"> | <hr width="100%"> | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M7_Slajd20.png]] | |valign="top" width="500px"|[[Grafika:PEE_M7_Slajd20.png|500px]] | ||
|valign="top"|Równania obwodu w stanie ustalonym | |valign="top"|Równania obwodu w stanie ustalonym | ||
| Linia 463: | Linia 447: | ||
: <math>I_L=\frac{E-RI}{R+Z_L}=7,21e^{j11,31^o}</math> | : <math>I_L=\frac{E-RI}{R+Z_L}=7,21e^{j11,31^o}</math> | ||
: <math>U_C=Z_CI=\frac{4}{\sqrt 2}e^{-j135^ | : <math>U_C=Z_CI=\frac{4}{\sqrt 2}e^{-j135^o}</math> | ||
| Linia 512: | Linia 496: | ||
: <math>\begin{bmatrix}\frac{du_C}{dt}\\ \frac{di_L}{dt}\end{bmatrix}=\begin{bmatrix}0&-1/C\\1/L&0\end{bmatrix}\cdot\begin{bmatrix}u_C\\i_L\end{bmatrix}+\begin{bmatrix}0&1/C\\-1/L&0\end{bmatrix}\cdot\begin{bmatrix}e(t)\\i(t)\end{bmatrix}</math> | : <math>\begin{bmatrix}\frac{du_C}{dt}\\ \frac{di_L}{dt}\end{bmatrix}=\begin{bmatrix}0&-1/C\\1/L&0\end{bmatrix}\cdot\begin{bmatrix}u_C\\i_L\end{bmatrix}+\begin{bmatrix}0&1/C\\-1/L&0\end{bmatrix}\cdot\begin{bmatrix}e(t)\\i(t)\end{bmatrix}</math> | ||
---- | |||
''Zadanie 7.2'' | ''Zadanie 7.2'' | ||
Aktualna wersja na dzień 21:56, 15 wrz 2023

|

|
Równania obwodu w stanie ustalonym
|
| Zadania sprawdzające
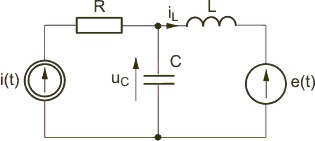
Napisać równanie stanu dla obwodu o strukturze przedstawionej na rysunku
Z praw Kirchhoffa napisanych dla obwodu z rysunku wynika
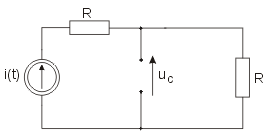
Zadanie 7.2 Określić przebieg czasowy napięcia na kondensatorze w stanie nieustalonym w obwodzie przedstawionym na rysunku Przyjąć następujące wartości parametrów: .
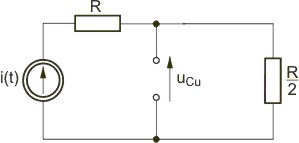
Warunki początkowe w obwodzie wynikają ze stanu ustalonego obwodu przed przełączeniem, który wobec wymuszenia stałego ma postać uproszczoną przedstawioną na rysunku Schemat obwodu w stanie ustalonym przed przełączeniem dla wymuszenia stałego
Schemat obwodu w stanie ustalonym po przełączeniu
Schemat obwodu w stanie przejściowym po przełączeniu
Stała czasowa obwodu jest więc równa . |