Analiza matematyczna 2/Wykład 13: Równania różniczkowe zwyczajne: Różnice pomiędzy wersjami
| (Nie pokazano 56 wersji utworzonych przez 4 użytkowników) | |||
| Linia 16: | Linia 16: | ||
Rozważmy kilka z tych problemów. | Rozważmy kilka z tych problemów. | ||
[[File:Am2w13.0010.svg|375x375px|thumb|left|Rysunek do przykładu 13.1.]] | |||
{{przyklad|13.1.|| | {{przyklad|13.1.|| | ||
(stygnięcie, ogrzewanie pewnej | (stygnięcie, ogrzewanie pewnej | ||
substancji) Z obserwacji wynika, że substancja stygnie | substancji) Z obserwacji wynika, że substancja stygnie | ||
(odpowiednio: ogrzewa się) tym szybciej, im większa jest różnica | (odpowiednio: ogrzewa się) tym szybciej, im większa jest różnica | ||
temperatury tej substancji i otoczenia. Jeśli <math> | temperatury tej substancji i otoczenia. Jeśli <math>x(t)</math> oznacza | ||
temperaturę substancji w chwili <math> | temperaturę substancji w chwili <math>t</math>, obserwację można sformułować | ||
następująco: zmiana temperatury substancji <math> | następująco: zmiana temperatury substancji <math>x(t+h)-x(t)</math> po | ||
upływie czasu <math> | upływie czasu <math>h</math> od pomiaru temperatury w chwili <math>t</math> jest | ||
proporcjonalna do różnicy temperatur <math> | proporcjonalna do różnicy temperatur <math>x(t)-x^*</math>, gdzie <math>x^*</math> | ||
oznacza temperaturę otoczenia, co można zapisać za pomocą równości | oznacza temperaturę otoczenia, co można zapisać za pomocą równości | ||
<center><math> | <center> | ||
\frac{x(t+h)-x(t)}{h}\approx-\lambda (x(t)-x^*), \ \ x(t_0)=x_0 | <math> | ||
</math></center> | \frac{x(t+h)-x(t)}{h}\approx-\lambda (x(t)-x^*), \ \ x(t_0)=x_0</math>, | ||
</center> | |||
gdzie <math> | gdzie <math>\lambda>0</math> jest pewną stałą, a <math>x_0</math> oznacza temperaturę | ||
substancji, którą zanotowaliśmy na początku obserwacji w chwili | substancji, którą zanotowaliśmy na początku obserwacji w chwili | ||
<math> | <math>t_0</math>. Znak minus, który poprzedza różnicę <math>x(t)-x^*</math> bierze się | ||
stąd, że substancja stygnie (czyli <math> | stąd, że substancja stygnie (czyli <math>x(t+h)-x(t)<0</math> po upływie | ||
czasu <math> | czasu <math>h>0</math>), gdy ma wyższą temperaturę niż otoczenie (tj. gdy | ||
<math> | <math>x(t)-x^*>0</math>) albo ogrzewa się (czyli <math>x(t+h)-x(t)>0</math> po upływie | ||
czasu <math> | czasu <math>h>0</math>), gdy otoczenie ma wyższą temperaturę niż obserwowana | ||
substancja (tj. gdy <math> | substancja (tj. gdy <math>x(t)-x^*<0</math>). Jeśli odcinki czasu pomiędzy | ||
kolejnymi pomiarami temperatury będą małe, w granicy zależność, | kolejnymi pomiarami temperatury będą małe, w granicy zależność, | ||
którą sformułowaliśmy, przyjmie postać: | którą sformułowaliśmy, przyjmie postać: | ||
<center><math> | <center> | ||
\frac{dx}{dt}(t)\ = -\lambda (x(t)-x^*), \ \ x(t_0)=x_0 | <math> | ||
</math></center> | \frac{dx}{dt}(t)\ = -\lambda (x(t)-x^*), \ \ x(t_0)=x_0</math> | ||
</center> | |||
Nietrudno odgadnąć (na przykład przyjmując wpierw dla ułatwienia | Nietrudno odgadnąć (na przykład przyjmując wpierw dla ułatwienia | ||
zadania, że temperatura otoczenia <math> | zadania, że temperatura otoczenia <math>x^*=0</math> jest zerowa), że | ||
zależność <math> | zależność <math>\frac{dx}{dt}(t) = -\lambda x(t)</math> spełnia funkcja | ||
wykładnicza <math> | wykładnicza <math>t\mapsto \exp (-\lambda t)</math>, a także każdy iloczyn | ||
tej funkcji przez stałą. Nasze doświadczenie podpowiada nam, że w | tej funkcji przez stałą. Nasze doświadczenie podpowiada nam, że w | ||
trakcie obserwacji dwóch identycznych próbek substancji, które | trakcie obserwacji dwóch identycznych próbek substancji, które | ||
| Linia 53: | Linia 56: | ||
stojące obok siebie), po upływie określonego czasu zauważymy, że | stojące obok siebie), po upływie określonego czasu zauważymy, że | ||
obie będą mieć taką samą temperaturę. Zbudowany model matematyczny | obie będą mieć taką samą temperaturę. Zbudowany model matematyczny | ||
<center><math> | <center> | ||
\frac{dx}{dt}(t)\ = -\lambda x(t), \ \ x(t_0)=x_0 | <math> | ||
</math></center> | \frac{dx}{dt}(t)\ = -\lambda x(t), \ \ x(t_0)=x_0</math>, | ||
</center> | |||
dostarcza dokładnie jednego rozwiązania i jest nim funkcja | dostarcza dokładnie jednego rozwiązania i jest nim funkcja | ||
<center><math> | <center> | ||
x(t)=x_0 \exp (-\lambda (t-t_0)) | <math> | ||
</math></center> | x(t)=x_0 \exp (-\lambda (t-t_0))</math>, | ||
</center> | |||
która spełnia warunek | która spełnia warunek | ||
<math> | <math>x(t_0)=x_0</math>, oznaczający, że temperatura substancji na początku | ||
obserwacji wynosiła <math> | obserwacji wynosiła <math>x_0</math>. | ||
Otrzymane rozwiązanie możemy również łatwo zmodyfikować tak, aby | Otrzymane rozwiązanie możemy również łatwo zmodyfikować tak, aby | ||
odpowiadało obserwacji w przypadku, gdy temperatura otoczenia | odpowiadało obserwacji w przypadku, gdy temperatura otoczenia | ||
<math> | <math>x^*</math> jest dowolna: | ||
<center><math> | <center><math>x(t)=x^* +(x_0-x^*) \exp (-\lambda (t-t_0)).</math></center> | ||
Naszkicujmy rodzinę krzywych, odpowiadających różnym wartościom | Naszkicujmy rodzinę krzywych, odpowiadających różnym wartościom | ||
temperatury początkowej.<br> | temperatury początkowej (patrz rysunek powyżej).<br> | ||
Niezależnie od temperatury początkowej <math>x_0</math> (w momencie <math>t_0=0</math>) | |||
wszystkie krzywe <math>t\mapsto x^* +(x_0-x^*) \exp (-\lambda t)</math> | |||
Niezależnie od temperatury początkowej <math> | zmierzają asymptotycznie do prostej <math>x=x^*</math>, co odpowiada | ||
wszystkie krzywe <math> | |||
zmierzają asymptotycznie do prostej <math> | |||
wielokrotnie czynionej przez nas obserwacji: wraz z upływem czasu | wielokrotnie czynionej przez nas obserwacji: wraz z upływem czasu | ||
wszystkie przedmioty, które znajdują się w pewnym pomieszczeniu (a | wszystkie przedmioty, które znajdują się w pewnym pomieszczeniu (a | ||
| Linia 94: | Linia 97: | ||
swobodnie w polu grawitacyjnym, spotkaliśmy się już w szkole na | swobodnie w polu grawitacyjnym, spotkaliśmy się już w szkole na | ||
lekcjach fizyki. Można przyjąć, że przyśpieszenie ziemskie jest (w | lekcjach fizyki. Można przyjąć, że przyśpieszenie ziemskie jest (w | ||
pobliżu powierzchni Ziemi) wielkością stałą <math> | pobliżu powierzchni Ziemi) wielkością stałą <math>g=9.81 | ||
\frac{m}{s^2}</math>. Pamiętając, że przyśpieszenie jest pochodną rzędu | \frac{m}{s^2}</math>. Pamiętając, że przyśpieszenie jest pochodną rzędu | ||
drugiego funkcji położenia <math> | drugiego funkcji położenia <math>t\mapsto x(t)</math>, otrzymujemy równanie | ||
<center><math> | <center><math>x''(t)=g</math>,</center> | ||
które po jednokrotnym całkowaniu spełnia przyjmuje | które po jednokrotnym całkowaniu spełnia przyjmuje | ||
postać | postać | ||
<center><math> | <center><math>x'(t)=gt+v_0</math>,</center> | ||
gdzie <math> | gdzie <math>v_0</math> jest prędkością w chwili <math>t_0=0</math>. Kolejne całkowanie | ||
prowadzi do znanego wzoru na położenie punktu materialnego w | prowadzi do znanego wzoru na położenie punktu materialnego w | ||
chwili <math> | chwili <math>t</math> w ruchu jednostajnie przyspieszonym: | ||
<center><math> | <center><math>x(t)=\frac{1}{2}gt^2+v_0t+x_0</math>,</center> | ||
gdzie <math> | gdzie <math>x_0</math> jest położeniem | ||
punktu w chwili początkowej <math> | punktu w chwili początkowej <math>t_0=0</math>.}} | ||
{{przyklad|13.3.|| | {{przyklad|13.3.|| | ||
| Linia 117: | Linia 120: | ||
organizmów w jednostce czasu jest proporcjonalna do liczby | organizmów w jednostce czasu jest proporcjonalna do liczby | ||
organizmów w danej chwili. Prowadzi to do równania | organizmów w danej chwili. Prowadzi to do równania | ||
<center><math> | <center><math>\frac{x(t+h)-x(t)}{h}\approx \lambda x(t)</math>,</center> | ||
w którym <math> | w którym <math>x(t)</math> oraz <math>x(t+h)</math> oznaczają liczebność grupy | ||
organizmów w chwili <math> | organizmów w chwili <math>t</math> oraz po upływie czasu <math>h</math>, natomiast | ||
<math> | <math>\lambda</math> jest stałą charakteryzującą tempo rozmnażania się danej | ||
grupy organizmów. Przy <math> | grupy organizmów. Przy <math>h\to 0</math> otrzymujemy równanie różniczkowe | ||
<center><math> | <center><math>x'=\lambda x</math>,</center> | ||
które spełnia funkcja <center><math> | które spełnia funkcja <center><math>x(t)=N_0 \exp(\lambda t)</math>,</center> | ||
gdzie stała | gdzie stała | ||
<math> | <math>N_0</math> oznacza liczebność grupy organizmów na początku obserwacji w | ||
chwili <math> | chwili <math>t=0</math>. Otrzymane równanie stanowi ilustrację '''''prawa | ||
Malthusa''''', które głosi, że wzrost liczebności organizmów jest | Malthusa''''', które głosi, że wzrost liczebności organizmów jest | ||
wykładniczy. | wykładniczy. | ||
}} | }} | ||
[[File:am2w13.0020.svg|375x375px|thumb|left|Rysunek do przykładu 13.4.]] | |||
{{przyklad|13.4.|| | [[grafika:Bernoulli.jpg|thumb|right||Jakob Bernoulli (1654-1705)<br>[[Biografia Bernoulli|Zobacz biografię]]]] | ||
{{przyklad|13.4.|prz_13_4| | |||
(zmodyfikowany model rozwoju grupy | (zmodyfikowany model rozwoju grupy | ||
organizmów) W realnym świecie wykładniczy wzrost liczby organizmów | organizmów) W realnym świecie wykładniczy wzrost liczby organizmów | ||
| Linia 140: | Linia 143: | ||
ograniczona, rozwój grupy organizmów lepiej niż prawo Malthusa | ograniczona, rozwój grupy organizmów lepiej niż prawo Malthusa | ||
opisuje równanie | opisuje równanie | ||
<center><math> | <center> | ||
x'=\lambda x(N-x) | <math> | ||
</math></center> | x'=\lambda x(N-x)</math>, | ||
</center> | |||
gdzie <math> | gdzie <math>N</math> jest pewną stałą. Jest to równanie Bernoullego | ||
<math> | <math>x'-N\lambda x=-\lambda x^2</math> (omawiamy je szerzej w ramach | ||
następnego modułu). Łatwo spostrzec, że spełniają je dwie funkcje | następnego modułu). Łatwo spostrzec, że spełniają je dwie funkcje | ||
stałe <math> | stałe <math>x(t)=N</math> oraz <math>x(t)=0</math>. Po podstawieniu <math>z=\frac{1}{x}</math> | ||
otrzymujemy równanie liniowe niejednorodne (które także omawiamy w | otrzymujemy równanie liniowe niejednorodne (które także omawiamy w | ||
ramach następnego modułu) | ramach następnego modułu) | ||
<center> | <center> | ||
<math> | <math> | ||
z'+\lambda N z=\lambda | z'+\lambda N z=\lambda</math>, | ||
</math> | |||
</center> | </center> | ||
| Linia 159: | Linia 161: | ||
spełnia każda funkcja postaci | spełnia każda funkcja postaci | ||
<center> | <center> | ||
<math> | <math> | ||
z(t)=\frac{1}{N}+C\exp(-\lambda N t) | z(t)=\frac{1}{N}+C\exp(-\lambda N t)</math>, | ||
</math> | |||
</center> | </center> | ||
gdzie <math> | gdzie <math>C</math> jest stałą. Jej wartość można określić, biorąc pod | ||
uwagę liczebność grupy <math> | uwagę liczebność grupy <math>N_0</math> w chwili <math>t=0</math>, czyli biorąc | ||
<math> | <math>z(0)=\frac{1}{N_0}</math>. Otrzymamy stąd | ||
<math> | <math>C=\frac{1}{N_0}-\frac{1}{N}</math>. Ostatecznie więc rozwiązaniem | ||
równania <math> | równania <math>x'=\lambda x(N-x)</math> jest funkcja | ||
<center> | <center> | ||
<math> | <math> | ||
x(t)= | x(t)= | ||
\left(\frac{1}{N}+\left(\frac{1}{N_0}-\frac{1}{N}\right) | \left(\frac{1}{N}+\left(\frac{1}{N_0}-\frac{1}{N}\right) | ||
\exp(-\lambda N t)\right)^{-1} | \exp(-\lambda N t)\right)^{-1}</math> | ||
</math> | |||
</center> | </center> | ||
Rozwiązanie stałe <math> | Rozwiązanie stałe <math>x(t)=N</math> jest szczególnym przypadkiem | ||
otrzymanego rozwiązania, gdy <math> | otrzymanego rozwiązania, gdy <math>N=N_0</math>.<br> | ||
Warto zwrócić uwagę na parę własności tego rozwiązania. Mamy | Warto zwrócić uwagę na parę własności tego rozwiązania. Mamy | ||
<math> | <math>x(t)\to N</math>, gdy <math>t\to \infty</math>, niezależnie od liczebności grupy w | ||
chwili początkowej. Stała <math> | chwili początkowej. Stała <math>N</math> ma naturalną interpretację | ||
biologiczną: jest to pojemność ekosystemu, zależna od m.in. ilości | biologiczną: jest to pojemność ekosystemu, zależna od m.in. ilości | ||
pożywienia dostępnego grupie organizmów na określonym obszarze. | pożywienia dostępnego grupie organizmów na określonym obszarze. | ||
Ponadto, jeśli <math> | Ponadto, jeśli <math>N_0<N</math> (odpowiednio: <math>N_0>N</math>), to liczebność grupy | ||
<math> | <math>t\mapsto x(t)</math> rośnie (odpowiednio: maleje) i zmierza | ||
asymptotycznie do <math> | asymptotycznie do <math>N</math>. Zauważmy także, że żadne z rozwiązań | ||
<math> | <math>t\mapsto x(t)</math> nie zmierza do zera, gdy tylko <math>N_0>0</math>. | ||
}} | }} | ||
| Linia 201: | Linia 199: | ||
opisuje równanie | opisuje równanie | ||
<center> | <center> | ||
<math> | <math>x''=-k^2x</math>,</center> | ||
gdzie <math> | gdzie <math>x</math> jest wielkością odkształcenia, a <math>k^2</math> | ||
jest stałą charakteryzującą ciało, które ulega odkształceniu | jest stałą charakteryzującą ciało, które ulega odkształceniu | ||
sprężystemu. Otrzymane równanie (równanie liniowe rzędu drugiego o | sprężystemu. Otrzymane równanie (równanie liniowe rzędu drugiego o | ||
stałych współczynnikach, które szerzej omawiamy w kolejnym module) | stałych współczynnikach, które szerzej omawiamy w kolejnym module) | ||
spełnia każda funkcja postaci | spełnia każda funkcja postaci | ||
<center><math> | <center><math> | ||
x(t)=A \cos(kt)+B\sin (kt) | x(t)=A \cos(kt)+B\sin (kt)</math>, | ||
</math> | |||
</center> | </center> | ||
gdzie <math> | gdzie <math>A, B</math> są stałymi, których wartość można określić na | ||
podstawie np. położenia <math> | podstawie np. położenia <math>x_0</math> i prędkości <math>v_0</math> w chwili | ||
początkowej <math> | początkowej <math>t=0</math>. Mamy bowiem <math>x'(t)=-Ak \sin(kt)+Bk\cos (kt)</math>, | ||
skąd | skąd | ||
<center><math> | <center><math> | ||
\left\{\ | \left\{\begin{align} x_0&=x(0)=A \cos(k\cdot 0)+B\sin (k\cdot 0)=A\\ | ||
v_0&=x'(0)=-Ak \sin(k\cdot 0)+Bk\cos (k\cdot 0)=Bk,\ | v_0&=x'(0)=-Ak \sin(k\cdot 0)+Bk\cos (k\cdot 0)=Bk,\end{align} \right.</math></center> | ||
</math></center> | |||
czyli <math> | czyli <math>A=x_0</math>, <math>B=\frac{v_0}{k}</math>. Zatem ruch końca sprężyny, który | ||
w chwili <math> | w chwili <math>t=0</math> odchylono o <math>x_0</math> i puszczono z prędkością | ||
początkową <math> | początkową <math>v_0</math>, opisuje równanie | ||
<center><math> | <center><math>x(t)=x_0 \cos(kt)+\frac{v_0}{k}\sin (kt)</math>.</center> | ||
Zauważmy, że otrzymana funkcja jest okresowa o okresie | Zauważmy, że otrzymana funkcja jest okresowa o okresie | ||
<math> | <math>T=\frac{2\pi}{k}</math> i ma stałą amplitudę, co w przypadku realnej | ||
sprężyny nie jest prawdą. Nasz model zaniedbuje bowiem tarcie, na | sprężyny nie jest prawdą. Nasz model zaniedbuje bowiem tarcie, na | ||
skutek którego ruch zanika (amplituda maleje do zera), gdy <math> | skutek którego ruch zanika (amplituda maleje do zera), gdy <math>t\to | ||
\infty</math>.}} | \infty</math>.}} | ||
| Linia 240: | Linia 236: | ||
{{definicja|13.6.|| | {{definicja|13.6.|| | ||
Niech <math> | Niech <math>F: \mathbb{R}^{n+1}\supset U\mapsto | ||
\mathbb{R}</math> będzie funkcją ciągłą na zbiorze otwartym <math> | \mathbb{R}</math> będzie funkcją ciągłą na zbiorze otwartym <math>U</math>. Równanie | ||
<center><math> | <center><math> | ||
F\left(t, x(t), x'(t), x''(t), \dots , x^{(n)}(t)\right)=0 | F\left(t, x(t), x'(t), x''(t), \dots , x^{(n)}(t)\right)=0</math>,</center> | ||
</math></center> | |||
z niewiadomą | z niewiadomą | ||
<math> | <math>t\mapsto x(t)</math> (tj. funkcją <math>n</math> krotnie różniczkowalną <math>t\mapsto | ||
x(t)</math>), w którym oprócz niewiadomej <math> | x(t)</math>), w którym oprócz niewiadomej <math>x</math> występują także jej | ||
pochodne <math> | pochodne <math>x', \ x'', \dots, x^{(n)}</math> nazywamy '''''równaniem | ||
różniczkowym zwyczajnym rzędu <math> | różniczkowym zwyczajnym rzędu <math>n</math>'''''. | ||
Niech <math> | Niech <math>\Delta\subset \mathbb{R}</math> będzie przedziałem (z końcami lub bez, | ||
ograniczonym lub nieograniczonym). Funkcję <center><math> | ograniczonym lub nieograniczonym). Funkcję <center><math>u:\Delta\to \mathbb{R}</math></center> | ||
nazywamy '''''rozwiązaniem''''' równania różniczkowego <math> | nazywamy '''''rozwiązaniem''''' równania różniczkowego <math> | ||
F\left(t, x(t), x'(t), x''(t), \dots , x^{(n)}(t)\right)=0 | F\left(t, x(t), x'(t), x''(t), \dots , x^{(n)}(t)\right)=0</math>, jeśli | ||
</math> jeśli | |||
1. <math> | 1. <math>u</math> jest <math>n</math>-krotnie różniczkowalna w każdym punkcie przedziału | ||
<math> | <math>\Delta</math> (przy czym na końcach przedziału, o ile do niego należą, | ||
bierzemy pod uwagę pochodne jednostronne); | bierzemy pod uwagę pochodne jednostronne); | ||
2. wykres funkcji <math> | 2. wykres funkcji <math>u</math> zawiera się w zbiorze <math>U</math>; | ||
3. dla dowolnego <math> | 3. dla dowolnego <math>t\in\Delta</math> zachodzi równość <math> | ||
F\left(t, u(t), u'(t), u''(t), \dots , u^{(n)}(t)\right)=0 | F\left(t, u(t), u'(t), u''(t), \dots , u^{(n)}(t)\right)=0 | ||
</math>. }} | </math>. }} | ||
| Linia 272: | Linia 266: | ||
zmiennych i równanie zawiera zależność od pochodnych cząstkowych | zmiennych i równanie zawiera zależność od pochodnych cząstkowych | ||
tej funkcji, na przykład | tej funkcji, na przykład | ||
<center><math> | <center><math> | ||
F\left(t,s, x(t,s), \frac{\partial x}{\partial t}, \frac{\partial x}{\partial | F\left(t,s, x(t,s), \frac{\partial x}{\partial t}, \frac{\partial x}{\partial | ||
s}, \dots \right)=0 | s}, \dots \right)=0</math>,</center> | ||
</math></center> | |||
to równanie tego typu nazywamy | to równanie tego typu nazywamy | ||
| Linia 281: | Linia 274: | ||
zajmować się równaniami zwyczajnym rzędu pierwszego w '''''postaci | zajmować się równaniami zwyczajnym rzędu pierwszego w '''''postaci | ||
normalnej''''' | normalnej''''' | ||
<center><math> | <center><math> | ||
x'(t)=f(t, x(t)) | x'(t)=f(t, x(t))</math>,</center> | ||
</math></center> | |||
tj. takiej postaci, w której pochodna niewiadomej <math> | tj. takiej postaci, w której pochodna niewiadomej <math>x</math> jest funkcją | ||
tej niewiadomej i zmiennej niezależnej <math> | tej niewiadomej i zmiennej niezależnej <math>t</math>. Mając bowiem dane | ||
równanie różniczkowe zwyczajne rzędu <math> | równanie różniczkowe zwyczajne rzędu <math>n</math> w postaci normalnej | ||
<center><math> | <center><math>x^{(n)}=f(t, x, x' , x'', \dots, x^{(n-1)})</math></center> | ||
możemy je zastąpić układem równań różniczkowych zwyczajnych rzędu | możemy je zastąpić układem równań różniczkowych zwyczajnych rzędu | ||
pierwszego w postaci normalnej: | pierwszego w postaci normalnej: | ||
<center><math> | <center><math>\left\{ \begin{align} | ||
x_0' | &x_0'=x_1 \\ &x_1 '=x_2 \\ &x_2'=x_3 \\ &\vdots \\ &x_{n-2}'=x_{n-1}\\ | ||
x_{n-1}' | &x_{n-1}'=f(t, x_0, x_1, x_2, \dots, x_{n-2}, x_{n-1}), | ||
\ | \end{align} \right.</math></center> | ||
</math></center> | |||
w którym zmienne <center><math> | w którym zmienne <center><math>x_0, \ x_1, \ x_2, \dots, \ x_{n-2}, x_{n-1}</math></center> | ||
x_{n-1}</math></center> | odpowiadają funkcji niewiadomej <math>x</math> oraz jej pochodnym | ||
odpowiadają funkcji niewiadomej <math> | <center><math>x, \ x', \ x'', \dots, \ x^{(n-2)}, \ x^{(n-1)}</math>.</center> | ||
<center><math> | |||
Bardzo często zmienną niezależną <math> | Bardzo często zmienną niezależną <math>t</math> w równaniu różniczkowym | ||
nazywamy '''''czasem''''' (ze względu na liczne modele matematyczne, w | nazywamy '''''czasem''''' (ze względu na liczne modele matematyczne, w | ||
których właśnie czas przeważnie jest zmienną niezależną). Pochodną | których właśnie czas przeważnie jest zmienną niezależną). Pochodną | ||
funkcji <math> | funkcji <math>t\mapsto x(t)</math> oznaczamy tradycyjnie symbolami | ||
<center><math> | <center><math>x', \ \ \frac{dx}{dt}, \ \ \frac{d}{dt}x, \ \ \dot{x}</math>.</center> | ||
Ostatnie | Ostatnie | ||
z oznaczeń pochodnej (za pomocą kropki nad niewiadomą <math> | z oznaczeń pochodnej (za pomocą kropki nad niewiadomą <math>\dot{x}</math>) | ||
jest charakterystyczne dla równań różniczkowych. | jest charakterystyczne dla równań różniczkowych. | ||
Odpowiednio drugą, trzecią i pochodne wyższego rzędu oznaczamy | Odpowiednio drugą, trzecią i pochodne wyższego rzędu oznaczamy | ||
tradycyjnie symbolami: | tradycyjnie symbolami: | ||
<center><math>\ | <center><math>\begin{align} | ||
&x'', | &x'', &\frac{d^2x}{dt^2}, &\frac{d^2}{dt^2}x, &\ddot{x} \\ | ||
&\ddot{x} | &x''', &\frac{d^3x}{dt^3}, &\frac{d^3}{dt^3}x, &\ddot{x} \\ | ||
\\ | &x^{(n)}, &\frac{d^n x}{dt^n}, &\frac{d^n}{dt^n}x, & x^{(n)}. | ||
&x''', | \end{align}</math></center> | ||
&\ | |||
&x^{(n)}, | |||
x^{(n)}. | |||
\ | |||
{{uwaga|13.7.|| | {{uwaga|13.7.|| | ||
Wraz z równaniem różniczkowym w postaci | Wraz z równaniem różniczkowym w postaci | ||
normalnej <math> | normalnej <math>\dfrac{dx}{dt}=f(t,x)</math> rozważamy też często równanie w | ||
'''''postaci różniczkowej''''' <center><math> | '''''postaci różniczkowej''''' <center><math>dx=f(t,x)dt</math>,</center> | ||
bądź w bardziej | bądź w bardziej | ||
ogólnej postaci | ogólnej postaci | ||
<center><math> | <center><math> | ||
P(t,x)dt+Q(t,x)dx=0 | P(t,x)dt+Q(t,x)dx=0</math>,</center> | ||
</math></center> | |||
gdzie <math> | gdzie <math>P, Q</math> są danymi funkcjami zmiennych <math>t,x</math>. Zadajemy wówczas | ||
pytanie o istnienie takiej funkcji różniczkowalnej <math> | pytanie o istnienie takiej funkcji różniczkowalnej <math>F: | ||
(t,x)\mapsto F(t,x)</math>, której różniczka <center><math> | (t,x)\mapsto F(t,x)</math>, której różniczka <center><math>dF=\frac{\partial | ||
F}{\partial t}dt+\frac{\partial F}{\partial x}dx</math></center> | F}{\partial t}dt+\frac{\partial F}{\partial x}dx</math></center> | ||
jest tożsama z | jest tożsama z | ||
lewą stroną równania w postaci różniczkowej <math> | lewą stroną równania w postaci różniczkowej <math>P(t,x)dt+Q(t,x)dx=0</math>. | ||
Otrzymujemy wówczas rozwiązanie <center><math> | Otrzymujemy wówczas rozwiązanie <center><math>t\mapsto x(t)\ \text{ lub } | ||
x\mapsto t(x)</math></center> | x\mapsto t(x)</math></center> | ||
dane w postaci uwikłanej <center><math> | dane w postaci uwikłanej <center><math>F(t, x(t))=C \ \text{ lub } F(t(x),x)=C</math>,</center> | ||
lub } F(t(x),x)=C | gdzie <math>C</math> jest pewną stałą. | ||
gdzie <math> | |||
}} | }} | ||
| Linia 351: | Linia 335: | ||
Dane jest równanie różniczkowe | Dane jest równanie różniczkowe | ||
zwyczajne rzędu pierwszego w postaci normalnej | zwyczajne rzędu pierwszego w postaci normalnej | ||
<center><math> | <center><math>\frac{dx}{dt}=-\frac{x+2t}{2x+t}</math>.</center> | ||
Zauważmy, że postaci | Zauważmy, że postaci | ||
różniczkowej przyjmuje ono wyjątkowo prostą postać | różniczkowej przyjmuje ono wyjątkowo prostą postać | ||
<center><math> | <center><math>(2x+t)dx+(x+2t)dt=0</math>,</center> | ||
gdyż <center><math> | gdyż <center><math>2xdx+2tdt=d(x^2+t^2) \text{ oraz } tdx+xdt=d(tx)</math>,</center> | ||
stąd | stąd | ||
równanie w postaci różniczkowej jest tożsame z równaniem | równanie w postaci różniczkowej jest tożsame z równaniem | ||
<center><math> | <center><math>d(x^2+xt+t^2)=0</math>,</center> | ||
czyli <math> | czyli <math>x^2+xt+t^2=C</math>, gdzie <math>C</math> jest pewną stałą. Funkcje | ||
<math> | <math>t\mapsto x(t)</math> w postaci uwikłanej <center><math>x(t)^2+x(t)t+t^2=C</math></center> | ||
spełniają dane równanie. | spełniają dane równanie. | ||
| Linia 373: | Linia 357: | ||
Zagadnienie | Zagadnienie | ||
<center> | <center> | ||
<math> | <math> | ||
\left\{\ | \left\{\begin{align} x'(t)&=f(t, x(t))\\ | ||
x(t_0)&=x_0\ | x(t_0)&=x_0\end{align} \right.</math> | ||
</math> | |||
</center> | </center> | ||
polegające na znalezieniu takiego | polegające na znalezieniu takiego | ||
rozwiązania <math> | rozwiązania <math>t\mapsto x(t)</math> równania różniczkowego <math>x'(t)=f(t, | ||
x(t))</math>, które spełnia '''''warunek początkowy''''' <math> | x(t))</math>, które spełnia '''''warunek początkowy''''' <math>x(t_0)=x_0</math> (gdzie | ||
<math> | <math>x_0</math> jest zadaną wartością, którą szukane rozwiązanie ma | ||
przyjmować w ustalonej chwili początkowej <math> | przyjmować w ustalonej chwili początkowej <math>t_0</math>) nazywamy | ||
'''''problemem początkowym Cauchy'ego'''''. }} | '''''problemem początkowym Cauchy'ego'''''. }} | ||
| Linia 388: | Linia 371: | ||
rozwiązanie i czy jest ono jednoznaczne? Przypomnijmy, że problem | rozwiązanie i czy jest ono jednoznaczne? Przypomnijmy, że problem | ||
<center> | <center> | ||
<math> | <math>\left\{\begin{align} &\frac{dx}{dt}(t)\ = -\lambda x(t) \\ &x(t_0)=x_0,\end{align}\right.</math>. | ||
</center> | </center> | ||
który rozwiązaliśmy opisując proces stygnięcia (ogrzewania) ma | który rozwiązaliśmy opisując proces stygnięcia (ogrzewania), ma | ||
zawsze rozwiązanie | zawsze rozwiązanie | ||
<center> | <center> | ||
<math> | <math>x(t)=x^* +(x_0-x^*) \exp (-\lambda (t-t_0))</math> | ||
</center> | </center> | ||
| Linia 400: | Linia 383: | ||
z prognozowaniem pogody) podpowiada nam, że nie wszystkie procesy, | z prognozowaniem pogody) podpowiada nam, że nie wszystkie procesy, | ||
które przebiegają w czasie, obok nas, mają jednoznaczne | które przebiegają w czasie, obok nas, mają jednoznaczne | ||
rozwiązanie, którego rezultat można przewidzieć w chwili <math> | rozwiązanie, którego rezultat można przewidzieć w chwili <math>t</math> na | ||
podstawie warunku początkowego. Rozważmy prosty przykład | podstawie warunku początkowego. Rozważmy prosty przykład. | ||
{{przyklad|13.10.|| | {{przyklad|13.10.|| | ||
Rozważmy problem początkowy Cauchy'ego | Rozważmy problem początkowy Cauchy'ego | ||
<center> | <center> | ||
<math> | <math>\left\{\begin{align} | ||
&\frac{dx}{dt}(t)\ = \sqrt{x(t)} \\ | &\frac{dx}{dt}(t)\ = \sqrt{x(t)} \\ | ||
&x(t_0)=x_0,\ | &x(t_0)=x_0,\end{align}\right.</math>. | ||
</center> | </center> | ||
Łatwo zauważyć, że równanie <math> | Łatwo zauważyć, że równanie <math>x'=\sqrt{x}</math> spełnia funkcja stała | ||
<math> | <math>x(t)=0</math>. Ponadto po zapisaniu równania w postaci różniczkowej | ||
<math> | <math>\frac{dx}{\sqrt{x} }=dt</math> wskazujemy rodzinę funkcji, które je | ||
spełniają: | spełniają: | ||
<center> | <center> | ||
<math> | <math> | ||
2\sqrt{x}=t+C | 2\sqrt{x}=t+C</math>,</center> | ||
</math></center> | |||
gdzie <math> | gdzie <math>C</math> jest stałą (zauważmy, że równanie to ma sens tylko jeśli | ||
<math> | <math>t+C\geq 0</math>). Stąd <math>x(t)=\big(\frac{t+C}{2}\big)^2</math>, o ile | ||
<math> | <math>t+C\geq 0</math>. A więc problem Cauchy'ego | ||
a) ma dokładnie jedno rozwiązanie, gdy <math> | a) ma dokładnie jedno rozwiązanie, gdy <math>x_0>0</math>: | ||
<center><math> | <center><math> | ||
x(t)=\left\{\ | x(t)=\left\{\begin{align} &\frac{1}{4}(t+C)^2,&& {\rm gdy}\; t>-C\\ | ||
&0,&& {\rm gdy} \; t\leq -C\ | &0,&& {\rm gdy} \; t\leq -C\end{align} \right., \quad \text{ gdzie } \ C=2\sqrt{x_0}-t_0</math>,</center> | ||
</math></center> | |||
b) nie ma rozwiązania, gdy <math> | b) nie ma rozwiązania, gdy <math>x_0<0</math>, | ||
c) ma dwa rozwiązania <center><math> | c) ma dwa rozwiązania <center><math>x=0 \quad \text{ oraz }\quad | ||
x(t)=\left\{\ | x(t)=\left\{\begin{align} &\frac{1}{4}(t-t_0)^2,&& {\rm gdy}\; t>t_0\\ | ||
&0,&& {\rm gdy} \; t\leq t_0\ | &0,&& {\rm gdy} \; t\leq t_0\end{align} \right.</math>,</center> | ||
</math></center> | |||
gdy <math> | gdy <math>x_0=0</math>. | ||
}} | }} | ||
Okazuje się jednak, że przy | Okazuje się jednak, że przy | ||
naturalnych założeniach o funkcji <math> | naturalnych założeniach o funkcji <math>f</math> problem Cauchy'ego ma | ||
rozwiązanie i jest ono jednoznaczne. | rozwiązanie i jest ono jednoznaczne. | ||
{{twierdzenie|13.11.|| | {{twierdzenie|13.11.|| | ||
(twierdzenie Picarda) Jeśli funkcja | (twierdzenie Picarda) Jeśli funkcja | ||
<math> | <math>\mathbb{R}^2\ni (t,x)\mapsto f(t,x)\in \mathbb{R}</math> jest ciągła w pewnym | ||
otoczeniu <math> | otoczeniu <math>(t_0-a, t_0+a)\times (x_0-b, x_0+b)</math> punktu <math>(t_0, | ||
x_0)</math> i spełnia warunek Lipschitza względem drugiej zmiennej, tzn. | x_0)</math> i spełnia warunek Lipschitza względem drugiej zmiennej, tzn. | ||
<center><math> | <center><math>\exists L : \forall x_1, x_2\in (x_0-b, x_0+b) \ : \ |f(t, | ||
x_1)-f(t, x_2)|\leq L|x_1-x_2|, \text{ dla } t\in (t_0-a, t_0+a) | x_1)-f(t, x_2)|\leq L|x_1-x_2|, \text{ dla } t\in (t_0-a, t_0+a)</math>,</center> | ||
</math></center> | |||
to problem początkowy Cauchy'ego | to problem początkowy Cauchy'ego | ||
<center><math> | <center><math>\left\{\begin{align} | ||
&x'(t)\ = f(t, x(t)) \\ | &x'(t)\ = f(t, x(t)) \\ | ||
&x(t_0)=x_0,\ | &x(t_0)=x_0,\end{align}\right.</math>.</center> | ||
ma rozwiązanie i jest ono jedyne. | ma rozwiązanie i jest ono jedyne. | ||
}} | }} | ||
| Linia 466: | Linia 445: | ||
kolejnych przybliżeń rozwiązania danego równania. | kolejnych przybliżeń rozwiązania danego równania. | ||
{{dowod| | {{dowod|13.11.|| | ||
[szkic] Zauważmy, że funkcja <math>t\mapsto x(t)</math> spełnia podany | |||
problem początkowy Cauchy'ego wtedy i tylko wtedy, gdy spełnione | problem początkowy Cauchy'ego wtedy i tylko wtedy, gdy spełnione | ||
jest równanie całkowe z niewiadomą <math> | jest równanie całkowe z niewiadomą <math>t\mapsto x(t)</math> | ||
<center><math> | <center><math>x(t)-x(t_0)=\int_{t_0}^t f(s, x(s))ds</math>,</center> | ||
czyli <center><math> | czyli <center><math>x(t)=x_0+\int_{t_0}^t f(s, x(s))ds</math>.</center> | ||
Niech | Niech | ||
<center><math> | <center><math>X:=\{x:[t_0-\alpha, t_0+\alpha]\ni t\mapsto x(t)\in [x_0-\beta, x_0+\beta], \text{ ciągła }\}</math></center> | ||
będzie przestrzenią funkcji ciągłych na przedziale <math> | będzie przestrzenią funkcji ciągłych na przedziale <math>[t_0-\alpha, | ||
t_0+\alpha]</math> o wartościach w przedziale <math> | t_0+\alpha]</math> o wartościach w przedziale <math>[x_0-\beta, x_0+\beta]</math>, | ||
gdzie <math> | gdzie <math>\alpha <a</math>, <math>\beta < b</math>. Przestrzeń <math>X</math> jest przestrzenią | ||
metryczną zupełną z metryką zadaną przez normę supremum, tj. | metryczną zupełną z metryką zadaną przez normę supremum, tj. | ||
<center><math> | <center><math>d(x_1, x_2)=\|x_1-x_2\|:=\sup\{|x_1(t)-x_2(t)|, t\in [t_0-\alpha, | ||
t_0+\alpha]\} | t_0+\alpha]\}</math>.</center> | ||
Określmy na tej przestrzeni odwzorowanie: | Określmy na tej przestrzeni odwzorowanie: | ||
<center><math> | <center><math> | ||
P: X\ni x\mapsto P(x), \qquad {\rm gdzie}\;\; P(x)(t):=x_0+\int_{t_0}^t f(s, x(s))ds | P: X\ni x\mapsto P(x), \qquad {\rm gdzie}\;\; P(x)(t):=x_0+\int_{t_0}^t f(s, x(s))ds</math></center> | ||
</math></center> | |||
Wykazuje się (pomijamy szczegóły, które można znaleźć np. w | Wykazuje się (pomijamy szczegóły, które można znaleźć np. w | ||
podręczniku Ryszarda Rudnickiego, Wykłady z analizy | podręczniku Ryszarda Rudnickiego, Wykłady z analizy | ||
matematycznej, Wydawnictwo Naukowe PWN, Warszawa 2001), że | matematycznej, Wydawnictwo Naukowe PWN, Warszawa 2001), że | ||
można dobrać stałe <math> | można dobrać stałe <math>\alpha</math> oraz <math>\beta</math> tak, że | ||
* odwzorowanie <math>P: X\mapsto X</math>, tzn. jest określone na <math>X</math> i | |||
przyjmuje wartości w przestrzeni <math> | przyjmuje wartości w przestrzeni <math>X</math>, tzn. | ||
<center><math> | <center><math>\|P(x(t))-x_0\|<\beta;</math></center> | ||
* jest zwężające (czyli spełnia warunek Lipschitza ze stałą | |||
mniejszą od 1), tzn. istnieje stała <math> | mniejszą od 1), tzn. istnieje stała <math>M<1</math> taka, że | ||
<center><math> | <center><math>\|P(x_1)-P(x_2)\|\leq M \|x_1-x_2\|</math></center> | ||
dla dowolnych <math> | dla dowolnych <math>x_1, x_2</math> z przestrzeni <math>X</math>. Na mocy twierdzenia | ||
Banacha o punkcie stałym w przestrzeni <math> | Banacha o punkcie stałym w przestrzeni <math>X</math> istnieje dokładnie | ||
jeden punkt <math> | jeden punkt <math>x^*</math>, do którego zmierza ciąg iteracji odwzorowania | ||
<math> | <math>P</math>: | ||
<center><math>\ | <center><math>\begin{align} | ||
&x_0\\ | &x_0\\ | ||
&x_1=P(x_0)\\ | &x_1=P(x_0)\\ | ||
| Linia 512: | Linia 490: | ||
&x_{n+1}=P(x_n)\\ | &x_{n+1}=P(x_n)\\ | ||
&\downarrow n\to \infty\\ | &\downarrow n\to \infty\\ | ||
&x^*.\ | &x^*.\end{align}</math></center> | ||
Punkt <math> | Punkt <math>x^*</math> jest punktem stałym odwzorowania | ||
<math> | <math>P</math>, tzn. <math>P(x^*)=x^*</math>, czyli | ||
<center><math> | <center><math>P(x^* (t))=x_0+\int_{t_0}^t f(s, x^* (s))ds</math></center> | ||
co oznacza, że jest rozwiązaniem danego problemu Cauchy'ego i | co oznacza, że jest rozwiązaniem danego problemu Cauchy'ego i | ||
rozwiązanie to jest jedyne, gdyż (na mocy twierdzenia Banacha o | rozwiązanie to jest jedyne, gdyż (na mocy twierdzenia Banacha o | ||
punkcie stałym) ciąg iteracji <math> | punkcie stałym) ciąg iteracji <math>x_{n+1}=P(x_n)</math> zawsze zmierza do | ||
tego samego punktu <math> | tego samego punktu <math>x^*</math> (punktu stałego odwzorowania <math>P</math>, który | ||
jest jedyny) niezależnie od wyboru pierwszego punktu <math> | jest jedyny) niezależnie od wyboru pierwszego punktu <math>x_0</math> w ciągu | ||
iteracji, byleby został on wybrany z przestrzeni <math> | iteracji, byleby został on wybrany z przestrzeni <math>X</math>, w której | ||
odwzorowanie <math> | odwzorowanie <math>P</math> jest zwężające. }} | ||
{{uwaga|13.12.|| | {{uwaga|13.12.|| | ||
Założenie o spełnianiu przez funkcję | Założenie o spełnianiu przez funkcję | ||
<math> | <math>(t,x)\mapsto f(t,x)</math> warunku Lipschitza jest istotne. Funkcja | ||
<math> | <math>(t,x)\mapsto \sqrt{x}</math> nie spełnia warunku Lipschitza względem | ||
drugiej zmiennej w otoczeniu punktu <math> | drugiej zmiennej w otoczeniu punktu <math>x_0</math>. Przypomnijmy, że | ||
problem | problem | ||
<center><math> | <center><math>\left\{\begin{align} | ||
&\frac{dx}{dt}(t)\ = \sqrt{x(t)} \\ | &\frac{dx}{dt}(t)\ = \sqrt{x(t)} \\ | ||
&x(t_0)=0,\ | &x(t_0)=0,\end{align}\right.</math>.</center> | ||
ma rozwiązanie, ale nie jest ono | ma rozwiązanie, ale nie jest ono | ||
jednoznaczne. }} | jednoznaczne. }} | ||
| Linia 542: | Linia 520: | ||
Ciąg określony w dowodzie twierdzenia | Ciąg określony w dowodzie twierdzenia | ||
Picarda | Picarda | ||
<center><math> | <center><math>\left\{\begin{align} | ||
x_1(t) | &x_1(t)=x_0+\int_{t_0}^t f(s, x_0)ds\\ | ||
x_2(t) | &x_2(t)=x_0+\int_{t_0}^t f(s, x_1(s))ds\\ | ||
x_3(t) | &x_3(t)=x_0+\int_{t_0}^t f(s, x_2(s))ds\\ | ||
&\vdots\\ | &\vdots\\ | ||
x_{n+1}(t) | &x_{n+1}(t)=x_0+\int_{t_0}^t f(s, x_{n} (s))ds\\ | ||
&\vdots\ | &\vdots\end{align}\right.</math>.</center> | ||
nazywamy '''''ciągiem kolejnych | nazywamy '''''ciągiem kolejnych | ||
przybliżeń Picarda'''''. }} | przybliżeń Picarda'''''. }} | ||
| Linia 562: | Linia 540: | ||
Wyznaczmy metodą Picarda rozwiązanie | Wyznaczmy metodą Picarda rozwiązanie | ||
problemu Cauchy'ego | problemu Cauchy'ego | ||
<center><math> | <center><math>\left\{\begin{align} | ||
&x'(t)\ = x(t) \\ | &x'(t)\ = x(t) \\ | ||
&x(0)=1 | &x(0)=1.\end{align}\right.</math>.</center> | ||
Zgodnie z określeniem ciągu Picarda | Zgodnie z określeniem ciągu Picarda | ||
mamy | mamy | ||
<center><math>\begin{array}{lll} | <center><math>\begin{array}{lll} | ||
x_1&=1+\int_0^t ds&=1+t\\ | |||
x_2&=1+\int_0^t(1+s)ds&=1+t+\frac{1}{2}t^2\\ | x_2&=1+\int_0^t(1+s)ds&=1+t+\frac{1}{2}t^2\\ | ||
x_3&=1+\int_0^t(1+s+\frac{1}{2}s^2)ds&=1+t+\frac{1}{2}t^2+\frac{1}{6}t^3\\ | x_3&=1+\int_0^t(1+s+\frac{1}{2}s^2)ds&=1+t+\frac{1}{2}t^2+\frac{1}{6}t^3\\ | ||
| Linia 580: | Linia 558: | ||
</math></center> | </math></center> | ||
Jak łatwo zauważyć <math> | Jak łatwo zauważyć <math>n</math>-ty wyraz ciągu Picarda jest identyczny z | ||
<math> | <math>n</math>-tą sumą częściową szeregu definiującego funkcję wykładniczą | ||
<center><math> | <center><math>\exp t=\sum_{k=0}^\infty \frac{t^n}{n!}=1+t+\frac{1}{2}t^2+\frac{1}{6}t^3+\frac{1}{24}t^4+\dots+\frac{1}{n!}t^n+\dots</math></center> | ||
Ciąg <math> | Ciąg <math>x_n</math> zmierza więc do funkcji <math>x(t)=\exp t</math>, która jest | ||
jedynym rozwiązaniem danego problemu Cauchy'ego. }} | jedynym rozwiązaniem danego problemu Cauchy'ego. }} | ||
[[grafika:Euler-portret.jpg|thumb|right||Leonhard Euler (1707-1783)<br>[[Biografia Euler|Zobacz biografię]]]] | [[grafika:Euler-portret.jpg|thumb|right||Leonhard Euler (1707-1783)<br>[[Biografia Euler|Zobacz biografię]]]] | ||
Prześledźmy także na tym samym przykładzie inną metodę | Prześledźmy także na tym samym przykładzie inną metodę | ||
przybliżonego rozwiązywania problemu Cauchy'ego, zwaną '''''metodą | przybliżonego rozwiązywania problemu Cauchy'ego, zwaną '''''metodą | ||
łamanych Eulera''''' | łamanych Eulera'''''. | ||
{{uwaga|13.15.|| | {{uwaga|13.15.|| | ||
Przypomnijmy, że na początku wykładu | Przypomnijmy, że na początku wykładu, | ||
omawiając proces stygnięcia (ogrzewania) substancji, zastąpiliśmy | omawiając proces stygnięcia (ogrzewania) substancji, zastąpiliśmy | ||
iloraz różnicowy | iloraz różnicowy | ||
<center><math> | <center> | ||
<math>\frac{x(t+h)-x(t)}{h}\approx-\lambda (x(t)-x^*), \ \ x(t_0)=x_0</math>, | |||
</center> | |||
równaniem różniczkowym | równaniem różniczkowym | ||
<center><math> | <center> | ||
<math>\frac{dx}{dt}(t)\ = -\lambda (x(t)-x^*), \ \ x(t_0)=x_0</math>. | |||
</center> | |||
Odwróćmy teraz kolejność postępowania i lewą stronę równania | Odwróćmy teraz kolejność postępowania i lewą stronę równania | ||
różniczkowego w postaci normalnej <center><math> | różniczkowego w postaci normalnej | ||
x(t_0)=x_0</math></center> | <center> | ||
<math>\frac{dx}{dt}=f(t,x), | |||
x(t_0)=x_0</math> | |||
</center> | |||
zastąpmy ilorazem różnicowym | zastąpmy ilorazem różnicowym | ||
<center><math> | <center> | ||
<math>\frac{x(t+h)-x(t)}{h}\approx f(t,x)</math>. | |||
</center> | |||
Stąd <center><math> | Stąd <center><math>x(t+h)\approx x(t)+f(t,x)h</math>.</center> | ||
Podzielmy przedział od <math> | Podzielmy przedział od <math>t_0</math> | ||
do <math> | do <math>t</math> na <math>n</math> równych części punktami | ||
<center><math> | <center> | ||
<math>t_k:=t_0+\frac{k}{n}(t-t_0), \ \ \ k=0,1,2,\dots, n</math>. | |||
</center> | |||
Określmy (skończony) ciąg punktów <math> | Określmy (skończony) ciąg punktów <math>x_k</math> następująco: | ||
<center><math> | <center> | ||
<math>\left\{\begin{align} | |||
&x_0=x(t_0) \\ | &x_0=x(t_0) \\ | ||
&x_1=x_0+f(t_0, x_0)h\\ | &x_1=x_0+f(t_0, x_0)h\\ | ||
| Linia 621: | Linia 611: | ||
&\vdots \\ | &\vdots \\ | ||
&x_n=x_{n-1}+f(t_{n-1}, x_{n-1})h, | &x_n=x_{n-1}+f(t_{n-1}, x_{n-1})h, | ||
\ | \end{align}\right.</math> | ||
</math></center> | </center> | ||
biorąc stały przyrost <math> | biorąc stały przyrost <math>h=\frac{t}{n}</math>: | ||
<center><math> | <center><math>h=t_1-t_0=t_2-t_1=t_3-t_2=\dots=t_{k+1}-t_k=\dots=t_n-t_{n-1}</math>.</center> | ||
Wówczas <math> | Wówczas <math>x_k</math> stanowi przybliżoną wartość rozwiązania równania w | ||
chwili <math> | chwili <math>t_k</math>, tj. <math>x_k\approx x(t_k)</math>. Im gęściej podzielimy | ||
przedział od <math> | przedział od <math>t_0</math> do <math>t</math> za pomocą punktów <math>t_k</math> (tzn. gdy <math>n</math> | ||
jest dużą liczbą), tym przybliżenie to jest lepsze. Łamaną, | jest dużą liczbą), tym przybliżenie to jest lepsze. Łamaną, | ||
łączącą punkty <math> | łączącą punkty <math>(t_k, x_k)</math> nazywamy '''''łamaną Eulera'''''. Stanowi | ||
ona przybliżenie wykresu <math> | ona przybliżenie wykresu <math>t\mapsto x(t)</math> rozwiązania danego | ||
problemu Cauchy'ego w przedziale od <math> | problemu Cauchy'ego w przedziale od <math>t_0</math> do <math>t</math>. }} | ||
{{przyklad|13.16.|| | {{przyklad|13.16.|| | ||
| Linia 639: | Linia 629: | ||
Zastosujmy opisany algorytm do znalezienia przybliżonej wartości | Zastosujmy opisany algorytm do znalezienia przybliżonej wartości | ||
rozwiązania problemu Cauchy'ego: | rozwiązania problemu Cauchy'ego: | ||
<center><math> | <center><math>\left\{\begin{align} | ||
&x'(t)\ = x(t) \\ | &x'(t)\ = x(t) \\ | ||
&x(0)=1,\ | &x(0)=1,\end{align}\right.</math></center> | ||
który rozwiązaliśmy już metodą | który rozwiązaliśmy już metodą | ||
kolejnych przybliżeń Picarda. Określamy kolejne '''''węzły łamanej | kolejnych przybliżeń Picarda. Określamy kolejne '''''węzły łamanej | ||
Eulera''''': | Eulera''''': | ||
<center><math>\ | <center><math>\begin{align} | ||
&x_0=x(t_0)=1 \\ | &x_0=x(t_0)=1 \\ | ||
&x_1=x_0+f(t_0, x_0)h=1+h\\ | &x_1=x_0+f(t_0, x_0)h=1+h\\ | ||
| Linia 654: | Linia 644: | ||
&\vdots\\ | &\vdots\\ | ||
&x_n=x_{n-1}+f(t_{n-1}, x_{n-1})h=(1+h)^n | &x_n=x_{n-1}+f(t_{n-1}, x_{n-1})h=(1+h)^n | ||
\ | \end{align} | ||
</math></center> | </math></center> | ||
Biorąc pod uwagę, że <math> | Biorąc pod uwagę, że <math>h=\frac{t}{n}</math>, otrzymujemy | ||
<center><math> | <center><math>x_n=\big(1+\frac{t}{n}\big)^n</math>.</center> | ||
Stąd <math> | Stąd <math>x_n (t)\approx \exp t</math>, gdyż ciąg | ||
<math> | <math>\big(1+\frac{t}{n}\big)^n</math> zmierza do <math>\exp t</math>, gdy <math>n\to\infty</math>. | ||
}} | }} | ||
| Linia 675: | Linia 665: | ||
skończonej liczby operacji na funkcjach elementarnych całek z | skończonej liczby operacji na funkcjach elementarnych całek z | ||
funkcji | funkcji | ||
<center><math> | <center><math>\exp(-x^2), \ \ \ \frac{\sin x}{x}, \ \ \ \frac{1}{\ln x}</math>.</center> | ||
i | i | ||
wielu innych. Funkcje te pojawiają się w wielu ważnych | wielu innych. Funkcje te pojawiają się w wielu ważnych | ||
zagadnieniach nauki, np. funkcja dana za pomocą całki oznaczonej | zagadnieniach nauki, np. funkcja dana za pomocą całki oznaczonej | ||
<center><math> | <center><math>\Phi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^x | ||
\exp(-\frac{1}{2}t^2)dt</math></center> | \exp(-\frac{1}{2}t^2)dt</math></center> | ||
jest | jest dystrybuantą rozkładu normalnego, | ||
jednego z najważniejszych rozkładów prawdopodobieństwa, który | jednego z najważniejszych rozkładów prawdopodobieństwa, który | ||
służy do modelowania wielu zjawisk w biologii, ekonomii i in. | służy do modelowania wielu zjawisk w biologii, ekonomii i in. | ||
| Linia 687: | Linia 677: | ||
Wracając do teorii równań różniczkowych, można na przykład | Wracając do teorii równań różniczkowych, można na przykład | ||
wykazać, że nie da się elementarnie rozwiązać równania | wykazać, że nie da się elementarnie rozwiązać równania | ||
<center><math> | <center><math>x'=x^2-t</math></center> | ||
(przykład tego prostego równania podaje W.I.Arnold, Równania | (przykład tego prostego równania podaje W.I.Arnold, Równania | ||
różniczkowe zwyczajne, Państwowe Wydawnictwo Naukowe, Warszawa | różniczkowe zwyczajne, Państwowe Wydawnictwo Naukowe, Warszawa | ||
1975, | 1975, s. 40). Zauważmy jednak, że funkcja <math>f(t,x)=x^2 -t</math> | ||
spełnia założenia twierdzenia Picarda w przedziałach | spełnia założenia twierdzenia Picarda w przedziałach | ||
<math> | <math>-\infty<t<\infty</math>, <math>-\infty<x<\infty</math>, a więc problem początkowy | ||
Cauchy'ego dla tego równania ma rozwiązanie i jest ono jedyne przy | Cauchy'ego dla tego równania ma rozwiązanie i jest ono jedyne przy | ||
dowolnym warunku początkowym. | dowolnym warunku początkowym. | ||
| Linia 717: | Linia 707: | ||
Powróćmy do przykładu z początku | Powróćmy do przykładu z początku | ||
wykładu. Równanie | wykładu. Równanie | ||
<center><math> | <center><math>x'=\lambda x(N-x)</math></center> | ||
pojawia się w modelu opisu rozwoju grupy | pojawia się w modelu opisu rozwoju grupy | ||
organizmów przy założeniu, że pojemność ekosystemu jest | organizmów przy założeniu, że pojemność ekosystemu jest | ||
ograniczona. Bez rozwiązywania równania możemy zauważyć, że dwie | ograniczona. Bez rozwiązywania równania możemy zauważyć, że dwie | ||
funkcje stałe <math> | funkcje stałe <math>x(t)=0</math> oraz <math>x(t)=N</math> spełniają to równanie. | ||
Ponadto, gdy <math> | Ponadto, gdy <math>x>N</math>, pochodna <math>x'<0</math>, czyli funkcja <math>t\mapsto x(t)</math> | ||
maleje, a z kolei, gdy <math> | maleje, a z kolei, gdy <math>0<x<N</math> mamy <math>x'>0</math>, czyli funkcja | ||
<math> | <math>t\mapsto x(t)</math> rośnie. Zwróćmy uwagę, że z tej prostej obserwacji | ||
wynika, że liczebność grupy organizmów rośnie (odpowiednio: | wynika, że liczebność grupy organizmów rośnie (odpowiednio: | ||
maleje), gdy jest ich mniej (odpowiednio: więcej) niż wynosi | maleje), gdy jest ich mniej (odpowiednio: więcej) niż wynosi | ||
pojemność ekosystemu. Zauważmy, że wyciągnęliśmy dokładnie ten sam | pojemność ekosystemu. Zauważmy, że wyciągnęliśmy dokładnie ten sam | ||
wniosek, który w | wniosek, który w [[#prz_13_4|przykładzie 13.4.]] pojawił się po | ||
analizie wyznaczonego rozwiązania równania różniczkowego. | analizie wyznaczonego rozwiązania równania różniczkowego. | ||
}} | }} | ||
Pamiętamy, że interpretacją geometryczną pochodnej funkcji | Pamiętamy, że interpretacją geometryczną pochodnej funkcji | ||
jednej zmiennej <math> | jednej zmiennej <math>t\mapsto x(t)</math> różniczkowalnej w punkcie <math>t_0</math> | ||
jest współczynnik kierunkowy stycznej do wykresu tej funkcji w | jest współczynnik kierunkowy stycznej do wykresu tej funkcji w | ||
punkcie <math> | punkcie <math>(t_0, x(t_0))</math>. Odwróćmy teraz sytuację i mając dane | ||
równanie różniczkowe zwyczajne rzędu pierwszego w postaci | równanie różniczkowe zwyczajne rzędu pierwszego w postaci | ||
normalnej | normalnej | ||
<center><math> | <center><math>x'(t)=f(t,x(t))</math>,</center> | ||
narysujmy | narysujmy | ||
wektory zaczepione w punktach <math> | wektory zaczepione w punktach <math>(t,x)</math> należących do dziedziny | ||
funkcji <math> | funkcji <math>f</math>, które tworzą z osią rzędnych (tj. z osią zmiennej | ||
<math> | <math>t</math>) kąt, którego tangens jest równy <math>f(t,x)</math>. | ||
Otrzymamy w ten sposób obraz | Otrzymamy w ten sposób obraz | ||
<center><math> | <center><math>\mathbb{R}^2 \supset \mathrm{dom}\, f\ni (t,x)\mapsto (t,x)+\big(1, f(t,x)\big)\in \mathbb{R}^2</math>,</center> | ||
'''''pola wektorowego''''' | '''''pola wektorowego''''' | ||
<center><math> | <center><math>\mathbb{R}^2 \supset\mathrm{dom}\, f\ni (t,x)\mapsto \big(1, f(t,x)\big)\in \mathbb{R}^2</math>,</center> | ||
którego przebieg jest ściśle związany z przebiegiem rozwiązań | którego przebieg jest ściśle związany z przebiegiem rozwiązań | ||
danego równania. Zgodnie z interpretacją pochodnej, wektor <math> | danego równania. Zgodnie z interpretacją pochodnej, wektor <math>[1, | ||
f(t,x)]</math> zaczepiony w punkcie <math> | f(t,x)]</math> zaczepiony w punkcie <math>(t_0, x_0)</math> jest styczny w tym | ||
punkcie do wykresu funkcji <math> | punkcie do wykresu funkcji <math>t\mapsto x(t)</math> będącej rozwiązaniem | ||
problemu początkowego Cauchy'ego | problemu początkowego Cauchy'ego | ||
<center><math> | <center><math>x'=f(x,t), \ \ x(t_0)=x_0</math>.</center> | ||
Jeśli więc nawet nie potrafimy rozwiązać danego równania | Jeśli więc nawet nie potrafimy rozwiązać danego równania | ||
| Linia 764: | Linia 753: | ||
danym równaniem i na podstawie obrazu pola wektorowego określić w | danym równaniem i na podstawie obrazu pola wektorowego określić w | ||
przybliżeniu przebieg rozwiązań równania różniczkowego. | przybliżeniu przebieg rozwiązań równania różniczkowego. | ||
[[File:am2w13.0030.svg|253x253px|thumb|right|Rysunek do przykładu 13.19.]] | |||
Często zamiast szkicować wektory | |||
<br> | |||
<center><math> | <center> | ||
<math>\mathbb{R}^2 \supset\mathrm{dom}\, f\ni (t,x)\mapsto \big(1, f(t,x)\big)\in \mathbb{R}^2</math>, | |||
</center> | |||
<br> | |||
rezygnujemy z informacji o długości wektora i rysujemy na | rezygnujemy z informacji o długości wektora i rysujemy na | ||
płaszczyźnie zmiennych <math> | płaszczyźnie zmiennych <math>(t,x)</math> odcinki o takiej samej długości | ||
(np. jednostkowej), nachylone do osi zmiennej <math> | (np. jednostkowej), nachylone do osi zmiennej <math>t</math> pod kątem, | ||
którego tangens wynosi <math> | którego tangens wynosi <math>f(t,x)</math>. Tę reprezentację równania | ||
różniczkowego nazywamy '''''polem kierunków''''' równania | różniczkowego nazywamy '''''polem kierunków''''' równania | ||
różniczkowego. | różniczkowego. | ||
Zauważmy, że jeśli w równaniu <math> | Zauważmy, że jeśli w równaniu <math>x'=f(t,x)</math> funkcja <math>(t,x)\mapsto | ||
f(t,x)</math> nie zależy od zmiennej <math> | f(t,x)</math> nie zależy od zmiennej <math>t</math>, pole kierunków zacieśnione do | ||
którejkolwiek prostej <math> | którejkolwiek prostej <math>t=Const</math> jest takie samo. Stąd w przypadku | ||
równań typu <math> | równań typu <math>x'=f(x)</math> do analizowania pola kierunków i przebiegu | ||
rozwiązań równania różniczkowego wystarczy prosta zmiennej <math> | rozwiązań równania różniczkowego wystarczy prosta zmiennej <math>x</math>. | ||
{{przyklad|13.19.|| | {{przyklad|13.19.|| | ||
Pole wektorowe związane z równaniem <math> | Pole wektorowe związane z równaniem <math>x'=2</math>.<br>}} | ||
}} | |||
{{przyklad|13.20.|| | {{przyklad|13.20.|| | ||
Pole wektorowe związane z równaniem <math> | Pole wektorowe związane z równaniem <math>x'=t</math>.<br> | ||
Zwróćmy uwagę, że rysując gęściej wektory pola kierunków związanego z danym równaniem, otrzymujemy lepsze wyobrażenie o przebiegu krzywych <math>t\mapsto (t, x(t))</math>, które stanowią rozwiązanie równania.}} | |||
{ | {| border="0" align="center" cellspacing="10" | ||
|[[File:am2w13.0040a.svg|253x253px|thumb|center|Rysunek do przykładu 13.20.]] | |||
|[[File:am2w13.0040b.svg|253x253px|thumb|center|Rysunek do przykładu 13.20.]] | |||
|[[File:am2w13.0040c.svg|253x253px|thumb|center|Rysunek do przykładu 13.20.]] | |||
|} | |||
{{przyklad|13.21.|| | {{przyklad|13.21.|| | ||
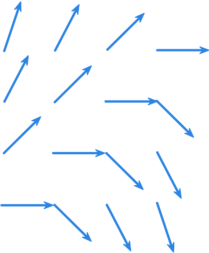
Pole wektorowe związane z równaniem <math> | Pole wektorowe związane z równaniem <math>x'=x-t</math>.<br> | ||
Podobnie jak poprzednio: im więcej wektorów pola, tym lepsze wyobrażenie o przebiegu rozwiązania równania różniczkowego. }} | |||
{ | {| border="0" align="center" cellspacing="10" | ||
|[[File:am2w13.0050a.svg|253x253px|thumb|center|Rysunek do przykładu 13.21.]] | |||
|[[File:am2w13.0050b.svg|253x253px|thumb|center|Rysunek do przykładu 13.21.]] | |||
|[[File:am2w13.0050c.svg|253x253px|thumb|center|Rysunek do przykładu 13.21.]] | |||
|} | |||
{{przyklad|13.22.|| | {{przyklad|13.22.|| | ||
Pole wektorowe związane z równaniem <math> | Pole wektorowe związane z równaniem <math>x'=x^2-t</math>. | ||
Równania tego nie da się rozwiązać za pomocą algorytmu o | Równania tego nie da się rozwiązać za pomocą algorytmu o skończonej liczbie etapów. Jednak, zgodnie z twierdzeniem | ||
skończonej liczbie etapów. Jednak | Picarda, dla każdego punktu <math>(t_0, x_0)</math> na płaszczyźnie istnieje dokładnie jedno rozwiązanie problemu Cauchy'ego: | ||
Picarda | <center><math>\left\{\begin{align} x'=x^2-t\\ x(t_0)=x_0. \end{align}\right.</math></center> | ||
istnieje dokładnie jedno rozwiązanie problemu Cauchy'ego: | |||
<center><math> | |||
Rysując pole kierunków, możemy wyobrazić sobie przebieg krzywych stanowiących rozwiązanie problemu Cauchy'ego dla poszczególnych punktów <math>(t_0, x_0)</math>. | |||
}} | |||
{| border="0" align="center" cellspacing="10" | |||
|[[File:am2w13.0060a.svg|253x253px|thumb|center|Rysunek do przykładu 13.22.]] | |||
|[[File:am2w13.0060b.svg|253x253px|thumb|center|Rysunek do przykładu 13.22.]] | |||
|[[File:am2w13.0060c.svg|253x253px|thumb|center|Rysunek do przykładu 13.22.]] | |||
|} | |||
{{przyklad|13.23.|| | {{przyklad|13.23.|| | ||
Pole wektorowe związane z równaniem <math> | Pole wektorowe związane z równaniem <math>x'=\ln |x|</math>. | ||
Także tego równania nie potrafimy rozwiązać dokładnie za pomocą | Także tego równania nie potrafimy rozwiązać dokładnie za pomocą algorytmu o skończonej liczbie etapów.<br> | ||
algorytmu o skończonej liczbie etapów.<br> | |||
Rysując pole kierunków, możemy jednak z łatwością wyobrazić sobie przebieg rozwiązań tego równania. }} | |||
{| border="0" align="center" cellspacing="10" | |||
|[[File:am2w13.0070a.svg|253x253px|thumb|center|Rysunek do przykładu 13.23.]] | |||
|[[File:am2w13.0070b.svg|253x253px|thumb|center|Rysunek do przykładu 13.23.]] | |||
|[[File:am2w13.0070c.svg|253x253px|thumb|center|Rysunek do przykładu 13.23.]] | |||
|} | |||
Aktualna wersja na dzień 19:16, 12 wrz 2023
Równania różniczkowe zwyczajne.
Przedstawiamy kilka praktycznych problemów, których opis w języku matematyki prowadzi do równań różniczkowych. Dowodzimy twierdzenia Picarda o istnieniu i jednoznaczności rozwiązania problemu początkowego Cauchy'ego. Przedstawiamy dwie metody przybliżonego rozwiązywania równań różniczkowych (metodę kolejnych przybliżeń Picarda i metodę łamanych Eulera). Pokazujemy też jak za pomocą analizy pola kierunków można określić przybliżony przebieg rozwiązań równania różniczkowego.
Modele matematyczne, które prowadzą do równań różniczkowych
Opis wielu zagadnień praktycznych korzysta z modeli, w których w naturalny sposób pojawia się zależność od pochodnej. Rozważmy kilka z tych problemów.
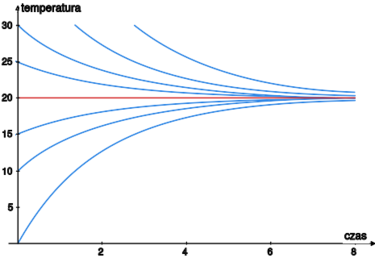
Przykład 13.1.
(stygnięcie, ogrzewanie pewnej substancji) Z obserwacji wynika, że substancja stygnie (odpowiednio: ogrzewa się) tym szybciej, im większa jest różnica temperatury tej substancji i otoczenia. Jeśli oznacza temperaturę substancji w chwili , obserwację można sformułować następująco: zmiana temperatury substancji po upływie czasu od pomiaru temperatury w chwili jest proporcjonalna do różnicy temperatur , gdzie oznacza temperaturę otoczenia, co można zapisać za pomocą równości
,
gdzie jest pewną stałą, a oznacza temperaturę substancji, którą zanotowaliśmy na początku obserwacji w chwili . Znak minus, który poprzedza różnicę bierze się stąd, że substancja stygnie (czyli po upływie czasu ), gdy ma wyższą temperaturę niż otoczenie (tj. gdy ) albo ogrzewa się (czyli po upływie czasu ), gdy otoczenie ma wyższą temperaturę niż obserwowana substancja (tj. gdy ). Jeśli odcinki czasu pomiędzy kolejnymi pomiarami temperatury będą małe, w granicy zależność, którą sformułowaliśmy, przyjmie postać:
Nietrudno odgadnąć (na przykład przyjmując wpierw dla ułatwienia zadania, że temperatura otoczenia jest zerowa), że zależność spełnia funkcja wykładnicza , a także każdy iloczyn tej funkcji przez stałą. Nasze doświadczenie podpowiada nam, że w trakcie obserwacji dwóch identycznych próbek substancji, które stygną w tych samych warunkach (np. dwie identyczne filiżanki kawy stojące obok siebie), po upływie określonego czasu zauważymy, że obie będą mieć taką samą temperaturę. Zbudowany model matematyczny
,
dostarcza dokładnie jednego rozwiązania i jest nim funkcja
,
która spełnia warunek , oznaczający, że temperatura substancji na początku obserwacji wynosiła .
Otrzymane rozwiązanie możemy również łatwo zmodyfikować tak, aby odpowiadało obserwacji w przypadku, gdy temperatura otoczenia jest dowolna:
Naszkicujmy rodzinę krzywych, odpowiadających różnym wartościom
temperatury początkowej (patrz rysunek powyżej).
Niezależnie od temperatury początkowej (w momencie ) wszystkie krzywe zmierzają asymptotycznie do prostej , co odpowiada wielokrotnie czynionej przez nas obserwacji: wraz z upływem czasu wszystkie przedmioty, które znajdują się w pewnym pomieszczeniu (a nie są w jakiś sposób izolowane przed ciepłem), osiągają
temperaturę otoczenia.Niemal każda dziedzina nauki (fizyka, chemia, biologia, ekonomia, demografia, meteorologia i wiele innych) tworzy modele, w których pojawiają się zależności od funkcji i jej pochodnej (lub pochodnych wyższego rzędu).
Przykład 13.2.
(ruch jednostajnie przyśpieszony, spadek swobodny) Z opisem ruchu punktu materialnego, który spada swobodnie w polu grawitacyjnym, spotkaliśmy się już w szkole na lekcjach fizyki. Można przyjąć, że przyśpieszenie ziemskie jest (w pobliżu powierzchni Ziemi) wielkością stałą . Pamiętając, że przyśpieszenie jest pochodną rzędu drugiego funkcji położenia , otrzymujemy równanie
które po jednokrotnym całkowaniu spełnia przyjmuje postać
gdzie jest prędkością w chwili . Kolejne całkowanie prowadzi do znanego wzoru na położenie punktu materialnego w chwili w ruchu jednostajnie przyspieszonym:
gdzie jest położeniem
punktu w chwili początkowej .Przykład 13.3.
(rozwój kolonii bakterii, prawo Malthusa) Obserwacja grupy jednakowych organizmów (np. kolonii bakterii), rozwijających się i rozmnażających w środowisku, w którym jest nieograniczona ilość pożywienia i nie ma naturalnych wrogów, prowadzi do obserwacji, że liczba nowo powstałych organizmów w jednostce czasu jest proporcjonalna do liczby organizmów w danej chwili. Prowadzi to do równania
w którym oraz oznaczają liczebność grupy organizmów w chwili oraz po upływie czasu , natomiast jest stałą charakteryzującą tempo rozmnażania się danej grupy organizmów. Przy otrzymujemy równanie różniczkowe
gdzie stała oznacza liczebność grupy organizmów na początku obserwacji w chwili . Otrzymane równanie stanowi ilustrację prawa Malthusa, które głosi, że wzrost liczebności organizmów jest wykładniczy.

Zobacz biografię
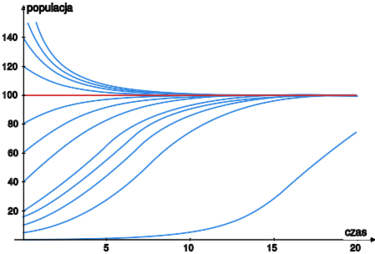
Przykład 13.4.
(zmodyfikowany model rozwoju grupy organizmów) W realnym świecie wykładniczy wzrost liczby organizmów obserwujemy rzadko. W sytuacji, gdy ilość pożywienia jest ograniczona, rozwój grupy organizmów lepiej niż prawo Malthusa opisuje równanie
,
gdzie jest pewną stałą. Jest to równanie Bernoullego (omawiamy je szerzej w ramach następnego modułu). Łatwo spostrzec, że spełniają je dwie funkcje stałe oraz . Po podstawieniu otrzymujemy równanie liniowe niejednorodne (które także omawiamy w ramach następnego modułu)
,
które spełnia każda funkcja postaci
,
gdzie jest stałą. Jej wartość można określić, biorąc pod uwagę liczebność grupy w chwili , czyli biorąc . Otrzymamy stąd . Ostatecznie więc rozwiązaniem równania jest funkcja
Rozwiązanie stałe jest szczególnym przypadkiem
otrzymanego rozwiązania, gdy .
Warto zwrócić uwagę na parę własności tego rozwiązania. Mamy , gdy , niezależnie od liczebności grupy w chwili początkowej. Stała ma naturalną interpretację biologiczną: jest to pojemność ekosystemu, zależna od m.in. ilości pożywienia dostępnego grupie organizmów na określonym obszarze. Ponadto, jeśli (odpowiednio: ), to liczebność grupy rośnie (odpowiednio: maleje) i zmierza asymptotycznie do . Zauważmy także, że żadne z rozwiązań nie zmierza do zera, gdy tylko .
Przykład 13.5.
(równanie sprężyny, prawo Hooke'a) Zgodnie z prawem Hooke'a siła, którą należy wywrzeć na ciało sprężyste, aby je odkształcić, jest wprost proporcjonalna do wielkości odkształcenia. Prawo to w przypadku jednowymiarowym (np. ściskanie i rozciąganie sprężyny) opisuje równanie
gdzie jest wielkością odkształcenia, a jest stałą charakteryzującą ciało, które ulega odkształceniu sprężystemu. Otrzymane równanie (równanie liniowe rzędu drugiego o stałych współczynnikach, które szerzej omawiamy w kolejnym module) spełnia każda funkcja postaci
gdzie są stałymi, których wartość można określić na podstawie np. położenia i prędkości w chwili początkowej . Mamy bowiem , skąd
czyli , . Zatem ruch końca sprężyny, który w chwili odchylono o i puszczono z prędkością początkową , opisuje równanie
Zauważmy, że otrzymana funkcja jest okresowa o okresie i ma stałą amplitudę, co w przypadku realnej sprężyny nie jest prawdą. Nasz model zaniedbuje bowiem tarcie, na
skutek którego ruch zanika (amplituda maleje do zera), gdy .W ramach ćwiczeń omawiamy także rozpad promieniotwórczy izotopu oraz zagadnienie ciągłej kapitalizacji odsetek. Problemy te także prowadzą do konstrukcji modeli matematycznych, w których głównym narzędziem jest pewne równanie różniczkowe.
Równanie różniczkowe w postaci normalnej i różniczkowej
Definicja 13.6.
Niech będzie funkcją ciągłą na zbiorze otwartym . Równanie
z niewiadomą (tj. funkcją krotnie różniczkowalną ), w którym oprócz niewiadomej występują także jej pochodne nazywamy równaniem różniczkowym zwyczajnym rzędu .
Niech będzie przedziałem (z końcami lub bez,
ograniczonym lub nieograniczonym). Funkcjęnazywamy rozwiązaniem równania różniczkowego , jeśli
1. jest -krotnie różniczkowalna w każdym punkcie przedziału (przy czym na końcach przedziału, o ile do niego należą, bierzemy pod uwagę pochodne jednostronne);
2. wykres funkcji zawiera się w zbiorze ;
3. dla dowolnego zachodzi równość .Jeśli w równaniu niewiadomą jest funkcja dwóch lub większej liczby zmiennych i równanie zawiera zależność od pochodnych cząstkowych tej funkcji, na przykład
to równanie tego typu nazywamy równaniem różniczkowym cząstkowym. W dalszym ciągu będziemy zajmować się równaniami zwyczajnym rzędu pierwszego w postaci normalnej
tj. takiej postaci, w której pochodna niewiadomej jest funkcją tej niewiadomej i zmiennej niezależnej . Mając bowiem dane równanie różniczkowe zwyczajne rzędu w postaci normalnej
możemy je zastąpić układem równań różniczkowych zwyczajnych rzędu pierwszego w postaci normalnej:
w którym zmienne
odpowiadają funkcji niewiadomej oraz jej pochodnym
Bardzo często zmienną niezależną w równaniu różniczkowym nazywamy czasem (ze względu na liczne modele matematyczne, w których właśnie czas przeważnie jest zmienną niezależną). Pochodną funkcji oznaczamy tradycyjnie symbolami
Ostatnie z oznaczeń pochodnej (za pomocą kropki nad niewiadomą ) jest charakterystyczne dla równań różniczkowych.
Odpowiednio drugą, trzecią i pochodne wyższego rzędu oznaczamy tradycyjnie symbolami:
Wraz z równaniem różniczkowym w postaci normalnej rozważamy też często równanie w
postaci różniczkowejbądź w bardziej ogólnej postaci
gdzie są danymi funkcjami zmiennych . Zadajemy wówczas
pytanie o istnienie takiej funkcji różniczkowalnej , której różniczkajest tożsama z lewą stroną równania w postaci różniczkowej .
Otrzymujemy wówczas rozwiązaniegdzie jest pewną stałą.
Przykład 13.8.
Dane jest równanie różniczkowe zwyczajne rzędu pierwszego w postaci normalnej
Zauważmy, że postaci różniczkowej przyjmuje ono wyjątkowo prostą postać
stąd równanie w postaci różniczkowej jest tożsame z równaniem
czyli , gdzie jest pewną stałą. Funkcje
w postaci uwikłanejspełniają dane równanie.
Istnienie i jednoznaczność rozwiązania problemu Cauchy'ego

Zobacz biografię
Definicja 13.9.
Zagadnienie
polegające na znalezieniu takiego rozwiązania równania różniczkowego , które spełnia warunek początkowy (gdzie jest zadaną wartością, którą szukane rozwiązanie ma przyjmować w ustalonej chwili początkowej ) nazywamy
problemem początkowym Cauchy'ego.Powstaje naturalne pytanie, czy zawsze problem Cauchy'ego ma rozwiązanie i czy jest ono jednoznaczne? Przypomnijmy, że problem
.
który rozwiązaliśmy opisując proces stygnięcia (ogrzewania), ma zawsze rozwiązanie
i jest ono jednoznaczne. Jednak nasze doświadczenie (np. związane z prognozowaniem pogody) podpowiada nam, że nie wszystkie procesy, które przebiegają w czasie, obok nas, mają jednoznaczne rozwiązanie, którego rezultat można przewidzieć w chwili na podstawie warunku początkowego. Rozważmy prosty przykład.
Przykład 13.10.
Rozważmy problem początkowy Cauchy'ego
.
Łatwo zauważyć, że równanie spełnia funkcja stała . Ponadto po zapisaniu równania w postaci różniczkowej wskazujemy rodzinę funkcji, które je spełniają:
gdzie jest stałą (zauważmy, że równanie to ma sens tylko jeśli ). Stąd , o ile . A więc problem Cauchy'ego
a) ma dokładnie jedno rozwiązanie, gdy :
b) nie ma rozwiązania, gdy ,
c) ma dwa rozwiązaniagdy .
Okazuje się jednak, że przy naturalnych założeniach o funkcji problem Cauchy'ego ma rozwiązanie i jest ono jednoznaczne.
Twierdzenie 13.11.
(twierdzenie Picarda) Jeśli funkcja jest ciągła w pewnym otoczeniu punktu i spełnia warunek Lipschitza względem drugiej zmiennej, tzn.
to problem początkowy Cauchy'ego
ma rozwiązanie i jest ono jedyne.
Przedstawimy szkic dowodu tego twierdzenia. Zawiera on bowiem ciekawą ideę, która pozwala opracować praktyczną metodę numerycznego rozwiązywania równania różniczkowego za pomocą ciągu kolejnych przybliżeń rozwiązania danego równania.
Dowód 13.11.
[szkic] Zauważmy, że funkcja spełnia podany problem początkowy Cauchy'ego wtedy i tylko wtedy, gdy spełnione jest równanie całkowe z niewiadomą
Niech
będzie przestrzenią funkcji ciągłych na przedziale o wartościach w przedziale , gdzie , . Przestrzeń jest przestrzenią metryczną zupełną z metryką zadaną przez normę supremum, tj.
Określmy na tej przestrzeni odwzorowanie:
Wykazuje się (pomijamy szczegóły, które można znaleźć np. w podręczniku Ryszarda Rudnickiego, Wykłady z analizy matematycznej, Wydawnictwo Naukowe PWN, Warszawa 2001), że można dobrać stałe oraz tak, że
- odwzorowanie , tzn. jest określone na i
przyjmuje wartości w przestrzeni , tzn.
- jest zwężające (czyli spełnia warunek Lipschitza ze stałą
mniejszą od 1), tzn. istnieje stała taka, że
dla dowolnych z przestrzeni . Na mocy twierdzenia Banacha o punkcie stałym w przestrzeni istnieje dokładnie jeden punkt , do którego zmierza ciąg iteracji odwzorowania :
Punkt jest punktem stałym odwzorowania , tzn. , czyli
co oznacza, że jest rozwiązaniem danego problemu Cauchy'ego i rozwiązanie to jest jedyne, gdyż (na mocy twierdzenia Banacha o punkcie stałym) ciąg iteracji zawsze zmierza do tego samego punktu (punktu stałego odwzorowania , który jest jedyny) niezależnie od wyboru pierwszego punktu w ciągu iteracji, byleby został on wybrany z przestrzeni , w której
odwzorowanie jest zwężające.Założenie o spełnianiu przez funkcję warunku Lipschitza jest istotne. Funkcja nie spełnia warunku Lipschitza względem drugiej zmiennej w otoczeniu punktu . Przypomnijmy, że problem
ma rozwiązanie, ale nie jest ono
jednoznaczne.Uwagi o przybliżonym rozwiązywaniu równań różniczkowych
Definicja 13.13.
Ciąg określony w dowodzie twierdzenia Picarda
nazywamy ciągiem kolejnych
przybliżeń Picarda.Większość metod numerycznych świetnie radzi sobie z wyznaczaniem przybliżonych rozwiązań równań różniczkowych, pod jednym jednak warunkiem: problem Cauchy'ego musi mieć jednoznaczne rozwiązanie. Nie będziemy rozwijać tego zagadnienia, prześledźmy jednak praktyczną realizację metody zawartej w dowodzie twierdzenia Picarda.
Przykład 13.14.
Wyznaczmy metodą Picarda rozwiązanie problemu Cauchy'ego
Zgodnie z określeniem ciągu Picarda mamy
Jak łatwo zauważyć -ty wyraz ciągu Picarda jest identyczny z -tą sumą częściową szeregu definiującego funkcję wykładniczą
Ciąg zmierza więc do funkcji , która jest
jedynym rozwiązaniem danego problemu Cauchy'ego.
Zobacz biografię
Prześledźmy także na tym samym przykładzie inną metodę przybliżonego rozwiązywania problemu Cauchy'ego, zwaną metodą łamanych Eulera.
Przypomnijmy, że na początku wykładu, omawiając proces stygnięcia (ogrzewania) substancji, zastąpiliśmy iloraz różnicowy
,
równaniem różniczkowym
.
Odwróćmy teraz kolejność postępowania i lewą stronę równania różniczkowego w postaci normalnej
zastąpmy ilorazem różnicowym
.
Podzielmy przedział od do na równych części punktami
.
Określmy (skończony) ciąg punktów następująco:
biorąc stały przyrost :
Wówczas stanowi przybliżoną wartość rozwiązania równania w chwili , tj. . Im gęściej podzielimy przedział od do za pomocą punktów (tzn. gdy jest dużą liczbą), tym przybliżenie to jest lepsze. Łamaną, łączącą punkty nazywamy łamaną Eulera. Stanowi ona przybliżenie wykresu rozwiązania danego
problemu Cauchy'ego w przedziale od do .Przykład 13.16.
Zastosujmy opisany algorytm do znalezienia przybliżonej wartości rozwiązania problemu Cauchy'ego:
który rozwiązaliśmy już metodą kolejnych przybliżeń Picarda. Określamy kolejne węzły łamanej Eulera:
Biorąc pod uwagę, że , otrzymujemy
Stąd , gdyż ciąg zmierza do , gdy .
Metody przybliżone rozwiązywania równań różniczkowych są ważnym narzędziem ze względu na fakt, że wielu równań (co można wykazać) nie da się rozwiązać za pomocą metod dokładnych, w tym sensie, że nie istnieje algorytm o skończonej liczbie kroków,
którego wynikiem byłoby dokładne rozwiązanie równania.Można na przykład wykazać, że nie da się wyrazić za pomocą skończonej liczby operacji na funkcjach elementarnych całek z funkcji
i wielu innych. Funkcje te pojawiają się w wielu ważnych zagadnieniach nauki, np. funkcja dana za pomocą całki oznaczonej
jest dystrybuantą rozkładu normalnego, jednego z najważniejszych rozkładów prawdopodobieństwa, który służy do modelowania wielu zjawisk w biologii, ekonomii i in.
Wracając do teorii równań różniczkowych, można na przykład wykazać, że nie da się elementarnie rozwiązać równania
(przykład tego prostego równania podaje W.I.Arnold, Równania różniczkowe zwyczajne, Państwowe Wydawnictwo Naukowe, Warszawa 1975, s. 40). Zauważmy jednak, że funkcja spełnia założenia twierdzenia Picarda w przedziałach , , a więc problem początkowy Cauchy'ego dla tego równania ma rozwiązanie i jest ono jedyne przy dowolnym warunku początkowym.
W kolejnym module dokonujemy przeglądu wybranych typów równań różniczkowych zwyczajnych, które można rozwiązać w sposób dokładny za pomocą algorytmu o skończonej liczbie etapów. Zwróćmy jednak uwagę, że nie istnieje jeden uniwersalny algorytm znajdowania rozwiązania równania różniczkowego (np. podobny do wzoru na pierwiastki trójmianu kwadratowego).
Pole wektorowe. Pole kierunków
Niezależnie od tego, czy równanie różniczkowe ma rozwiązanie, które można uzyskać za pomocą algorytmu o skończonej liczbie etapów, czy też nie, może zdarzyć się, że nie potrafimy znaleźć tego rozwiązania, bo po prostu nie znamy algorytmu, bądź nie zależy nam na znalezieniu dokładnego rozwiązania, gdy jest ono dla nas mniej interesujące niż na przykład asymptotyczne zachowanie rozwiązań.
Przykład 13.18.
Powróćmy do przykładu z początku wykładu. Równanie
pojawia się w modelu opisu rozwoju grupy organizmów przy założeniu, że pojemność ekosystemu jest ograniczona. Bez rozwiązywania równania możemy zauważyć, że dwie funkcje stałe oraz spełniają to równanie. Ponadto, gdy , pochodna , czyli funkcja maleje, a z kolei, gdy mamy , czyli funkcja rośnie. Zwróćmy uwagę, że z tej prostej obserwacji wynika, że liczebność grupy organizmów rośnie (odpowiednio: maleje), gdy jest ich mniej (odpowiednio: więcej) niż wynosi pojemność ekosystemu. Zauważmy, że wyciągnęliśmy dokładnie ten sam wniosek, który w przykładzie 13.4. pojawił się po analizie wyznaczonego rozwiązania równania różniczkowego.
Pamiętamy, że interpretacją geometryczną pochodnej funkcji jednej zmiennej różniczkowalnej w punkcie jest współczynnik kierunkowy stycznej do wykresu tej funkcji w punkcie . Odwróćmy teraz sytuację i mając dane równanie różniczkowe zwyczajne rzędu pierwszego w postaci normalnej
narysujmy wektory zaczepione w punktach należących do dziedziny funkcji , które tworzą z osią rzędnych (tj. z osią zmiennej ) kąt, którego tangens jest równy .
Otrzymamy w ten sposób obraz
pola wektorowego
którego przebieg jest ściśle związany z przebiegiem rozwiązań danego równania. Zgodnie z interpretacją pochodnej, wektor zaczepiony w punkcie jest styczny w tym punkcie do wykresu funkcji będącej rozwiązaniem problemu początkowego Cauchy'ego
Jeśli więc nawet nie potrafimy rozwiązać danego równania różniczkowego w postaci dokładnej, możemy (np. wspierając się programem do obliczeń symbolicznych Maple, Mathematica lub innym, który pozwala kreślić wykresy) narysować pole wektorowe związane z danym równaniem i na podstawie obrazu pola wektorowego określić w przybliżeniu przebieg rozwiązań równania różniczkowego.

Często zamiast szkicować wektory
,
rezygnujemy z informacji o długości wektora i rysujemy na płaszczyźnie zmiennych odcinki o takiej samej długości (np. jednostkowej), nachylone do osi zmiennej pod kątem, którego tangens wynosi . Tę reprezentację równania różniczkowego nazywamy polem kierunków równania różniczkowego.
Zauważmy, że jeśli w równaniu funkcja nie zależy od zmiennej , pole kierunków zacieśnione do którejkolwiek prostej jest takie samo. Stąd w przypadku równań typu do analizowania pola kierunków i przebiegu rozwiązań równania różniczkowego wystarczy prosta zmiennej .
Przykład 13.19.
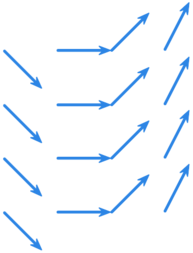
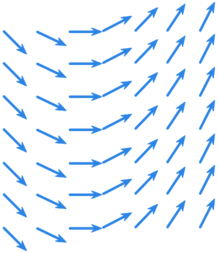
Przykład 13.20.
Pole wektorowe związane z równaniem .
 |
 |
 |
Przykład 13.21.
Pole wektorowe związane z równaniem .
 |
 |
 |
Przykład 13.22.
Pole wektorowe związane z równaniem .
Równania tego nie da się rozwiązać za pomocą algorytmu o skończonej liczbie etapów. Jednak, zgodnie z twierdzeniem Picarda, dla każdego punktu na płaszczyźnie istnieje dokładnie jedno rozwiązanie problemu Cauchy'ego:
Rysując pole kierunków, możemy wyobrazić sobie przebieg krzywych stanowiących rozwiązanie problemu Cauchy'ego dla poszczególnych punktów .
 |
 |
 |
Przykład 13.23.
Pole wektorowe związane z równaniem .
Także tego równania nie potrafimy rozwiązać dokładnie za pomocą algorytmu o skończonej liczbie etapów.
 |
 |