TC Moduł 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „,...,” na „,\ldots,” |
||
| (Nie pokazano 10 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd1.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd1.png]] | ||
|valign="top"| | |valign="top"|Redukcja argumentów | ||
|} | |} | ||
| Linia 8: | Linia 8: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd2.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd2.png]] | ||
|valign="top"| | |valign="top"|Minimalizacja funkcji boolowskich jest podstawową procedurą syntezy logicznej w komputerowych systemach projektowania układów cyfrowych. Skuteczność i szybkość działania tej procedury może być decydująca o jakości implementacji sprzętowych wielu systemów cyfrowych o różnorodnych zastosowaniach. | ||
Niestety ze względu na heurystyczny sposób obliczeń w programie Espresso uzyskany wynik <math>F_M\,</math> może nie być pokryciem minimalnym, co przy wzrastającej złożoności układów realizowanych w nowoczesnych technologiach może okazać się istotną barierą. | |||
Niniejszy wykład omawia oryginalną metodę zmniejszania złożoności obliczeniowej algorytmów minimalizacji funkcji boolowskich. Istotą tej metody jest zastosowanie algorytmu redukcji argumentów, jako oddzielnej procedury poprzedzającej właściwą minimalizację. Redukcja argumentów jest procedurą do tej pory rzadko stosowaną w komputerowych systemach syntezy logicznej. Jedną z przyczyn takiej sytuacji jest brak świadomości, że złożone układy cyfrowe są – od strony pojedynczych wyjść - reprezentowane funkcjami boolowskimi o znacznie nadmiarowych zależnościach wejściowych. | |||
|} | |} | ||
| Linia 15: | Linia 20: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd3.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd3.png]] | ||
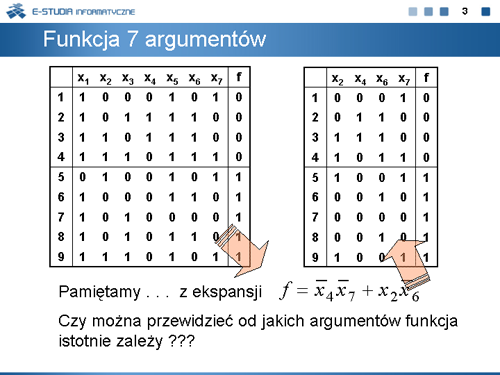
|valign="top"| | |valign="top"|Celem wprowadzenia wróćmy do przykładu funkcji omawianej w poprzednim wykładzie. Jej tablica prawdy podana na planszy ma 7 argumentów. Ale na poprzednim wykładzie obliczyliśmy metodą ekspansji, że minimalne wyrażenie boolowskie tej funkcji zawiera wyłącznie 4 argumenty. Gdybyśmy to wiedzieli wcześniej, to zadanie minimalizacji moglibyśmy skutecznie uprościć. Wystarczyłoby w tym celu usunąć z tablicy prawdy tej funkcji kolumny odpowiadające nadmiarowym argumentom. Zatem problem obliczania od jakich argumentów funkcja istotnie zależy jest bardzo ważny w zmniejszaniu złożoności obliczeniowej procedur minimalizacji. | ||
|} | |} | ||
| Linia 22: | Linia 28: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd4.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd4.png]] | ||
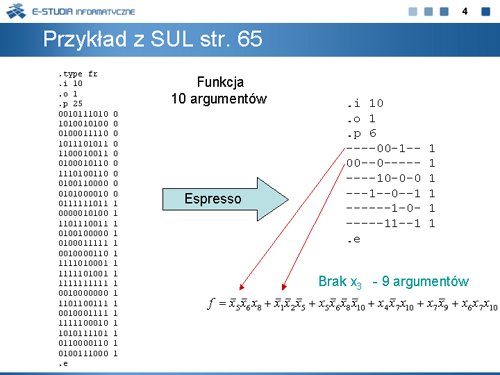
|valign="top"| | |valign="top"|W innym przykładzie funkcji 10 argumentowej, dla której programem Espresso zostało obliczone minimalne wyrażenie boolowskie zauważamy, że w wyrażeniu tym brak jest zmiennej <math>x_3\,</math>. Czyli według Espresso funkcja ta zależy od 9 argumentów. | ||
|} | |} | ||
| Linia 29: | Linia 36: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd5.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd5.png]] | ||
|valign="top"| | |valign="top"|Można jednak obliczyć (programem Pandor), że funkcja ta w rzeczywistości jest zależna od 7 argumentów. Czyli Espresso doskonale redukuje składniki iloczynowe funkcji, ale w przypadku argumentów jego obliczenia nie są skuteczne. Potwierdza to sygnalizowany już mankament metody i programu Espresso. | ||
|} | |} | ||
| Linia 36: | Linia 44: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd6.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd6.png]] | ||
|valign="top"| | |valign="top"|Z powyższych przykładów wynika, że obliczanie minimalnej liczby argumentów | ||
od których funkcja istotnie zależy jest bardzo istotne w redukowaniu złożoności obliczeniowej procedur minimalizacji funkcji boolowskich, a w konsekwencji może się przyczynić do uzyskiwania lepszych rezultatów. Do obliczeń w metodzie redukcji argumentów będziemy stosować rachunek podziałów. Niezbędne pojęcia tego rachunku podajemy na planszach 7, 8 oraz 9. | |||
|} | |} | ||
| Linia 43: | Linia 53: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd7.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd7.png]] | ||
|valign="top"| | |valign="top"|''Podziałem'' na zbiorze <math>S\,</math> jest system zbiorów <math>\pi=\left \{ Bi \right\}\,</math>, którego bloki są rozłączne, czyli | ||
:<math>B_i\cap B_j=\varnothing</math> , jeśli tylko <math>i\neq j</math> . | |||
Na przykład dla <math>S = \left \{1,2,3,4,5,6\right \} \,</math> , <math>\left \{\left \{1,2\right \} , \left \{3,5\right \}, \left \{4,6\right \}\right \}</math> jest podziałem na <math>S\,</math>, co zapisujemy: | |||
:<math>\pi=(\overline{1,2};\overline{3,4};\overline{5,6})</math> | |||
Dla podziałów – podobnie jak dla zbiorów –definiuje się relację porządku oraz typowe działania iloczynu, sumy itp., | |||
|} | |} | ||
| Linia 50: | Linia 69: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd8.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd8.png]] | ||
|valign="top"| | |valign="top"|Powiemy, że podział <math>\pi_1\,</math> jest nie większy od <math>\pi_2\,</math> (co oznaczamy: <math>\pi_1\le \pi_2</math>), jeśli każdy blok z <math>\pi_1\,</math> jest zawarty w pewnym bloku z <math>\pi_2\,</math>. | ||
Wprowadzamy oznaczenia odpowiednio dla podziału najmniejszego <math>\pi (0)\,</math> oraz największego <math>\pi (1)\,</math>. Podział <math>\pi (0)\,</math> jest podziałem, którego bloki są elementami zbioru <math>S\,</math>. Podział <math>\pi (1)\,</math> jest podziałem o jednym bloku wyczerpującym cały zbiór <math>S\,</math>. Na przykład: dla <math>S = \left\{1, 2, 3}\right\}\,</math>, <math>\pi (0) = \left\{\overline{1}, \overline{2}, \overline{3}}\right\}\,</math> , <math>\pi (1) = \left\{\overline{1,2,3}}\right\}\,</math> . | |||
|} | |} | ||
| Linia 57: | Linia 79: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd9.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd9.png]] | ||
|valign="top"| | |valign="top"|Iloczynem podziałów <math>\pi_1\bullet \pi_2\,</math> nazywamy największy (względem relacji <math>\le\,</math>) podział, który jest nie większy od <math>\pi_1\,</math> oraz <math>\pi_2\,</math>. | ||
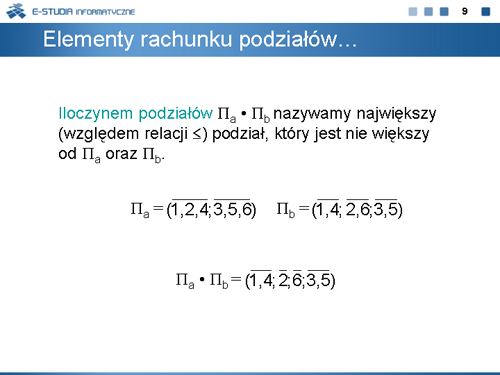
<math>\Pi_a=(\overline{1,2,4}; \overline{3,5,6})</math> | |||
<math>\Pi_b=(\overline{1,4}; \overline{2,6}; \overline{3,5})</math> | |||
<math>\Pi_1\bullet \Pi_2=(\overline{1,4}; \overline{2}; \overline{6}; \overline{3,5})</math> | |||
Symetrycznie, ''sumą <math>\pi_1+ \pi_2\,</math>'' nazywamy najmniejszy podział nie mniejszy od <math>\pi_1\,</math> oraz <math>\pi_2\,</math>. | |||
<math>\Pi_a=(\overline{1,2}; \overline{3,4}; \overline{5,6}; \overline{7,8,9})</math> | |||
<math>\Pi_b=(\overline{1,6}; \overline{2,3}; \overline{4,5}; \overline{7,8}; \overline{9})</math> | |||
<math>\Pi_1+ \Pi_2=(\overline{1,2,3,4,5,6}; \overline{7,8,9})</math> | |||
|} | |} | ||
| Linia 64: | Linia 101: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd10.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd10.png]] | ||
|valign="top"| | |valign="top"|Rachunek podziałów zastosujemy do reprezentacji funkcji boolowskich. Dla funkcji EXTL, której tablicę prawdy powtarzamy na niniejszej planszy jej zapis w postaci podziałów jest następujący: | ||
<math>P_1=(\overline{5}; \overline{1,2,3,4,6,7,8,9})</math> | |||
<math>P_2=(\overline{1,2,6,7,8}; \overline{3,4,5,9})</math> | |||
<math>P_3=(\overline{1,3,5,6}; \overline{2,4,7,8,9})</math> | |||
<math>P_4=(\overline{1,4,5,6,7,8,9}; \overline{2,3})</math> | |||
<math>P_5=(\overline{7}; \overline{1,2,3,4,5,6,8,9})</math> | |||
<math>P_6=(\overline{1,5,7,9}; \overline{2,3,4,6,8})</math> | |||
<math>P_7=(\overline{2,3,6,7,8}; \overline{1,4,5,9})</math> | |||
<math>P_f=(\overline{1,2,3,4}; \overline{5,6,7,8,9})</math> | |||
|} | |} | ||
| Linia 71: | Linia 125: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd11.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd11.png]] | ||
|valign="top"| | |valign="top"|Jeżeli wektory <math>X_a\,</math> oraz <math>X_b\,</math>: <math>f\,(X_a)\neq f\,(X_b)</math> , różnią się dokładnie dla jednej zmiennej to nazywamy ją zmienną niezbędną. Sens fizyczny zmiennej niezbędnej wynika z faktu, że usunięcie kolumny odpowiadającej tej zmiennej w tablicy prawdy tworzy tablicę, w której dwa takie same wektory mają różne wartości (są sprzeczne). | ||
|} | |} | ||
| Linia 78: | Linia 133: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd12.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd12.png]] | ||
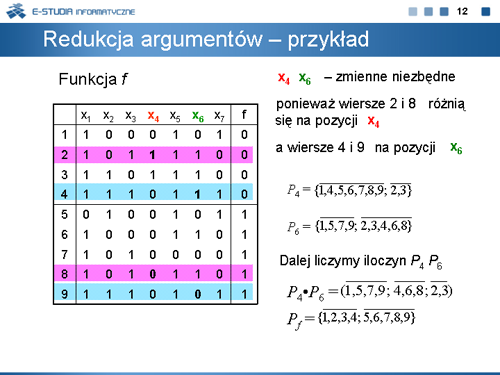
|valign="top"| | |valign="top"|Na przykładzie funkcji EXTL wyjaśniamy poszukiwanie zmiennych niezbędnych. | ||
Zmiennymi niezbędnymi tej funkcji są <math>x_4\,</math> , <math>x_6\,</math>. Co łatwo sprawdzić, gdyż wiersze o numerach 2 i 8 (zaznaczone kolorem różowym) różnią się wyłącznie na pozycji <math>x_4\,</math>, natomiast wiersze 4 i 9 (zaznaczone kolorem niebieskim) różnią się tylko na pozycji <math>x_6\,</math>. | |||
Po wyznaczeniu zmiennych niezbędnych obliczamy iloczyn podziałów <math>P = P_4\cdot P_6\,</math> . | |||
|} | |} | ||
| Linia 85: | Linia 144: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd13.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd13.png]] | ||
|valign="top"| | |valign="top"|Iloczyn podziałów wyznaczonych przez zmienne niezbędne ma bardzo ważną interpretację. | ||
Zauważmy, że kolejne bloki iloczynu <math>P = (B_1,\ldots,B_3)\,</math> są <math>B_1=\left \{1,5,7,9 \right \}</math> , <math>B_2=\left \{4,6,8\right \}</math> , <math>B_3 = {2,3\}</math>.Blok <math>B_3\,</math> jest zawarty w jednym bloku podziału <math>P_f\,</math>. Ale bloki <math>B_1\,</math> i <math>B_2\,</math> zawierają elementy należące do dwóch różnych bloków podziału <math>P_f\,</math>, czyli same zmienne <math>x_4\,</math> , <math>x_6\,</math> nie wystarczają do oddzielenia wektorów prawdziwych od fałszywych realizowanej funkcji. | |||
|} | |} | ||
| Linia 92: | Linia 154: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd14.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd14.png]] | ||
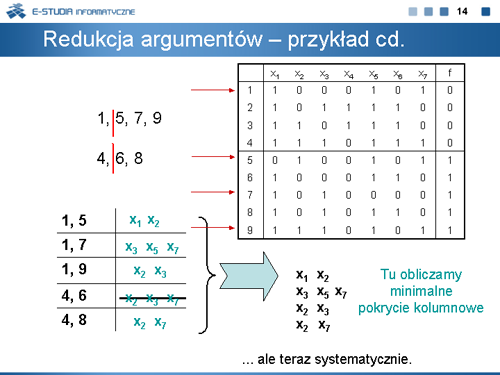
|valign="top"| | |valign="top"|Zatem należy się zastanowić jakie argumenty należy dołożyć do argumentów niezbędnych, aby zapewnić jednoznaczną realizację tej funkcji. Obserwując zbiory <math>B_1=\left \{1,5,7,9\right \}</math>, <math>B_2=\left \{4,6,8\right \}</math> , łatwo stwierdzić, że wystarczy w tym celu dobrać takie argumenty, aby „oddzielić” wektory (wiersze) o numerach 1 od 5, 7, 9 oraz 4 od 6, 8. Zatem należy oddzielić 1 od 5, 1 od 7 itd. Zapisujemy zbiory argumentów, dla których różnią się wiersze 1 i 5, 1 i 7 itd. w formie stosownej tabelki (jak na planszy). W tabelce tej zbiór w wierszu oznaczonym 4, 6 pokrywa zbiór z wiersza 1, 9. Zatem wiersz „większy” usuwamy. | ||
Ogólnie usuwamy każdy zbiór <math>Z\,</math> dla którego istnieje <math>Z': Z'\subseteq Z\,</math>. Tak wyznaczana tabelka (w szczególności) zredukowana może być interpretowana jako zadanie obliczania minimalnego pokrycia kolumnowego. | |||
|} | |} | ||
| Linia 99: | Linia 164: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd15.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd15.png]] | ||
|valign="top"| | |valign="top"|Chcąc zatem obliczyć minimalne zbiory argumentów zapisujemy zredukowaną tabelkę w postaci wyrażenia boolowskiego typu „iloczyn sum”. Kolejną czynnością jest przekształcenie „iloczynu sum” w wyrażenie typu „suma iloczynów” W czynności tej oczywiście stosujemy zasady algebry Boole’a. I w rezultacie uzyskujemy wyrażenie: | ||
<math>x_2x_3+x_2x_5+x_2x_7+x_1x_3x_7+</math> | |||
które interpretujemy następująco. Wszystkie składniki tego wyrażenia o minimalnej liczbie czynników (zmiennych <math>x_i\,</math>) reprezentują minimalne zbiory argumentów, które łącznie ze zmiennymi niezbędnymi tworzą minimalne zbiory argumentów wystarczające do realizacji funkcji: | |||
<math>\left \{x_2, x_3, x_4, x_6\right \}, \left \{x_2, x_3, x_5, x_6\right \}, \left \{x_2, x_3, x_6, x_7\right \}</math> . | |||
Stąd wniosek, że siedmio-argumentowa funkcja f w rzeczywistości jest zależna wyłącznie od czterech argumentów. | |||
|} | |} | ||
| Linia 106: | Linia 180: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd16.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd16.png]] | ||
|valign="top"| | |valign="top"|Zauważmy też, że ostatnie z podanych rozwiązań oznacza usunięcie z tablicy funkcji <math>f\,</math> kolumn odpowiadających zmiennym <math>x1, x3, x5\,</math> . W rezultacie uzyskujemy tablicę, której wymiary umożliwiają zastosowanie nawet najprostszej metody minimalizacji jaką jest tablica Karnaugha. | ||
|} | |} | ||
| Linia 113: | Linia 188: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd17.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd17.png]] | ||
|valign="top"| | |valign="top"|Omówioną metodę zrealizowaną w postaci oddzielnego modułu oprogramowania można traktować jako procedurę wspomagająca metodę i program Espresso. W celu przekonania się o skuteczności wspomagania minimalizacji funkcji boolowskich dodatkową procedurą redukcji argumentów omówimy kilka eksperymentów wykonanych programami Espresso i Pandor. W eksperymentach tych dokonamy minimalizacji dwóch typowych funkcji boolowskich: TL27 i KAZ. W szczególności porównamy wyniki minimalizacji uzyskane programem Espresso z wynikami uzyskanymi przy wspomaganiu minimalizacji dodatkową procedura redukcji argumentów. | ||
|} | |} | ||
| Linia 120: | Linia 196: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd18.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd18.png]] | ||
|valign="top"| | |valign="top"|Eksperyment z funkcją TL27. Na planszy z lewej strony podany jest plik wejściowy programu Espresso z zapisaną funkcją TL27. Z prawej strony tej planszy podany jest wynik minimalizacji tej funkcji programem Espresso. Jak widać espresso minimalizuje tę funkcję do 6 termów (składników iloczynowych) z łączną liczbą 9 argumentów. | ||
|} | |} | ||
| Linia 127: | Linia 204: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd19.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd19.png]] | ||
|valign="top"| | |valign="top"|Za pomocą programu Pandor można obliczyć, że funkcja ta ma 10 rozwiązań dla minimalnych zbiorów argumentów. Jedno z tych rozwiązań jest podane na planszy. Jest zrozumiałe, że funkcja o mniejszej liczbie argumentów jest „łatwiejsza” do minimalizacji. Zatem tak zredukowaną funkcję można poddać obliczeniom za pomocą programu Pandor. | ||
|} | |} | ||
| Linia 134: | Linia 212: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd20.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd20.png]] | ||
|valign="top"| | |valign="top"|Porównajmy wyniki tak przeprowadzanych minimalizacji. | ||
Wynik Espresso – 9 argumentów, 6 termów | |||
<math>f=\overline{x}_5\overline{x}_6x_8+\overline{x}_1\overline{x}_2\overline{x}_5+x_5\overline{x}_6\overline{x}_8\overline{x}_{10}+x_4\overline{x}_7x_{10}+x_7\overline{x}_9+x_6x_7x_{10}</math> | |||
Wynik Pandora – 7 argumentów, 5 termów | |||
<math>f=\overline{x}_1\overline{x}_2\overline{x}_7+x_1x_2x_4+\overline{x}_1x_{10}+\overline{x}_1\overline{x}_4\overline{x}_6+x_7\overline{x}_9</math> | |||
|} | |} | ||
| Linia 141: | Linia 228: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd21.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd21.png]] | ||
|valign="top"| | |valign="top"|Eksperyment z funkcją KAZ. Na planszy z lewej strony podany jest plik wejściowy programu Espresso z zapisaną funkcją KAZ. Z prawej strony tej planszy podany jest wynik redukcji argumentów tej funkcji programem Pandor. Jak widać Pandor oblicza, że funkcja ta w rzeczywistości (mimo pierwotnej specyfikacji o 21 argumentach) istotnie zależy wyłącznie od 5 argumentów. Zatem tak zredukowaną funkcję można poddać obliczeniom za pomocą systematycznej procedury ekspansji wbudowanej do programu Pandor. | ||
|} | |} | ||
| Linia 148: | Linia 236: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:TC_M5_Slajd22.png]] | |valign="top" width="450px"|[[Grafika:TC_M5_Slajd22.png]] | ||
|valign="top"| | |valign="top"|Możemy więc porównać wynik minimalizacji programem Espresso: | ||
<math>f=\overline{x}_2x_{14}\overline{x}_{19}x_{21}+x_7\overline{x}_8\overline{x}_{12}+x_5x_8\overline{x}_{20}</math> | |||
z minimalizacją systematyczną wspomaganą procedurą redukcji argumentów. | |||
<math>f=\overline{x}_2\overline{x}_4x_9\overline{x}_{19}+\overline{x}_2x_4\overline{x}_9+x_2x_{19}\overline{x}_{20}</math> | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"></math> | ||
Aktualna wersja na dzień 21:58, 15 wrz 2023

|
Redukcja argumentów |
|
Iloczynem podziałów nazywamy największy (względem relacji ) podział, który jest nie większy od oraz .
Symetrycznie, sumą nazywamy najmniejszy podział nie mniejszy od oraz .
|

|
Rachunek podziałów zastosujemy do reprezentacji funkcji boolowskich. Dla funkcji EXTL, której tablicę prawdy powtarzamy na niniejszej planszy jej zapis w postaci podziałów jest następujący:
|

|
Porównajmy wyniki tak przeprowadzanych minimalizacji.
Wynik Espresso – 9 argumentów, 6 termów
Wynik Pandora – 7 argumentów, 5 termów
|

|
Możemy więc porównać wynik minimalizacji programem Espresso:
z minimalizacją systematyczną wspomaganą procedurą redukcji argumentów.
|
</math>