PF Moduł 8: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 16 wersji utworzonych przez 4 użytkowników) | |||
| Linia 1: | Linia 1: | ||
__TOC__ | |||
= Wykład = | |||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:PF_M8_Slajd1.png]] | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd1.png]] | ||
| Linia 33: | Linia 36: | ||
|valign="top" width="450px"|[[Grafika:PF_M8_Slajd3.png]] | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd3.png]] | ||
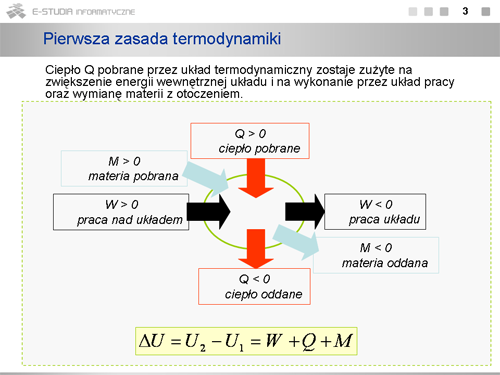
|valign="top"|W ten sposób pierwsza zasada termodynamiki wskazuje na trzy różne sposoby zmiany energii wewnętrznej układu: na drodze wykonywania pracy nad układem bądź przez układ oraz poprzez wymianę ciepła lub/i materii pomiędzy układem a otoczeniem. | |valign="top"|W ten sposób pierwsza zasada termodynamiki wskazuje na trzy różne sposoby zmiany energii wewnętrznej układu: na drodze wykonywania pracy nad układem bądź przez układ oraz poprzez wymianę ciepła lub/i materii pomiędzy układem a otoczeniem. | ||
'''W naszych dalszych rozważaniach będziemy omawiać układy nie wymieniające materii z otoczeniem, dla których M=0'''. | |||
|} | |} | ||
| Linia 39: | Linia 43: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika:PF_M8_Slajd4.png]] | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd4.png]] | ||
|valign="top"| | |valign="top"|Zmiana energii wewnętrznej <math>\Delta U</math> układu o stałej masie dokonuje się poprzez wymianę ciepła <math>Q</math>, co zachodzi w warunkach różnicy temperatur pomiędzy układem i otoczeniem, lub/i poprzez pracę <math>W</math> wykonaną nad układem lub przez układ nad otoczeniem. | ||
: <math>\Delta Q=Q+W</math>. | : <math>\Delta Q=Q+W</math>. | ||
| Linia 45: | Linia 49: | ||
Wprowadzamy tu konwencję, którą będziemy stosować w dalszych rozważaniach dla układów nie wymieniających materii z otoczeniem. | Wprowadzamy tu konwencję, którą będziemy stosować w dalszych rozważaniach dla układów nie wymieniających materii z otoczeniem. | ||
Praca <math>W\ | Praca <math>W\ </math>, jest dodatnia <math>(W > 0)</math>, jeżeli jest wykonywana przez siły zewnętrzne (otoczenie) nad układem fizycznym. Kiedy układ fizyczny wykonuje pracę nad otoczeniem (kosztem swej energii wewnętrznej) praca ta jest ujemna <math>(W < 0)</math>. Podobnie, ciepło jest dodatnie <math>(Q > 0)</math>, jeśli przepływa z otoczenia do układu, a ujemne <math>(Q < 0)</math>, jeśli przepływa z układu do otoczenia. Dla przykładu, kiedy siły zewnętrzne (otoczenie) wykonują pracę sprężając gaz <math>(\Delta V < 0)</math>, to wykonana praca jest dodatnia, kiedy gaz wykonuje pracę nad otoczeniem rozprężając się <math>(\Delta V > 0)</math>, praca jest ujemna. | ||
|} | |} | ||
| Linia 57: | Linia 61: | ||
: <math>dU=\delta Q + \delta W</math> | : <math>dU=\delta Q + \delta W</math> | ||
'''UWAGA:''' Symbolami <math>\delta Q</math> i <math>\delta W</math> oznaczamy różniczkowe porcje (a nie skończone przyrosty) wymienianego przez układ ciepła i wykonanej pracy przy nieskończenie małych (infinitezymalnych) zmianach parametrów stanu układu. Wynika, to z faktu, ze ciepło i praca nie są funkcjami stanu, bowiem jak zobaczymy, zależą od drogi przejścia pomiędzy stanami. Mówimy, że są '''funkcjami procesu'''. Symbol <math>dU\ | '''UWAGA:''' Symbolami <math>\delta Q</math> i <math>\delta W</math> oznaczamy różniczkowe porcje (a nie skończone przyrosty) wymienianego przez układ ciepła i wykonanej pracy przy nieskończenie małych (infinitezymalnych) zmianach parametrów stanu układu. Wynika, to z faktu, ze ciepło i praca nie są funkcjami stanu, bowiem jak zobaczymy, zależą od drogi przejścia pomiędzy stanami. Mówimy, że są '''funkcjami procesu'''. Symbol <math>dU\ </math>, oznacza zmianę energii wewnętrznej, która jest funkcją stanu. W przemianie kołowej, kiedy układ powraca do stanu początkowego, jego energia wewnętrzna mieć będzie taką samą wartość jak w stanie początkowym, co zapisujemy w postaci | ||
: <math>\oint dU=0</math> | : <math>\oint dU=0</math> | ||
| Linia 71: | Linia 75: | ||
|valign="top"|'''Przemiana izochoryczna''' to proces, w którym objętość układu pozostaje stała, czyli <math>V=const</math>. W przemianie tej '''nie jest wykonywana praca'''. W oparciu o pierwszą zasadę termodynamiki mamy dla przemiany izochorycznej relację | |valign="top"|'''Przemiana izochoryczna''' to proces, w którym objętość układu pozostaje stała, czyli <math>V=const</math>. W przemianie tej '''nie jest wykonywana praca'''. W oparciu o pierwszą zasadę termodynamiki mamy dla przemiany izochorycznej relację | ||
: <math>\delta Q_v= | : <math>\delta Q_v=dU</math>, | ||
co oznacza, że w przemianie izochorycznej możemy zmienić energię wewnętrzną układu jedynie na drodze wymiany ciepła. | co oznacza, że w przemianie izochorycznej możemy zmienić energię wewnętrzną układu jedynie na drodze wymiany ciepła. | ||
| Linia 198: | Linia 202: | ||
: <math>{p \cdot V \over R} \cdot V^{\kappa -1}=const</math> lub <math>{p \cdot V^\kappa \over R}=const</math>. | : <math>{p \cdot V \over R} \cdot V^{\kappa -1}=const</math> lub <math>{p \cdot V^\kappa \over R}=const</math>. | ||
Powyższe wzory pozostaną w mocy, jeśli stałą gazową <math>R\ | Powyższe wzory pozostaną w mocy, jeśli stałą gazową <math>R\ </math>, włączymy do stałej po prawej stronie. Otrzymamy wtedy | ||
: <math>p \cdot V^\kappa=const</math>. | : <math>p \cdot V^\kappa=const</math>. | ||
Związek ten jest równaniem adiabaty i nosi nazwę '''równania Poissona'''. Postępując podobnie można otrzymać równania określające zależności między innymi parametrami stanu dla przemiany adiabatycznej | |} | ||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:PF_M8_Slajd10.png]] | |||
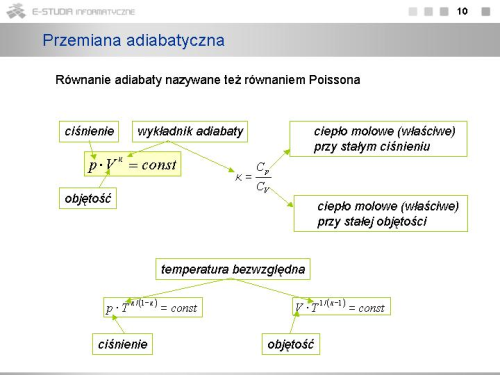
|valign="top"|Związek ten jest równaniem adiabaty i nosi nazwę '''równania Poissona'''. Postępując podobnie można otrzymać równania określające zależności między innymi parametrami stanu dla przemiany adiabatycznej | |||
: <math>p \cdot T^{\kappa / (1-\kappa)}=const, \ V \cdot T^{1/(\kappa -1)}=const</math>. | : <math>p \cdot T^{\kappa / (1-\kappa)}=const, \ V \cdot T^{1/(\kappa -1)}=const</math>. | ||
| Linia 213: | Linia 223: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd11.png]] | ||
|valign="top"|Jeśli w czasie przemiany pojemność cieplna ciała pozostaje stała, czyli '''C=const''', to mówimy, że zachodzi '''przemiana politropowa'''. Znajdźmy dla gazu doskonałego związek pomiędzy ciśnieniem i objętością w takiej przemianie, czyli równanie politropy. | |valign="top"|Jeśli w czasie przemiany pojemność cieplna ciała pozostaje stała, czyli '''C=const''', to mówimy, że zachodzi '''przemiana politropowa'''. Znajdźmy dla gazu doskonałego związek pomiędzy ciśnieniem i objętością w takiej przemianie, czyli równanie politropy. | ||
| Linia 222: | Linia 232: | ||
Wzór ten można też zapisać inaczej | Wzór ten można też zapisać inaczej | ||
: <math>n_M \cdot (C-C_v) \cdot dT=p \cdot dV </math> lub <math>dT={p \cdot dV \over n_M \cdot (C-C_v)}</math>. | : <math>n_M \cdot (C-C_v) \cdot dT=p \cdot dV</math> lub <math>dT={p \cdot dV \over n_M \cdot (C-C_v)}</math>. | ||
Wykorzystamy także równanie stanu gazu doskonałego, różniczkując je mamy | Wykorzystamy także równanie stanu gazu doskonałego, różniczkując je mamy | ||
| Linia 228: | Linia 238: | ||
: <math>p \cdot dV \cdot + V \cdot dp=n_M \cdot R \cdot dT</math>. | : <math>p \cdot dV \cdot + V \cdot dp=n_M \cdot R \cdot dT</math>. | ||
Teraz wstawiając wyrażenie na <math>dT\ | Teraz wstawiając wyrażenie na <math>dT\ </math>, do ostatniego równania otrzymujemy po prostych przekształceniach | ||
: <math>(C-C_v-R) \cdot p \cdot dV + (C-C_v) \cdot V \cdot dp = 0</math>. | : <math>(C-C_v-R) \cdot p \cdot dV + (C-C_v) \cdot V \cdot dp = 0</math>. | ||
| Linia 249: | Linia 259: | ||
nazywa się wykładnikiem politropy. (Pamiętajmy by nie mylić tego oznaczenia z oznaczeniem, także literą '''"n"''', liczby cząsteczek w jednostce objętości. Nie wprowadzamy tu nowych oznaczeń, by pozostać w zgodności z ogólnie przyjętym nazewnictwem.) | nazywa się wykładnikiem politropy. (Pamiętajmy by nie mylić tego oznaczenia z oznaczeniem, także literą '''"n"''', liczby cząsteczek w jednostce objętości. Nie wprowadzamy tu nowych oznaczeń, by pozostać w zgodności z ogólnie przyjętym nazewnictwem.) | ||
Można teraz obliczyć ciepło molowe '''C''' w zależności od wykładnika '''n''' | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:PF_M8_Slajd12.png]] | |||
|valign="top"|Można teraz obliczyć ciepło molowe '''C''' w zależności od wykładnika '''n''' | |||
: <math>C={n \cdot C_v - C_p \over n-1}</math>. | : <math>C={n \cdot C_v - C_p \over n-1}</math>. | ||
| Linia 269: | Linia 286: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd13.png]] | ||
|valign="top"|Pierwsza zasada termodynamiki nie wystarcza do pełnego opisu procesów zachodzących w przyrodzie. Dla przykładu, całkowicie zgodna z pierwszą zasadą termodynamiki byłaby zamiana na pracę nieprzebranej ilości energii cieplnej tkwiącej w wodach mórz i oceanów, w powietrzu, czy skorupie ziemskiej. Wiemy, że energia ta nie może być w całości zamieniona na pracę. | |valign="top"|Pierwsza zasada termodynamiki nie wystarcza do pełnego opisu procesów zachodzących w przyrodzie. Dla przykładu, całkowicie zgodna z pierwszą zasadą termodynamiki byłaby zamiana na pracę nieprzebranej ilości energii cieplnej tkwiącej w wodach mórz i oceanów, w powietrzu, czy skorupie ziemskiej. Wiemy, że energia ta nie może być w całości zamieniona na pracę. | ||
Wymieńmy jeszcze inne przykłady procesów, które nie mogą zachodzić, chociaż nie są sprzeczne z zasadą zachowania energii. | Wymieńmy jeszcze inne przykłady procesów, które nie mogą zachodzić, chociaż nie są sprzeczne z zasadą zachowania energii. | ||
| Linia 289: | Linia 306: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd14.png]] | ||
|valign="top"|W silnikach (maszynach) cieplnych ciepło zamieniane jest na pracę. Elementami silnika są: źródło ciepła (grzejnik) o temperaturze <math>T_1</math>, chłodnica o temperaturze <math>T_2</math> i substancja robocza, którą jest gaz. Pracę silnika charakteryzuje sprawność (wydajność). Sprawność silnika określa, jaka część energii pobranej na sposób ciepła może być przekazana innemu układowi na sposób pracy, w jednym cyklu. | |valign="top"|W silnikach (maszynach) cieplnych ciepło zamieniane jest na pracę. Elementami silnika są: źródło ciepła (grzejnik) o temperaturze <math>T_1</math>, chłodnica o temperaturze <math>T_2</math> i substancja robocza, którą jest gaz. Pracę silnika charakteryzuje sprawność (wydajność). Sprawność silnika określa, jaka część energii pobranej na sposób ciepła może być przekazana innemu układowi na sposób pracy, w jednym cyklu. | ||
| Linia 303: | Linia 320: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd15.png]] | ||
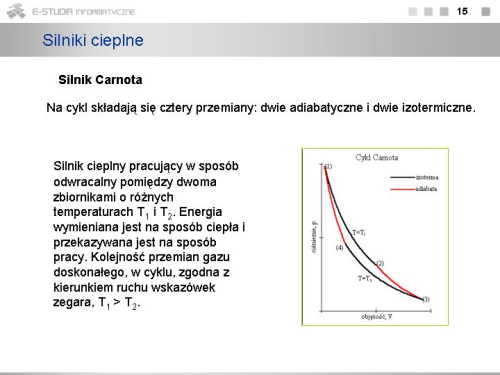
|valign="top"|Silnik cieplny pracujący w sposób odwracalny pomiędzy dwoma zbiornikami o różnych temperaturach <math>T_ 1</math> i <math>T_2</math>. Energia wymieniana jest na sposób ciepła i przekazywana jest na sposób pracy. Kolejność przemian gazu doskonałego, w cyklu, zgodna z kierunkiem ruchu wskazówek zegara, <math>T_1 > T_2</math>. | |valign="top"|Silnik cieplny pracujący w sposób odwracalny pomiędzy dwoma zbiornikami o różnych temperaturach <math>T_ 1</math> i <math>T_2</math>. Energia wymieniana jest na sposób ciepła i przekazywana jest na sposób pracy. Kolejność przemian gazu doskonałego, w cyklu, zgodna z kierunkiem ruchu wskazówek zegara, <math>T_1 > T_2</math>. | ||
Na cykl składają się cztery przemiany: dwie adiabatyczne i dwie izotermiczne. Zakładamy, że cykl rozpoczyna się stanem (1) opisanym przez <math>p_1, V_1, T_1</math> i odpowiednio poprzez kolejne stany (2), (3), (4) kończy powrotem do stanu (1). | Na cykl składają się cztery przemiany: dwie adiabatyczne i dwie izotermiczne. Zakładamy, że cykl rozpoczyna się stanem (1) opisanym przez <math>p_1, V_1, T_1</math> i odpowiednio poprzez kolejne stany (2), (3), (4) kończy powrotem do stanu (1). | ||
| Linia 312: | Linia 329: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd16.png]] | ||
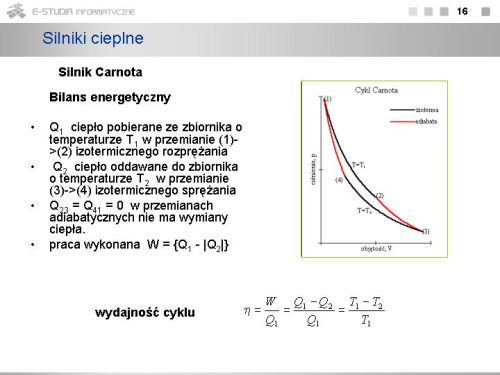
|valign="top"|W przemianie (1)->(2) izotermicznego rozprężania gaz pobiera ciepło <math>Q_1</math> ze zbiornika o temperaturze <math>T_1</math>. Przemiana zachodzi przy stałej temperaturze, więc energia wewnętrzna gazu nie ulega zmianie oraz | |valign="top"|W przemianie (1)->(2) izotermicznego rozprężania gaz pobiera ciepło <math>Q_1</math> ze zbiornika o temperaturze <math>T_1</math>. Przemiana zachodzi przy stałej temperaturze, więc energia wewnętrzna gazu nie ulega zmianie oraz | ||
| Linia 347: | Linia 364: | ||
: <math>{\bar Q_2 \over Q_1}={T_2 \over T_1}</math> lub <math>{Q_1 \over T_1}={\bar Q_2 \over T_2}</math>. | : <math>{\bar Q_2 \over Q_1}={T_2 \over T_1}</math> lub <math>{Q_1 \over T_1}={\bar Q_2 \over T_2}</math>. | ||
Wynika z tego, że '''sprawność silnika Carnota''' może być przedstawiona w postaci | |} | ||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="450px"|[[Grafika:PF_M8_Slajd17.png]] | |||
|valign="top"|Wynika z tego, że '''sprawność silnika Carnota''' może być przedstawiona w postaci | |||
: <math>\eta = 1-{T_2 \over T_1}={T_1-T_2 \over T_1}</math>. | : <math>\eta = 1-{T_2 \over T_1}={T_1-T_2 \over T_1}</math>. | ||
| Linia 375: | Linia 398: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd18.png]] | ||
|valign="top"|Pracę czterosuwowego silnika benzynowego, z dobrym przybliżeniem, opisuje cykl Otta, na który składa się sześć następujących procesów | |valign="top"|Pracę czterosuwowego silnika benzynowego, z dobrym przybliżeniem, opisuje cykl Otta, na który składa się sześć następujących procesów | ||
#(0)->(1) izobaryczne wessanie powietrza zawierającego pary benzyny do cylindra, o pojemności minimalnej <math>V_2</math> oraz maksymalnej <math>V_1</math>. | #(0)->(1) izobaryczne wessanie powietrza zawierającego pary benzyny do cylindra, o pojemności minimalnej <math>V_2</math> oraz maksymalnej <math>V_1</math>. | ||
| Linia 390: | Linia 413: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd19.png]] | ||
|valign="top"|Przy obliczaniu wydajności cykli odwracalnych posługujemy się najwygodniejszymi charakterystykami rozważanego cyklu. | |valign="top"|Przy obliczaniu wydajności cykli odwracalnych posługujemy się najwygodniejszymi charakterystykami rozważanego cyklu. | ||
W procesie (2) -> (3) izochorycznego ogrzewania gaz pobiera ciepło | W procesie (2) -> (3) izochorycznego ogrzewania gaz pobiera ciepło | ||
| Linia 417: | Linia 440: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd20.png]] | ||
|valign="top"|'''Cykl Diesla''' opisuje pracę czterosuwowego silnika wysokoprężnego. Stan gazów w cylindrze opisany jest za pomocą sześciu następujących po sobie przemian odwracalnych. | |valign="top"|'''Cykl Diesla''' opisuje pracę czterosuwowego silnika wysokoprężnego. Stan gazów w cylindrze opisany jest za pomocą sześciu następujących po sobie przemian odwracalnych. | ||
#(0)->(1) izobaryczne wessanie powietrza do całkowitego wypełnienia objętości cylindra. | #(0)->(1) izobaryczne wessanie powietrza do całkowitego wypełnienia objętości cylindra. | ||
| Linia 432: | Linia 455: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd21.png]] | ||
|valign="top"|Przy obliczaniu wydajności cykli odwracalnych posługujemy się najwygodniejszymi charakterystykami rozważanego cyklu. | |valign="top"|Przy obliczaniu wydajności cykli odwracalnych posługujemy się najwygodniejszymi charakterystykami rozważanego cyklu. | ||
W procesie (2) -> (3) izobarycznego ogrzewania gaz pobiera ciepło | W procesie (2) -> (3) izobarycznego ogrzewania gaz pobiera ciepło | ||
| Linia 465: | Linia 488: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd22.png]][[Grafika:PF_M8_Slajd23.png]] | ||
|valign="top"|Entropię możemy tu zdefiniować następująco:, jeżeli w danym procesie odwracalnym układ pobiera ciepło <math>dQ</math> w temperaturze <math>T</math>, to przyrost entropii układu wynosi <math>dS = dQ / T</math>. | |valign="top"|Entropię możemy tu zdefiniować następująco:, jeżeli w danym procesie odwracalnym układ pobiera ciepło <math>dQ</math> w temperaturze <math>T</math>, to przyrost entropii układu wynosi <math>dS = dQ / T</math>. | ||
Entropia <math>S</math> jest funkcja stanu układu termodynamicznego. Dla każdego układu izolowanego i we wszystkich możliwych procesach wartość entropii nie zmniejsza się. | Entropia <math>S</math> jest funkcja stanu układu termodynamicznego. Dla każdego układu izolowanego i we wszystkich możliwych procesach wartość entropii nie zmniejsza się. | ||
Stwierdzenie to znane jest jako '''prawo wzrostu entropii'''. | Stwierdzenie to znane jest jako '''prawo wzrostu entropii'''. | ||
'''Entropia układu izolowanego, w którym zachodzą procesy nieodwracalne może tylko rosnąć.''' | '''Entropia układu izolowanego, w którym zachodzą procesy nieodwracalne może tylko rosnąć.''' | ||
Jeżeli w układzie zachodzą wyłącznie procesy odwracalne, albo układ osiągnął stan równowagi termodynamicznej wtedy entropia pozostaje stała.<br> | Jeżeli w układzie zachodzą wyłącznie procesy odwracalne, albo układ osiągnął stan równowagi termodynamicznej wtedy entropia pozostaje stała.<br> | ||
Ponieważ <math>dS={\delta Q \over T}</math>, to dla kołowego procesu odwracalnego mamy <math>\oint_{C}{\delta Q \over T}=\oint_{C}dS=0</math>. Dla przemiany przeprowadzającej w sposób odwracalny układ ze stanu '''A''' do stanu '''B''' | Ponieważ <math>dS={\delta Q \over T}</math>, to dla kołowego procesu odwracalnego mamy <math>\oint_{C}{\delta Q \over T}=\oint_{C}dS=0</math>. Dla przemiany przeprowadzającej w sposób odwracalny układ ze stanu '''A''' do stanu '''B''' | ||
| Linia 484: | Linia 503: | ||
Dla wyznaczenia entropii układu w danym stanie musielibyśmy znać wartość bezwzględną entropii stanu początkowego. Możemy jednak wyznaczyć przyrost entropii w danym procesie i to (jak zobaczymy) ma zasadnicze znaczenie dotyczące określenia możliwości zachodzenia oraz kierunku przebiegu procesów w przyrodzie. Ważną cechą entropii jest także jej '''addytywność''', co oznacza, że entropia układu jest sumą entropii podukładów. Warto też zwrócić uwagę, że ponieważ w przemianie adiabatycznej, odwracalnej mamy <math>\delta Q=0</math>, to wartość entropii jest dla tej przemiany stała; <math>S=const, dS=0</math>. Proces adiabatyczny, odwracalny nazywa się, dlatego '''procesem izoentropowym'''. | Dla wyznaczenia entropii układu w danym stanie musielibyśmy znać wartość bezwzględną entropii stanu początkowego. Możemy jednak wyznaczyć przyrost entropii w danym procesie i to (jak zobaczymy) ma zasadnicze znaczenie dotyczące określenia możliwości zachodzenia oraz kierunku przebiegu procesów w przyrodzie. Ważną cechą entropii jest także jej '''addytywność''', co oznacza, że entropia układu jest sumą entropii podukładów. Warto też zwrócić uwagę, że ponieważ w przemianie adiabatycznej, odwracalnej mamy <math>\delta Q=0</math>, to wartość entropii jest dla tej przemiany stała; <math>S=const, dS=0</math>. Proces adiabatyczny, odwracalny nazywa się, dlatego '''procesem izoentropowym'''. | ||
Zauważmy, że w przypadku procesów nieodwracalnych wzrasta oddane otoczeniu ciepło o znaku ujemnym w stosunku do ciepła pobranego, któremu przypisaliśmy znak dodatni. Przyczyną jest niekwazistatyczny przebieg procesu, niedoskonała izolacja układu itp. | Zauważmy, że w przypadku procesów nieodwracalnych wzrasta oddane otoczeniu ciepło o znaku ujemnym w stosunku do ciepła pobranego, któremu przypisaliśmy znak dodatni. Przyczyną jest niekwazistatyczny przebieg procesu, niedoskonała izolacja układu itp. | ||
| Linia 492: | Linia 510: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd24.png]] | ||
|valign="top"|Dla gazów rzeczywistych obserwuje się odstępstwa od równania gazu doskonałego przy wysokich ciśnieniach i niskich temperaturach. Uwzględnienie w równaniu stanu gazu dwu poprawek – na objętość cząsteczek i oddziaływania międzycząsteczkowe, prowadzi do równania van der Waalsa. Równanie to opisuje zachowanie się gazów rzeczywistych w szerokim zakresie gęstości. Zawiera dwie, wyznaczone doświadczalnie, stałe van der Waalsa a oraz b. | |valign="top"|Dla gazów rzeczywistych obserwuje się odstępstwa od równania gazu doskonałego przy wysokich ciśnieniach i niskich temperaturach. Uwzględnienie w równaniu stanu gazu dwu poprawek – na objętość cząsteczek i oddziaływania międzycząsteczkowe, prowadzi do równania van der Waalsa. Równanie to opisuje zachowanie się gazów rzeczywistych w szerokim zakresie gęstości. Zawiera dwie, wyznaczone doświadczalnie, stałe van der Waalsa a oraz b. | ||
| Linia 530: | Linia 532: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd25.png]] | ||
|valign="top"|Zależność ciśnienia od objętości przy stałej temperaturze dla jednego mola gazu wynikająca z równania van der Waalsa ma postać | |valign="top"|Zależność ciśnienia od objętości przy stałej temperaturze dla jednego mola gazu wynikająca z równania van der Waalsa ma postać | ||
| Linia 536: | Linia 538: | ||
Przykładowe izotermy van der Waalsa dla dwutlenku węgla, <math>CO_2</math> pokazane są na wykresie. Temperatury: 264 K, 284 K, 304 K, 334 K, 364 K, 404 K. | Przykładowe izotermy van der Waalsa dla dwutlenku węgla, <math>CO_2</math> pokazane są na wykresie. Temperatury: 264 K, 284 K, 304 K, 334 K, 364 K, 404 K. | ||
Z postaci wzorów oraz kształtu izoterm widzimy, że sprężając gaz przy stałej temperaturze mamy dla temperatur wysokich systematyczny wzrost ciśnienia przy zmniejszaniu się objętości, podobnie jak dla gazu doskonałego. Najmniejsza wartość objętości równa jest parametrowi '''b''', który opisuje efektywną objętość zajmowaną przez jeden mol cząsteczek gazu. Kiedy objętość staje się bliska '''b''', to ciśnienie dąży do nieskończoności, bowiem różnica w mianowniku wyrażenia <math>RT/(V-b)</math> dąży do zera. Z kolei, wyrażenie <math>-a/V^2</math> obniża wartość ciśnienia, co przy stosunkowo niskich temperaturach powoduje powstanie lokalnego minimum w obszarze pomiędzy punktami '''C''' i '''B'''. | Z postaci wzorów oraz kształtu izoterm widzimy, że sprężając gaz przy stałej temperaturze mamy dla temperatur wysokich systematyczny wzrost ciśnienia przy zmniejszaniu się objętości, podobnie jak dla gazu doskonałego. Najmniejsza wartość objętości równa jest parametrowi '''b''', który opisuje efektywną objętość zajmowaną przez jeden mol cząsteczek gazu. Kiedy objętość staje się bliska '''b''', to ciśnienie dąży do nieskończoności, bowiem różnica w mianowniku wyrażenia <math>RT/(V-b)</math> dąży do zera. Z kolei, wyrażenie <math>-a/V^2</math> obniża wartość ciśnienia, co przy stosunkowo niskich temperaturach powoduje powstanie lokalnego minimum w obszarze pomiędzy punktami '''C''' i '''B'''. | ||
Naturalnym wnioskiem z analizy izoterm van der Waalsa jest to, że dla określonej temperatury (izoterma krytyczna) nie pojawia się minimum, ale jedynie punkt przegięcia na krzywej. Punkt ten zwany jest '''punktem krytycznym''' i na rysunku oznaczony jest literą '''K'''. Odpowiadające temu punktowi wartości ciśnienia, objętości i gęstości gazu noszą nazwę '''wartości krytycznych'''. Parametry krytyczne można wyznaczyć, zauważając, że dla izotermy krytycznej pierwiastki równania van der Waalsa są sobie równe: <math>V_1 = V_2 = V_3 = V_{kr}</math>. Można też analitycznie zbadać przebieg zmienności funkcji <math>p (V) \ dla T = const</math>. W punkcie krytycznym styczna do izotermy jest pozioma, co oznacza zerowanie się pierwszej pochodnej ciśnienia względem objętości. Punkt ten jest też punktem przegięcia, co oznacza zerowanie się drugiej pochodnej. Mamy, zatem dla <math>T = const</math> | Naturalnym wnioskiem z analizy izoterm van der Waalsa jest to, że dla określonej temperatury (izoterma krytyczna) nie pojawia się minimum, ale jedynie punkt przegięcia na krzywej. Punkt ten zwany jest '''punktem krytycznym''' i na rysunku oznaczony jest literą '''K'''. Odpowiadające temu punktowi wartości ciśnienia, objętości i gęstości gazu noszą nazwę '''wartości krytycznych'''. Parametry krytyczne można wyznaczyć, zauważając, że dla izotermy krytycznej pierwiastki równania van der Waalsa są sobie równe: <math>V_1 = V_2 = V_3 = V_{kr}</math>. Można też analitycznie zbadać przebieg zmienności funkcji <math>p (V) \ dla T = const</math>. W punkcie krytycznym styczna do izotermy jest pozioma, co oznacza zerowanie się pierwszej pochodnej ciśnienia względem objętości. Punkt ten jest też punktem przegięcia, co oznacza zerowanie się drugiej pochodnej. Mamy, zatem dla <math>T = const</math> | ||
| Linia 563: | Linia 563: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd26.png]] | ||
|valign="top"| | |valign="top"|Przeanalizujmy nieco dokładniej postać izoterm van der Waalsa, dla różnych wartości temperatur. Przykładowe kształty izoterm dla trzech różnych temperatur spełniających warunek <math>T_1<T_{kr}<T_2</math> przedstawia rysunek. Zacznijmy od przypadku temperatury niższej od temperatury krytycznej. Kiedy poprzez zmniejszanie objętości naczynia sprężamy izotermiczne gaz rozpoczynając od dużej objętości i małego ciśnienia w temperaturze poniżej temperatury krytycznej (punkt oznaczony symbolem temperatury <math>T_1</math>) - przesuwamy się po krzywej w kierunku punktów '''A''' i '''B'''. W punkcie '''B''' krzywa ma lokalne maksimum. Dalsze zwiększanie siły wywieranej na tłok powinno spowodować obniżenie ciśnienia wewnątrz naczynia. Musiałoby to doprowadzić do raptownego przejścia układu do stanu '''E''' o tym samym ciśnieniu, bowiem ciśnienie zewnętrzne byłoby większe od ciśnienia wewnętrznego. Tak się jednak nie dzieje. W punkcie '''A''' rozpoczyna się nowe zjawisko - '''skraplanie''', czyli tworzenie się fazy ciekłej. | ||
Para nienasycona, będąc w fazie gazowej, wskutek sprężania zwiększa swą gęstość i w punkcie '''A''' osiąga gęstość pary nasycanej w temperaturze <math>T_1</math>, czyli staje się parą nasyconą. Dalsze zmniejszanie objętości powoduje skraplanie pary nasyconej. Proces ten odbywa się wzdłuż prostej '''AD''', przy stałym ciśnieniu. | |||
Przy zmniejszeniu się objętości na odcinku <math>AD</math> coraz więcej gazu ulega skropleniu. W naczyniu współistnieją wtedy dwie fazy - ciecz i '''para nasycona'''. W punkcie '''D''' cały gaz ulega skropleniu i następuje gwałtowny wzrost ciśnienia, ponieważ ściśliwość cieczy jest wielokrotnie mniejsza od ściśliwości gazów.<br> | |||
Fakt, że w punkcie '''A''' rozpoczyna się skraplanie nie oznacza, że odcinek krzywej '''AB''' jest dla gazu nieosiągalny. Proces skraplania rozpoczyna się na istniejących zwykle w gazie niejednorodnościach, które są centrami kondensacji. Jeśli proces sprężania przeprowadzany jest ostrożnie a gaz nie zawiera zanieczyszczeń możliwe jest przemieszczenie się do punktu '''B'''. Gaz w takim stanie nazywamy '''parą przesyconą'''. | |||
Analogicznie do efektu powstawania pary przesyconej możliwe jest przejście w odwrotnym kierunku - od punktu '''D''' do punktu '''C'''. Uzyskujemy wtedy stan cieczy przegrzanej. Stany te są '''stanami metastabilnymi'''. Oznacza to, że wystarczy niewielkie zaburzenie, aby wyprowadzić ciecz lub gaz z takiego stanu. Następuje wtedy gwałtowna kondensacja (w przypadku pary przesyconej) lub wrzenie cieczy (w przypadku cieczy przegrzanej). Proces skraplania bądź wrzenia rozpoczyna się na występujących niejednorodnościach, a następnie obejmuje cała objętość. | |||
|} | |} | ||
| Linia 570: | Linia 575: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd27.png]] | ||
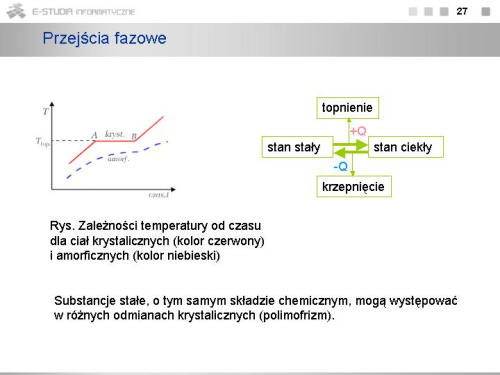
|valign="top"| | |valign="top"|Proces przechodzenia ze stanu stałego w stan ciekły nazywamy topnieniem. Proces ten wymaga dostarczenia ciepła, które dla jednostkowej masy substancji nosi nazwę '''ciepła topnienia'''. Proces ten dla substancji krystalicznych zachodzi w określonej temperaturze. Zakładając, że ilość dostarczanego ciepła na jednostkę czasu ma wartość stałą otrzymamy zależność temperatury od czasu dla ciała, które podlega procesowi topnienia w postaci przedstawionej na rysunku. Kolorem czerwonym pokazana jest zależność temperatury od czasu dla ciał krystalicznych. Temperatura ciała wzrasta wraz z upływem czasu, kiedy dostarczane jest ciepło. Po osiągnięciu temperatury topnienia, punkt '''A''', ciepło zużywane jest na proces topnienia i temperatura pozostaje stała. Kiedy stopieniu ulega cała masa, punkt '''B''', temperatura fazy ciekłej zaczyna dalej wzrastać. | ||
W przypadku ciał amorficznych nie ma określonej temperatury topnienia. Przechodzenia ciała w stan ciekły odbywa się w określonym przedziale temperatury. Jest to rezultatem podobnej struktury ciał amorficznych i cieczy (brakiem uporządkowania atomów i cząsteczek na dużych odległościach). | |||
Trzeba tu dodać, że rysunek jest schematyczny. Nachylenia odcinków do punktu '''A''' i od punktu '''B''' będą różne, gdyż zależą one od ciepła właściwego, które dla fazy ciekłej ma inną wartość niż dla fazy stałej. | |||
Procesem odwrotnym do topnienia jest proces krzepnięcia albo inaczej - krystalizacji. W procesie tym ciało oddaje ciepło, a sam proces rozpoczyna się także na centrach krystalizacji, podobnie jak na centrach kondensacji w przypadku skraplania. Także podobnie i tu możliwy jest proces przechłodzenia cieczy i pozostawanie jej w stanie metastabilnym. Drobna niejednorodność w postaci zanieczyszczenia może wówczas spowodować proces krystalizacji (bardziej ogólnie - solidyfikacji, gdyż nie zawsze powstający stan stały ma strukturę krystaliczną). W przypadku silnych, gwałtownych przechłodzeń możliwe jest przejście cieczy w stan amorficzny ciała stałego. | |||
|} | |} | ||
| Linia 577: | Linia 586: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="450px"|[[Grafika: | |valign="top" width="450px"|[[Grafika:PF_M8_Slajd28.png]] | ||
|valign="top"| | |valign="top"|Przejścia pomiędzy różnymi fazami substancji zależne są od tego, w jakiej temperaturze i pod jakim ciśnieniem substancja się znajduje. Ilustruje te zależności rysunek. Trzy krzywe odpowiadają tu trzem typom przejść fazowych: parowaniu, topnieniu i '''sublimacji''', czyli bezpośredniemu przejściu pomiędzy stanem stałym i gazowym. Trzy obszary oddzielone tym krzywymi określają wartości ciśnienia i temperatury, w której istnieje tylko jedna faza danej substancji: ciało stałe, ciecz lub gaz. Punkty na krzywych odpowiadają równowagowym stanom koegzystencji dwóch faz. Punkt <math>P_p</math>, w którym wszystkie trzy krzywe się spotykają odpowiada stanowi, w którym współistnieją trzy fazy w stanie równowagi. Punkt ten nazywa się '''punktem potrójnym''', a wykres nazywa się '''wykresem stanu'''. Odpowiadające temu punktowi wartości ciśnienia i temperatury zaznaczone są na osiach wykresu <math>(p_{tr}, T_{tr})</math>. | ||
Kiedy układ znajduje się w jakimś punkcie na czerwonej krzywej, to jest w równowagowym stanie cieczy i gazu. Jeśli teraz będziemy odbierać od układu ciepło bez zmiany objętości, to maleć będzie temperatura i ciśnienie, a stan układu będzie odpowiadał punktom na krzywej coraz bliższym punktowi potrójnemu. Przy dalszym odbieraniu ciepła rozpocznie się proces krystalizacji (krzepnięcia) przy stałych wartościach ciśnienia i temperatury. Oddawane w tym procesie ciepło nazywa się ciepłem krystalizacji. Kiedy proces krystalizacji będzie zakończony, przestaje istnieć faza ciekła i przy dalszym odbieraniu ciepła układ przesuwać się będzie w dół po krzywej niebieskiej oznaczającej współistnienie fazy stałej i gazowej. Przy ogrzewaniu substancji będącej w stanie stałym, po osiągnięciu punktu potrójnego rozpocznie się proces topnienia przebiegający wzdłuż krzywej zielonej. | |||
Ogrzewanie pod stałym ciśnieniem substancji znajdującej się w stanie określonym przez położenie punktu '''A''' przeprowadza układ w kierunku punktu '''B''' kolejno przez trzy fazy: stałą, ciekłą i gazową. Kiedy jednak proces ogrzewania rozpoczyna się w punkcie '''C''' wówczas przejście do stanu gazowego (punktu '''D''') odbędzie się z pominięciem fazy ciekłej (sublimacja). | |||
Zwróćmy uwagę jeszcze na jedną ważną własność wykresu fazowego. Krzywa parowania kończy się w warunkach, kiedy osiągany jest stan krytyczny oznaczający ciągłe przejście pomiędzy fazą ciekłą i gazową. Na rysunku punkt ten oznaczony jest literą '''K'''. Przy wyższych temperaturach i ciśnieniach mamy do czynienia wyłącznie ze stanem gazowym. Inaczej jest w przypadku przejścia pomiędzy stanem krystalicznym, a stanami: ciekłym i gazowym. Struktura stanu krystalicznego różni się, bowiem zasadniczo od struktury cieczy lub gazu. Cechą charakterystyczną struktury krystalicznej jest anizotropia w rozkładzie przestrzennym atomów i przejście do izotropowej fazy ciekłej lub gazowej musi mieć charakter skokowy. Krzywe sublimacji i topnienia nie urywają się, ale oddzielają stan krystaliczny od stanu ciekłego lub gazowego. Oczywiście możliwe są także bezpośrednie przejścia ze stanu lotnego (gaz) do stanu ciała stałego, bez przejścia poprzez fazę cieczy. Taki proces nazywa się '''resublimacją'''. Podobnie, procesem odwrotnym do parowania jest '''skraplanie''', a do topnienia - '''krzepnięcie'''. | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
= Materiały do ćwiczeń = | |||
'''Zadanie 8.2''' | |||
Oblicz ciepło molowe gazu doskonałego w przemianie politropowej o równaniu | |||
#<math>pV^2 = const</math>, | |||
#<math>p^2V = const</math>. | |||
W której z przemian, podczas rozszerzania, gaz ten ogrzewa się a w której oziębia? | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | |||
#<math>C = C_v - R</math>, oziębianie, | |||
#<math>C = C_p + R</math>, ogrzewanie. | |||
</div></div> | |||
---- | |||
'''Zadanie 8.3''' | |||
Silnik cieplny pracuje według cyklu składającego się z izotermy, izobary i izochory. Objętość gazu w czasie cyklu zmienia się dziesięciokrotnie, a temperatura przemiany izotermicznej jest równa 400 K. Gazem roboczym jest 1 kmol gazu doskonałego o cząsteczkach jednoatomowych. Oblicz sprawność cyklu. | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | |||
<math>\eta = 0,38</math> | |||
</div></div> | |||
---- | |||
'''Zadanie 8.4''' | |||
Oblicz zmianę entropii w cyklu Carnota. | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | |||
Entropia jest funkcją stanu, <math>\Delta S = 0</math> | |||
</div></div> | |||
---- | |||
'''Zadanie 8.5''' | |||
W naczyniu o objętości <math>V</math>, w temperaturze <math>t^\circ C</math>, znajduje się n moli gazu rzeczywistego spełniającego równanie van der Waalsa, o znanych parametrach a, b. | |||
*Jakie jest jego ciśnienie? | |||
*O ile zmieni się to ciśnienie, jeśli temperatura tego gazu wzrośnie dwukrotnie przy stałej objętości? | |||
*Odpowiedz też na powyższe pytania zakładając, że jest to gaz doskonały | |||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Odpowidź </span><div class="mw-collapsible-content" style="display:none"> | |||
< | <math>p={nR(273+t) \over V-nb}-{n^2 a \over V^2}</math>, <math>\Delta p={nRt \over V-nb}</math>, dla gazu doskonałego a = 0 i b = 0 | ||
</div></div> | |||
<hr width="100%"> | <hr width="100%"> | ||
= Słowniczek = | |||
*'''pierwsza zasada termodynamiki''' - Przyrost energii wewnętrznej układu równy jest sumie dostarczonej do układu energii cieplnej, wykonanej nad układem pracy oraz energii uzyskanej wskutek wymiany materii z otoczeniem. Przyrost ten w procesach kwazistatycznych i odwracalnych nie zależy od sposobu, w jaki dokonuje się przejście, a określony jest całkowicie przez początkowy i końcowy stan układu | |||
*'''pojemność cieplna''' - ilość ciepła potrzebna do podwyższenia temperatury ciała o jeden kelwin | |||
*'''molowe ciepło właściwe''' - ilość ciepła potrzebna do podwyższenia temperatury jednego mola substancji o jeden kelwin | |||
*'''przemiana izotermiczna''' - proces, który zachodzi w stałej temperaturze; '''T = const''' | |||
*'''prawo Boyle'a Mariotte'a''' - odnosi się do przemiany izotermicznej: '''pV = const'''. W stałej temperaturze iloczyn ciśnienia i objętości jest stały lub - ciśnienie zmienia się odwrotnie proporcjonalnie do objętości. | |||
*'''przemiana izochoryczna''' - proces, który zachodzi przy stałej objętości; '''V = const''' | |||
*'''przemiana izobaryczna''' - proces, który zachodzi przy stałym ciśnieniu; '''p = const''' | |||
*'''przemiana adiabatyczna''' - przemiana, która zachodzi bez wymiany ciepła z otoczeniem | |||
*'''przemiana politropowa''' - przemiana, w czasie której pojemność cieplna ciała pozostaje stała | |||
*'''cykl Carnota''' - cykl odwracalny składający się z dwóch przemian izotermicznych oraz dwóch adiabatycznych | |||
*'''twierdzenia Carnota''' - 1. Wszystkie silniki pracujące w odwracalnym cyklu Carnota pomiędzy tymi samymi temperaturami mają tę samą sprawność.<br>2. Sprawność cyklu nieodwracalnego jest zawsze mniejsza od sprawności cyklu odwracalnego. | |||
*'''ciepło zredukowane''' - stosunek ilości ciepła pobranego z danego źródła do jego temperatury bezwzględnej | |||
*'''entropia''' - 1. funkcja stanu której przyrost w przemianie odwracalnej równy jest przyrostowi ciepła zredukowanego<br>2. wielkość proporcjonalna do logarytmu prawdopodobieństwa termodynamicznego stanu układu | |||
*'''proces izoentropowy''' - proces, w którym entropia zachowuje wartość stałą. Procesem takim jest każdy proces adiabatyczny, odwracalny. | |||
*'''nierówność Clausiusa''' - suma wartości ciepeł zredukowanych w każdej przemianie zamkniętej jest nie większa od zera | |||
*'''prawo wzrostu entropii ''' - Entropia układu izolowanego, w którym zachodzą procesy nieodwracalne może tylko rosnąć. | |||
*'''druga zasada termodynamiki''' - 1. Niemożliwe jest przekazywanie ciepła przez ciało o temperaturze niższej ciału o temperaturze wyższej bez wprowadzenia innych zmian w obu ciałach i w otoczeniu<br>2. Niemożliwe jest pobieranie ciepła z jednego termostatu i zamiana go na pracę bez wprowadzania innych zmian w układzie i w otoczeniu.<br>3. Skonstruowanie perpetuum mobile drugiego rodzaju jest niemożliwe<br>4. Entropia układu izolowanego nie może maleć. | |||
*'''cykl Otta''' - cykl termodynamiczny składający się z dwóch adiabat i dwóch izochor. Do cyklu Otta zbliżony jest cykl pracy silnika benzynowego. | |||
*'''cykl Diesla''' - cykl termodynamiczny składający się z dwóch adiabat izochory i izobary. Opisuje pracę silnika Diesla. | |||
*'''równanie van der Waalsa''' - równanie stanu gazu rzeczywistego biorące pod uwagę objętość cząsteczek gazu i siły ich wzajemnych oddziaływań | |||
*'''stan (punkt) krytyczny''' - stan, w którym znikają różnice pomiędzy własnościami cieczy, pary nasyconej i gazu. Gęstości substancji w tych trzech stanach są jednakowe. | |||
*'''wartości krytyczne''' - wartości ciśnienia, temperatury i gęstości w punkcie krytycznym | |||
*'''faza substancji''' - stan substancji charakteryzujący się jednoznacznie określonymi własnościami | |||
*'''przejście fazowe''' - proces w rezultacie którego zmienia się faza substancji | |||
*'''parowanie''' - proces polegający na przejściu z fazy ciekłej do gazowej | |||
*'''skraplanie''' - proces polegający na przejściu z fazy gazowej do fazy ciekłej | |||
*'''sublimacja''' - proces polegający na przejściu z fazy gazowej do fazy stałej | |||
*'''stan równowagi dynamicznej''' - stan którego własności makroskopowe nie zmieniają się w czasie pomimo zachodzących procesów w skali mikroskopowej | |||
*'''anizotropia''' - zależność własności fizycznych ciała od kierunku | |||
*'''stan metastabilny''' - stan układu, który może być zmieniony wskutek bardzo niewielkiego zaburzenia warunków w jakich układ się znajduje | |||
*'''para nasycona''' - para o maksymalnej możliwej gęstości w danej temperaturze | |||
*'''para przesycona''' - metastabilny stan pary, w warunkach ciśnienia i temperatury odpowiadających stanowi ciekłemu danej substancji | |||
*'''ciecz przegrzana''' - metastabilny stan cieczy, w warunkach ciśnienia i temperatury odpowiadających stanowi gazowemu danej substancji | |||
*'''punkt potrójny''' - punkt określający warunki ciśnienia i temperatury, w których mogą istnieć w równowadze trzy stany skupienia danej substancji: stała, ciekła i gazowa | |||
*'''wykres stanu''' - wykres we współrzędnych temperatury i ciśnienia określający warunki współistnienia faz danej substancji | |||
Aktualna wersja na dzień 12:04, 5 wrz 2023
Wykład

|
Wprowadzenie
Omówione są tu ogólne prawa makroskopowe opisujące prawidłowo zjawiska cieplne i pozwalające ilościowo przewidywać skutki różnych procesów. |
Materiały do ćwiczeń
Zadanie 8.2
Oblicz ciepło molowe gazu doskonałego w przemianie politropowej o równaniu
- ,
- .
W której z przemian, podczas rozszerzania, gaz ten ogrzewa się a w której oziębia?
Zadanie 8.3
Silnik cieplny pracuje według cyklu składającego się z izotermy, izobary i izochory. Objętość gazu w czasie cyklu zmienia się dziesięciokrotnie, a temperatura przemiany izotermicznej jest równa 400 K. Gazem roboczym jest 1 kmol gazu doskonałego o cząsteczkach jednoatomowych. Oblicz sprawność cyklu.
Zadanie 8.4
Oblicz zmianę entropii w cyklu Carnota.
Zadanie 8.5
W naczyniu o objętości , w temperaturze , znajduje się n moli gazu rzeczywistego spełniającego równanie van der Waalsa, o znanych parametrach a, b.
- Jakie jest jego ciśnienie?
- O ile zmieni się to ciśnienie, jeśli temperatura tego gazu wzrośnie dwukrotnie przy stałej objętości?
- Odpowiedz też na powyższe pytania zakładając, że jest to gaz doskonały
Słowniczek
- pierwsza zasada termodynamiki - Przyrost energii wewnętrznej układu równy jest sumie dostarczonej do układu energii cieplnej, wykonanej nad układem pracy oraz energii uzyskanej wskutek wymiany materii z otoczeniem. Przyrost ten w procesach kwazistatycznych i odwracalnych nie zależy od sposobu, w jaki dokonuje się przejście, a określony jest całkowicie przez początkowy i końcowy stan układu
- pojemność cieplna - ilość ciepła potrzebna do podwyższenia temperatury ciała o jeden kelwin
- molowe ciepło właściwe - ilość ciepła potrzebna do podwyższenia temperatury jednego mola substancji o jeden kelwin
- przemiana izotermiczna - proces, który zachodzi w stałej temperaturze; T = const
- prawo Boyle'a Mariotte'a - odnosi się do przemiany izotermicznej: pV = const. W stałej temperaturze iloczyn ciśnienia i objętości jest stały lub - ciśnienie zmienia się odwrotnie proporcjonalnie do objętości.
- przemiana izochoryczna - proces, który zachodzi przy stałej objętości; V = const
- przemiana izobaryczna - proces, który zachodzi przy stałym ciśnieniu; p = const
- przemiana adiabatyczna - przemiana, która zachodzi bez wymiany ciepła z otoczeniem
- przemiana politropowa - przemiana, w czasie której pojemność cieplna ciała pozostaje stała
- cykl Carnota - cykl odwracalny składający się z dwóch przemian izotermicznych oraz dwóch adiabatycznych
- twierdzenia Carnota - 1. Wszystkie silniki pracujące w odwracalnym cyklu Carnota pomiędzy tymi samymi temperaturami mają tę samą sprawność.
2. Sprawność cyklu nieodwracalnego jest zawsze mniejsza od sprawności cyklu odwracalnego. - ciepło zredukowane - stosunek ilości ciepła pobranego z danego źródła do jego temperatury bezwzględnej
- entropia - 1. funkcja stanu której przyrost w przemianie odwracalnej równy jest przyrostowi ciepła zredukowanego
2. wielkość proporcjonalna do logarytmu prawdopodobieństwa termodynamicznego stanu układu - proces izoentropowy - proces, w którym entropia zachowuje wartość stałą. Procesem takim jest każdy proces adiabatyczny, odwracalny.
- nierówność Clausiusa - suma wartości ciepeł zredukowanych w każdej przemianie zamkniętej jest nie większa od zera
- prawo wzrostu entropii - Entropia układu izolowanego, w którym zachodzą procesy nieodwracalne może tylko rosnąć.
- druga zasada termodynamiki - 1. Niemożliwe jest przekazywanie ciepła przez ciało o temperaturze niższej ciału o temperaturze wyższej bez wprowadzenia innych zmian w obu ciałach i w otoczeniu
2. Niemożliwe jest pobieranie ciepła z jednego termostatu i zamiana go na pracę bez wprowadzania innych zmian w układzie i w otoczeniu.
3. Skonstruowanie perpetuum mobile drugiego rodzaju jest niemożliwe
4. Entropia układu izolowanego nie może maleć. - cykl Otta - cykl termodynamiczny składający się z dwóch adiabat i dwóch izochor. Do cyklu Otta zbliżony jest cykl pracy silnika benzynowego.
- cykl Diesla - cykl termodynamiczny składający się z dwóch adiabat izochory i izobary. Opisuje pracę silnika Diesla.
- równanie van der Waalsa - równanie stanu gazu rzeczywistego biorące pod uwagę objętość cząsteczek gazu i siły ich wzajemnych oddziaływań
- stan (punkt) krytyczny - stan, w którym znikają różnice pomiędzy własnościami cieczy, pary nasyconej i gazu. Gęstości substancji w tych trzech stanach są jednakowe.
- wartości krytyczne - wartości ciśnienia, temperatury i gęstości w punkcie krytycznym
- faza substancji - stan substancji charakteryzujący się jednoznacznie określonymi własnościami
- przejście fazowe - proces w rezultacie którego zmienia się faza substancji
- parowanie - proces polegający na przejściu z fazy ciekłej do gazowej
- skraplanie - proces polegający na przejściu z fazy gazowej do fazy ciekłej
- sublimacja - proces polegający na przejściu z fazy gazowej do fazy stałej
- stan równowagi dynamicznej - stan którego własności makroskopowe nie zmieniają się w czasie pomimo zachodzących procesów w skali mikroskopowej
- anizotropia - zależność własności fizycznych ciała od kierunku
- stan metastabilny - stan układu, który może być zmieniony wskutek bardzo niewielkiego zaburzenia warunków w jakich układ się znajduje
- para nasycona - para o maksymalnej możliwej gęstości w danej temperaturze
- para przesycona - metastabilny stan pary, w warunkach ciśnienia i temperatury odpowiadających stanowi ciekłemu danej substancji
- ciecz przegrzana - metastabilny stan cieczy, w warunkach ciśnienia i temperatury odpowiadających stanowi gazowemu danej substancji
- punkt potrójny - punkt określający warunki ciśnienia i temperatury, w których mogą istnieć w równowadze trzy stany skupienia danej substancji: stała, ciekła i gazowa
- wykres stanu - wykres we współrzędnych temperatury i ciśnienia określający warunki współistnienia faz danej substancji