Laboratorium wirtualne 1/Moduł 5 - ćwiczenie 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 1 pośredniej wersji utworzonej przez tego samego użytkownika) | |||
| Linia 34: | Linia 34: | ||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:LW1_M5_Slajd4.png]] | ||
|valign="top"|Krótkoczasowa transformata Fouriera (STFT – Short-Time Fourier Transform) stanowi wzorcowy przykład algorytmu analizy czasowo-częstotliwościowej. Umożliwia ona wydobycie z sygnału informacji o tym, jak zmienia się jego widmo w czasie, czyli jednoczesną obserwację jego właściwości zarówno w dziedzinie czasu jak i częstotliwości. Wycinek sygnału (blok próbek o rozmiarze L) przeznaczony do analizy jest sukcesywnie dzielony na segmenty, z których każdy podlega analizie widmowej niezależnie. Podobnie jak w przypadku tradycyjnym, aby usunąć gwałtowne zmiany (cięcia) sygnału na krańcach przedziałów, stosuje się różne okna czasowe w odniesieniu do wspomnianych segmentów. Przesuwając okno w czasie, wzdłuż sygnału, wyznacza się jego zawartość widmową wewnątrz przedziału czasowego, którego długość jest określona szerokością okna. | |valign="top"|Krótkoczasowa transformata Fouriera (STFT – Short-Time Fourier Transform) stanowi wzorcowy przykład algorytmu analizy czasowo-częstotliwościowej. Umożliwia ona wydobycie z sygnału informacji o tym, jak zmienia się jego widmo w czasie, czyli jednoczesną obserwację jego właściwości zarówno w dziedzinie czasu jak i częstotliwości. Wycinek sygnału (blok próbek o rozmiarze L) przeznaczony do analizy jest sukcesywnie dzielony na segmenty, z których każdy podlega analizie widmowej niezależnie. Podobnie jak w przypadku tradycyjnym, aby usunąć gwałtowne zmiany (cięcia) sygnału na krańcach przedziałów, stosuje się różne okna czasowe w odniesieniu do wspomnianych segmentów. Przesuwając okno w czasie, wzdłuż sygnału, wyznacza się jego zawartość widmową wewnątrz przedziału czasowego, którego długość jest określona szerokością okna. | ||
Krótkoczasową transformatę Fouriera sygnału <math>x(t)\ | Krótkoczasową transformatę Fouriera sygnału <math>x(t)\ </math>,, w odniesieniu do okna <math>\varphi(t)\ </math>, rozmieszczonego w pozycji <math>(\tau, \xi)\ </math>, na płaszczyźnie t/f zdefiniować można jako (1). W odróżnieniu od tradycyjnej transformaty Fouriera, dla której do wyznaczenia pojedynczej składowej konieczna jest znajomość funkcji <math>x(t)\ </math>, na całej osi czasu, w tym przypadku, wymagana jest znajomość <math>x(t)\ </math>, tylko w przedziale określonym przez położenie <math>\varphi (t-\tau)\ </math>,. | ||
Dyskretna wersja powyższego równania przyjmuje postać: | Dyskretna wersja powyższego równania przyjmuje postać: | ||
| Linia 41: | Linia 41: | ||
gdzie <math>T_p\ | gdzie <math>T_p\ </math>, oznacza okres próbkowania sygnału. Dla przypadku unormowanego, gdy <math>T_p=1\ </math>, otrzymujemy zależność (2). | ||
|} | |} | ||
| Linia 48: | Linia 48: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:LW1_M5_Slajd5.png]] | ||
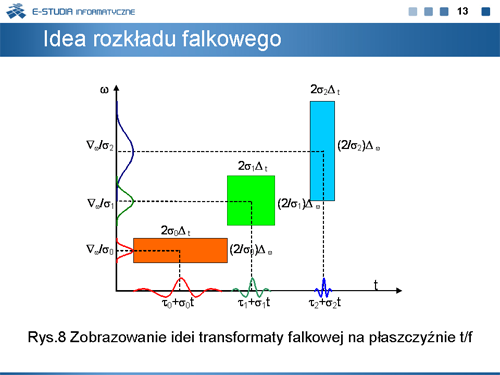
|valign="top"|Kształt okna czasowego <math>\varphi(t)\ | |valign="top"|Kształt okna czasowego <math>\varphi(t)\ </math>, rozmieszczonego w pozycji <math>(\tau, \xi)\ </math>, na płaszczyźnie t/f odgrywa kluczową rolę w przypadku STFT. Iloczyn szerokości okna w dziedzinie czasu <math>\Delta_t\ </math>, i szerokości okna w dziedzinie częstotliwości <math>\Delta_{\omega}\ </math>, jest wielkością stałą dla danego okna. Stąd też, poprawiając rozdzielczość w dziedzinie czasu, będziemy ją pogarszać w dziedzinie częstotliwości i odwrotnie. Zatem szerokość okna wybierana jest na drodze kompromisu. Interpretacja położenia okna czasowo-częstotliwościowego na płaszczyźnie t/f przedstawiona jest na rysunku 1. | ||
|} | |} | ||
| Linia 59: | Linia 59: | ||
<math>x(t)=sin2\pi f_1t+sin2\pi f_2t+\alpha [\delta(t-t_1)+\delta(t-t_2)]</math> | <math>x(t)=sin2\pi f_1t+sin2\pi f_2t+\alpha [\delta(t-t_1)+\delta(t-t_2)]</math> | ||
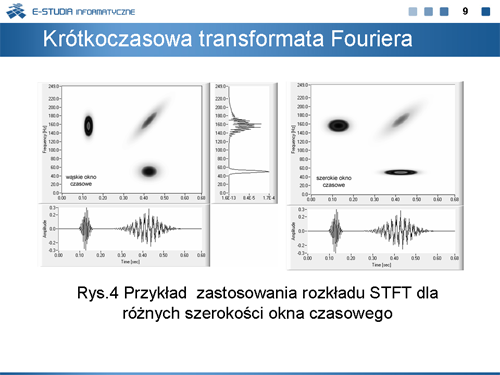
dla różnych szerokości (promieni) <math>\Delta_t\ | dla różnych szerokości (promieni) <math>\Delta_t\ </math>, okna czasowego <math>\varphi(t)\ </math>,. W przypadku zastosowania szerokiego okna czasowego, otrzymuje się bardzo dużą rozdzielczość częstotliwościową i bardzo małą rozdzielczość czasową. W miarę zwężania okna czasowego poprawia się rozdzielczość czasowa kosztem częstotliwościowej. | ||
|} | |} | ||
| Linia 70: | Linia 70: | ||
<math>\Phi (\omega)=G_{\alpha}(\omega)=e^{-\alpha \omega^2}, \alpha>0</math> | <math>\Phi (\omega)=G_{\alpha}(\omega)=e^{-\alpha \omega^2}, \alpha>0</math> | ||
Okno to, od nazwiska pierwszego użytkownika, nosi miano okna Gabora. Iloczyn szerokości okna Gabora w dziedzinie czasu <math>\Delta_t\ | Okno to, od nazwiska pierwszego użytkownika, nosi miano okna Gabora. Iloczyn szerokości okna Gabora w dziedzinie czasu <math>\Delta_t\ </math>, i szerokości okna w dziedzinie częstotliwości <math>\Delta_{\omega}\ </math>, osiąga minimum i wynosi: | ||
: <math>\Delta_t \Delta_{\omega}=\frac{1}{2}</math> | : <math>\Delta_t \Delta_{\omega}=\frac{1}{2}</math> | ||
| Linia 88: | Linia 88: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:LW1_M5_Slajd8.png]] | ||
|valign="top"|Praktyczny algorytm obliczeniowy dyskretnego rozkładu Gabora ma postać określoną wzorem (5). Współczynniki rozkładu Gabora są wyznaczane za pomocą algorytmu STFT z równania (6) gdzie <math>N\ | |valign="top"|Praktyczny algorytm obliczeniowy dyskretnego rozkładu Gabora ma postać określoną wzorem (5). Współczynniki rozkładu Gabora są wyznaczane za pomocą algorytmu STFT z równania (6) gdzie <math>N\ </math>, oznacza liczbę przedziałów częstotliwości, <math>T_p\ </math>, okres próbkowania, <math>\gamma [n]\ </math>, funkcję dualną do <math>g_{\alpha}[n]\ </math>,. | ||
|} | |} | ||
| Linia 121: | Linia 121: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:LW1_M5_Slajd10.png]] | ||
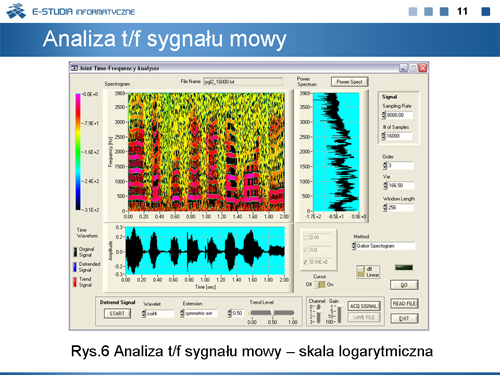
|valign="top"|Na rysunku 4 pokazane są wyniki analizy STFT otrzymane przy wykorzystaniu opisywanego wyżej wirtualnego przyrządu pomiarowego do przeprowadzania analiz czasowo-częstotliwościowych. Sygnał badany, spróbkowany z częstotliwością 500Hz, składa się z dwóch części wyciętych oknami Gaussa (przedziały czasowe <math>0.08 \div 0.15sek.\ | |valign="top"|Na rysunku 4 pokazane są wyniki analizy STFT otrzymane przy wykorzystaniu opisywanego wyżej wirtualnego przyrządu pomiarowego do przeprowadzania analiz czasowo-częstotliwościowych. Sygnał badany, spróbkowany z częstotliwością 500Hz, składa się z dwóch części wyciętych oknami Gaussa (przedziały czasowe <math>0.08 \div 0.15sek.\ </math>, i <math>0.25\div 0.58sek.\ </math>,). Część pierwszą stanowi sygnał sinusoidalny o częstotliwości 156Hz, część druga to złożenie dwóch sygnałów: sinusoidalnego o częstotliwości 50Hz oraz sinusoidalnego o częstotliwości liniowo zmiennej w zakresie <math>90\div 240Hz\ </math>,. Na dole rysunku 11 pokazany jest przebieg czasowy tego sygnału. Po środku przedstawiony jest obraz widma mocy badanego sygnału. Z widma mocy można wywnioskować, jakie składowe częstotliwościowe występują w sygnale badanym, ale nic nie można powiedzieć o chwilach czasu występowania składowych sygnału związanego z tymi częstotliwościowymi. Równie trudno jest określić charakter zmian częstotliwościowych. Natomiast obserwując rozkład na płaszczyźnie t/f, możemy podać zarówno czas występowania składowych sygnału o określonej zawartości częstotliwościowej, jak i charakter zmian częstotliwościowych. Niestety wartości czasu i częstotliwości można określić tylko z pewnym prawdopodobieństwem wyznaczonym przez parametry okna. Zastosowanie wąskiego okna czasowego (i tym samym szerokiego w dziedzinie częstotliwości) objawia się dużym rozmyciem umiejscowienia prążków w dziedzinie częstotliwości i stosunkowo dobrym umiejscowieniem prążków w czasie (rysunek z prawej). Zastosowanie szerokiego okna czasowego (rysunek z lewej) daje dobrą lokalizację częstotliwościową i złą czasową. | ||
|} | |} | ||
| Linia 203: | Linia 203: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd19.png]] | |valign="top" width="500px"|[[Grafika:LW1_M5_Slajd19.png]] | ||
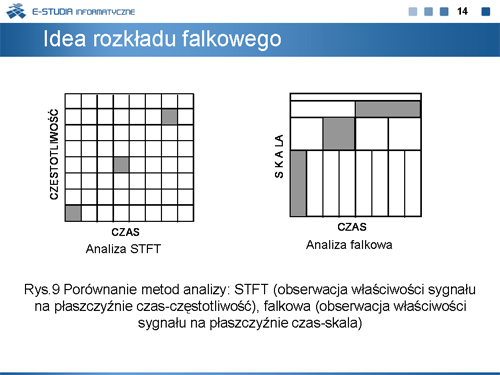
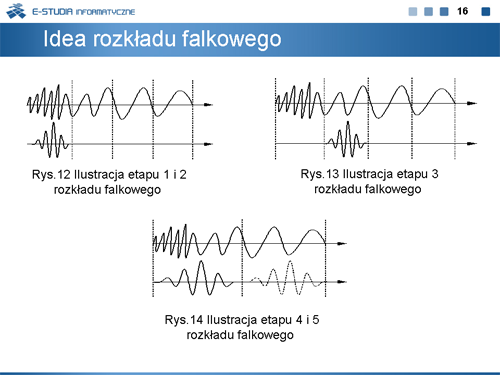
|valign="top"|Bardzo efektywna metoda implementacji algorytmu DWT dokonanej z użyciem filtrów opracowana została w 1988 roku przez Mallata. Nawiązuje ona do, znanej z analizy częstotliwościowej, metody kodowania w podpasmach i realizuje tzw. szybką transformatę falkową (Fast Wavelet Transform: FWT). Do analizy falkowej wprowadzono dwa pojęcia: aproksymacji i detalu. Pod pojęciem aproksymacji rozumie się niskoczęstotliwościowe składowe sygnału. Detale to składowe wysokoczęstotliwościowe. Wspomniany proces filtracji, obejmuje dwa filtry: dolnopasmowy (H) i górnopasmowy (G). Oryginalny sygnał S przechodzi przez parę komplementarnych filtrów, które rozdzielają go na dwie składowe <math>a_1\ | |valign="top"|Bardzo efektywna metoda implementacji algorytmu DWT dokonanej z użyciem filtrów opracowana została w 1988 roku przez Mallata. Nawiązuje ona do, znanej z analizy częstotliwościowej, metody kodowania w podpasmach i realizuje tzw. szybką transformatę falkową (Fast Wavelet Transform: FWT). Do analizy falkowej wprowadzono dwa pojęcia: aproksymacji i detalu. Pod pojęciem aproksymacji rozumie się niskoczęstotliwościowe składowe sygnału. Detale to składowe wysokoczęstotliwościowe. Wspomniany proces filtracji, obejmuje dwa filtry: dolnopasmowy (H) i górnopasmowy (G). Oryginalny sygnał S przechodzi przez parę komplementarnych filtrów, które rozdzielają go na dwie składowe <math>a_1\ </math>, (aproksymacja) i <math>d_1\ </math>, (detal) (rys.15). W przypadku filtracji cyfrowej podwaja się liczba danych, przeznaczonych do dalszego przetwarzania. Wygodnym sposobem ograniczenia tej liczby w metodzie falkowej jest decymacja, polegająca na odrzuceniu co drugiej próbki danych. Pełny proces dekompozycji zawiera szereg członów tworzących tzw. drzewo dekompozycji falkowej. | ||
|} | |} | ||
| Linia 213: | Linia 213: | ||
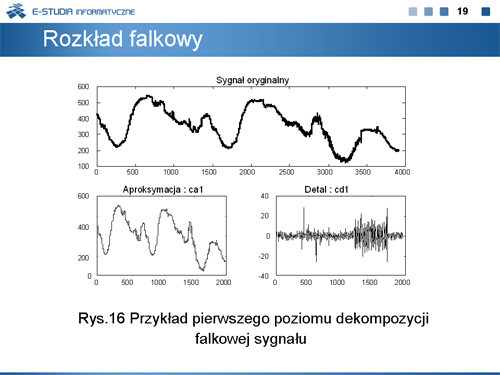
|valign="top"|Przykład pierwszego poziomu dekompozycji falkowej pewnego rzeczywistego sygnału pomiarowego zamieszczono na rysunku 16. | |valign="top"|Przykład pierwszego poziomu dekompozycji falkowej pewnego rzeczywistego sygnału pomiarowego zamieszczono na rysunku 16. | ||
Należy zauważyć, że dobór charakterystyk filtrów rozkładu falkowego jest podyktowany doborem kształtu falki tego rozkładu. Ściśle rzecz ujmując, kształt falki <math>\psi(t)\ | Należy zauważyć, że dobór charakterystyk filtrów rozkładu falkowego jest podyktowany doborem kształtu falki tego rozkładu. Ściśle rzecz ujmując, kształt falki <math>\psi(t)\ </math>, jest jednoznacznie związany z charakterystyką filtru górnopasmowego wyodrębniającego detal w rozkładzie falkowym. Istnieje jeszcze jedna bardzo charakterystyczna funkcja związana ze zbiorami falek. Jest to tzw. funkcja skalująca, oznaczana symbolem <math>\varphi(t)\ </math>,. Jej kształt związany jest z charakterystykami dolnopasmowych kwadraturowych filtrów lustrzanych odpowiedzialnych za wyodrębnienie aproksymacji sygnału. Kształt funkcji skalującej jest zbliżony do kształtu odpowiadającej jej falki, z tym że zawiera ona składową stałą. Definiuje się ją w rekurencyjnym zapisie matematycznym za pomocą równania dylatacyjnego: | ||
<math>\varphi(t)=\sqrt{2}\sum_{k=0}^{N-1} {h_k \varphi (2t-k)}</math> | <math>\varphi(t)=\sqrt{2}\sum_{k=0}^{N-1} {h_k \varphi (2t-k)}</math> | ||
| Linia 223: | Linia 223: | ||
Współczynniki <math>H=\left \{h_k \right \}\ | Współczynniki <math>H=\left \{h_k \right \}\ </math>,, oraz <math>G=\left \{g_k \right \}\ </math>, są rozumiane jako współczynniki pary kwadraturowych filtrów lustrzanych. W przypadku bazy ortonormalnej związane są zależnością wzajemną: | ||
<math>g_k=(-1)^k h_{N-k}</math>. | <math>g_k=(-1)^k h_{N-k}</math>. | ||
Aktualna wersja na dzień 12:05, 5 wrz 2023
wersja beta
LABORATORIUM WIRTUALNE 1
Ćwiczenie 5 - Analiza czasowo - częstotliwościowa sygnałów

|

|

|

|