Języki, automaty i obliczenia/Wykład 8: Dalsze algorytmy dla języków regularnych. Problemy rozstrzygalne: Różnice pomiędzy wersjami
Matiunreal (dyskusja | edycje) Nie podano opisu zmian |
m Zastępowanie tekstu – „,...,” na „,\ldots,” |
||
| (Nie pokazano 50 wersji utworzonych przez 5 użytkowników) | |||
| Linia 1: | Linia 1: | ||
W tym wykładzie przedstawimy algorytmy konstrukcji gramatyki regularnej, automatu skończenie stanowego oraz wyrażeń regularnych opisujących ten sam język <math> | W tym wykładzie przedstawimy algorytmy konstrukcji gramatyki regularnej, automatu skończenie stanowego oraz wyrażeń regularnych opisujących ten sam język <math>L</math>. Omówimy także problemy rozstrzygalne algorytmicznie w klasie języków regularnych. | ||
__FORCETOC__ | |||
== | ==Dalsze algorytmy języków regularnych== | ||
Dowód twierdzenia z ostatniego wykładu, w którym udowodniliśmy równoważność | Dowód twierdzenia z ostatniego wykładu, w którym udowodniliśmy równoważność | ||
rozpoznawania języka <math> | rozpoznawania języka <math>L</math> i generowania tego języka przez gramatykę regularną | ||
daje podstawę do określenia dwóch algorytmów. Algorytmu konstruującego | daje podstawę do określenia dwóch algorytmów. Algorytmu konstruującego | ||
automat skończony w oparciu o daną gramatykę regularną i oczywiście | automat skończony w oparciu o daną gramatykę regularną i oczywiście | ||
| Linia 13: | Linia 13: | ||
Idea działania algorytmu ''Automat2GReg'' jest następująca: każdy | Idea działania algorytmu ''Automat2GReg'' jest następująca: każdy | ||
symbol nieterminalny <math> | symbol nieterminalny <math>v</math> tworzonej | ||
gramatyki odpowiada pewnemu stanowi <math> | gramatyki odpowiada pewnemu stanowi <math>s_v</math> automatu. Jeśli w automacie pod wpływem | ||
litery <math> | litery <math>a</math> następuje przejście | ||
ze stanu <math> | ze stanu <math>s_v</math> do stanu <math>s_w</math>, to do zbioru praw gramatyki dodawane jest prawo | ||
<math> | <math>s_v \rightarrow as_w</math>. Ponadto, | ||
jeśli stan <math> | jeśli stan <math>s_w</math> jest stanem końcowym, to dodajemy także prawo <math>s_w \rightarrow 1</math>, | ||
aby w danym miejscu wywód słowa | aby w danym miejscu wywód słowa | ||
mógł zostać zakończony. | mógł zostać zakończony. | ||
{{algorytm|''Automat2GReg'' | {{algorytm|''Automat2GReg'' - buduje gramatykę regularną dla | ||
zadanego automatu skończonego.|| | zadanego automatu skończonego.|| | ||
1 Wejście: <math> | 1 Wejście: <math>\mathcal{A}=(S, A, f, s_0, T)</math> - automat niedeterministyczny. | ||
2 Wyjście: <math> | 2 Wyjście: <math>G=(V_N, V_T, P, v_0)</math> - gramatyka regularna taka, że <math>L(G)=L(\mathcal{A})</math>. | ||
3 <math> | 3 <math>V_N \leftarrow \{v_0,v_1,\ldots,v_{|S|-1}\}</math>; | ||
4 <math> | 4 <math>V_T \leftarrow A</math>; | ||
5 <math> | 5 <math>v_0 \leftarrow s_0</math>; | ||
6 <math> | 6 <math>P \leftarrow \emptyset</math>; | ||
7 '''for''' '''each ''' <math> | 7 '''for''' '''each ''' <math>s_i\in S</math> '''do''' | ||
8 '''for''' '''each ''' <math> | 8 '''for''' '''each ''' <math>a\in A</math> '''do''' | ||
9 '''if''' <math> | 9 '''if''' <math>f(s_i,a)\neq</math>'''NULL''' '''then''' | ||
10 <math> | 10 <math>s_j \leftarrow f(s_i,a)</math>; <math>\triangleright</math> funkcja <math>f</math> jest określona na <math>(s_i,a)</math> | ||
11 <math>P \leftarrow P \cup \{s_i \rightarrow as_j\}</math>; | |||
12 '''if''' <math> | 12 '''if''' <math>s_j \in T</math> '''then''' | ||
13 <math> | 13 <math>P \leftarrow P \cup \{s_j \rightarrow 1\}</math>; | ||
14 '''end if''' | 14 '''end if''' | ||
15 '''end if''' | 15 '''end if''' | ||
16 '''end for''' | 16 '''end for''' | ||
17 '''end for''' | 17 '''end for''' | ||
18 '''return''' <math> | 18 '''return''' <math>G</math>; | ||
}} | }} | ||
Oznaczmy przez <math> | Oznaczmy przez <math>E(\mathcal{A})</math> ilość krawędzi w grafie | ||
<math> | <math>n</math>-stanowego automatu niedeterministycznego <math>\mathcal{A}</math>. | ||
Złożoność czasowa liczona względem <math> | Złożoność czasowa liczona względem <math>E(\mathcal{A})</math> jest liniowa i | ||
równa <math> | równa <math>O(E(\mathcal{A}))</math>. Również złożoność pamięciowa jest liniowa | ||
i wynosi <math> | i wynosi <math>O(|S|+E(\mathcal{A}))</math>. | ||
{{przyklad|1.1|| | <span id="przyklad_1_1">{{przyklad|1.1|| | ||
Niech dany będzie automat <math> | Niech dany będzie automat <math>\mathcal{A}</math> pokazany na rysunku 1. Zbudujemy gramatykę, która będzie | ||
generowała język akceptowany przez <math>\mathcal{A}</math>.}} | |||
generowała język akceptowany przez <math> | |||
<center> | <center> | ||
[[File:ja-lekcja08-w-rys1.svg|250x150px|thumb|center|Rysunek 1]] | |||
</center> | </center> | ||
Ponieważ <math> | Ponieważ <math>f(s_0,a)=s_0</math>, a ponadto <math>s_0</math> jest stanem końcowym, do | ||
<math> | <math>P</math> dodajemy produkcje <math>v_0 \rightarrow av_0</math> oraz <math>v_0 \rightarrow | ||
1</math>. Dodajemy także produkcję <math> | 1</math>. Dodajemy także produkcję <math>v_0 \rightarrow bv_1</math>, gdyż mamy | ||
<math> | <math>f(s_0,b)=s_1</math>. | ||
Fakt, że <math> | Fakt, że <math>f(s_1,b)=s_1</math> oraz <math>f(s_1,a)=s_2</math> sprawia, że do <math>P</math> | ||
dodajemy: <math> | dodajemy: <math>v_1\ \rightarrow bv_1</math>, <math>v_1 \rightarrow av_2</math>. | ||
Ponieważ <math> | Ponieważ <math>f(s_2, a)=s_1</math> do <math>P</math> dodajemy: <math>v_2 \rightarrow av_1</math> | ||
oraz <math> | oraz <math>v_2 \rightarrow 1</math>, gdyż <math>s_2 \in T</math>. | ||
Symbolem początkowym nowej gramatyki jest symbol | Symbolem początkowym nowej gramatyki jest symbol | ||
<math> | <math>v_0</math>. Ostatecznie gramatyka ma postać: | ||
<center><math>\ | <center><math>\begin{align} v_0 & \rightarrow & av_0\ |\ bv_1 \ |\ 1\\ | ||
v_1 & \rightarrow & bv_1\ |\ av_2 \\ | |||
v_2 & \rightarrow & av_1\ |\ 1 | |||
\ | \end{align}</math></center> | ||
Zwróćmy uwagę na wygodny zapis produkcji gramatyki, jaki został | Zwróćmy uwagę na wygodny zapis produkcji gramatyki, jaki został | ||
| Linia 92: | Linia 88: | ||
Zauważmy, że gramatyka podana na wejściu algorytmu nie może zawierać | Zauważmy, że gramatyka podana na wejściu algorytmu nie może zawierać | ||
produkcji postaci <math> | produkcji postaci <math>v \rightarrow x</math>, gdzie <math>v \in V_N</math>, <math>x \in (V_N | ||
\cup V_T)</math>. Jeśli gramatyka zawiera takie produkcje, to możemy się | \cup V_T)</math>. Jeśli gramatyka zawiera takie produkcje, to możemy się | ||
ich łatwo pozbyć, zgodnie z Twierdzeniem 2.2 z Wykładu 7, uzyskując | ich łatwo pozbyć, zgodnie z Twierdzeniem 2.2 z Wykładu 7 (patrz [[Języki, automaty i obliczenia/Wykład 7: Twierdzenie Kleene'ego. Własności języków i gramatyk regularnych#twierdzenie_2_2|twierdzenie 2.2 wykład 7]]), uzyskując oczywiście gramatykę równoważną. | ||
oczywiście gramatykę równoważną. | |||
Idea działania algorytmu jest podobna do poprzedniej | Idea działania algorytmu jest podobna do poprzedniej - każdy | ||
tworzony stan automatu odpowiadać będzie pewnemu symbolowi | tworzony stan automatu odpowiadać będzie pewnemu symbolowi | ||
nieterminalnemu gramatyki wejściowej. Zależnie od postaci produkcji | nieterminalnemu gramatyki wejściowej. Zależnie od postaci produkcji | ||
gramatyki, niektóre stany będą stanami końcowymi. | gramatyki, niektóre stany będą stanami końcowymi. | ||
Zapis <math> | Zapis <math>f \leftarrow\emptyset</math> w linii 7. symbolicznie oznacza, że | ||
funkcja przejść nie jest jeszcze określona. | funkcja przejść nie jest jeszcze określona. | ||
W pętli 8.-15. pozbywamy się produkcji, w których występuje więcej | W pętli 8.-15. pozbywamy się produkcji, w których występuje więcej | ||
niż jeden terminal; każdą taką produkcję "rozbijamy" na sekwencję | niż jeden terminal; każdą taką produkcję "rozbijamy" na sekwencję | ||
produkcji postaci <math> | produkcji postaci <math>v \rightarrow aw</math>, gdzie <math>v,w \in V_N,\ a \in | ||
V_T</math>. | V_T</math>. | ||
{{algorytm|''GReg2Automat'' | {{algorytm|''GReg2Automat'' - buduje automat dla zadanej | ||
gramatyki regularnej.|| | gramatyki regularnej.|| | ||
1 Wejście: <math> | 1 Wejście: <math>G=(V_N, V_T, P, v_0)</math> - gramatyka regularna. | ||
2 Wyjście: <math> | 2 Wyjście: <math>\mathcal{A}=(S, A, f, v_0, T)</math> - automat taki, że <math>L(\mathcal{A})=L(G)</math>. | ||
3 <math> | 3 <math>S \leftarrow V_N</math>; | ||
4 <math> | 4 <math>A \leftarrow V_T</math>; | ||
5 <math> | 5 <math>T \leftarrow \emptyset</math>; <math>\triangleright</math> nie ma jeszcze stanów końcowych | ||
6 <math> | 6 <math>s_0 \leftarrow v_0</math>; | ||
7 <math> | 7 <math>f \leftarrow \emptyset</math>; <math>\triangleright</math> funkcja <math>f</math> nie jest określona dla żadnego argumentu | ||
8 '''for''' '''each ''' <math> | 8 '''for''' '''each ''' <math>(v_i \rightarrow a_1a_2...a_nv_j) \in P</math> '''do''' | ||
9 '''if''' <math> | 9 '''if''' <math>n>1</math> '''then''' | ||
10 <math> | 10 <math>V_N \leftarrow V_N \cup \{v^{a_1}, ..., v^{a_{n-1}}\}</math>; <math>\triangleright</math> rozbijamy produkcję na kilka prostszych | ||
11 <math> | 11 <math>P \leftarrow P \backslash \{v_i \rightarrow a_1a_2...a_nv_j\}</math>; <math>\triangleright</math> w tym celu usuwamy produkcję z <math>P</math> | ||
12 <math> | 12 <math>P \leftarrow P \cup \{v_i \rightarrow a_1v^{a_1}, v^{a_{n-1}} \rightarrow a_nv_j\}</math>; <math>\triangleright</math> w zamian dodając ciąg krótszych | ||
13 <math> | 13 <math>P \leftarrow P \cup \{v^{a_1} \rightarrow a_2v^{a_2}, \ldots, v^{a_{n-2}} \rightarrow a_{n-1}v^{a_{n-1}} \}</math>; | ||
14 '''end if''' | 14 '''end if''' | ||
15 '''end for''' | 15 '''end for''' | ||
16 <math> | 16 <math>\triangleright</math> wszystkie produkcje są postaci <math>u\rightarrow a v</math> lub <math>u\rightarrow 1</math>, gdzie <math>u,v\in V_N</math>, <math>a\in V_T</math> | ||
17 '''for''' '''each '''<math> | 17 '''for''' '''each '''<math>(s_i \rightarrow as_j) \in P</math> '''do''' | ||
18 <math> | 18 <math>f(s_i, a) \leftarrow s_j</math>; | ||
19 '''end for''' | 19 '''end for''' | ||
20 '''for''' '''each ''' <math> | 20 '''for''' '''each ''' <math>(v_i \rightarrow 1) \in P</math> '''do''' | ||
21 <math> | 21 <math>T \leftarrow T \cup \{v_i\}</math>; | ||
22 '''end for''' | 22 '''end for''' | ||
23 '''return''' <math> | 23 '''return''' <math>\mathcal{A}=(S, A, f, s_0, T)</math>; | ||
}} | }}</span> | ||
{{przyklad|1.2|| | {{przyklad|1.2|| | ||
Jako wejście algorytmu rozważmy gramatykę z przykładu | Jako wejście algorytmu rozważmy gramatykę z przykładu 1.1 (patrz [[#przyklad_1_1|przykład 1.1.]]) | ||
[[# | Używając algorytmu | ||
''Greg2Automat'', zbudujemy dla niej automat akceptujący język | ''Greg2Automat'', zbudujemy dla niej automat akceptujący język | ||
przez nią generowany. | przez nią generowany. | ||
Mamy <math> | Mamy <math>S=\{s_0, s_1, s_2\}</math>. W liniach 17. -- 19. określana jest | ||
funkcja przejścia: <math> | funkcja przejścia: <math>f(s_0, a)=s_0</math>, <math>f(s_0, b)=s_1</math>, <math>f(s_1, | ||
b)=s_1</math>, <math> | b)=s_1</math>, <math>f(s_1, a)=s_2</math> oraz <math>f(s_2, a)=s_1</math>. | ||
Pętla w liniach 20. | Pętla w liniach 20. - 22. przebiega po dwóch produkcjach: <math>v_0 | ||
\rightarrow 1</math> oraz <math> | \rightarrow 1</math> oraz <math>v_2 \rightarrow 1</math>, dodaje zatem do zbioru <math>T</math> | ||
stanów końcowych stany <math> | stanów końcowych stany <math>s_0</math> oraz <math>s_2</math>. Szukany automat to automat z poprzedniego przykładu; przedstawiony jest na rysunku 1. | ||
}} | }} | ||
Automat powstały w wyniku działania algorytmu ''GReg2Automat'' | Automat powstały w wyniku działania algorytmu ''GReg2Automat'' | ||
nie musi być automatem deterministycznym (wystarczy, że w zbiorze | nie musi być automatem deterministycznym (wystarczy, że w zbiorze | ||
produkcji znajdą się dwie produkcje postaci <math> | produkcji znajdą się dwie produkcje postaci <math>v_i \rightarrow av_j</math> | ||
oraz <math> | oraz <math>v_i \rightarrow av_k</math> dla pewnego <math>a \in A</math>), jednak po jego | ||
determinizacji i minimalizacji otrzymujemy minimalny automat | determinizacji i minimalizacji otrzymujemy minimalny automat | ||
deterministyczny akceptujący język, który jest generowany przez | deterministyczny akceptujący język, który jest generowany przez | ||
gramatyke podaną na wejście algorytmu. | gramatyke podaną na wejście algorytmu. | ||
Złożoność czasowa jak i pamięciowa algorytmu wynosi <math> | Złożoność czasowa jak i pamięciowa algorytmu wynosi <math>O(p)</math>, gdzie | ||
<math> | <math>p</math> jest liczbą produkcji występujących w zbiorze praw <math>P</math> | ||
gramatyki. | gramatyki. | ||
| Linia 175: | Linia 169: | ||
regularnego. | regularnego. | ||
Niech <math> | Niech <math>a \in A, r,s \in \mathcal{WR}</math>. Najpierw pokażemy, że językom | ||
odpowiadającym wyrażeniom regularnym , <math> | odpowiadającym wyrażeniom regularnym , <math>1</math>, <math>a</math>, <math>r+s</math>, <math>rs</math> oraz | ||
<math> | <math>r^*</math> można przyporządkować automaty akceptujące te języki, a | ||
następnie podamy algorytm konstruowania automatu rozpoznającego | następnie podamy algorytm konstruowania automatu rozpoznającego | ||
dowolne wyrażenie regularne. | dowolne wyrażenie regularne. | ||
Na rysunku | Na rysunku 2 przedstawione są trzy automaty. | ||
Automat a) rozpoznaje język pusty, automat b) | Automat a) rozpoznaje język pusty, automat b) - język <math>\{1\}</math>, a | ||
automat c) | automat c) - język <math>\{a\}</math>, dla <math>a \in A</math>. | ||
< | <center> | ||
[[File:ja-lekcja08-w-rys3.svg|250x250px|thumb|center|Rysunek 2]] | |||
</center> | |||
Niech dane będą automaty: <math> | Niech dane będą automaty: <math>M_1</math>, akceptujący język opisywany | ||
wyrażeniem <math> | wyrażeniem <math>r</math> oraz <math>M_2</math>, akceptujący język opisywany wyrażeniem | ||
<math> | <math>s</math>. Na rysunku 3 przedstawiono konstrukcje | ||
automatów akceptujących wyrażenia regularne <math> | automatów akceptujących wyrażenia regularne <math>r+s</math> (automat a)), | ||
<math> | <math>(rs)</math> (automat b)) oraz <math>r^*</math> (automat c)). | ||
<center> | |||
[[File:ja-lekcja08-w-rys4.svg|250x250px|thumb|center|Rysunek 3]] | |||
</center> | |||
< | W automacie a) stan <math>q_0</math> jest stanem początkowym, stan <math>f_0</math> - | ||
stanem końcowym, stany <math>q_1,q_2</math> oraz <math>f_1,f_2</math> oznaczają | |||
odpowiednio stany początkowe automatów <math>M_1</math> i <math>M_2</math> oraz stany | |||
końcowe automatów <math>M_1</math> i <math>M_2</math>. | |||
W automacie | W automacie b) stan <math>q_0</math> jest jednocześnie jego stanem początkowym | ||
oraz stanem początkowym automatu <math>M_1</math>, stan <math>f_1</math> jest stanem | |||
końcowym automatu b) i jednocześnie stanem końcowym automatu <math>M_2</math>. | |||
Stan <math>f_0</math> jest stanem końcowym w <math>M_1</math>, a <math>q_1</math> - początkowym w | |||
<math>M_2</math>. | |||
W automacie c) stan <math>q_0</math> jest jego stanem początkowym a <math>f_0</math> | |||
końcowym. Stany <math>q_1</math> oraz <math>f_1</math> to odpowiednio początkowy i końcowy | |||
stan automatu <math>M_1</math>. | |||
W automacie c) stan <math> | |||
końcowym. Stany <math> | |||
stan automatu <math> | |||
Wyrażenia regularne można przedstawiać w postaci drzewa, w którym | Wyrażenia regularne można przedstawiać w postaci drzewa, w którym | ||
| Linia 216: | Linia 213: | ||
{{przyklad|1.3|| | {{przyklad|1.3|| | ||
Rozważmy wyrażenie regularne <math> | Rozważmy wyrażenie regularne <math>r=(a^*b)(ab+c)</math>. Drzewo odpowiadające | ||
<math> | <math>r</math> przedstawione jest na rysunku 4. Korzeniem | ||
jest wierzchołek z małą wchodzącą strzałką. | jest wierzchołek z małą wchodzącą strzałką. | ||
}} | }} | ||
<center> | |||
< | [[File:ja-lekcja08-w-rys5.svg|350x250px|thumb|center|Rysunek 4]] | ||
</center> | |||
Powyższe konstrukcje będą stosowane podczas iteracyjnej budowy | Powyższe konstrukcje będą stosowane podczas iteracyjnej budowy | ||
| Linia 228: | Linia 226: | ||
będzie przeszukiwane metodą post-order (zaczynając od korzenia), | będzie przeszukiwane metodą post-order (zaczynając od korzenia), | ||
tzn. najpierw rekurencyjnie przeszukiwane są poddrzewa danego węzła | tzn. najpierw rekurencyjnie przeszukiwane są poddrzewa danego węzła | ||
<math> | <math>x</math>, a na końcu sam węzeł <math>x</math>. Dzięki temu, wchodząc do węzła <math>x</math> | ||
drzewa etykietowanego daną operacją na wyrażeniu regularnym oba | drzewa etykietowanego daną operacją na wyrażeniu regularnym oba | ||
poddrzewa <math> | poddrzewa <math>P</math> i <math>L</math> wierzchołka <math>x</math> będą już reprezentowane przez | ||
automaty <math> | automaty <math>\mathcal{A}_P</math> oraz <math>\mathcal{A}_L</math>. Teraz wystarczy | ||
zastosować jedną z konstrukcji z rysunku | zastosować jedną z konstrukcji z rysunku 2 lub 3. Procedurę powtarzamy do momentu, aż | ||
przechodzenie drzewa zakończy się w korzeniu. Szukanym przez nas | przechodzenie drzewa zakończy się w korzeniu. Szukanym przez nas | ||
automatem będzie automat "odpowiadający" korzeniowi drzewa. | automatem będzie automat "odpowiadający" korzeniowi drzewa. | ||
| Linia 242: | Linia 239: | ||
Wykorzystamy także dwie procedury, mianowicie | Wykorzystamy także dwie procedury, mianowicie | ||
''CreateAutomata''(''type'') oraz | ''CreateAutomata''(''type'') oraz | ||
''JoinAutomata''(''type'',<math> | ''JoinAutomata''(''type'',<math>\mathcal{M}_1,\mathcal{M}_2</math>). | ||
Zmienna ''type'' może przyjmować wartości '<math> | Zmienna ''type'' może przyjmować wartości '<math>a</math>', '<math>b</math>' lub '<math>c</math>'. | ||
Funkcja zwraca automat ''CreateAutomata''(''type'') | Funkcja zwraca automat ''CreateAutomata''(''type'') | ||
przedstawiony (zależnie od zmiennej ''type'') na rysunku | przedstawiony (zależnie od zmiennej ''type'') na rysunku 2. Procedura | ||
''JoinAutomata''(''type'',<math>\mathcal{M}_1,\mathcal{M}_2</math>) | |||
''JoinAutomata''(''type'',<math> | natomiast konstruuje na podstawie automatów <math>\mathcal{M}_1</math>, | ||
natomiast konstruuje na podstawie automatów <math> | <math>\mathcal{M}_2</math> automat z rysunku 2, przy | ||
<math> | czym dla przypadku ''type''<nowiki>=</nowiki><math>c</math> automat <math>\mathcal{M}_2</math> jest bez | ||
czym dla przypadku ''type''<nowiki>=</nowiki><math> | |||
znaczenia. Ostatnią wykorzystaną procedurą będzie | znaczenia. Ostatnią wykorzystaną procedurą będzie | ||
''BuildTree''(r), tworząca drzewo (binarne) dla wyrażenia | ''BuildTree''(r), tworząca drzewo (binarne) dla wyrażenia | ||
regularnego. Zakładamy, że studentowi doskonale jest znana Odwrotna | regularnego. Zakładamy, że studentowi doskonale jest znana Odwrotna | ||
Notacja Polska i budowa takiego drzewa nie będzie dla niego | Notacja Polska i budowa takiego drzewa nie będzie dla niego | ||
stanowiła problemu. Dla ustalenia uwagi zakładamy, że symbol <math> | stanowiła problemu. Dla ustalenia uwagi zakładamy, że symbol <math>*</math> | ||
prowadzi zawsze do lewego dziecka. | prowadzi zawsze do lewego dziecka. | ||
Poniżej przedstawiamy oznaczenia standardowych funkcji operujących | Poniżej przedstawiamy oznaczenia standardowych funkcji operujących | ||
na drzewach. Funkcja <math>\ | na drzewach. Funkcja <math>\text{Root}(T)</math> zwraca korzeń drzewa <math>T</math>, | ||
funkcje <math>\ | funkcje <math>\text{LeftChild}(T,v)</math> oraz <math>\text{RightChild}(T,v)</math> | ||
zwracają lewe i prawe dziecko wierzchołka <math> | zwracają lewe i prawe dziecko wierzchołka <math>v</math> (ew. '''NULL''', | ||
gdy brak lewego lub prawego dziecka), natomiast funkcja | gdy brak lewego lub prawego dziecka), natomiast funkcja | ||
<math>\ | <math>\text{Label}(T,v)</math> zwraca etykietę wierzchołka <math>v</math> drzewa <math>T</math>. | ||
Funkcja <math>\ | Funkcja <math>\text{IsLeaf}(T,v)</math> zwraca wartość <math>\textbf{true}</math>, gdy | ||
<math> | <math>v</math> jest liściem w drzewie <math>T</math> oraz <math>\textbf{false}</math> w przypadku | ||
przeciwnym. | przeciwnym. | ||
| Linia 271: | Linia 267: | ||
opisywany wyrażeniem regularnym|| | opisywany wyrażeniem regularnym|| | ||
Wejście: <math> | 1 Wejście: <math>r</math> -- wyrażenie regularne. | ||
2 Wyjście: <math>\mathcal{A}=(S, A, f, s_0, T)</math> -- automat rozpoznający język opisywany wyrażeniem <math>r</math>. | |||
Wyjście: <math> | 3 <math>T\leftarrow \text{BuildTree}(r)</math>; | ||
rozpoznający język opisywany wyrażeniem <math> | 4 <math>v_0 \leftarrow \text{Root}(T)</math>; | ||
5 <math>\mathcal{A} \leftarrow</math> ''PostOrder''(<math>T,v_0</math>); | |||
<math> | 6 '''return''' <math>\mathcal{A}</math>; | ||
<math> | |||
<math> | |||
'''return''' <math> | |||
}} | }} | ||
{{przyklad|1.4|| | {{przyklad|1.4|| | ||
Zastosujemy algorytm ''Wr2Automat'' do konstrukcji automatu dla | Zastosujemy algorytm ''Wr2Automat'' do konstrukcji automatu dla | ||
wyrażenia regularnego <math> | wyrażenia regularnego <math>w=(a^*b)(ab+c)</math>. | ||
}} | }} | ||
<center> | |||
[[File:ja-lekcja08-w-anim1.svg|350x350px|thumb|center|Animacja 1]] | |||
</center> | |||
Automat <math>\mathcal{A}_{10}</math> jest zwrócony przez algorytm jako automat | |||
akceptujący język opisywany wyrażeniem <math>r=(a^*b)(ab+c)</math>. Automat ten przedstawiony jest na rysunku 5. | |||
Automat <math> | <center> | ||
akceptujący język opisywany wyrażeniem <math> | [[File:ja-lekcja08-w-rys6.svg|500x350px|thumb|center|Rysunek 5]] | ||
przedstawiony jest na rysunku [[ | </center> | ||
Ramkami zaznaczono i opisano automaty budowane w trakcie działania | Ramkami zaznaczono i opisano automaty budowane w trakcie działania | ||
| Linia 366: | Linia 299: | ||
wcześniej algorytmów ''UsuńPustePrzejścia'' oraz | wcześniej algorytmów ''UsuńPustePrzejścia'' oraz | ||
''Determinizuj''. | ''Determinizuj''. | ||
{{algorytm|Procedure PostOrder|| | |||
1 '''procedure''' ''PostOrder'' (<math>T</math>: drzewo, <math>v</math>: wierzchołek) | |||
2 '''if''' ''IsLeaf''(<math>T,v</math>) '''then''' | |||
3 '''if''' <math>v</math><nowiki>=</nowiki>'''NULL''' '''then''' | |||
4 <math>\mathcal{A}_v \leftarrow</math> ''CreateAutomata''('<math>a</math>'); | |||
5 '''else''' | |||
6 '''if''' ''Label''(<math>T,v</math>)<nowiki>=</nowiki>'1' '''then''' | |||
7 <math>\mathcal{A}_v \leftarrow</math> ''CreateAutomata''('<math>b</math>'); | |||
8 '''else''' | |||
9 <math>\mathcal{A}_v \leftarrow</math> ''CreateAutomata''('<math>c</math>'); <math>\triangleright</math> ''Label''<math>(T,v)\in A</math> | |||
10 '''end if''' | |||
11 '''end if''' | |||
12 '''return''' <math>\mathcal{A}_v</math>; | |||
13 '''else''' | |||
14 <math>\mathcal{A}_L \leftarrow</math> ''PostOrder''(<math>T</math>, LeftChild<math>(T,v)</math>); | |||
15 <math>\mathcal{A}_P \leftarrow</math> ''PostOrder''(<math>T</math>, RightChild<math>(T,v)</math>); | |||
16 '''if''' ''Label''(<math>T,v</math>)<nowiki>=</nowiki>'<math>+</math>' '''then''' | |||
17 <math>\mathcal{A}_{LP}\leftarrow</math>''JoinAutomata''('<math>a</math>'<math>,\mathcal{A}_L,\mathcal{A}_P</math>); | |||
18 '''end if''' | |||
19 '''if''' ''Label''(<math>T,v</math>)<nowiki>=</nowiki>'<math>\cdot</math>' '''then''' | |||
20 <math>\mathcal{A}_{LP}\leftarrow</math>''JoinAutomata''('<math>b</math>'<math>,\mathcal{A}_L,\mathcal{A}_P</math>); | |||
21 '''end if''' | |||
22 '''if''' ''Label''(<math>T,v</math>)<nowiki>=</nowiki>'<math>*</math>' '''then''' | |||
23 <math>\mathcal{A}_{LP}\leftarrow</math>''JoinAutomata''('<math>c</math>'<math>,\mathcal{A}_L,\mathcal{A}_P</math>); | |||
24 '''end if''' | |||
25 '''return''' <math>\mathcal{A}_{LP}</math>; | |||
26 '''end if''' | |||
27 '''end procedure''' | |||
}} | |||
Procedura tworzenia drzewa dla wyrażenia regularnego działa w czasie | Procedura tworzenia drzewa dla wyrażenia regularnego działa w czasie | ||
| Linia 380: | Linia 344: | ||
przedstawimy w ćwiczeniach do tego wykładu. | przedstawimy w ćwiczeniach do tego wykładu. | ||
Niech dany będzie automat <math> | Niech dany będzie automat <math>\mathcal{A}=(S, A, f, s_1, T)</math>. Zbudujemy | ||
wyrażenie regularne opisujące język akceptowany przez <math> | wyrażenie regularne opisujące język akceptowany przez <math>\mathcal{A}</math>. | ||
Konstrukcja polega na obliczeniu zbiorów <math> | Konstrukcja polega na obliczeniu zbiorów <math>R_{ij}^k</math> (definicja | ||
poniżej), gdzie <math> | poniżej), gdzie <math>i,j=1,\ldots,|S|</math>, co jest równoważne konstrukcji | ||
pewnych wyrażeń regularnych <math> | pewnych wyrażeń regularnych <math>r_{ij}^k</math>. Szukany język będzie | ||
odpowiadał sumie pewnych zbiorów <math> | odpowiadał sumie pewnych zbiorów <math>R_{ij}^k</math>, a zatem opisywany | ||
będzie przez wyrażenie regularne postaci <math> | będzie przez wyrażenie regularne postaci <math>r_{ij_1}^k + ... + | ||
r_{ij_t}^k</math> dla pewnych <math> | r_{ij_t}^k</math> dla pewnych <math>j_l</math>, <math>i</math> oraz <math>k</math>. | ||
Załóżmy, że zbiór stanów automatu jest postaci <math> | Załóżmy, że zbiór stanów automatu jest postaci <math>S=\{s_1, s_2, ..., s_n\}</math>. | ||
Wprowadźmy porządek na | Wprowadźmy porządek na | ||
zbiorze <math> | zbiorze <math>S</math>, przyjmując: <center><math>s_i \prec s_j \Leftrightarrow i<j</math>.</center> | ||
Zbiory <math> | Zbiory <math>R_{ij}^k</math> definiujemy w następujący sposób: | ||
<center><math>\ | <math>\mbox{(1)}</math> | ||
<center><math>\begin{align} R_{ij}^0 &= \left\{ \begin{array} {ll} \{a \in A:\ f(s_i,a)=s_j\} | |||
& \mbox{ dla } i \not = j,\ 1 \leqslant i,j \leqslant n \\ \{a \in A\ f(s_i, | & \mbox{ dla } i \not = j,\ 1 \leqslant i,j \leqslant n \\ \{a \in A\ f(s_i, | ||
a)=s_j\} \cup \{ 1 \} & \mbox{ dla } i=j,\ 1 \leqslant i,j \leqslant n | a)=s_j\} \cup \{ 1 \} & \mbox{ dla } i=j,\ 1 \leqslant i,j \leqslant n | ||
\end{array} | \end{array} | ||
\right. \\ | \right. \\ | ||
R_{ij}^k &= R_{ik}^{k-1}(R_{kk}^{k-1})^*R_{kj}^{k-1} | |||
\cup R_{ij}^{k-1},\ 1 \leqslant i,j,k \leqslant n. | \cup R_{ij}^{k-1},\ 1 \leqslant i,j,k \leqslant n. | ||
\ | \end{align}</math></center> | ||
Intuicyjnie, zbiór <math> | Intuicyjnie, zbiór <math>R_{ij}^k</math> to ogół wszystkich słów <math>w</math> takich, że | ||
<math> | <math>f(s_i, w)=s_j</math>, a ponadto jeśli <math>w=a_1a_2...a_m</math>, to <math>\forall 1 | ||
\leqslant j \leqslant m-1 f(s_i, a_1a_2...a_j) = s_l \wedge l \leqslant k</math>. | \leqslant j \leqslant m-1 f(s_i, a_1a_2...a_j) = s_l \wedge l \leqslant k</math>. | ||
Zamiast obliczać zbiory <math> | Zamiast obliczać zbiory <math>R_{ij}^k</math> wygodniej będzie od razu | ||
zapisywać odpowiadające im wyrażenia regularne, które oznaczać | zapisywać odpowiadające im wyrażenia regularne, które oznaczać | ||
będziemy poprzez <math> | będziemy poprzez <math>r_{ij}^k</math>. | ||
Przez analogię mamy wzór rekurencyjny: | Przez analogię mamy wzór rekurencyjny: | ||
<center><math> | <math>\mbox{(2)}</math> | ||
\leqslant i,j,k \leqslant n | <center><math>r_{ij}^k=r_{ik}^{k-1}(r_{kk}^{k-1})^*r_{kj}^{k-1} + r_{ij}^{k-1},\ 1 | ||
</math></center> | \leqslant i,j,k \leqslant n</math></center> | ||
Pozostaje wyjaśnić jak wyglądają wyrażenia <math> | Pozostaje wyjaśnić jak wyglądają wyrażenia <math>r_{ij}^0</math>. Jeśli | ||
<math> | <math>R_{ij}^k=\{a_1,a_2,\dots,a_s\}</math> to | ||
<center><math> | {{kotwica|prz.3|}}<math>\mbox{(3)}</math> | ||
<center><math>r_{ij}^0=a_1+a_2+\dots+a_s | |||
</math></center> | </math></center> | ||
{{twierdzenie|1.1|| | {{kotwica|prz.1|}}{{twierdzenie|1.1|| | ||
Niech <math> | Niech <math>\mathcal{A}</math> oraz <math>R_{ij}^k</math> będą zdefiniowane jak powyżej i | ||
niech zbiór stanów końcowych dla <math> | niech zbiór stanów końcowych dla <math>\mathcal{A}</math> ma postać | ||
<math> | <math>T=\{s_{j_1}, s_{j_2}, ..., s_{j_t}\}</math>. Wtedy | ||
<center><math> | <center><math>L(\mathcal{A})=r_{1j_1}^n + r_{1j_2}^n + ... + r_{1j_t}^n</math>.</center> | ||
}} | }} | ||
| Linia 439: | Linia 405: | ||
opisujące język akceptowany przez automat skończony.|| | opisujące język akceptowany przez automat skończony.|| | ||
Wejście: <math> | 1 Wejście: <math>\mathcal{A}=(S=\{s_1, s_2, ..., s_n\}, A, f, s_1, T)</math>. | ||
T)</math>. | 2 Wyjście: <math>w</math> - wyrażenie regularne opisujące język <math>L=L(\mathcal{A})</math>. | ||
3 '''for''' <math>i\leftarrow 1</math> '''to''' <math>n</math> '''do''' | |||
Wyjście: <math> | 4 '''for''' <math>j\leftarrow 1</math> '''to''' <math>n</math> '''do''' | ||
<math> | 5 '''oblicz''' <math>r_{ij}^0</math> <math>\triangleright</math> stosujemy wzór (3); | ||
6 '''end for''' | |||
'''for''' <math> | 7 '''end for''' | ||
8 '''for''' <math>k \leftarrow 1</math> '''to''' <math>n</math> '''do''' | |||
'''for''' <math> | 9 '''for''' <math>i\leftarrow 1</math> '''to''' <math>n</math> '''do''' | ||
10 '''for''' <math>j\leftarrow 1</math> '''to''' <math>n</math> '''do''' | |||
'''oblicz''' <math> | 11 <math>r_{ij}^k \leftarrow r_{ik}^{k-1}(r_{kk}^{k-1})^*r_{kj}^{k-1} + r_{ij}^{k-1}</math>; <math>\triangleright</math> dokonujemy katenacji słów | ||
wzór ( | 12 '''end for''' | ||
13 '''end for''' | |||
''' | 14 '''end for''' | ||
15 <math>r \leftarrow</math> ""; <math>\triangleright</math> podstaw pod <math>r</math> słowo puste | |||
''' | 16 '''for''' <math>i\leftarrow 1</math> '''to''' <math>n</math> | ||
17 '''if''' <math>\ s_i \in T</math> | |||
'''for''' <math> | 18 '''if''' r<nowiki>=</nowiki>"" | ||
19 <math>r\leftarrow r_{1i}^{n}</math>; <math>\triangleright</math> stosujemy Twierdzenie 1.1 | |||
'''for''' <math> | 20 '''else''' | ||
21 <math>r \leftarrow r + r_{1i}^{n}</math>; | |||
'''for''' <math> | 22 '''end if''' | ||
+ r_{ij}^{k-1}</math>; <math> | 23 '''end if''' | ||
katenacji słów | 24 '''end for''' | ||
25 '''return''' <math>r</math>; | |||
''' | |||
''' | |||
''' | |||
<math> | |||
słowo puste | |||
'''for''' <math> | |||
'''if''' <math> | |||
'''if''' r<nowiki>=</nowiki>"" | |||
<math> | |||
stosujemy Twierdzenie | |||
'''else''' | |||
<math> | |||
''' | |||
''' | |||
''' | |||
'''return''' <math> | |||
}} | }} | ||
Podczas obliczania wyrażeń <math> | Podczas obliczania wyrażeń <math>r_{ij}^k</math> należy je w miarę możliwości | ||
upraszczać, gdyż, szczególnie przy dużej liczbie stanów, | upraszczać, gdyż, szczególnie przy dużej liczbie stanów, | ||
nieskracane, mogą rozrastać się do bardzo dużych rozmiarów. | nieskracane, mogą rozrastać się do bardzo dużych rozmiarów. | ||
| Linia 500: | Linia 439: | ||
Znajdziemy wyrażenie regularne opisujące język akceptowany przez | Znajdziemy wyrażenie regularne opisujące język akceptowany przez | ||
automat z rysunku | automat z rysunku 6. | ||
}} | }} | ||
<center> | <center> | ||
[[File:ja-lekcja08-w-rys7.svg|250x250px|thumb|center|Rysunek 6]] | |||
</center> | </center> | ||
Mamy <math> | Mamy <math>|S|=3</math>, <math>i,j \in \{1, 2, 3\}</math>, <math>k \in \{0, 1, 2, 3\}</math>, | ||
<math> | <math>T=\{s_3\}</math>. Szukamy zatem wyrażenia regularnego <math>r = r_{13}^3</math>. | ||
Najpierw musimy obliczyć <math> | Najpierw musimy obliczyć <math>r_{ij}^0</math> dla wszystich <math>i,j \in | ||
\{1,2,3\}</math>. Mamy na przykład <math> | \{1,2,3\}</math>. Mamy na przykład <math>r_{31}^0=a+b</math>, gdyż z definicji | ||
zachodzi: <math> | zachodzi: <math>R_{31}^0 = \{a \in A:\ f(s_3, a)=s_1\}=\{a, b\}</math>. | ||
Gdy mamy wyliczone wszystkie <math> | Gdy mamy wyliczone wszystkie <math>r_{ij}^0</math>, przystępujemy do obliczeń | ||
dla <math> | dla <math>k=1</math>. | ||
Na przykład: | Na przykład: | ||
<center><math> | <center><math>r_{31}^1=r_{31}^0(r_{11}^0)^*r_{11}^0+r_{31}^0=(a+b)(a+1)^*(a+1)+(a+b)</math>,</center> | ||
co po zredukowaniu daje | co po zredukowaniu daje | ||
<center><math> | <center><math>r_{31}^1=(a+b)(a+1)^++(a+b)=(a+b)a^*+(a+b)=(a+b)a^*=a^++ba^*</math>.</center> | ||
[ | Obliczone wyrażenia <math>r_{ij}^k</math> dla <math>k=0,1,2</math> oraz dla wszystkich | ||
<math>i,j</math> przedstawione są w tabeli [[#tab.1|1]]. | |||
{| border=1 | {| border=1 align=center | ||
|- | |- | ||
| || <math> | | || <math>k=0</math> || <math>k=1</math> || <math>k=2</math> | ||
|- | |- | ||
| <math> | | <math>r_{11}^k</math> || <math>a+1</math> || <math>a^*</math> || <math>a^*b(a^+b)^*a^++a^*</math> | ||
|- | |- | ||
| <math> | | <math>r_{12}^k</math> || <math>b</math> || <math>a^*b</math> || <math>a^*b(a^+b)^*</math> | ||
|- | |- | ||
| <math> | | <math>r_{13}^k</math> || <math>\phi</math> || <math>\phi</math> || <math>a^*b(a^+b)^*b</math> | ||
|- | |- | ||
| <math> | | <math>r_{21}^k</math> || <math>a</math> || <math>a^+</math> || <math>(a^+b)^*a^+</math> | ||
|- | |- | ||
| <math> | | <math>r_{22}^k</math> || <math>1</math> || <math>a^+b+1</math> || <math>(a^+b)^*</math> | ||
|- | |- | ||
| <math> | | <math>r_{23}^k</math> || <math>b</math> || <math>b</math> || <math>(a^+b)^*b</math> | ||
|- | |- | ||
| <math> | | <math>r_{31}^k</math> || <math>a+b</math> || <math>a^++ba^*</math> || <math>(1+(a^+b+ba^*b)(a^+b)^*)a^++ba^*</math> | ||
|- | |- | ||
| <math> | | <math>r_{32}^k</math> || <math>\phi</math> || <math>a^+b+ba^*b</math> || <math>(a^+b+ba^*b)(a^+b)^*</math> | ||
|- | |- | ||
| <math> | | <math>r_{33}^k</math> || <math>1</math> || <math>1</math> || <math>(a^+b+ba^*b)(a^+b)^*b+1</math> | ||
|} | |} | ||
{Obliczone wartości <math> | {{kotwica|tab.1|}}<center><tt>Tabela 1. Obliczone wartości <math>r_{ij}^k</math> dla automatu z rys. 6</tt></center> | ||
Ponieważ <math> | Ponieważ <math>T=\{s_3\}</math>, szukanym wyrażeniem regularnym będzie | ||
<math> | <math>r=r_{13}^3</math>. Obliczamy zatem: | ||
<center><math>\ | <center><math>\begin{align} r_{13}^3 &= r_{13}^2(r_{33}^2)^*r_{33}^2+r_{13}^2 \\ | ||
&= | |||
a^*b(a+b)^*b(a^+b+ba^*b)(a^ | a^*b(a^+b)^*b((a^+b+ba^*b)(a^+b)^*b+1)^++a^*b(a^+b)^*b \\ | ||
&= a^*b(a^+b)^*b((a^+b+ba^*b)(a^+b)^*b)^*. | |||
\ | \end{align}</math></center> | ||
== | ==Problemy rozstrzygalne algorytmicznie== | ||
Kończąc część wykładu prezentującą języki regularne, wskażemy | Kończąc część wykładu prezentującą języki regularne, wskażemy | ||
| Linia 583: | Linia 515: | ||
{{twierdzenie|2.1|| | {{twierdzenie|2.1|| | ||
W klasie języków regularnych <math> | W klasie języków regularnych <math>\mathcal{REG}(A^{*})</math> następujące | ||
problemy są rozstrzygalne: | problemy są rozstrzygalne: | ||
# problem niepustości języka, <math> | # problem niepustości języka, <math>L\neq \emptyset</math> | ||
# problem nieskończoności języka, <math> | # problem nieskończoności języka, <math>card\, L=\aleph _{0}</math> | ||
# problem równości języków, <math> | # problem równości języków, <math>L_{1}=L_{2}</math> | ||
# problem należenia słowa do języka, <math> | # problem należenia słowa do języka, <math>w\in L</math> | ||
}} | }} | ||
| Linia 594: | Linia 526: | ||
{{dowod||| | {{dowod||| | ||
1. | |||
Aby uzasadnić ten fakt zauważmy, że wystarczy sprawdzić niepustość | Aby uzasadnić ten fakt zauważmy, że wystarczy sprawdzić niepustość | ||
skończonego podzbioru języka | skończonego podzbioru języka | ||
<math> | <math>L</math> co wynika z równoważności: | ||
<center><math> | <center><math>L\neq \oslash \ : \Leftrightarrow \ : \exists w\in L\, :\, \mid w\mid <N</math>,</center> | ||
gdzie <math> | gdzie <math>N</math> stała z lematu o pompowaniu. | ||
Implikacji <math> | Implikacji <math>\Leftarrow</math> jest oczywista. Natomiast fakt, że | ||
do niepustego języka należy słowo o długości ograniczonej | do niepustego języka należy słowo o długości ograniczonej | ||
przez <math> | przez <math>N</math> , wynika z lematu o pompowaniu. Jeśli mianowicie | ||
<math> | <math>w\in L</math> i <math>\mid w\mid \geqslant N</math> , to | ||
rozkładamy słowo <math> | rozkładamy słowo <math>w</math> następująco: | ||
<center><math> | <center><math>w=v_{1}uv_{2},\; \; u\neq 1,\; \; \forall i=0,1,2\ldots \ : v_{1}u^{i}v_{2}\in L</math></center> | ||
Przyjmując teraz wartość <math> | Przyjmując teraz wartość <math>i=0</math> , uzyskujemy: | ||
<center><math> | <center><math>v_{1}v_{2}\in L,\; \mid v_{1}v_{2}\mid <\mid w\mid</math></center> | ||
Po skończonej ilości powtórzeń powyższego rozkładu uzyskamy | Po skończonej ilości powtórzeń powyższego rozkładu uzyskamy | ||
słowo należące do języka, o długości ograniczonej | słowo należące do języka, o długości ograniczonej | ||
przez <math> | przez <math>N</math> . | ||
2. | |||
Wystarczy udowodnić nastepującą równoważność: | Wystarczy udowodnić nastepującą równoważność: | ||
<center><math> | <center><math>L \mbox{ nieskończony } \;\; \Longleftrightarrow \;\;\exists w \in L \;\; : \;\; N \leqslant \mid w \mid < 2N</math>.</center> | ||
Jeśli <math> | Jeśli <math>L</math> jest językiem nieskończonym, to znajdziemy w <math>L</math> | ||
słowo <math> | słowo <math>w</math> dowolnie długie. Niech <math>\mid w\mid \geqslant N | ||
</math> ''.'' Jeśli słowo <math> | </math> ''.'' Jeśli słowo <math>w</math> nie spełnia ograniczenia <math>\mid | ||
w\mid <2N | w\mid <2N</math> , to podobnie jak poprzednio korzystamy z lematu o | ||
pompowaniu i po skończonej ilości kroków otrzymamy słowo krótsze | pompowaniu i po skończonej ilości kroków otrzymamy słowo krótsze | ||
od <math> | od <math>2N</math> . Istotne jest, że wykorzystując lemat o pompowaniu, | ||
możemy założyć, że usuwane słowo <math> | możemy założyć, że usuwane słowo <math>u</math> ma długość ograniczoną | ||
przez <math> | przez <math>N</math> . Zatem oznacza to, że ze słowa dłuższego od <math>2N</math> | ||
nie | nie | ||
dostaniemy słowa krótszego od <math> | dostaniemy słowa krótszego od <math>N</math> . <br> | ||
Jeśli teraz do języka <math> | Jeśli teraz do języka <math>L</math> należy słowo <math>w</math> o długości | ||
większej lub równej <math> | większej lub równej <math>N</math> , to znów z lematu o pompowaniu wnioskujemy, że | ||
<center><math> | <center><math>w=v_{1}uv_{2},\ : u\neq 1\;\;\; i\;\;\; v_{1}u^{*}v_{2}\subset L</math></center> | ||
Istnieje więc nieskończony podzbiór języka <math> | Istnieje więc nieskończony podzbiór języka <math>L</math> , a więc i sam język | ||
<math> | <math>L</math> jest nieskończony. | ||
3. | |||
Rozważmy <math> | Rozważmy <math>L=(L_{1}\cap \overline{L_{2}})\cup (\overline{L_{1}}\cap L_{2})</math> . | ||
Język <math> | Język <math>L</math> jest regularny, co wynika z domkniętości | ||
klasy <math> | klasy <math>\mathcal{L}_{3}</math> na operaje boolowskie. Równoważność | ||
<center><math> | <center><math>L\neq \emptyset \Longleftrightarrow L_{1}\neq L_{2}</math></center> | ||
sprowadza problem równości języków do problemu | sprowadza problem równości języków do problemu | ||
niepustości omówionego powyżej. | niepustości omówionego powyżej. | ||
4. | |||
Konstruujemy automat <math> | Konstruujemy automat <math>\mathcal{A} =(S,f,s_0,T)</math> rozpoznający język | ||
<math> | <math>L</math> i sprawdzamy, czy <math>f(s_{0},w)\in T</math>. | ||
}} | |||
Na podstawie dowodu powyższego twierdzenia nietrudno jest określić algorytmy | Na podstawie dowodu powyższego twierdzenia nietrudno jest określić algorytmy | ||
| Linia 665: | Linia 597: | ||
{{algorytm|''NależenieDoJęzyka'' -- sprawdza, czy dane słowo | {{algorytm|''NależenieDoJęzyka'' -- sprawdza, czy dane słowo | ||
należy do języka <math> | należy do języka <math>L</math> akceptowanego przez zadany automat | ||
<math> | <math>\mathcal{A}</math>|| | ||
1 Wejście: <math> | 1 Wejście: <math>\mathcal{A}=(S, A, f, s_0, T)</math> - automat akceptujący język <math>L</math> oraz <math>w=w_1w_2\ldots w_n \in A^*</math> - słowo. | ||
2 Wyjście: Odpowiedź '''true''' (tak) lub '''false''' (nie). | 2 Wyjście: Odpowiedź '''true''' (tak) lub '''false''' (nie). | ||
3 <math> | 3 <math>k \leftarrow |w|</math>; | ||
4 <math> | 4 <math>s \leftarrow s_0</math>; | ||
5 '''for''' <math> | 5 '''for''' <math>i\leftarrow 1</math> '''to''' <math>k</math> '''do''' | ||
6 <math> | 6 <math>s \leftarrow f(s,w_i)</math>; | ||
7 '''end for''' | 7 '''end for''' | ||
8 '''if''' <math> | 8 '''if''' <math>s \in T</math> '''then''' | ||
9 '''return true'''; | 9 '''return true'''; | ||
10 '''else''' | 10 '''else''' | ||
| Linia 682: | Linia 614: | ||
}} | }} | ||
Algorytm działa w czasie <math> | Algorytm działa w czasie <math>O(|w|)</math> i posiada złożoność pamięciową | ||
<math> | <math>O(|A| \cdot |S|)</math>, co spowodowane jest koniecznością przechowywania funkcji | ||
przejść automatu <math> | przejść automatu <math>\mathcal{A}</math>. | ||
Jeśli język zadany jest nie automatem, a gramatyką regularną, to | Jeśli język zadany jest nie automatem, a gramatyką regularną, to | ||
Aktualna wersja na dzień 21:58, 15 wrz 2023
W tym wykładzie przedstawimy algorytmy konstrukcji gramatyki regularnej, automatu skończenie stanowego oraz wyrażeń regularnych opisujących ten sam język . Omówimy także problemy rozstrzygalne algorytmicznie w klasie języków regularnych.
Dalsze algorytmy języków regularnych
Dowód twierdzenia z ostatniego wykładu, w którym udowodniliśmy równoważność rozpoznawania języka i generowania tego języka przez gramatykę regularną daje podstawę do określenia dwóch algorytmów. Algorytmu konstruującego automat skończony w oparciu o daną gramatykę regularną i oczywiście akceptujący język generowany przez tę gramatykę oraz algorytmu budowy gramatyki regularnej dla zadanego automatu. Bez utraty ogólności przyjmujemy, że automat jest deterministyczny.
Idea działania algorytmu Automat2GReg jest następująca: każdy symbol nieterminalny tworzonej gramatyki odpowiada pewnemu stanowi automatu. Jeśli w automacie pod wpływem litery następuje przejście ze stanu do stanu , to do zbioru praw gramatyki dodawane jest prawo . Ponadto, jeśli stan jest stanem końcowym, to dodajemy także prawo , aby w danym miejscu wywód słowa mógł zostać zakończony.
Algorytm Automat2GReg - buduje gramatykę regularną dla zadanego automatu skończonego.
1 Wejście: - automat niedeterministyczny. 2 Wyjście: - gramatyka regularna taka, że . 3 ; 4 ; 5 ; 6 ; 7 for each do 8 for each do 9 if NULL then 10 ; funkcja jest określona na 11 ; 12 if then 13 ; 14 end if 15 end if 16 end for 17 end for 18 return ;
Oznaczmy przez ilość krawędzi w grafie -stanowego automatu niedeterministycznego . Złożoność czasowa liczona względem jest liniowa i równa . Również złożoność pamięciowa jest liniowa i wynosi .
Przykład 1.1
Niech dany będzie automat pokazany na rysunku 1. Zbudujemy gramatykę, która będzie
generowała język akceptowany przez .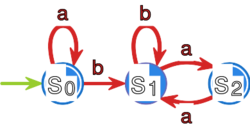
Ponieważ , a ponadto jest stanem końcowym, do dodajemy produkcje oraz . Dodajemy także produkcję , gdyż mamy .
Fakt, że oraz sprawia, że do dodajemy: , .
Ponieważ do dodajemy: oraz , gdyż .
Symbolem początkowym nowej gramatyki jest symbol . Ostatecznie gramatyka ma postać:
Zwróćmy uwagę na wygodny zapis produkcji gramatyki, jaki został użyty powyżej. Produkcje o tej samej lewej stronie (wspólnym symbolu nieterminalnym) zapisywane są razem, a prawe strony tych produkcji oddzielane są pionowymi kreskami.
Przedstawiony poniżej algorytm GReg2Automat konstruuje automat skończenie stanowy, akceptujący język generowany przez zadaną gramatykę.
Zauważmy, że gramatyka podana na wejściu algorytmu nie może zawierać produkcji postaci , gdzie , . Jeśli gramatyka zawiera takie produkcje, to możemy się ich łatwo pozbyć, zgodnie z Twierdzeniem 2.2 z Wykładu 7 (patrz twierdzenie 2.2 wykład 7), uzyskując oczywiście gramatykę równoważną.
Idea działania algorytmu jest podobna do poprzedniej - każdy tworzony stan automatu odpowiadać będzie pewnemu symbolowi nieterminalnemu gramatyki wejściowej. Zależnie od postaci produkcji gramatyki, niektóre stany będą stanami końcowymi.
Zapis w linii 7. symbolicznie oznacza, że funkcja przejść nie jest jeszcze określona.
W pętli 8.-15. pozbywamy się produkcji, w których występuje więcej niż jeden terminal; każdą taką produkcję "rozbijamy" na sekwencję produkcji postaci , gdzie .
Algorytm GReg2Automat - buduje automat dla zadanej gramatyki regularnej.
1 Wejście: - gramatyka regularna. 2 Wyjście: - automat taki, że . 3 ; 4 ; 5 ; nie ma jeszcze stanów końcowych 6 ; 7 ; funkcja nie jest określona dla żadnego argumentu 8 for each do 9 if then 10 ; rozbijamy produkcję na kilka prostszych 11 ; w tym celu usuwamy produkcję z 12 ; w zamian dodając ciąg krótszych 13 ; 14 end if 15 end for 16 wszystkie produkcje są postaci lub , gdzie , 17 for each do 18 ; 19 end for 20 for each do 21 ; 22 end for 23 return ;
Przykład 1.2
Jako wejście algorytmu rozważmy gramatykę z przykładu 1.1 (patrz przykład 1.1.) Używając algorytmu Greg2Automat, zbudujemy dla niej automat akceptujący język przez nią generowany.
Mamy . W liniach 17. -- 19. określana jest funkcja przejścia: , , , oraz .
Pętla w liniach 20. - 22. przebiega po dwóch produkcjach: oraz , dodaje zatem do zbioru stanów końcowych stany oraz . Szukany automat to automat z poprzedniego przykładu; przedstawiony jest na rysunku 1.
Automat powstały w wyniku działania algorytmu GReg2Automat nie musi być automatem deterministycznym (wystarczy, że w zbiorze produkcji znajdą się dwie produkcje postaci oraz dla pewnego ), jednak po jego determinizacji i minimalizacji otrzymujemy minimalny automat deterministyczny akceptujący język, który jest generowany przez gramatyke podaną na wejście algorytmu.
Złożoność czasowa jak i pamięciowa algorytmu wynosi , gdzie jest liczbą produkcji występujących w zbiorze praw gramatyki.
Przedstawimy teraz algorytmy związane z wyrażeniami regularnymi. Pierwszy z nich prowadzi do konstrukcji automatu skończenie stanowego, rozpoznającego język opisany wyrażeniem regularnym. Drugi, mając na wejściu automat, konstruuje wyrażenie regularne opisujące język rozpoznawany przez ten automat.
Rozpoczynamy od algorytmu prowadzącego do konstrukcji automatu na podstawie wyrażenia regularnego.
Niech . Najpierw pokażemy, że językom odpowiadającym wyrażeniom regularnym , , , , oraz można przyporządkować automaty akceptujące te języki, a następnie podamy algorytm konstruowania automatu rozpoznającego dowolne wyrażenie regularne.
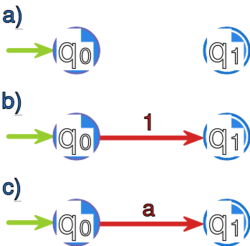
Na rysunku 2 przedstawione są trzy automaty. Automat a) rozpoznaje język pusty, automat b) - język , a automat c) - język , dla .
Niech dane będą automaty: , akceptujący język opisywany wyrażeniem oraz , akceptujący język opisywany wyrażeniem . Na rysunku 3 przedstawiono konstrukcje automatów akceptujących wyrażenia regularne (automat a)), (automat b)) oraz (automat c)).
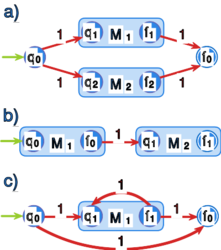
W automacie a) stan jest stanem początkowym, stan - stanem końcowym, stany oraz oznaczają odpowiednio stany początkowe automatów i oraz stany końcowe automatów i .
W automacie b) stan jest jednocześnie jego stanem początkowym oraz stanem początkowym automatu , stan jest stanem końcowym automatu b) i jednocześnie stanem końcowym automatu . Stan jest stanem końcowym w , a - początkowym w .
W automacie c) stan jest jego stanem początkowym a końcowym. Stany oraz to odpowiednio początkowy i końcowy stan automatu .
Wyrażenia regularne można przedstawiać w postaci drzewa, w którym liśćmi są litery, słowo puste 1 lub zbiór pusty , a węzły symbolizują operacje na wyrażeniach regularnych, czyli sumę, konkatenację lub iterację, czyli gwiazdkę Kleene'ego.
Przykład 1.3
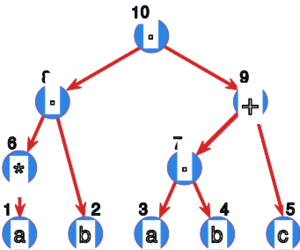
Rozważmy wyrażenie regularne . Drzewo odpowiadające przedstawione jest na rysunku 4. Korzeniem jest wierzchołek z małą wchodzącą strzałką.
Powyższe konstrukcje będą stosowane podczas iteracyjnej budowy automatu. Algorytm do tego celu będzie wykorzystywał drzewo odpowiadające wyrażeniu regularnemu w następujący sposób: drzewo będzie przeszukiwane metodą post-order (zaczynając od korzenia), tzn. najpierw rekurencyjnie przeszukiwane są poddrzewa danego węzła , a na końcu sam węzeł . Dzięki temu, wchodząc do węzła drzewa etykietowanego daną operacją na wyrażeniu regularnym oba poddrzewa i wierzchołka będą już reprezentowane przez automaty oraz . Teraz wystarczy zastosować jedną z konstrukcji z rysunku 2 lub 3. Procedurę powtarzamy do momentu, aż przechodzenie drzewa zakończy się w korzeniu. Szukanym przez nas automatem będzie automat "odpowiadający" korzeniowi drzewa.
Poniżej przedstawiony jest algorytm konstrukcji automatu w oparciu o wyrażenie regularne. Jego istotną część składową stanowi procedura PostOrder, której pseudo-kod jest przedstawiony poniżej. Wykorzystamy także dwie procedury, mianowicie CreateAutomata(type) oraz JoinAutomata(type,). Zmienna type może przyjmować wartości '', '' lub ''. Funkcja zwraca automat CreateAutomata(type) przedstawiony (zależnie od zmiennej type) na rysunku 2. Procedura JoinAutomata(type,) natomiast konstruuje na podstawie automatów , automat z rysunku 2, przy czym dla przypadku type= automat jest bez znaczenia. Ostatnią wykorzystaną procedurą będzie BuildTree(r), tworząca drzewo (binarne) dla wyrażenia regularnego. Zakładamy, że studentowi doskonale jest znana Odwrotna Notacja Polska i budowa takiego drzewa nie będzie dla niego stanowiła problemu. Dla ustalenia uwagi zakładamy, że symbol prowadzi zawsze do lewego dziecka.
Poniżej przedstawiamy oznaczenia standardowych funkcji operujących na drzewach. Funkcja zwraca korzeń drzewa , funkcje oraz zwracają lewe i prawe dziecko wierzchołka (ew. NULL, gdy brak lewego lub prawego dziecka), natomiast funkcja zwraca etykietę wierzchołka drzewa . Funkcja zwraca wartość , gdy jest liściem w drzewie oraz w przypadku przeciwnym.
Algorytm Wr2Automat -- buduje automat rozpoznający język opisywany wyrażeniem regularnym
1 Wejście: -- wyrażenie regularne. 2 Wyjście: -- automat rozpoznający język opisywany wyrażeniem . 3 ; 4 ; 5 PostOrder(); 6 return ;
Przykład 1.4
Zastosujemy algorytm Wr2Automat do konstrukcji automatu dla wyrażenia regularnego .
Automat jest zwrócony przez algorytm jako automat akceptujący język opisywany wyrażeniem . Automat ten przedstawiony jest na rysunku 5.
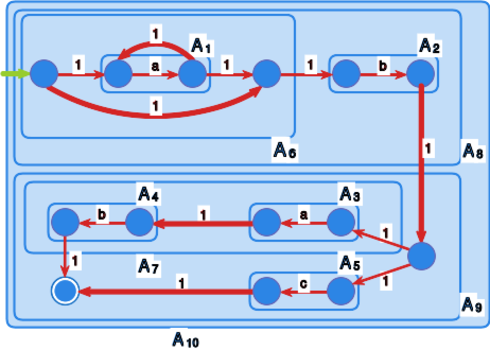
Ramkami zaznaczono i opisano automaty budowane w trakcie działania procedury PostOrder.
Rezultat działania algorytmu Wr2Automat może nie być zadawalający, gdyż wynikiem działania algorytmu nie jest automat deterministyczny, lecz automat z pustymi przejściami. Automat ten można więc poddać procesowi usunięcia przejść pustych oraz determinizacji, co można przeprowadzić przy pomocy omówionych wcześniej algorytmów UsuńPustePrzejścia oraz Determinizuj.
Algorytm Procedure PostOrder
1 procedure PostOrder (: drzewo, : wierzchołek)
2 if IsLeaf() then
3 if =NULL then
4 CreateAutomata('');
5 else
6 if Label()='1' then
7 CreateAutomata('');
8 else
9 CreateAutomata(''); Label
10 end if
11 end if
12 return ;
13 else
14 PostOrder(, LeftChild);
15 PostOrder(, RightChild);
16 if Label()='' then
17 JoinAutomata('');
18 end if
19 if Label()='' then
20 JoinAutomata('');
21 end if
22 if Label()='' then
23 JoinAutomata('');
24 end if
25 return ;
26 end if
27 end procedure
Procedura tworzenia drzewa dla wyrażenia regularnego działa w czasie
liniowym ze względu na długość napisu reprezentującego wyrażenie
regularne -- napis ten można najpierw przekształcić do równoważnego
mu, zapisanego w Odwrotnej Notacji Polskiej, a następnie,
przechodząc
od lewej strony do prawej, konstruować po kolei fragmenty drzewa.
Przechodzimy teraz do algorytmów konstruujących wyrażenie regularne na podstawie zadanego automatu. Pierwszą metodę, można powiedzieć klasyczną i omawianą w większości podręczników, prezentujemy poniżej. Drugą, nieco prostszą i wygodniejszą w zastosowaniu, przedstawimy w ćwiczeniach do tego wykładu.
Niech dany będzie automat . Zbudujemy wyrażenie regularne opisujące język akceptowany przez .
Konstrukcja polega na obliczeniu zbiorów (definicja poniżej), gdzie , co jest równoważne konstrukcji pewnych wyrażeń regularnych . Szukany język będzie odpowiadał sumie pewnych zbiorów , a zatem opisywany będzie przez wyrażenie regularne postaci dla pewnych , oraz .
Załóżmy, że zbiór stanów automatu jest postaci . Wprowadźmy porządek na
zbiorze
, przyjmując:
Zbiory definiujemy w następujący sposób:
Intuicyjnie, zbiór to ogół wszystkich słów takich, że , a ponadto jeśli , to .
Zamiast obliczać zbiory wygodniej będzie od razu zapisywać odpowiadające im wyrażenia regularne, które oznaczać będziemy poprzez . Przez analogię mamy wzór rekurencyjny:
Pozostaje wyjaśnić jak wyglądają wyrażenia . Jeśli to
Twierdzenie 1.1
Niech oraz będą zdefiniowane jak powyżej i niech zbiór stanów końcowych dla ma postać . Wtedy
Powyższą metodę ujmiemy formalnie w ramy algorytmu (algorytm Automat2WR1).
Algorytm Automat2WR1 -- buduje wyrażenie regularne opisujące język akceptowany przez automat skończony.
1 Wejście: . 2 Wyjście: - wyrażenie regularne opisujące język . 3 for to do 4 for to do 5 oblicz stosujemy wzór (3); 6 end for 7 end for 8 for to do 9 for to do 10 for to do 11 ; dokonujemy katenacji słów 12 end for 13 end for 14 end for 15 ""; podstaw pod słowo puste 16 for to 17 if 18 if r="" 19 ; stosujemy Twierdzenie 1.1 20 else 21 ; 22 end if 23 end if 24 end for 25 return ;
Podczas obliczania wyrażeń należy je w miarę możliwości upraszczać, gdyż, szczególnie przy dużej liczbie stanów, nieskracane, mogą rozrastać się do bardzo dużych rozmiarów.
Przykład 1.5
Znajdziemy wyrażenie regularne opisujące język akceptowany przez automat z rysunku 6.
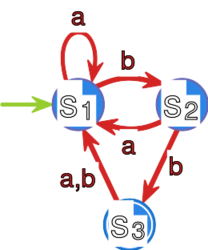
Mamy , , , . Szukamy zatem wyrażenia regularnego .
Najpierw musimy obliczyć dla wszystich . Mamy na przykład , gdyż z definicji zachodzi: .
Gdy mamy wyliczone wszystkie , przystępujemy do obliczeń dla .
Na przykład:
co po zredukowaniu daje
Obliczone wyrażenia dla oraz dla wszystkich przedstawione są w tabeli 1.
Ponieważ , szukanym wyrażeniem regularnym będzie . Obliczamy zatem:
Problemy rozstrzygalne algorytmicznie
Kończąc część wykładu prezentującą języki regularne, wskażemy problemy rozstrzygalne algorytmicznie w zakresie tej rodziny języków formalnych. Ponieważ pojęcia rozstrzygalności i nierozstrzygalności możemy uznać za znane (były wprowadzone na innych wykładach) nie będziemy tutaj ich definiować ani kreślić tła teorii rozstrzygalności.
W obrębie rodziny języków regularnych wszystkie podstawowe problemy są algorytmicznie rozstrzygalne. Uzasadnienia są proste. Część z nich opiera się na lemacie o pompowaniu, a część wynika bezpośrednio z algorytmicznej struktury automatu skończenie stanowego, czy też gramatyki regularnej.
Twierdzenie 2.1
W klasie języków regularnych następujące problemy są rozstrzygalne:
- problem niepustości języka,
- problem nieskończoności języka,
- problem równości języków,
- problem należenia słowa do języka,
Dowód
1. Aby uzasadnić ten fakt zauważmy, że wystarczy sprawdzić niepustość skończonego podzbioru języka co wynika z równoważności:
gdzie stała z lematu o pompowaniu. Implikacji jest oczywista. Natomiast fakt, że do niepustego języka należy słowo o długości ograniczonej przez , wynika z lematu o pompowaniu. Jeśli mianowicie i , to rozkładamy słowo następująco:
Przyjmując teraz wartość , uzyskujemy:
Po skończonej ilości powtórzeń powyższego rozkładu uzyskamy słowo należące do języka, o długości ograniczonej przez .
2. Wystarczy udowodnić nastepującą równoważność:
Jeśli jest językiem nieskończonym, to znajdziemy w
słowo dowolnie długie. Niech . Jeśli słowo nie spełnia ograniczenia , to podobnie jak poprzednio korzystamy z lematu o
pompowaniu i po skończonej ilości kroków otrzymamy słowo krótsze
od . Istotne jest, że wykorzystując lemat o pompowaniu,
możemy założyć, że usuwane słowo ma długość ograniczoną
przez . Zatem oznacza to, że ze słowa dłuższego od
nie
dostaniemy słowa krótszego od .
Jeśli teraz do języka należy słowo o długości większej lub równej , to znów z lematu o pompowaniu wnioskujemy, że
Istnieje więc nieskończony podzbiór języka , a więc i sam język jest nieskończony.
3. Rozważmy . Język jest regularny, co wynika z domkniętości klasy na operaje boolowskie. Równoważność
sprowadza problem równości języków do problemu niepustości omówionego powyżej.
4. Konstruujemy automat rozpoznający język i sprawdzamy, czy .
Na podstawie dowodu powyższego twierdzenia nietrudno jest określić algorytmy rozstrzygające przedstawione problemy. Poniżej prezentujemy algorytm rozstrzygający problem należenia słowa do języka regularnego zadanego automatem. Bez straty ogólności możemy założyć, że automat jest deterministyczny.
Algorytm NależenieDoJęzyka -- sprawdza, czy dane słowo należy do języka akceptowanego przez zadany automat
1 Wejście: - automat akceptujący język oraz - słowo. 2 Wyjście: Odpowiedź true (tak) lub false (nie). 3 ; 4 ; 5 for to do 6 ; 7 end for 8 if then 9 return true; 10 else 11 return false; 12 end if
Algorytm działa w czasie i posiada złożoność pamięciową , co spowodowane jest koniecznością przechowywania funkcji przejść automatu .
Jeśli język zadany jest nie automatem, a gramatyką regularną, to gramatykę można przekształcić na automat poznanym na początku wykładu algorytmem GReg2Automat, następnie zdeterminizować ten automat i podać go jako wejście dla algorytmu NależenieDoJęzyka.
Jeśli język zadany jest wyrażeniem regularnym, to mając wyrażenie regularne, można zbudować odpowiadający mu automat przy pomocy algorytmu WR2Automat. A zatem, na przykład, z powyższego twierdzenia wynika, iż problem równoważności wyrażeń regularnych jest rozstrzygalny.