PEE Zadania egzaminacyjne: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 7 wersji utworzonych przez 2 użytkowników) | |||
| Linia 5: | Linia 5: | ||
Zad. 1 | Zad. 1 | ||
Obliczyć prąd <math>I_x\ | Obliczyć prąd <math>I_x\ </math>, w obwodzie metodą Thevenina | ||
[[Grafika:PEE_Zadania_egz_zes1_1.jpg]] | [[Grafika:PEE_Zadania_egz_zes1_1.jpg]] | ||
Dane: <math>i(t)=5\sqrt{2}sin(\omega t+90^\circ)\ | Dane: <math>i(t)=5\sqrt{2}sin(\omega t+90^\circ)\quad</math>, <math>e(t)=10\sqrt{2}sin(\omega t-90^\circ)\quad</math>, <math>R=50\Omega\quad</math>, <math>\omega L=3\Omega</math> | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 19: | Linia 19: | ||
[[Grafika:PEE_Zadania_egz_zes1_2.jpg]] | [[Grafika:PEE_Zadania_egz_zes1_2.jpg]] | ||
Dane: <math>e_1(t)=50V\ | Dane: <math>e_1(t)=50V\ </math>,, <math>e_2(t)=60\sqrt{2}sin(\omega t+90^\circ)\ </math>,, <math>R=10\Omega</math>, <math>C=0,1F\ </math>, | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 29: | Linia 29: | ||
[[Grafika:PEE_Zadania_egz_zes1_3.jpg]] | [[Grafika:PEE_Zadania_egz_zes1_3.jpg]] | ||
Dane: <math>R=5\Omega</math>, <math>L=1H\ | Dane: <math>R=5\Omega</math>, <math>L=1H\ </math>,, <math>C=0,5F\ </math>, | ||
<hr width="100%"> | <hr width="100%"> | ||
Zad. 4 | |||
Wykazać, że kondunktancja dynamiczna <math>g_D</math> diody półprzewodnikowej jest wprost proporcjonalna do natężenia prądu przewodzenia <math>I_D</math>. | |||
<hr width="100%"> | |||
Zad. 5 | |||
Wyznaczyć wzmocnienie napięciowe w układzie wzmacniacza jak na rysunku. Dane: <math>U_{CC}</math>, <math>R_1</math>, <math>R_2</math>, <math>R_3</math>, <math>R_4</math>, <math>r_{BE}</math>, <math>\beta</math>, <math>k_f \to 0</math>, <math>r_{CE} \to \inf</math>. | |||
[[Grafika:PEE_Zadania_egz_zes1_5.jpg]] | |||
<hr width="100%"> | |||
| Linia 52: | Linia 65: | ||
[[Grafika:PEE_Zadania_egz_zes2_2.jpg]] | [[Grafika:PEE_Zadania_egz_zes2_2.jpg]] | ||
Dane: <math>X_{L1}=\omega L_1=40\Omega</math>, <math>X_{L2}=\omega L_2=20\Omega</math>, <math>X_M=\omega M=20\Omega</math>, <math>R=20\Omega</math>, <math>|U_f|=100V\ | Dane: <math>X_{L1}=\omega L_1=40\Omega</math>, <math>X_{L2}=\omega L_2=20\Omega</math>, <math>X_M=\omega M=20\Omega</math>, <math>R=20\Omega</math>, <math>|U_f|=100V\ </math> | ||
<hr width="100%"> | <hr width="100%"> | ||
| Linia 62: | Linia 75: | ||
[[Grafika:PEE_Zadania_egz_zes2_3.jpg]] | [[Grafika:PEE_Zadania_egz_zes2_3.jpg]] | ||
Dane: <math>R_1=30\Omega</math>, <math>R_2=20\Omega</math>, <math>C=0,01F\ | Dane: <math>R_1=30\Omega</math>, <math>R_2=20\Omega</math>, <math>C=0,01F\ </math>,, <math>e_1(t)=200V\ </math>,, <math>e_2(t)=15V\ </math>, | ||
<hr width="100%"> | |||
Zad. 4 | |||
Wykazać, że rezystancja wejściowa tranzystora bipolarnego <math>r_{BE}</math>, jeżeli temperatura złącza jest stała, jest odwrotnie proporcjonalna do natężenia prądu bazy. | |||
<hr width="100%"> | |||
Zad. 5 | |||
Wyznaczyć wzmocnienie napięciowe w układzie wzmacniacza jak na rysunku. Dane: <math>U_{CC}</math>, <math>R_1</math>, <math>R_2</math>, <math>R_3</math>, <math>S</math>, <math>r_{DS}</math>. | |||
[[Grafika:PEE_Zadania_egz_zes2_5.jpg]] | |||
<hr width="100%"> | <hr width="100%"> | ||
Aktualna wersja na dzień 12:02, 5 wrz 2023
Zadania egzaminacyjne
Zestaw 1
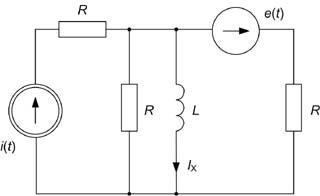
Zad. 1
Obliczyć prąd , w obwodzie metodą Thevenina
Dane: , , ,
Zad. 2
Obliczyć przebieg w stanie nieustalonym po przełączeniu w obwodzie
Dane: ,, ,, , ,
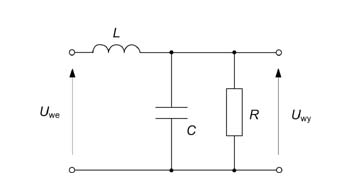
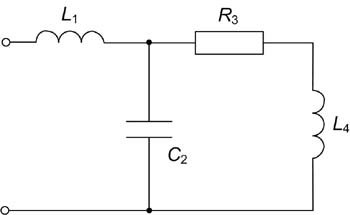
Zad. 3
Określić transmitancję napięciową, odpowiedź impulsową i charakterystyki częstotliwościowe
Dane: , ,, ,
Zad. 4
Wykazać, że kondunktancja dynamiczna diody półprzewodnikowej jest wprost proporcjonalna do natężenia prądu przewodzenia .
Zad. 5
Wyznaczyć wzmocnienie napięciowe w układzie wzmacniacza jak na rysunku. Dane: , , , , , , , , .
Zestaw 2
Zad. 1
Narysować wykres wektorowy dla obwodu
Zad. 2
Obliczyć moce elementów w obwodzie i sporządzić bilans mocy.
Dane: , , , ,
Zad. 3
Obliczyć przebieg w stanie nieustalonym po przełączeniu w obwodzie
Dane: , , ,, ,, ,
Zad. 4
Wykazać, że rezystancja wejściowa tranzystora bipolarnego , jeżeli temperatura złącza jest stała, jest odwrotnie proporcjonalna do natężenia prądu bazy.
Zad. 5
Wyznaczyć wzmocnienie napięciowe w układzie wzmacniacza jak na rysunku. Dane: , , , , , .