Języki, automaty i obliczenia/Wykład 1: Słowa, katenacja - elementy teorii półgrup, półgrupy i monoidy wolne: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „,...,” na „,\ldots,” |
||
| (Nie pokazano 26 wersji utworzonych przez 5 użytkowników) | |||
| Linia 1: | Linia 1: | ||
__FORCETOC__ | |||
==Definicje, oznaczenia i podstawowe własności== | ==Definicje, oznaczenia i podstawowe własności== | ||
Przyjmijmy, że <math>\mathbb{N}=\left\{ 1,2,\ldots \right\}</math> oznacza zbiór liczb naturalnych, | |||
Przyjmijmy, że <math>\mathbb{N}=\left\{ 1,2,\ldots \right\} | a <math>\mathbb{N}_{0}</math> zbiór liczb naturalnych wraz z '''0'''. Przypomnimy teraz podstawowe wiadomości z wykładu Algebra Liniowa dotyczące struktur algebraicznych, a dokładniej struktur najprostszych, półgrup i monoidów, posiadających jedno tylko działanie. | ||
a <math>\mathbb{N}_{0} </math> zbiór liczb naturalnych wraz z '''0'''. Przypomnimy teraz podstawowe wiadomości z wykładu Algebra Liniowa dotyczące struktur algebraicznych, a dokładniej struktur najprostszych, półgrup i monoidów, posiadających jedno tylko działanie. | |||
{{definicja|1.1|| | {{definicja|1.1|| | ||
Zbiór <math>S </math>, w którym określone jest działanie łączne, to znaczy spełniające warunek | Zbiór <math>S</math>, w którym określone jest działanie łączne, to znaczy spełniające warunek | ||
<center><math>\forall x,y,z \in S \;\;\; x\cdot (y\cdot z)=(x\cdot y)\cdot z</math></center> | <center><math>\forall x,y,z \in S \;\;\; x\cdot (y\cdot z)=(x\cdot y)\cdot z</math></center> | ||
| Linia 14: | Linia 14: | ||
{{przyklad|1.1|| | {{przyklad|1.1|| | ||
Zbiór liczb naturalnych z dodawaniem <math>(\mathbb{N},+) </math> tworzy półgrupę. | Zbiór liczb naturalnych z dodawaniem <math>(\mathbb{N},+)</math> tworzy półgrupę. | ||
}} | }} | ||
{{definicja|1.2|| | {{definicja|1.2|| | ||
Półgrupę <math>M </math>, w której istnieje element neutralny działania, to znaczy element <math>1_{M}\in M </math> spełniający warunek | Półgrupę <math>M</math>, w której istnieje element neutralny działania, to znaczy element <math>1_{M}\in M</math> spełniający warunek | ||
<center><math> \forall x\in M \;\;\;1_M \cdot x=x\cdot 1_M=x</math></center> | <center><math>\forall x\in M \;\;\;1_M \cdot x=x\cdot 1_M=x</math></center> | ||
nazywamy '''monoidem'''. | nazywamy '''monoidem'''. | ||
| Linia 26: | Linia 26: | ||
{{przyklad|1.2|| | {{przyklad|1.2|| | ||
: (1) Zbiór liczb naturalnych z mnożeniem <math>(\mathbb{N},\cdot ,1) </math> jest monoidem. | : (1) Zbiór liczb naturalnych z mnożeniem <math>(\mathbb{N},\cdot ,1)</math> jest monoidem. | ||
: (2) Zbiór liczb naturalnych z zerem <math>(\mathbb{N}_{0},+,0) </math> jest monoidem ze względu na dodawanie. | : (2) Zbiór liczb naturalnych z zerem <math>(\mathbb{N}_{0},+,0)</math> jest monoidem ze względu na dodawanie. | ||
: (3) Monoidem jest <math>(A^A,\circ,id_A)</math> - zbiór odwzorowań dowolnego zbioru <math>{A}</math> w siebie ze składaniem jako działaniem i identycznością jako elementem neutralnym. | : (3) Monoidem jest <math>(A^A,\circ,id_A)</math> - zbiór odwzorowań dowolnego zbioru <math>{A}</math> w siebie ze składaniem jako działaniem i identycznością jako elementem neutralnym. | ||
| Linia 39: | Linia 39: | ||
Dla uproszczenia notacji będziemy opuszczać kropkę "<math>\cdot</math>" oznaczającą działanie oraz | Dla uproszczenia notacji będziemy opuszczać kropkę "<math>\cdot</math>" oznaczającą działanie oraz | ||
używać nazwy "jedynka" na element neutralny. Jeśli nie będzie zaznaczone inaczej, to | używać nazwy "jedynka" na element neutralny. Jeśli nie będzie zaznaczone inaczej, to | ||
<math>(\mathbf{S},\cdot ) </math> będzie oznaczać półgrupę, a <math>(\mathbf{M},\cdot ,\, 1_{\mathbf{M}}) </math> monoid. Ze względu na łączność działania zarówno w półgrupie, jak i w monoidzie iloczyn <math>x_1...x_n | <math>(\mathbf{S},\cdot )</math> będzie oznaczać półgrupę, a <math>(\mathbf{M},\cdot ,\, 1_{\mathbf{M}})</math> monoid. Ze względu na łączność działania zarówno w półgrupie, jak i w monoidzie iloczyn <math>x_1...x_n</math>, a także <math>x^n=x...x</math> (n razy) jest określony jednoznacznie bez potrzeby wprowadzania nawiasów. Dla dowolnych liczb naturalnych <math>m,n\in \mathbb{N}</math> zachodzą wzory | ||
<center><math>\begin{array} {c} | <center><math>\begin{array} {c} | ||
| Linia 46: | Linia 46: | ||
\end{array}</math></center> | \end{array}</math></center> | ||
Dla dowolnego <math>x \in M</math> przyjmujemy z definicji <center><math>x^0 = 1_{M} | Dla dowolnego <math>x \in M</math> przyjmujemy z definicji <center><math>x^0 = 1_{M}</math>.</center> | ||
Strukturę monoidu <math> M</math> przenosimy na zbiór potęgowy <math>\mathcal{P}(M) </math> | Strukturę monoidu <math>M</math> przenosimy na zbiór potęgowy <math>\mathcal{P}(M)</math> | ||
wszystkich podzbiorów monoidu <math>M </math>, określając dla dowolnych <math>A,B \in\mathcal{P}(M) </math> działanie | wszystkich podzbiorów monoidu <math>M</math>, określając dla dowolnych <math>A,B \in\mathcal{P}(M)</math> działanie | ||
<center><math> | <center><math> | ||
A\cdot B=\left\{ x\in {\bf M}\ | A\cdot B=\left\{ x\in {\bf M}\ :\ \exists a\in A,\ \exists b\in B,\ x=ab\right\} | ||
</math></center> | </math></center> | ||
<math>(\mathcal{P}(M),\cdot, \{1_{M}\}) </math> jest monoidem. <br> | <math>(\mathcal{P}(M),\cdot, \{1_{M}\})</math> jest monoidem. <br> | ||
Podobnie przenosimy strukturę półgrupy z <math>S </math> na <math>\mathcal{P}(S) </math>.<br> | Podobnie przenosimy strukturę półgrupy z <math>S</math> na <math>\mathcal{P}(S)</math>.<br> | ||
Dla dowolnego podzbioru monoidu | Dla dowolnego podzbioru monoidu | ||
(półgrupy) i dla dowolnej liczby <math>n \in \mathbb{N} </math> zapis <math>A^n</math> oznacza n-krotny iloczyn | (półgrupy) i dla dowolnej liczby <math>n \in \mathbb{N}</math> zapis <math>A^n</math> oznacza n-krotny iloczyn | ||
zbioru <math>\ | zbioru <math>\text{A}</math> przez siebie rozumiany w powyższym sensie. <br> | ||
W szczególności <math>A^{1}=A | W szczególności <math>A^{1}=A</math> | ||
W przypadku monoidu przyjmujemy z definicji <center><math>A^0 = \{ 1_{ M} \} | W przypadku monoidu przyjmujemy z definicji <center><math>A^0 = \{ 1_{ M} \}</math>.</center> | ||
{{definicja|1.3|| | {{definicja|1.3|| | ||
'''Homomorfizmem''' '''półgrup''' <math>(S,\cdot)\;,\;\;(S',*)</math> nazywamy | '''Homomorfizmem''' '''półgrup''' <math>(S,\cdot)\;,\;\;(S',*)</math> nazywamy | ||
odwzorowanie | odwzorowanie | ||
<math>h~:S~\longmapsto~S'</math> takie, że <center><math> \forall x,y \in S \;\;\; h(x\cdot y)=h(x)*h(y) | <math>h~:S~\longmapsto~S'</math> takie, że <center><math>\forall x,y \in S \;\;\; h(x\cdot y)=h(x)*h(y)</math>.</center> | ||
'''Homomorfizmem monoidów''' <math>(M,\cdot,1_{M}),\;(M',*,1_{M'})</math> nazywamy | '''Homomorfizmem monoidów''' <math>(M,\cdot,1_{M}),\;(M',*,1_{M'})</math> nazywamy | ||
odwzorowanie <math>h:M \longmapsto M'</math> | odwzorowanie <math>h:M \longmapsto M'</math> | ||
takie, że <center><math> \forall x,y \in {M} \;\;\;h(x\cdot y)=h(x)*h(y) \;\;\; i \;\;\; h(1_{M})= 1_{M'} | takie, że <center><math>\forall x,y \in {M} \;\;\;h(x\cdot y)=h(x)*h(y) \;\;\; i \;\;\; h(1_{M})= 1_{M'}</math>.</center> | ||
}} | }} | ||
{{przyklad|1.3|| | {{przyklad|1.3|| | ||
Odwzorowanie <math>h:{\mathbb{Z}}_{mod\, 3}\longrightarrow {\mathbb{Z}}_{mod\,6} </math> | Odwzorowanie <math>h:{\mathbb{Z}}_{mod\, 3}\longrightarrow {\mathbb{Z}}_{mod\,6}</math> | ||
takie, że | takie, że | ||
| Linia 81: | Linia 81: | ||
2\longrightarrow 2 | 2\longrightarrow 2 | ||
\end{array} | \end{array} | ||
\end{array} </math></center> | \end{array}</math></center> | ||
jest homomorfizmem półgrupy <math>(\mathbb{Z}_{mod\,3},\cdot ) </math> w półgrupę | jest homomorfizmem półgrupy <math>(\mathbb{Z}_{mod\,3},\cdot )</math> w półgrupę | ||
<math>(\mathbb{Z}_{mod\,6},\cdot ) </math>, ale nie jest homomorfizmem monoidu <math>(\mathbb{Z}_{mod\,3},\cdot,1 ) </math> w monoid | <math>(\mathbb{Z}_{mod\,6},\cdot )</math>, ale nie jest homomorfizmem monoidu <math>(\mathbb{Z}_{mod\,3},\cdot,1 )</math> w monoid | ||
<math>(\mathbb{Z}_{mod\,6},\cdot,1 ) </math>, bo wartością '''1''' z monoidu <math>(\mathbb{Z}_{mod\,3},\cdot, 1 ) </math> | <math>(\mathbb{Z}_{mod\,6},\cdot,1 )</math>, bo wartością '''1''' z monoidu <math>(\mathbb{Z}_{mod\,3},\cdot, 1 )</math> | ||
nie jest jedynka monoidu <math>(\mathbb{Z}_{mod\,6},\cdot,1 ) </math>. | nie jest jedynka monoidu <math>(\mathbb{Z}_{mod\,6},\cdot,1 )</math>. | ||
}} | }} | ||
{{ | {{zainteresowani||| | ||
'''Definicja 1.4.''' | |||
Niech <math>(S,\cdot),\;\;(M,\cdot,1_{M})</math> będą odpowiednio dowolną półgrupą, monoidem. | Niech <math>(S,\cdot),\;\;(M,\cdot,1_{M})</math> będą odpowiednio dowolną półgrupą, monoidem. | ||
* <math>(T,\cdot)</math> nazywamy '''podpółgrupą '''<math>{S}</math> wtedy i tylko wtedy, gdy <math>T\subset S</math> i <math>T^2 \subset T | * <math>(T,\cdot)</math> nazywamy '''podpółgrupą '''<math>{S}</math> wtedy i tylko wtedy, gdy <math>T\subset S</math> i <math>T^2 \subset T</math>. | ||
* <math>(N,\cdot,1_{M})</math> nazywamy '''podmonoidem''' <math>M</math> wtedy i tylko wtedy, gdy <math>N</math> jest podpółgrupą <math>M</math> i <math>1_{M} \in N | * <math>(N,\cdot,1_{M})</math> nazywamy '''podmonoidem''' <math>M</math> wtedy i tylko wtedy, gdy <math>N</math> jest podpółgrupą <math>M</math> i <math>1_{M} \in N</math> | ||
'''Przykład 1.4.''' | |||
<math>(\mathbb{Z}_{mod\,6},\cdot ) </math> jest monoidem. Podzbiór <math>\{2,4\} </math>, jako zamknięty na działanie <math>\cdot _{mod\, 6} </math>, tworzy podpółgrupę <math>\mathbb{Z}_{mod\, 6} </math>. <math>(\{2,4\},\cdot _{mod\, 6}) </math> jest monoidem z | <math>(\mathbb{Z}_{mod\,6},\cdot )</math> jest monoidem. Podzbiór <math>\{2,4\}</math>, jako zamknięty na działanie <math>\cdot _{mod\, 6}</math>, tworzy podpółgrupę <math>\mathbb{Z}_{mod\, 6}</math>. <math>(\{2,4\},\cdot _{mod\, 6})</math> jest monoidem z | ||
<math>4 </math> jako elementem neutralnym, ale nie podmonoidem <math>\mathbb{Z}_{mod\, 6} </math>. | <math>4</math> jako elementem neutralnym, ale nie podmonoidem <math>\mathbb{Z}_{mod\, 6}</math>. | ||
Niech <math>X</math> będzie dowolnym podzbiorem monoidu <math>M</math>. Zbiór | Niech <math>X</math> będzie dowolnym podzbiorem monoidu <math>M</math>. Zbiór | ||
| Linia 117: | Linia 119: | ||
:2. Dla dowolnego monoidu istnieje zbiór generatorów, jest nim w szczególności zbiór <math>{M}</math>. | :2. Dla dowolnego monoidu istnieje zbiór generatorów, jest nim w szczególności zbiór <math>{M}</math>. | ||
Podobnie dla dowolnego podzbioru <math>X </math> półgrupy <math>{S}</math> zbiór | Podobnie dla dowolnego podzbioru <math>X</math> półgrupy <math>{S}</math> zbiór | ||
| Linia 124: | Linia 126: | ||
jest podpółgrupą <math>{S}</math> i to najmniejszą w sensie inkluzji zawierającą zbiór <math>X</math>. <br> Powyższe uwagi dotyczące zbioru generatorów monoidów przenoszą się odpowiednio dla półgrup. | jest podpółgrupą <math>{S}</math> i to najmniejszą w sensie inkluzji zawierającą zbiór <math>X</math>. <br> Powyższe uwagi dotyczące zbioru generatorów monoidów przenoszą się odpowiednio dla półgrup. | ||
W monoidzie <math>(\mathbb{N}_{0},+,0) </math> podmonoid generowany przez zbiór generatorów | '''Przykład 1.5.''' | ||
<math>X=\{2\} </math> składa się z liczb parzystych i nieujemnych. | |||
W monoidzie <math>(\mathbb{N}_{0},+,0)</math> podmonoid generowany przez zbiór generatorów | |||
<math>X=\{2\}</math> składa się z liczb parzystych i nieujemnych. | |||
}} | }} | ||
{{definicja|1.5|| | {{definicja|1.5|| | ||
Niech <math>S </math> będzie półgrupą. Relację równoważności <math>\rho \subset {S}^2 </math> nazywamy: | Niech <math>S</math> będzie półgrupą. Relację równoważności <math>\rho \subset {S}^2</math> nazywamy: | ||
: (1) '''prawą kongruencją''' w półgrupie <math>{S}</math>, jeśli <center><math> \forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow xz\;\rho\; yz | : (1) '''prawą kongruencją''' w półgrupie <math>{S}</math>, jeśli <center><math>\forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow xz\;\rho\; yz</math>,</center> | ||
: (2) '''lewą kongruencją''' w półgrupie <math>{S}</math>, jeśli <center><math> \forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow zx\;\rho\; zy | : (2) '''lewą kongruencją''' w półgrupie <math>{S}</math>, jeśli <center><math>\forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow zx\;\rho\; zy</math>,</center> | ||
: (3) '''kongruencją''', jeśli jest prawą i lewą kongruencją, tzn. <center><math> \forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow zx\;\rho\; zy \;\; i \;\; xz\;\rho\; yz | : (3) '''kongruencją''', jeśli jest prawą i lewą kongruencją, tzn. <center><math>\forall x,y,z \in {S} \;\;\; x\;\rho\; y \Rightarrow zx\;\rho\; zy \;\; i \;\; xz\;\rho\; yz</math>.</center> | ||
Zastępując w powyższej definicji półgrupę <math>S </math> na monoid <math>M </math> otrzymamy dualnie pojęcia prawej kongruencji, | Zastępując w powyższej definicji półgrupę <math>S</math> na monoid <math>M</math> otrzymamy dualnie pojęcia prawej kongruencji, | ||
lewej kongruencji i kongruencji zdefiniowane w monoidzie. <br> | lewej kongruencji i kongruencji zdefiniowane w monoidzie. <br> | ||
Mając kongruencję <math>\rho</math> określoną w półgrupie <math>{S}</math> (monoidzie | Mając kongruencję <math>\rho</math> określoną w półgrupie <math>{S}</math> (monoidzie | ||
<math>M) </math> możemy utworzyć półgrupę ilorazową <math>{S}/\rho</math> (monoid ilorazowy <math>{M}/\rho</math>), której elementami | <math>M)</math> możemy utworzyć półgrupę ilorazową <math>{S}/\rho</math> (monoid ilorazowy <math>{M}/\rho</math>), której elementami | ||
są klasy równoważności (abstrakcji) relacji <math>\rho | są klasy równoważności (abstrakcji) relacji <math>\rho</math>.<br> | ||
Dla dowolnego homomorfizmu półgrup <math>h:{S}\longmapsto {S}'</math> określamy relację | Dla dowolnego homomorfizmu półgrup <math>h:{S}\longmapsto {S}'</math> określamy relację | ||
<center><math>Ker_h = \{ (x,y)\in {S}\times {S}\;:\;\; h(x)=h(y) \} | <center><math>Ker_h = \{ (x,y)\in {S}\times {S}\;:\;\; h(x)=h(y) \}</math>.</center> Relacja <math>Ker_h</math> jest kongruencją w półgrupie <math>{S}</math>. <br> | ||
Dla homomorfizmu monoidów <math>h:{M}\longmapsto {M}'</math> relacja <math>Ker_h</math> jest kongruencją | Dla homomorfizmu monoidów <math>h:{M}\longmapsto {M}'</math> relacja <math>Ker_h</math> jest kongruencją | ||
w monoidzie <math>M </math>. | w monoidzie <math>M</math>. | ||
Podstawowe twierdzenie o epimorfizmie dla struktur algebraicznych przyjmuje dla półgrup i odpowiednio dla monoidów następującą postać. | Podstawowe twierdzenie o epimorfizmie dla struktur algebraicznych przyjmuje dla półgrup i odpowiednio dla monoidów następującą postać. | ||
| Linia 156: | Linia 158: | ||
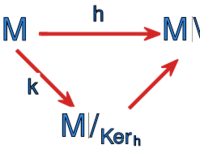
{{twierdzenie|1.1|| | {{twierdzenie|1.1|| | ||
Niech <math>h:{S}\longmapsto {S}'</math> będzie dowolnym epimorfizmem półgrupy <math>{S}</math> na półgrupę <math>{S}' | Niech <math>h:{S}\longmapsto {S}'</math> będzie dowolnym epimorfizmem półgrupy <math>{S}</math> na półgrupę <math>{S}'</math>. Półgrupa <math>{S}'</math> jest | ||
izomorficzna z półgrupą ilorazową <math>{S}/_{Ker_h}</math>. | izomorficzna z półgrupą ilorazową <math>{S}/_{Ker_h}</math>. | ||
}} | }} | ||
<center> | <center> | ||
<div class="thumb"><div style="width: | <div class="thumb"><div style="width:200px;"><flash>file=Ja-1-1.swf|width=200|height=200</flash> | ||
<flash>file=Ja-1-1.swf|width= | <div.thumbcaption>Rysunek 1</div> | ||
<div.thumbcaption> | |||
</div></div> | </div></div> | ||
</center> | </center> | ||
{{twierdzenie|1.2|| | {{twierdzenie|1.2|| | ||
Niech <math>h:{M}\longmapsto {M}'</math> będzie dowolnym epimorfizmem monoidu <math>{M}</math> na | Niech <math>h:{M}\longmapsto {M}'</math> będzie dowolnym epimorfizmem monoidu <math>{M}</math> na | ||
monoid <math>{M}' | monoid <math>{M}'</math>. Monoid <math>{M}'</math> jest izomorficzny z monoidem ilorazowym <math>{M}/_{Ker_h}</math>. | ||
}} | }} | ||
<center> | <center> | ||
[[File:Ja-1-2.svg|200x200px|thumb|center|Rysunek 2]] | |||
</center> | </center> | ||
| Linia 187: | Linia 186: | ||
'''Wolnym monoidem''' <math>A^*</math> '''o bazie''' <math>{A}</math> nazywamy zbiór wszystkich skończonych ciągów: | '''Wolnym monoidem''' <math>A^*</math> '''o bazie''' <math>{A}</math> nazywamy zbiór wszystkich skończonych ciągów: | ||
<center> | <center> | ||
<math>A^*=\{ (a_1, | <math>A^*=\{ (a_1,\ldots,a_n)\;\;:\;\;n \geq 0\;\;,\;\;a_i \in A \}</math></center> wraz z działaniem | ||
<center> | <center> | ||
<math> (a_1, | <math>(a_1,\ldots,a_n)\cdot (b_1,\ldots,b_m) = (a_1,\ldots,a_n,b_1,\ldots,b_m)</math></center> | ||
Ciąg pusty <math>{(n=0)}</math> oznaczamy symbolem "'''1'''" i z definicji jest on elementem neutralnym określonego powyżej | Ciąg pusty <math>{(n=0)}</math> oznaczamy symbolem "'''1'''" i z definicji jest on elementem neutralnym określonego powyżej | ||
działania, nazywanego '''katenacją''' lub '''konkatenacją'''. | działania, nazywanego '''katenacją''' lub '''konkatenacją'''. | ||
Przyjmujemy następującą konwencję zapisu: <center><math>(a)\equiv a,\;\;\;(a_1, | Przyjmujemy następującą konwencję zapisu: <center><math>(a)\equiv a,\;\;\;(a_1,\ldots,a_n)\equiv a_1...a_n</math>.</center> W oparciu o nią możemy stwierdzić inkluzję <math>A\subset A^*</math>. | ||
}} | }} | ||
{{ | {{zainteresowani||| | ||
Ta inkluzja uzasadnia użycie wprowadzonego wcześniej | Ta inkluzja uzasadnia użycie wprowadzonego wcześniej oznaczenia <math>A^*</math>.<br> | ||
<math>A^*</math> jest najmniejszym podmonoidem | <math>A^*</math> jest najmniejszym podmonoidem | ||
monoidu <math>A^*</math> zawierającym <math>A | monoidu <math>A^*</math> zawierającym <math>A</math>. | ||
}} | }} | ||
{{definicja|2.2|| | {{definicja|2.2|| | ||
| Linia 206: | Linia 205: | ||
''' Wolną półgrupą''' <math>A^+</math> '''nad alfabetem''' | ''' Wolną półgrupą''' <math>A^+</math> '''nad alfabetem''' | ||
<math>A</math> nazywamy zbiór wszystkich skończonych ciągów: | <math>A</math> nazywamy zbiór wszystkich skończonych ciągów: | ||
<center><math>A^+=\{ (a_1, | <center><math>A^+=\{ (a_1,\ldots,a_n)\;\;:\;\;n > 0,\;\;\;a_i \in A \}</math></center> wraz z działaniem katenacji. | ||
Używa się także określeń - wolny monoid o bazie <math>A </math> | Używa się także określeń - wolny monoid o bazie <math>A</math> | ||
i wolna półgrupa o bazie <math>A </math>. | i wolna półgrupa o bazie <math>A</math>. | ||
* Elementy alfabetu <math>{A}</math> nazywamy '''literami'''. | * Elementy alfabetu <math>{A}</math> nazywamy '''literami'''. | ||
* Elementy wolnego monoidu (półgrupy) nazywamy '''słowami''' i oznaczać bedziemy w wykładzie najczęściej literami <math>u,v,w </math>. | * Elementy wolnego monoidu (półgrupy) nazywamy '''słowami''' i oznaczać bedziemy w wykładzie najczęściej literami <math>u,v,w</math>. | ||
* Dowolny podzbiór wolnego monoidu (półgrupy) nazywamy '''językiem'''. | * Dowolny podzbiór wolnego monoidu (półgrupy) nazywamy '''językiem'''. | ||
| Linia 229: | Linia 228: | ||
{{definicja|2.3|| | {{definicja|2.3|| | ||
Niech <math>A </math> i <math>B </math> będą alfabetami. '''Podstawieniem''' nazywamy homomorfizm | Niech <math>A</math> i <math>B</math> będą alfabetami. '''Podstawieniem''' nazywamy homomorfizm | ||
<center><math>s:A^{*}\longrightarrow \mathcal{P}(B^{*}) | <center><math>s:A^{*}\longrightarrow \mathcal{P}(B^{*})</math>.</center> | ||
Odwzorowanie <math>s </math> jako homomorfizm monoidu <math>A^{*} </math> w monoid <math>\mathcal{P}(B^{*}) </math> spełnia dla dowolnych <math>v,w\in A^{*} </math> równość <center><math> s(vw)=s(v)s(w) \;\; \text{oraz}\;\; s(1)=\{1\} | Odwzorowanie <math>s</math> jako homomorfizm monoidu <math>A^{*}</math> w monoid <math>\mathcal{P}(B^{*})</math> spełnia dla dowolnych <math>v,w\in A^{*}</math> równość <center><math>s(vw)=s(v)s(w) \;\; \text{oraz}\;\; s(1)=\{1\}</math></center> | ||
}} | }} | ||
<span id="zainteresowani_2"> | |||
</span> | |||
{{zainteresowani||| | |||
'''Twierdzenie 2.1.''' | |||
Niech <math>{A}</math> oznacza dowolny zbiór, a <math>({M},\cdot,1_{M})</math> dowolny monoid. | Niech <math>{A}</math> oznacza dowolny zbiór, a <math>({M},\cdot,1_{M})</math> dowolny monoid. | ||
| Linia 242: | Linia 244: | ||
: (1) Każde odwzorowanie | : (1) Każde odwzorowanie | ||
<center><math>f:A\longmapsto {M} </math></center> | <center><math>f:A\longmapsto {M}</math></center> | ||
: daje się jednoznacznie rozszerzyć do homomorfizmu <center><math>h:A^*\longmapsto {M} | : daje się jednoznacznie rozszerzyć do homomorfizmu <center><math>h:A^*\longmapsto {M}</math>.</center> | ||
: (2) Homomorfizm <math>{h}</math> jest epimorfizmem wtedy i tylko wtedy, gdy <math>f(A)</math> jest zbiorem generatorów <math>{M} | : (2) Homomorfizm <math>{h}</math> jest epimorfizmem wtedy i tylko wtedy, gdy <math>f(A)</math> jest zbiorem generatorów <math>{M}</math>. | ||
''' | '''Dowód''' | ||
: (1) Przyjmujemy | : (1) Przyjmujemy | ||
<center><math>\forall\; a_1...a_n \in A^+\;\;\;\;h(a_1...a_n)=f(a_1)...f(a_n) \;\;\;\text{oraz}\; \;\;h(1)=1_{M} | <center><math>\forall\; a_1...a_n \in A^+\;\;\;\;h(a_1...a_n)=f(a_1)...f(a_n) \;\;\;\text{oraz}\; \;\;h(1)=1_{M}</math>.</center> | ||
: Tak określone <math>h</math> jest jedynym rozszerzeniem przekształcenia <math>f</math>. | : Tak określone <math>h</math> jest jedynym rozszerzeniem przekształcenia <math>f</math>. | ||
| Linia 258: | Linia 260: | ||
Przyjmując w powyższym twierdzeniu jako <math>A</math> dowolny zbiór generatorów monoidu <math>{M}</math> oraz jako funkcję <math>f</math> włożenie <math>id_{A}:A\longrightarrow \mathbf{M} </math> równe identyczności na <math>{A} </math> dochodzimy do następującego wniosku. | Przyjmując w powyższym twierdzeniu jako <math>A</math> dowolny zbiór generatorów monoidu <math>{M}</math> oraz jako funkcję <math>f</math> włożenie <math>id_{A}:A\longrightarrow \mathbf{M}</math> równe identyczności na <math>{A}</math> dochodzimy do następującego wniosku. | ||
'''Wniosek 2.1.''' | |||
Każdy monoid <math>{M}</math> jest homomorficznym obrazem wolnego monoidu <math>A^*</math> utworzonego nad dowolnym zbiorem generatorów <math>{M} | Każdy monoid <math>{M}</math> jest homomorficznym obrazem wolnego monoidu <math>A^*</math> utworzonego nad dowolnym zbiorem generatorów <math>{M}</math>. | ||
Udowodnione powyżej twierdzenie oraz sformułowany wniosek prawdziwy jest również dla półgrup.<br> | Udowodnione powyżej twierdzenie oraz sformułowany wniosek prawdziwy jest również dla półgrup.<br> | ||
Powyższe rezultaty określają rolę wolnych monoidów (półgrup) w klasie wszystkich monoidów (półgrup). | Powyższe rezultaty określają rolę wolnych monoidów (półgrup) w klasie wszystkich monoidów (półgrup). | ||
Monoid <math>{M}</math> jest wolny wtedy i tylko wtedy, gdy każdy element <math>m \in {S}={M}\setminus \{1\}</math> ma jednoznaczny rozkład na elementy zbioru <math>A={S}\setminus {S}^2 | '''Twierdzenie 2.2.''' | ||
Monoid <math>{M}</math> jest wolny wtedy i tylko wtedy, gdy każdy element <math>m \in {S}={M}\setminus \{1\}</math> ma jednoznaczny rozkład na elementy zbioru <math>A={S}\setminus {S}^2</math>. | |||
'''Dowod''' | '''Dowod''' | ||
Załóżmy, że monoid <math>{M}</math> jest wolny, to znaczy <math>{M}=B^*</math> dla pewnego zbioru (bazy) <math>B | Załóżmy, że monoid <math>{M}</math> jest wolny, to znaczy <math>{M}=B^*</math> dla pewnego zbioru (bazy) <math>B</math>. <br> | ||
:* Udowodnimy, że <math>A{}</math> jest zbiorem generatorów monoidu <math>M</math>. W tym celu wykażemy, że zachodzi inkluzja <center><math>{S}\subset ({S}\setminus {S}^2)^+ | :* Udowodnimy, że <math>A{}</math> jest zbiorem generatorów monoidu <math>M</math>. W tym celu wykażemy, że zachodzi inkluzja <center><math>{S}\subset ({S}\setminus {S}^2)^+</math>.</center> Dowód przeprowadzimy nie wprost. Załóżmy więc, że | ||
<center><math>{S}\setminus ({S}\setminus {S}^2)^+ \neq \emptyset</math></center> | <center><math>{S}\setminus ({S}\setminus {S}^2)^+ \neq \emptyset</math></center> | ||
: i niech <math>{m}</math> oznacza element z tego zbioru o najmniejszej długości w <math>B^* | : i niech <math>{m}</math> oznacza element z tego zbioru o najmniejszej długości w <math>B^*</math>. <br> Wnioskujemy stąd kolejno: | ||
<center> | <center> | ||
<math>m\notin ({S}\setminus {S}^2)^+</math><br> | <math>m\notin ({S}\setminus {S}^2)^+</math><br> | ||
| Linia 283: | Linia 285: | ||
<math>m=s_1s_2</math> dla pewnych <math>s_1,s_2\in {S}</math>, | <math>m=s_1s_2</math> dla pewnych <math>s_1,s_2\in {S}</math>, | ||
</center> | </center> | ||
: przy czym długość <math>s_1,s_2</math> jest silnie mniejsza niż długość <math>m | : przy czym długość <math>s_1,s_2</math> jest silnie mniejsza niż długość <math>m</math>. Zatem | ||
<center><math>s_1,s_2 \in ({S}\setminus {S}^2)^+ | <center><math>s_1,s_2 \in ({S}\setminus {S}^2)^+ | ||
| Linia 290: | Linia 292: | ||
: a to oznacza, że | : a to oznacza, że | ||
<center><math>m=s_1s_2 \in ({S}\setminus {S}^2)^+ | <center><math>m=s_1s_2 \in ({S}\setminus {S}^2)^+</math></center> | ||
</math></center> | |||
: Otrzymana sprzeczność kończy dowód faktu, że <math>A={S}\setminus {S}^2</math> jest zbiorem generatorów monoidu <math>{M} | : Otrzymana sprzeczność kończy dowód faktu, że <math>A={S}\setminus {S}^2</math> jest zbiorem generatorów monoidu <math>{M}</math>. | ||
:* Pokażemy teraz, że <math>A \subset B | :* Pokażemy teraz, że <math>A \subset B</math>. <br>Niech <math>m=b_1...b_k \in {S}\setminus {S}^2</math> dla pewnych <math>b_i \in B</math>, <math>i=1,\ldots,k</math>. <br>Jeśli <math>k>1</math>, to <math>m\in {S}^2</math>, co jest sprzeczne z wyborem <math>m</math>. Zatem <math>{k=1}</math>, co implikuje <math>A\subset B</math>. | ||
Z definicji wolnego monoidu wynika jednoznaczność rozkładu na elementy z bazy <math>B</math>, a to pociąga za sobą jednoznaczność rozkładu na elementy z podzbioru <math>A={S}\setminus {S}^2 | Z definicji wolnego monoidu wynika jednoznaczność rozkładu na elementy z bazy <math>B</math>, a to pociąga za sobą jednoznaczność rozkładu na elementy z podzbioru <math>A={S}\setminus {S}^2</math>.<br> | ||
Niech teraz <math>{M}</math> oznacza monoid z jednoznacznością rozkładu na elementy zbioru <math>A~=~S~\setminus~S^2</math>. Rozszerzamy identyczność <math>id_A:A\longmapsto {M}</math> do homomorfizmu <math>h:A^*\longmapsto {M} | Niech teraz <math>{M}</math> oznacza monoid z jednoznacznością rozkładu na elementy zbioru <math>A~=~S~\setminus~S^2</math>. Rozszerzamy identyczność <math>id_A:A\longmapsto {M}</math> do homomorfizmu <math>h:A^*\longmapsto {M}</math>. Z założenia wynika, że każdy element <math>m \in {S}</math> można przedstawić jako iloczyn | ||
<center><math>m=a_1...a_n \;\;\; gdzie \;\;\;a_i \in A \;\;\; | <center><math>m=a_1...a_n \;\;\; gdzie \;\;\;a_i \in A \;\;\; | ||
dla \;\;\; i=1, | dla \;\;\; i=1,\ldots,n</math>.</center> | ||
Zatem | Zatem | ||
<center><math>h(a_1...a_n)=h(a_1)...h(a_n) a_1...a_n | <center><math>h(a_1...a_n)=h(a_1)...h(a_n) a_1...a_n</math>.</center> | ||
Homomorfizm <math>h</math> jest izomorfizmem, więc monoid <math>{M}</math> jako izomorficzny z <math>A^*</math> jest wolny. | Homomorfizm <math>h</math> jest izomorfizmem, więc monoid <math>{M}</math> jako izomorficzny z <math>A^*</math> jest wolny. | ||
Powyższe twierdzenie posiada swój odpowiednik dla wolnych półgrup. | Powyższe twierdzenie posiada swój odpowiednik dla wolnych półgrup. | ||
'''Twierdzenie 2.3.''' | |||
Półgrupa <math>{S}</math> jest wolna wtedy i tylko wtedy, gdy każdy element <math>x \in {S}</math> ma jednoznaczny rozkład na elementy zbioru <math>{S}\setminus {S}^2 | |||
Półgrupa <math>{S}</math> jest wolna wtedy i tylko wtedy, gdy każdy element <math>x \in {S}</math> ma jednoznaczny rozkład na elementy zbioru <math>{S}\setminus {S}^2</math>. | |||
'''Wniosek 2.2.''' | |||
Baza wolnego monoidu (półgrupy) jest minimalym zbiorem generatorów. | Baza wolnego monoidu (półgrupy) jest minimalym zbiorem generatorów. | ||
: (1) Półgrupa <math>(\mathbb{N},+ ) </math> jest wolna. Każdy jej element można jednoznacznie zapisać jako sumę jedynek - <math>\mathbb{N}\setminus (\mathbb{N}+\mathbb{N})=\left\{ 1\right\} | '''Przyklad 2.2.''' | ||
: (1) Półgrupa <math>(\mathbb{N},+ )</math> jest wolna. Każdy jej element można jednoznacznie zapisać jako sumę jedynek - <math>\mathbb{N}\setminus (\mathbb{N}+\mathbb{N})=\left\{ 1\right\}</math>. | |||
: (2) Dla <math>\mathbb{N}_2=\{n \in \mathbb{N}:n\geq 2\}</math> półgrupa <math>(\mathbb{N}_2,+ ) </math> nie jest to półgrupą wolną.<br> Nie ma jednoznaczności rozkładu na elementy z <math>\mathbb{N}_2\setminus (\mathbb{N}_2+\mathbb{N}_2)=\{2,3\}</math>.<br> Na przykład <math>6=2+2+2=3+3</math>. | : (2) Dla <math>\mathbb{N}_2=\{n \in \mathbb{N}:n\geq 2\}</math> półgrupa <math>(\mathbb{N}_2,+ )</math> nie jest to półgrupą wolną.<br> Nie ma jednoznaczności rozkładu na elementy z <math>\mathbb{N}_2\setminus (\mathbb{N}_2+\mathbb{N}_2)=\{2,3\}</math>.<br> Na przykład <math>6=2+2+2=3+3</math>. | ||
}} | }} | ||
Aktualna wersja na dzień 21:58, 15 wrz 2023
Definicje, oznaczenia i podstawowe własności
Przyjmijmy, że oznacza zbiór liczb naturalnych, a zbiór liczb naturalnych wraz z 0. Przypomnimy teraz podstawowe wiadomości z wykładu Algebra Liniowa dotyczące struktur algebraicznych, a dokładniej struktur najprostszych, półgrup i monoidów, posiadających jedno tylko działanie.
Definicja 1.1
Zbiór , w którym określone jest działanie łączne, to znaczy spełniające warunek
nazywamy półgrupą.
Przykład 1.1
Zbiór liczb naturalnych z dodawaniem tworzy półgrupę.
Definicja 1.2
Półgrupę , w której istnieje element neutralny działania, to znaczy element spełniający warunek
nazywamy monoidem.
Przykład 1.2
- (1) Zbiór liczb naturalnych z mnożeniem jest monoidem.
- (2) Zbiór liczb naturalnych z zerem jest monoidem ze względu na dodawanie.
- (3) Monoidem jest - zbiór odwzorowań dowolnego zbioru w siebie ze składaniem jako działaniem i identycznością jako elementem neutralnym.
Dwa pierwsze monoidy są przemienne, czyli działanie jest przemienne, a trzeci jest nieprzemienny.
Każdy monoid jest półgrupą.
Dla uproszczenia notacji będziemy opuszczać kropkę "" oznaczającą działanie oraz używać nazwy "jedynka" na element neutralny. Jeśli nie będzie zaznaczone inaczej, to będzie oznaczać półgrupę, a monoid. Ze względu na łączność działania zarówno w półgrupie, jak i w monoidzie iloczyn , a także (n razy) jest określony jednoznacznie bez potrzeby wprowadzania nawiasów. Dla dowolnych liczb naturalnych zachodzą wzory
Dla dowolnego
przyjmujemy z definicji
Strukturę monoidu przenosimy na zbiór potęgowy wszystkich podzbiorów monoidu , określając dla dowolnych działanie
jest monoidem.
Podobnie przenosimy strukturę półgrupy z na .
Dla dowolnego podzbioru monoidu
(półgrupy) i dla dowolnej liczby zapis oznacza n-krotny iloczyn
zbioru przez siebie rozumiany w powyższym sensie.
W szczególności
W przypadku monoidu przyjmujemy z definicji
Definicja 1.3
Homomorfizmem półgrup nazywamy odwzorowanie
takie, żeHomomorfizmem monoidów nazywamy odwzorowanie
takie, żePrzykład 1.3
Odwzorowanie takie, że
jest homomorfizmem półgrupy w półgrupę , ale nie jest homomorfizmem monoidu w monoid , bo wartością 1 z monoidu nie jest jedynka monoidu .
Definicja 1.4.
Niech będą odpowiednio dowolną półgrupą, monoidem.
- nazywamy podpółgrupą wtedy i tylko wtedy, gdy i .
- nazywamy podmonoidem wtedy i tylko wtedy, gdy jest podpółgrupą i
Przykład 1.4.
jest monoidem. Podzbiór , jako zamknięty na działanie , tworzy podpółgrupę . jest monoidem z jako elementem neutralnym, ale nie podmonoidem .
Niech będzie dowolnym podzbiorem monoidu . Zbiór
jest podmonoidem monoidu .
Jest to najmniejszy, w sensie inkluzji podmonoid monoidu zawierający zbiór .
Gdy spełniona jest równość , to mówimy, że jest zbiorem generatorów monoidu .
Zachodzą następujące własności:
- 1. Zbiór generatorów nie jest wyznaczony jednoznacznie.
- 2. Dla dowolnego monoidu istnieje zbiór generatorów, jest nim w szczególności zbiór .
Podobnie dla dowolnego podzbioru półgrupy zbiór
jest podpółgrupą i to najmniejszą w sensie inkluzji zawierającą zbiór .
Powyższe uwagi dotyczące zbioru generatorów monoidów przenoszą się odpowiednio dla półgrup.
Przykład 1.5.
W monoidzie podmonoid generowany przez zbiór generatorów składa się z liczb parzystych i nieujemnych.
Definicja 1.5
Niech będzie półgrupą. Relację równoważności nazywamy:
- (1) prawą kongruencją w półgrupie , jeśli
,
- (2) lewą kongruencją w półgrupie , jeśli
,
- (3) kongruencją, jeśli jest prawą i lewą kongruencją, tzn.
.
Zastępując w powyższej definicji półgrupę na monoid otrzymamy dualnie pojęcia prawej kongruencji,
lewej kongruencji i kongruencji zdefiniowane w monoidzie.
Mając kongruencję określoną w półgrupie (monoidzie
możemy utworzyć półgrupę ilorazową (monoid ilorazowy ), której elementami
są klasy równoważności (abstrakcji) relacji .
Dla dowolnego homomorfizmu półgrup określamy relację
Dla homomorfizmu monoidów relacja jest kongruencją w monoidzie .
Podstawowe twierdzenie o epimorfizmie dla struktur algebraicznych przyjmuje dla półgrup i odpowiednio dla monoidów następującą postać.
Twierdzenie 1.1
Niech będzie dowolnym epimorfizmem półgrupy na półgrupę . Półgrupa jest izomorficzna z półgrupą ilorazową .
Twierdzenie 1.2
Niech będzie dowolnym epimorfizmem monoidu na monoid . Monoid jest izomorficzny z monoidem ilorazowym .
Półgrupy wolne i monoidy wolne
Niech oznacza dowolny zbiór.
Definicja 2.1
Wolnym monoidem o bazie nazywamy zbiór wszystkich skończonych ciągów:
Ciąg pusty oznaczamy symbolem "1" i z definicji jest on elementem neutralnym określonego powyżej działania, nazywanego katenacją lub konkatenacją.
Przyjmujemy następującą konwencję zapisu:Ta inkluzja uzasadnia użycie wprowadzonego wcześniej oznaczenia .
jest najmniejszym podmonoidem
monoidu zawierającym .
Definicja 2.2
Wolną półgrupą nad alfabetem nazywamy zbiór wszystkich skończonych ciągów:
Używa się także określeń - wolny monoid o bazie i wolna półgrupa o bazie .
- Elementy alfabetu nazywamy literami.
- Elementy wolnego monoidu (półgrupy) nazywamy słowami i oznaczać bedziemy w wykładzie najczęściej literami .
- Dowolny podzbiór wolnego monoidu (półgrupy) nazywamy językiem.
Długością słowa nazywamy liczbę będącą długością ciągu określającego to słowo. Słowo puste 1, czyli odpowiadające ciągowi pustemu ma długość równą 0.
Przykład 2.1
- (1) Wolna półgrupa składa się z ciągów binarnych.
- (2) Wolny monoid składa się z ciągów binarnych i ciągu pustego.
Definicja 2.3
Niech i będą alfabetami. Podstawieniem nazywamy homomorfizm
Twierdzenie 2.1.
Niech oznacza dowolny zbiór, a dowolny monoid.
- (1) Każde odwzorowanie
- daje się jednoznacznie rozszerzyć do homomorfizmu
.
- (2) Homomorfizm jest epimorfizmem wtedy i tylko wtedy, gdy jest zbiorem generatorów .
Dowód
- (1) Przyjmujemy
- Tak określone jest jedynym rozszerzeniem przekształcenia .
- (2) dla pewnego jest suriekcją.
Przyjmując w powyższym twierdzeniu jako dowolny zbiór generatorów monoidu oraz jako funkcję włożenie równe identyczności na dochodzimy do następującego wniosku.
Wniosek 2.1.
Każdy monoid jest homomorficznym obrazem wolnego monoidu utworzonego nad dowolnym zbiorem generatorów .
Udowodnione powyżej twierdzenie oraz sformułowany wniosek prawdziwy jest również dla półgrup.
Powyższe rezultaty określają rolę wolnych monoidów (półgrup) w klasie wszystkich monoidów (półgrup).
Twierdzenie 2.2.
Monoid jest wolny wtedy i tylko wtedy, gdy każdy element ma jednoznaczny rozkład na elementy zbioru .
Dowod
Załóżmy, że monoid jest wolny, to znaczy dla pewnego zbioru (bazy) .
- Udowodnimy, że jest zbiorem generatorów monoidu . W tym celu wykażemy, że zachodzi inkluzja
. Dowód przeprowadzimy nie wprost. Załóżmy więc, że
- Udowodnimy, że jest zbiorem generatorów monoidu . W tym celu wykażemy, że zachodzi inkluzja
- i niech oznacza element z tego zbioru o najmniejszej długości w .
Wnioskujemy stąd kolejno:
dla pewnych ,
- przy czym długość jest silnie mniejsza niż długość . Zatem
- a to oznacza, że
- Otrzymana sprzeczność kończy dowód faktu, że jest zbiorem generatorów monoidu .
- Pokażemy teraz, że .
Niech dla pewnych , .
Jeśli , to , co jest sprzeczne z wyborem . Zatem , co implikuje .
- Pokażemy teraz, że .
Z definicji wolnego monoidu wynika jednoznaczność rozkładu na elementy z bazy , a to pociąga za sobą jednoznaczność rozkładu na elementy z podzbioru .
Niech teraz oznacza monoid z jednoznacznością rozkładu na elementy zbioru . Rozszerzamy identyczność do homomorfizmu . Z założenia wynika, że każdy element można przedstawić jako iloczyn
Zatem
Homomorfizm jest izomorfizmem, więc monoid jako izomorficzny z jest wolny.
Powyższe twierdzenie posiada swój odpowiednik dla wolnych półgrup.
Twierdzenie 2.3.
Półgrupa jest wolna wtedy i tylko wtedy, gdy każdy element ma jednoznaczny rozkład na elementy zbioru .
Wniosek 2.2.
Baza wolnego monoidu (półgrupy) jest minimalym zbiorem generatorów.
Przyklad 2.2.
- (1) Półgrupa jest wolna. Każdy jej element można jednoznacznie zapisać jako sumę jedynek - .
- (2) Dla półgrupa nie jest to półgrupą wolną.
Nie ma jednoznaczności rozkładu na elementy z .
Na przykład .