Matematyka dyskretna 1/Wykład 12: Grafy: Różnice pomiędzy wersjami

Aktualna wersja na dzień 21:49, 11 wrz 2023

Czym jest graf

Wyruszając w daleką podróż zabieramy ze sobą mapę samochodową. Głównymi elementami graficznymi zawartymi w mapie są punkty (małe kółka) symbolizujące miasta, oraz odcinki (lub łuki) obrazujące drogi pomiędzy nimi. Taka mapa jest z grubsza przedstawieniem rzeczywistości za pomocą grafu. Chcąc na przykład znaleźć drogę z Bydgoszczy do Krakowa, szukamy ciągu kolejno połączonych miast zaczynającego się w Bydgoszczy i kończącego się w Krakowie. Jest to nic innego, jak znalezienie odpowiedniej ścieżki w grafie połączeń między miastami.

Graf to para $𝐆 = (V, E)$ , gdzie:

$V$ jest zbiorem wierzchołków,

(czasami zwanymi węzłami lub punktami grafu)

$E$ jest rodziną (być może powtarzających się) krawędzi,

czyli jedno- i dwu-elementowych podzbiorów $V$ .

Graf prosty to para $𝐆 = (V, E)$ , gdzie:

$V$ jest zbiorem wierzchołków,
$E$ jest zbiorem krawędzi między różnymi wierzchołkami,

czyli dwu-elementowych podzbiorów $V$ .

Graf ogólny (a.) oraz prosty (b.)

Uwaga

W grafie w odróżnieniu od grafu prostego dopuszczamy pętle oraz krawędzie wielokrotne. Wierzchołek nazywany jest czasem także węzłem, jak i punktem grafu. Krawędź łącząca $v$ z $w$ oznaczana będzie jako $v w$ . Jeśli istnieje krawędź $v w$ to mówimy, że $v$ i $w$ są sąsiadami; oraz że krawędź $v w$ jest incydentna do $v$ ( $w$ ). Ponadto, dla grafu $𝐆$ symbolem $V (𝐆)$ będziemy oznaczać jego zbiór wierzchołków, zaś symbolem $E (𝐆)$ jego zbiór krawędzi. Czasem, dla odróżnienia grafu od grafu prostego, graf będziemy nazywać też grafem ogólnym.

Stopień wierzchołka $v$ w grafie $𝐆$ to liczba krawędzi incydentnych z $v$ . Stopień wierzchołka $v$ oznaczany jest jako $d e g v$ .

Obserwacja 12.1

Jeśli $𝐆 = (V, E)$ jest grafem ogólnym, to

$\sum_{v \in V} d e g v = 2 | E |$

A zatem liczba wierzchołków o nieparzystym stopniu jest parzysta.

Dowód

Każda krawędź jest incydentna do dwóch wierzchołków. Zliczając krawędzie incydentne do kolejnych wierzchołków, a następnie sumując te wartości, każda krawędź $v w$ zostanie zliczona dwa razy: raz przy rozpatrywaniu wierzchołka $v$ , a drugi raz przy $w$ .

Jeśli $𝐆$ miałby nieparzyście wiele wierzchołków o nieparzystym stopniu to suma $\sum_{v \in V} d e g v$ byłaby nieparzysta, wbrew temu, że jest liczbą parzystą $2 | E |$ .

Ściągnięcie zbioru

{p, q, r}

do wierzchołku

x

(a.) Digraf oraz (b.) jego graf szkieletowy

Uwaga

Dla grafów $𝐆 = (V, E)$ , $𝐆_{1} = (V_{1}, E_{1})$ , $𝐆_{2} = (V_{2}, E_{2})$ definiujemy następujące pojęcia:

suma grafów $𝐆_{1} \cup 𝐆_{2} = (V_{1} \cup V_{2}, E_{1} \cup E_{2})$ ,

przecięcie grafów $𝐆_{1} \cap 𝐆_{2} = (V_{1} \cap V_{2}, E_{1} \cap E_{2})$ ,

różnica grafów $𝐆_{1} - 𝐆_{2} = (V_{1} - V_{2}, E_{1} - E_{2})$ ,

podgraf grafu $𝐆$ to graf $𝐇$ , w którym $V (𝐇) \subseteq V (𝐆)$ i $E (𝐇) \subseteq E (𝐆)$ ,

restrykcja grafu $𝐆$ do podzbioru $X \subseteq V$ to $𝐆 |_{X} = (X, {v w : v, w \in X})$ ,

podgraf indukowany grafu $𝐆$ to graf będący restrykcją grafu $𝐆$ ,

iloraz grafu $𝐆$ przez relację równoważności $θ \subseteq V \times V$ na zbiorze jego wierzchołków to graf postaci

$𝐆 / θ = (V / θ, {{v / θ, w / θ} : {v, w} \in E})$

ściągnięcie zbioru wierzchołków $X \subseteq V$ w grafie $𝐆$ to szczególny przypadek ilorazu $𝐆 / θ$ , w którym klasy równoważności wszystkich wierzchołków spoza $X$ są jednoelementowe, a $X$ stanowi dodatkową klasę, tzn. $V / θ = {{v} : v \in V - X} \cup {X}$ . W ten sposób zbiór $X$ został ściągnięty do punktu, którego sąsiadami są sąsiedzi jakiegokolwiek wierzchołka z $X$ . Z drugiej strony, jeśli $θ \subseteq V \times V$ jest relacją równoważności o klasach $X_{1}, \dots, X_{k}$ , to ściągając w grafie $𝐆$ kolejno zbiory $X_{1}, \dots, X_{k}$ otrzymamy graf ilorazowy $𝐆 / θ$ .

W dotychczasowej interpretacji grafów, jako mapy dróg zakładaliśmy, że istnienie drogi np. z Krakowa do Zakopanego, gwarantowało także możliwość powrotu po tej samej trasie. To oczywiście nie musi być zawsze prawdą, np. w miastach jest wiele dróg jednokierunkowych. Chcąc rozważać również takie jednokierunkowe trasy, tzn uwzględniać kierunek relacji między dwoma obiektami, będziemy mówić o grafach skierowanych.

Graf skierowany (lub inaczej digraf) to para $𝐃 = (V, E)$ , gdzie

$V$ jest zbiorem wierzchołków,

$E$ jest zbiorem krawędzi skierowanych, czyli $E \subseteq V \times V$ .

Uwaga

Krawędź digrafu (czyli uporządkowaną parę) $v w$ graficznie przedstawiamy jako strzałkę $v ∙ ⟶ ∙ w$ .

Graf szkieletowy digrafu $𝐃$ to graf otrzymany z $𝐃$ poprzez zaniedbanie (usunięcie) kierunku krawędzi, ale nie samych krawędzi.

Przegląd niektórych grafów

[[File:Grafy dwudzielne.svg|250x250px|thumb|left|Graf nie będący dwudzielnym (a), niepełny graf dwudzielny (b) oraz pełny graf dwudzielny $𝒦_{3, 4}$ (c)

Graf nieplanarny(a) oraz graf planarny (b) wraz z jego prezentacją w postaci grafu płaskiego (c)

Graf pusty to graf bez krawędzi. Antyklika lub graf niezależny to inne nazwy grafu pustego. Antyklikę o $n$ wierzchołkach oznaczać będziemy przez $𝒜_{n}$ .

Graf pełny to graf, w którym każde dwa wierzchołki połączone są krawędzią. Graf pełny nazywany jest także kliką i oznaczany przez $𝒦_{n}$ , gdzie $n$ jest liczbą jego wierzchołków.

Uwaga

Liczba krawędzi w klice $𝒦_{n}$ wynosi $\frac{n (n - 1)}{2}$ .

Graf dwudzielny to graf $𝐆 = (V, E)$ , w którym zbiór $V$ da się podzielić na dwa rozłączne podzbiory $V_{1}$ oraz $V_{2}$ tak, by żadne dwa wierzchołki w obrębie tego samego podzbioru $V_{i}$ nie były sąsiadami. Czasem, dla podkreślenia takiego podziału, graf dwudzielny będziemy oznaczać przez $(V_{1} \cup V_{2}, E)$ . Zauważmy jednak, że podział taki nie jest jednoznaczny -- np. w antyklice $𝒜_{n}$ dowolny podział zbioru wierzchołków na dwa podzbiory jest podziałem dwudzielnym.

Pełny graf dwudzielny to graf dwudzielny $𝐆 = (V_{1} \cup V_{2}, E)$ , w którym każdy wierzchołek z $V_{1}$ jest połączony z każdym wierzchołkiem z $V_{2}$ . Pełny graf dwudzielny oznaczać będziemy przez $𝒦_{r, s}$ , gdzie $r$ jest rozmiarem $V_{1}$ , a $s$ rozmiarem $V_{2}$ .

Graf płaski to para $\overline{G} = (\overline{V}, \overline{E})$ , gdzie:

$\overline{V}$ jest jakimś zbiorem punktów płaszczyzny $ℝ^{2}$ ,

$\overline{E}$ jest zbiorem nie przecinających się odcinków lub łuków w $R^{2}$ o końcach ze zbiorze $\overline{V}$ .

Graf planarny to graf, który jest prezentowalny jako graf płaski.

Ścieżki, Cykle, oraz Spójność

Grafy marszruta

Marszruta w grafie $𝐆$ z wierzchołka $w$ do wierzchołka $u$ to skończony ciąg krawędzi w postaci $w v_{1}, v_{1} v_{2}, \dots, v_{k - 1} u$ .
W skrócie marszrutę taką oznaczamy przez $w \to v_{1} \to v_{2} \to \dots \to v_{k - 1} \to u$ .
Wierzchołek $w$ nazywać będziemy początkowym, a $u$ końcowym wierzchołkiem marszruty.

Długość marszruty $w \to v_{1} \to v_{2} \to \dots \to v_{k - 1} \to u$ to liczba jej krawędzi.

Marszruta zamknięta to marszruta kończąca się w punkcie wyjścia, czyli taka, w której $w = u$ .

Uwaga

Marszruta może być również zdefiniowana w grafach skierowanych. Definiuje się ją analogicznie, uwzględniając jednak kierunek krawędzi. Marszruta taka, zgodna z kierunkiem krawędzi nazywana jest marszrutą skierowaną.

W grafie z rysunku Grafy marszruta ciąg $u \to v \to w \to z \to z \to y \to v \to w \to v$ jest marszrutą z $u$ do $v$ o długości $8$ . Widzimy, że niektóre jej wierzchołki, a nawet krawędzie, powtarzają się. Wygodnie jest móc wyróżniać marszruty bez powtarzających się wierzchołków.

Droga to marszruta bez powtarzających się wierzchołków. Droga nazywana jest też często ścieżką.

Cykl to marszruta zamknięta, w której jedynym powtarzającym się wierzchołkiem jest jej początek (będący oczywiście również jej końcem).

W grafie z rysunku Grafy marszruta marszruta $y \to v \to w \to u \to x$ jest drogą, zaś marszruta $x \to u \to v \to w \to y \to x$ jest cyklem.
Czasem wygodnie jest traktować marszrutę w grafie $𝐆$ (a więc w szczególności również cykle i ścieżki) jako podgraf

𝐌 = (V (𝐌), E (𝐌)) : = ({v_{0}, \dots, v_{k}}, {{v_{0}, v_{1}}, \dots, {v_{k - 1}, v_{k}}})

Graf spójny to graf, w którym między dwoma dowolnymi wierzchołkami istnieje droga. Graf niespójny to graf, który nie jest spójny.

Spójna składowa grafu $𝐆 = (V, E)$ to maksymalny (w sensie inkluzji) podzbiór $X \subseteq V$ , indukujący graf spójny $𝐆 |_{X}$ .

Graf z rysunku Grafy marszruta jest spójny.

Uwaga

Dowolnym graf $𝐆$ rozpada się na spójne składowe, tworzące podział zbioru $V$ . Grafy spójne mają jedynie jedną spójną składową, w przeciwieństwie do grafów niespójnych posiadających ich więcej.
Rozkład na spójne składowe wyznacza relacją równoważności $σ \subseteq V \times V$ , dla której graf ilorazowy $𝐆 / σ$ jest antykliką.

Wierzchołek izolowany to wierzchołek nie posiadający sąsiadów.

Uwaga

Punkty izolowane tworzą jednoelemetowe spójne składowe.

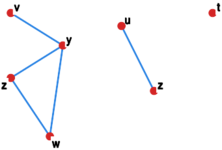
Graf z rysunku Grafy spojne skladowe ma trzy spójne składowe: ${v, w, y, x}, {u, z}, {t}$ . Ponadto $t$ jest punktem izolowanym.

Intuicyjnie wydaje się, że graf spójny powinien mieć dostatecznie dużo krawędzi w stosunku do liczby wierzchołków. Okazuje się jednak, że w grafie spójnym $𝐆 = (V, E)$ możemy wymusić jedynie $| V | - 1$ krawędzi. Z drugiej jednak strony, gdy graf $𝐆$ ma więcej niż $| V | \cdot (| V | - 1) / 2$ krawędzi, to musi być spójny. Rezultaty te można uzyskać z bardziej ogólnego wyniku:

Twierdzenie 12.2

W grafie prostym $𝐆 = (V, E)$ o $k$ składowych spójnych liczba jego krawędzi spełnia nierówności

| V | - k \leq | E | \leq \frac{(| V | - k) (| V | - k + 1)}{2}

Ponadto, są to najlepsze możliwe ograniczenia, tzn.

istnieje graf prosty $𝐆 = (V, E)$ o dokładnie $k$ składowych spójnych, w którym $| E | = | V | - k$ ,
istnieje graf prosty $𝐆 = (V, E)$ o dokładnie $k$ składowych spójnych, w którym $| E | = \frac{(| V | - k) (| V | - k + 1)}{2}$ .

Dowód

Niech $n$ będzie liczbą wierzchołków grafu $𝐆$ , a $m$ liczbą jego krawędzi. Dowód nierówności $n - k \leq m$ przeprowadzimy indukcyjnie względem liczby krawędzi $m$ w grafie $𝐆$ . Jeżeli $m = 0$ , to wszystkie wierzchołki są punktami izolowanymi czyli $k = n$ , co spełnia żądaną nierówność. Przy $m > 0$ usunięcie krawędzi może nie zmienić liczby składowych spójnych albo zwiększyć ją o jeden. W pierwszym przypadku z założenia indukcyjnego dostaniemy odrazu że $n - k \leq m - 1 \leq m$ , zaś w drugim, założenie indukcyjne daje $n - (k + 1) \leq m - 1$ , czyli rzeczywiście $n - k \leq m$ .

Dla dowodu górnego ograniczenia $m \leq (n - k) (n - k + 1) / 2$ na liczbę krawędzi załóżmy, że $𝐆$ posiada $k$ składowych spójnych i ma największą możliwą liczbę krawędzi wśród $n$ -elementowych grafów o $k$ składowych spójnych. Wtedy każda z tych składowych jest grafem pełnym, jako że inaczej moglibyśmy dołożyć krawędzie w takiej niepełnej składowej, nie zmieniając przy tym liczb $k$ i $n$ . Pokażemy dodatkowo, że co najwyżej jedna z tych składowych może mieć więcej niż jeden wierzchołek. Istotnie, gdyby były dwie składowe $V_{1}, V_{2}$ o odpowiednio $n_{1} \geq n_{2} > 1$ wierzchołkach, to - nie zmieniając pozostałych składowych, i - przenosząc jeden wierzchołek z $V_{2}$ do $V_{1}$ otrzymalibyśmy nowy graf. W oryginalnym grafie sumaryczna liczba krawędzi w (pełnych) składowych $V_{1}, V_{2}$ wynosi $(\binom{n_{1}}{2}) + (\binom{n_{2}}{2})$ , a w nowym grafie te zmodyfikowane (również pełne) składowe posiadają łącznie $(\binom{n_{1} + 1}{2}) + (\binom{n_{2} - 1}{2})$ krawędzi. Różnica między nową a starą liczbą krawędzi wynosi więc

\frac{(n_{1} + 1) n_{1} + (n_{2} - 1) (n_{2} - 2) - n_{1} (n_{1} - 1) - n_{2} (n_{2} - 1)}{2} = n_{1} - n_{2} + 1 \geq 1

co pokazuje, że nowy graf ma przynajmniej o jedną krawędź więcej. Dowodzi to, że graf $𝐆$ maksymalizujący liczbę krawędzi ma opisaną przez nas własność. To z kolei oznacza, że $k - 1$ jego składowych ma po jednym elemencie, a pozostała składowa jest grafem pełnym o $n - (k - 1)$ elementach. Taki graf ma oczywiście $(\binom{n - k + 1}{2})$ krawędzi.

Aby zobaczyć, że podanych ograniczeń na liczbę krawędzi nie można poprawić zauważmy, że

graf o $k$ składowych spójnych, z których każda jest indukowaną ścieżką o liczności odpowiednio $n_{1}, n_{2}, \dots, n_{k}$ ma dokładnie $(n_{1} - 1) + (n_{2} - 1) + \dots + (n_{k} - 1) = | V | - k$ krawędzi.
rozważany w dowodzie graf o dokładnie $k$ składowych spójnych, z których $k - 1$ to wierzchołki izolowane, a pozostałe $| V | - k$ wierzchołków tworzy klikę $𝒦_{n - k}$ , ma dokładnie $\frac{(| V | - k) (| V | - k + 1)}{2}$ krawędzi.

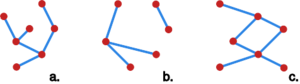
Las to graf nie zawierający cykli jako podgrafy.

Drzewo to graf spójny nie zawierający cykli, czyli spójny las.

Liść drzewa to wierzchołek o stopniu $1$ .

Gwiazda to drzewo, w którym co najwyżej jeden wierzchołek nie jest liściem.

Drzewo rozpinające grafu $𝐆$ to podgraf grafu $𝐆$ zawierający wszystkie jego wierzchołki i będący drzewem.

Drzewa można zdefiniować na kilka równoważnych sposobów:

Twierdzenie 12.3

Dla grafu $𝐓 = (V, E)$ następujące warunki są równoważne:

$𝐓$ jest drzewem,
$𝐓$ nie zawiera cykli i ma $| V | - 1$ krawędzi,
$𝐓$ jest spójny i ma $| V | - 1$ krawędzi,
$𝐓$ jest spójny, zaś usunięcie dowolnej krawędzi tworzy dokładnie dwie składowe,
dowolne dwa wierzchołki grafu $𝐓$ są połączone dokładnie jedną drogą,
$𝐓$ nie zawiera cykli, lecz dodanie dowolnej nowej krawędzi tworzy dokładnie jeden cykl.

Dowód

Dowód przeprowadzimy indukcyjnie ze względu na liczbę wierzchołków $| V |$ grafu $𝐓$ . Oczywiście dla $| V | = 1$ graf $𝐓$ nie ma krawędzi i tym samym spełnia wszystkie sześć warunków dowodzonego Twierdzenia.

1. $\Rightarrow$ 2. Ponieważ $𝐓$ nie posiada cykli, to usunięcie krawędzi rozspaja $𝐓$ na dwa drzewa: pierwsze o $n_{1}$ wierzchołkach oraz drugie o $n_{2}$ , przy czym $n_{1} + n_{2} = | V |$ oraz $0 < n_{1}, n_{2} < | V |$ . Założenie indukcyjne gwarantuje, że nowo powstałe drzewa mają odpowiednio $n_{1} - 1$ oraz $n_{2} - 1$ krawędzi. Sumując te krawędzie wraz z usuniętą otrzymujemy

| E | = (n_{1} - 1) + (n_{2} - 1) + 1 = | V | - 1

2. $\Rightarrow$ 3. Jeżeli $𝐓$ nie byłby spójny, to miałby $k \geq 2$ składowych spójnych. Ponieważ żadna składowa nie ma cykli, założenie indukcyjne daje, że w każdej z $k$ składowych krawędzi jest o jedną mniej niż wierzchołków. A więc, w całym grafie krawędzi jest o $k \geq 2$ mniej niż wierzchołków co daje sprzeczność z $| E | = | V | - 1$ .

3. $\Rightarrow$ 4. Usunięcie dowolnej krawędzi spowoduje, że nowy graf będzie miał $| V | - 2$ krawędzie. Na mocy Twierdzenia 12.2 okazuje się, że jest to za mało aby graf był spójny.

4. $\Rightarrow$ 5. Jeżeli istniałyby dwie różne ścieżki $P_{1}$ oraz $P_{2}$ o wspólnym początku i końcu, to usunięcie krawędzi $e \in P_{1} - P_{2}$ nierozspajałoby grafu $𝐓$ .

5. $\Rightarrow$ 6. Pomiędzy dwoma punktami dowolnego cyklu $C$ istnieją dwie rozłączne ścieżki zawarte w $C$ . Tak więc istnienie dokładnie jednej ścieżki pomiędzy dowolnymi punktami w $𝐓$ wyklucza istnienie cykli w $𝐓$ . Z drugiej zaś strony dodanie dodatkowej krawędzi $u v$ stworzy cykl składający się z krawędzi $u v$ oraz ścieżki łączącej wierzchołek $u$ z $v$ zawartej w grafie $𝐓$ . Powyższy cykl jest jedyny. Wynika to z tego, że jeżeli istnieją dwa cykle zawierające krawędź $u v$ , to musi istnieć trzeci cykl niezawierajacy $u v$ , czyli zawarty w $𝐓$ co nie jest możliwe.

6. $\Rightarrow$ 1. Gdyby, mimo spełniania warunku 6, graf $𝐓$ nie był spójny, to dodanie jednej krawędzi łączącej dwa wierzchołki w różnych składowych spójnych nie utworzy cyklu.

Z charakteryzacji drzew podanej w Twierdzeniu 12.3 natychmiast dostajemy następujący związek miedzy liczbą krawędzi i wierzchołków w dowolnym lesie.

Wniosek 12.4

Każdy las $𝐆 = (V, E)$ o $k$ składowych spójnych posiada $| E | = | V | - k$ krawędzi.

Matematyka dyskretna 1/Wykład 12: Grafy: Różnice pomiędzy wersjami

Aktualna wersja na dzień 21:49, 11 wrz 2023

Czym jest graf

Przegląd niektórych grafów

Ścieżki, Cykle, oraz Spójność

Menu nawigacyjne

Działania na stronie

Opcje strony

Narzędzia osobiste

Nawigacja

Szukaj

Narzędzia

@@ Linia 1: / Linia 1: @@
 ==Czym jest graf==
-<div class="thumb tright"><div style="width:320px;">
+[[File:Grafy mapa samochodowa.svg|250x250px|thumb|right|Bardzo uproszczona mapa samochodowa Polski]]
-<flash>file=Grafy mapa samochodowa.swf|width=300|height=300</flash>
-<div.thumbcaption>Bardzo uproszczona mapa samochodowa Polski.</div>
-</div></div>
 Wyruszając w daleką podróż zabieramy ze sobą mapę samochodową.
 Głównymi elementami graficznymi zawartymi w mapie są punkty (małe kółka)
@@ Linia 26: / Linia 23: @@
 * <math>E</math> jest zbiorem krawędzi między różnymi wierzchołkami,<br>
 czyli dwu-elementowych podzbiorów <math>V</math>.
+[[File:Grafy graf ogolny i prosty.mp4|250x250px|thumb|right|Graf ogólny (a.) oraz prosty (b.)]]
 {{uwaga|||
 W grafie w odróżnieniu od grafu prostego dopuszczamy pętle oraz krawędzie wielokrotne.
 Wierzchołek nazywany jest czasem także  ''węzłem'', jak i ''punktem'' grafu.
@@ Linia 34: / Linia 32: @@
 Jeśli istnieje krawędź <math>vw</math> to mówimy, że <math>v</math> i  <math>w</math> są sąsiadami;
 oraz że krawędź <math>vw</math> jest incydentna do <math>v</math> (<math>w</math>).
-Ponadto, dla grafu <math>\mathbf{G}</math> symbolem <math>{\sf V}\!\left(\mathbf{G}\right)</math>
+Ponadto, dla grafu <math>\mathbf{G}</math> symbolem <math>\mathsf{ V}\!\left(\mathbf{G}\right)</math>
 będziemy oznaczać  jego zbiór wierzchołków,
-zaś symbolem <math>{\sf E}\!\left(\mathbf{G}\right)</math> jego zbiór krawędzi.
+zaś symbolem <math>\mathsf{ E}\!\left(\mathbf{G}\right)</math> jego zbiór krawędzi.
 Czasem, dla odróżnienia grafu od grafu prostego,
 graf będziemy nazywać też ''grafem ogólnym''.
 }}
-{grafy_graf_ogolny_i_prosty}
-{Graf ogólny (a.) oraz prosty '''[Rysunek z pliku:''' <tt>grafygrafogolnyiprosty.eps</tt>''']'''}
 '''Stopień wierzchołka''' <math>v</math> w grafie <math>\mathbf{G}</math>
 to liczba krawędzi incydentnych z <math>v</math>.
-Stopień wierzchołka  <math>v</math> oznaczany jest jako <math>{\sf deg}\ v</math>.
+Stopień wierzchołka  <math>v</math> oznaczany jest jako <math>\mathsf{ deg}\ v</math>.
-{{obserwacja|1||
+{{obserwacja|12.1|obs 12.1|
+Jeśli <math>\mathbf{G}=\left( V,E \right)</math> jest grafem ogólnym, to
-Jeśli <math>\mathbf{G}=\left( V,E \right)</math> jest grafem ogólnym, to
-<center><math>\sum_{v\in V}{\sf deg}\ v=2\left\vert E \right\vert.
+<center>
-</math></center>
+<math>\sum_{v\in V}\mathsf{ deg}\ v=2\left\vert E \right\vert</math>
+</center>
 A zatem liczba wierzchołków o nieparzystym stopniu jest parzysta.
@@ Linia 59: / Linia 56: @@
 {{dowod|||
 Każda krawędź jest incydentna do dwóch wierzchołków.
 Zliczając krawędzie incydentne do kolejnych wierzchołków,
@@ Linia 67: / Linia 63: @@
 Jeśli <math>\mathbf{G}</math> miałby nieparzyście wiele wierzchołków o nieparzystym stopniu
-to suma <math>\sum_{v\in V}{\sf deg}\ v</math> byłaby nieparzysta,
+to suma <math>\sum_{v\in V}\mathsf{ deg}\ v</math> byłaby nieparzysta,
 wbrew temu, że jest liczbą parzystą <math>2\left\vert E \right\vert</math>.
 }}
+[[File:Grafy sciagniecie.mp4|250x250px|thumb|left|Ściągnięcie zbioru <math>\left\lbrace p,q,r \right\rbrace</math> do wierzchołku <math>x</math>]]
+[[File:Grafy digraf.mp4|250x250px|thumb|right|(a.) Digraf oraz (b.) jego graf szkieletowy]]
 {{uwaga|||
 Dla grafów
 <math>\mathbf{G}=\left( V,E \right)</math>,
@@ Linia 79: / Linia 78: @@
 *  '''suma grafów''' <math>\mathbf{G}_1\cup\mathbf{G}_2=\left( V_1\cup V_2,E_1\cup E_2 \right)</math>,
 *  '''przecięcie grafów''' <math>\mathbf{G}_1\cap\mathbf{G}_2=\left( V_1\cap V_2,E_1\cap E_2 \right)</math>,
 *  '''różnica grafów''' <math>\mathbf{G}_1-\mathbf{G}_2=\left( V_1- V_2,E_1- E_2 \right)</math>,
-*  '''podgraf''' grafu <math>\mathbf{G}</math> to graf <math>\mathbf{H}</math>, w którym <math>{\sf V}\!\left(\mathbf{H}\right)\subseteq{\sf V}\!\left(\mathbf{G}\right)</math> i <math>{\sf E}\!\left(\mathbf{H}\right)\subseteq{\sf E}\!\left(\mathbf{G}\right)</math>,
+*  '''podgraf''' grafu <math>\mathbf{G}</math> to graf <math>\mathbf{H}</math>, w którym <math>\mathsf{ V}\!\left(\mathbf{H}\right)\subseteq\mathsf{ V}\!\left(\mathbf{G}\right)</math> i <math>\mathsf{ E}\!\left(\mathbf{H}\right)\subseteq\mathsf{ E}\!\left(\mathbf{G}\right)</math>,
 *  '''restrykcja''' grafu <math>\mathbf{G}</math> do podzbioru <math>X\subseteq V</math> to <math>\mathbf{G}|_X=\left( X,\left\lbrace vw:v,w\in X \right\rbrace \right)</math>,
 *  '''podgraf indukowany''' grafu <math>\mathbf{G}</math> to graf będący restrykcją grafu <math>\mathbf{G}</math>,
-*  '''iloraz''' grafu <math>\mathbf{G}</math> przez relację równoważności <math>\theta\subseteq V\times V</math> na zbiorze jego wierzchołków to graf postaci <center><math>\mathbf{G}/\theta=\left( V/\theta,\left\lbrace \left\lbrace v/\theta,w/\theta \right\rbrace:\left\lbrace v,w \right\rbrace\in E \right\rbrace \right), </math></center>
+*  '''iloraz''' grafu <math>\mathbf{G}</math> przez relację równoważności <math>\theta\subseteq V\times V</math> na zbiorze jego wierzchołków to graf postaci
+<center>
+<math>\mathbf{G}/\theta=\left( V/\theta,\left\lbrace \left\lbrace v/\theta,w/\theta \right\rbrace:\left\lbrace v,w \right\rbrace\in E \right\rbrace \right)</math>
+</center>
 *  '''ściągnięcie''' zbioru wierzchołków <math>X\subseteq V</math> w grafie <math>\mathbf{G}</math> to szczególny przypadek ilorazu <math>\mathbf{G}/\theta</math>, w którym  klasy równoważności wszystkich wierzchołków spoza <math>X</math> są jednoelementowe, a <math>X</math> stanowi dodatkową klasę, tzn. <math>V/\theta=\left\lbrace \left\lbrace v \right\rbrace:v\in V- X \right\rbrace\cup\left\lbrace X \right\rbrace</math>. W ten sposób zbiór <math>X</math> został ściągnięty do punktu, którego sąsiadami są sąsiedzi jakiegokolwiek wierzchołka z <math>X</math>. Z drugiej strony, jeśli <math>\theta\subseteq V\times V</math> jest relacją równoważności o klasach <math>X_1,\ldots,X_k</math>, to ściągając w grafie <math>\mathbf{G}</math> kolejno zbiory <math>X_1,\ldots,X_k</math> otrzymamy graf ilorazowy <math>\mathbf{G}/\theta</math>.
 }}
-{grafy_sciagniecie}
-{Ściągnięcie zbioru <math>\left\lbrace p,q,r \right\rbrace</math> do wierzchołku <math>x</math>. '''[Rysunek z pliku:''' <tt>grafysciagniecie.eps</tt>''']'''}
 W dotychczasowej interpretacji grafów, jako mapy dróg
@@ Linia 104: / Linia 111: @@
 to para <math>\mathbf{D}=\left( V,E \right)</math>, gdzie
 * <math>V</math> jest zbiorem ''wierzchołków'',
 * <math>E</math> jest zbiorem ''krawędzi skierowanych'', czyli <math>E\subseteq V\times V</math>.
 {{uwaga|||
 Krawędź digrafu (czyli uporządkowaną parę) <math>vw</math>
 graficznie przedstawiamy jako strzałkę <math>v\ \bullet\!\longrightarrow\!\bullet\ w</math>.
@@ Linia 116: / Linia 123: @@
 ale nie samych krawędzi.
-{grafy_digraf}
+==Przegląd niektórych grafów==
-{(a.) Digraf oraz (b.) jego graf szkieletowy. '''[Rysunek z pliku:''' <tt>grafydigraf.eps</tt>''']'''}
+[[File:Grafy antyklika.svg|250x250px|thumb|left|Antyklika <math>\mathcal{A}_{5}</math>]]
+[[File:Grafy dwudzielne.svg|250x250px|thumb|left|Graf nie będący dwudzielnym (a), niepełny graf dwudzielny (b)
+oraz pełny graf dwudzielny <math>\mathcal{K}_{3,4}</math> (c)
-==Przegląd niektórych grafów==
+[[File:Grafy klika.svg|250x250px|thumb|right|Klika <math>\mathcal{K}_{5}</math>]]
-'''Graf pusty''' to graf bez krawędzi.<br>
+[[File:Grafy planarne.mp4|250x250px|thumb|right|Graf nieplanarny(a) oraz graf planarny (b) wraz z jego prezentacją w postaci grafu płaskiego (c)]]
-''Antyklika'' lub ''graf niezależny'' to inne nazwy grafu prostego.
-Antyklikę o <math>n</math> jest ilością wierzchołkach oznaczać będziemy przez <math>\mathcal{A}_{n}</math>.
-{grafy_antyklika}
+'''Graf pusty''' to graf bez krawędzi.
-{Antyklika <math>\mathcal{A}_{5}</math> '''[Rysunek z pliku:''' <tt>grafyantyklika.eps</tt>''']'''}
+''Antyklika'' lub ''graf niezależny'' to inne nazwy grafu pustego.
+Antyklikę o <math>n</math> wierzchołkach oznaczać będziemy przez <math>\mathcal{A}_{n}</math>.
 '''Graf pełny''' to graf, w którym każde dwa wierzchołki połączone są krawędzią.
@@ Linia 133: / Linia 143: @@
 {{uwaga|||
 Liczba krawędzi w klice <math>\mathcal{K}_{n}</math> wynosi <math>\frac{n(n-1)}{2}</math>.
 }}
-{grafy_klika}
-{Klika <math>\mathcal{K}_{5}</math> '''[Rysunek z pliku:''' <tt>grafyklika.eps</tt>''']'''}
 '''Graf dwudzielny''' to graf <math>\mathbf{G}=\left( V,E \right)</math>,
@@ Linia 155: / Linia 161: @@
 gdzie <math>r</math> jest rozmiarem <math>V_1</math>, a <math>s</math> rozmiarem <math>V_2</math>.
-{grafy_dwudzielne}
-{Graf nie będący dwudzielnym (a), niepełny graf dwudzielny (b)
-oraz pełny graf dwudzielny <math>\mathcal{K}_{3,4}</math> (c) graf '''[Rysunek z pliku:''' <tt>grafydwudzielne.eps</tt>''']'''}
 '''Graf płaski''' to para <math>\mathbf{\overline{G}}=\left( \overline{V},\overline{E} \right)</math>, gdzie:
 * <math>\overline{V}</math> jest  jakimś zbiorem punktów płaszczyzny <math>\mathbb{R}^2</math>,
-* <math>\overline{E}</math> jest zbiorem nie przecinających się odcinków lub łuków w <math>R^2</math>
-o końcach ze zbiorze <math>\overline{V}</math>.
+* <math>\overline{E}</math> jest zbiorem nie przecinających się odcinków lub łuków w <math>R^2</math> o końcach ze zbiorze <math>\overline{V}</math>.
 '''Graf planarny''' to graf, który jest prezentowalny jako graf płaski.
-{grafy_planarne}
+<table width="100%">
-{Graf nieplanarny(a) oraz graf planarny (b) wraz z jego prezentacją w postaci grafu płaskiego (c) '''[Rysunek z pliku:''' <tt>grafyplanarne.eps</tt>''']'''}
+<tr><td>&nbsp;</td></tr>
+</table>
 ==Ścieżki, Cykle, oraz Spójność==
+{{kotwica|marszruta||}}
+[[File:Grafy marszruta.mp4|250x250px|thumb|right|Grafy marszruta]]
 '''Marszruta''' w grafie <math>\mathbf{G}</math> z wierzchołka <math>w</math> do wierzchołka <math>u</math>
@@ Linia 184: / Linia 191: @@
 {{uwaga|||
 Marszruta może być również zdefiniowana w grafach skierowanych.
 Definiuje się ją analogicznie, uwzględniając jednak kierunek krawędzi.
@@ Linia 191: / Linia 197: @@
 }}
-{grafy_marszruta}
+W grafie z rysunku [[#marszruta|Grafy marszruta]] ciąg
-{ '''[Rysunek z pliku:''' <tt>grafymarszruta.eps</tt>''']'''}
-W grafie z rysunku [[##pict marszruta|Uzupelnic pict marszruta|]] ciąg
 <math>u\to v\to w\to z\to z\to y\to v\to w\to v</math> jest marszrutą z <math>u</math> do <math>v</math>
 o długości <math>8</math>.
@@ Linia 207: / Linia 210: @@
 (będący oczywiście również jej końcem).
-W grafie z rysunku [[##pict marszruta|Uzupelnic pict marszruta|]]
+W grafie z rysunku [[#marszruta|Grafy marszruta]]
 marszruta <math>y\to v\to w\to u\to x</math> jest drogą,
 zaś marszruta <math>x\to u\to v\to w\to y\to x</math> jest cyklem.
@@ Linia 214: / Linia 217: @@
 (a więc w szczególności również cykle i ścieżki)
 jako podgraf
-<center><math>\mathbf{M}=\left( {\sf V}\!\left(\mathbf{M}\right),{\sf E}\!\left(\mathbf{M}\right) \right)
+<center><math>\mathbf{M}=\left( \mathsf{ V}\!\left(\mathbf{M}\right),\mathsf{ E}\!\left(\mathbf{M}\right) \right)
-:=\left( \left\lbrace v_0,\ldots,v_k \right\rbrace,\left\lbrace \left\lbrace v_0,v_1 \right\rbrace,\ldots,\left\lbrace v_{k-1},v_k \right\rbrace \right\rbrace \right).
+:=\left( \left\lbrace v_0,\ldots,v_k \right\rbrace,\left\lbrace \left\lbrace v_0,v_1 \right\rbrace,\ldots,\left\lbrace v_{k-1},v_k \right\rbrace \right\rbrace \right)</math></center>
-</math></center>
 '''Graf spójny''' to graf, w którym między dwoma dowolnymi wierzchołkami
@@ Linia 226: / Linia 228: @@
 indukujący graf spójny <math>\mathbf{G}|_X</math>.
-Graf z rysunku [[##pict marszruta|Uzupelnic pict marszruta|]] jest spójny.
+Graf z rysunku [[#marszruta|Grafy marszruta]] jest spójny.
 {{uwaga|||
 Dowolnym graf <math>\mathbf{G}</math> rozpada się na spójne składowe,
 tworzące podział zbioru <math>V</math>.
@@ Linia 241: / Linia 242: @@
 {{uwaga|||
 Punkty izolowane tworzą jednoelemetowe spójne składowe.
 }}
-{grafy_spojne_skladowe}
+[[File:Grafy spojne skladowe.svg|250x150px|thumb|right|Grafy spójne skladowe]]
-{ '''[Rysunek z pliku:''' <tt>grafyspojneskladowe.eps</tt>''']'''}
-Graf z rysunku [[##pict spojne skladowe|Uzupelnic pict spojne skladowe|]] ma trzy spójne składowe:
+Graf z rysunku [[#grafy spojne skladowe|Grafy spojne skladowe]] ma trzy spójne składowe:
 <math>\left\lbrace v,w,y,x \right\rbrace,\left\lbrace u,z \right\rbrace,\left\lbrace t \right\rbrace</math>.
 Ponadto <math>t</math> jest punktem izolowanym.
@@ Linia 259: / Linia 258: @@
 Rezultaty te można uzyskać z bardziej ogólnego wyniku:
-{{twierdzenie|2||
+{{twierdzenie|12.2|tw 12.2|
 W grafie prostym <math>\mathbf{G}=\left(V,E\right)</math> o <math>k</math> składowych spójnych
 liczba jego krawędzi spełnia nierówności
-<center><math>\left\vert V \right\vert-k\leq \left\vert E \right\vert\leq\frac{(\left\vert V \right\vert-k)(\left\vert V \right\vert-k+1)}{2}.
-</math></center>
+<center><math>\left\vert V \right\vert-k\leq \left\vert E \right\vert\leq\frac{(\left\vert V \right\vert-k)(\left\vert V \right\vert-k+1)}{2}</math></center>
 Ponadto, są to najlepsze możliwe ograniczenia, tzn.
-* istnieje graf prosty <math>\mathbf{G}=\left(V,E\right)</math> o dokładnie <math>k</math>
+* istnieje graf prosty <math>\mathbf{G}=\left(V,E\right)</math> o dokładnie <math>k</math> składowych spójnych, w którym <math>\left\vert E \right\vert= \left\vert V \right\vert-k</math>,
-składowych spójnych, w którym <math>\left\vert E \right\vert= \left\vert V \right\vert-k</math>,
+* istnieje graf prosty <math>\mathbf{G}=\left(V,E\right)</math> o dokładnie <math>k</math> składowych spójnych, w którym <math>\left\vert E \right\vert= \frac{(\left\vert V \right\vert-k)(\left\vert V \right\vert-k+1)}{2}</math>.
-* istnieje graf prosty <math>\mathbf{G}=\left(V,E\right)</math> o dokładnie <math>k</math>
-składowych spójnych, w którym <math>\left\vert E \right\vert= \frac{(\left\vert V \right\vert-k)(\left\vert V \right\vert-k+1)}{2}</math>.
 }}
 {{dowod|||
 Niech <math>n</math> będzie liczbą wierzchołków grafu <math>\mathbf{G}</math>, a <math>m</math> liczbą jego krawędzi.
 Dowód nierówności <math>n-k\leq m</math> przeprowadzimy indukcyjnie
@@ Linia 289: / Linia 285: @@
 czyli rzeczywiście <math>n-k\leq m</math>.
-Dla dowodu górnego ograniczenia <math>m\leq (n-k)(n-k+1)/2 </math> na liczbę krawędzi
+Dla dowodu górnego ograniczenia <math>m\leq (n-k)(n-k+1)/2</math> na liczbę krawędzi
 załóżmy, że <math>\mathbf{G}</math> posiada <math>k</math> składowych spójnych
 i ma największą możliwą liczbę krawędzi wśród <math>n</math>-elementowych grafów
@@ Linia 300: / Linia 296: @@
 Istotnie, gdyby były dwie składowe <math>V_1, V_2</math>
 o odpowiednio <math>n_1 \geq n_2 >1</math> wierzchołkach,
-to -- nie zmieniając pozostałych składowych, i --
+to - nie zmieniając pozostałych składowych, i -
 przenosząc jeden wierzchołek z <math>V_2</math> do <math>V_1</math> otrzymalibyśmy nowy graf.
 W oryginalnym grafie sumaryczna liczba krawędzi w (pełnych) składowych <math>V_1, V_2</math>
 wynosi
-<math>{{n_1}\choose{2}} + {{n_2}\choose{2}},
+<math>{{n_1}\choose{2}} + {{n_2}\choose{2}}</math>,
-</math>
 a w nowym grafie te zmodyfikowane (również pełne) składowe posiadają łącznie
 <math>{{n_1+1}\choose{2}} + {{n_2-1}\choose{2}}
 </math>
 krawędzi. Różnica między nową a starą liczbą krawędzi wynosi więc
 <center><math>\frac{(n_1+1)n_1 + (n_2-1)(n_2-2) - n_1(n_1-1) - n_2(n_2-1)}{2}
 = n_1 - n_2 +1 \geq 1
 </math></center>
 co pokazuje, że nowy graf ma przynajmniej o jedną krawędź więcej.
@@ Linia 324: / Linia 321: @@
 Aby zobaczyć, że podanych ograniczeń na liczbę krawędzi nie można poprawić
 zauważmy, że
-* graf o <math>k</math> składowych spójnych, z których każda jest indukowaną ścieżką
+* graf o <math>k</math> składowych spójnych, z których każda jest indukowaną ścieżką o liczności odpowiednio <math>n_1,n_2,\ldots,n_k</math> ma dokładnie <math>(n_1-1)+(n_2-1)+\ldots+(n_k-1) =\left\vert V \right\vert-k</math> krawędzi.
-o liczności odpowiednio <math>n_1,n_2,\ldots,n_k</math> ma dokładnie
+* rozważany w dowodzie graf o dokładnie <math>k</math> składowych spójnych, z których <math>k-1</math> to wierzchołki izolowane, a pozostałe <math>\left\vert V \right\vert-k</math> wierzchołków tworzy klikę <math>\mathcal{K}_{n-k}</math>, ma dokładnie <math>\frac{(\left\vert V \right\vert-k)(\left\vert V \right\vert-k+1)}{2}</math> krawędzi.
-<math>(n_1-1)+(n_2-1)+\ldots+(n_k-1) =\left\vert V \right\vert-k</math> krawędzi.
-* rozważany w dowodzie graf o dokładnie <math>k</math> składowych spójnych, z których
-<math>k-1</math> to wierzchołki izolowane, a pozostałe <math>\left\vert V \right\vert-k</math> wierzchołków tworzy klikę
-<math>\mathcal{K}_{n-k}</math>, ma dokładnie <math>\frac{(\left\vert V \right\vert-k)(\left\vert V \right\vert-k+1)}{2}</math> krawędzi.
 }}
+[[File:Grafy las.svg|300x150px|thumb|left|Drzewo (a); las nie będący drzewem ale z dwiema gwiazdami jako składowymi spójnymi (b);
+oraz graf nie będący lasem (c)]]
+[[File:Grafy drzewo rozp.svg|250x250px|thumb|right|Drzewo rozpinające]]
 '''Las''' to graf nie zawierający cykli jako podgrafy.
@@ Linia 340: / Linia 338: @@
 '''Gwiazda''' to drzewo, w którym co najwyżej jeden wierzchołek nie jest liściem.
-{grafy_las}
-{Drzewo (a); las nie będący drzewem ale z dwiema gwiazdami jako składowymi spójnymi (b);
-oraz graf nie będący lasem (c) '''[Rysunek z pliku:''' <tt>grafylas.eps</tt>''']'''}
 '''Drzewo rozpinające''' grafu <math>\mathbf{G}</math> to podgraf
 grafu <math>\mathbf{G}</math> zawierający wszystkie jego wierzchołki i będący drzewem.
-{grafy_drzewo_rozp}
-{Drzewo rozpinające. '''[Rysunek z pliku:''' <tt>grafydrzeworozp.eps</tt>''']'''}
 Drzewa można zdefiniować na kilka równoważnych sposobów:
-{{twierdzenie|3||
+{{twierdzenie|12.3|tw 12.3|
 Dla grafu <math>\mathbf{T}=\left(V,E\right)</math> następujące warunki są równoważne:
 # <math>\mathbf{T}</math> jest drzewem,
@@ Linia 379: / Linia 369: @@
 <math>n_1-1</math> oraz <math>n_2-1</math> krawędzi.
 Sumując te krawędzie wraz z usuniętą otrzymujemy
-<center><math>\left\vert E \right\vert=(n_1-1)+(n_2-1)+1=\left\vert V \right\vert-1.
-</math></center>
+<center><math>\left\vert E \right\vert=(n_1-1)+(n_2-1)+1=\left\vert V \right\vert-1</math></center>
 . <math>\Rightarrow</math> 3.
@@ Linia 392: / Linia 384: @@
 . <math>\Rightarrow</math> 4.
 Usunięcie dowolnej krawędzi spowoduje, że nowy graf będzie miał <math>\left\vert V \right\vert-2</math> krawędzie.
-Na mocy Twierdzenia [[##th oszacowanie E|Uzupelnic th oszacowanie E|]] okazuje się,
+Na mocy [[#tw 12.2|Twierdzenia 12.2]] okazuje się,
 że jest to za mało aby graf był spójny.
@@ Linia 418: / Linia 410: @@
 }}
-Z charakteryzacji drzew podanej w Twierdzeniu [[##th warunki na drzewo|Uzupelnic th warunki na drzewo|]]
+Z charakteryzacji drzew podanej w [[#tw 12.3|Twierdzeniu 12.3]]
 natychmiast dostajemy następujący związek miedzy liczbą krawędzi i wierzchołków
 w dowolnym lesie.
-{{wniosek|||
+{{wniosek|12.4|wn 12.4|
 Każdy las <math>\mathbf{G}=\left(V,E\right)</math> o <math>k</math> składowych spójnych
 posiada <math>\left\vert E \right\vert=\left\vert V \right\vert-k</math> krawędzi.
 }}