PEE Moduł 4: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 17 wersji utworzonych przez 2 użytkowników) | |||
| Linia 1: | Linia 1: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd1.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd1.png|500px]] | ||
|valign="top"| | |valign="top"| | ||
|} | |} | ||
| Linia 7: | Linia 7: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd2.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd2.png|500px]] | ||
|valign="top"|'''Metoda równań Kirchhoffa''' | |valign="top"|'''Metoda równań Kirchhoffa''' | ||
W metodzie tej wykorzystuje się w bezpośredniej formie prawo prądowe i napięciowe Kirchhoffa uzupełnione o równania symboliczne opisujące poszczególne elementy obwodu. W efekcie zastosowania praw Kirchhoffa otrzymuje się układ równań algebraicznych o zespolonych współczynnikach. Jeśli założymy, że obwód posiada b gałęzi i n węzłów to w równaniach opisujących obwód wykorzystuje się (n-1) równań pochodzących z prawa prądowego Kirchhoffa. Pozostałe (b-n+1) równań wynika z prawa napięciowego Kirchhoffa dla (b-n+1) dowolnie wybranych oczek niezależnych w obwodzie (oczka uważa się za niezależne, jeśli równania napięciowe opisujące je są od siebie niezależne). | W metodzie tej wykorzystuje się w bezpośredniej formie prawo prądowe i napięciowe Kirchhoffa uzupełnione o równania symboliczne opisujące poszczególne elementy obwodu. W efekcie zastosowania praw Kirchhoffa otrzymuje się układ równań algebraicznych o zespolonych współczynnikach. Jeśli założymy, że obwód posiada <math>b</math> gałęzi i <math>n</math> węzłów to w równaniach opisujących obwód wykorzystuje się <math>(n-1)</math> równań pochodzących z prawa prądowego Kirchhoffa. Pozostałe <math>(b-n+1)</math> równań wynika z prawa napięciowego Kirchhoffa dla <math>(b-n+1)</math> dowolnie wybranych oczek niezależnych w obwodzie (oczka uważa się za niezależne, jeśli równania napięciowe opisujące je są od siebie niezależne). | ||
|} | |} | ||
| Linia 19: | Linia 16: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd3.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd3.png|500px]] | ||
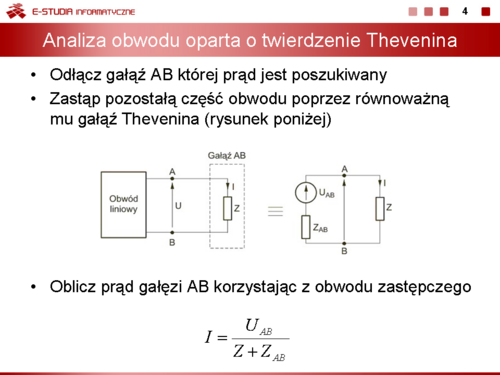
|valign="top"|'''Metoda oparta na twierdzeniu Thevenina''' | |valign="top"|'''Metoda oparta na twierdzeniu Thevenina''' | ||
| Linia 32: | Linia 29: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd4.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd4.png|500px]] | ||
|valign="top"|Na rysunku obok (slajd 4) przedstawiono sposób transformacji obwodu zgodnie z twierdzeniem Thevenina ułatwiający obliczenie prądu w wybranej gałęzi AB obwodu. | |valign="top"|Na rysunku obok (slajd 4) przedstawiono sposób transformacji obwodu zgodnie z twierdzeniem Thevenina ułatwiający obliczenie prądu w wybranej gałęzi AB obwodu. | ||
Prąd <math>I\ | Prąd <math>I\ </math>, występujący w gałęzi AB obwodu oryginalnego jest równy prądowi <math>I\ </math>, w tej samej gałęzi obwodu uproszczonego. Napięcie <math>U_{AB}</math> występujące na rysunku reprezentuje źródło zastępcze, natomiast impedancja <math>Z_{AB}</math> jest impedancją zastępczą obwodu. Przy założeniu, że gałąź AB w której obliczamy prąd reprezentowana jest przez impedancję <math>Z\ </math>,, prąd tej gałęzi można obliczyć korzystając z prawa napięciowego Kirchhoffa z którego wynika wyrażenie na prąd gałęzi w następującej postaci | ||
: <math>I={U_{AB} \over Z+Z_{AB}}</math> | : <math>I={U_{AB} \over Z+Z_{AB}}</math> | ||
| Linia 45: | Linia 42: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd5.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd5.png|500px]] | ||
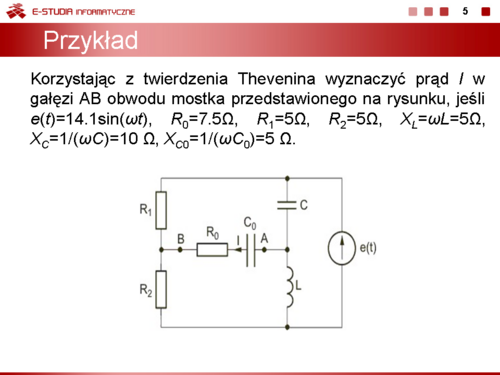
|valign="top"|Jako przykład rozpatrzymy obliczenie prądu w gałęzi AB obwodu przedstawionego na slajdzie. | |valign="top"|Jako przykład rozpatrzymy obliczenie prądu w gałęzi AB obwodu przedstawionego na slajdzie. | ||
| Linia 54: | Linia 51: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd6.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd6.png|500px]] | ||
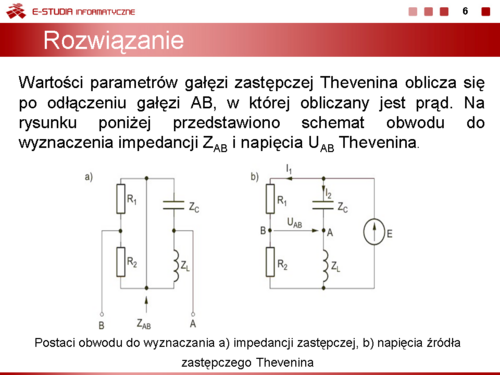
|valign="top"|W pierwszej kolejności należy wyznaczyć parametry zastępcze gałęzi Thevenina: <math>Z_{AB}</math> i <math>U_{AB}</math>. Slajd obok przedstawia schematy obwodów służące do obliczenia tych wielkości. | |valign="top"|W pierwszej kolejności należy wyznaczyć parametry zastępcze gałęzi Thevenina: <math>Z_{AB}</math> i <math>U_{AB}</math>. Slajd obok przedstawia schematy obwodów służące do obliczenia tych wielkości. | ||
| Linia 65: | Linia 62: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd7.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd7.png|500px]] | ||
|valign="top"|Łatwo pokazać, że impedancja zastępcza tego obwodu jest równa | |valign="top"|Łatwo pokazać, że impedancja zastępcza tego obwodu jest równa | ||
: <math>Z_{AB}={R_1R_2 \over R_1+R_2}+{Z_LZ_C \over Z_L+Z_C}={5 \cdot 5 \over 5+5}+{j5 \cdot (-j10) \over j5-j10}=2,5+j10</math> | : <math>Z_{AB}={R_1R_2 \over R_1+R_2}+{Z_LZ_C \over Z_L+Z_C}={5 \cdot 5 \over 5+5}+{j5 \cdot (-j10) \over j5-j10}=2,5+j10</math> | ||
Rys. b na slajdzie nr 6 przedstawia obwód do obliczenia wartości źródła zastępczego <math>U_{AB}</math> w schemacie zastępczym Thevenina. Obliczając kolejno prądy | Rys. b na slajdzie nr 6 przedstawia obwód do obliczenia wartości źródła zastępczego <math>U_{AB}</math> w schemacie zastępczym Thevenina. Obliczając kolejno prądy | ||
: <math>I_1={E \over R_1+R_2}=1</math> | |||
: <math>I_2={E \over jX_L-jX_C}=2j</math> | : <math>I_2={E \over jX_L-jX_C}=2j</math> | ||
Napięcie <math>U_{AB}</math> określa się ze wzoru | Napięcie <math>U_{AB}</math> określa się ze wzoru | ||
: <math>U_{AB}=R_1I_1-Z_CI_2=-15</math> | : <math>U_{AB}=R_1I_1-Z_CI_2=-15</math> | ||
| Linia 88: | Linia 81: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd8.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd8.png|500px]] | ||
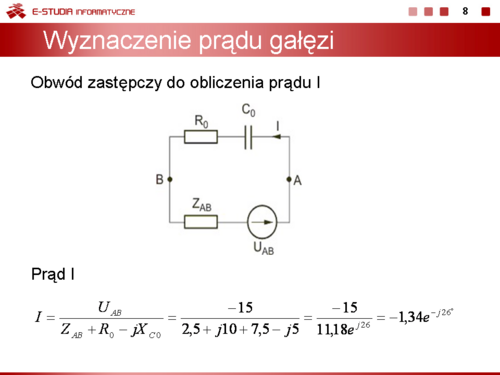
|valign="top"|Wykorzystując obwód zastępczy Thevenina z rysunku na slajdzie 8 i prawo napięciowe Kirchhoffa, wartość skuteczną zespoloną prądu <math>I\ | |valign="top"|Wykorzystując obwód zastępczy Thevenina z rysunku na slajdzie 8 i prawo napięciowe Kirchhoffa, wartość skuteczną zespoloną prądu <math>I\ </math>, określa się ze wzoru | ||
: <math>I={U_{AB} \over Z_{AB}+R_0-jX_{C0}}={-15 \over 2,5+j10+7,5-j5}={-15 \over 11,18e^{j26^\circ}}=-1,34e^{-j26^\circ}</math> | : <math>I={U_{AB} \over Z_{AB}+R_0-jX_{C0}}={-15 \over 2,5+j10+7,5-j5}={-15 \over 11,18e^{j26^\circ}}=-1,34e^{-j26^\circ}</math> | ||
Wartości chwilowe prądu <math>i(t)\ </math>, wyznaczane są z zależności | |||
Wartości chwilowe prądu <math>i(t)\ | |||
: <math>i(t)=-1,34\sqrt{2}sin(\omega t-26^\circ)A</math> | : <math>i(t)=-1,34\sqrt{2}sin(\omega t-26^\circ)A</math> | ||
Zauważmy, że zastosowanie twierdzenia Thevenina umożliwiło rozwiązanie obwodu względem jednego wybranego prądu bez konieczności rozwiązania układu równań algebraicznych. | Zauważmy, że zastosowanie twierdzenia Thevenina umożliwiło rozwiązanie obwodu względem jednego wybranego prądu bez konieczności rozwiązania układu równań algebraicznych. | ||
| Linia 107: | Linia 96: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd9.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd9.png|500px]] | ||
|valign="top"|'''Metoda oparta na twierdzeniu Nortona''' | |valign="top"|'''Metoda oparta na twierdzeniu Nortona''' | ||
| Linia 114: | Linia 103: | ||
'''Twierdzenie Nortona''' | '''Twierdzenie Nortona''' | ||
Dowolny aktywny obwód liniowy można od strony wybranych zacisków AB zastąpić obwodem równoważnym, złożonym z równoległego połączenia idealnego źródła prądu i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się w obwodzie oryginalnym jako prąd zwarciowy gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu i jest identyczna z impedancją zastępczą w twierdzeniu Thevenina. | Dowolny aktywny obwód liniowy można od strony wybranych zacisków AB zastąpić obwodem równoważnym, złożonym z równoległego połączenia idealnego źródła prądu i impedancji zastępczej obwodu. Wartość źródła zastępczego oblicza się w obwodzie oryginalnym jako prąd zwarciowy gałęzi AB. Impedancja zastępcza widziana z zacisków AB dotyczy obwodu po wyłączeniu gałęzi AB i po zwarciu wszystkich źródeł napięcia oraz rozwarciu źródeł prądu i jest identyczna z impedancją zastępczą w twierdzeniu Thevenina. | ||
|} | |} | ||
| Linia 123: | Linia 110: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd10.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd10.png|500px]] | ||
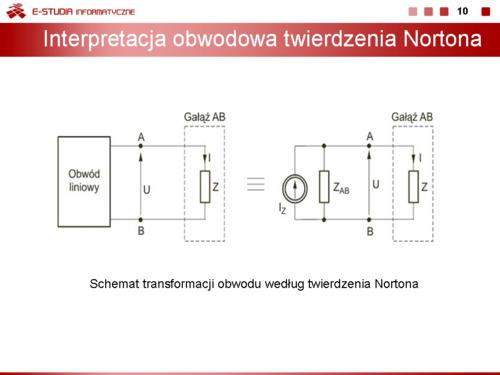
|valign="top"|Rysunek na slajdzie 10 przedstawia schemat transformacji obwodu zgodnie z twierdzeniem Nortona. | |valign="top"|Rysunek na slajdzie 10 przedstawia schemat transformacji obwodu zgodnie z twierdzeniem Nortona. | ||
Prąd <math>I\ | Prąd <math>I\ </math>, oraz napięcie <math>U\ </math>, występujące w gałęzi AB obwodu oryginalnego są równe odpowiednio prądowi <math>I\ </math>, oraz napięciu <math>U\ </math>, w tej samej gałęzi obwodu uproszczonego. Źródło prądowe <math>I_Z</math> występujące na rysunku reprezentuje źródło zastępcze, natomiast impedancja <math>Z_{AB}</math> jest impedancją zastępczą obwodu. Przy założeniu, że gałąź AB reprezentowana jest przez impedancję <math>Z\ </math>,, napięcie tej gałęzi oblicza się z prawa prądowego Kirchhoffa <math>I_Z-U({1 \over Z}+{1 \over Z_{AB}})=0</math>, które pozwala wyrazić poszukiwane napięcie gałęzi w postaci | ||
: <math>U={I_Z \over 1/Z+1/Z_{AB}}</math> | : <math>U={I_Z \over 1/Z+1/Z_{AB}}</math> | ||
Znajomość napięcia pozwala wyznaczyć na podstawie prawa Ohma prąd gałęzi korzystając z zależności <math>I=U/Z</math> Podobnie jak metoda Thevenina, zastosowanie twierdzenia Nortona umożliwia obliczenie prądu i napięcia tylko jednej gałęzi obwodu. Zwykle z punktu widzenia obliczeniowego wygodniejsze jest użycie metody Thevenina. | Znajomość napięcia pozwala wyznaczyć na podstawie prawa Ohma prąd gałęzi korzystając z zależności <math>I=U/Z</math> Podobnie jak metoda Thevenina, zastosowanie twierdzenia Nortona umożliwia obliczenie prądu i napięcia tylko jednej gałęzi obwodu. Zwykle z punktu widzenia obliczeniowego wygodniejsze jest użycie metody Thevenina. | ||
| Linia 138: | Linia 123: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd11.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd11.png|500px]] | ||
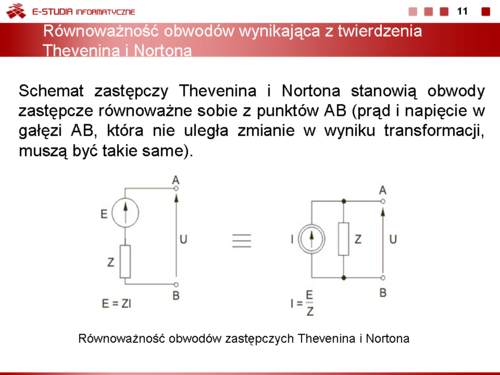
|valign="top"|'''Równoważność twierdzenia Thevenina i Nortona''' | |valign="top"|'''Równoważność twierdzenia Thevenina i Nortona''' | ||
Twierdzenia Thevenina i Nortona pozwalają wyznaczyć uproszczone schematy zastępcze tego samego układu elektrycznego z punktów AB obwodu wyjściowego. Oba schematy uproszczone stanowią więc obwody zastępcze równoważne sobie, co oznacza, że prąd i napięcie w gałęzi AB, która nie uległa zmianie w wyniku transformacji, są takie same. Oznacza to, że gałąź szeregowa zawierająca idealne źródło napięcia <math>E\ | Twierdzenia Thevenina i Nortona pozwalają wyznaczyć uproszczone schematy zastępcze tego samego układu elektrycznego z punktów AB obwodu wyjściowego. Oba schematy uproszczone stanowią więc obwody zastępcze równoważne sobie, co oznacza, że prąd i napięcie w gałęzi AB, która nie uległa zmianie w wyniku transformacji, są takie same. Oznacza to, że gałąź szeregowa zawierająca idealne źródło napięcia <math>E\ </math>, i impedancję <math>Z\ </math>, może być bez zmiany prądu w obwodzie zewnętrznym zastąpiona gałęzią równoległą zawierającą idealne źródło prądowe <math>I\ </math>, oraz impedancję <math>Z\ </math>,, jak to zilustrowano na rysunku obok (slajd 11). | ||
Wzajemne relacje między wartościami źródła prądu i napięcia określa wzór | Wzajemne relacje między wartościami źródła prądu i napięcia określa wzór | ||
| Linia 151: | Linia 136: | ||
: <math>E=ZI</math> | : <math>E=ZI</math> | ||
przy zamianie gałęzi równoległej na szeregową. Impedancja <math>Z\ | przy zamianie gałęzi równoległej na szeregową. Impedancja <math>Z\ </math>, w obu obwodach zastępczych pozostaje taka sama | ||
|} | |} | ||
| Linia 157: | Linia 142: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd12.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd12.png|500px]] | ||
|valign="top"|'''Metoda potencjałów węzłowych''' | |valign="top"|'''Metoda potencjałów węzłowych''' | ||
| Linia 168: | Linia 153: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd13.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd13.png|500px]] | ||
|valign="top"|Zostało wykazane, że każdy obwód liniowy RLC może być opisany równaniem macierzowym potencjałów węzłowych o postaci | |valign="top"|Zostało wykazane, że każdy obwód liniowy RLC może być opisany równaniem macierzowym potencjałów węzłowych o postaci | ||
<math>\mathbf{YV}=\mathbf{I}_{zr}</math> | : <math>\mathbf{YV}=\mathbf{I}_{zr}</math> | ||
<math>\mathbf{V}=\mathbf{Y}^{-1}\mathbf{I}_{zr}</math> | : <math>\mathbf{V}=\mathbf{Y}^{-1}\mathbf{I}_{zr}</math> | ||
w której <math>\mathbf{Y}</math>, jest macierzą węzłową o wymiarach <math>NxN\ </math>,, gdzie <math>N\ </math>, jest liczbą węzłów niezależnych w obwodzie, <math>\mathbf{V}\ </math>, jest wektorem niezależnych potencjałów węzłowych o wymiarze <math>N\ </math>, a <math>\mathbf{I}_{zr}</math> jest wektorem prądów źródłowych stanowiących wymuszenie. Macierz węzłowa <math>\mathbf{Y}</math>, określona jest w postaci | |||
<math>\mathbf{Y}=\begin{bmatrix} | : <math>\mathbf{Y}=\begin{bmatrix} | ||
Y_{11} & Y_{12} & \cdots & Y_{1N} \\ | Y_{11} & Y_{12} & \cdots & Y_{1N} \\ | ||
Y_{21} & Y_{22} & \cdots & Y_{2N} \\ | Y_{21} & Y_{22} & \cdots & Y_{2N} \\ | ||
| Linia 188: | Linia 173: | ||
a wektory <math>\mathbf{V}</math>, oraz <math>\mathbf{I}_{zr}</math> dane są jak następuje | a wektory <math>\mathbf{V}</math>, oraz <math>\mathbf{I}_{zr}</math> dane są jak następuje | ||
<math>\mathbf{V}=\begin{bmatrix} | |||
: <math>\mathbf{V}=\begin{bmatrix} | |||
V_1 \\ | V_1 \\ | ||
V_2 \\ | V_2 \\ | ||
| Linia 204: | Linia 190: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd14.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd14.png|500px]] | ||
|valign="top"|Elementy <math>Y_{ii}</math> położone na głównej diagonalnej macierzy <math>\mathbf{Y}\ | |valign="top"|Elementy <math>Y_{ii}</math> położone na głównej diagonalnej macierzy <math>\mathbf{Y}\ </math>, nazywane są '''admitancjami własnymi''' węzła <math>i\ </math>,-tego. W przypadku obwodów RLC bez źródeł sterowanych admitancja własna węzła <math>i\ </math>,-tego jest równa sumie admitancji wszystkich gałęzi włączonych w <math>i\ </math>,-tym węźle. Elementy <math>Y_{ij}</math> położone poza główną diagonalną są '''admitancjami wzajemnymi''' między węzłem <math>i\ </math>,-tym oraz <math>j\ </math>,-tym. Admitancja wzajemna dwu węzłów jest równa admitancji łączącej te węzły wziętej ze znakiem minus. Admitancja wzajemna węzła <math>i\ </math>,-tego oraz <math>j\ </math>,-tego jest taka sama jak węzła <math>j\ </math>,-tego oraz <math>i\ </math>,-tego, tzn. <math>Y_{ij}=Y_{ji}</math>. Macierz admitancyjna <math>\mathbf{Y}\ </math>, dla obwodów RLC bez źródeł sterowanych jest więc macierzą symetryczną. | ||
Elementy wektora wymuszeń prądowych <math>\mathbf{I}_{zr}</math> są równe sumie wszystkich prądów źródłowych wpływających do danego węzła, przy czym prąd źródłowy dopływający do węzła bierze się ze znakiem plus a prąd odpływający od węzła ze znakiem minus. | Elementy wektora wymuszeń prądowych <math>\mathbf{I}_{zr}</math> są równe sumie wszystkich prądów źródłowych wpływających do danego węzła, przy czym prąd źródłowy dopływający do węzła bierze się ze znakiem plus a prąd odpływający od węzła ze znakiem minus. | ||
| Linia 213: | Linia 199: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd15.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd15.png|500px]] | ||
|valign="top"|Podsumowując, analiza obwodów w stanie ustalonym metoda węzłową wymaga wykonania następujących etapów: | |valign="top"|Podsumowując, analiza obwodów w stanie ustalonym metoda węzłową wymaga wykonania następujących etapów: | ||
*Opis obwodu równaniem macierzowym potencjałów węzłowych (zmienne poszukiwane: wektor potencjałów <math>\mathbf{V}\ | *Opis obwodu równaniem macierzowym potencjałów węzłowych (zmienne poszukiwane: wektor potencjałów <math>\mathbf{V}\ </math>,) | ||
*Rozwiązanie układu równań <math>\mathbf{V}=\mathbf{Y}^{-1}\mathbf{I}_{zr}</math> | *Rozwiązanie układu równań <math>\mathbf{V}=\mathbf{Y}^{-1}\mathbf{I}_{zr}</math> | ||
*Określenie prądów gałęziowych z prawa napięciowego Kirchhoffa przy znanych potencjałach węzłowych prąd gałęziowy jest równy iloczynowi admitancji elementu i napięcia na nim wyrażonego poprzez potencjały węzłowe. | *Określenie prądów gałęziowych z prawa napięciowego Kirchhoffa przy znanych potencjałach węzłowych prąd gałęziowy jest równy iloczynowi admitancji elementu i napięcia na nim wyrażonego poprzez potencjały węzłowe. | ||
| Linia 225: | Linia 211: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd16.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd16.png|500px]] | ||
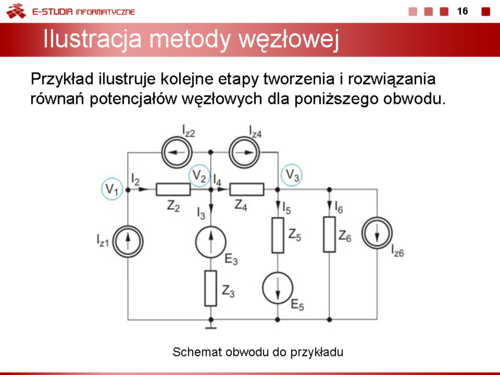
|valign="top"|Sposób formułowania równań węzłowych zilustrujemy na przykładzie obwodu przedstawionego na rysunku obok. | |valign="top"|Sposób formułowania równań węzłowych zilustrujemy na przykładzie obwodu przedstawionego na rysunku obok. | ||
Korzystając z przedstawionych reguł formułowania równań węzłowych należy napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku. | Korzystając z przedstawionych reguł formułowania równań węzłowych należy napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku. | ||
| Linia 235: | Linia 220: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd17.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd17.png|500px]] | ||
|valign="top"|Obwód zawiera 3 węzły niezależne: <math>V_1</math>, <math>V_2</math> oraz <math>V_3</math> mierzone względem węzła odniesienia jak to oznaczono na rysunku. Oznaczając admitancje przez <math>Y_i\ | |valign="top"|Obwód zawiera 3 węzły niezależne: <math>V_1</math>, <math>V_2</math> oraz <math>V_3</math> mierzone względem węzła odniesienia jak to oznaczono na rysunku. Oznaczając admitancje przez <math>Y_i\ </math>,, gdzie <math>Y_i=1/Z_i</math> otrzymuje się macierz potencjałów węzłowych <math>\mathbf{Y}\ </math>, oraz wektor prądów wymuszających <math>\mathbf{I}_{zr}</math> w postaci | ||
<math>\begin{bmatrix} | <math>\begin{bmatrix} | ||
| Linia 256: | Linia 242: | ||
</math> | </math> | ||
: <math>\mathbf{I}_{zr}= | |||
: <math>\mathbf{Y}=\begin{bmatrix} | |||
Y_2 & -Y_2 & 0 \\ | |||
-Y_2 & Y_2+Y_3+Y_4 & -Y_4 \\ | |||
0 & -Y_4 & Y_4+Y_5+Y_6 | |||
\end{bmatrix}</math>, <math>\mathbf{I}_{zr}= | |||
\begin{bmatrix} | \begin{bmatrix} | ||
I_{Z1}+I_{Z2}\\ | I_{Z1}+I_{Z2}\\ | ||
| Linia 277: | Linia 268: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd18.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd18.png|500px]] | ||
|valign="top"|Na podstawie obliczonych wartości napięć węzłowych obwodu można w prosty sposób korzystając z prawa napięciowego Kirchhoffa dla poszczególnych gałęzi obwodu wyznaczyć prądy gałęziowe. Wystarczy w tym celu zastosować bądź prawo Ohma (jeśli gałąź zawiera jedynie element pasywny) lub równanie napięciowe Kirchoffa dla gałęzi szeregowej zawierającej źródło napięcia i element pasywny. Przykładowo dla obwodu z rysunku na slajdzie 16 odpowiednie zależności przyjmują postać: | |valign="top"|Na podstawie obliczonych wartości napięć węzłowych obwodu można w prosty sposób korzystając z prawa napięciowego Kirchhoffa dla poszczególnych gałęzi obwodu wyznaczyć prądy gałęziowe. Wystarczy w tym celu zastosować bądź prawo Ohma (jeśli gałąź zawiera jedynie element pasywny) lub równanie napięciowe Kirchoffa dla gałęzi szeregowej zawierającej źródło napięcia i element pasywny. Przykładowo dla obwodu z rysunku na slajdzie 16 odpowiednie zależności przyjmują postać: | ||
: <math>I_2=Y_2(V_1-V_2)</math> | : <math>I_2=Y_2(V_1-V_2)</math> | ||
: <math>I_3=Y_3(V_2-E_3)</math> | : <math>I_3=Y_3(V_2-E_3)</math> | ||
: <math>I_4=Y_4(V_2-V_3)</math> | : <math>I_4=Y_4(V_2-V_3)</math> | ||
: <math>I_5=Y_5(V_3+E_5)</math> | : <math>I_5=Y_5(V_3+E_5)</math> | ||
: <math>I_6=Y_6V_3</math> | : <math>I_6=Y_6V_3</math> | ||
Należy podkreślić, że metoda potencjałów węzłowych wymaga rozwiązania układu <math>N\ | Należy podkreślić, że metoda potencjałów węzłowych wymaga rozwiązania układu <math>N\ </math>, równań, gdzie <math>N\ </math>, oznacza liczbę węzłów niezależnych. Zwykle liczba węzłów jest dużo mniejsza niż liczba gałęzi obwodu, stąd metoda potencjałów węzłowych jest znacznie efektywniejsza niż metoda klasyczna wykorzystująca bezpośrednio prawa Kirchhoffa. | ||
|} | |} | ||
| Linia 292: | Linia 287: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd19.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd19.png|500px]] | ||
|valign="top"|Reguły tworzenia opisu węzłowego przedstawione powyżej zakładały istnienie jedynie elementów pasywnych RLC oraz źródeł wymuszających typu prądowego. Dzięki takiemu założeniu są one bardzo proste i łatwe w stosowaniu. | |valign="top"|Reguły tworzenia opisu węzłowego przedstawione powyżej zakładały istnienie jedynie elementów pasywnych RLC oraz źródeł wymuszających typu prądowego. Dzięki takiemu założeniu są one bardzo proste i łatwe w stosowaniu. | ||
W przypadku wystąpienia źródeł sterowanych oraz idealnych źródeł napięciowych włączonych między węzłami trudno jest podać formułę ogólną pozwalającą określić zarówno macierz admitancyjną jak i wektor wymuszeń prądowych. Zasada tworzenia opisu admitancyjnego w takim przypadku korzysta bezpośrednio ze stwierdzenia, że opis admitancyjny powstaje jako uporządkowany zbiór równań wynikających z prawa prądowego Kirchhoffa, w których wszystkie prądy gałęziowe zostały wyrażone poprzez potencjały węzłowe i wartości źródeł wymuszających. Macierz admitancyjna <math>\mathbf{Y}\ | W przypadku wystąpienia źródeł sterowanych oraz idealnych źródeł napięciowych włączonych między węzłami trudno jest podać formułę ogólną pozwalającą określić zarówno macierz admitancyjną jak i wektor wymuszeń prądowych. Zasada tworzenia opisu admitancyjnego w takim przypadku korzysta bezpośrednio ze stwierdzenia, że opis admitancyjny powstaje jako uporządkowany zbiór równań wynikających z prawa prądowego Kirchhoffa, w których wszystkie prądy gałęziowe zostały wyrażone poprzez potencjały węzłowe i wartości źródeł wymuszających. Macierz admitancyjna <math>\mathbf{Y}\ </math>, wynika wówczas z uporządkowania macierzowego powstałego układu równań. | ||
|} | |} | ||
| Linia 301: | Linia 296: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd20.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd20.png|500px]] | ||
|valign="top"|'''Metoda prądów oczkowych (oczkowa)''' | |valign="top"|'''Metoda prądów oczkowych (oczkowa)''' | ||
W metodzie prądów oczkowych, zwanej również metodą oczkową, wprowadza się prądy oczkowe jako zmienne, czyli prądy przypisane niezależnym oczkom występującym w obwodzie. Przykładowy wybór oczek niezależnych i oznaczenie prądów oczkowych obwodu przedstawiono na rysunku obok (slajd 20). | W metodzie prądów oczkowych, zwanej również metodą oczkową, wprowadza się prądy oczkowe jako zmienne, czyli prądy przypisane niezależnym oczkom występującym w obwodzie. Przykładowy wybór oczek niezależnych i oznaczenie prądów oczkowych obwodu przedstawiono na rysunku obok (slajd 20). | ||
|} | |} | ||
| Linia 311: | Linia 305: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd21.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd21.png|500px]] | ||
|valign="top"|Oznaczmy w ogólności wektor prądów oczkowych w postaci | |valign="top"|Oznaczmy w ogólności wektor prądów oczkowych w postaci | ||
: <math>\mathbf{I}_o= | : <math>\mathbf{I}_o= | ||
| Linia 322: | Linia 317: | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
w której <math>I_{ok}</math> oznacza prąd oczkowy <math>k\ | |||
w której <math>I_{ok}</math> oznacza prąd oczkowy <math>k\ </math>,-tego oczka. Dla uzyskania opisu oczkowego wykorzystuje się prawo napięciowe Kirchhoffa napisane dla wszystkich oczek niezależnych obwodu. Następnie wyraża się wszystkie prądy gałęziowe poprzez prądy oczkowe (prąd gałęziowy jest równy sumie lub różnicy prądów oczkowych przeprowadzonych przez daną gałąź) i otrzymuje opis obwodu w postaci układu równań oczkowych | |||
: <math>\mathbf{ZI}_o=\mathbf{E}</math> | : <math>\mathbf{ZI}_o=\mathbf{E}</math> | ||
gdzie macierz oczkowa <math>\mathbf{Z}\ </math>, oraz wektor napięć wymuszających <math>\mathbf{E}\ </math>, przyjmują postać | |||
: <math>\mathbf{Z}= | : <math>\mathbf{Z}= | ||
| Linia 335: | Linia 331: | ||
\cdots & \cdots & \cdots & \cdots\\ | \cdots & \cdots & \cdots & \cdots\\ | ||
Z_{N1} & Z_{N2} & \cdots & Z_{NN} | Z_{N1} & Z_{N2} & \cdots & Z_{NN} | ||
\end{bmatrix}</math> | \end{bmatrix}</math>, <math>\mathbf{E}= | ||
\begin{bmatrix} | \begin{bmatrix} | ||
E_{o1}\\ | E_{o1}\\ | ||
| Linia 349: | Linia 343: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd22.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd22.png|500px]] | ||
|valign="top"|Elementy <math>Z_{ii}</math> położone na głównej diagonalnej macierzy <math>\mathbf{Z}\ | |valign="top"|Elementy <math>Z_{ii}</math> położone na głównej diagonalnej macierzy <math>\mathbf{Z}\ </math>, nazywamy '''impedancjami własnymi''' oczka <math>i\ </math>,-tego. Elementy <math>Z_{ij}</math> położone poza główną diagonalną są '''impedancjami wzajemnymi''' między oczkiem <math>i\ </math>,-tym oraz <math>j\ </math>,-tym. Impedancja wzajemna dwu oczek przy identycznym zwrocie wszystkich prądów oczkowych jest równa impedancji wspólnej dla obu oczek wziętej ze znakiem minus. | ||
|} | |} | ||
| Linia 356: | Linia 350: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd23.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd23.png|500px]] | ||
|valign="top"|Przy założeniu, że wszystkie prądy oczkowe mają identyczny zwrot, dla obwodów RLC bez źródeł sterowanych impedancja własna oczka <math>i\ | |valign="top"|Przy założeniu, że wszystkie prądy oczkowe mają identyczny zwrot, dla obwodów RLC bez źródeł sterowanych impedancja własna oczka <math>i\ </math>,-tego jest równa sumie impedancji wszystkich gałęzi występujących w oczku. | ||
Impedancja wzajemna oczka <math>i\ | Impedancja wzajemna oczka <math>i\ </math>,-tego oraz <math>j\ </math>,-tego jest taka sama jak oczka <math>j\ </math>,-tego oraz <math>i\ </math>,-tego, tzn. <math>Z_{ij}=Z_{ji}</math>. Macierz <math>\mathbf{Z}\ </math>, jest więc macierzą symetryczną. | ||
Element <math>k\ | Element <math>k\ </math>,-ty wektora wymuszeń napięciowych <math>\mathbf{E}\ </math>, jest równy sumie wszystkich napięć źródłowych występujących w <math>k\ </math>,-tym oczku. Przy założonej orientacji oczka napięcie źródłowe dodaje się ze znakiem plus jeśli jego zwrot jest identyczny z tą orientacją a ze znakiem minus jeśli ten zwrot jest przeciwny. | ||
|} | |} | ||
| Linia 367: | Linia 361: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd24.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd24.png|500px]] | ||
|valign="top"|Sposób tworzenia opisu oczkowego zilustrujemy na przykładzie obwodu z rysunku na slajdzie. | |valign="top"|Sposób tworzenia opisu oczkowego zilustrujemy na przykładzie obwodu z rysunku na slajdzie. | ||
Dla podanego obwodu napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku. Obwód zawiera 3 oczka niezależne, stąd wymiar macierzy oczkowej <math>\mathbf{Z}</math> jest równy 3, podobnie jak liczba nieznanych składników wektora prądów oczkowych oraz liczba znanych składników wektora napięć wymuszających. | |||
Dla podanego obwodu napisać równanie prądów oczkowych przy założeniu układu oczek niezależnych jak na rysunku. Obwód | |||
|} | |} | ||
| Linia 377: | Linia 369: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd25.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd25.png|500px]] | ||
|valign="top"| | |valign="top"|Korzystając z podanej wcześniej reguły tworzenia opisu oczkowego otrzymuje się | ||
: <math>Z= | |||
: <math>\mathbf{Z}= | |||
\begin{bmatrix} | \begin{bmatrix} | ||
Z_1+Z_2+Z_3 & -Z_3 & -Z_1\\ | Z_1+Z_2+Z_3 & -Z_3 & -Z_1\\ | ||
| Linia 387: | Linia 380: | ||
\end{bmatrix}</math> | \end{bmatrix}</math> | ||
: <math>E= | |||
: <math>\mathbf{E}= | |||
\begin{bmatrix} | \begin{bmatrix} | ||
-E_1-E_3\\ | -E_1-E_3\\ | ||
| Linia 395: | Linia 389: | ||
Biorąc pod uwagę że obwód zawiera trzy nieznane prądy oczkowe tworzące wektor prądów <math> | Biorąc pod uwagę że obwód zawiera trzy nieznane prądy oczkowe tworzące wektor prądów <math>\mathbf{I}_o= \left [ I_{o1} \ I_{o2} \ I_{o3} \right ] ^T</math>, równanie oczkowe <math>\mathbf{ZI}_o=\mathbf{E}</math> stanowi zbiór trzech równań liniowych. Rozwiązanie tego układu równań pozwala określić te zmienne. | ||
|} | |} | ||
| Linia 401: | Linia 395: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd26.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd26.png|500px]] | ||
|valign="top"| | |valign="top"|Znajomość prądów oczkowych pozwala wyznaczyć wszystkie prądy gałęziowe obwodu. Mianowicie | ||
: <math>I_1=I_{03}-I_{01}</math> | : <math>I_1=I_{03}-I_{01}</math> | ||
| Linia 414: | Linia 409: | ||
: <math>I_6=-I_{03}</math> | : <math>I_6=-I_{03}</math> | ||
|} | |} | ||
| Linia 421: | Linia 414: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd27.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd27.png|500px]] | ||
|valign="top"| | |valign="top"|Metoda prądów oczkowych wymaga rozwiązania układu <math>N\ </math>, równań, gdzie <math>N\ </math>, oznacza liczbę oczek niezależnych. Podobnie jak w metodzie węzłowej liczba oczek jest zwykle dużo mniejsza niż liczba gałęzi obwodu, stąd metoda prądów oczkowych jest dużo bardziej efektywna niż metoda klasyczna wykorzystująca bezpośrednio prawa Kirchhoffa. | ||
|} | |} | ||
| Linia 428: | Linia 421: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:PEE_M4_Slajd28.png]] | |valign="top" width="500px"|[[Grafika:PEE_M4_Slajd28.png|500px]] | ||
|valign="top"|'''Zasada superpozycji''' | |valign="top"|'''Zasada superpozycji''' | ||
Omówione wcześniej metody analizy symbolicznej stanowią dobry i skuteczny sposób rozwiązania problemu przy istnieniu w obwodzie źródeł sinusoidalnych o tej samej częstotliwości, gdyż dla każdego źródła elementy reaktancyjne LC przedstawiają sobą te same wartości reaktancji. Istotna trudność występuje dopiero przy istnieniu w obwodzie wielu źródeł o różnych częstotliwościach. W takim przypadku nie istnieje pojęcie impedancji wspólnej dla każdego źródła, co uniemożliwia zastosowanie metody symbolicznej. Jedynym rozwiązaniem pozostaje wtedy zastosowanie zasady '''superpozycji'''. Obowiązuje ona '''tylko''' dla obwodów liniowych. Jej treść jest następująca. | Omówione wcześniej metody analizy symbolicznej stanowią dobry i skuteczny sposób rozwiązania problemu przy istnieniu w obwodzie źródeł sinusoidalnych o tej samej częstotliwości, gdyż dla każdego źródła elementy reaktancyjne LC przedstawiają sobą te same wartości reaktancji. Istotna trudność występuje dopiero przy istnieniu w obwodzie wielu źródeł o różnych częstotliwościach. W takim przypadku nie istnieje pojęcie impedancji wspólnej dla każdego źródła, co uniemożliwia zastosowanie metody symbolicznej. Jedynym rozwiązaniem pozostaje wtedy zastosowanie zasady '''superpozycji'''. Obowiązuje ona '''tylko''' dla obwodów liniowych. Jej treść jest następująca. | ||
''Zasada superpozycji | <hr> | ||
''Zasada superpozycji'' | |||
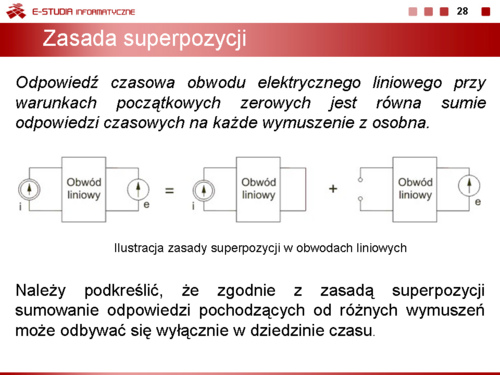
Odpowiedź czasowa obwodu elektrycznego liniowego przy warunkach początkowych zerowych jest równa sumie odpowiedzi czasowych na każde wymuszenie z osobna.'' | ''Odpowiedź czasowa obwodu elektrycznego liniowego przy warunkach początkowych zerowych jest równa sumie odpowiedzi czasowych na każde wymuszenie z osobna.'' | ||
<hr> | |||
Tak ogólnie sformułowana zasada obowiązuje zarówno w stanie ustalonym jak i nieustalonym obwodu. W przypadku analizy stanów ustalonych jej zastosowanie w analizie obwodów polega na rozbiciu danego obwodu o wielu wymuszeniach na wiele obwodów zawierających po jednym wymuszeniu, rozwiązaniu każdego z nich oddzielnie a następnie zsumowaniu odpowiedzi czasowych każdego obwodu. Należy pamiętać przy tym o zasadzie, że eliminowane źródła są zastępowane zwarciem (jeśli źródło jest napięciowe) lub rozwarciem (gdy źródło jest prądowe). | Tak ogólnie sformułowana zasada obowiązuje zarówno w stanie ustalonym jak i nieustalonym obwodu. W przypadku analizy stanów ustalonych jej zastosowanie w analizie obwodów polega na rozbiciu danego obwodu o wielu wymuszeniach na wiele obwodów zawierających po jednym wymuszeniu, rozwiązaniu każdego z nich oddzielnie a następnie zsumowaniu odpowiedzi czasowych każdego obwodu. Należy pamiętać przy tym o zasadzie, że eliminowane źródła są zastępowane zwarciem (jeśli źródło jest napięciowe) lub rozwarciem (gdy źródło jest prądowe). | ||
Należy podkreślić, że zgodnie z zasadą superpozycji sumowanie odpowiedzi pochodzących od różnych wymuszeń może odbywać się wyłącznie w dziedzinie czasu. Sumowanie wartości zespolonych od poszczególnych wymuszeń byłoby poważnym błędem, gdyż sugerowałoby istnienie rozwiązania obwodu zawierającego tylko jedną harmoniczną. Ilustrację stosowania zasady superpozycji w analizie obwodów przedstawiono na rysunku obok (slajd 28). | Należy podkreślić, że zgodnie z zasadą superpozycji sumowanie odpowiedzi pochodzących od różnych wymuszeń może odbywać się wyłącznie w dziedzinie czasu. Sumowanie wartości zespolonych od poszczególnych wymuszeń byłoby poważnym błędem, gdyż sugerowałoby istnienie rozwiązania obwodu zawierającego tylko jedną harmoniczną. Ilustrację stosowania zasady superpozycji w analizie obwodów przedstawiono na rysunku obok (slajd 28). | ||
|} | |} | ||
| Linia 454: | Linia 448: | ||
[[Grafika:PEE_M4_zadanie_4_1.png]] | [[Grafika:PEE_M4_zadanie_4_1.png]] | ||
''Rozwiązanie'' | ''Rozwiązanie'' | ||
Impedancja z zacisków AB obwodu jest równa | Impedancja z zacisków AB obwodu (rysunek a) jest równa | ||
[[Grafika:PEE_M4_zadanie_4_1_a.png]] | [[Grafika:PEE_M4_zadanie_4_1_a.png]] | ||
<math>Z_{AB}={R_1R_3 \over R_1+R_3}+{R_2R_4 \over R_2+R_4}=2,93</math> | : <math>Z_{AB}={R_1R_3 \over R_1+R_3}+{R_2R_4 \over R_2+R_4}=2,93</math> | ||
Prądy w obwodzie z rys. b: | Prądy w obwodzie z rys. b: | ||
<math>I_1={E \over R_1+R_3}={30 \over 6}=5</math> | : <math>I_1={E \over R_1+R_3}={30 \over 6}=5</math> | ||
: <math>I_2={E \over R_2+R_4}={30 \over 10}=3</math> | |||
Napięcie <math>U_{AB}</math> | Napięcie <math>U_{AB}</math> | ||
<math>U_{AB}=R_2I_2-R_1I_1=4</math> | : <math>U_{AB}=R_2I_2-R_1I_1=4</math> | ||
Poszukiwany prąd <math>I_x</math> z obwodu zastępczego Thevenina (rys. c) | Poszukiwany prąd <math>I_x</math> z obwodu zastępczego Thevenina (rys. c) | ||
<math>I_x={U_{AB} \over Z_{AB}}=1,36A</math> | : <math>I_x={U_{AB} \over Z_{AB}}=1,36A</math> | ||
---- | |||
''Zadanie 4.2'' | ''Zadanie 4.2'' | ||
| Linia 489: | Linia 488: | ||
Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci | Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci | ||
<math> | |||
: <math> | |||
\begin{bmatrix} | \begin{bmatrix} | ||
Y_1+Y_2 & -Y_2 & 0\\ | Y_1+Y_2 & -Y_2 & 0\\ | ||
| Linia 509: | Linia 509: | ||
---- | |||
''Zadanie 4.3'' | ''Zadanie 4.3'' | ||
| Linia 519: | Linia 520: | ||
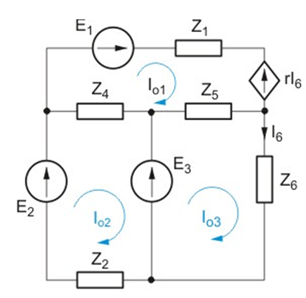
Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci | Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci | ||
: <math> | : <math> | ||
Aktualna wersja na dzień 12:04, 5 wrz 2023

|

|
Znajomość prądów oczkowych pozwala wyznaczyć wszystkie prądy gałęziowe obwodu. Mianowicie
|
| Zadania sprawdzające
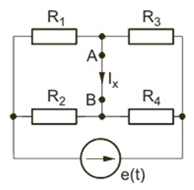
Stosując metodę Thevenina obliczyć prąd w gałęzi AB obwodu przedstawionego na rysunku poniżej. Dane liczbowe elementów: , , , , .
Impedancja z zacisków AB obwodu (rysunek a) jest równa
Zadanie 4.2 Napisać równanie potencjałów węzłowych dla obwodu przedstawionego na rysunku ponizej. Rozwiązanie Przy podanych na rysunku oznaczeniach potencjałów węzłów mierzonych względem węzła odniesienia bezpośrednie zastosowanie prawa prądowego Kirchhoffa do wszystkich węzłów obwodu i wyrażenie prądów poprzez potencjały węzłowe pozwala uzyskać równanie węzłowe w postaci
Zadanie 4.3 Napisać macierzowe równanie oczkowe dla obwodu przedstawionego na rysunku poniżej: Rozwiązanie Z prawa napięciowego Kirchhoffa zastosowanego do trzech oczek zaznaczonych na rysunku po wyrażeniu prądów gałęziowych poprzez prądy oczkowe otrzymujemy równanie oczkowe o postaci
|