Matematyka dyskretna 1/Ćwiczenia 12: Grafy: Różnice pomiędzy wersjami
Nie podano opisu zmian |
m Zastępowanie tekstu – „.↵</math>” na „</math>” |
||
| (Nie pokazano 14 wersji utworzonych przez 4 użytkowników) | |||
| Linia 1: | Linia 1: | ||
==Grafy I== | ==Grafy I== | ||
[[File:Cw grafy operation.svg|300x150px|thumb|right" id="cw_grafy_operation|1. Grafy <math>\mathbf{G}_1</math> oraz <math>\mathbf{G}_2</math>]] | |||
{{cwiczenie| | {{cwiczenie|1|cw 1| | ||
Niech <math>\mathbf{G}_1</math> oraz <math>\mathbf{G}_2</math> | |||
Niech <math> | będą grafami przedstawionymi na [[#cw grafy operation|rysunku 1]]. | ||
będą grafami przedstawionymi na | Przedstaw sumę <math>\mathbf{G}_1\cup\mathbf{G}_2</math> , | ||
Przedstaw sumę <math> | przecięcie <math>\mathbf{G}_1\cap\mathbf{G}_2</math> , | ||
przecięcie <math> | oraz różnicę <math>\mathbf{G}_1-\mathbf{G}_2</math> . | ||
oraz różnicę <math> | |||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
| Linia 21: | Linia 16: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
[[File:Cw grafy operation.svg|300x150px|thumb|left" id="cw_grafy_operation_sum|2. Grafy <math>\mathbf{G}_1\cup\mathbf{G}_2</math>]] | |||
[ | [[File:Cw grafy operation.svg|300x150px|thumb|right" id="cw_grafy_operation_p_m|3. Przecięcie <math>\mathbf{G}_1\cap\mathbf{G}_2</math> oraz różnica <math>\mathbf{G}_1-\mathbf{G}_2</math>]] | ||
{ | Suma <math>\mathbf{G}_1\cup\mathbf{G}_2</math> jest przedstawiona na [[#cw grafy operation sum|rysunku 2]], | ||
zaś przecięcie <math>\mathbf{G}_1\cap\mathbf{G}_2</math> | |||
oraz różnica <math>\mathbf{G}_1-\mathbf{G}_2</math> | |||
na [[#cw grafy operation p m|rysunku 3]]. | |||
</div></div> | </div></div> | ||
<table width="100%"><tr><td> </td></tr></table> | |||
[[File:Cw grafy iloraz.svg|300x250px|thumb|right" id="cw_grafy_iloraz|4. Graf <math>\mathbf{G}</math>]] | |||
Graf <math> | {{cwiczenie|2|cw 2| | ||
na | Graf <math>\mathbf{G}=\left( V,E \right)</math> jest przedstawiony | ||
Przedstaw graf ilorazowy <math> | na [[#cw grafy iloraz|rysunku 4]]. | ||
<math> | Przedstaw graf ilorazowy <math>\mathbf{G}/\!\triangleq</math> dla relacji równoważności | ||
<math>\triangleq\ \subseteq V\times V</math> | |||
zdefiniowanej przez: | zdefiniowanej przez: | ||
<center><math> | <center> | ||
</math></center> | <math>v_i \triangleq v_j\quad</math> w.t.w. <math>\quad \left\vert i-j \right\vert\ </math> jest wielokrotnością <math>\ 4</math> | ||
</center> | |||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
| Linia 62: | Linia 49: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
[! | [[File:Cw grafy iloraz odp.svg|300x200px|thumb|left" id="cw_grafy_iloraz_odp|5. Graf <math>\mathbf{G}/\!\triangleq</math>]] | ||
{ | Iloraz <math>V/\triangleq</math> zbioru <math>V=\left\lbrace v_0,v_1,v_2,v_3,v_4,v_5,v_6,v_7,v_8,v_9 \right\rbrace</math> to | ||
<math>\left\lbrace \left\lbrace v_0,v_4,v_8 \right\rbrace,\left\lbrace v_1,v_5,v_9 \right\rbrace,\left\lbrace v_2,v_6 \right\rbrace,\left\lbrace v_3,v_7 \right\rbrace \right\rbrace</math> . | |||
Z faktu, że <math>v_0 v_2 \in E</math> wynika, że wierzchołki | |||
<math>\left\lbrace v_0,v_4,v_8 \right\rbrace</math> oraz <math>\left\lbrace v_2,v_6 \right\rbrace</math> | |||
są sąsiednie w grafie <math>\mathbf{G}/\!\triangleq</math> . | |||
Z kolei krawędzie <math>v_1 v_4, v_3 v_5 \in E</math> dają krawędzie | |||
<math>\left\lbrace \left\lbrace v_0,v_4,v_8 \right\rbrace,\left\lbrace v_1,v_5,v_9 \right\rbrace \right\rbrace</math> | |||
oraz <math>\left\lbrace \left\lbrace v_1,v_5,v_9 \right\rbrace,\left\lbrace v_3,v_7 \right\rbrace \right\rbrace</math> | |||
w grafie <math>\mathbf{G}/\!\triangleq</math> . | |||
Ponadto nie występują tu już żadne inne krawędzie. | |||
Graf <math>\mathbf{G}/\!\triangleq</math> został przedstawiony na [[#cw grafy iloraz odp|rysunku 5]]. | |||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|3|cw 3| | ||
Niech <math>\mathbf{G}</math> będzie grafem prostym z co najmniej dwoma wierzchołkami. | |||
Niech <math> | Wykaż, że <math>\mathbf{G}</math> zawiera dwa wierzchołki tego samego stopnia. | ||
Wykaż, że <math> | |||
}} | }} | ||
| Linia 93: | Linia 77: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math> | Niech <math>\mathbf{G}</math> ma <math>n\geq 2</math> wierzchołków. | ||
Wierzchołek <math> | Wierzchołek <math>v\in\mathsf{ V}\!\left(\mathbf{G}\right)</math> | ||
nie może mieć więcej niż <math> | nie może mieć więcej niż <math>\left\vert \mathsf{ V}\!\left(\mathbf{G}\right)-\left\lbrace v \right\rbrace \right\vert=n-1</math> sąsiadów. | ||
Stopień dowolnego wierzchołka z <math>\ | Stopień dowolnego wierzchołka z <math>\mathsf{ V}\!\left(\mathbf{G}\right)</math> | ||
leży więc w zbiorze <math> | leży więc w zbiorze <math>\left\lbrace 0,1,2,\ldots,n-1 \right\rbrace</math> . | ||
Jeśli jakiś wierzchołek ma stopień <math> | Jeśli jakiś wierzchołek ma stopień <math>0</math> , czyli jest izolowany, | ||
to każdy inny wierzchołek może mieć co najwyżej <math> | to każdy inny wierzchołek może mieć co najwyżej <math>n-2</math> sąsiadów. | ||
Z kolei gdyby istniał punkt <math> | Z kolei gdyby istniał punkt <math>w</math> o stopniu równym <math>n-1</math> , | ||
to każdy wierzchołek ze zbioru <math>\ | to każdy wierzchołek ze zbioru <math>\mathsf{ V}\!\left(\mathbf{G}\right)-\left\lbrace w \right\rbrace</math> | ||
byłby sąsiadem <math> | byłby sąsiadem <math>w</math> , więc nie mogłby mieć stopnia równego <math>0</math> . | ||
Zbiór <math> | Zbiór <math>S</math> stopni wierzchołków grafu <math>\mathbf{G}</math> zawiera się więc albo w zbiorze | ||
<math> | <math>\left\lbrace 0,1,2,\ldots,n-2 \right\rbrace</math> , albo w <math>\left\lbrace 1,2,3,\ldots,n-1 \right\rbrace</math> , | ||
więc <math> | więc <math>S</math> jest co najwyżej <math>\left( n-1 \right)</math> -elementowy. | ||
Wszystkich wierzchołków jest <math> | Wszystkich wierzchołków jest <math>n</math> , | ||
więc z Zasady Szufladkowej Dirichleta otrzymujemy, | więc z Zasady Szufladkowej Dirichleta otrzymujemy, | ||
że istnieją dwa wierzchołki o tym samym stopniu. | że istnieją dwa wierzchołki o tym samym stopniu. | ||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|4|cw 4| | ||
Wykaż, że w grupie sześciu osób zawsze znajdą się trzy, | Wykaż, że w grupie sześciu osób zawsze znajdą się trzy, | ||
które albo znają się nawzajem, albo żadna z nich nie zna dwóch pozostałych. | które albo znają się nawzajem, albo żadna z nich nie zna dwóch pozostałych. | ||
| Linia 126: | Linia 109: | ||
Wybierzmy dowolną osobę z rozważanej szóstki i oznaczmy ją za pomocą inicjału A. | Wybierzmy dowolną osobę z rozważanej szóstki i oznaczmy ją za pomocą inicjału A. | ||
Załóżmy, że A w zbiorze pięciu pozostałych osób ma więcej znajomych niż nieznajomych. | Załóżmy, że A w zbiorze pięciu pozostałych osób ma więcej znajomych niż nieznajomych. | ||
A ma więc <math> | A ma więc <math>3</math> , <math>4</math> , lub <math>5</math> znajomych. | ||
Jeżeli istnieje chociaż jedna para w tym gronie, | Jeżeli istnieje chociaż jedna para w tym gronie, | ||
która się zna, to wraz z A tworzy poszukiwaną trójkę. | która się zna, to wraz z A tworzy poszukiwaną trójkę. | ||
| Linia 134: | Linia 117: | ||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|5|cw 5| | ||
Dopełnienie grafu <math>\mathbf{G}=\left( V,E \right)</math> to graf | |||
Dopełnienie grafu <math> | <math>\overline{\mathbf{G}}=\left( V,\mathcal{P}_{2}\!\left( V \right)- E \right)</math> . | ||
<math> | Przedstaw dopełnienie grafu pełnego <math>\mathcal{K}_{n}</math> | ||
Przedstaw dopełnienie grafu pełnego <math> | oraz dwudzielnego grafu pełnego <math>\mathcal{K}_{m,n}</math> . | ||
oraz dwudzielnego grafu pełnego <math> | |||
Przedstaw graf, którego dopełnienie jest z nim izomorficzne. | Przedstaw graf, którego dopełnienie jest z nim izomorficzne. | ||
| Linia 150: | Linia 132: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Dopełnieniem grafu pełnego jest graf pusty, tzn. | Dopełnieniem grafu pełnego jest graf pusty, tzn. | ||
<math> | <math>\overline{\mathcal{K}_{n}}=\mathcal{A}_{n}</math> . | ||
Na odwrót dopełnienie grafu pustego jest grafem pełnym: | Na odwrót dopełnienie grafu pustego jest grafem pełnym: | ||
<math> | <math>\overline{\mathcal{A}_{n}}=\mathcal{K}_{n}</math> . | ||
Z kolei dopełnienie pełnego grafu dwudzielnego <math> | Z kolei dopełnienie pełnego grafu dwudzielnego <math>\mathcal{K}_{n,n}</math> | ||
jest rozłączną sumą dwóch klik <math> | jest rozłączną sumą dwóch klik <math>\mathcal{K}_{m}\cup\mathcal{K}_{n}</math> . | ||
Cykl piecioelementowy oraz ścieżka czteroelementowa są przykładami | Cykl piecioelementowy oraz ścieżka czteroelementowa są przykładami | ||
| Linia 160: | Linia 142: | ||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|6|cw 6| | ||
Niech <math>\mathbf{G}</math> będzie grafem prostym, | |||
Niech <math> | w którym każdy wierzchołek ma co najmniej <math>r\geq 2</math> sąsiadów. | ||
w którym każdy wierzchołek ma co najmniej <math> | Wykaż, że <math>\mathbf{G}</math> zawiera cykl o długości co najmniej <math>r+1</math> . | ||
Wykaż, że <math> | |||
}} | }} | ||
| Linia 170: | Linia 151: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Spróbuj budować indukcyjnie możliwie długą ścieżkę. | Spróbuj budować indukcyjnie możliwie długą ścieżkę. | ||
Pokaż, że musi mieć co najmniej <math> | Pokaż, że musi mieć co najmniej <math>r</math> elementów. | ||
Aby znaleźć cykl, rozważ sąsiadów ostatniego wierzchołka na tej ścieżce. | Aby znaleźć cykl, rozważ sąsiadów ostatniego wierzchołka na tej ścieżce. | ||
</div></div> | </div></div> | ||
| Linia 176: | Linia 157: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Wskażemy odpowiednią ścieżkę definiując ją indukcyjnie. | Wskażemy odpowiednią ścieżkę definiując ją indukcyjnie. | ||
Załóżmy, że istnieje ścieżka o długości <math> | Załóżmy, że istnieje ścieżka o długości <math>k< r</math> tzn. <math>v_1\to v_2\to\ldots\to v_k</math> . | ||
Wierzchołek <math> | Wierzchołek <math>v_k</math> ma co najmniej <math>r</math> sąsiadów, | ||
musi więc mieć sąsiada <math> | musi więc mieć sąsiada <math>v_{k+1}</math> poza <math>k</math> -elementowym zbiorem | ||
<math> | <math>\left\lbrace v_1,v_2,\ldots,v_k \right\rbrace</math> . | ||
Skonstruowaliśmy więc ścieżkę <math> | Skonstruowaliśmy więc ścieżkę <math>v_1\to v_2\to\ldots\to v_k\to v_{k+1}</math> | ||
odwiedzającą <math> | odwiedzającą <math>k+1</math> wierzchołków. | ||
Powtarzając tę czynność tak długo jak <math> | Powtarzając tę czynność tak długo jak <math>k< r</math> , otrzymujemy <math>r</math> -elementową ścieżkę: | ||
<center><math>v_1\to v_2\to\ldots\to v_r</math></center> | |||
Wiemy więc, że ścieżka o możliwie największej długości ma <math> | Wiemy więc, że ścieżka o możliwie największej długości ma <math>k\geq r</math> wierzchołków. | ||
Niech <math> | Niech <math>w_1\to w_2\to\ldots\to w_k</math> będzie taką ścieżką. | ||
Z jej maksymalności wiemy, że wszyscy sąsiedzi <math> | Z jej maksymalności wiemy, że wszyscy sąsiedzi <math>w_k</math> są już na tej ścieżce, | ||
bo inaczej można by ją było przedłużyć. | bo inaczej można by ją było przedłużyć. | ||
Niech więc <math> | Niech więc <math>w_i</math> będzie sąsiadem <math>w_k</math> o najmniejszym indeksie. | ||
Ścieżka <math> | Ścieżka <math>w_i\to w_{i+1}\to\ldots\to w_k</math> odwiedza <math>r</math> | ||
sąsiadów wierzchołka <math> | sąsiadów wierzchołka <math>w_k</math> , więc jest długości co najmniej równej <math>r</math> . | ||
Wraz z wierzchołkiem <math> | Wraz z wierzchołkiem <math>w_k</math> tworzy więc cykl: | ||
<center><math> | |||
<center><math>w_i\to w_{i+1}\to\ldots\to w_k\to w_i | |||
</math></center> | </math></center> | ||
o długości co najmniej <math> | |||
o długości co najmniej <math>r+1</math> . | |||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|7|cw 7| | ||
Niech <math>\mathbf{G}</math> będzie grafem prostym o <math>2k</math> wierzchołkach, | |||
Niech <math> | |||
niezawierającym trójkątów. | niezawierającym trójkątów. | ||
Wykaż, że <math> | Wykaż, że <math>\mathbf{G}</math> ma co najwyżej <math>k^2</math> krawędzi | ||
i podaj przykład grafu, w którym to górne oszacowanie jest osiągnięte. | i podaj przykład grafu, w którym to górne oszacowanie jest osiągnięte. | ||
| Linia 212: | Linia 195: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
Zastosuj indukcję względem <math> | Zastosuj indukcję względem <math>k</math> usuwając z grafu jedną krawędź, jej końce, a także | ||
krawędzie incydentne z tymi końcami. | krawędzie incydentne z tymi końcami. | ||
</div></div> | </div></div> | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Dowód zostanie przeprowadzony indukcyjnie ze względu na <math> | Dowód zostanie przeprowadzony indukcyjnie ze względu na <math>k</math> . | ||
Dla <math> | Dla <math>k=1</math> mamy po prostu graf bez krawędzi. | ||
Załóżmy więc, że ograniczenie liczby krawędzi | Załóżmy więc, że ograniczenie liczby krawędzi | ||
zachodzi dla wszystkich grafów o <math> | zachodzi dla wszystkich grafów o <math>2k\geq 2</math> wierzchołkach. | ||
Niech teraz graf <math> | Niech teraz graf <math>\mathbf{G}</math> posiada <math>2k+2</math> wierzchołków. | ||
Jeśli <math> | Jeśli <math>\mathbf{G}</math> nie posiada krawędzi, to nie ma czego dowodzić. | ||
Załóżmy więc, że <math> | Załóżmy więc, że <math>vw\in\mathsf{ E}\!\left(\mathbf{G}\right)</math> . | ||
Na mocy założenia indukcyjnego podgraf <math> | Na mocy założenia indukcyjnego podgraf <math>\mathbf{G}|_{\mathsf{ V}\!\left(\mathbf{G}\right)-\left\lbrace v,w \right\rbrace}</math> | ||
posiada co najwyżej <math> | posiada co najwyżej <math>k^2</math> krawędzi. | ||
Ponadto, gdyby istniał <math> | Ponadto, gdyby istniał <math>u\in\mathsf{ V}\!\left(\mathbf{G}\right)</math> sąsiadujący zarazem z <math>v</math> jak i <math>w</math> , | ||
to <math> | to <math>\left\lbrace v,w,u \right\rbrace</math> byłby trójkątem. | ||
Tak więc zbiór sąsiadów <math> | Tak więc zbiór sąsiadów <math>v</math> jest rozłączny ze zbiorem sąsiadów <math>w</math> . | ||
Zbiór krawędzi łączących wierzchołki <math> | Zbiór krawędzi łączących wierzchołki <math>v</math> oraz <math>w</math> z wierzchołkami | ||
<math>\ | <math>\mathsf{ V}\!\left(\mathbf{G}\right)-\left\lbrace v,w \right\rbrace</math> jest więc nie większy niż rozmiar | ||
<math>\ | <math>\mathsf{ V}\!\left(\mathbf{G}\right)-\left\lbrace v,w \right\rbrace</math> , czyli ograniczony przez <math>2k</math> . | ||
Zbiór wszystkich krawędzi w <math> | Zbiór wszystkich krawędzi w <math>\mathbf{G}</math> składa się z: | ||
* krawędzi grafu <math> | * krawędzi grafu <math>\mathbf{G}-\left\lbrace v,w \right\rbrace</math> , | ||
* krawędzi łączących wierzchołki <math> | * krawędzi łączących wierzchołki <math>v</math> oraz <math>w</math> z wierzchołkami <math>\mathsf{ V}\!\left(\mathbf{G}\right)-\left\lbrace v,w \right\rbrace</math> , | ||
* krawędzi <math> | * krawędzi <math>vw</math> . | ||
W sumie więc rozmiar zbioru krawędzi grafu <math>\mathbf{G}</math> jest ograniczony przez | |||
<center><math>\left\vert \mathsf{ E}\!\left(\mathbf{G}\right) \right\vert\leq k^2+2k+1=\left( k+1 \right)^2</math></center> | |||
</div></div> | </div></div> | ||
[[File:Cw grafy petersen.svg|250x150px|thumb|right" id="cw_grafy_petersen|6. Graf Petersena]] | |||
Wskaż jakieś drzewo rozpinające w grafie Petersena z | {{cwiczenie|8|cw 8| | ||
Wskaż jakieś drzewo rozpinające w grafie Petersena z [[#cw grafy petersen|rysunku 6]]. | |||
}} | }} | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> | ||
| Linia 260: | Linia 240: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
<div class="thumb tleft" id="cw_grafy_petersen_tree"><div style="width:250px;"> | |||
<flash>file="Cw grafy petersen tree.swf"|width=250|height=150</flash> | |||
<div.thumbcaption>7. Drzewo rozpinające w grafie Petersena</div></div> | |||
</div> | |||
Prykładowe drzewo rozpinające w grafie Petersena zostało przedstawione | |||
na [[#cw grafy petersen tree|rysunku 7]]. | |||
</div></div> | </div></div> | ||
<table width="100%"><tr><td> </td></tr></table> | |||
{{cwiczenie| | {{cwiczenie|9|cw 9| | ||
Pokaż, że w dowolnym drzewie o co najmniej dwu wierzchołkach, | Pokaż, że w dowolnym drzewie o co najmniej dwu wierzchołkach, | ||
istnieją co najmniej dwa wierzchołki o stopniu równym jeden. | istnieją co najmniej dwa wierzchołki o stopniu równym jeden. | ||
| Linia 284: | Linia 265: | ||
<div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> | ||
Niech <math> | Niech <math>n</math> będzie liczbą wierzchołków drzewa. | ||
Drzewo jest grafem spójnym, więc każdy wierzchołek ma stopień co najmniej jeden. | Drzewo jest grafem spójnym, więc każdy wierzchołek ma stopień co najmniej jeden. | ||
Załóżmy, że co najwyżej jeden wierzchołek ma stopień jeden, | Załóżmy, że co najwyżej jeden wierzchołek ma stopień jeden, | ||
czyli jest co najmniej <math> | czyli jest co najmniej <math>n-1</math> wierzchołków o stopniu równym <math>2</math> lub więcej. | ||
Sumując teraz stopnie tych wierzchołków i pamiętając, | Sumując teraz stopnie tych wierzchołków i pamiętając, | ||
że suma taka to podwojona liczba krawędzi, dostajemy, | że suma taka to podwojona liczba krawędzi, dostajemy, | ||
że liczba krawędzi jest równa co najmniej | że liczba krawędzi jest równa co najmniej | ||
Przeczy to faktowi, że drzewo o <math> | <center><math>\frac{2\left( n-1 \right)+1}{2}=n-\frac{1}{2}</math></center> | ||
Przeczy to faktowi, że drzewo o <math>n</math> wierzchołkach ma <math>n-1</math> krawędzi. | |||
</div></div> | </div></div> | ||
{{cwiczenie| | {{cwiczenie|10|cw 10| | ||
''Centrum'' spójnego grafu <math>\mathbf{G}</math> | |||
''Centrum'' spójnego grafu <math> | to taki wierzchołek <math>v</math> , dla którego maksymalna odległość pomiędzy <math>v</math> | ||
to taki wierzchołek <math> | i dowolnym innym wierzchołkiem grafu <math>\mathbf{G}</math> jest możliwie najmniejsza. | ||
i dowolnym innym wierzchołkiem grafu <math> | |||
Udowodnij, że każde drzewo ma albo dokładnie jedno centrum, albo dwa sąsiednie centra. | Udowodnij, że każde drzewo ma albo dokładnie jedno centrum, albo dwa sąsiednie centra. | ||
| Linia 315: | Linia 296: | ||
* ''W drzewie o co najmniej trzech wierzchołkach żaden liść nie może być centrum.'' | * ''W drzewie o co najmniej trzech wierzchołkach żaden liść nie może być centrum.'' | ||
Niech <math> | Niech <math>v</math> będzie liściem, oraz <math>w</math> jedynym jego sąsiadem. | ||
Ścieżka pomiędzy liściem <math> | Ścieżka pomiędzy liściem <math>v</math> , a dowolnym innym wierzchołkiem | ||
musi przechodzić przez wierzchołek <math> | musi przechodzić przez wierzchołek <math>w</math> . | ||
Jeśli tylko w drzewie istnieje jeszcze jakiś wierzchołek <math> | Jeśli tylko w drzewie istnieje jeszcze jakiś wierzchołek <math>u</math> poza <math>v,w</math> , | ||
to <math> | to <math>w</math> leży bliżej <math>u</math> niż <math>v</math> . | ||
* ''Gdy <math> | * ''Gdy <math>x</math> jest wierzchołkiem drzewa, to wierzchołek najbardziej oddalony od <math>x</math> jest liściem.'' | ||
jest liściem.'' | |||
Rozważmy dowolny wierzchołek <math> | Rozważmy dowolny wierzchołek <math>y</math> realizujący największą odległość od <math>x</math> | ||
i załóżmy, że nie jest on liściem w drzewie <math> | i załóżmy, że nie jest on liściem w drzewie <math>\mathbf{T}</math> . | ||
Usunięcie <math> | Usunięcie <math>y</math> rozspaja drzewo <math>\mathbf{T}</math> na dwa niepuste drzewa | ||
<math> | <math>\mathbf{T}_1</math> oraz <math>\mathbf{T}_2</math> . | ||
Bez straty ogólności załóżmy, że <math> | Bez straty ogólności załóżmy, że <math>x\in \mathbf{T}_1</math> . | ||
Ścieżka w <math> | Ścieżka w <math>\mathbf{T}</math> z <math>x</math> do dowolnego wierzchołka | ||
z <math> | z <math>\mathbf{T}_2</math> odwiedza <math>y</math> , | ||
tak więc jest dłuższa niż ścieżka pomiędzy <math> | tak więc jest dłuższa niż ścieżka pomiędzy <math>x</math> i <math>y</math> . | ||
A zatem <math> | A zatem <math>y</math> nie może być najdalej oddalonym wierzchołkiem od <math>x</math> . | ||
* ''Usunięcie liści nie zmienia zbioru centrów w drzewie.'' | * ''Usunięcie liści nie zmienia zbioru centrów w drzewie.'' | ||
Usunięcie liścia nie zmienia odległości pomiędzy pozostałymi wierzchołkami. | Usunięcie liścia nie zmienia odległości pomiędzy pozostałymi wierzchołkami. | ||
Ustalmy wierzchołek <math> | Ustalmy wierzchołek <math>v</math> i przez <math>k</math> oznaczmy odległość <math>v</math> | ||
od wierzchołków najbardziej oddalonych od <math> | od wierzchołków najbardziej oddalonych od <math>v</math> . | ||
Usuwając wszystkie liście, usuwamy między innymi najbardziej oddalone wierzchołki | Usuwając wszystkie liście, usuwamy między innymi najbardziej oddalone wierzchołki | ||
od wierzchołka <math> | od wierzchołka <math>v</math> . | ||
W tym zmniejszonym drzewie, parametr <math> | W tym zmniejszonym drzewie, parametr <math>k</math> zmienia się więc na <math>k-1</math> . | ||
A zatem, usunięcie wszystkich liści, | A zatem, usunięcie wszystkich liści, | ||
zmniejsza każdemu wierzchołkowi | zmniejsza każdemu wierzchołkowi | ||
| Linia 349: | Linia 329: | ||
które nie może być liściem. | które nie może być liściem. | ||
Wyposażeni w te obserwacje, z drzewa <math> | Wyposażeni w te obserwacje, z drzewa <math>\mathbf{T}^0:=\mathbf{T}</math> konstruujemy | ||
sukcesywnie drzewa <math> | sukcesywnie drzewa <math>\mathbf{T}^j</math> usuwając wszystkie liście drzewa <math>\mathbf{T}^{j-1}</math> | ||
tak długo, jak długo otrzymane drzewa są niepuste. | tak długo, jak długo otrzymane drzewa są niepuste. | ||
A zatem ostatnie ma jeden lub dwa (ale wtedy połączone) wierzchołki, które są | A zatem ostatnie ma jeden lub dwa (ale wtedy połączone) wierzchołki, które są | ||
wobec tego centrami wyjściowego drzewa <math> | wobec tego centrami wyjściowego drzewa <math>\mathbf{T}^0=\mathbf{T}</math> . | ||
</div></div> | </div></div> | ||
Aktualna wersja na dzień 21:31, 11 wrz 2023
Grafy I
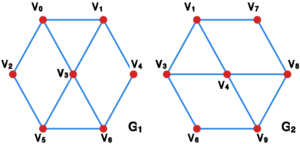
Ćwiczenie 1
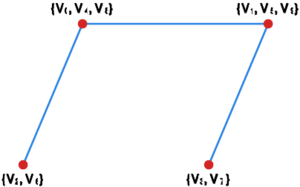
Niech oraz będą grafami przedstawionymi na rysunku 1. Przedstaw sumę , przecięcie , oraz różnicę .
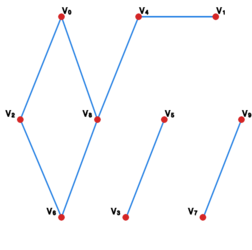
Ćwiczenie 2
Graf jest przedstawiony na rysunku 4. Przedstaw graf ilorazowy dla relacji równoważności zdefiniowanej przez:
w.t.w. jest wielokrotnością
Ćwiczenie 3
Niech będzie grafem prostym z co najmniej dwoma wierzchołkami. Wykaż, że zawiera dwa wierzchołki tego samego stopnia.
Ćwiczenie 4
Wykaż, że w grupie sześciu osób zawsze znajdą się trzy, które albo znają się nawzajem, albo żadna z nich nie zna dwóch pozostałych.
Ćwiczenie 5
Dopełnienie grafu to graf . Przedstaw dopełnienie grafu pełnego oraz dwudzielnego grafu pełnego . Przedstaw graf, którego dopełnienie jest z nim izomorficzne.
Ćwiczenie 6
Niech będzie grafem prostym, w którym każdy wierzchołek ma co najmniej sąsiadów. Wykaż, że zawiera cykl o długości co najmniej .
Ćwiczenie 7
Niech będzie grafem prostym o wierzchołkach, niezawierającym trójkątów. Wykaż, że ma co najwyżej krawędzi i podaj przykład grafu, w którym to górne oszacowanie jest osiągnięte.
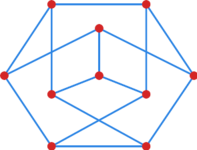
Ćwiczenie 8
Wskaż jakieś drzewo rozpinające w grafie Petersena z rysunku 6.
Prykładowe drzewo rozpinające w grafie Petersena zostało przedstawione na rysunku 7.
Ćwiczenie 9
Pokaż, że w dowolnym drzewie o co najmniej dwu wierzchołkach, istnieją co najmniej dwa wierzchołki o stopniu równym jeden.
Ćwiczenie 10
Centrum spójnego grafu to taki wierzchołek , dla którego maksymalna odległość pomiędzy i dowolnym innym wierzchołkiem grafu jest możliwie najmniejsza. Udowodnij, że każde drzewo ma albo dokładnie jedno centrum, albo dwa sąsiednie centra.