Języki, automaty i obliczenia/Wykład 7: Twierdzenie Kleene'ego. Własności języków i gramatyk regularnych: Różnice pomiędzy wersjami
m Zastępowanie tekstu – „<math> ” na „<math>” |
|||
| (Nie pokazano 23 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
W wykładzie udowodnimy twierdzenie Kleene'ego, które orzeka, że | W wykładzie udowodnimy twierdzenie Kleene'ego, które orzeka, że | ||
rodzina języków regularnych jest identyczna z rodziną języków rozpoznawanych przez automaty o skończonej liczbie stanów. Przedstawimy własności języków regularnych i gramatyk typu '''(3)'''. Na koniec uzasadnimy, że rodziny języków regularnych, rozpoznawalnych oraz generowanych przez gramatyki typu '''(3)''', są tożsame. | rodzina języków regularnych jest identyczna z rodziną języków rozpoznawanych przez automaty o skończonej liczbie stanów. Przedstawimy własności języków regularnych i gramatyk typu '''(3)'''. Na koniec uzasadnimy, że rodziny języków regularnych, rozpoznawalnych oraz generowanych przez gramatyki typu '''(3)''', są tożsame. | ||
__FORCETOC__ | |||
==Twierdzenie Kleene== | ==Twierdzenie Kleene== | ||
Wiemy już, z poprzednich wykładów, że rodzina wyrażeń regularnych | [[grafika:Kleene.gif|thumb|right||Stephen Cole Kleene (1909-1994)<br>[[Biografia Kleene|Zobacz biografię]]]]Wiemy już, z poprzednich wykładów, że rodzina wyrażeń regularnych | ||
określa rodzinę języków regularnych. Celem pierwszej części tego | określa rodzinę języków regularnych. Celem pierwszej części tego | ||
wykładu jest ustalenie związku pomiędzy rodziną języków regularnych | wykładu jest ustalenie związku pomiędzy rodziną języków regularnych | ||
| Linia 13: | Linia 13: | ||
<span id="twierdzenie_1_1">{{twierdzenie|1.1.|| | <span id="twierdzenie_1_1">{{twierdzenie|1.1.|| | ||
Dla dowolnego skończonego alfabetu <math> | Dla dowolnego skończonego alfabetu <math>A</math> | ||
<center><math> | <center> | ||
<math>\mathcal{REG}(A^{*})=\mathcal{REC}(A^{*})</math> | |||
</center> | |||
}}</span> | }}</span> | ||
| Linia 21: | Linia 23: | ||
{{dowod||| | {{dowod||| | ||
Dowód pierwszej części twierdzenia, czyli inkluzja <math> | Dowód pierwszej części twierdzenia, czyli inkluzja <math>\mathcal{REG}(A^{*})\subseteq \mathcal{REC}(A^{*})</math> , będzie | ||
prowadzony zgodnie ze strukturą definicji rodziny języków | prowadzony zgodnie ze strukturą definicji rodziny języków | ||
regularnych <math> | regularnych <math>\mathcal{REG}(A^{*})</math> . | ||
1. Język pusty <math> | 1. Język pusty <math>\emptyset</math> jest rozpoznawany przez dowolny | ||
automat <math> | automat <math>\mathcal{A} =(S,A,f,s_0,T)</math>, w którym zbiór stanów końcowych <math>T</math> jest pusty. | ||
2. Język a złożony z dowolnej litery <math> | 2. Język a złożony z dowolnej litery <math>a \in A</math> jest rozpoznawany przez automat}} | ||
<center> | |||
[[File:ja-lekcja07-w-rys1.svg|250x150px|thumb|center|Rysunek 1]] | |||
</center> | |||
Dla dalszej części dowodu ustalmy, iż dane są języki <math>L_1, L_2</math> rozpoznawane odpowiednio | |||
przez automaty deterministyczne <math>\mathcal{A}_{i} = (S_i,f_i,{s_0}^i,T_i)</math>, gdzie <math>i=1,2</math>. | |||
3. Sumę mnogościową języków <math>L_1, L_2</math>, | |||
czyli język <math>L = L_1 \cup L_2</math> rozpoznaje automat <math>\mathcal{A} | |||
= (S,f,{s_0},T)</math>, dla którego <math>S = S_1 \times S_2</math>, <math>s_0 = | |||
({s_0}^1,{s_0}^2)</math>, <math>\ : T = T_1 \times S_2\; \cup \;S_1 \times | |||
T_2</math> oraz dla dowolnego stanu <math>(s_{1},s_{2})\in S</math> i litery <math>a\in A</math> funkcja przejść określona jest równością | |||
<center><math>f((s_{1},s_{2}),a)=(f_{1}(s_{1},a),f_{2}(s_{2},a))</math>.</center> | |||
<center><math> | |||
4. | 4. | ||
Katenację języków <math> | Katenację języków <math>L_1, L_2</math>, czyli | ||
język <math> | język <math>L = L_1 \cdot L_2</math> rozpoznaje | ||
automat <math> | automat <math>\mathcal{A} = (S,f,{s_0},T)</math>, dla którego | ||
<math> | <math>S=S_{1}\times \mathcal{P}(S_{2}),\quad s_{0}=\left( | ||
s_{0}^{1},\emptyset \right) | s_{0}^{1},\emptyset \right)</math> oraz dla dowolnego stanu <math>(s_1,S'_2) | ||
\in S</math> i litery <math> | \in S</math> i litery <math>a\in A</math> funkcja przejść określona jest | ||
następująco: | następująco: | ||
<center><math> | <center><math>f((s_1,S'_2),a) = \left\{ \begin{array} {ll} (f_1(s_1,a),f_2(S'_2,a)) & \text{gdy} f_1(s_1,a) \notin T_1 ,\\ (f_1(s_1,a),f_2(S'_2,a) \cup \{ {s_0}^2\}) & \text{gdy}f_1(s_1,a) \in T_1, \end{array} \right</math>.</center> | ||
a zbiorem stanów końcowych jest | a zbiorem stanów końcowych jest | ||
<center><math> | <center><math>T=S_{1}\times \left\{ S'\in \mathcal{P}(S_{2})\, :\, S'\cap T_{2}\neq \emptyset \right\}</math>.</center> | ||
5. | 5. | ||
Załóżmy, że język <math> | Załóżmy, że język <math>L</math> rozpoznaje automat <math>\mathcal{A} | ||
=(S,f,s_0,T)</math>. Określimy automat niedeterministyczny, który | |||
będzie rozpoznawał gwiazdkę Kleene języka <math> | będzie rozpoznawał gwiazdkę Kleene języka <math>L</math>, czyli <math>L^*</math>. Automat | ||
niedeterministyczny <math> | niedeterministyczny <math>\mathcal{A}' =(S,f',\{ s_0\},T)</math>, | ||
w którym | w którym | ||
<center><math> | <center><math>f'(s,a) = \left\{ \begin{array} {ll} \{ f(s,a)\} & \text{gdy} f(s,a) \notin T ,\\ | ||
\{ f(s,a),s_0 \} & \ | \{ f(s,a),s_0 \} & \text{gdy} f(s,a) \in T \end{array} \right</math>.</center> | ||
rozpoznaje język język <math> | rozpoznaje język język <math>L^+</math>. Dowód tego faktu jest indukcyjny i pozostawiamy go na ćwiczenia. | ||
ćwiczenia. | Zauważmy teraz, że język <math>\{1\}</math> rozpoznaje automat | ||
Zauważmy teraz, że język <math> | <center> | ||
[[File:ja-lekcja07-w-rys2.svg|250x150px|thumb|center|Rysunek 2]] | |||
</center> | |||
Ponieważ <math>L^{*}=L^{+}\cup \left\{ 1\right\}</math> , to | |||
Ponieważ <math> | |||
korzystając z udowodnionej już zamkniętości języków rozpoznawanych | korzystając z udowodnionej już zamkniętości języków rozpoznawanych | ||
ze względu na sumę mnogościową, stwierdzamy, że istnieje automat | ze względu na sumę mnogościową, stwierdzamy, że istnieje automat | ||
rozpoznający język <math> | rozpoznający język <math>L^*</math>. | ||
Zatem dowód | Zatem dowód | ||
inkluzji <math> | inkluzji <math>\mathcal{REG}(A^{*})\subseteq \mathcal{REC}(A^{*})</math> jest zakończony. | ||
Przejdziemy teraz do dowodu inkluzji | Przejdziemy teraz do dowodu inkluzji | ||
<math> | <math>\mathcal{REG}(A^{*})\supseteq \mathcal{RE}C(A^{*})</math> . | ||
Niech <math> | Niech <math>L</math> oznacza dowolny język rozpoznawany przez automat | ||
<math> | <math>\mathcal{A} = (S,f,s_0,T)</math>. Dowód polega na rozbiciu języka | ||
<math> | <math>L</math> na fragmenty, dla których stwierdzenie, że są to języki | ||
regularne będzie dość oczywiste. Natomiast sam język <math> | regularne będzie dość oczywiste. Natomiast sam język <math>L</math> będzie | ||
wynikiem operacji regularnych określonych na tych właśnie | wynikiem operacji regularnych określonych na tych właśnie | ||
fragmentach. Poniżej przeprowadzamy defragmentację języka <math> | fragmentach. Poniżej przeprowadzamy defragmentację języka <math>L</math>. | ||
Dla <math> | Dla <math>s,t \in S</math> niech | ||
<center><math> | <center><math>L(s,t) = \{w \in A^* : f(s,w) = t \}</math>.</center> | ||
Jest to język złożony ze słów, które przeprowadzają stan <math> | Jest to język złożony ze słów, które przeprowadzają stan <math>s</math> | ||
automatu <math> | automatu <math>\mathcal{A}</math> w stan <math>t</math> . Ogół liter alfabetu <math>A | ||
</math> przeprowadzających stan <math> | </math> przeprowadzających stan <math>s</math> w <math>t</math> oznaczymy przez | ||
<center><math> | <center><math>A(s,t) = \{a \in A : f(s,a) = t \}</math>.</center> | ||
Dla stanów <math> | Dla stanów <math>s,t \in S</math> i zbioru <math>S_1 \subseteq S</math> niech | ||
<center><math> | <center><math>L(s,S_1,t) = \{ w \in A^* : f(s,w) =t, f(s,w_1) \in S_1\;:\;w= w_1v,\; w_1, v \in A^* \}</math>.</center> | ||
Jest to język, który można przedstawić graficznie następująco:<br> | Jest to język, który można przedstawić graficznie następująco:<br> | ||
<center> | |||
[[File:ja-lekcja07-w-rys3.svg|350x150px|thumb|center|Rysunek 3]] | |||
</center> | |||
Na koniec przyjmijmy <center><math>\overline{L}(s,S_2,t) = \{ w \in A^* : f(s,w) | |||
=t, f(s,w_1) \in S_2\; : \;w = w_1v,\; w_1,v \in A^+ \}</math>,</center> | |||
Na koniec przyjmijmy <center><math> | |||
=t, f(s,w_1) \in S_2\; : \;w = w_1v,\; w_1,v \in A^+ \} | |||
określony | określony | ||
dla <math> | dla <math>S_2 \subseteq S</math> i <math>s,t \in S - S_2</math> | ||
Język ten jest graficznie interpretowany poniżej.<br> | Język ten jest graficznie interpretowany poniżej.<br> | ||
<center> | |||
[[File:ja-lekcja07-w-rys4.svg|350x150px|thumb|center|Rysunek 4]] | |||
</center> | |||
Wprost z określeń wynika, że wszystkie wprowadzone powyżej języki są | Wprost z określeń wynika, że wszystkie wprowadzone powyżej języki są | ||
regularne, czyli należą do rodziny <math> | regularne, czyli należą do rodziny <math>\mathcal{REG}(A^{*})</math> . Dowód | ||
tego faktu przebiega indukcyjnie ze względu na liczbę | tego faktu przebiega indukcyjnie ze względu na liczbę | ||
elementów zbiorów <math> | elementów zbiorów <math>S_1</math> i <math>S_2</math>. Szczegóły tego dowodu pominiemy. | ||
Natomiast warto wskazać rolę, jaką spełniają w dowodzie wprowadzone | Natomiast warto wskazać rolę, jaką spełniają w dowodzie wprowadzone | ||
wyżej języki. A mianowicie: | wyżej języki. A mianowicie: | ||
<center><math> | <center><math>L(s,\left\{ s\right\} ,s)=A(s,s)^{*}</math>,</center> | ||
<center><math> | <center><math>\overline{L}(s,\left\{ r\right\} ,t)=A(s,r)A(r,r)^{*}A(r,t)</math>,</center> | ||
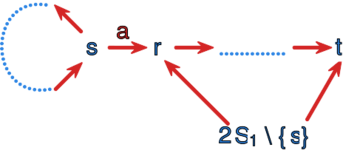
<center><math> | <center><math>L(s,S_1,t) = \overline{L}(s,S_1 \setminus \{s\},s)^*\; | ||
[\bigcup_{r \in S_1 \setminus \{s\}}A(s,r)L(r,S_1 - | |||
\{s\},t)\; | \{s\},t)\;]</math>.</center> | ||
Tę ostatnią równość przedstawia poniższy rysunek.<br> | Tę ostatnią równość przedstawia poniższy rysunek.<br> | ||
<center> | |||
[[File:ja-lekcja07-w-rys5.svg|350x150px|thumb|center|Rysunek 5]] | |||
</center> | |||
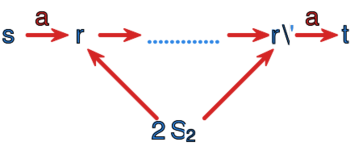
<center><math>\overline{L}(s,S_2,t) = \bigcup_{r,r' \in S_2} A(s,r) L(r,S_2,r') A(r',t)</math>,</center> | |||
<center><math> | |||
co graficznie można przedstawić następująco:<br> | co graficznie można przedstawić następująco:<br> | ||
<center> | |||
[[File:ja-lekcja07-w-rys6.svg|350x150px|thumb|center|Rysunek 6]] | |||
</center> | |||
Dochodzimy więc do konkluzji, iż | Dochodzimy więc do konkluzji, iż | ||
jezyki <math> | jezyki <math>L(s,S_{1},t)</math> oraz <math>\overline{L}(s,S_{2},t)</math> są regularne. | ||
W szczególności zatem regularny jest język | W szczególności zatem regularny jest język | ||
<math> | <math>L(s_{0},S,t)=L(s_{0},t)</math>. | ||
Język <math> | Język <math>L</math> możemy przedstawić w następującej postaci: | ||
<center><math> | <center><math>L = \bigcup_{t \in T} \{w \in A^* : f(s_0,w) = t \} = \bigcup_{t \in T} L(s_0,t)</math>,</center> | ||
co w połączeniu z ustaleniami punktu 3 z poprzedniej części dowodu uzasadnia tezę, że | co w połączeniu z ustaleniami punktu 3 z poprzedniej części dowodu uzasadnia tezę, że | ||
język <math> | język <math>L</math> należy do rodziny <math>\mathcal{REG}(A^{*})</math>. | ||
==Własności języków regularnych i gramatyk regularnych== | ==Własności języków regularnych i gramatyk regularnych== | ||
| Linia 167: | Linia 173: | ||
<span id="definicja_2_1">{{definicja|2.1.|| | <span id="definicja_2_1">{{definicja|2.1.|| | ||
Odbiciem zwierciadlanym słowa <math> | Odbiciem zwierciadlanym słowa <math>w = a_1 \ldots a_n \in A^*</math> nazywamy | ||
słowo <math> | słowo <math>\stackrel{\leftarrow}{w} = a_n \ldots a_1</math>. Odbiciem zwierciadlanym języka <math>L \subset A^*</math> | ||
nazywamy język <math> | nazywamy język <math>\stackrel{\leftarrow}{L} = \{ \stackrel{\leftarrow}{w} \in A^* \; : \; w \in L \}</math>. | ||
}}</span> | }}</span> | ||
| Linia 175: | Linia 181: | ||
<span id="twierdzenie_2_1">{{twierdzenie|2.1.|| | <span id="twierdzenie_2_1">{{twierdzenie|2.1.|| | ||
Rodzina <math> | Rodzina <math>\mathcal{REG}(A^{*})=\mathcal{REC}(A^{*})</math> jest zamknięta ze względu na: | ||
:(1) sumę mnogościową, przecięcie, różnicę i uzupełnienie, | :(1) sumę mnogościową, przecięcie, różnicę i uzupełnienie, | ||
:(2) katenację i operację iteracji <math> | :(2) katenację i operację iteracji <math>* </math> | ||
:(3) obraz homomorficzny, | :(3) obraz homomorficzny, | ||
:(4) podstawienie regularne, | :(4) podstawienie regularne, | ||
| Linia 187: | Linia 193: | ||
{{dowod||| | {{dowod||| | ||
1. Zamkniętość rodziny języków <math> | 1. Zamkniętość rodziny języków <math>\mathcal{REG}(A^{*})</math> ze względu na sumę mnogościową wynika z twierdzenia Kleene'ego. Automat akceptujący iloczyn języków otrzymujemy, zmieniając odpowiednio zbiór stanów końcowych w automacie rozpoznającym sumę. Bowiem pozostając przy oznaczeniach punktu 3 z dowodu twierdzenia Kleene'ego, automat <math>\mathcal{A} =(S,f,{s_0},F)</math>, gdzie <math>F = T_1 \times T_2</math>, rozpoznaje język <math>L_1 \cap L_2</math>. Jeśli automat <math>\mathcal{A} =(S,f,s_0,T)</math> akceptuje język <math>L</math>, to automat <math>\overline{\mathcal{A}} =(S,f,s_0,S\backslash T)</math> akceptuje język <math>\overline{L}=A^{*}\setminus L</math>. Ostatnia własność implikuje zamkniętość ze względu na uzupełnienie. | ||
2 Z twierdzenia Kleene'ego, punkt 4 i 5, wynika zamkniętość ze względu na katenację i operację iteracji <math> | 2 Z twierdzenia Kleene'ego, punkt 4 i 5, wynika zamkniętość ze względu na katenację i operację iteracji <math>*</math>. | ||
3. Niech <math> | 3. Niech <math>h: A^* \longrightarrow B^*</math> będzie homomorfizmem. Dowód implikacji | ||
<center><math> | <center><math>L\in \mathcal{REG}(A^{*})\Longrightarrow \ : h(L)\in \mathcal{REG}(B^{*})</math></center> | ||
przeprowadzimy zgodnie ze strukturą definicji rodziny języków regularnych. | przeprowadzimy zgodnie ze strukturą definicji rodziny języków regularnych. | ||
Dla <math> | Dla <math>L=\emptyset</math> i dla <math>L=\{a\}</math> | ||
gdzie <math> | gdzie <math>a</math> jest dowolną literą alfabetu <math>A</math> , implikacja jest | ||
oczywista. W pierwszym przypadku obrazem homomorficznym jest język | oczywista. W pierwszym przypadku obrazem homomorficznym jest język | ||
pusty, a w drugim język <math> | pusty, a w drugim język <math>\{w\}</math> , gdzie <math>w</math> jest pewnym | ||
słowem nad alfabetem <math> | słowem nad alfabetem <math>B</math> . Dla dowolnych języków regularnych <math>X, | ||
Y \in | Y \in\mathcal{REG}(A^{*})</math> prawdziwe są równości: | ||
* <math> | * <math>h( X \cup Y)=h(X) \cup h(Y) \in\mathcal{REG}(B^{*})</math> , | ||
* <math> | * <math>h( X \cdot Y) = h(X) \cdot h(Y) \in\mathcal{REG}(B^{*})</math> , | ||
* <math> | * <math>{h(X^*)=h( \bigcup_{n=0} ^\infty X^n) = \bigcup_{n=0} ^\infty (h(X))^n = (h(X))^* \in}\mathcal{REG}(B^{*})</math> | ||
co kończy dowód tego punktu. | co kończy dowód tego punktu. | ||
4. Uzasadnienie jest podobne jak dla homomorfizmu. Jedyna różnica tkwi w tym, że dla podstawienia regularnego <math> | 4. Uzasadnienie jest podobne jak dla homomorfizmu. Jedyna różnica tkwi w tym, że dla podstawienia regularnego <math>s:A^{*}\longrightarrow \mathcal{P}(B^{*})</math> i dla dowolnej litery <math>a \in A</math> wartość podstawienia na literze jest pewnym językiem regularnym <math>s(a)=L\in \mathcal{REG}(B^{*})</math> , a nie słowem jak w przypadku | ||
homomorfizmu. | homomorfizmu. | ||
5. Niech <math> | 5. Niech <math>h: A^* \longrightarrow B^*</math> będzie homomorfizmem. | ||
Aby udowodnić implikację | Aby udowodnić implikację | ||
<center><math> | <center><math>L\in \mathcal{REG}(B^{*})\Longrightarrow \ : h^{-1}(L)\in | ||
\mathcal{REG}(A^{*}) | \mathcal{REG}(A^{*})</math>,</center> | ||
odwołamy się do własności, że dla języka <math> | odwołamy się do własności, że dla języka <math>L | ||
\in | \in\mathcal{REG}(B^{*})</math> istnieje | ||
skończony monoid <math> | skończony monoid <math>\; M \;</math> i | ||
homomorfizm <math> | homomorfizm <math>\varphi : B^* \longrightarrow M</math> taki, że | ||
<math> | <math>L = \varphi^{-1}(\varphi (L))</math>. Dla | ||
homomorfizmu <math> | homomorfizmu <math>\varphi \circ h : A^* \longrightarrow M</math> mamy równość: <center><math>((\varphi \circ h)^{-1} \circ (\varphi \circ h))(h^{-1} (L)) = h^{-1}(L)</math>.</center> | ||
Korzystając teraz z | Korzystając teraz z punktu 4 twierdzenia 1.2 z wykładu 3 (patrz [[Języki, automaty i obliczenia/Wykład 3: Automat skończenie stanowy #twierdzenie_1_2|twierdzenie 1.2. wykład 3]]), wnioskujemy, że | ||
punktu | <math>h^{-1}(L) \in\mathcal{REG}(A^{*})</math> . | ||
<math> | |||
6. Wykorzystamy tutaj zapis języka regularnego | 6. Wykorzystamy tutaj zapis języka regularnego | ||
przez wyrażenie regularne. Niech | przez wyrażenie regularne. Niech | ||
dla języka <math> | dla języka <math>L \in\mathcal{REG}(A^{*})</math> wyrażenie regularne <math>\alpha \in \mathcal{WR}</math> | ||
będzie takie, że <math> | będzie takie, że <math>L = \mid {\bf \alpha} \mid</math>. Wtedy język <math>\stackrel{\leftarrow}{L}</math> | ||
jest opisany przez wyrażenie regularne <math> | jest opisany przez wyrażenie regularne <math>\stackrel{\leftarrow}{\bf \alpha}</math>, | ||
które uzyskujemy z <math> | które uzyskujemy z <math>{\bf \alpha}</math> przez odbicie zwierciadlane, a dokładniej odwrócenie | ||
kolejności katenacji w każdej sekwencji tego działania występującej w | kolejności katenacji w każdej sekwencji tego działania występującej w | ||
wyrażeniu regularnym. | wyrażeniu regularnym. | ||
| Linia 240: | Linia 245: | ||
W wykładzie drugim wprowadziliśmy pojęcie gramatyki. Wracamy do tego pojęcia, a w | W wykładzie drugim wprowadziliśmy pojęcie gramatyki. Wracamy do tego pojęcia, a w | ||
szczególności do gramatyki typu '''(3)''', czyli regularnej. Przypomnijmy, że | szczególności do gramatyki typu '''(3)''', czyli regularnej. Przypomnijmy, że | ||
produkcje takiej gramatyki <math> | produkcje takiej gramatyki <math>G=(V_N ,V_T ,v_0 ,P )</math> mają postać: | ||
<center><math> | <center><math>v \rightarrow v' x \;\; lub \;\;\; v \rightarrow x</math></center> | ||
gdzie <math> | gdzie <math>v,v' \in V_N , \; x \in {V_T}^*</math>. Gramatykę typu | ||
'''(3)''', nazywamy inaczej lewostronną lub lewoliniową. Określa się też gramatykę regularną | '''(3)''', nazywamy inaczej lewostronną lub lewoliniową. Określa się też gramatykę regularną | ||
prawostronną | prawostronną | ||
(prawoliniową). Jest to | (prawoliniową). Jest to | ||
gramatyka <math> | gramatyka <math>G=(V_N ,V_T ,v _0 ,P)</math>, której produkcje są postaci: | ||
<center><math> | <center><math>v \rightarrow xv' \;\; lub \;\;\; v \rightarrow x</math></center> | ||
gdzie <math> | gdzie <math>v,v' \in V_N , \; x \in {V_T}^*</math>. Jeśli język <math>L=L(G)</math> jest | ||
generowany przez gramatykę typu '''(3)''' (lewoliniową), to | generowany przez gramatykę typu '''(3)''' (lewoliniową), to | ||
jego odbiciem zwierciadlanym jest <math> | jego odbiciem zwierciadlanym jest <math>\stackrel{\leftarrow}{L} =L ( | ||
\stackrel{\leftarrow}{G})</math>, gdzie <math> | \stackrel{\leftarrow}{G})</math>, gdzie <math>\stackrel{\leftarrow}{G}</math> jest | ||
gramatyką prawoliniową, którą uzyskuje się z gramatyki <math> | gramatyką prawoliniową, którą uzyskuje się z gramatyki <math>G</math> przez | ||
odbicie zwierciadlane prawych stron produkcji. Oznacza to, iż | odbicie zwierciadlane prawych stron produkcji. Oznacza to, iż | ||
zmieniamy produkcje według następujących zasad: | zmieniamy produkcje według następujących zasad: | ||
<center><math> | <center><math>v \rightarrow v' x \;\;</math> zastępujemy przez <math>\;\;\; v \rightarrow \stackrel{\leftarrow}{x}v'</math></center> | ||
<center><math> | <center><math>v \rightarrow x \;\;</math> zastępujemy przez <math>\;\;\; v \rightarrow \stackrel{\leftarrow}{x}</math>.</center> | ||
Oczywiście, jeśli <math> | Oczywiście, jeśli <math>L</math> jest językiem generowanym przez gramatykę prawoliniową, to | ||
<math> | <math>\stackrel{\leftarrow}{L}</math> jest | ||
generowany przez odpowiednią gramatykę lewoliniową. | generowany przez odpowiednią gramatykę lewoliniową. | ||
Podamy teraz charakterystykę rodziny języków regularnych <math> | Podamy teraz charakterystykę rodziny języków regularnych <math>\mathcal{REG}(A^{*})</math> | ||
przez rodzinę gramatyk prawoliniowych. | przez rodzinę gramatyk prawoliniowych. | ||
<span id="twierdzenie_2_2">{{twierdzenie|2.2.|| | <span id="twierdzenie_2_2">{{twierdzenie|2.2.|| | ||
Niech <math> | Niech <math>L \subset A^*</math>. Język <math>L \in\mathcal{REG}(A^{*})</math> wtedy i tylko wtedy, | ||
gdy <math> | gdy <math>L =L(G)</math> dla pewnej gramatyki prawoliniowej <math>G</math>. | ||
}}</span> | }}</span> | ||
| Linia 277: | Linia 282: | ||
{{dowod||| | {{dowod||| | ||
Załóżmy, że automat <math> | Załóżmy, że automat <math>\mathcal{A} =(S,A,f,s_0,T)</math> rozpoznaje język <math>L</math> . | ||
Definiujemy gramatykę <math> | Definiujemy gramatykę <math>G = (V_N , V_T , v_0 ,P)</math> | ||
przyjmując <math> | przyjmując <math>V_N = S,\;\; V_T = A, \;\; v_0 = s_0</math> oraz określając w następujący sposób | ||
zbiór produkcji | zbiór produkcji | ||
<center><math> | <center><math>P = \{ s \rightarrow a f(s ,a) ; :s \in S, a \in A \} \cup \{ s \rightarrow 1 ; : s \in T \}</math>.</center> | ||
Dla dowolnego stanu <math> | Dla dowolnego stanu <math>s \in S</math> i słowa <math>w \in A^+</math> prawdziwa jest równoważność | ||
<center><math> | <center><math>s_0 \mapsto^* ws \ ;\ ; \Longleftrightarrow \ ;\ ; f(s_0 ,w) = s</math>.</center> | ||
Dowód przeprowadzimy indukcyjnie ze względu na długość słowa <math> | Dowód przeprowadzimy indukcyjnie ze względu na długość słowa <math>w</math>. Niech <math>w = a</math> dla pewnego <math>a \in A</math>. | ||
Z definicji zbioru produkcji <math> | Z definicji zbioru produkcji <math>P</math> wynika równoważność | ||
<center><math> | <center><math>s_0 \rightarrow as \; \Longleftrightarrow \; s = f(s_0 ,a)</math>.</center> | ||
Rozważmy teraz <math> | Rozważmy teraz <math>w = a_1 \ldots a_n</math> oraz <math>s_0 \mapsto^* ws</math>. Z założenia indukcyjnego | ||
wynika, że <center><math> | wynika, że <center><math>f(s_0 , a_1 \ldots a_{n-1}) =s' \Longleftrightarrow s_0 \mapsto^* a_1 \ldots a_{n-1}s'</math></center> | ||
oraz, że <math> | oraz, że <math>s = f(s' ,a_n )</math> wtedy | ||
i tylko wtedy, gdy <math> | i tylko wtedy, gdy <math>s' \mapsto a_n s</math>. A więc fakt, że | ||
<math> | <math>s=f(s_{0},w)=f(s_{0},a_{1}\ldots a_{n})=f(f(s_{0},a_{1}\ldots a_{n-1}),a_{n})</math> jest | ||
równoważny temu, | równoważny temu, | ||
że <math> | że <math>s'=f(s_{0},a_{1}\ldots a_{n-1})\mapsto a_{n}s</math> . A to z kolei równoważne jest | ||
<center><math> | <center><math>s_{0}\mapsto^{*}a_{1}\ldots a_{n-1}s',\;\;\;s'\mapsto a_{n}s</math></center> | ||
i ostatecznie równoważne faktowi, że <math> | i ostatecznie równoważne faktowi, że <math>s_{0}\mapsto ^{*}a_{1}\ldots a_{n-1}a_{n}s</math> . | ||
A zatem dowodzona równoważność jest prawdziwa dla <math> | A zatem dowodzona równoważność jest prawdziwa dla <math>w \in A^+</math>, ponieważ | ||
<center><math> | <center><math>w\in L(\mathcal{A})\ : \Longleftrightarrow \ : s=f(s_{0},w)\in T\ : \Longleftrightarrow \ : s_{o}\mapsto ^{*}ws,\, s\rightarrow 1\in P\ : \Longleftrightarrow \ : w\in L(G)</math>.</center> | ||
Dla <math> | Dla <math>w=1</math> mamy <math>1\in L(\mathcal{A})\ : \Longleftrightarrow \ : s_{0}\rightarrow 1\in P\ : \Longleftrightarrow \ : 1\in L(G)</math> | ||
co kończy dowód w jedną stronę. | co kończy dowód w jedną stronę. | ||
Rozważmy teraz język <math> | Rozważmy teraz język <math>L = L(G)</math> generowany przez pewna gramatykę prawoliniową | ||
<math> | <math>G = (V_N , V_T , v_0 ,P)</math>. Skonstruujemy gramatykę równoważną | ||
<math> | <math>G</math> i taką, w której wszystkie produkcje są postaci | ||
<math> | <math>v \rightarrow a v'</math> lub <math>v \rightarrow 1</math>, gdzie <math>v,v' \in V_N , a \in A</math>. | ||
Będziemy zamieniać produkcje występujące w gramatyce <math> | Będziemy zamieniać produkcje występujące w gramatyce <math>G</math> na inne, o | ||
żądanej postaci, zgodnie z następująmi zasadami: | żądanej postaci, zgodnie z następująmi zasadami: | ||
1. Produkcje typu <math> | 1. Produkcje typu <math>v \rightarrow v'</math>, gdzie <math>v,v' \in V_N</math> | ||
Z symbolem nieterminalnym <math> | Z symbolem nieterminalnym <math>v \in V_N</math> kojarzymy określony poniżej zbiór | ||
<center><math> | <center><math>V_N(v) = \{ v' \in V_N \; : \; v \rightarrow v_1 \rightarrow \ldots \rightarrow v_n \rightarrow v' \; w \; G \}</math></center> | ||
oraz zbiór produkcji | oraz zbiór produkcji | ||
<center><math> | <center><math>P(v) = \{ v \rightarrow xv'' \; : \; x \neq 1 , \; \exists v' \in V_N(v) , v' \rightarrow xv'' \in P \} \cup</math></center> | ||
<center><math> | <center><math>\cup \{ v \rightarrow x \; : \; \exists v' \in V_N(v) , v' \rightarrow x \in P \}</math>.</center> | ||
Dla każdego takiego symbolu <math> | Dla każdego takiego symbolu <math>v \in V_N</math> usuwamy ze zbioru <math>P</math> wszystkie produkcje | ||
<math> | <math>v \rightarrow v'</math> i wprowadzamy na to | ||
miejsce wszystkie produkcje ze zbioru <math> | miejsce wszystkie produkcje ze zbioru <math>P(v)</math>. | ||
2. Produkcje typu <math> | 2. Produkcje typu <math>v \rightarrow x</math> dla <math>x \neq 1</math>. | ||
Jeśli produkcja taka występuje w <math> | Jeśli produkcja taka występuje w <math>P</math> i <math>x \neq 1</math>, to do alfabetu | ||
nieterminalnego <math> | nieterminalnego <math>V_N</math> dodajemy nowy symbol <math>v_x</math>. Następnie ze | ||
zbioru <math> | zbioru <math>P</math> usuwamy powyższą produkcję i dodajemy dwie nowe: | ||
<center><math> | <center><math>v \rightarrow xv_x , \;\; v_x \rightarrow 1</math>.</center> | ||
Zauważmy, że jeśli <math> | Zauważmy, że jeśli <math>x\neq y</math>, to <math>v_x \neq v_y</math>. | ||
3. Produkcje typu <math> | 3. Produkcje typu <math>v \rightarrow x v'</math> dla <math>\mid x \mid > 1</math>. | ||
Jeśli <math> | Jeśli <math>v \rightarrow a_1 \ldots a_n v' \in P</math>, przy czym <math>n \geq 2</math>, to do alfabetu | ||
nieterminalnego <math> | nieterminalnego <math>V_N</math> dodajemy | ||
nowe symbole <math> | nowe symbole <math>v_1 , \ldots v_n</math>, produkcję <math>v \rightarrow a_1 \ldots a_n v'</math> usuwamy ze | ||
zbioru <math> | zbioru <math>P</math> i | ||
dodajemy produkcje: <center><math> | dodajemy produkcje: <center><math>v \rightarrow a_1 v_1 , v_1 \rightarrow a_2 v_2 , \ldots ,v_{n-1} \rightarrow a_n v'</math>.</center> | ||
Po opisanych powyżej trzech modyfikacjach gramatyki <math> | Po opisanych powyżej trzech modyfikacjach gramatyki <math>G</math> | ||
generowany język, co łatwo zauważyć, nie ulega zmianie. Zatem | generowany język, co łatwo zauważyć, nie ulega zmianie. Zatem | ||
skonstruowana gramatyka jest równoważna wyjściowej. Dla | skonstruowana gramatyka jest równoważna wyjściowej. Dla | ||
otrzymanej gramatyki określamy teraz automat niedeterministyczny | otrzymanej gramatyki określamy teraz automat niedeterministyczny | ||
<math> | <math>\mathcal{A} =(S,A,f,\{s_0\},T)</math>, przyjmując <math>S= V_N</math>, <math>A= V_T</math> | ||
oraz <math> | oraz <math>s_0 = v_0</math> i definiując następująco funkcję przejść: <math>f(v,a) = | ||
\{ v' \in V_N \; : \; v \rightarrow av' \in P \} | \{ v' \in V_N \; : \; v \rightarrow av' \in P \}</math>. Przjmując | ||
<math> | <math>T = \{ v \in V_N \; : \; v \rightarrow 1 \in P \}</math> jako zbiór stanów końcowych, stwierdzamy, | ||
że automat <math> | że automat <math>\mathcal{A}</math> rozpoznaje język | ||
<center><math> | <center><math>L(\mathcal{A})=\{w\in V_{T}^{*}\ : :\ : f(s_{0})\cap T\neq \emptyset \}=L</math>.</center> | ||
Uzyskany rezultat, w świetle równości <math> | Uzyskany rezultat, w świetle równości <math>\mathcal{REG}(A^{*})=\mathcal{RE}C(A^{*})</math> , | ||
kończy dowód twierdzenia. | kończy dowód twierdzenia. | ||
| Linia 367: | Linia 372: | ||
w następnym wykładzie. Przykłady ilustrujące twierdzenie zamieszczamy poniżej. | w następnym wykładzie. Przykłady ilustrujące twierdzenie zamieszczamy poniżej. | ||
{{przyklad|2.1.|| | <span id="przyklad__">{{przyklad|2.1.|| | ||
1. Niech <math>\mathcal{A}=(S,A,f,s_0,T)</math> będzie automatem takim, że<br> | |||
<math> | <math>S=\{ s_0,s_1, s_2 \}, A=\{a,b\}, T=\{s_1\}</math>, a graf przejść wygląda następująco:}} | ||
<center> | |||
[[File:ja-lekcja07-w-rys7.svg|250x250px|thumb|center|Rysunek 7]] | |||
</center> | |||
Gramatyka <math>G=(S,A,s_0,P)</math>, gdzie | |||
<center><math>P=\{s_0 \rightarrow as_1, s_0 \rightarrow bs_2, s_1 \rightarrow as_2, s_1 \rightarrow bs_0, s_1 \rightarrow 1, | |||
Gramatyka <math> | |||
<center><math> | |||
s_2 \rightarrow as_0, s_2 \rightarrow bs_1\}</math></center> | s_2 \rightarrow as_0, s_2 \rightarrow bs_1\}</math></center> | ||
akceptuje język <math> | akceptuje język <math>L(\mathcal{A})</math>. <br> | ||
Zauważmy, że język <center><math> | Zauważmy, że język <center><math>L(\mathcal{A})=L(G)=\{ w \in A^* : \#_aw-\#_bw=1 mod 3\}</math>.</center> | ||
2. Niech <math>G=(\{v_0,v_1\},\{a,b\},v_0,P)</math>, gdzie | |||
<center><math> | <center><math>P=\{v_0 \rightarrow av_0, v_0 \rightarrow ab, v_0 \rightarrow bv_1, v_1 \rightarrow 1 \}</math>.</center> | ||
Gramatykę <math> | Gramatykę <math>G</math> przekształcamy w równoważną gramatykę | ||
<center><math> | <center><math>G'=(\{v_0,v_1,v_2,v_b\},\{a,b\},v_0,P')</math>,</center> | ||
gdzie | gdzie | ||
<center><math> | <center><math>P'=\{v_0 \rightarrow av_0, v_0 \rightarrow av_2, v_0 \rightarrow bv_1 , v_2 \rightarrow bv_b, | ||
v_1 \rightarrow 1 , v_b \rightarrow 1\} | v_1 \rightarrow 1 , v_b \rightarrow 1\}</math>.</center> | ||
Niedeterministyczny automat <math> | Niedeterministyczny automat <math>\mathcal{A}_{ND}=(\{v_0,v_1,v_2,v_b\},\{a,b\},f,v_0,\{v_1,v_b\})</math>, gdzie graf przejśc | ||
wygląda następująco:< | wygląda następująco: | ||
<center> | |||
[[File:ja-lekcja07-w-rys8.svg|250x250px|thumb|center|Rysunek 8]] | |||
</center> | |||
<center><math> | <center><math>L(G)=L(\mathcal{A}_{ND})=a^*b</math></center> | ||
</span> | |||
Wykorzystując udowodnione do tej pory własności rodziny języków | Wykorzystując udowodnione do tej pory własności rodziny języków | ||
| Linia 401: | Linia 409: | ||
właśnie rodzina, czyli ogół języków | właśnie rodzina, czyli ogół języków | ||
typu '''(3)''' w hierarchii | typu '''(3)''' w hierarchii | ||
Chomsky'ego pokrywa się z rodziną <math> | Chomsky'ego pokrywa się z rodziną <math>\mathcal{REG}(A^{*})</math> . | ||
<span id="twierdzenie_2_3">{{twierdzenie|2.3.|| | <span id="twierdzenie_2_3">{{twierdzenie|2.3.|| | ||
Dla dowolnego alfabetu <math> | Dla dowolnego alfabetu <math>A</math> rodziny języków regularnych <math>A^{*}</math> | ||
oraz języków generowanych przez gramatyki regularne są równe, czyli | oraz języków generowanych przez gramatyki regularne są równe, czyli | ||
<math> | <math>\mathcal{REG}(A^{*})=\mathcal{L}_{3}</math> . | ||
}}</span> | }}</span> | ||
| Linia 413: | Linia 421: | ||
{{dowod||| | {{dowod||| | ||
Odbicie zwierciadlane dowolnego języka <math> | Odbicie zwierciadlane dowolnego języka <math>L\in \mathcal{REG}(A^{*})</math> , czyli język | ||
<math> | <math>\overleftarrow{L}</math> należy również do rodziny <math>\mathcal{REG}(A^{*})</math> , | ||
co oznacza, że <math> | co oznacza, że <math>\overleftarrow{L}\in \mathcal{RE}C(A^{*})</math> . | ||
Na podstawie twierdzenia [[# | Na podstawie twierdzenia 2.2. (patrz [[#twierdzenie_2_2|twierdzenie 2.2.]]) istnieje więc gramatyka prawoliniowa | ||
<math> | <math>G</math> taka, że <math>\overleftarrow{L}=L(G)</math> . A stąd wniosek, że | ||
<math> | <math>L=\overleftarrow{\overleftarrow{L}}=L(\overline{G})</math> | ||
dla pewnej gramatyki <math> | dla pewnej gramatyki <math>\overline{G}</math> typu '''(3)'''. Zatem <math>L\in \mathcal{L}_{3}</math> . | ||
Rozważmy teraz język <math> | Rozważmy teraz język <math>L</math> typu '''(3)''', czyli <math>L=L(G)</math> dla pewnej | ||
gramatyki regularnej. A więc <math> | gramatyki regularnej. A więc <math>\overleftarrow{L}=L(\overline{G})</math> | ||
dla pewnej gramatyki prawoliniowej i <math> | dla pewnej gramatyki prawoliniowej i <math>\overleftarrow{L}\in \mathcal{RE}C(A^{*})</math> . | ||
Z twierdzenia Kleene'ego wynika, że <math> | Z twierdzenia Kleene'ego wynika, że <math>\overleftarrow{L}\in \mathcal{REG}(A^{*})</math> | ||
i ostatecznie <math> | i ostatecznie <math>L=\overleftarrow{\overleftarrow{L}}\in \mathcal{REG}(A^{*})</math> , | ||
co kończy dowód twierdzenia. | co kończy dowód twierdzenia. | ||
| Linia 432: | Linia 440: | ||
Zamkniemy rozważania następującą konkluzją podsumowującą główne rezultaty tego wykładu. | Zamkniemy rozważania następującą konkluzją podsumowującą główne rezultaty tego wykładu. | ||
Dla dowolnego skończonego alfabetu <math> | Dla dowolnego skończonego alfabetu <math>A</math> prawdziwe są równości: | ||
<center><math> | <center><math>\mathcal{REG}(A^{*})=\mathcal{REC}(A^{*})= \mathcal{L}_{3}</math></center> | ||
czyli | czyli | ||
wprowadzone pojęcia rodziny języków regularnych, rozpoznawalnych | wprowadzone pojęcia rodziny języków regularnych, rozpoznawalnych | ||
oraz generowanych przez gramatyki typu '''(3)''' są tożsame. | oraz generowanych przez gramatyki typu '''(3)''' są tożsame. | ||
Aktualna wersja na dzień 22:14, 11 wrz 2023
W wykładzie udowodnimy twierdzenie Kleene'ego, które orzeka, że rodzina języków regularnych jest identyczna z rodziną języków rozpoznawanych przez automaty o skończonej liczbie stanów. Przedstawimy własności języków regularnych i gramatyk typu (3). Na koniec uzasadnimy, że rodziny języków regularnych, rozpoznawalnych oraz generowanych przez gramatyki typu (3), są tożsame.
Twierdzenie Kleene

Zobacz biografię
Wiemy już, z poprzednich wykładów, że rodzina wyrażeń regularnych
określa rodzinę języków regularnych. Celem pierwszej części tego wykładu jest ustalenie związku pomiędzy rodziną języków regularnych a rodziną języków rozpoznawanych przez automaty o skończonej liczbie stanów. Twierdzenie, udowodnione przez S.C.Kleene'ego w roku 1956, orzeka, iż te dwie rodziny języków są identyczne.
Twierdzenie 1.1.
Dla dowolnego skończonego alfabetu
Dowód
Dowód pierwszej części twierdzenia, czyli inkluzja , będzie prowadzony zgodnie ze strukturą definicji rodziny języków regularnych .
1. Język pusty jest rozpoznawany przez dowolny automat , w którym zbiór stanów końcowych jest pusty.
2. Język a złożony z dowolnej litery jest rozpoznawany przez automat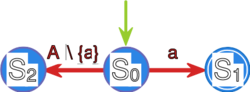
Dla dalszej części dowodu ustalmy, iż dane są języki rozpoznawane odpowiednio przez automaty deterministyczne , gdzie .
3. Sumę mnogościową języków , czyli język rozpoznaje automat , dla którego , , oraz dla dowolnego stanu i litery funkcja przejść określona jest równością
4. Katenację języków , czyli język rozpoznaje automat , dla którego oraz dla dowolnego stanu i litery funkcja przejść określona jest następująco:
a zbiorem stanów końcowych jest
5. Załóżmy, że język rozpoznaje automat . Określimy automat niedeterministyczny, który będzie rozpoznawał gwiazdkę Kleene języka , czyli . Automat niedeterministyczny , w którym
rozpoznaje język język . Dowód tego faktu jest indukcyjny i pozostawiamy go na ćwiczenia. Zauważmy teraz, że język rozpoznaje automat
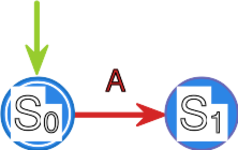
Ponieważ , to korzystając z udowodnionej już zamkniętości języków rozpoznawanych ze względu na sumę mnogościową, stwierdzamy, że istnieje automat rozpoznający język .
Zatem dowód inkluzji jest zakończony.
Przejdziemy teraz do dowodu inkluzji .
Niech oznacza dowolny język rozpoznawany przez automat . Dowód polega na rozbiciu języka na fragmenty, dla których stwierdzenie, że są to języki regularne będzie dość oczywiste. Natomiast sam język będzie wynikiem operacji regularnych określonych na tych właśnie fragmentach. Poniżej przeprowadzamy defragmentację języka .
Dla niech
Jest to język złożony ze słów, które przeprowadzają stan automatu w stan . Ogół liter alfabetu przeprowadzających stan w oznaczymy przez
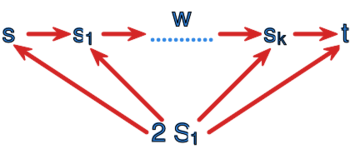
Dla stanów i zbioru niech
Jest to język, który można przedstawić graficznie następująco:
Na koniec przyjmijmy
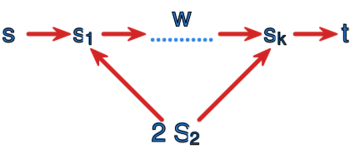
określony dla i
Język ten jest graficznie interpretowany poniżej.
Wprost z określeń wynika, że wszystkie wprowadzone powyżej języki są regularne, czyli należą do rodziny . Dowód tego faktu przebiega indukcyjnie ze względu na liczbę elementów zbiorów i . Szczegóły tego dowodu pominiemy. Natomiast warto wskazać rolę, jaką spełniają w dowodzie wprowadzone wyżej języki. A mianowicie:
Tę ostatnią równość przedstawia poniższy rysunek.
co graficznie można przedstawić następująco:
Dochodzimy więc do konkluzji, iż jezyki oraz są regularne. W szczególności zatem regularny jest język .
Język możemy przedstawić w następującej postaci:
co w połączeniu z ustaleniami punktu 3 z poprzedniej części dowodu uzasadnia tezę, że język należy do rodziny .
Własności języków regularnych i gramatyk regularnych
W tej części wykładu omówimy własności rodziny języków i gramatyk regularnych, czyli typu (3) w hierarchii Chomsky'ego. Ustalimy też związek pomiędzy językami a gramatykami regularnymi. Zbadamy zamkniętość rodziny języków regularnych ze względu na operacje mnogościowe, czyli ze względu na sumę, przecięcie, różnicę i uzupełnienie. Rozpoczniemy jednak tę część wykładu od wprowadzenia jednoargumentowego działania na słowach zwanego odbiciem zwierciadlanym.
Definicja 2.1.
Odbiciem zwierciadlanym słowa nazywamy słowo . Odbiciem zwierciadlanym języka nazywamy język .
Twierdzenie 2.1.
Rodzina jest zamknięta ze względu na:
- (1) sumę mnogościową, przecięcie, różnicę i uzupełnienie,
- (2) katenację i operację iteracji
- (3) obraz homomorficzny,
- (4) podstawienie regularne,
- (5) przeciwobraz homomorficzny,
- (6) odbicie zwierciadlane.
Dowód
1. Zamkniętość rodziny języków ze względu na sumę mnogościową wynika z twierdzenia Kleene'ego. Automat akceptujący iloczyn języków otrzymujemy, zmieniając odpowiednio zbiór stanów końcowych w automacie rozpoznającym sumę. Bowiem pozostając przy oznaczeniach punktu 3 z dowodu twierdzenia Kleene'ego, automat , gdzie , rozpoznaje język . Jeśli automat akceptuje język , to automat akceptuje język . Ostatnia własność implikuje zamkniętość ze względu na uzupełnienie.
2 Z twierdzenia Kleene'ego, punkt 4 i 5, wynika zamkniętość ze względu na katenację i operację iteracji .
3. Niech będzie homomorfizmem. Dowód implikacji
przeprowadzimy zgodnie ze strukturą definicji rodziny języków regularnych. Dla i dla gdzie jest dowolną literą alfabetu , implikacja jest oczywista. W pierwszym przypadku obrazem homomorficznym jest język pusty, a w drugim język , gdzie jest pewnym słowem nad alfabetem . Dla dowolnych języków regularnych prawdziwe są równości:
- ,
- ,
co kończy dowód tego punktu.
4. Uzasadnienie jest podobne jak dla homomorfizmu. Jedyna różnica tkwi w tym, że dla podstawienia regularnego i dla dowolnej litery wartość podstawienia na literze jest pewnym językiem regularnym , a nie słowem jak w przypadku homomorfizmu.
5. Niech będzie homomorfizmem. Aby udowodnić implikację
odwołamy się do własności, że dla języka istnieje skończony monoid i homomorfizm taki, że . Dla
homomorfizmu mamy równość:Korzystając teraz z punktu 4 twierdzenia 1.2 z wykładu 3 (patrz twierdzenie 1.2. wykład 3), wnioskujemy, że .
6. Wykorzystamy tutaj zapis języka regularnego przez wyrażenie regularne. Niech dla języka wyrażenie regularne będzie takie, że . Wtedy język jest opisany przez wyrażenie regularne , które uzyskujemy z przez odbicie zwierciadlane, a dokładniej odwrócenie kolejności katenacji w każdej sekwencji tego działania występującej w wyrażeniu regularnym.
W wykładzie drugim wprowadziliśmy pojęcie gramatyki. Wracamy do tego pojęcia, a w szczególności do gramatyki typu (3), czyli regularnej. Przypomnijmy, że produkcje takiej gramatyki mają postać:
gdzie . Gramatykę typu (3), nazywamy inaczej lewostronną lub lewoliniową. Określa się też gramatykę regularną prawostronną (prawoliniową). Jest to gramatyka , której produkcje są postaci:
gdzie . Jeśli język jest generowany przez gramatykę typu (3) (lewoliniową), to jego odbiciem zwierciadlanym jest , gdzie jest gramatyką prawoliniową, którą uzyskuje się z gramatyki przez odbicie zwierciadlane prawych stron produkcji. Oznacza to, iż zmieniamy produkcje według następujących zasad:
Oczywiście, jeśli jest językiem generowanym przez gramatykę prawoliniową, to jest generowany przez odpowiednią gramatykę lewoliniową.
Podamy teraz charakterystykę rodziny języków regularnych przez rodzinę gramatyk prawoliniowych.
Twierdzenie 2.2.
Niech . Język wtedy i tylko wtedy, gdy dla pewnej gramatyki prawoliniowej .
Dowód
Załóżmy, że automat rozpoznaje język . Definiujemy gramatykę przyjmując oraz określając w następujący sposób zbiór produkcji
Dla dowolnego stanu i słowa prawdziwa jest równoważność
Dowód przeprowadzimy indukcyjnie ze względu na długość słowa . Niech dla pewnego . Z definicji zbioru produkcji wynika równoważność
Rozważmy teraz oraz . Z założenia indukcyjnego
wynika, żeoraz, że wtedy i tylko wtedy, gdy . A więc fakt, że jest równoważny temu, że . A to z kolei równoważne jest
i ostatecznie równoważne faktowi, że . A zatem dowodzona równoważność jest prawdziwa dla , ponieważ
Dla mamy co kończy dowód w jedną stronę.
Rozważmy teraz język generowany przez pewna gramatykę prawoliniową . Skonstruujemy gramatykę równoważną i taką, w której wszystkie produkcje są postaci lub , gdzie . Będziemy zamieniać produkcje występujące w gramatyce na inne, o żądanej postaci, zgodnie z następująmi zasadami:
1. Produkcje typu , gdzie
Z symbolem nieterminalnym kojarzymy określony poniżej zbiór
oraz zbiór produkcji
Dla każdego takiego symbolu usuwamy ze zbioru wszystkie produkcje i wprowadzamy na to miejsce wszystkie produkcje ze zbioru .
2. Produkcje typu dla .
Jeśli produkcja taka występuje w i , to do alfabetu nieterminalnego dodajemy nowy symbol . Następnie ze zbioru usuwamy powyższą produkcję i dodajemy dwie nowe:
Zauważmy, że jeśli , to .
3. Produkcje typu dla .
Jeśli , przy czym , to do alfabetu nieterminalnego dodajemy nowe symbole , produkcję usuwamy ze zbioru i
dodajemy produkcje:Po opisanych powyżej trzech modyfikacjach gramatyki generowany język, co łatwo zauważyć, nie ulega zmianie. Zatem skonstruowana gramatyka jest równoważna wyjściowej. Dla otrzymanej gramatyki określamy teraz automat niedeterministyczny , przyjmując , oraz i definiując następująco funkcję przejść: . Przjmując jako zbiór stanów końcowych, stwierdzamy, że automat rozpoznaje język
Uzyskany rezultat, w świetle równości , kończy dowód twierdzenia.
Algorytmiczną stroną równoważności udowodnionej w powyższym twierdzeniu zajmiemy się w następnym wykładzie. Przykłady ilustrujące twierdzenie zamieszczamy poniżej.
Przykład 2.1.
1. Niech będzie automatem takim, że
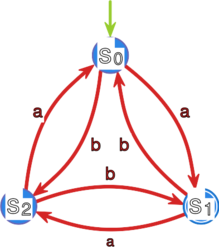
Gramatyka , gdzie
akceptuje język .
Zauważmy, że język
2. Niech , gdzie
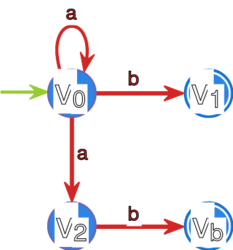
Gramatykę przekształcamy w równoważną gramatykę
gdzie
Niedeterministyczny automat , gdzie graf przejśc wygląda następująco:
Wykorzystując udowodnione do tej pory własności rodziny języków generowanych przez gramatyki regularne, uzasadnimy teraz, iż ta właśnie rodzina, czyli ogół języków typu (3) w hierarchii Chomsky'ego pokrywa się z rodziną .
Twierdzenie 2.3.
Dla dowolnego alfabetu rodziny języków regularnych oraz języków generowanych przez gramatyki regularne są równe, czyli .
Dowód
Odbicie zwierciadlane dowolnego języka , czyli język należy również do rodziny , co oznacza, że . Na podstawie twierdzenia 2.2. (patrz twierdzenie 2.2.) istnieje więc gramatyka prawoliniowa taka, że . A stąd wniosek, że dla pewnej gramatyki typu (3). Zatem .
Rozważmy teraz język typu (3), czyli dla pewnej gramatyki regularnej. A więc dla pewnej gramatyki prawoliniowej i . Z twierdzenia Kleene'ego wynika, że i ostatecznie , co kończy dowód twierdzenia.
Zamkniemy rozważania następującą konkluzją podsumowującą główne rezultaty tego wykładu.
Dla dowolnego skończonego alfabetu prawdziwe są równości:
czyli wprowadzone pojęcia rodziny języków regularnych, rozpoznawalnych oraz generowanych przez gramatyki typu (3) są tożsame.