|
|
| (Nie pokazano 20 wersji utworzonych przez 4 użytkowników) |
| Linia 1: |
Linia 1: |
| {{cwiczenie|||
| | ==Ćwiczenia 7== |
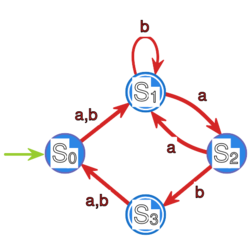
| Zastosuj algorytm ''Automat2GReg'' do automatu o następującej
| |
| funkcji przejść:
| |
|
| |
|
| <center><math>\displaystyle \begin{array} {c|c|c|c|c|} f & s_0 & s_1 & s_2 & s_3\\
| | {{cwiczenie|1|| |
| \hline a & s_1 & s_2 & s_0 & s_2\\
| |
| \hline b & s_3 & s_2 & s_2 & s_2\\
| |
| \hline \end{array} </math></center>
| |
|
| |
|
| gdzie <math>\displaystyle s_0</math> jest stanem początkowym oraz <math>\displaystyle T=\{s_0,s_2\}</math>.
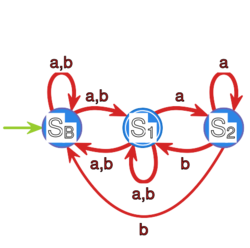
| | Niech <math>A = \{a,b\}</math>. Dla automatów<center><math>{\mathcal B} = (S_{\mathcal B},A,f_{\mathcal B},s_{\mathcal B},F_{\mathcal B}),\;\;\;\; {\mathcal C} = |
| | (S_{\mathcal C},A,f_{\mathcal C},s_{\mathcal C},F_{\mathcal C})</math></center> |
| | <center><math>S_{\mathcal B} = \{s_{\mathcal B},s_1,s_2\}, |
| | \;\;F_{\mathcal B} = \{s_2\},\;\;\; S_{\mathcal C} = \{s_{\mathcal C},s\},\;\; F_{\mathcal C} = \{s\}</math>,</center> |
| | gdzie |
|
| |
|
| }} | | <center><math>\begin{array} {c|c|c|c|} f_{\mathcal B} &s_{\mathcal B} &s_1 & s_2 \\ |
| | \hline a & s_2 & s_1 & s_2 \\ \hline b & s_1 & s_1 & s_2\\ |
| | \hline \end{array} \begin{array} {c|c|c|} f_{\mathcal C} &s_{\mathcal C} &s \\ \hline a & s & s \\ |
| | \hline b & s_{\mathcal C} & s_{\mathcal C} \\ \hline \end{array}</math></center> |
|
| |
|
| ROZWIĄZANIE. Pętla w liniach 7.--17. do zbioru <math>\displaystyle P</math> doda następujące
| | skonstruuj automat <math>\mathcal A</math> taki, że <center><math>L({\mathcal A}) = L({\mathcal B}) \cap L({\mathcal C})</math>,</center> |
| produkcje: <math>\displaystyle v_0 \rightarrow av_1</math>, <math>\displaystyle v_0 \rightarrow bv_3</math>, <math>\displaystyle v_1
| |
| \rightarrow av_2</math>, <math>\displaystyle v_1 \rightarrow bv_2</math>, <math>\displaystyle v_2 \rightarrow av_0</math>, | |
| <math>\displaystyle v_2 \rightarrow bv_2</math>, <math>\displaystyle v_3 \rightarrow av_2</math>, <math>\displaystyle v_3 \rightarrow
| |
| bv_2</math>. Ponieważ stanami końcowymi są <math>\displaystyle s_0</math> i <math>\displaystyle s_2</math>, w pętli (w
| |
| liniach 12.--14.) dodane zostaną jeszcze produkcje <math>\displaystyle v_0 \rightarrow
| |
| 1</math> oraz <math>\displaystyle v_2 \rightarrow 1</math>.
| |
| | |
| {{cwiczenie|||
| |
| Zbuduj automaty akceptujące języki generowane następującymi
| |
| gramatykami (<math>\displaystyle v_i</math> oznaczają symbole nieterminalne, <math>\displaystyle a,b</math> --
| |
| terminalne):
| |
| # <math>\displaystyle v_0 \rightarrow av_0</math>, <math>\displaystyle v_0 \rightarrow bv_1</math>, <math>\displaystyle v_0
| |
| \rightarrow bv_2</math>, <math>\displaystyle v_1 \rightarrow bv_0</math>, <math>\displaystyle v_1 \rightarrow av_2</math>,
| |
| <math>\displaystyle v_2 \rightarrow av_0</math>, <math>\displaystyle v_2 \rightarrow 1</math>.
| |
| # <math>\displaystyle v_0 \rightarrow av_1</math>, <math>\displaystyle v_0 \rightarrow b</math>, <math>\displaystyle v_1 \rightarrow
| |
| bv_0</math>, <math>\displaystyle v_1 \rightarrow av_1</math>, <math>\displaystyle v_1 \rightarrow 1</math>.
| |
|
| |
|
| }} | | }} |
|
| |
|
| ROZWIĄZANIE punktu 1. Postępując zgodnie z algorytmem
| | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"><math>L({\mathcal A})= (S_{\mathcal B}\times S_{\mathcal C},A,f_{\mathcal A},(s_{\mathcal B},s_{\mathcal C}), |
| ''GReg2Automat'', obliczamy funkcję przejść tworzonego automatu
| | F_{\mathcal B}\times F_{\mathcal C})</math>. Funkcja przejść zadana jest grafem |
| (w tym przypadku niedeterministycznego) o stanach <math>\displaystyle s_0, s_1, s_2</math>
| |
| (stanem początkowym jest <math>\displaystyle s_0</math>):
| |
|
| |
|
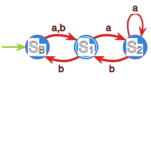
| <math>\displaystyle f(s_0,a)=\{f_0\}</math>, <math>\displaystyle f(s_0,b)=\{s_1,s_2\}</math>, <math>\displaystyle f(s_1,b)=\{s_0,s_2\}</math>, | | <center> |
| <math>\displaystyle f(s_2,a)=s_0</math>. Ponieważ w gramatyce istnieje produkcja <math>\displaystyle v_2
| | [[File:ja-lekcja07-c-rys1.svg|250x250px|thumb|center|Rysunek 1]] |
| \rightarrow 1</math>, stan <math>\displaystyle s_2</math> oznaczamy jako końcowy.
| | </center> |
|
| |
|
| ROZWIĄZANIE punktu 2. Ponieważ w gramatyce występuje produkcja <math>\displaystyle v_0
| | Zauważ, że otrzymany automat nie jest minimalny. Jakie języki akceptują automaty <math>{\mathcal A}</math>, <math>{\mathcal B}</math> i <math>{\mathcal C}</math>? |
| \rightarrow b</math>, która ma postać niezgodną z postacią produkcji
| | </div></div> |
| będących wejściem algorytmu, przekształcamy gramatykę, usuwając tę
| | {{cwiczenie|2|| |
| produkcję i dodając dwie inne: <math>\displaystyle v_0 \rightarrow bv_k</math> oraz <math>\displaystyle v_k
| |
| \rightarrow 1</math>. Teraz możemy skonstruować automat. Jego zbiór stanów
| |
| to <math>\displaystyle s_0, s_1, s_k</math>, stanem początkowym jest <math>\displaystyle s_0</math>, a funkcja przejść
| |
| zdefiniowana jest następująco:
| |
|
| |
|
| <math>\displaystyle f(s_0,a)= s_1</math>, <math>\displaystyle f(s_0,b)=s_k</math>, <math>\displaystyle f(s_1,a)=s_1</math>, <math>\displaystyle s(s_1,b)=s_0</math>. | | Niech <math>A = \{a,b\}</math>. Dla automatu <center><math>{\mathcal B} = (S_{\mathcal |
| | B},A,f_{\mathcal B},s_{\mathcal B},F_{\mathcal B})</math>,</center> |
| | gdzie |
| | <center><math>S_{\mathcal B} = \{s_{\mathcal B},s_1,s_2\}, |
| | \;\;F_{\mathcal B} = \{s_1\}</math>,</center> |
| | a funkcja przejść zdefiniowana jest |
| | następująco: |
|
| |
|
| Ponieważ w gramatyce wystąpiły produkcje <math>\displaystyle v_1 \rightarrow 1</math> oraz
| | <center><math>\begin{array} {c|c|c|c|} f_{\mathcal B} &s_{\mathcal B} &s_1 & s_2 \\ |
| <math>\displaystyle v_k \rightarrow 1</math>, stany <math>\displaystyle v_1</math> oraz <math>\displaystyle v_k</math> są stanami końcowymi.
| | \hline a & s_1 & s_2 & s_2 \\ \hline b & s_1 & s_{\mathcal{B}} & s_1\\ |
| | \hline \end{array}</math></center> |
|
| |
|
| W wykładzie podany został algorytm ''Automat2WR1'' budujący
| | skonstruuj automat deterministyczny <math>\mathcal A</math> taki, że |
| wyrażenie regularne na podstawie zadanego automatu. Opiszemy teraz
| | <center><math>L({\mathcal A}) = L({\mathcal B})^*</math>.</center> |
| inną metodę rozwiązania tego problemu, wykorzystującą równania na
| |
| językach.
| |
|
| |
|
| Dany niech będzie automat <math>\displaystyle \mathcal{A}=(S, A, f, s_0, T)</math>. Chcemy
| |
| zbudować wyrażenie regularne opisujące język akceptowany przez
| |
| <math>\displaystyle \mathcal{A}</math>. Do wyprowadzenia metody potrzebować będziemy lematu
| |
| Ardena.
| |
|
| |
| {{lemat|||
| |
| '''(Arden)''' Niech <math>\displaystyle R \subseteq A^+</math> i
| |
| <math>\displaystyle S \subseteq A^*</math> będą językami regularnymi. Wtedy równanie <center><math>\displaystyle X = XR
| |
| + S</math></center>
| |
| posiada jedyne rozwiązanie <math>\displaystyle X=SR^*</math>, które jest językiem
| |
| regularnym.
| |
| }} | | }} |
|
| |
|
| Zdefiniujmy najpierw <math>\displaystyle L_i</math> jako język tych słów, które byłyby
| | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none">Pomocne może być użycie automatu z pustymi przejściami. |
| akceptowane przez <math>\displaystyle \mathcal{A}</math>, gdyby stanem końcowym był stan
| | </div></div> |
| <math>\displaystyle s_i</math>, tzn. gdyby <math>\displaystyle T=\{s_i\}</math>: <center><math>\displaystyle L_i=\{w \in A^*:\ f(s_0,w)=s_i\}.</math></center> | | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> |
| | | Automat <math>\mathcal{B}</math> pokazany jest na rysunku 2. |
| Zauważmy, że jeśli do stanu <math>\displaystyle s_t</math> wchodzą strzałki prowadzące ze
| | <center> |
| stanów <math>\displaystyle s_{i_1}, s_{i_2}, ..., s_{i_n}</math> odpowiednio z etykietami
| | [[File:ja-lekcja07-c-rys2.svg|250x150px|thumb|center|Rysunek 2]] |
| <math>\displaystyle a_1, a_2,..., a_n</math> (i tylko takie), to
| | </center> |
| <center><math>\displaystyle L_t=\sum_{j=1}^n L_{i_j}a_j.</math></center>
| |
| | |
| Obserwacja ta jest podstawą do konstrukcji metody otrzymywania
| |
| wyrażenia regularnego na podstawie automatu. Będziemy budować układ
| |
| równań, w którym każde równanie będzie postaci <math>\displaystyle L_i=\sum_{j \in
| |
| I}L_ja_j</math>, <math>\displaystyle I=\{i_1,i_2,...,i_n\}</math>
| |
| , gdzie <math>\displaystyle L_i</math> traktowane są jak
| |
| niewiadome. Następnie układ taki rozwiążemy ze względu na każdą
| |
| zmienną <math>\displaystyle L_i</math> (tu pomocny będzie lemat Ardena). Szukanym przez nas
| |
| wyrażeniem regularnym będzie wyrażenie postaci <math>\displaystyle \sum_{i\in I}L_i</math>,
| |
| gdzie <math>\displaystyle I</math> jest zbiorem indeksów <math>\displaystyle i</math> stanów końcowych <math>\displaystyle s_i</math> automatu
| |
| <math>\displaystyle \mathcal{A}</math>.
| |
| | |
| Można postawić w tym momencie pytanie, czy budowany układ równań ma
| |
| rozwiązanie, a jeśli tak, to czy jest ono jedyne. Okazuje się że w
| |
| rozważanej przez nas sytuacji ma to miejsce, choć dowód tego faktu
| |
| nie jest natychmiastowy. Fakt ten, podobnie jak lemat Ardena,
| |
| podajemy tutaj bez dowodu.
| |
| | |
| {{algorytm|||
| |
| | |
| {''Automat2WR2'' - buduje inną metodą wyrażenie
| |
| regularne opisujące język akceptowany przez automat skończony.}
| |
| | |
| [1]
| |
| Wejście: <math>\displaystyle \mathcal{A}=(S, A, f, s_0, T)</math> -- automat
| |
| akceptujący język <math>\displaystyle L</math>.
| |
| | |
| Wyjście: <math>\displaystyle r</math> -- wyrażenie regularne opisujące język <math>\displaystyle L</math>.
| |
| | |
| '''for''' '''each '''<math>\displaystyle s \in S</math>
| |
| | |
| '''for''' '''each '''<math>\displaystyle t \in S</math>
| |
| | |
| '''for''' '''each ''' <math>\displaystyle a \in A\displaystyle L_s \leftarrow "";\displaystyle \triangleright</math>
| |
| wyrażenie puste
| |
| '''if''' <math>\displaystyle f(t,a)=s</math>
| |
| | |
| '''if''' <math>\displaystyle L_s=""\displaystyle L_s \leftarrow L_ta</math>;
| |
| <math>\displaystyle \triangleright</math> podstawiamy wyrażenie regularne | |
| '''else'''
| |
| <math>\displaystyle L_s \leftarrow L_s + L_ta</math>; <math>\displaystyle \triangleright</math> podstawiamy wyrażenie regularne | |
| '''endif'''
| |
| '''endif'''
| |
| | |
| '''endfor'''
| |
| | |
| '''endfor'''
| |
| | |
| '''if''' <math>\displaystyle s=s_0</math> ''' and ''' <math>\displaystyle s \in T\displaystyle L_s \leftarrow L_s + 1</math>; <math>\displaystyle \triangleright</math> podstawiamy
| |
| wyrażenie regularne
| |
| | |
| '''endif'''
| |
|
| |
|
| '''endfor'''
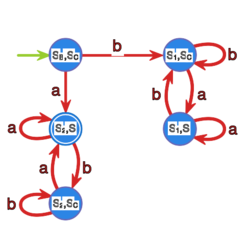
| | Aby skonstruować automat akceptujący język <math>L(\mathcal{B})^*</math>, |
| | wystarczy dodać przejście <math>f(s_1,1)=s_{\mathcal{B}}</math> (dlaczego?). |
| | Automat z pustymi przejściami akceptujący <math>L(\mathcal{B})^*</math> |
| | pokazany jest na rysunku 3. |
| | <center> |
| | [[File:ja-lekcja07-c-rys3.svg|250x150px|thumb|center|Rysunek 3]] |
| | </center> |
|
| |
|
| '''rozwiąż''' <math>\displaystyle \{L_i = \sum_{t \in S} L_t
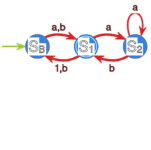
| | Po usunięciu pustych przejść otrzymujemy automat z rysunku 4: |
| \}_{i=0,...,|S|-1}</math>;
| | <center> |
| | [[File:ja-lekcja07-c-rys4.svg|250x250px|thumb|center|Rysunek 4]] |
| | </center> |
|
| |
|
| <math>\displaystyle r \leftarrow \sum_{s_i \in T} L_i</math>; | | Teraz wystarczy skonstruować równoważny automat deterministyczny. |
| | </div></div> |
|
| |
|
| '''return''' <math>\displaystyle r</math>;
| | {{cwiczenie|3|| |
|
| |
|
| }} | | Dane są dwa automaty nad tym samym alfabetem <math>A</math><br> |
| | <math>\mathcal{A}=(S,f,s_{0},T)</math> i <math>\mathcal{B}=(Q,g,t_{0},F)</math>. Udowodnij, |
| | że istnieje liczba <math>p\in{\Bbb N}_{0}</math> taka, że jeśli dla każdego słowa <math>w</math> o długości <math>|w|\leq p</math> spełniona jest implikacja |
| | <math>w\in L(\mathcal{A})\Rightarrow w\in L(\mathcal{B})</math>, |
| | to |
|
| |
|
| Funkcja '''rozwiąż''' w algorytmie ''Automat2Wr2''
| | <center><math>L(\mathcal{A})\subseteq L(\mathcal{B})</math></center> |
| rozwiązuje układ równań (mający na podstawie wcześniejszych uwag
| |
| jednoznaczne rozwiązania), zwraca obliczone języki <math>\displaystyle L_i</math>, <math>\displaystyle i=0, ..., |S|-1</math>.
| |
|
| |
|
| Rozwiązanie można wykonać metodą rugowania, przechodząc od <math>\displaystyle L_n</math> do
| |
| <math>\displaystyle L_1</math>. Równanie <math>\displaystyle L_i=\sum_{t \in S} L_t</math> rozwiązujemy, korzystając
| |
| ze wzoru w lemacie Ardena (rolę <math>\displaystyle X</math> w lemacie odgrywa <math>\displaystyle L_i</math>) i
| |
| podstawiamy do pozostałych równań (tzn. równań dla <math>\displaystyle i=0,\dots,i-1</math>).
| |
| Mając już wyliczone <math>\displaystyle L_0</math>, wyliczamy kolejne <math>\displaystyle L_i</math> idąc od <math>\displaystyle 1</math> do
| |
| <math>\displaystyle |S|-1</math>. Dla lepszego zrozumienia metody przedstawiamy następujący
| |
| przykład.
| |
|
| |
| {{przyklad|||
| |
|
| |
| Dany niech będzie automat pokazany na rysunku
| |
| [[##ja-lekcja8-c-rys1|Uzupelnic ja-lekcja8-c-rys1|]] (pominęliśmy tu dla uproszczenia jedną
| |
| strzałkę wychodzącą ze stanu <math>\displaystyle s_2</math> w celu uniknięcia zwiększenia
| |
| liczby stanów, gdyż chcąc formalnie narysować automat
| |
| deterministyczny, musielibyśmy dodać stan <math>\displaystyle s_3</math> i zdefiniować
| |
| <math>\displaystyle f(s_2, a)=s_3</math>, <math>\displaystyle f(s_3,a)=f(s_3,b)=s_3</math>, ale widać, że wcale nie
| |
| trzeba wtedy obliczać języka <math>\displaystyle L_3</math>, gdyż z tego stanu nie da się już
| |
| wyjść - jest to tzw. sink state).
| |
| }} | | }} |
|
| |
|
| RYSUNEK ja-lekjca8-c-rys1
| | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> |
| | Niech <math>\mathcal{C}</math> będzie automatem takim, że <math>L(\mathcal{C})=L(\mathcal{A})\cup L(\mathcal{B})</math>. Wówczas, |
| | <center><math>L(\mathcal{C})\subseteq L(\mathcal{B})\Leftrightarrow L(\mathcal{A})\subseteq L(\mathcal{B})</math>.</center> |
|
| |
|
| Ułóżmy równania do naszego układu równań. Mamy:
| | Udowodnimy więc inkluzję <math>L(\mathcal{C})\subseteq L(\mathcal{B})</math>, gdzie |
| | <center><math>\mathcal{C}=(S\times Q,f\times g,(s_0,t_0), (S\times F \cup T\times Q))</math>.</center> |
|
| |
|
| <center><math>\displaystyle \left\{ \begin{array} {l} | | Przyjmijmy <math>p=|S| \cdot |Q|</math>. Niech <math>w \in L(\mathcal{C})</math> |
| L_0 = L_0b + L_2b + 1 \\
| | # Jeśli <math>|w|\leq p</math>, to z założenia <math>w \in L(\mathcal{B})</math> |
| L_1 = L_0a + L_1a \\
| | # Jeśli <math>|w|>p</math>, to z lematu o pompowaniu wynika, że <math>\exists v_1 v_2 \in A^*</math>, <math>\exists u \in A^+</math> takie, że <math>w=v_1 uv_2</math>, <math>v_1 v_2 \in L(\mathcal{C})</math> i <math>|v_1v_2|<|w|</math>. |
| L_2 = L_1b
| | <center><math>(f\times g)((s_0,t_0),w) = (f\times g)((s_0,t_0),v_1 v_2)=(f(s_0,v_1v_2),g(t_0,v_1v_2)) |
| \end{array} \right. \Leftrightarrow \left\{ \begin{array} {l}
| | \in S\times F \cup T\times Q </math></center> |
| L_0 = L_0b + L_1bb + 1 \\
| | Mamy dwie możliwości: |
| L_1 = L_0a + L_1a \\
| |
| \end{array} \right. \Leftrightarrow L_0=L_0b+L_0aa^*bb^*+1.</math></center> | |
|
| |
|
| Mamy więc <math>\displaystyle L_0=L_0(b+a^+bb) + 1</math>. Korzystając z lematu Ardena,
| | :(a) <math>g(t_0,v_1v_2) \in F</math>, co oznacza <math>v_1v_2 \in L(\mathcal{B})</math>, <math>w \in |
| otrzymujemy <math>\displaystyle L_0=1(b+a^+bb)^*=(b+a^+bb)^*</math>. Podstawiając obliczone
| | L(\mathcal{B})</math>, |
| <math>\displaystyle L_0</math> do równania i obliczając pozostałe <math>\displaystyle L_i</math>, otrzymujemy | |
| ostatecznie:
| |
|
| |
|
| <center><math>\displaystyle \left\{ \begin{array} {l} | | :(b) <math>f(s_0,v_1v_2)\in T</math>, co oznacza <math>v_1v_2 \in L(\mathcal{A})</math>. <br> |
| L_0 = (b+a^+bb)^* \\
| | : Jeśli <math>|v_1v_2|<p</math>, to <math>v_1v_2 \in L(\mathcal{B})</math>, <math>w \in L(\mathcal{B})</math>.<br> |
| L_1 = (b+a^+bb)^*a^+ \\
| | : Jeśli <math>|v_1v_2|>p</math>, to powtarzamy punkt 2. |
| L_2 = (b+a^+bb)^*a^+b.
| |
| \end{array} \right. </math></center> | |
|
| |
|
| Ponieważ <math>\displaystyle T=\{s_0,s_1,s_2\}</math>, rozwiązaniem jest:
| | Po każdym kroku długość rozważanego słowa silnie maleje, więc po skończonej ilości kroków uzyskamy oczekiwany efekt.<br> |
| <center><math>\displaystyle w=L_0+L_1+L_2=(b+a^+bb)^*(1 + a^+(1 + b)).</math></center>
| | Zauważ, że z zadania tego wynika |
| | rozstrzygalność problemu równoważności automatów. Algorytmiczny aspekt tego problemu rozważymy w ćwiczeniach 8. |
| | </div></div> |
|
| |
|
| {{cwiczenie||| | | {{cwiczenie|4|| |
| Niech dany będzie automat
| |
| <math>\displaystyle \mathcal{A}(S=\{s_0,s_1,s_2,s_3\},A=\{a,b\},f,s_0,T=\{s_0\})</math> o
| |
| następującej funkcji przejść:
| |
| | |
| <center><math>\displaystyle \begin{array} {c|c|c|c|c|} f & s_0 & s_1 & s_2 & s_3\\
| |
| \hline a & s_1 & s_2 & s_0 & s_3\\
| |
| \hline b & s_3 & s_2 & s_2 & s_3\\
| |
| \hline \end{array} </math></center>
| |
| | |
| Wykorzystując algorytm ''Automat2WR2'', wyznacz wyrażenie
| |
| regularne odpowiadające językowi akceptowanemu przez <math>\displaystyle \mathcal{A}</math>.
| |
|
| |
|
| | Niech <math>A</math> będzie dowolnym alfabetem, a <math>L \subset A^*</math> językiem regularnym. Udowodnij, że język |
| | <math>L'=\{a^{|w|} :w \in L\}</math> jest też językiem regularnym. |
| }} | | }} |
|
| |
|
| ROZWIĄZANIE. Po pierwsze zauważmy, że w obliczeniach nie musimy
| | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie </span><div class="mw-collapsible-content" style="display:none"> |
| uwzględniać stanu <math>\displaystyle s_3</math> ani języka <math>\displaystyle L_3</math> stowarzyszonego z tym
| | Rozważmy homomorfizm <math>h:A^* \longrightarrow \{a\}^*</math> taki, że <math>\forall |
| stanem. Układ równań będzie więc posiadał 3 równania o 3
| | x \in A\quad f(x)=a</math>. Dla tak zdefiniowanego <math>h</math> język <math>L'</math> jest homomorficzym obrazem języka regularnego <math>L'=h(L)</math>, |
| niewiadomych <math>\displaystyle L_0</math>, <math>\displaystyle L_1</math> oraz <math>\displaystyle L_2</math>:
| | a więc jest regularny. |
| | | </div></div> |
| <center><math>\displaystyle \left\{ \begin{array} {l} | |
| L_0 = L_2a+1 \\
| |
| L_1 = L_0a \\
| |
| L_2 = L_1(a+b)+L_2b
| |
| \end{array} \right. </math></center>
| |
| | |
| W równaniu drugim zamieniamy <math>\displaystyle L_0</math> na <math>\displaystyle L_2a+1</math> i otrzymujemy
| |
|
| |
|
| <center><math>\displaystyle \left\{ \begin{array} {l}
| | {{cwiczenie|5|| |
| L_1 = (L_2a+1)a = L_2a^2+a \\
| |
| L_2 = L_1(a+b)+L_2b.
| |
| \end{array} \right. </math></center>
| |
|
| |
|
| Teraz <math>\displaystyle L_1</math> w równaniu drugim zastępujemy prawą stroną równania
| | Udowodnij, że następujące języki nie są regularne: |
| pierwszego: <center><math>\displaystyle L_2 = L_1(a+b)+L_2b = (L_2a^2+a)(a+b)+L_2b =
| | # <math>L = \{a^n : n \; \text{nie jest liczbą pierwszą;} \}</math>, |
| L_2(a^3+a^2b+b)+a^2+ab.</math></center>
| | # <math>L=\left\{ a^{n}b^{m}:0\leq n,m;\;n\neq m\right\}</math>. |
| | |
| Korzystamy z lematu Ardena i otrzymujemy
| |
| <math>\displaystyle L_2=(a^2+ab)(a^3+a^2b+b)^*</math>. Podstawiamy to do równania
| |
| <math>\displaystyle L_0=L_2a+1</math> i otrzymujemy ostatecznie:
| |
| <center><math>\displaystyle L_0=(a^2+ab)(a^3+a^2b+b)^*a+1= (a^2+ab)(a^2(a+b)+b)^*a+1.</math></center>
| |
| | |
| Można pokazać, że wyrażenie to jest równoważne następującemu:
| |
| <center><math>\displaystyle L_0=(a(a+b)b^*a)^*.</math></center>
| |
| | |
| {{cwiczenie|||
| |
| | |
| Dane niech będą automaty: <math>\displaystyle n_A</math>-stanowy <math>\displaystyle \mathcal{A}</math> i
| |
| <math>\displaystyle n_B</math>-stanowy <math>\displaystyle \mathcal{B}</math>, oba nad alfabetem <math>\displaystyle A</math> i akceptujące
| |
| odpowiednio języki <math>\displaystyle L(\mathcal{A})</math> i <math>\displaystyle L(\mathcal{B})</math>. Pokaż, że
| |
| problem stwierdzenia, czy dla dowolnego <math>\displaystyle w \in A^*</math> zachodzi <math>\displaystyle w \in
| |
| L(\mathcal{A}) \cap L(\mathcal{B})</math>, jest rozstrzygalny:
| |
| # poprzez skonstruowanie niedeterministycznego automatu posiadającego <math>\displaystyle O(n_A+n_B)</math> stanów,
| |
| # poprzez skonstruowanie deterministycznego automatu <math>\displaystyle n_A \cdot
| |
| n_B</math>-stanowego.
| |
|
| |
|
| }} | | }} |
|
| |
|
| ROZWIĄZANIE punktu 1. Niech <math>\displaystyle \mathcal{A}=(S_A, A, f_A, s_A^0, T_A)</math>
| | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie punktu 1</span><div class="mw-collapsible-content" style="display:none"> |
| oraz <math>\displaystyle \mathcal{B}=(S_B, A, f_B, s_B^0, T_B)</math> będą zadanymi
| | Skorzystamy z faktu, że język <math>L' = \{a^n : n |
| automatami. Konstruujemy automat <math>\displaystyle \mathcal{C}=(S, A, f, s_0, T)</math>
| | \; \text{ jest liczbą pierwszą;} \}</math> nie jest akceptowany ( |
| taki, że <math>\displaystyle S = S_A \cup S_B \backslash \{s_B^0\}</math>, <math>\displaystyle s_0=s_A^0</math>,
| | ćwiczenie 8), a więc nie jest regularny. |
| <math>\displaystyle T=T_B</math>, gdy <math>\displaystyle s_B^0 \not \in T_B</math>, <math>\displaystyle T=T_B \cup T_A</math>, gdy <math>\displaystyle s_B^0 \in | | <center><math>a^*=L \cup L', L\cap L' = \emptyset, \;\text {a więc}\;L'=\overline{L}</math></center> |
| T_B</math>, a funkcja przejść <math>\displaystyle f</math> jest zdefiniowana następująco:
| |
| | |
| <center><math>\displaystyle \aligned \forall s \in S_A, a \in A\ f(s,a) &=f_A(s,a) \\ \forall s \in S_B
| |
| \backslash \{s_B^0\}, a \in A\ f(s,a) &= f_B(s,a)
| |
| \\
| |
| \forall s \in T_A, a \in A\ f(s,a) &= f(s_B^0,a).
| |
| \endaligned</math></center>
| |
| | |
| Zbiór stanów końcowych automatu <math>\displaystyle \mathcal{A}</math> staje się więc zbiorem
| |
| stanów początkowych dla automatu <math>\displaystyle \mathcal{B}</math>, przy czym, jeśli
| |
| <math>\displaystyle s_B^0 \in T_B</math>, to każdy ze stanów <math>\displaystyle T_A</math> jest równocześnie stanem
| |
| końcowym w automacie <math>\displaystyle \mathcal{C}</math>. Zauważ, że:
| |
| | |
| <center><math>\displaystyle w \in L(\mathcal{A}) \cap L(\mathcal{B}) \Longleftrightarrow | |
| ww \in L(\mathcal{C}) \wedge f(s_0,w) \cap T_A \not = \emptyset.</math></center>
| |
| | |
| Oba warunki występujące po prawej stronie równoważności są
| |
| algorytmicznie weryfikowalne i da się je sprawdzić w czasie
| |
| <math>\displaystyle O(|w|)</math>. Konstrukcja automatu <math>\displaystyle \mathcal{C}</math> w oczywisty sposób
| |
| również jest algorytmizowalna i da się ją wykonać w czasie
| |
| <math>\displaystyle O(|A|(n_A+n_B))</math>.
| |
| Ponieważ <math>\displaystyle |S|=n_A+n_B-1</math>, więc <math>\displaystyle \mathcal{C}</math> posiada <math>\displaystyle O(n_A+n_B)</math> stanów. <br>
| |
|
| |
|
| ROZWIĄZANIE punktu 2. Skorzystaj z konstrukcji z ćwiczenia
| | Ponieważ klasa języków regularnych jest zamknięta ze względu na |
| [[##ja-lekcja7-c-cw1.1|Uzupelnic ja-lekcja7-c-cw1.1|]]
| | uzupełnienie, to <math>L \notin \mathcal{REG}</math>. |
| | </div></div> |
| | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Rozwiązanie punktu 2</span><div class="mw-collapsible-content" style="display:none"> |
| | Język <math>L'=\left\{ a^{n}b^{n}:0\leq n \right\}</math> nie jest akceptowany |
| | (patrz [[Języki, automaty i obliczenia/Wykład 6: Automat niedeterministyczny. Lemat o pompowaniu#przyklad_3_1|3.1. z wykładu 6]]), a więc nie jest regularny. |
| | <center><math>a^*b^* =L \cup L',L\cap L' = \emptyset,\;\text {a więc}\;L'=a^* b^* \cap\overline{L}</math>.</center> |
|
| |
|
| {{cwiczenie||| | | Ponieważ klasa języków regularnych jest zamknięta ze względu na |
| Skonstruuj algorytm (oraz określ jego złożoność) dla następującego
| | uzupełnienie i przecięcie, to <math>L \notin \mathcal{REG}</math>. |
| problemu (tym samym dowodząc jego rozstrzygalności):
| | </div></div> |
| | <center>ZADANIA DOMOWE</center> |
|
| |
|
| Dany jest automat <math>\displaystyle \mathcal{A}=(S, A, f, s_0, T)</math>. Czy
| | {{cwiczenie|6|| |
| <math>\displaystyle L(\mathcal{A})=\emptyset</math>?
| |
| }}
| |
|
| |
|
| ROZWIĄZANIE. Bez straty ogólności możemy założyć, że automat jest
| | Niech <math>A = \{a,b\}</math>. Skonstruuj automat <math>\mathcal A</math>, taki że |
| deterministyczny. W algorytmie wykorzystamy procedurę
| | 1. <math>L({\mathcal A}) = L({\mathcal B}) \cup L({\mathcal C})</math>, gdzie <center><math>{\mathcal B} = |
| ''Zaznacz'' przedstawioną poniżej. | | (S_{\mathcal B},A,f_{\mathcal B},s_{\mathcal B},F_{\mathcal B}),\;\;\;\; {\mathcal C} = |
| | (S_{\mathcal C},A,f_{\mathcal C},s_{\mathcal C},F_{\mathcal C})</math>,</center> |
| | <center><math>S_{\mathcal B} = |
| | \{s_{\mathcal B},s_1,s_2\}, \;\;F_{\mathcal B} = \{s_2\},\;\;\; S_{\mathcal C} = |
| | \{s_{\mathcal C},{s'}_1,{s'}_2\},\;\; F_{\mathcal C} = \{{s'}_2\}</math>,</center> |
|
| |
|
| {{algorytm|||
| |
|
| |
|
| {''PustośćJęzyka'' -- sprawdza, czy język akceptowany | | <center><math>\begin{array} {c|c|c|c|} f_{\mathcal B} &s_{\mathcal B} &s_1 & s_2 \\ |
| przez zadany automat jest pusty.}
| | \hline a & s_2 & s_1 & s_2 \\ \hline b & s_1 & s_1 & s_2\\ \hline \end{array} |
| | \begin{array} {c|c|c|c|} f_{\mathcal C} &s_{\mathcal C} &{s'}_1&{s'}_2 \\ \hline a & {s'}_1 & {s'}_1& {s'}_2 \\ |
| | \hline b & {s'}_2 & {s'}_1& {s'}_2 \\ \hline \end{array}</math></center> |
| | 2. <math>L({\mathcal A}) = L({\mathcal B})^*</math>, gdzie <center><math>{\mathcal B} = |
| | (S_{\mathcal B},A,f_{\mathcal B},s_{\mathcal B},F_{\mathcal B})</math>,</center> |
|
| |
|
| [1]
| | <center><math>S_{\mathcal B} = \{s_{\mathcal B},s_1,s_2,s_3\}, \;\;F_{\mathcal |
| Wejście: <math>\displaystyle \mathcal{A}=(S, A, f, s_0, T)</math> -- deterministyczny
| | B} = \{s_2\}</math>,</center> |
| automat akceptujący język <math>\displaystyle L</math>.
| |
|
| |
|
| Wyjście: Odpowiedź '''true''' (tak) lub '''false'''
| |
| (nie).
| |
|
| |
|
| ''Zaznacz''<math>\displaystyle (s_0)</math>;
| | <center><math>\begin{array} {c|c|c|c|c|} f_{\mathcal B} &s_{\mathcal B} &s_1 & s_2 & s_3\\ \hline a & s_1 & s_3 & s_3 & s_3 \\ |
| | \hline b & s_3 & s_2 & s_3 &s_3\\ \hline \end{array}</math></center> |
|
| |
|
| '''for''' '''each '''<math>\displaystyle s \in T</math>
| | Podaj dwie konstrukcje: |
| | | # opartą na dowodzie twierdzenia Kleene'ego, |
| '''if''' <math>\displaystyle \textbf{zaznaczone}[s] = 1</math> | | # z wykorzystaniem automatu z pustymi przejściami. |
| '''return false'''
| |
| '''endif'''
| |
| | |
| '''endfor'''
| |
| | |
| '''return true''';
| |
|
| |
|
| }} | | }} |
|
| |
|
| {{algorytm||| | | {{cwiczenie|7|| |
|
| |
|
| [1]
| | Skonstruuj minimalny automat <math>\mathcal{A}</math>, taki że |
| '''procedure''' ''Zaznacz''(<math>\displaystyle s \in S</math>)
| | <math>L(\mathcal{A})=L(\mathcal{B})^*</math>, gdzie <math>\mathcal{B}</math> opisany jest |
| | poniższym grafem:}} |
| | <center> |
| | [[File:ja-lekcja07-c-rys5.svg|250x250px|thumb|center|Rysunek 5]] |
| | </center> |
|
| |
|
| <math>\displaystyle \textbf{zaznaczone}[s] \leftarrow 1</math>;
| |
|
| |
|
| '''for''' '''each ''' <math>\displaystyle a \in A</math>
| | {{cwiczenie|8|| |
| | |
| '''if''' '''zaznaczone'''<math>\displaystyle [f(s,a)]\neq 1</math>
| |
| ''Zaznacz''<math>\displaystyle (f(s,a))</math>;
| |
| '''endif'''
| |
| | |
| '''endfor'''
| |
| | |
| '''end procedure'''
| |
|
| |
|
| | Udowodnij, że następujące języki nie są regularne: |
| | # <math>L=\left\{ a^{n}b^{m}c^n:0<n,m\right\}</math>, |
| | # <math>L = \{(ab)^n(bc)^n : n \geq 0 \}</math>. <br> |
| }} | | }} |
| | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka do punktu 2 </span><div class="mw-collapsible-content" style="display:none"> |
| | Wykorzystaj fakt, że język <math>\left\{ a^{n}b^{n}:n \geq 0\right\}</math> nie jest regularny oraz |
| | domkniętość klasy języków regularnych ze względu na homomorfizm. |
| | </div></div> |
|
| |
|
| Algorytm wykonuje przeszukanie automatu metodą DFS. Jego złożoność
| | {{cwiczenie|9|| |
| jest więc <math>\displaystyle O(|A| \cdot |S|)</math> - liniowa ze względu na ilość stanów
| |
| automatu. Złożoność pamięciowa także wynosi <math>\displaystyle O(|A| \cdot |S|)</math>.
| |
| | |
| ZADANIA DOMOWE
| |
| | |
| {{cwiczenie|||
| |
| Zastosuj algorytm ''Automat2GReg'' do automatu o następującej
| |
| funkcji przejść:
| |
| | |
| <center><math>\displaystyle \begin{array} {c|c|c|c|c|} f & s_0 & s_1 & s_2 & s_3\\
| |
| \hline a & s_1 & s_3 & s_3 & s_3\\
| |
| \hline b & s_2 & s_2 & s_0 & s_0\\
| |
| \hline \end{array} </math></center>
| |
| | |
| gdzie <math>\displaystyle s_0</math> jest stanem początkowym oraz <math>\displaystyle T=\{s_1\}</math>.
| |
| | |
| }}
| |
| | |
| {{cwiczenie|||
| |
| Zbuduj automaty akceptujące języki generowane następującymi
| |
| gramatykami (<math>\displaystyle v_i</math> oznaczają symbole nieterminalne, <math>\displaystyle a,b</math> --
| |
| terminalne):
| |
| # <math>\displaystyle v_0 \rightarrow av_1</math>, <math>\displaystyle v_0 \rightarrow bv_2</math>, <math>\displaystyle v_0
| |
| \rightarrow bv_0</math>, <math>\displaystyle v_1 \rightarrow bv_1</math>, <math>\displaystyle v_1 \rightarrow av_0</math>,
| |
| <math>\displaystyle v_2 \rightarrow bv_0</math>, <math>\displaystyle v_2 \rightarrow bv_2</math>, <math>\displaystyle v_2 \rightarrow 1</math>.
| |
| # <math>\displaystyle v_0 \rightarrow bv_2</math>, <math>\displaystyle v_0 \rightarrow b</math>, <math>\displaystyle v_1 \rightarrow
| |
| bv_0</math>, <math>\displaystyle v_1 \rightarrow av_1</math>, <math>\displaystyle v_1 \rightarrow 1</math>, <math>\displaystyle v_2 \rightarrow
| |
| av_1</math>.
| |
| | |
| }}
| |
| | |
| {{cwiczenie||| | |
| Zbuduj automaty (z pustymi przejściami) akceptujące poniższe języki:
| |
| # <math>\displaystyle b((a+b)^*+a)</math>,
| |
| # <math>\displaystyle (a+b)^*(a^*b^*)</math>,
| |
| # <math>\displaystyle a(b^*a^*)^*+1</math>.
| |
|
| |
|
| | Zbuduj automat akceptujący język będący ogółem skończonych sekwencji |
| | binarnych, w których liczba zer jest podzielna przez dwa, a liczba |
| | jedynek przez 3, a następnie gramatykę generującą ten język. |
| }} | | }} |
| | | <div class="mw-collapsible mw-made=collapsible mw-collapsed"><span class="mw-collapsible-toogle mw-collapsible-toogle-default style="font-variant:small-caps">Wskazówka </span><div class="mw-collapsible-content" style="display:none"> |
| WSKAZÓWKA. Zastosuj algorytm ''WR2Automat''.
| | Stany automatu niech będą postaci <math>(x,y)</math>, gdzie <math>x \in |
| | | \{0, 1\}</math>, <math>y \in \{0, 1, 2\}</math>. Stan początkowy to <math>(0,0)</math>. Określ |
| {{cwiczenie|||
| | funkcję przejść w ten sposób, że po przeczytaniu przez automat słowa |
| Niech dany będzie automat
| | zawierającego <math>k</math> symboli 0 oraz <math>l</math> symboli 1 automat znajdzie się |
| <math>\displaystyle \mathcal{A}(S=\{s_0,s_1,s_2,s_3\},A=\{a,b\},f,s_0,T=\{s_0\})</math> o | | w stanie <math>(k \mod 2, l \mod 3)</math>. Zastanów się, który stan będzie |
| następującej funkcji przejść:
| | stanem końcowym. Na podstawie automatu określ gramatykę. |
| | | </div></div> |
| <center><math>\displaystyle \begin{array} {c|c|c|c|c|} f & s_0 & s_1 & s_2 & s_3\\
| |
| \hline a & s_1 & s_2 & s_0 & s_2\\
| |
| \hline b & s_3 & s_2 & s_2 & s_2\\
| |
| \hline \end{array} </math></center>
| |
| | |
| Wykorzystując algorytm ''Automat2WR2'', wyznacz wyrażenie
| |
| regularne odpowiadające językowi akceptowanemu przez <math>\displaystyle \mathcal{A}</math>.
| |
| | |
| }}
| |
| | |
| {{cwiczenie|||
| |
| Skonstruuj algorytmy dla następujących problemów rozstrzygalnych:
| |
| # Równoważność dowolnych automatyów <math>\displaystyle \mathcal{A}</math> i <math>\displaystyle \mathcal{B}</math>.
| |
| # Nieskończoność języka <math>\displaystyle L(\mathcal{A})</math> dla dowolnego automatu <math>\displaystyle \mathcal{A}</math>.
| |
| | |
| }}
| |
| | |
| WSKAZÓWKA do punktu 1. Metoda pierwsza: istnieje dokładnie jeden
| |
| automat minimalny. Metoda druga: rozważ automat akceptujący
| |
| przecięcie <math>\displaystyle L(\mathcal{A}) \cap L(\mathcal{B}) </math> tak jak w punkcie
| |
| (2) zadania [[##cw_ai|Uzupelnic cw_ai|]]. Jaki warunek muszą spełniać stany <math>\displaystyle s \in
| |
| S_A, t \in S_B</math>, aby <math>\displaystyle (s,t) \in T</math>?
| |
| | |
| WSKAZÓWKI do punktu 2.
| |
| # Automat akceptuje nieskończenie wiele słów,
| |
| gdy w wyrażeniu regularnym odpowiadającym temu automatowi występuje
| |
| gwiazdka Kleene'ego. Użyj metody z twierdzenia Kleene'ego
| |
| (Twierdzenie 1.1, punkt 5.).
| |
| # <math>\displaystyle \exists s \in S, w_1, w_2 \in A^*:\
| |
| f(s_0, w_1)=s \wedge f(s,w_2)=s...</math>
| |
| | |
| {{cwiczenie|||
| |
| | |
| <center><math>\displaystyle \begin{array} {c|c|c|c|c|} f & s_0 & s_1 & s_2 \\
| |
| \hline a & s_1 & s_1 & s_2 \\
| |
| \hline b & s_2 & s_0 & s_0 \\
| |
| \hline \end{array} </math></center>
| |
| | |
| }}
| |
| | |
| Dla automatów <math>\displaystyle \mathcal{A}=(S_A, A, f_A,
| |
| s_A^0, T_A)</math> oraz <math>\displaystyle \mathcal{B}=(S_B, A, f_B, s_B^0, T_B)</math>
| |
| konstruujemy następujący automat <math>\displaystyle \mathcal{C}=(S, A, f, s_0, T)</math>:
| |
| * <math>\displaystyle S = S_A \times S_B,</math>
| |
| * <math>\displaystyle s_0 = (s_A^0,s_B^0),</math>
| |
| * <math>\displaystyle T = \{(s,t): s \in T_A, t \in T_B\}</math>
| |
| * <math>\displaystyle f((s,t),a)=(f_A(s,a),f_B(s,a)).</math>
| |
| | |
| Zachodzi <center><math>\displaystyle w \in L(\mathcal{A}) \cap L(\mathcal{B})
| |
| \Longleftrightarrow w \in L(\mathcal{C}).</math></center>
| |