Matematyka dyskretna 1/Wykład 5: Współczynniki dwumianowe: Różnice pomiędzy wersjami
Matiunreal (dyskusja | edycje) Nie podano opisu zmian |
|||
| (Nie pokazano 73 wersji utworzonych przez 7 użytkowników) | |||
| Linia 1: | Linia 1: | ||
==Zliczanie podzbiorów raz jeszcze== | ==Zliczanie podzbiorów raz jeszcze== | ||
[[grafika:Ettingshausen-portret.jpg|thumb|right||Andreas Freiherr von Ettingshausen (1796-1878) <br>[[Biografia Ettingshausena|Zobacz biografię]]]] | |||
Wiemy już, że dowolny zbiór <math>n</math>-elementowy ma dokładnie <math>2^n</math> podzbiorów. Teraz zajmiemy się pytaniem ile taki zbiór ma podzbiorów o dokładnie <math>k</math> elementach. Policzymy zatem liczność rodziny <math>k</math>-elemetowych podzbiorów zbioru <math>X</math>. Rodzinę tę oznaczać będziemy przez <math>{\mathcal P}_k(X)</math>. | |||
{{kotwica|wspoldwu|'''Współczynnik dwumianowy'''}} <math>{n\choose k}</math> | |||
to liczba <math>k</math>-elementowych podzbiorów zbioru <math>n</math>-elementowego, tzn. <math>{n\choose k} = {|{\mathcal P}_k(\mathbb{Z}_n)|}</math>. Wyrażenie <math>{n\choose k}</math> czytamy <math>n</math> po <math>k</math>. | |||
Prawdopodobnie jako pierwszy tej notacji użył Andreas von Ettingshausen w 1826. Jednak liczby te już wcześniej pojawiały się wielokrotnie, choćby w [[#trojPas|Trójkącie Pascala]]. Sama nazwa "współczynniki dwumianowe" bierze się stąd, że liczby te pojawiają się w rozwinięciu dwumianu <math>(x+y)^n</math>. Zobaczymy to dokładnie w [[#tw_5.7|Twierdzeniu 5.7]] | |||
{{przyklad||| | |||
Aby policzyć <math>{4\choose 2}</math> wypiszmy wszystkie <math>2</math>-elementowe podzbiory <math>4</math>-elementowego zbioru <math>\mathbb{Z}_4=\{0,1,2,3\}</math>. Sa to | |||
<math>\{0,1\}</math>, <math>\{0,2\}</math>, <math>\{0,3\}</math>, <math>\{1,2\}</math>, <math>\{1,3\}</math>, <math>\{2,3\}</math>, | |||
skąd <math>{4\choose 2}=6</math>.}} | |||
{{przyklad| | |||
Aby policzyć <math>{4\choose 2}</math> wypiszmy wszystkie <math>2</math>-elementowe podzbiory | |||
<math>4</math>-elementowego zbioru <math>\mathbb{Z} | |||
Sa to | |||
<math> | |||
skąd <math>{4\choose 2}=6</math>. | |||
Bezpośrednio z definicji liczb <math>{n\choose k}</math> dostajemy: | Bezpośrednio z definicji liczb <math>{n\choose k}</math> dostajemy: | ||
{{obserwacja|1|obs 1| | {{obserwacja|5.1|obs 5.1| | ||
Dla <math>n,k \in \mathbb{R}</math> zachodzi: | |||
Dla <math>n,k \in | |||
* <math>{n\choose 0}={n\choose n}=1</math>, | * <math>{n\choose 0}={n\choose n}=1</math>, | ||
| Linia 44: | Linia 29: | ||
}} | }} | ||
{{dowod| | {{dowod||| | ||
Pierwszy punkt jest natychmiastową konsekwencją faktu, że dowolny zbiór <math>n</math>-elementowy ma tylko jeden <math>0</math>-elementowy podzbiór -podzbiór pusty i tylko jeden podzbiór <math>n</math>-elementowy - cały zbiór. | |||
Drugi punkt jest oczywisty, jako że zbiór <math>n</math>-elementowy nie może mieć podzbiorów o <math>k>n</math> elementach. | |||
że | |||
Dla dowodu trzeciego punktu, zauważmy jedynie, że podzbiorów jednoelementowych jest dokładnie tyle ile elementów w zbiorze. | |||
Wreszcie dla dowodu ostatniego punktu załóżmy, że <math>|{X}|=n\geqslant k\geqslant 0</math>. Wtedy funkcja | |||
że | |||
<center><math>{\mathcal P}_k(X)\ni A \mapsto | <center><math>{\mathcal P}_k(X)\ni A \mapsto Xminus A \in {\mathcal P}_{n-k}(X) | ||
</math></center> | </math></center> | ||
jest bijekcją. A zatem istotnie <math>{n\choose k}={n\choose n-k}</math>. | jest bijekcją. A zatem istotnie <math>{n\choose k}={n\choose n-k}</math>. | ||
| Linia 66: | Linia 47: | ||
}} | }} | ||
Nasza następna obserwacja stanowi fundament dla rekurencyjnej procedury obliczania | Nasza następna obserwacja stanowi fundament dla rekurencyjnej procedury obliczania współczynników dwumianowych. | ||
współczynników dwumianowych. | |||
{{obserwacja|2|obs 2| | {{obserwacja|5.2|obs 5.2| | ||
Dla <math>0<k \leqslant n</math> mamy: | |||
<center><math>{n\choose k}={n-1\choose k-1}+{n-1\choose k} | <center><math>{n\choose k}={n-1\choose k-1}+{n-1\choose k}</math></center> | ||
</math></center> | |||
}} | }} | ||
{{dowod| | {{dowod||| | ||
Podobnie jak przy budowaniu zależności rekurencyjnej przy zliczaniu wszystkich podzbiorów zbioru <math>n</math>-elementowego załóżmy, że <math>|{Z}|=n</math>. Wtedy, po usunięciu ze zbioru <math>Z</math> elementu <math>a\in Z</math> dostajemy <math>(n-1)</math> -elementowy zbiór <math>Z'</math>. | |||
Oczywiście wszystkie <math>k</math> -elementowe podzbiory zbioru <math>Z</math> można podzielić na dwa typy: | |||
*albo mają w sobie element <math>a</math>, | |||
albo mają | *albo go nie mają. | ||
W drugim przypadku są to <math>k</math> -elementowe podzbiory <math>(n-1)</math> -elementowego zbioru <math>Z'</math>. Jest więc ich dokładnie <math>{n-1 \choose k}</math>. | |||
Każdy zaś podzbiór pierwszego typu, czyli <math>A \in {\mathcal P}_k(Z)</math> takie, że <math>a\in A</math> jest jednoznacznie wyznaczony przez swoje pozostałe <math>k-1</math> elementów, czyli <math>A=A'\cup \{a\}</math> dla pewnego <math>A' \in {\mathcal P}_{k-1}(Z')</math>. A zatem | |||
<center><math>{n \choose k} = | <center><math>{n \choose k} = {|{\mathcal P}_k(Z)|} | ||
= | = {|{\mathcal P}_k(Z')|} + {|{\mathcal P}_{k-1}(Z')|} | ||
= {n-1\choose k}+{n-1\choose k-1} | = {n-1\choose k}+{n-1\choose k-1} | ||
</math></center> | </math></center> | ||
}} | }} | ||
[[grafika:Pascal-portret.jpg|thumb|right||Blaise Pascal (1623-1662)<br>[[Biografia Pascal|Zobacz biografię]]]] | |||
< | {{kotwica|trojPas|'''Trójkąt Pascala'''}} (nazwany na cześć Blaise'a Pascala, który napisał znakomitą rozprawę o współczynnikach dwumianowych) bazuje na własności <math>{n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}</math> i ustawia liczby w następujący sposób: | ||
(nazwany na cześć Blaise'a Pascala, | |||
który napisał znakomitą rozprawę o współczynnikach dwumianowych) | |||
bazuje na własności <math>{n \choose k} = {n-1 \choose k-1} + {n-1 \choose k}</math> | |||
i ustawia liczby w następujący sposób: | |||
* wiersze trójkąta numerowane są kolejnymi liczbami naturalnymi <br> | * wiersze trójkąta numerowane są kolejnymi liczbami naturalnymi <br> | ||
| Linia 118: | Linia 85: | ||
* w każdym wierszy trójkąta występuje dokładnie <math>n+1</math> liczb. <br> | * w każdym wierszy trójkąta występuje dokładnie <math>n+1</math> liczb. <br> | ||
Są to kolejno | Są to kolejno <math>{n \choose 0}, {n \choose 1}, {n \choose 2},\ldots, {n \choose n-1},{n \choose n}</math> | ||
<math>{n \choose 0}, {n \choose 1}, {n \choose 2},\ldots, {n \choose n-1},{n \choose n}</math> | <center> | ||
{| border=1 | {| border=1 | ||
|+ <span style="font-variant:small-caps"> | |+ <span style="font-variant:small-caps"></span> | ||
|- | |- | ||
| || || || || || <math>0\choose 0</math> || || || || || | | || || || || || <math>0\choose 0</math> || || || || || | ||
| Linia 141: | Linia 107: | ||
|} | |} | ||
</center> | |||
Przesunięcie w wierszach, pozwala wyliczyć <math>{n \choose k}</math> jako sumę <math>{n-1 \choose k-1} + {n-1 \choose k}</math> dwu liczb stojących bezpośrednio nad <math>{n \choose k}</math>: | |||
<center> | |||
<div class="thumb"><flashwrap>file=Trojkat pascala.swf|size=large</flashwrap></div> | |||
</center> | |||
{| | {{przyklad||| | ||
Napisz program drukujący trójkąt Pascala, ale z liczbami <math>{n \choose k}</math> modulo <math>2</math>, tzn. w miejsce <math>{n \choose k}</math> wstaw jedynie resztę <math>0</math> lub <math>1</math> z dzielenia liczby <math>{n \choose k}</math> przez <math>2</math>. Zaobserwuj na wydruku powstały fraktal. Wyjaśnij dlaczego tak się dzieje. | |||
W trójkącie Pascala współczynniki o tym samym górnym indeksie, np. | |||
<center> | |||
<math>\left \langle {4\choose 0},{4\choose 1},{4\choose 2},{4\choose 3},{4\choose 4}\right \rangle =\left \langle {1,4,6,4,1}\right \rangle | |||
</math> | |||
</center>}} | |||
tworzą {{kotwica|wiersz|'''wiersz'''}}; natomiast współczynniki o ustalonym dolnym indeksie, np. | |||
<center> | <center> | ||
<math>\left \langle {5\choose 5},{6\choose 5},{7\choose 5},{8\choose 5},{\ldots}\right \rangle =\left \langle {1,6,21,56,\ldots}\right \rangle</math> | |||
</center> | |||
</math></center> | |||
tworzą {{kotwica|przekatna|'''przekątną'''}}. | |||
Trójkat Pascala ma zera na obrzeżach, a jego wiersze są symetryczne względem pionowej osi przebiegającej przez środek trójkąta. Jest to konsekwencja [[#obs_5.1|Obserwacji 5.1]]. Współczynniki dwumianowe spełniają bardzo wiele ciekawych zależności. Wymienimy tylko te najważniejsze. Zaczniemy od wzoru w postaci zwartej. | |||
{{obserwacja|5.3|obs 5.3| | |||
Dla dowolnych <math>0\leqslant k\leqslant n</math> | Dla dowolnych <math>0\leqslant k\leqslant n</math> | ||
<center><math>{n\choose k}=\frac{n!}{(n-k)!k!} | <center> | ||
</math></center> | <math>{n\choose k}=\frac{n!}{(n-k)!k!} | ||
</math> | |||
</center> | |||
}} | }} | ||
{{dowod| | {{dowod||| | ||
Podamy dwa dowody: kombinatoryczny i indukcyjny. | Podamy dwa dowody: kombinatoryczny i indukcyjny. | ||
'''Dowód kombinatoryczny.''' | '''Dowód kombinatoryczny.''' | ||
Ustalmy pewien <math>n</math>-elementowy zbiór <math>X</math>, i wybierajmy po kolei <math>k</math> różnych jego elementów, | Ustalmy pewien <math>n</math>-elementowy zbiór <math>X</math>, i wybierajmy po kolei <math>k</math> różnych jego elementów, tzn. utwórzmy injekcję <math>\mathbb{Z}_k X</math>. Z wykładu o zliczaniu zbiorów i funkcji wiemy, ze takich injekcji jest <math>\frac{n!}{(n-k)!}</math>. | ||
tzn. utwórzmy injekcję <math>\mathbb{Z} | W wyniku takiego wyboru, dostajemy wszakże pewien uporządkowany ciąg <math>k</math> elementów zbioru <math>X</math>. Wiele takich ciągów wyznacza ten sam <math>k</math>-elementowy podzbiór zbioru <math>X</math>. Ciągi takie różnią sie jedynie kolejnością elementów, a zatem jest ich tyle ile permutacji zbioru <math>k</math>-elemetowego, czyli <math>k!</math>. Zatem jest dokładnie | ||
Z wykładu o zliczaniu zbiorów i funkcji wiemy, ze takich injekcji jest | |||
<math>\frac{n!}{(n-k)!}</math>. | |||
W wyniku takiego wyboru, dostajemy wszakże pewien uporządkowany ciąg <math>k</math> elementów | |||
zbioru <math>X</math>. Wiele takich ciągów wyznacza ten sam <math>k</math>-elementowy podzbiór zbioru <math>X</math>. | |||
Ciągi takie różnią sie jedynie kolejnością elementów, a zatem jest ich tyle | |||
ile permutacji zbioru <math>k</math>-elemetowego, czyli <math>k!</math>. | |||
Zatem jest dokładnie | |||
<center><math>\frac{n(n-1)\cdot\ldots\cdot(n-k+1)}{k!}=\frac{n!}{(n-k)!k!} | <center><math>\frac{n(n-1)\cdot\ldots\cdot(n-k+1)}{k!}=\frac{n!}{(n-k)!k!} | ||
</math></center> | </math></center> | ||
podzbiorów <math>k</math>-elementowych zbioru <math>n</math>-elementowego. | podzbiorów <math>k</math>-elementowych zbioru <math>n</math>-elementowego. | ||
'''Dowód indukcyjny.''' | '''Dowód indukcyjny.''' | ||
Indukcję poprowadzimy względem górnego indeksu <math>n</math>. | Indukcję poprowadzimy względem górnego indeksu <math>n</math>. Dla <math>n=0</math> mamy tylko jeden interesujący nas współczynnik <math>{0\choose 0}=1</math>, i rzeczywiście <math>\frac{0!}{(0-0)!0!}=1</math>. Załóżmy zatem, że wszystkie współczynniki w <math>n</math>-tym wierszu spełniają wzór z tezy | ||
Dla <math>n=0</math> mamy tylko jeden interesujący nas współczynnik <math>{0\choose 0}=1</math>, | i rozważmy <math>{n+1\choose k}</math> dla <math>k\in\{0,\ldots,n+1\}</math>. Jeśli <math>k=0</math> to <math>{n+1\choose k}=1=\frac{n!}{(n-0)!0!}</math>. Załóżmy więc, że <math>k>0</math>. Wtedy: | ||
i rzeczywiście <math>\frac{0!}{(0-0)!0!}=1</math>. | |||
Załóżmy zatem, że wszystkie współczynniki w <math>n</math>-tym wierszu spełniają wzór z tezy | |||
i rozważmy <math>{n+1\choose k}</math> dla <math>k\in | <center><math>\begin{align}{n+1\choose k}&={n\choose k-1}+{n\choose k}\\ | ||
Jeśli <math>k=0</math> to <math>{n+1\choose k}=1=\frac{n!}{(n-0)!0!}</math>. | &=\frac{n!}{(n-k+1)!(k-1)!}+\frac{n!}{(n-k)!k!}\\ | ||
Załóżmy więc, że <math>k>0</math>. Wtedy: | &=\frac{n!}{(n-k)!(k-1)!}\cdot\left(\frac{1}{n-k+1}+\frac{1}{k}\right)\\ | ||
&=\frac{n!}{(n-k)!(k-1)!}\cdot\frac{k+(n-k+1)}{(n-k+1)k}\\ | |||
&=\frac{(n+1)!}{(n-k+1)!k!} | |||
\end{align}</math></center> | |||
}} | }} | ||
{{przyklad| | {{przyklad||| | ||
<center><math>{15\choose 3}=\frac{15!}{(15-3)!3!}=\frac{13\cdot14\cdot15}{2\cdot3}=13\cdot7\cdot5=455 | <center><math>{15\choose 3}=\frac{15!}{(15-3)!3!}=\frac{13\cdot14\cdot15}{2\cdot3}=13\cdot7\cdot5=455 | ||
</math></center> | </math></center> | ||
}} | |||
[[File:MD1-4.2.svg|250x100px|thumb|right|MD1-4.2.swf]] | |||
[[File:MD1-4.3.svg|250x100px|thumb|right|MD1-4.3.swf]] | |||
{{przyklad||| | |||
Wyobraźmy sobie, że znajdujemy się w mieście zbudowanym na planie prostopadle przecinających się ulic. Powiedzmy, że znajdujemy się w punkcie <math>A</math> i chcemy dojść do punktu <math>B</math>, tak jak zaznaczono na rysunku. | |||
Łatwo zauważyć, że jest wiele najkrótszych dróg prowadzących z <math>A</math> do <math>B</math>. | Łatwo zauważyć, że jest wiele najkrótszych dróg prowadzących z <math>A</math> do <math>B</math>. Dla przykładu: możemy pójść <math>3</math> razy na północ i potem cały czas na wschód, ale także możemy iść najpierw <math>6</math> razy na na wschód i dopiero wtedy skręcić na północ. | ||
Dla przykładu: | |||
możemy pójść <math>3</math> razy na północ i potem cały czas na wschód, | |||
ale także możemy iść najpierw <math>6</math> razy na na wschód i dopiero wtedy skręcić na północ. | |||
Ile jest najkrótszych dróg z <math>A</math> do <math>B</math>? | Ile jest najkrótszych dróg z <math>A</math> do <math>B</math>? | ||
Zauważmy, że każda najkrótsza droga biegnie przez dokładnie <math>9</math> skrzyżowań | Zauważmy, że każda najkrótsza droga biegnie przez dokładnie <math>9</math> skrzyżowań (licząc skrzyżowanie w punkcie <math>A</math> i nie licząc skrzyżowania w punkcie <math>B</math>). Na każdym takim skrzyżowaniu musimy podjąć decyzję, czy pójść na wschód czy na północ, przy czym musimy iść | ||
(licząc skrzyżowanie w punkcie <math>A</math> i nie licząc skrzyżowania w punkcie <math>B</math>). | |||
Na każdym takim skrzyżowaniu musimy podjąć decyzję, | |||
czy pójść na wschód czy na północ, przy czym musimy iść | |||
dokładnie <math>3</math> razy na północ i dokładnie <math>6</math> razy na wschód. | dokładnie <math>3</math> razy na północ i dokładnie <math>6</math> razy na wschód. | ||
< | Zatem liczba najkrótszych dróg z <math>A</math> do <math>B</math> to liczba wyborów spośród <math>9</math> skrzyżowań, trzech, na których pójdziemy na północ, bądź <math>6</math> na których pójdziemy na wschód. A zatem liczba ta wynosi <math>{9\choose 3}={9\choose 6}=94</math>. | ||
W ogólności załóżmy, że mamy kratkę <math>m\times n</math> i chcemy narysować najkrótszą łamaną po krawędziach kratki łączącą lewy dolny wierzchołek z prawym górnym. Na ile sposobów możemy narysować taką łamaną? | |||
Widzimy, że musimy narysować <math>m+n</math> odcinków jednostkowych, | |||
i | z których dokładnie <math>m</math> jest pionowych i dokładnie <math>n</math> jest poziomych. Zatem jest | ||
<center><math>{m+n\choose m}={m+n\choose n}=\frac{(m+n)!}{m!n!} | <center><math>{m+n\choose m}={m+n\choose n}=\frac{(m+n)!}{m!n!} | ||
</math></center> | </math></center> | ||
sposobów połączenia dwóch przeciwległych wierzchołków.}} | |||
[[File:4.4-4.5.mp4|250x250px|thumb|right|4.4-4.5.swf]] | |||
{{przyklad||| | |||
Ile rozwiązań ma równanie | Ile rozwiązań ma równanie | ||
<center> | |||
<math>x_0+x_1+x_2+x_3+x_4=7 | |||
</math> | |||
</center> | |||
< | gdzie <math>x_i</math> są liczbami naturalnymi? | ||
< | Użyjmy kratki rozważanej w poprzednim przykładzie do połączenia przeciwległych jej rogów. W kratce rozmiaru <math>4\times7</math> suma poziomych odcinków daje <math>7</math> i jest dokładnie <math>5</math> takich odcinków, po jednym na każdym poziomie. Jeśli długości tych odcinków oznaczymy odpowiednio przez <math>x_0,x_1,x_2,x_3,x_4</math>, to każda taka droga (łamana) na kratce ustala pewne rozwiązanie naszego równania, i każde rozwiązanie równania wyznacza dokładnie jedna drogę (łamaną). Dla przykładu - animacja obok. | ||
Zatem istnieje <math>{7+4\choose 4}=330</math> rozwiązań naszego równania. | Zatem istnieje <math>{7+4\choose 4}=330</math> rozwiązań naszego równania. | ||
| Linia 318: | Linia 234: | ||
W ogólności, równanie | W ogólności, równanie | ||
<center> | |||
<math>x_0+x_1+\ldots+x_{k-1}=n | |||
</math> | |||
</center> | |||
{{ | ma dokładnie tyle rozwiązań w liczbach naturalnych gdzie <math>x_i</math>, ile jest łamanych w kratce <math>k \times n</math>, czyli <math>{n+k-1\choose n}={n+k-1\choose k-1}</math>.}} | ||
[[File:SW 6.1.svg|250x100px|thumb|right|SW 6.1.swf]] | |||
[[File:SW 6.2.svg|250x200px|thumb|right|SW 6.2.swf]] | |||
{{przyklad||| | |||
Ile rozwiązań ma równanie | |||
<center><math>x_0+\ldots+x_{k-1}=n | <center> | ||
</math></center> | <math>x_0+\ldots+x_{k-1}=n | ||
</math> | |||
</center> | |||
gdzie <math>x_i</math> są '''dodatnimi''' liczbami naturalnymi? | gdzie <math>x_i</math> są '''dodatnimi''' liczbami naturalnymi? | ||
Zauważmy, że każde rozwiązanie tego równania z warunkami <math>x_i\geqslant 1</math>, | Zauważmy, że każde rozwiązanie tego równania z warunkami <math>x_i\geqslant 1</math>, można otrzymać z rozwiązania w liczbach naturalnych równania | ||
można otrzymać z rozwiązania w liczbach naturalnych równania | |||
<center> | |||
<math>y_0+\ldots+y_{k-1}=n-k | |||
</math> | |||
</center> | |||
poprzez podstawienie <math>x_i=y_i+1</math>. Na podstawie poprzedniego przykładu poszukiwanych rozwiązań jest zatem <math>n-1 \choose k-1</math>. | |||
Rozważmy <math>n</math> obiektów (np. punktów) ustawionych w ciągu jeden przy drugim. | |||
< | Separatorem nazywamy pionową kreskę położoną pomiędzy dwoma punktami. Zatem pomiędzy <math>n</math> punktami mamy <math>n-1</math> możliwych pozycji dla separatora. Zauważmy, że każde rozwiązanie naszego równania jednoznacznie odpowiada jednemu z możliwych rozmieszczeń <math>k-1</math> separatorów wśród <math>n-1</math> pozycji. Liczba punktów do pierwszego separatora to wartość <math>x_0</math>, liczba punktów pomiędzy pierwszym a drugim separatorem to <math>x_1</math>, itd., liczba punktów za ostatnim <math>k-1</math>-szym separatorem to <math>x_{k-1}</math>. Dla przykładu: | ||
Na odwrót każde rozwiązanie <math>x_0,x_1,\ldots,x_{k-1}</math> naszego równania | Na odwrót każde rozwiązanie <math>x_0,x_1,\ldots,x_{k-1}</math> naszego równania wyznacza jednoznacznie rozłożenie <math>k-1</math> separatorów: | ||
wyznacza jednoznacznie rozłożenie <math>k-1</math> separatorów: | |||
pierwszy kładziemy po <math>x_0</math> punktach, drugi po <math>x_0+x_1</math>, itd. | pierwszy kładziemy po <math>x_0</math> punktach, drugi po <math>x_0+x_1</math>, itd. | ||
Zatem liczba rozwiązań naszego równania to liczba rozmieszczeń <math>k-1</math> separatorów | Zatem liczba rozwiązań naszego równania to liczba rozmieszczeń <math>k-1</math> separatorów na <math>n-1</math> pozycjach, czyli <math>{n-1\choose k-1}</math>.}} | ||
na <math>n-1</math> pozycjach, czyli <math>{n-1\choose k-1}</math>. | |||
[[File:MD1-4.11.svg|250x150px|thumb|right|MD1-4.11.swf]] | |||
{{przyklad| | {{przyklad||| | ||
Rozważmy znów kratkę, tym razem kwadratową, wielkości <math>n\times n</math>, | |||
i policzmy na ile sposobów można w jej wnętrzu narysować prostokąt tak, aby wszystkie jego boki były równoległe do krawędzi kratki? | |||
Zauważmy, że każdy taki prostokąt jest jednoznacznie wyznaczony przez dwie linie poziome (spośród <math>n+1</math>) oraz dwie linie pionowe (znów spośród <math>n+1</math>). Rzeczywiście, dowolny prostokąt wyznacza dwie linie poziome i dwie pionowe (te przylegające do jego boków). I na odwrót dowolny wybór linii pozwoli nam nakreślić jednoznacznie prostokąt w kratce. | |||
i | |||
< | Poziome linie możemy wybrać na <math>{n+1\choose 2}</math> sposobów i pionowe linie także na <math>{n+1\choose 2}</math> sposobów. Zatem prostokąt w kratce <math>n\times n</math> możemy narysować na dokładnie | ||
<center><math>{n+1\choose 2}^2=\left(\frac{n(n+1)}{2}\right)^2 | <center><math>{n+1\choose 2}^2=\left(\frac{n(n+1)}{2}\right)^2 | ||
</math></center> | </math></center> | ||
sposobów. W przykładowej kratce na rysunku wymiarów <math>5\times 5</math> możemy więc umieścić <math>\left(\frac{5(5+1)}{2}\right)^2=225</math> prostokątów.}} | |||
Przechodzimy teraz do kolejnych własności współczynników dwumianowych. | |||
Rozpoczniemy od sumowania liczb na przekątnej trójkąta Pascala. Przekątna taka jest oczywiście nieskończona - sumujemy więc tylko jej początkowy fragment. | |||
[[File:4.6.mp4|250x250px|thumb|right|4.6.swf]] | |||
<center><math>\sum_{i=0}^{n}{i\choose k}={n+1\choose k+1} | {{obserwacja|5.4 [reguła sumowania po górnym indeksie]|obs 5.4| | ||
</math></center> | Dla <math>n,k\in\mathbb{N}</math> mamy | ||
<center> | |||
<math>\sum_{i=0}^{n}{i\choose k}={n+1\choose k+1} | |||
</math> | |||
</center> | |||
}} | }} | ||
< | {{dowod||| | ||
Ustalmy <math>(n+1)</math>-elementowy zbiór <math>X=\{x_0,\ldots,x_n\}</math> Rozważając jego <math>(k+1)</math>-elementowe podzbiory zwracamy uwagę na element tego podzbioru, który ma największy indeks. Oczywiście jest <math>i\geqslant k</math>, gdyż <math>X=\{x_0,\ldots,x_{k-1}\}</math> nie ma <math>(k+1)</math>-elementowych podzbiorów. Równie łatwo jest zauważyć, | |||
że jest dokładnie jeden podzbiór <math>(k+1)</math>-elementowy w którym <math>x_{k}</math> jest elementem o najwyższym indeksie, jest to zbiór <math>\{x_0,\ldots,x_{k-1}\}</math>. | |||
{{ | Policzmy teraz podzbiory zbioru <math>X</math>, w których <math>x_i</math> jest elementem o największym indeksie, przy czym <math>i>k</math>. Oprócz elementu <math>x_i</math> każdy taki zbiór ma dokładnie <math>k</math> elementów wybranych z <math>i</math>-elementowego zbioru <math>\{x_0,\ldots,x_{i-1}\}</math>. Wyboru tych elementów można dokonać na <math>{i\choose k}</math> sposobów. Zatem podzbiorów zbioru <math>X</math>, w których <math>x_i</math> jest elementem o największym indeksie jest dokładnie <math>{i\choose k}</math>. | ||
Sumując po wszystkich możliwych <math>i</math>, czyli <math>i\in\{k,\ldots,n\}</math> otrzymujemy: | |||
<center><math>\sum_{i=0}^n{i\choose k}=\sum_{i=k}^n{i\choose k}={n+1\choose k+1}</math>.</center> | |||
}} | }} | ||
Podobnie możemy sumować liczby położone | Podobnie możemy sumować liczby położone na linii "prostopadłej" do przekątnych Trójkąta Pascala, czyli liczby postaci <math>{n+i\choose i}</math>. | ||
na linii "prostopadłej" do przekątnych Trójkąta Pascala, | |||
czyli liczby postaci <math>{n+i\choose i}</math>. | |||
[[File:4.7.mp4|250x250px|thumb|right|4.7.swf]] | |||
Dla <math>n,k\in | {{obserwacja|5.5 [reguła sumowania równoległego]|obs 5.5| | ||
Dla <math>n,k\in\mathbb{N}</math> mamy: | |||
<center><math>\sum_{i=0}^{k}{n+i\choose i}={n+k+1\choose k} | <center> | ||
</math></center> | <math>\sum_{i=0}^{k}{n+i\choose i}={n+k+1\choose k} | ||
</math> | |||
</center> | |||
}} | }} | ||
{{dowod||| | |||
Tożsamość tę udowodnimy wykorzystując dwukrotnie {regułę symetrii} oraz {regułę sumowania po górnym indeksie}: | |||
{{dowod| | |||
<center><math>\ | <center> | ||
<math>\begin{align}\sum_{i=0}^{k}{n+i\choose i}&=\sum_{i=0}^k{n+i\choose (n+i)-i} | |||
=\sum_{i=0}^k{n+i\choose n} | =\sum_{i=0}^k{n+i\choose n} | ||
=\sum_{i=n}^{n+k}{i\choose n}\\ | =\sum_{i=n}^{n+k}{i\choose n}\\ | ||
&= | &={n+k+1\choose n+1}={n+k+1\choose k}. | ||
\ | \end{align}</math> | ||
</center> | |||
}} | }} | ||
{{obserwacja|6 | {{obserwacja|5.6 [tożsamość Cauchy'ego, splot Vandermonde'a]|obs 5.6| | ||
Dla liczb naturalnych <math>m,n,k</math> mamy: | Dla liczb naturalnych <math>m,n,k</math> mamy: | ||
<center><math>\sum_{i=0}^k{m\choose i}{n\choose k-i}={m+n\choose k} | <center><math>\sum_{i=0}^k{m\choose i}{n\choose k-i}={m+n\choose k} | ||
</math></center> | </math></center> | ||
}} | }} | ||
{{dowod| | {{dowod||| | ||
Policzymy liczbę wszystkich wyborów <math>k</math> osób z grona <math>m</math> mężczyzn i <math>n</math> kobiet, czyli liczbę <math>{m+n\choose k}</math> | |||
Policzymy liczbę wszystkich wyborów <math>k</math> osób | na jeszcze jeden sposób. Wybierając <math>k</math> osób wybieramy najpierw <math>i</math> mężczyzn na <math>{m\choose i}</math> sposobów, a potem <math>k-i</math> kobiet na <math>{n\choose k-i}</math> sposobów. Pozostaje teraz zsumować po wszystkich możliwych wartościach parametru <math>i</math>. | ||
z grona <math>m</math> mężczyzn i <math>n</math> kobiet, czyli liczbę <math>{m+n\choose k}</math> | |||
na jeszcze jeden sposób. | |||
Wybierając <math>k</math> osób wybieramy najpierw <math>i</math> mężczyzn na <math>{m\choose i}</math> sposobów, | |||
a potem <math>k-i</math> kobiet na <math>{n\choose k-i}</math> sposobów. | |||
Pozostaje teraz zsumować po wszystkich możliwych wartościach parametru <math>i</math>. | |||
}} | }} | ||
| Linia 485: | Linia 366: | ||
==Dwumiany== | ==Dwumiany== | ||
Poniższe Twierdzenie o Dwumianie wyjaśnia | Poniższe Twierdzenie o Dwumianie wyjaśnia pochodzenie tajemniczej nazwy "współczynniki dwumianowe". Twierdzenie to często przypisuje się Pascalowi. Tymczasem było ono już znane indyjskiemu matematykowi Pingala w III wieku p.n.e.. | ||
pochodzenie tajemniczej nazwy "współczynniki dwumianowe". | |||
Twierdzenie to często przypisuje się Pascalowi. | |||
Tymczasem było ono już znane indyjskiemu matematykowi Pingala w III wieku p.n.e.. | |||
{{obserwacja|7 | {{obserwacja|5.7 [Twierdzenie o Dwumianie]|obs 5.7| | ||
Dla <math>x,y\in \mathbb{R}</math> i <math>n\in \mathbb{N}</math> | |||
<center><math>(x+y)^n=\sum_{i=0}^n{n\choose i}x^iy^{n-i} | <center><math>(x+y)^n=\sum_{i=0}^n{n\choose i}x^iy^{n-i}</math></center> | ||
</math></center> | |||
}} | }} | ||
{{dowod| | {{dowod||| | ||
Przedstawmy najpierw potęgę <math>(x+y)^n</math> w rozwiniętej formie iloczynu: | |||
<center><math>\underbrace{(x+y)\cdot\ldots\cdot(x+y)}_{n\ razy}</math></center> | |||
Korzystając z rozdzielności mnożenia, wyrażenie to staje się sumą składników. | Korzystając z rozdzielności mnożenia, wyrażenie to staje się sumą składników. | ||
Każdy taki składnik to iloczyn pewnej liczby <math>x</math>-ów i pewnej liczby <math>y</math>-ów, | Każdy taki składnik to iloczyn pewnej liczby <math>x</math>-ów i pewnej liczby <math>y</math>-ów, przy czym łącznie iloczyn taki ma <math>n</math> czynników. | ||
przy czym łącznie iloczyn taki ma <math>n</math> czynników. | A zatem każdy składnik ma postać <math>x^k y^{n-k}</math>. Powstaje on poprzez wybór <math>k</math> (spośród <math>n</math>) czynników w iloczynie <math>(x+y)\cdot\ldots\cdot(x+y)</math>, z których do składnika postaci <math>x^k y^{n-k}</math> wchodzi <math>x</math> (a tym samym <math>(n-k)</math> składników, z których wchodzi <math>y</math>). Tym samym składników postaci <math>x^k y^{n-k}</math> jest tyle, ile <math>k</math>-elementowych podzbiorów zbioru <math>n</math>-elementowego, czyli <math>x^k y^{n-k}</math> pojawi się w sumie <math>{n\choose k}</math>-krotnie. | ||
A zatem każdy składnik ma postać <math>x^k y^{n-k}</math>. | |||
Powstaje on poprzez wybór <math>k</math> (spośród <math>n</math>) | |||
czynników w iloczynie <math>(x+y)\cdot\ldots\cdot(x+y)</math>, z których do składnika | |||
postaci <math>x^k y^{n-k}</math> wchodzi <math>x</math> (a tym samym <math>(n-k)</math> składników, z których wchodzi <math>y</math>). | |||
Tym samym składników postaci <math>x^k y^{n-k}</math> jest tyle, ile <math>k</math>-elementowych podzbiorów | |||
zbioru <math>n</math>-elementowego, czyli <math>x^k y^{n-k}</math> pojawi się | |||
}} | }} | ||
Twierdzenie o Dwumianie można też udowodnić za pomocą indukcji, | Twierdzenie o Dwumianie można też udowodnić za pomocą indukcji, co pozostawiamy jako ćwiczenie. | ||
co pozostawiamy jako ćwiczenie. | |||
{{przyklad||| | |||
{{ | <center><math>\begin{align}(a+b)^2&=a^2+2ab+b^2,\\ | ||
(a+b)^3&=a^3+3a^2b+3ab^2+b^3,\\ | |||
(a+b)^4&=a^4+4a^3b+6a^2b^2+4ab^3+b^4. | |||
\end{align}</math></center> | |||
}} | }} | ||
{{wniosek|8| | [[File:MD1-4.8.mp4|250x250px|thumb|right|MD1-4.8.swf]] | ||
{{wniosek|5.8|wn 5.8| | |||
Dla dowolnego <math>n\geqslant0</math> | |||
* <math>(1+x)^n=\sum_{i=0}^n{n\choose i}x^i</math>, | * <math>(1+x)^n=\sum_{i=0}^n{n\choose i}x^i</math>, | ||
| Linia 535: | Linia 411: | ||
* <math>{n\choose 0}+{n\choose 1}+\ldots+{n\choose n}=2^n</math>, | * <math>{n\choose 0}+{n\choose 1}+\ldots+{n\choose n}=2^n</math>, | ||
* <math>{n\choose 0}-{n\choose 1}+\ldots+(-1)^n{n\choose n}=0^n</math>. | * <math>{n\choose 0}-{n\choose 1}+\ldots+(-1)^n{n\choose n}=0^n</math>. (Uwaga: <math>{0\choose0}=1=0^0</math>) | ||
}} | }} | ||
< | {{dowod||| | ||
Wszystkie punkty wynikają trywialnie z Twierdzenia o Dwumianie. (Pierwszy jest oczywisty. Dla dwu pozostałych zauważmy jedynie, że <math>(1+1)^n=2^n</math>, <math>(1-1)^n=0</math>.) Jednak drugi i trzeci punkt mają ładną interpretację kombinatoryczną. | |||
{{ | Istotnie, liczba podzbiorów zbiorów <math>n</math> elementowego to <math>2^n</math>. Z drugiej strony licząc te podzbiory, możemy kolejno zliczać | ||
podzbiory <math>0,1,2,\ldots</math>-elementowe - jest ich <math>{n\choose 0},{n\choose 1},{n\choose 2},\ldots</math>. | |||
Nieco dłuższy jest argument kombinatoryczny dla naprzemiennej sumy | |||
<math>{n\choose 0}-{n\choose 1}+\ldots+(-1)^n{n\choose n}=0</math>. Dla <math>n=0</math> jest to oczywiste. Natomiast dla <math>n>0</math> jest to równoważne stwierdzeniu, że dla <math>n</math>-elementowego zbioru <math>X</math> | |||
* liczba podzbiorów zbioru <math>X</math> o parzystej liczbie elementów jest równa liczbie podzbiorów <math>X</math> o nieparzystej liczbie elementów. | |||
jest | |||
Załóżmy najpierw, że <math>n</math> jest nieparzyste. Wtedy każdy podzbiór zbioru <math>X</math> o parzystej liczbie elementów ma dopełnienie o nieparzystej liczbie elementów, a każdy podzbiór zbioru <math>X</math> o nieparzystej liczbie elementów ma dopełnienie o parzystej liczbie elementów. | |||
Ta bijektywna odpowiedniość dowodzi, że w istocie jest ich tyle samo. | |||
Załóżmy zatem, że <math>n</math> jest parzyste i ustalmy <math>x\in X</math>. | |||
Zdefiniujmy funkcję <math>f:\mathcal{P}(X)\mathcal{P}(X)</math>, kładąc | |||
<center><math>f(Y)= \begin{cases} | |||
(X - Y)-\{x\} & \mbox{, jeśli } {x} \not \in {Y}\subseteq {X}\\ | |||
(X - Y)\cup\{x\} & \mbox{, jeśli } {x} \in {Y}\subseteq {X}.\end{cases}</math></center> | |||
Zauważmy, że <math>f</math> jest permutacją <math>\mathcal{P}(X)</math>. | Zauważmy, że <math>f</math> jest permutacją <math>\mathcal{P}(X)</math>. Rzeczywiście, dla różnych podzbiorów <math>Y_1,Y_2\subseteq X</math> mamy: | ||
Rzeczywiście, dla różnych podzbiorów <math>Y_1,Y_2\subseteq X</math> mamy: | |||
* jeśli <math>x\notin Y_1</math> i <math>x\notin Y_2</math> to | * jeśli <math>x\notin Y_1</math> i <math>x\notin Y_2</math> to | ||
<center><math>f(Y_1)=(X-Y_1)- | <center><math>f(Y_1)=(X-Y_1)-\{x\}=X-Y_1\neq X-Y_2=(X-Y_2)-\{x\}=f(Y_2)</math>,</center> | ||
</math></center> | |||
* jeśli <math>x\in Y_1</math> i <math>x\in Y_2</math> to | * jeśli <math>x\in Y_1</math> i <math>x\in Y_2</math> to | ||
<center><math>f(Y_1)=(X-Y_1)\cup | <center><math>f(Y_1)=(X-Y_1)\cup\{x\}\neq(X-Y_1)\cup\{x\}=f(Y_2)</math>,</center> | ||
</math></center> | |||
* jeśli <math>x\in Y_1</math> i <math>x\notin Y_2</math> to <math>x\in f(Y_1)</math> i <math>x\notin f(Y_2)</math>, zatem <math>f(Y_1)\neq f(Y_2)</math>. | * jeśli <math>x\in Y_1</math> i <math>x\notin Y_2</math> to <math>x\in f(Y_1)</math> i <math>x\notin f(Y_2)</math>, zatem <math>f(Y_1)\neq f(Y_2)</math>. | ||
To dowodzi, że <math>f</math> jest injekcją. Dla dowodu surjektywności weźmy dowolne <math>Z\subseteq X</math>. Jeśli <math>x\in Z</math> to <math>f((X-Z)\cup | To dowodzi, że <math>f</math> jest injekcją. Dla dowodu surjektywności weźmy dowolne <math>Z\subseteq X</math>. Jeśli <math>x\in Z</math> to <math>f((X-Z)\cup\{x\})=Z</math>, jeśli zaś <math>x\notin Z</math> to <math>f((X-Z)-\{x\})=Z</math>. Zatem <math>f</math> jest permutacją zbioru <math>\mathcal{P}(X)</math>. Co więcej łatwo zauważyć, że dla <math>Y</math> o parzystej (nieparzystej) liczbie elementów <math>f(Y)</math> ma nieparzystą (parzystą) liczbę elementów. To dowodzi, że dla parzystego <math>n</math> podzbiorów <math>X</math> o parzystej liczbie elementów jest tyle samo co podzbiorów <math>X</math> o nieparzystej liczbie elementów. | ||
}} | }} | ||
==Uogólniony współczynnik dwumianowy== | ==Uogólniony współczynnik dwumianowy== | ||
[[#wn_5.8|Wniosek 5.8]] pozwala na ustalenie wartość sumy całego wiersza w Trójkącie Pascala i wartość naprzemiennej sumy całego wiersza Trójkąta Pascala. | |||
wartość sumy całego wiersza w Trójkącie Pascala i | W praktyce często pojawia się konieczność (naprzemiennego) sumowania tylko pewnego fragmentu takiego wiersza.Do tego pomocne mogłyby być sumy postaci: | ||
wartość naprzemiennej sumy całego wiersza Trójkąta Pascala. | |||
W praktyce często pojawia się konieczność (naprzemiennego) | |||
sumowania tylko pewnego fragmentu takiego wiersza. | |||
Do tego pomocne mogłyby być sumy postaci: | |||
<center><math>\begin{array} { | <center><math>\begin{array} {lllc} | ||
\sum_{i=0}^m{n\choose i}&= | \sum_{i=0}^m{n\choose i}&={n\choose0}+{n\choose1}+\ldots+{n\choose m}&\qquad(*)\\ | ||
\sum_{i=0}^m(-1)^i{n\choose i}&= | \sum_{i=0}^m(-1)^i{n\choose i}&={n\choose0}-{n\choose1}+\ldots+(-1)^m{n\choose m}&\qquad(**) | ||
\end{array} | \end{array} | ||
</math></center> | </math></center> | ||
dla <math>0\leqslant m<n</math>. | dla <math>0\leqslant m<n</math>. | ||
Niestety nie jest znana żadna zwarta postać <math>(*)</math>. | Niestety nie jest znana żadna zwarta postać <math>(*)</math>. Zaskakująca jest natomiast zwarta postać modyfikacji tej sumy polegającej na wymnożeniu każdego składnika przez jego odległość od środka trójkąta. Indukcyjny dowód tak powstałej zależności pozostawiamy jako ćwiczenie. | ||
Zaskakująca jest natomiast zwarta postać modyfikacji tej sumy | |||
polegającej na wymnożeniu każdego składnika przez jego odległość od środka trójkąta. | |||
Indukcyjny dowód tak powstałej zależności pozostawiamy jako ćwiczenie. | |||
{{obserwacja|9|obs 9| Dla <math>m,n\geqslant0</math> | {{obserwacja|5.9|obs 5.9| | ||
Dla <math>m,n\geqslant0</math> | |||
<center><math>\sum_{i=0}^m{\frac{n}{2}-i}\cdot{n\choose i}=\frac{m+1}{2}{n\choose m+1}</math></center> | |||
}} | }} | ||
Natomiast naprzemienna częściowa suma <math>(**)</math> wiersza Trójkąta Pascala ma postać zwartą. Wyprowadzenie takiej postaci odwołuje się do | Natomiast naprzemienna częściowa suma <math>(**)</math> wiersza Trójkąta Pascala ma postać zwartą. Wyprowadzenie takiej postaci odwołuje się do uogólnienia współczynnika dwumianowego na dowolne rzeczywiste indeksy górne, i dowolne całkowite indeksy dolne. Wykorzystuje to poznane już przy okazji rachunku róznicowego pojęcie dolnej silni <math>r^{\underline{k}}</math>. | ||
{{kotwica|uwspoldwu|'''Uogólniony współczynnik dwumianowy'''}} <math>{r\choose k}</math> dla <math>r\in\mathbb{R}</math> i <math>k\in\mathbb{Z}</math> to: | |||
<center><math>{r\choose k} = \begin{cases} \frac{r(r-1)\cdot\ldots\cdot(r-k+1)}{k(k-1)\cdot\ldots\cdot1}=\frac{r^{\underline{k}}}{k!}, &\mbox{dla }{k\geqslant0},\\0,& \mbox{dla }{k<0}. \end{cases}</math></center> | <center><math>{r\choose k} = \begin{cases} \frac{r(r-1)\cdot\ldots\cdot(r-k+1)}{k(k-1)\cdot\ldots\cdot1}=\frac{r^{\underline{k}}}{k!}, &\mbox{dla }{k\geqslant0},\\0,& \mbox{dla }{k<0}. \end{cases}</math></center> | ||
{{obserwacja|10|obs 10| Dla <math>r\in\mathbb{R}\real</math> i <math>k\in\mathbb{Z} | Zauważmy, że w istocie dla <math>r,k\in\mathbb{N}</math> wartości <math>{r\choose k}</math> pozostają niezmienione. Oczywiście, dla <math>r\in\mathbb{N}</math>, interpretacja <math>{r\choose k}</math> jako <math>k</math>-elementowych liczby podzbiorów zbioru <math>r</math>-elementowego pozostaje w mocy. Nie jest natomiast znana sensowna kombinatoryczna interpretacja uogólnionego współczynnika dwumianowego dla pozostałych rzeczywistych wartosci <math>r</math>. Odnotujmy tylko, że <math>{r\choose k}</math> jest wielomianem <math>k</math>-tego stopnia zmiennej <math>r</math>. Sporo własności współczynnika dwumianowego przenosi się na wersję uogólnioną. Poniższe zostawiamy bez dowodu jako ćwiczenie. | ||
{{obserwacja|5.10|obs 5.10| | |||
Dla <math>r\in\mathbb{R}\real</math> i <math>k\in\mathbb{Z}</math> mamy | |||
* <math>{r\choose0}=1</math>, | * <math>{r\choose0}=1</math>, | ||
| Linia 650: | Linia 502: | ||
}} | }} | ||
{{przyklad| | {{przyklad||| | ||
Z uwagi na to, że w indeksie dolnym mogą występować jedynie liczby całkowite, | |||
nie ma sensu reguła symetrii <math>{r \choose k}= {r \choose k-1}</math>. Ale nawet dla całkowitych wartości <math>r</math> zawodzi: | |||
<center><math>{-1\choose k}\neq{-1\choose -1-k}, \qquad\mbox{dla dowolnych }{k} | <center><math>{-1\choose k}\neq{-1\choose -1-k}, \qquad\mbox{dla dowolnych }{k}</math>.</center> | ||
* jeśli <math>k<0</math>, to <math>{-1\choose k}\neq{-1\choose -1-k}=(-1)^{-1-k+1}</math>, | * jeśli <math>k<0</math>, to <math>{-1\choose k}\neq{-1\choose -1-k}=(-1)^{-1-k+1}</math>, | ||
| Linia 664: | Linia 515: | ||
}} | }} | ||
Zachowana jest natomiast < | Zachowana jest natomiast reguła dodawania. | ||
{{obserwacja|5.11|obs 5.11| | |||
Dla <math>r\in\mathbb{R}\real</math> i <math>k\in\mathbb{Z}</math> | |||
<center><math>{r\choose k}={r-1\choose k}+{r-1\choose k-1} | <center><math>{r\choose k}={r-1\choose k}+{r-1\choose k-1}</math></center> | ||
</math></center> | |||
}} | }} | ||
{{dowod| | {{dowod||| | ||
Dla ujemnych wartości <math>k</math> wszystkie współczynniki równe są <math>0</math> i tożsamość trywialnie zachodzi. Niech teraz <math>r\in\mathbb{R}\real</math> i <math>k\geqslant0</math>. Oczywiście różnica | |||
<center><math>{r\choose k}-{r-1\choose k}-{r-1\choose k-1} | <center><math>{r\choose k}-{r-1\choose k}-{r-1\choose k-1} | ||
</math></center> | </math></center> | ||
jest wielomianem co najwyżej <math>k</math>. | |||
Może więc, o ile nie jest wielomianem stale równym zero, | jest wielomianem co najwyżej <math>k</math>. Może więc, o ile nie jest wielomianem stale równym zero, mieć co najwyżej <math>k</math> miejsc zerowych. | ||
mieć co najwyżej <math>k</math> miejsc zerowych. | Z drugiej strony wiemy już, że ta różnica zeruje się dla wszystkich liczb naturalnych <math>r</math>, więc musi być zawsze równa <math>0</math>. | ||
Z drugiej strony wiemy już, | |||
że ta różnica zeruje się dla wszystkich liczb naturalnych <math>r</math>, | |||
więc musi być zawsze równa <math>0</math>. | |||
}} | }} | ||
[[File:4.9.svg|250x250px|thumb|right|4.9.swf]] | |||
Uogólniona reguła dodawania z [[#obs_5.11|Obserwacji 5.11]] pozwala rozszerzyć Trójkąt Pascala na współczynniki o ujemnych wartościach górnego indeksu. | |||
Kolejne wartości "ujemnej części" możemy wyliczać w następującej kolejności: | Kolejne wartości "ujemnej części" możemy wyliczać w następującej kolejności: | ||
Przyjrzyjmy się wartościom <math>{n\choose k}</math> dla ustalonego <math>k</math> i całkowitych wartości <math>n</math>. | <center> | ||
Zauważalny jest pewien rodzaj symetrii między tymi wartościami. | <math>{-1\choose 0},{-2\choose0},{-1\choose1},{-3\choose0},{-2\choose 1},{-1\choose2},\ldots</math> | ||
W istocie zachodzi on | </center> | ||
Przyjrzyjmy się wartościom <math>{n\choose k}</math> dla ustalonego <math>k</math> i całkowitych wartości <math>n</math>. Zauważalny jest pewien rodzaj symetrii między tymi wartościami. W istocie zachodzi on dla wszystkich rzeczywistych wartości górnego indeksu. | |||
{{obserwacja|5.12 [reguła negacji górnego indeksu]|obs 5.12| | |||
Dla <math>r\in\mathbb{R}\real</math>, <math>k\in\mathbb{Z}</math>: | |||
<center> | |||
<math>(-1)^k{r\choose k}={k-r-1\choose k}</math> | |||
</center> | |||
}} | }} | ||
{{dowod| | {{dowod||| | ||
Policzymy wartość obu stron po uprzednim wymnożeniu przez wspólny mianownik <math>k!</math>: | |||
<center><math>\ | <center><math>\begin{align}(-1)^k r^{\underline{k}} | ||
&= | &=(-1)^k r(r-1)\cdot\ldots\cdot(r-k+1)\\ | ||
&= | &=(-r)(1-r)\cdot\ldots\cdot(k-1-r)\\ | ||
&= | &=(k-r-1)^{\underline{k}}. | ||
\ | \end{align}</math></center> | ||
}} | }} | ||
Znaną nam już z | Znaną nam już z [[#obs_5.5|Obserwacji 5.5]] regułę równoległego sumowania możemy uogólnić za pomocą argumentu podobnego do użytego w dowodzie [[#obs_5.11|Obserwacji 5.11]]. | ||
regułę równoległego sumowania możemy uogólnić za pomocą argumentu podobnego do | |||
użytego w dowodzie | |||
{{obserwacja|13|obs 13| Dla <math>r\in\mathbb{R}\real</math>, <math>k\in\mathbb{Z}\ | {{obserwacja|5.13|obs 5.13| | ||
Dla <math>r\in\mathbb{R}\real</math>, <math>k\in\mathbb{Z}</math> | |||
<center><math>\sum_{i\leqslant k}{r+i\choose i}={r+k+1\choose k}</math></center> | |||
}} | }} | ||
Zauważmy, że rozważana suma jest tylko pozornie nieskończona, | Zauważmy, że rozważana suma jest tylko pozornie nieskończona, gdyż dla wszystkich ujemnych wartości <math>i</math> odpowiednie składniki zerują się. | ||
gdyż dla wszystkich ujemnych wartości <math>i</math> odpowiednie składniki | W dalszych ciągu przyjmiemy będziemy również rozważać podobne sumy "nieskończone", ale przy założeniu, że tylko skończenie wiele składników jest niezerowych. | ||
zerują się. | |||
W dalszych ciągu przyjmiemy będziemy również rozważać podobne sumy "nieskończone", | Wyposażeni w regułę negacji górnego indeksu wracamy teraz my do naprzemiennej, cześciowej sumy wierszy w Trójkącie Pascala, czyli do <math>(**)</math>. | ||
ale przy założeniu, że tylko skończenie wiele składników jest niezerowych. | |||
{{obserwacja|5.14|obs 5.14| | |||
Dla <math>r\in\mathbb{R}\real</math>, <math>m\in\mathbb{Z}</math> | |||
<center><math>\sum_{i\leqslant m}(-1)^i{r\choose i}=(-1)^m{r-1\choose m}</math></center> | |||
}} | }} | ||
{{dowod| | {{dowod||| | ||
<center><math>\begin{align}\sum_{i\leqslant m}(-1)^i{r\choose i} | |||
&=\sum_{i\leqslant m}{i-r-1\choose i} | |||
\qquad\text{z reguły negacji górnego indeksu}\\ | |||
&={-m+r\choose m} | |||
\qquad\qquad\text{z Obserwacji 5.13}\\ | |||
&=(-1)^m{r-1\choose m}. | |||
\qquad\text{z reguły negacji górnego indeksu} | |||
\end{align}</math></center> | |||
}} | }} | ||
| Linia 771: | Linia 618: | ||
szczególnych permutacji. Zaczniemy od pomocniczej obserwacji. | szczególnych permutacji. Zaczniemy od pomocniczej obserwacji. | ||
{{obserwacja|15 | {{obserwacja|5.15 [przestawienie trójmianowe]|obs 5.15| | ||
Dla <math>r\in\mathbb{R}\real</math>, <math>i,j\in\mathbb{Z}\ | Dla <math>r\in\mathbb{R}\real</math>, <math>i,j\in\mathbb{Z}</math> | ||
<center><math>{r\choose i}{i\choose j}={r\choose j}{r-j\choose i-j}</math></center> | |||
}} | }} | ||
{{dowod| | {{dowod||| | ||
Zauważmy, że dla <math>i<j</math> obie strony równości się zerują. Także dla <math>i<0</math> teza jest trywialna. Zatem możemy założyć, że <math>0\leqslant i<j</math>. Wtedy: | |||
<center><math>\begin{align}{r\choose i}{i\choose j}&=\frac{r^{\underline{i}}}{i!}\cdot\frac{i^{\underline{j}}}{j!}\\ | |||
&=\frac{r(r-1\cdot\ldots\cdot(r-i+1))}{i!}\cdot\frac{i(i-1)\cdot\ldots\cdot(i-j+1)}{j!}\\ | |||
&=\frac{r(r-1)\cdot\ldots\cdot(r-j+1)}{j!}\cdot\frac{(r-j)(r-j-1)\cdot\ldots\cdot(r-i+1)}{(i-j)!}\\ | |||
&={r\choose j}{r-j\choose i-j}. | |||
\end{align}</math></center> | |||
}} | }} | ||
{{obserwacja|16 | {{obserwacja|5.16 [reguła odwracania]|obs 5.16| | ||
Dla funkcji <math>f,g:\mathbb{Z} | Dla funkcji <math>f,g:\mathbb{Z}\mathbb{R}\real</math> | ||
<center><math>f(n)=\sum_{i\in\mathbb{Z} | <center><math>f(n)=\sum_{i\in\mathbb{Z}}{n\choose i}(-1)^ig(i) | ||
</math></center> | </math></center> | ||
wtedy i tylko wtedy, gdy | wtedy i tylko wtedy, gdy | ||
{{dowod| | <center><math>g(n)=\sum_{i\in\mathbb{Z}}{n\choose i}(-1)^if(i)</math></center> | ||
}} | |||
{{dowod||| | |||
Z uwagi na symetrię założeń wystarczy udowodnić tylko jedne implikację. Zakładamy zatem, że <math>f(n)=\sum_{i\in\mathbb{Z}}{n\choose i}(-1)^ig(i)</math> by dostać: | |||
<center><math>\begin{align}\sum_i{n\choose i}(-1)^if(i) | |||
&=\sum_{i\in\mathbb{Z}}{n\choose i}(-1)^i\sum_{j\in\mathbb{Z}}{i\choose j}(-1)^jg(j)\\ | |||
&=\sum_{j\in\mathbb{Z}} g(j)\sum_{i\in\mathbb{Z}\mathbb{Z}}{n\choose i}{i\choose j}(-1)^{i+j}\\ | |||
&=\sum_{j\in\mathbb{Z}} g(j)\sum_{i\in\mathbb{Z}\mathbb{Z}} {n\choose j}{n-j\choose i-j}(-1)^{i+j}\\ | |||
&=\sum_{j\in\mathbb{Z}} g(j){n\choose j}\sum_{i\in\mathbb{Z}} {n-j\choose i-j}(-1)^{i+j}\\ | |||
&=\sum_{j\in\mathbb{Z}} g(j){n\choose j}\sum_{i\in\mathbb{Z}} {n-j\choose i}(-1)^i, | |||
\end{align}</math></center> | |||
gdzie druga równość wynika ze zmiana kolejności sumowania, trzecia z przestawienia trójmianowego, a ostatnia przez podstawienie <math>i:=i+j</math>. | |||
Z [[#wn_5.8|Wniosku 5.8]] wiemy, że suma <math>\sum_{i\in\mathbb{Z}}{n-j\choose i}(-1)^i</math> jest niezerowa (i wynosi <math>1</math>) tylko dla <math>j=n</math>. Zatem kontynuując: | |||
<center><math>\ | <center><math>\begin{align} &=\sum_{j\in\mathbb{Z}} g(j){n\choose j}\sum_{i\in\mathbb{Z}}{n-j\choose i}(-1)^i\\ | ||
&= | &=g(n){n\choose n} | ||
= g(n). | = g(n). | ||
\ | \end{align}</math></center> | ||
}} | }} | ||
| Linia 835: | Linia 683: | ||
===Permutacje bez punktów stałych=== | ===Permutacje bez punktów stałych=== | ||
{Nieporządek} na zbiorze <math>X</math> to permutacja <math>\alpha:X\ | {{kotwica|nieporz|'''Nieporządek'''}} na zbiorze <math>X</math> to permutacja <math>\alpha:X\to X</math> taka, że <math>\alpha(x)\neq x</math> dla dowolnego <math>x\in X</math>, czyli permutacja "bez punktów stałych". | ||
że <math>\alpha(x)\neq x</math> dla dowolnego <math>x\in X</math>, | |||
czyli permutacja "bez punktów stałych". | |||
{Podsilnia} liczby <math>n</math>, w skrócie <math> | {{kotwica|podsilnia|'''Podsilnia'''}} liczby <math>n</math>, w skrócie <math>!n</math>, to liczba nieporządków zbioru <math>n</math>-elementowego. Przyjmujemy, że <math>!0=1</math>, jako ze jedyna permutacja zbioru pustego - funkcja pusta - w oczywisty sposób nie ma punktów stałych. | ||
to liczba nieporządków zbioru <math>n</math>-elementowego. | |||
Przyjmujemy, że <math> | |||
funkcja pusta | |||
{{przyklad| | {{przyklad||| | ||
Zbiór <math>\mathbb{Z}_4=\{0,1,2,3\}</math> ma <math>4!=24</math> permutacje, ale tylko <math>9</math> z nich to nieporządki. Oto ich lista: | |||
<center><math>\begin{array} {cccccccccccccc} | <center><math>\begin{array} {cccccccccccccc} | ||
| Linia 863: | Linia 705: | ||
\end{array} | \end{array} | ||
</math></center> | </math></center> | ||
}} | }} | ||
{{obserwacja|17|obs 17| | {{obserwacja|5.17|obs 5.17| | ||
<math> | <math>!n = n!\sum_{i=0}^n\frac{(-1)^i}{i!}</math>. | ||
}} | }} | ||
{{dowod| | {{dowod||| | ||
Zauważmy najpierw, że liczba permutacji <math>\alpha</math> zbioru <math>n</math>-elementowego takich, że <math>\alpha(x)\neq x</math> dla dokładnie <math>i</math> elementów <math>x\in X</math>, | |||
wynosi <math>{n\choose i}!i</math>. Stąd: | |||
<center><math>n!= | <center><math>n!= | ||
\sum_{i=0}^n {n\choose i} | \sum_{i=0}^n {n\choose i}!i | ||
=\sum_{i=0}^n (-1)^i{n\choose i}(-1)^i | =\sum_{i=0}^n (-1)^i{n\choose i}(-1)^i(!i)</math></center> | ||
</math></center> | |||
Stosując teraz regułę odwracania, dostajemy: | |||
<center><math>\begin{align}!n&=\sum_{i=0}^n(-1)^{n-i}{n\choose i}i!\\ | |||
&=\sum_{i=0}^n(-1)^{n-i}\frac{n!}{(n-i)!}\\ | |||
&=n!\sum_{i=0}^n\frac{(-1)^i}{i!}. | |||
\end{align}</math></center> | |||
}} | }} | ||
==Współczynniki multimianowe== | ==Współczynniki multimianowe== | ||
Współczynniki dwumianowe pojawiały się przy rozwinięciu dwumianu <math>(x+y)^n</math>. | Współczynniki dwumianowe pojawiały się przy rozwinięciu dwumianu <math>(x+y)^n</math>. | ||
Odpowiadały one wyborom dwuwartościowym. | Odpowiadały one wyborom dwuwartościowym. | ||
| Linia 905: | Linia 750: | ||
oczywiście <math>k_1+\ldots k_r=n</math>. | oczywiście <math>k_1+\ldots k_r=n</math>. | ||
{Współczynnik multimianowy} <math>{n\choose k_1,k_2\ldots,k_{r}}</math>, | {{kotwica|wspolmulti|'''Współczynnik multimianowy'''}} <math>{n\choose k_1,k_2\ldots,k_{r}}</math>, dla <math>n\in\mathbb{Z}</math>, <math>r\geqslant2</math> oraz całkowitych <math>k_1,\ldots,k_r</math> takich, że <math>k_1+\ldots k_r=n</math>, to liczba sposobów umieszczenia <math>n</math> obiektów w <math>r</math> pudełkach z odpowiednio <math>k_1</math> obiektami w pierwszym pudełku, <math>k_2</math> w drugim, itd., oraz <math>k_r</math> w <math>r</math>-tym. Jeśli którakolwiek z liczb <math>k_i</math> jest ujemna to współczynnik jest równy <math>0</math>. | ||
dla <math>n\in\mathbb{Z} | Zauważmy, że z uwagi na symetrię dolnych indeksów, ich kolejność nie jest istotna. Oczywiście <math>{n \choose k}</math> to w nowej notacji <math>{n \choose k,n-k}</math>. | ||
oraz całkowitych <math>k_1,\ldots,k_r</math> takich, że <math>k_1+\ldots k_r=n</math>, | |||
to liczba sposobów umieszczenia <math>n</math> obiektów w <math>r</math> pudełkach z odpowiednio | |||
<math>k_1</math> obiektami w pierwszym pudełku, <math>k_2</math> w drugim, itd., | |||
oraz <math>k_r</math> w <math>r</math>-tym. | |||
Jeśli którakolwiek z liczb <math>k_i</math> jest ujemna to współczynnik jest równy <math>0</math>. | |||
Zauważmy, że z uwagi na symetrię dolnych indeksów, | |||
ich kolejność nie jest istotna. | |||
Oczywiście <math>{n \choose k}</math> to w nowej notacji <math>{n \choose k,n-k}</math>. | |||
Następna obserwacja wynika wprost z definicji współczynników multimianowych. | Następna obserwacja wynika wprost z definicji współczynników multimianowych. | ||
{{obserwacja|18|obs 18| Dla <math>n\in\mathbb{Z} | {{obserwacja|5.18|obs 5.18| | ||
zachodzi: | Dla <math>n\in\mathbb{Z}</math>, <math>k,l,k_1,\ldots,k_r\in\mathbb{Z}</math> takich, że <math>k_1+\ldots k_r=n= k+l</math> zachodzi: | ||
* <math>{n\choose n,0,\ldots,0}=1</math>, | * <math>{n\choose n,0,\ldots,0}=1</math>, | ||
| Linia 929: | Linia 766: | ||
* <math>{n\choose l,l,0,\ldots,0}={n\choose k}={n\choose l}</math>, | * <math>{n\choose l,l,0,\ldots,0}={n\choose k}={n\choose l}</math>, | ||
* <math>{n\choose k_1,\ldots,k_r} = {n\choose k_{\sigma(1)},\ldots,k_{\sigma(r)}}</math>, | * <math>{n\choose k_1,\ldots,k_r} = {n\choose k_{\sigma(1)},\ldots,k_{\sigma(r)}}</math>, dla dowolnej permutacji <math>\sigma</math> zbioru <math>\{1,2,\ldots,r\}</math>. | ||
dla dowolnej permutacji <math>\sigma</math> zbioru <math> | |||
}} | }} | ||
| Linia 936: | Linia 772: | ||
Następna obserwacja wymaga krótkiego uzasadnienia. | Następna obserwacja wymaga krótkiego uzasadnienia. | ||
{{obserwacja|19|obs 19| Dla <math>n,k_1,\ldots,k_r\geqslant0</math> takich, że <math>k_1+\ldots+k_r=n</math> | {{obserwacja|5.19|obs 5.19| | ||
Dla <math>n,k_1,\ldots,k_r\geqslant0</math> takich, że <math>k_1+\ldots+k_r=n</math> | |||
<center><math>{n\choose k_1,\ldots,k_r} | <center><math>{n\choose k_1,\ldots,k_r} | ||
={n\choose k_1}{n-k_1\choose k_2}{n-(k_1+k_2)\choose k_3} | ={n\choose k_1}{n-k_1\choose k_2}{n-(k_1+k_2)\choose k_3} | ||
\cdot\ldots\cdot{n-(k_1+\ldots+k_{r-1})\choose k_r} | \cdot\ldots\cdot{n-(k_1+\ldots+k_{r-1})\choose k_r}</math></center> | ||
</math></center> | |||
}} | }} | ||
{{dowod| | {{dowod||| | ||
Rozmieszczenie <math>n</math>-obiektów w <math>r</math> pudełkach po <math>k_i</math> w każdym, polega na: | Rozmieszczenie <math>n</math>-obiektów w <math>r</math> pudełkach po <math>k_i</math> w każdym, polega na: | ||
* wyborze <math>k_1</math> obiektów spośród wszystkich <math>n</math> | * wyborze <math>k_1</math> obiektów spośród wszystkich <math>n</math> i umieszczeniu ich w pierwszym pudełku - możemy to uczynić na <math>{n\choose k_1}</math> sposobów, | ||
i umieszczeniu ich w pierwszym pudełku | |||
* wyborze <math>k_2</math> obiektów spośród pozostałych <math>n-k_1</math> | * wyborze <math>k_2</math> obiektów spośród pozostałych <math>n-k_1</math> i umieszczeniu ich w drugim pudełku - możemy to uczynić na <math>{n-k_1\choose k_2}</math> sposobów, | ||
i umieszczeniu ich w drugim pudełku | |||
* wyborze <math>k_3</math> obiektów spośród pozostałych <math>n-(k_1+k_2)</math> | * wyborze <math>k_3</math> obiektów spośród pozostałych <math>n-(k_1+k_2)</math> | ||
i umieszczeniu ich w trzecim pudełku | i umieszczeniu ich w trzecim pudełku - możemy to uczynić na <math>{n-(k_1+k_2)\choose k_3}</math> sposobów, | ||
* ... | * ... | ||
* wyborze <math>k_r</math> obiektów spośród pozostałych <math>n-(k_1+\ldots+k_{r-1})=k_r</math> | * wyborze <math>k_r</math> obiektów spośród pozostałych <math>n-(k_1+\ldots+k_{r-1})=k_r</math> i umieszczeniu ich w ostatnim pudełku - możemy to uczynić na <math>{n-(k_1+\ldots+k_{r-1})\choose k_r}={k_r\choose k_r}=1</math> sposobów. | ||
i umieszczeniu ich w ostatnim pudełku | |||
Zatem wszystkich możliwych rozmieszczeń zgodnie z wymogami z definicji | Zatem wszystkich możliwych rozmieszczeń zgodnie z wymogami z definicji | ||
współczynnika multimianowego jest dokładnie | współczynnika multimianowego jest dokładnie <math>{n\choose k_1}{n-k_1\choose k_2}{n-(k_1+k_2)\choose k_3} \cdot\ldots\cdot{n-(k_1+\ldots+k_{r-1})\choose k_r}</math>.}} | ||
<math>{n\choose k_1}{n-k_1\choose k_2}{n-(k_1+k_2)\choose k_3} | |||
\cdot\ldots\cdot{n-(k_1+\ldots+k_{r-1})\choose k_r}</math>. | {{wniosek|5.20|wn 5.20| | ||
}} | Dla <math>n,k_1,\ldots,k_r\geqslant0</math> takich, że <math>k_1+\ldots+k_r=n</math> | ||
<center><math>{n\choose k_1,\ldots,k_r}=\frac{n!}{k_1!\cdot\ldots\cdot k_r!}</math></center> | |||
}} | }} | ||
{{dowod| | {{dowod||| | ||
<center><math>\ | |||
&= | <center><math>\begin{align}{n\choose k_1,\ldots,k_r} | ||
&= | &={n\choose k_1}{n-k_1\choose k_2}{n-(k_1+k_2)\choose k_3}\cdot\ldots\cdot{n-(k_1+\ldots+k_{r-1})\choose k_r}\\ | ||
&=\frac{n!}{(n-k_1)!k_1!}\cdot\frac{(n-k_1)!}{(n-(k_1+k_2))!k_2!} | |||
\cdot\ldots\cdot\frac{(n-(k_1+\ldots+k_{r-1}))!}{(n-(k_1+\ldots+k_r))!k_r!}\\ | \cdot\ldots\cdot\frac{(n-(k_1+\ldots+k_{r-1}))!}{(n-(k_1+\ldots+k_r))!k_r!}\\ | ||
&= | &=\frac{n!}{k_1!\cdot\ldots\cdot k_r!\cdot(n-(k_1+\ldots+k_r))!}\\ | ||
&= | &=\frac{n!}{k_1!\cdot\ldots\cdot k_r!}. | ||
\ | \end{align}</math></center> | ||
}} | }} | ||
{{przyklad| | {{przyklad||| | ||
Ile liczb możemy ułożyć zapisując w dowolnej kolejności <math>11</math> cyfr: <math>1,1,3,4,5,5,5,6,7,7,9</math>? | Ile liczb możemy ułożyć zapisując w dowolnej kolejności <math>11</math> cyfr: <math>1,1,3,4,5,5,5,6,7,7,9</math>? | ||
Zauważmy, że każda taka liczba | Zauważmy, że każda taka liczba powstaje przez wybór dwu pozycji dla cyfry <math>1</math>, jednej dla cyfry <math>3</math>, jednej dla cyfry <math>4</math>, trzech dla cyfry <math>5</math>, jednej dla cyfry <math>6</math>, dwu dla cyfry <math>7</math> i wreszcie jednej pozycji dla cyfry <math>9</math>. Zatem <math>11</math> pozycji to nasze obiekty, które rozmieszczamy w siedmiu pudełkach etykietowanych cyframi: <math>1,3,4,5,6,7,9</math>. Zatem z definicji współczynnika multimianowego mamy: | ||
powstaje przez wybór dwu pozycji dla cyfry <math>1</math>, | |||
jednej dla cyfry <math>3</math>, | |||
jednej dla cyfry <math>4</math>, | <center><math>{11\choose 2,1,1,3,1,2,1}=\frac{11!}{2!\cdot3!\cdot2!}=1663200</math></center> | ||
trzech dla cyfry <math>5</math>, | |||
jednej dla cyfry <math>6</math>, | |||
dwu dla cyfry <math>7</math> | |||
i wreszcie jednej pozycji dla cyfry <math>9</math>. | |||
Zatem <math>11</math> pozycji to nasze obiekty, | |||
które rozmieszczamy w siedmiu pudełkach etykietowanych cyframi: <math>1,3,4,5,6,7,9</math>. | |||
Zatem z definicji współczynnika multimianowego mamy: | |||
}} | }} | ||
{{przyklad| | {{przyklad||| | ||
Rozważmy raz jeszcze podróż w mieście o ulicach na planie siatki. Tym razem jednak... <math>3</math>-wymiarową wersję. Mamy więc do dyspozycji trójwymiarową, prostopadłościenną kratownicę <math>a\times b\times c</math>. | |||
Na ile sposobów można połączyć przeciwległe wierzchołki prostopadłoscianu | |||
najkrótszą możliwą łamaną Zauważmy, że każda najkrótsza możliwa łamana składa się z dokładnie <math>a+b+c</math> odcinków jednostkowych. Przy czym dokładnie <math>a</math> z nich jest poziomych, <math>b</math> pionowych i <math>c</math> idzie w głąb. Zatem najkrótszych łamanych jest tyle co rozmieszczeń <math>a+b+c</math> odcinków (obiekty) w <math>3</math> pudełkach: "poziomy", "pionowy", "w głąb" tak, by w było ich odpowiednio <math>a,b</math> i <math>c</math>. Z definicji współczynnika multimianowego mamy zatem: | |||
<center><math>{a+b+c\choose a,b,c}=\frac{(a+b+c)!}{a!b!c!}</math>,</center> | |||
łamanych. | łamanych. | ||
Kratka z rysunku o wymiarach <math>3\times4\times2</math> ma zatem: | Kratka z rysunku o wymiarach <math>3\times4\times2</math> ma zatem: | ||
<math>{9\choose3,4,2}=\frac{9!}{3!\cdot4!\cdot2!}=420</math> interesujących nas łamanych. | <math>{9\choose3,4,2}=\frac{9!}{3!\cdot4!\cdot2!}=420</math> interesujących nas łamanych. | ||
}} | }} | ||
| Linia 1041: | Linia 851: | ||
Współczynniki multimianowe także zachowują pewną regułę dodawania. | Współczynniki multimianowe także zachowują pewną regułę dodawania. | ||
{{obserwacja|21|obs 21| Dla <math>n>0</math>, całkowitych <math>k_1,\ldots,k_r</math> takich, że <math>k_1+\ldots+k_r=n</math> | {{obserwacja|5.21|obs 5.21| | ||
Dla <math>n>0</math>, całkowitych <math>k_1,\ldots,k_r</math> takich, że <math>k_1+\ldots+k_r=n</math> | |||
<center><math>{n\choose k_1}={n-1\choose k_1-1,k_2,\ldots,k_r}+{n-1\choose k_1,k_2-1,\ldots,k_r}+\ldots+{n-1\choose k_1,k_2,\ldots,k_r-1}</math></center> | |||
}} | }} | ||
{{dowod| | {{dowod||| | ||
Ponieważ <math>n>0</math>, możemy wybrać i ustalić ulubiony obiekt <math>x</math>. Możemy go umieścić w jednym z <math>r</math> pudełek. Jeśli jednak umieścimy go w pierwszym, to pozostałe <math>n-1</math> obiektów musimy rozłożyć do <math>r</math> pudeł zgodnie z warunkami wyjściowymi, ale do pierwszej szuflady mamy włożyć już <math>1</math> obiekt mniej (<math>k_1-1</math> a nie <math>k_1</math>). Rozłożenia tego możemy dokonać na <math>{n\choose k_1-1,k_2,\ldots,k_r}</math>. Analogicznie gdy <math>x</math> umieścimy w drugim pudle, to pozostałe przedmioty rozkładamy w pudłach odpowiednio po <math>k_1, k_2-1, k_3,\ldots,k_r</math>. Po przesumowaniu po numerach pudła, w którym jest <math>x</math> dostajemy nasz wzór. | |||
Ponieważ <math>n>0</math>, możemy wybrać i ustalić ulubiony obiekt <math>x</math>. | |||
Możemy go umieścić w jednym z <math>r</math> pudełek. | |||
Jeśli jednak umieścimy go w pierwszym, | |||
to pozostałe <math>n-1</math> obiektów musimy rozłożyć do <math>r</math> pudeł | |||
zgodnie z warunkami wyjściowymi, | |||
ale do pierwszej szuflady mamy włożyć już <math>1</math> obiekt mniej (<math>k_1-1</math> a nie <math>k_1</math>). | |||
Rozłożenia tego możemy dokonać na <math>{n\choose k_1-1,k_2,\ldots,k_r}</math>. | |||
Analogicznie gdy <math>x</math> umieścimy w drugim pudle, | |||
to pozostałe przedmioty rozkładamy w pudłach odpowiednio po <math>k_1, k_2-1, k_3,\ldots,k_r</math>. | |||
Po przesumowaniu po numerach pudła, w którym jest <math>x</math> dostajemy nasz wzór. | |||
}} | }} | ||
Jako ćwiczenie pozostawiamy dowód następującego uogólnienia wzoru dwumiennego: | Jako ćwiczenie pozostawiamy dowód następującego uogólnienia wzoru dwumiennego: | ||
{{obserwacja|22|obs 22| | {{obserwacja|5.22|obs 5.22| | ||
<center><math>(x_1+\ldots +x_r)^n | <center><math>(x_1+\ldots +x_r)^n | ||
= \sum_{k_1+\ldots+k_r=n} | = \sum_{k_1+\ldots+k_r=n} | ||
{n \choose k_1,\ldots,k_r} x_1^{k_1} x_2^{k_2}\ldots x_r^{k_r} | {n \choose k_1,\ldots,k_r} x_1^{k_1} x_2^{k_2}\ldots x_r^{k_r}</math></center> | ||
</math></center> | |||
}} | }} | ||
Aktualna wersja na dzień 22:30, 15 wrz 2023
Zliczanie podzbiorów raz jeszcze

Zobacz biografię
Wiemy już, że dowolny zbiór -elementowy ma dokładnie podzbiorów. Teraz zajmiemy się pytaniem ile taki zbiór ma podzbiorów o dokładnie elementach. Policzymy zatem liczność rodziny -elemetowych podzbiorów zbioru . Rodzinę tę oznaczać będziemy przez .
Współczynnik dwumianowy to liczba -elementowych podzbiorów zbioru -elementowego, tzn. . Wyrażenie czytamy po .
Prawdopodobnie jako pierwszy tej notacji użył Andreas von Ettingshausen w 1826. Jednak liczby te już wcześniej pojawiały się wielokrotnie, choćby w Trójkącie Pascala. Sama nazwa "współczynniki dwumianowe" bierze się stąd, że liczby te pojawiają się w rozwinięciu dwumianu . Zobaczymy to dokładnie w Twierdzeniu 5.7
Przykład
Aby policzyć wypiszmy wszystkie -elementowe podzbiory -elementowego zbioru . Sa to , , , , , ,
skąd .
Bezpośrednio z definicji liczb dostajemy:
Obserwacja 5.1
Dla zachodzi:
- ,
- , dla ,
- , dla ,
- , dla .
Dowód
Pierwszy punkt jest natychmiastową konsekwencją faktu, że dowolny zbiór -elementowy ma tylko jeden -elementowy podzbiór -podzbiór pusty i tylko jeden podzbiór -elementowy - cały zbiór.
Drugi punkt jest oczywisty, jako że zbiór -elementowy nie może mieć podzbiorów o elementach.
Dla dowodu trzeciego punktu, zauważmy jedynie, że podzbiorów jednoelementowych jest dokładnie tyle ile elementów w zbiorze.
Wreszcie dla dowodu ostatniego punktu załóżmy, że . Wtedy funkcja
jest bijekcją. A zatem istotnie .
Nasza następna obserwacja stanowi fundament dla rekurencyjnej procedury obliczania współczynników dwumianowych.
Obserwacja 5.2
Dla mamy:
Dowód
Podobnie jak przy budowaniu zależności rekurencyjnej przy zliczaniu wszystkich podzbiorów zbioru -elementowego załóżmy, że . Wtedy, po usunięciu ze zbioru elementu dostajemy -elementowy zbiór . Oczywiście wszystkie -elementowe podzbiory zbioru można podzielić na dwa typy:
- albo mają w sobie element ,
- albo go nie mają.
W drugim przypadku są to -elementowe podzbiory -elementowego zbioru . Jest więc ich dokładnie .
Każdy zaś podzbiór pierwszego typu, czyli takie, że jest jednoznacznie wyznaczony przez swoje pozostałe elementów, czyli dla pewnego . A zatem

Zobacz biografię
Trójkąt Pascala (nazwany na cześć Blaise'a Pascala, który napisał znakomitą rozprawę o współczynnikach dwumianowych) bazuje na własności i ustawia liczby w następujący sposób:
- wiersze trójkąta numerowane są kolejnymi liczbami naturalnymi
,
- w każdym wierszy trójkąta występuje dokładnie liczb.
Są to kolejno
| ... | ... | ... | ... | ... | ||||||
Przesunięcie w wierszach, pozwala wyliczyć jako sumę dwu liczb stojących bezpośrednio nad :
Przykład
Napisz program drukujący trójkąt Pascala, ale z liczbami modulo , tzn. w miejsce wstaw jedynie resztę lub z dzielenia liczby przez . Zaobserwuj na wydruku powstały fraktal. Wyjaśnij dlaczego tak się dzieje.
W trójkącie Pascala współczynniki o tym samym górnym indeksie, np.
tworzą wiersz; natomiast współczynniki o ustalonym dolnym indeksie, np.
tworzą przekątną.
Trójkat Pascala ma zera na obrzeżach, a jego wiersze są symetryczne względem pionowej osi przebiegającej przez środek trójkąta. Jest to konsekwencja Obserwacji 5.1. Współczynniki dwumianowe spełniają bardzo wiele ciekawych zależności. Wymienimy tylko te najważniejsze. Zaczniemy od wzoru w postaci zwartej.
Obserwacja 5.3
Dla dowolnych
Dowód
Podamy dwa dowody: kombinatoryczny i indukcyjny.
Dowód kombinatoryczny. Ustalmy pewien -elementowy zbiór , i wybierajmy po kolei różnych jego elementów, tzn. utwórzmy injekcję . Z wykładu o zliczaniu zbiorów i funkcji wiemy, ze takich injekcji jest . W wyniku takiego wyboru, dostajemy wszakże pewien uporządkowany ciąg elementów zbioru . Wiele takich ciągów wyznacza ten sam -elementowy podzbiór zbioru . Ciągi takie różnią sie jedynie kolejnością elementów, a zatem jest ich tyle ile permutacji zbioru -elemetowego, czyli . Zatem jest dokładnie
podzbiorów -elementowych zbioru -elementowego.
Dowód indukcyjny. Indukcję poprowadzimy względem górnego indeksu . Dla mamy tylko jeden interesujący nas współczynnik , i rzeczywiście . Załóżmy zatem, że wszystkie współczynniki w -tym wierszu spełniają wzór z tezy i rozważmy dla . Jeśli to . Załóżmy więc, że . Wtedy:
Przykład

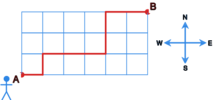
Przykład
Wyobraźmy sobie, że znajdujemy się w mieście zbudowanym na planie prostopadle przecinających się ulic. Powiedzmy, że znajdujemy się w punkcie i chcemy dojść do punktu , tak jak zaznaczono na rysunku.
Łatwo zauważyć, że jest wiele najkrótszych dróg prowadzących z do . Dla przykładu: możemy pójść razy na północ i potem cały czas na wschód, ale także możemy iść najpierw razy na na wschód i dopiero wtedy skręcić na północ.
Ile jest najkrótszych dróg z do ?
Zauważmy, że każda najkrótsza droga biegnie przez dokładnie skrzyżowań (licząc skrzyżowanie w punkcie i nie licząc skrzyżowania w punkcie ). Na każdym takim skrzyżowaniu musimy podjąć decyzję, czy pójść na wschód czy na północ, przy czym musimy iść dokładnie razy na północ i dokładnie razy na wschód.
Zatem liczba najkrótszych dróg z do to liczba wyborów spośród skrzyżowań, trzech, na których pójdziemy na północ, bądź na których pójdziemy na wschód. A zatem liczba ta wynosi .
W ogólności załóżmy, że mamy kratkę i chcemy narysować najkrótszą łamaną po krawędziach kratki łączącą lewy dolny wierzchołek z prawym górnym. Na ile sposobów możemy narysować taką łamaną?
Widzimy, że musimy narysować odcinków jednostkowych, z których dokładnie jest pionowych i dokładnie jest poziomych. Zatem jest
Przykład
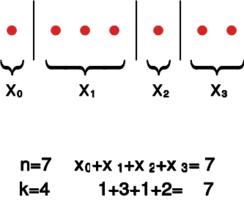
Ile rozwiązań ma równanie
gdzie są liczbami naturalnymi?
Użyjmy kratki rozważanej w poprzednim przykładzie do połączenia przeciwległych jej rogów. W kratce rozmiaru suma poziomych odcinków daje i jest dokładnie takich odcinków, po jednym na każdym poziomie. Jeśli długości tych odcinków oznaczymy odpowiednio przez , to każda taka droga (łamana) na kratce ustala pewne rozwiązanie naszego równania, i każde rozwiązanie równania wyznacza dokładnie jedna drogę (łamaną). Dla przykładu - animacja obok.
Zatem istnieje rozwiązań naszego równania.
W ogólności, równanie

Przykład
Ile rozwiązań ma równanie
gdzie są dodatnimi liczbami naturalnymi?
Zauważmy, że każde rozwiązanie tego równania z warunkami , można otrzymać z rozwiązania w liczbach naturalnych równania
poprzez podstawienie . Na podstawie poprzedniego przykładu poszukiwanych rozwiązań jest zatem .
Rozważmy obiektów (np. punktów) ustawionych w ciągu jeden przy drugim.
Separatorem nazywamy pionową kreskę położoną pomiędzy dwoma punktami. Zatem pomiędzy punktami mamy możliwych pozycji dla separatora. Zauważmy, że każde rozwiązanie naszego równania jednoznacznie odpowiada jednemu z możliwych rozmieszczeń separatorów wśród pozycji. Liczba punktów do pierwszego separatora to wartość , liczba punktów pomiędzy pierwszym a drugim separatorem to , itd., liczba punktów za ostatnim -szym separatorem to . Dla przykładu:
Na odwrót każde rozwiązanie naszego równania wyznacza jednoznacznie rozłożenie separatorów: pierwszy kładziemy po punktach, drugi po , itd.
Zatem liczba rozwiązań naszego równania to liczba rozmieszczeń separatorów na pozycjach, czyli .
Przykład
Rozważmy znów kratkę, tym razem kwadratową, wielkości , i policzmy na ile sposobów można w jej wnętrzu narysować prostokąt tak, aby wszystkie jego boki były równoległe do krawędzi kratki?
Zauważmy, że każdy taki prostokąt jest jednoznacznie wyznaczony przez dwie linie poziome (spośród ) oraz dwie linie pionowe (znów spośród ). Rzeczywiście, dowolny prostokąt wyznacza dwie linie poziome i dwie pionowe (te przylegające do jego boków). I na odwrót dowolny wybór linii pozwoli nam nakreślić jednoznacznie prostokąt w kratce.
Poziome linie możemy wybrać na sposobów i pionowe linie także na sposobów. Zatem prostokąt w kratce możemy narysować na dokładnie
Przechodzimy teraz do kolejnych własności współczynników dwumianowych.
Rozpoczniemy od sumowania liczb na przekątnej trójkąta Pascala. Przekątna taka jest oczywiście nieskończona - sumujemy więc tylko jej początkowy fragment.
Obserwacja 5.4 [reguła sumowania po górnym indeksie]
Dla mamy
Dowód
Ustalmy -elementowy zbiór Rozważając jego -elementowe podzbiory zwracamy uwagę na element tego podzbioru, który ma największy indeks. Oczywiście jest , gdyż nie ma -elementowych podzbiorów. Równie łatwo jest zauważyć, że jest dokładnie jeden podzbiór -elementowy w którym jest elementem o najwyższym indeksie, jest to zbiór .
Policzmy teraz podzbiory zbioru , w których jest elementem o największym indeksie, przy czym . Oprócz elementu każdy taki zbiór ma dokładnie elementów wybranych z -elementowego zbioru . Wyboru tych elementów można dokonać na sposobów. Zatem podzbiorów zbioru , w których jest elementem o największym indeksie jest dokładnie . Sumując po wszystkich możliwych , czyli otrzymujemy:
Podobnie możemy sumować liczby położone na linii "prostopadłej" do przekątnych Trójkąta Pascala, czyli liczby postaci .
Obserwacja 5.5 [reguła sumowania równoległego]
Dla mamy:
Dowód
Tożsamość tę udowodnimy wykorzystując dwukrotnie {regułę symetrii} oraz {regułę sumowania po górnym indeksie}:
Obserwacja 5.6 [tożsamość Cauchy'ego, splot Vandermonde'a]
Dla liczb naturalnych mamy:
Dowód
Policzymy liczbę wszystkich wyborów osób z grona mężczyzn i kobiet, czyli liczbę na jeszcze jeden sposób. Wybierając osób wybieramy najpierw mężczyzn na sposobów, a potem kobiet na sposobów. Pozostaje teraz zsumować po wszystkich możliwych wartościach parametru .
Dwumiany
Poniższe Twierdzenie o Dwumianie wyjaśnia pochodzenie tajemniczej nazwy "współczynniki dwumianowe". Twierdzenie to często przypisuje się Pascalowi. Tymczasem było ono już znane indyjskiemu matematykowi Pingala w III wieku p.n.e..
Obserwacja 5.7 [Twierdzenie o Dwumianie]
Dla i
Dowód
Przedstawmy najpierw potęgę w rozwiniętej formie iloczynu:
Korzystając z rozdzielności mnożenia, wyrażenie to staje się sumą składników.
Każdy taki składnik to iloczyn pewnej liczby -ów i pewnej liczby -ów, przy czym łącznie iloczyn taki ma czynników.
A zatem każdy składnik ma postać . Powstaje on poprzez wybór (spośród ) czynników w iloczynie , z których do składnika postaci wchodzi (a tym samym składników, z których wchodzi ). Tym samym składników postaci jest tyle, ile -elementowych podzbiorów zbioru -elementowego, czyli pojawi się w sumie -krotnie.
Twierdzenie o Dwumianie można też udowodnić za pomocą indukcji, co pozostawiamy jako ćwiczenie.
Przykład
Wniosek 5.8
Dla dowolnego
- ,
- ,
- . (Uwaga: )
Dowód
Wszystkie punkty wynikają trywialnie z Twierdzenia o Dwumianie. (Pierwszy jest oczywisty. Dla dwu pozostałych zauważmy jedynie, że , .) Jednak drugi i trzeci punkt mają ładną interpretację kombinatoryczną.
Istotnie, liczba podzbiorów zbiorów elementowego to . Z drugiej strony licząc te podzbiory, możemy kolejno zliczać podzbiory -elementowe - jest ich .
Nieco dłuższy jest argument kombinatoryczny dla naprzemiennej sumy . Dla jest to oczywiste. Natomiast dla jest to równoważne stwierdzeniu, że dla -elementowego zbioru
- liczba podzbiorów zbioru o parzystej liczbie elementów jest równa liczbie podzbiorów o nieparzystej liczbie elementów.
Załóżmy najpierw, że jest nieparzyste. Wtedy każdy podzbiór zbioru o parzystej liczbie elementów ma dopełnienie o nieparzystej liczbie elementów, a każdy podzbiór zbioru o nieparzystej liczbie elementów ma dopełnienie o parzystej liczbie elementów. Ta bijektywna odpowiedniość dowodzi, że w istocie jest ich tyle samo.
Załóżmy zatem, że jest parzyste i ustalmy . Zdefiniujmy funkcję , kładąc
Zauważmy, że jest permutacją . Rzeczywiście, dla różnych podzbiorów mamy:
- jeśli i to
- jeśli i to
- jeśli i to i , zatem .
To dowodzi, że jest injekcją. Dla dowodu surjektywności weźmy dowolne . Jeśli to , jeśli zaś to . Zatem jest permutacją zbioru . Co więcej łatwo zauważyć, że dla o parzystej (nieparzystej) liczbie elementów ma nieparzystą (parzystą) liczbę elementów. To dowodzi, że dla parzystego podzbiorów o parzystej liczbie elementów jest tyle samo co podzbiorów o nieparzystej liczbie elementów.
Uogólniony współczynnik dwumianowy
Wniosek 5.8 pozwala na ustalenie wartość sumy całego wiersza w Trójkącie Pascala i wartość naprzemiennej sumy całego wiersza Trójkąta Pascala. W praktyce często pojawia się konieczność (naprzemiennego) sumowania tylko pewnego fragmentu takiego wiersza.Do tego pomocne mogłyby być sumy postaci:
dla .
Niestety nie jest znana żadna zwarta postać . Zaskakująca jest natomiast zwarta postać modyfikacji tej sumy polegającej na wymnożeniu każdego składnika przez jego odległość od środka trójkąta. Indukcyjny dowód tak powstałej zależności pozostawiamy jako ćwiczenie.
Obserwacja 5.9
Dla
Natomiast naprzemienna częściowa suma wiersza Trójkąta Pascala ma postać zwartą. Wyprowadzenie takiej postaci odwołuje się do uogólnienia współczynnika dwumianowego na dowolne rzeczywiste indeksy górne, i dowolne całkowite indeksy dolne. Wykorzystuje to poznane już przy okazji rachunku róznicowego pojęcie dolnej silni .
Uogólniony współczynnik dwumianowy dla i to:
Zauważmy, że w istocie dla wartości pozostają niezmienione. Oczywiście, dla , interpretacja jako -elementowych liczby podzbiorów zbioru -elementowego pozostaje w mocy. Nie jest natomiast znana sensowna kombinatoryczna interpretacja uogólnionego współczynnika dwumianowego dla pozostałych rzeczywistych wartosci . Odnotujmy tylko, że jest wielomianem -tego stopnia zmiennej . Sporo własności współczynnika dwumianowego przenosi się na wersję uogólnioną. Poniższe zostawiamy bez dowodu jako ćwiczenie.
Obserwacja 5.10
Dla i mamy
- ,
- ,
- ,
- , dla .
Przykład
Z uwagi na to, że w indeksie dolnym mogą występować jedynie liczby całkowite, nie ma sensu reguła symetrii . Ale nawet dla całkowitych wartości zawodzi:
- jeśli , to ,
- jeśli , to .
Zachowana jest natomiast reguła dodawania.
Obserwacja 5.11
Dla i
Dowód
Dla ujemnych wartości wszystkie współczynniki równe są i tożsamość trywialnie zachodzi. Niech teraz i . Oczywiście różnica
jest wielomianem co najwyżej . Może więc, o ile nie jest wielomianem stale równym zero, mieć co najwyżej miejsc zerowych.
Z drugiej strony wiemy już, że ta różnica zeruje się dla wszystkich liczb naturalnych , więc musi być zawsze równa .
Uogólniona reguła dodawania z Obserwacji 5.11 pozwala rozszerzyć Trójkąt Pascala na współczynniki o ujemnych wartościach górnego indeksu.
Kolejne wartości "ujemnej części" możemy wyliczać w następującej kolejności:
Przyjrzyjmy się wartościom dla ustalonego i całkowitych wartości . Zauważalny jest pewien rodzaj symetrii między tymi wartościami. W istocie zachodzi on dla wszystkich rzeczywistych wartości górnego indeksu.
Obserwacja 5.12 [reguła negacji górnego indeksu]
Dla , :
Dowód
Znaną nam już z Obserwacji 5.5 regułę równoległego sumowania możemy uogólnić za pomocą argumentu podobnego do użytego w dowodzie Obserwacji 5.11.
Obserwacja 5.13
Dla ,
Zauważmy, że rozważana suma jest tylko pozornie nieskończona, gdyż dla wszystkich ujemnych wartości odpowiednie składniki zerują się. W dalszych ciągu przyjmiemy będziemy również rozważać podobne sumy "nieskończone", ale przy założeniu, że tylko skończenie wiele składników jest niezerowych.
Wyposażeni w regułę negacji górnego indeksu wracamy teraz my do naprzemiennej, cześciowej sumy wierszy w Trójkącie Pascala, czyli do .
Obserwacja 5.14
Dla ,
Dowód
Przedstawimy teraz tożsamość, której później użyjemy do zliczenia pewnych, szczególnych permutacji. Zaczniemy od pomocniczej obserwacji.
Obserwacja 5.15 [przestawienie trójmianowe]
Dla ,
Dowód
Zauważmy, że dla obie strony równości się zerują. Także dla teza jest trywialna. Zatem możemy założyć, że . Wtedy:
Obserwacja 5.16 [reguła odwracania]
Dla funkcji
wtedy i tylko wtedy, gdy
Dowód
Z uwagi na symetrię założeń wystarczy udowodnić tylko jedne implikację. Zakładamy zatem, że by dostać:
gdzie druga równość wynika ze zmiana kolejności sumowania, trzecia z przestawienia trójmianowego, a ostatnia przez podstawienie .
Z Wniosku 5.8 wiemy, że suma jest niezerowa (i wynosi ) tylko dla . Zatem kontynuując:
Permutacje bez punktów stałych
Nieporządek na zbiorze to permutacja taka, że dla dowolnego , czyli permutacja "bez punktów stałych".
Podsilnia liczby , w skrócie , to liczba nieporządków zbioru -elementowego. Przyjmujemy, że , jako ze jedyna permutacja zbioru pustego - funkcja pusta - w oczywisty sposób nie ma punktów stałych.
Przykład
Zbiór ma permutacje, ale tylko z nich to nieporządki. Oto ich lista:
Obserwacja 5.17
.
Dowód
Zauważmy najpierw, że liczba permutacji zbioru -elementowego takich, że dla dokładnie elementów , wynosi . Stąd:
Stosując teraz regułę odwracania, dostajemy:
Współczynniki multimianowe
Współczynniki dwumianowe pojawiały się przy rozwinięciu dwumianu . Odpowiadały one wyborom dwuwartościowym. Podobnie rozważając trójmian , czy ogólnie , pojawią się współczynniki odpowiadające wyborom odpowiedni trój- i -wartościowym. Wybieranie podzbioru -elementowego ze zbioru -elementowego to podział zbioru na dwie części o odpowiednio i elementach. Naturalnym uogólnieniem, będzie podział zbioru -elementowego na części o odpowiednio elementach, przy czym oczywiście .
Współczynnik multimianowy , dla , oraz całkowitych takich, że , to liczba sposobów umieszczenia obiektów w pudełkach z odpowiednio obiektami w pierwszym pudełku, w drugim, itd., oraz w -tym. Jeśli którakolwiek z liczb jest ujemna to współczynnik jest równy . Zauważmy, że z uwagi na symetrię dolnych indeksów, ich kolejność nie jest istotna. Oczywiście to w nowej notacji .
Następna obserwacja wynika wprost z definicji współczynników multimianowych.
Obserwacja 5.18
Dla , takich, że zachodzi:
- ,
- ,
- ,
- ,
- , dla dowolnej permutacji zbioru .
Następna obserwacja wymaga krótkiego uzasadnienia.
Obserwacja 5.19
Dla takich, że
Dowód
Rozmieszczenie -obiektów w pudełkach po w każdym, polega na:
- wyborze obiektów spośród wszystkich i umieszczeniu ich w pierwszym pudełku - możemy to uczynić na sposobów,
- wyborze obiektów spośród pozostałych i umieszczeniu ich w drugim pudełku - możemy to uczynić na sposobów,
- wyborze obiektów spośród pozostałych
i umieszczeniu ich w trzecim pudełku - możemy to uczynić na sposobów,
- ...
- wyborze obiektów spośród pozostałych i umieszczeniu ich w ostatnim pudełku - możemy to uczynić na sposobów.
Zatem wszystkich możliwych rozmieszczeń zgodnie z wymogami z definicji
współczynnika multimianowego jest dokładnie .Wniosek 5.20
Dla takich, że
Dowód
Przykład
Ile liczb możemy ułożyć zapisując w dowolnej kolejności cyfr: ?
Zauważmy, że każda taka liczba powstaje przez wybór dwu pozycji dla cyfry , jednej dla cyfry , jednej dla cyfry , trzech dla cyfry , jednej dla cyfry , dwu dla cyfry i wreszcie jednej pozycji dla cyfry . Zatem pozycji to nasze obiekty, które rozmieszczamy w siedmiu pudełkach etykietowanych cyframi: . Zatem z definicji współczynnika multimianowego mamy:
Przykład
Rozważmy raz jeszcze podróż w mieście o ulicach na planie siatki. Tym razem jednak... -wymiarową wersję. Mamy więc do dyspozycji trójwymiarową, prostopadłościenną kratownicę . Na ile sposobów można połączyć przeciwległe wierzchołki prostopadłoscianu najkrótszą możliwą łamaną Zauważmy, że każda najkrótsza możliwa łamana składa się z dokładnie odcinków jednostkowych. Przy czym dokładnie z nich jest poziomych, pionowych i idzie w głąb. Zatem najkrótszych łamanych jest tyle co rozmieszczeń odcinków (obiekty) w pudełkach: "poziomy", "pionowy", "w głąb" tak, by w było ich odpowiednio i . Z definicji współczynnika multimianowego mamy zatem:
łamanych.
Kratka z rysunku o wymiarach ma zatem: interesujących nas łamanych.
Współczynniki multimianowe także zachowują pewną regułę dodawania.
Obserwacja 5.21
Dla , całkowitych takich, że
Dowód
Ponieważ , możemy wybrać i ustalić ulubiony obiekt . Możemy go umieścić w jednym z pudełek. Jeśli jednak umieścimy go w pierwszym, to pozostałe obiektów musimy rozłożyć do pudeł zgodnie z warunkami wyjściowymi, ale do pierwszej szuflady mamy włożyć już obiekt mniej ( a nie ). Rozłożenia tego możemy dokonać na . Analogicznie gdy umieścimy w drugim pudle, to pozostałe przedmioty rozkładamy w pudłach odpowiednio po . Po przesumowaniu po numerach pudła, w którym jest dostajemy nasz wzór.
Jako ćwiczenie pozostawiamy dowód następującego uogólnienia wzoru dwumiennego:
Obserwacja 5.22