Matematyka dyskretna 1/Wykład 14: Grafy III

Grafy planarne

Load video

Local File

Local File might collect personal data.

Continue Dismiss

Graf nieplanarny (a) oraz graf planarny (b) wraz z jego prezentacją w postaci grafu płaskiego (c)

Grafy k33

Grafy k332

Graf płaski to para: $\bar{\mathbf{G}}=(\bar{V},\bar{E})$, gdzie

• $\bar{V}$ jest jakimś zbiorem punktów płaszczyzny ${\mathbb{ℝ}}^2$,
• $\bar{E}$ jest zbiorem nie przecinających się odcinków lub łuków w $R^2$ o końcach w zbiorze $\bar{V}$.

Graf planarny to graf, który jest prezentowalny jako graf płaski.

Obserwacja 14.1

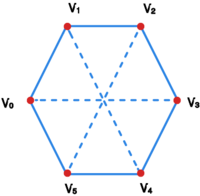
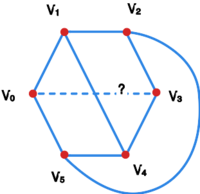
Grafy ${{𝒦}}_5$ i ${{𝒦}}_{3,3}$ nie są planarne.

Dowód

Graf ${{𝒦}}_{3,3}$ ma sześcio-elementowy cykl Hamiltona $H$. Musi on być narysowany w dowolnej płaskiej prezentacji. Przykładowe umiejscowienie tego cyklu prezentuje rysunekGrafy k33.

Spośród krawędzi $v_1{v}_4$ i $v_2{v}_5$ jedna musi leżeć wewnątrz cyklu a druga musi leżeć na zewnątrz. W konsekwencji nie da się narysować krawędzi $v_3{v}_0$ nie przecinając krawędzi $v_1{v}_4$ lub $v_2{v}_5$.

Dowód dla ${{𝒦}}_5$ jest analogiczny, rozpoczynając od pięcio-elementowego cyklu Hamiltona.

Z Obserwacji 14.1 natychmiast wynika, że żaden graf zawierający ${{𝒦}}_5$ lub ${{𝒦}}_{3,3}$ nie jest planarny. Ale również graf powstały np. z ${{𝒦}}_5$ poprzez umieszczenie na jednej krawędzi dodatkowego wierzchołka nie jest planarny mimo, że nie zawiera podgrafu ${{𝒦}}_5$ ani ${{𝒦}}_{3,3}$. Dla scharakteryzowania grafów planarnych potrzebne nam będzie następujące pojęcie homeomorficzności grafów.

Graf ${\mathbf{𝐆}}_1$ jest homeomorficzny z grafem ${\mathbf{𝐆}}_2$, jeśli jeden otrzymamy z drugiego poprzez wykonanie skończenie wielu poniższych operacji:

• Dodawanie wierzchołków stopnia dwa na krawędzi.
  Jeśli $uw\in \mathsf{E}\left({\mathbf{𝐆}}_1\right)$ oraz $x\in ̸\mathsf{V}\left({\mathbf{𝐆}}_1\right)$, to operacja ta zastępuje graf $(\mathsf{V}\left({\mathbf{𝐆}}_1\right),\mathsf{E}\left({\mathbf{𝐆}}_1\right))$ grafem $(\mathsf{V}\left({\mathbf{𝐆}}_1\right)\cup \left\{x\right\},\mathsf{E}\left({\mathbf{𝐆}}_1\right)\cup \{ux,xw\}-\left\{uw\right\})$.
• Usuwanie wierzchołków stopnia dwa.
  Jeśli $x\in \mathsf{V}\left({\mathbf{𝐆}}_1\right)$ ma jedynie dwóch sąsiadów $u,w$, to operacja ta zastępuje graf $(\mathsf{V}\left({\mathbf{𝐆}}_1\right),\mathsf{E}\left({\mathbf{𝐆}}_1\right))$ grafem $(\mathsf{V}\left({\mathbf{𝐆}}_1\right)-\left\{x\right\},\mathsf{E}\left({\mathbf{𝐆}}_1\right)\cup \left\{uw\right\}-\{ux,xw\})$.

Grafy homeomorficzne

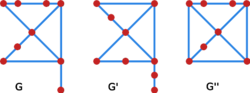
Przykład

Grafy $\mathbf{𝐆},{\mathbf{𝐆}}^{\prime }$ przedstawione na rysunku Grafy homeomorficzne są ze sobą homeomorficzne, zaś ${\mathbf{𝐆}}^{″}$ nie jest homeomorficzny ani z $\mathbf{𝐆}$ ani z ${\mathbf{𝐆}}^{\prime }$.

Następne twierdzenie podaje prostą charakteryzację grafów planarnych. Niestety dowód tego twierdzenia nie jest prosty i go pominiemy.

Twierdzenie 14.2 [Kuratowski 1930]

Graf jest planarny wtedy i tylko wtedy, gdy żaden jego podgraf nie jest homeomorficzny z ${{𝒦}}_5$ ani z ${{𝒦}}_{3,3}$.

Kolejne charakterystyka grafów planarnych odwołuje się do znanego nam już pojęcia sciągalności, lub grafu ilorazowego. Przypomnijmy, że

• iloraz grafu $\mathbf{𝐆}$ przez relację równoważności $\theta \subseteq V\times V$ na zbiorze jego wierzchołków to graf postaci

$\mathbf{𝐆}/\theta =(V/\theta ,\{\{v/\theta ,w/\theta \}:\{v,w\}\in E\})$

• ściągnięcie zbioru wierzchołków $X\subseteq V$ w grafie $\mathbf{𝐆}$ to szczególny przypadek ilorazu $\mathbf{𝐆}/\theta$, w którym klasy równoważności wszystkich wierzchołków spoza $X$ są jednoelementowe, a $X$ stanowi dodatkową klasę, tzn. $V/\theta =\{\left\{v\right\}:v\in V-X\}\cup \left\{X\right\}$. W ten sposób zbiór $X$ został ściągnięty do punktu, którego sąsiadami są sąsiedzi jakiegokolwiek wierzchołka z $X$. Z drugiej strony, jeśli $\theta \subseteq V\times V$ jest relacją równoważności o klasach $X_1,\dots ,X_k$, to ściągając w grafie $\mathbf{𝐆}$ kolejno zbiory $X_1,\dots ,X_k$ otrzymamy graf ilorazowy $\mathbf{𝐆}/\theta$.

Dowód charakteryzacji grafów planarnych w terminach ściągalności również pomijamy. Grafy sciagalne k33

<flashwrap>file=Grafy sciagalne k33.swf|size=small</flashwrap>

<div.thumbcaption>Graf posiadający podgraf ściągalny do ${{𝒦}}_{3,3}$

Graf posiadający cztery ściany: $f_0,f_1,f_2,f_3$

Twierdzenie 14.3

Graf jest planarny wtedy i tylko wtedy, gdy nie zawiera podgrafu ściągalnego do ${{𝒦}}_5$ lub ${{𝒦}}_{3,3}$.

Przykład

W grafie przedstawionym na rysunku Grafy ściagalne k33 ściągnięcie zbiorów wierzchołków otoczonych przerywaną linią prowadzi do grafu zawierającego ${{𝒦}}_{3,3}$. A więc, na mocy Twierdzenia 14.3, graf ten nie jest planarny.

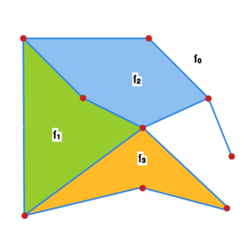
W grafach płaskich poza wierzchołkami oraz krawędziami można rozważać również ściany, czyli obszary płaszczyzny otoczone krawędziami.

Ściana w grafie płaskim $\mathbf{𝐆}$ to spójny obszar płaszczyzny po usunięciu linii reprezentujących krawędzie, tzn. $R^2-\bigcup \mathsf{E}\left(\mathbf{𝐆}\right)$. Innym słowy ściana to zbiór punktów płaszczyzny, które da się połączyć krzywą nieprzecinającą żadnej krawędzi.

Ściana $f_0$ w grafie z rysunku Graf o czterech ścianach jest ścianą nieograniczoną, która nazywana jest też ścianą nieskończoną. Nie tylko ten graf, ale wszystkie grafy płaskie mają dokładnie jedną ścianę nieskończoną. Zauważmy, że las jest grafem planarnym, ale w żadnej reprezentacji płaskiej nie posiada ścian ograniczonych. Tak więc posiada w ogóle tylko jedną ścianę. Tym samym, następne twierdzenie jest uogólnieniem związku $\left|E\right|=\left|V\right|-k$ między liczbą wierzchołków, krawędzi i drzew (tzn. spójnych składowych) w lesie.

Twierdzenie 14.4 [Euler 1750]

W grafie płaskim $\mathbf{𝐆}=(V,E)$ o $f$ ścianach i $k\ge 1$ składowych spójnych zachodzi

$\left|V\right|-\left|E\right|+f=k+1$

Dowód

Dowód poprowadzimy indukcją ze względu na liczbę krawędzi. Jeżeli graf $\mathbf{𝐆}$ jest pusty to $\left|E\right|=0,k=\left|V\right|,f=1$, które to wartości spełniają podaną równość. Załóżmy, że $\left|E\right|>1$. Wybierzmy dowolną krawędź $uv\in E$. Jeżeli $uv$ nie leży na żadnym cyklu grafu $\mathbf{𝐆}$, to usunięcie $uv$ zwiększy o $1$ liczbę składowych ale nie zmieni liczby ścian. Tak więc, na mocy założenia indukcyjnego, $\left|V\right|-(\left|E\right|-1)+f=(k+1)+1$, co daje żądaną równość. Załóżmy więc, że $uv$ leży na jakimś cyklu $C$. Tym samym $uv$ jest granicą pomiędzy dwoma różnymi ścianami, jako że dowolna krzywa przechodząca z jednej strony na drugą stronę granicy wyznaczonej przez krawędź $uv$ musi przecinać jakąś krawędź z cyklu $C$. Tak więc usunięcie krawędzi $uv$ zmniejszy liczbę ścian o jeden. Ale teraz usunięcie krawędzi $uv$ nie zmienia liczby składowych. Założenie indukcyjne daje nam więc $\left|V\right|-(\left|E\right|-1)+(f-1)=k+1$, czyli żądaną równość dla grafu $\mathbf{𝐆}$.

Uwaga

Ważną konsekwencją Twierdzenia 14.4 jest to, że liczba ścian zależy jedynie od liczby wierzchołków, krawędzi, oraz spójnych składowych. Tak więc w każdej reprezentacji płaskiej musi być taka sama.

Uzasadnienie dwu kolejnych wniosków z Twierdzenia 14.4 pozostawiamy jako ćwiczenie.

Wniosek 14.5

Jeśli $\mathbf{𝐆}=(V,E)$ jest spójnym grafem planarnym o co najmniej $3$ wierzchołkach, to

$\left|E\right|\le 3\left|V\right|-6$

Wniosek 14.6

Spójny graf planarny o $\left|V\right|\ge 1$ posiada wierzchołek o stopniu nie większym niż $5$.

Graf (w kolorze czerwono-niebieskim) oraz graf do niego dualny geometrycznie (w kolorze żółto-szarym)

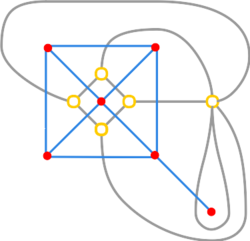
Graf dualny geometrycznie do grafu płaskiego $\mathbf{𝐆}=(V,E)$ to graf płaski ${\mathbf{𝐆}}^{*}=(V^{*},E^{*})$ skonstruowany w następujący sposób:

• Z każdej ściany grafu $\mathbf{𝐆}$ wybieramy po jednym punkcie. Tak wybrane punkty tworzą zbiór wierzchołków $V^{*}$.
• Jeśli krawędź po jednej stronie sąsiadowała ze ścianą $f_1$, a po drugiej z $f_2$ to w grafie ${\mathbf{𝐆}}^{*}$ odpowiadające ścianom $f_1,f_2$ wierzchołki $v_1^{*},v_2^{*}$ łączymy krawędzią $v_1^{*}{v}_2^{*}$. Tak wybrane krawędzie tworzą zbiór $E^{*}$.

Twierdzenie 14.7

Jeśli $\mathbf{𝐆}$ jest spójnym grafem płaskim, to ${\mathbf{𝐆}}^{**}$ jest izomorficzny z $\mathbf{𝐆}$.

Dowód

Każda ściana grafu ${\mathbf{𝐆}}^{*}$ reprezentowana jest jednym wierzchołkiem ${\mathbf{𝐆}}^{**}$. Z drugiej strony, w każdej ścianie grafu ${\mathbf{𝐆}}^{*}$ znajduje się dokładnie jeden wierzchołek grafu $\mathbf{𝐆}$. Ponadto, jeśli wierzchołki $v_1,v_2$ grafu $\mathbf{𝐆}$ są sąsiednie, to ściany $f_1^{*},f_2^{*}$ grafu ${\mathbf{𝐆}}^{*}$ zawierające odpowiednio $v_1$ i $v_2$ graniczą ze sobą. To kolei oznacza, że wierzchołki $v_1^{**},v_2^{**}$ grafu ${\mathbf{𝐆}}^{**}$ odpowiadające ścianom $f_1^{*}$ oraz $f_2^{*}$ są sąsiednie. Oczywiście, przy przejściu z $\mathbf{𝐆}$ do ${\mathbf{𝐆}}^{*}$ i potem do ${\mathbf{𝐆}}^{**}$ wierzchołki $v_1$ i $v_2$ przechodzą w $v_1^{**},v_2^{**}$. Analogicznie jeżeli $v_1^{**}$ jest połączony krawędzią z $v_2^{**}$ w ${\mathbf{𝐆}}^{**}$, to i również $v_1$ z $v_2$ w $\mathbf{𝐆}$.

Twierdzenie 14.8

Niech ${\mathbf{𝐆}}^{*}$ będzie grafem geometrycznie dualnym do grafu płaskiego $\mathbf{𝐆}$. Wtedy podzbiór $C$ krawędzi grafu $\mathbf{𝐆}$ jest cyklem w grafie $\mathbf{𝐆}$ wtedy i tylko wtedy, gdy zbiór krawędzi dualnych do krawędzi zbioru $C$ jest rozcięciem grafu ${\mathbf{𝐆}}^{*}$.

Grafy cykl rozC

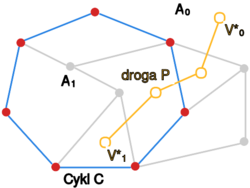
Dowód

Niech $C$ będzie cyklem w grafie $\mathbf{𝐆}$. W grafie płaskim cykl dzieli płaszczyznę ${\mathbb{ℝ}}^2$ na dwie spójne części $A_1$ oraz $A_0$, przy czym załóżmy, że $A_1$ jest ograniczona przez $C$, a $A_0$ jest nieograniczona. Niech $f_1$ będzie dowolną ścianą we wnętrzu $A_1$, zaś $f_0$ ścianą nieskończoną, czyli zawartą w $A_0$ a $v_1^{*},v_0^{*}$ niech będą odpowiadającymi tym ścianom punktami grafu dualnego ${\mathbf{𝐆}}^{*}$. Tak więc, $v_1^{*}\in A_1$, a $v_0^{*}\in A_0$. A zatem dowolnie wybrana droga $P$ z $v_1^{*}$ do $v_0^{*}$ musi przeciąć cykl $C$ co najmniej raz. Przecinające się krawędzie, jedna z drogi $P$ i druga z cyklu $C$, są wzajemnie dualne (przy przejściu z $\mathbf{𝐆}$ do ${\mathbf{𝐆}}^{*}$ i z powrotem do ${\mathbf{𝐆}}^{**}\approx \mathbf{𝐆}$). Tak więc, zbiór $C^{*}$ krawędzi dualnych do krawędzi z cyklu $C$ tworzy zbiór rozspajający wierzchołki $v_1^{*},v_0^{*}$.

Pokażemy, że zbiór $C^{*}$ jest rozcięciem, czyli minimalnym zbiorem rozspajającym. Zmniejszenie $C^{*}$ powstaje oczywiście poprzez zmniejszenie zbioru $C$. Usunięcie jednakże krawędzi $e$ z $C$, powoduje połączenie obszaru $A_1$ z obszarem $A_0$. Pozwala to tworzyć krzywe łączące dowolne dwa punkty $A_0\cup A_1$ i nie przecinające krawędzi ze zbioru $C-\left\{e\right\}$. W konsekwencji pozwala to na tworzenie ścieżek między dowolnymi wierzchołkami grafu ${\mathbf{𝐆}}^{*}$ omijając krawędzie z $C-\left\{e\right\}$.

Dowód implikacji w drugą stronę jest analogiczny.

Kolorowanie grafów

W tej części wykładu zajmiemy się problemami związanymi z kolorowaniem grafów. Intuicyjnie kolorowanie to przypisanie wierzchołkom grafu kolorów w taki sposób, by każde dwa sąsiednie wierzchołki miały różne kolory.

Kolorowanie grafu $\mathbf{𝐆}=(V,E)$ to funkcja $c:V⟶\mathbb{\mathbb{N}}$ taka, że $c(v)\ne c(w)$ ilekroć $vw$ jest krawędzią grafu $\mathbf{𝐆}$.

Kolorowanie grafu $\mathbf{𝐆}$ na $k$ kolorów wyznacza rozbicie zbioru $V$ na sumę rozłączną $V=V_0\cup V_1\cup \dots \cup V_{k-1}$ jednobarwnych zbiorów $V_i$, przy czym każdy graf indukowany postaci $\mathbf{𝐆}{|}_{V_i}$ jest antykliką. Na odwrót, rozbicie $V=V_0\cup V_1\cup \dots \cup V_{k-1}$ pozwala na pokolorowanie grafu $\mathbf{𝐆}$ na $k$ kolorów.

Kolorowanie grafu nieoptymalne (a), optymalne (b) oraz niepoprawne (c)

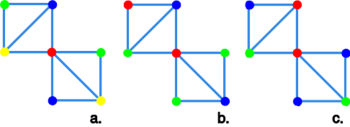
Graf $k$-kolorowalny ($k$-barwny) to graf dający się pokolorować $k$ barwami.

Liczba chromatyczna grafu, $\chi \left(\mathbf{𝐆}\right)$, to najmniejsza liczba barw, którymi można pokolorować graf $\mathbf{𝐆}$.

Optymalne kolorowanie grafu $\mathbf{𝐆}$ to kolorowanie używające dokładnie $\chi \left(\mathbf{𝐆}\right)$ kolorów.

Twierdzenie 14.9

Graf, którego wszystkie wierzchołki mają stopień nie większy niż $k$ jest $(k+1)$-kolorowalny.

Dowód

Dowód poprowadzimy indukcyjnie ze względu na liczbę wierzchołków w grafie $\mathbf{𝐆}=(V,E)$. Jeśli graf ma jeden wierzchołek, to oczywiście wystarcza jeden kolor. Załóżmy więc, że $\left|V\right|\ge 2$. Wybierzmy dowolny wierzchołek $v\in V$ i rozważmy graf $\mathbf{𝐆}{|}_{V-\left\{v\right\}}$. Na mocy założenia indukcyjnego da się go pokolorować $k+1$ barwami. Zauważmy, że $v$ ma co najwyżej $k$ sąsiadów. Wśród $k+1$ kolorów użytych w kolorowaniu grafu $\mathbf{𝐆}{|}_{V-\left\{x\right\}}$ jest więc kolor nie przypisany żadnemu sąsiadowi wierzchołka $v$. Wybieramy więc ten kolor jako barwę dla $v$. Udało się pokolorować graf $\mathbf{𝐆}$ zbiorem $k+1$ kolorów, co kończy dowód.

Ograniczenia górnego, na liczbę chromatyczną grafu, podanego w Twierdzeniu 14.9 nie można w ogólności wzmocnić. Istotnie, każde kolorowanie kliki ${{𝒦}}_{k+1}$ wymaga dokładnie $k+1$ kolorów, mimo iż stopień każdego wierzchołka to $k$. Następne twierdzenie wzmacnia jednak znacznie Twierdzenia 14.9, ale podajemy je bez dowodu.

Twierdzenie 14.10 [Brooks 1941]

Niech $\mathbf{𝐆}$ będzie spójnym grafem prostym, który nie jest kliką. Jeśli wszystkie wierzchołki grafu $\mathbf{𝐆}$ mają stopień nie większy niż $k$ i $k\ge 3$, to $\mathbf{𝐆}$ jest $\rho$-kolorowalny.

Oczywiście nie powinno dziwić nas, że dla grafów specjalnego typu można na ogół powiedzieć więcej o ich liczbie chromatycznej.

Obserwacja 14.11

Graf jest dwudzielny wtedy i tylko wtedy, gdy jest $2$-kolorowalny.

Dowód

Zauważmy najpierw, że w grafie dwudzielnym $\mathbf{𝐆}=(V_1\cup V_2,E)$, podgrafy indukowane $\mathbf{𝐆}{|}_{V_1}$ oraz $\mathbf{𝐆}{|}_{V_2}$ są antyklikami. Wystarczy więc pokolorować wierzchołki z $V_1$ jednym kolorem, a wierzchołki z $V_2$ drugim. Z drugiej strony wierzchołki grafu $2$-kolorowalnego daje się oczywiście rozbić na dw zbiory indukujące antykliki, jak tego wymaga dwudzielność.

Twierdzenie 14.12

Każdy graf planarny jest $5$-kolorowalny.

Grafy 5barw planar

Grafy 5barw planar2

Dowód

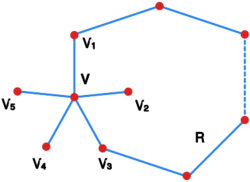
Dowód przeprowadzimy indukcyjnie ze względu na liczbę wierzchołków w grafie $\mathbf{𝐆}=(V,E)$. Dla $\left|V\right|=1$ teza jest oczywista. Niech więc $\left|V\right|\ge 2$. Z Wniosku 14.6 wiemy, że $\mathbf{𝐆}$ ma jakiś wierzchołek $v$ o stopniu niewiększym niż $5$. Na mocy założenia indukcyjnego wiemy, że graf $\mathbf{𝐆}{|}_{V-\left\{v\right\}}$ jest $5$-kolorowalny. Jeżeli $v$ ma mniej niż $5$-ciu sąsiadów, to można go pokolorować kolorem niewystępującym u żadnego sąsiada, co kończyłoby dowód. Podobnie, gdyby jakiś kolor występował u co najmniej dwóch sąsiadów wierzchołka $v$, to także można byłoby zakończyć dowód, gdyż Wśród $5$-ciu kolorów dostępnych do kolorowania grafu $\mathbf{𝐆}$ jest kolor nie przypisany żadnemu sąsiadowi wierzchołka $v$ i może być wobec tego użyty dla $v$. Możemy więc założyć, że $v$ ma $5$ sąsiadów $v_1,v_2,v_3,v_4,v_5$ odpowiednio o kolorach: $1,2,3,4,5$. Bez straty ogólności ich ułożenie może wyglądać jak na rysunku Grafy 5barw planar.

Niech ${\mathbf{𝐏}}_{i,j}$ będzie restrykcją grafu $\mathbf{𝐆}$ do zbioru wszystkich jego wierzchołków o barwach $i$ oraz $j$. Jeśli $v_1$ i $v_3$ nie są w tej samej spójnej składowej grafu ${\mathbf{𝐏}}_{1,3}$, to można zamienić kolory $1$ i $3$ w spójnej składowej wierzchołka $v_1$. Tak więc, z racji, że teraz $v_1$ otrzymał kolor $3$, koloru $1$ można użyć do pokolorowania wierzchołka $v$. Pozostał przypadek, gdy $v_1$ oraz $v_3$ są w tej samej spójnej składowej grafu ${\mathbf{𝐏}}_{1,3}$. Oznaczy to, że istnieje ścieżka $R$ zawarta w ${\mathbf{𝐏}}_{1,3}$ i łącząca $v_1$ z $v_3$. W efekcie otrzymujemy cykl $v\to v_1\to R\to v_3\to v$, który ogranicza obszar zawierający wierzchołek $v_2$ i nie zawierający $v_4$.

Z planarności dostajemy więc, że wierzchołki $v_2$ oraz $v_4$ nie mogą być w tej samej spójnej składowej grafu ${\mathbf{𝐏}}_{2,4}$. W takim razie podobnie, jak powyżej możemy podmienić kolory w spójnej składowej wierzchołka $v_2$ tak, że $v_2$ otrzyma kolor $4$. Ale teraz możemy pokolorować wierzchołek $v$ na kolor $2$, co kończy dowód.

Okazuje się że prawdziwe jest mocniejsze i słynne twierdzenie o czterech barwach. Jego długi i skomplikowany dowód został otrzymany przy użyciu specjalnie napisanego programu do rozważenia bardzo wielu przypadków. Dowód ten pomijamy.

Twierdzenie 14.13

Każdy graf planarny jest $4$-kolorowalny.

Mapa to graf płaski nie zawierający mostów.

W mapach rozważa się kolorowanie ścian.

Mapa ma $k$-kolorowalne ściany jeśli jej ściany można pokolorować $k$ kolorami w ten sposób, by żadne dwie graniczące ze sobą ściany nie miały tego samego koloru. Innymi słowy, mapa $\mathbf{𝐌}$ ma $k$-kolorowalne ściany, jeśli jej geometrycznie dualny graf ${\mathbf{𝐌}}^{*}$ jest $k$ kolorowalny.

Twierdzenie 14.14

Mapa $\mathbf{𝐌}$ ma $2$-kolorowalne ściany wtedy i tylko wtedy, gdy graf $\mathbf{𝐌}$ jest eulerowski.

Dowód

Załóżmy najpierw, że ściany są pomalowane dwoma kolorami. Wtedy każdy wierzchołek $v$ musi być incydentny z parzystą liczbą ścian, a zatem musi mieć parzysty stopień. Na mocy Twierdzenia Eulera otrzymujemy więc, że $\mathbf{𝐌}$ jest eulerowski.

Niech teraz $\mathbf{𝐌}$ będzie grafem eulerowskim. Wtedy, na mocy wniosku z Twierdzenia Eulera, jego krawędzie można podzielić na rozłączne krawędziowo cykle $C_1,\dots ,C_k$. Kolorowanie ścian mapy $\mathbf{𝐌}$ zdefiniujmy poprzez przypisanie ścianie pierwszego koloru, jeśli jest otoczona nieparzystą liczbą cykli spośród $C_1,\dots ,C_k$, albo poprzez przypisanie drugiego koloru, jeśli jest otoczona parzystą liczbą cykli. Kolorowanie to jest poprawne, gdyż jeśli dwie ściany graniczą ze sobą poprzez krawędź jakiegoś cyklu $C_i$, to jedna z tych ścian leży wewnątrz cyklu $C_i$, a druga na zewnątrz $C_i$. W stosunku do pozostałych cykli spośród $C_1,\dots ,C_k$, albo obie ściany są wewnątrz, albo obie na zewnątrz. Tak więc różni je parzystość liczby cykli, we wnętrzu których leżą. Tym samym, w zdefiniowanym kolorowaniu, otrzymają różne kolory.

Z Twierdzenia 14.13, poprzez przejście od mapy $\mathbf{𝐌}$ do grafu geometrycznie dualnego ${\mathbf{𝐌}}^{*}$ dostajemy natychmiast następujący wniosek.

Wniosek 14.15

Każda mapa ma $4$-kolorowalne ściany.

Z powodu dużego znaczenia kolorowania tak w samej teorii grafów, jak i w algorytmice, problemy kolorowania doczekały się bardzo rozbudowanych pojęć i narzędzi. Poznamy teraz jeszcze jedno z nich.

Liczba stopniowa grafu. Niech $\mathbf{𝐆}=(\{v_1,\dots ,v_n\},E)$ będzie grafem prostym. Przy każdej permutacji $\rho :\{1,\dots ,n\}⟶\{1,\dots ,n\}$ każdemu wierzchołkowi $v_{\rho \left(i\right)}$ przypisana jest liczba sąsiadów $n_{\rho \left(i\right)}^{\rho }$ w zbiorze wierzchołków o indeksie mniejszym niż $\rho \left(i\right)$. Liczba stopniowa jest równa

${\chi }_s\left(\mathbf{𝐆}\right)=\underset{\rho }{\min }\underset{i=1,\dots ,n}{\max }{n}_i^{\rho }$

Grafy liczba stopniowa 1

Graf ${\mathbf{𝐆}}_1$ z wierzchołkami w porządku wyznaczonym przez $\rho$

Kolorowanie grafu ${\mathbf{𝐆}}_1$

Load video

Local File

Local File might collect personal data.

Continue Dismiss

Animacja

Przykład

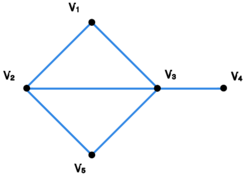
Rozważmy graf ${\mathbf{𝐆}}_1=(\{v_1,v_2,v_3,v_4,v_5\},E)$ przedstawiony na rysunku Grafy liczba stopniowa 1.

Dla permutacji $\rho$ zadanej przez

$\begin{array}{cccccc}n& 1& 2& 3& 4& 5\\ \rho \left(n\right)& 5& 2& 3& 1& 4\end{array}$

mamy $\underset{i=1,\dots ,n}{\max }{n}_i^{\rho }=2$ i wartość ta jest realizowana przez wierzchołki $v_3$ i $v_1$. Wierzchołki ułożone w porządku $v_{\rho \left(1\right)},\dots ,v_{\rho \left(5\right)}$ przedstawione są na rysunku Graf G_1 z wierzchołkami....

Przeglądając z kolei wszystkie możliwe permutacje możemy stwierdzić, że nasza permutacja $\rho$ realizuje minimum $\underset{\rho }{\min }\underset{i=1,\dots ,n}{\max }{n}_i^{\rho }$, a zatem ${\chi }_s\left(\mathbf{𝐆}\right)=2$.

Graf ${\mathbf{𝐆}}_1$ można teraz pokolorować następującą procedurą. Wybierając kolejno wierzchołki $v_{\rho \left(1\right)},v_{\rho \left(2\right)},\dots ,v_{\rho \left(5\right)}$ nadajemy im kolor niewykorzystany dla żadnego dotąd rozpatrywanego sąsiada. Otrzymujemy wtedy kolorowanie przedstawione na rysunku Kolorowanie grafu.

Waga wprowadzonej liczby stopniowej wynika z poniższej obserwacji.

Obserwacja 14.16

Jeżeli $\mathbf{𝐆}$ jest grafem prostym, to

$\chi \left(\mathbf{𝐆}\right)\le {\chi }_s\left(\mathbf{𝐆}\right)+1$

Dowód

Niech $v_1,\dots ,v_n$ będzie ciągiem wierzchołków grafu $\mathbf{𝐆}$ w porządku realizującym wartość ${\chi }_s\left(\mathbf{𝐆}\right)$. Wskażemy kolorowanie za pomocą ${\chi }_s\left(\mathbf{𝐆}\right)+1$ barw. Wierzchołki kolorowane są kolejno zgodnie z ich numeracją. Załóżmy, że pokolorowane zostały już wierzchołki $v_1,\dots ,v_{i-1}$. Wierzchołek $v_i$ ma co najwyżej ${\chi }_s\left(\mathbf{𝐆}\right)$ sąsiadów w zbiorze $\{v_1,\dots ,v_{i-1}\}$, tak więc w zbiorze ${\chi }_s\left(\mathbf{𝐆}\right)+1$ kolorów jest jeszcze co najmniej jeden kolor nie wykorzystany dla tych wcześniejszych sąsiadów $v_i$. Przydzielamy go więc wierzchołkowi $v_i$. Czynność ta jest powtarzana, aż do momentu pokolorowania wszystkich wierzchołków w $\mathsf{V}\left(\mathbf{𝐆}\right)$.