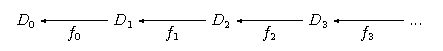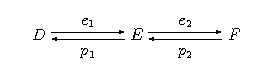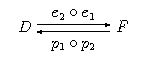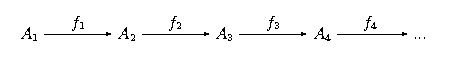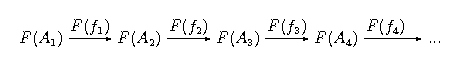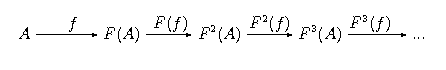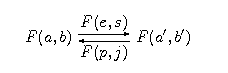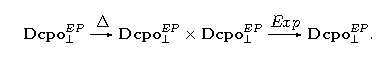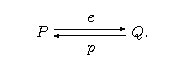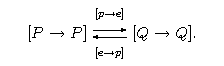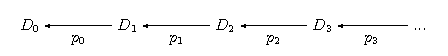TKI Moduł 13: Różnice pomiędzy wersjami
mNie podano opisu zmian |
m Zastępowanie tekstu – „<math> ” na „<math>” |
||
| (Nie pokazano 7 wersji utworzonych przez 2 użytkowników) | |||
| Linia 7: | Linia 7: | ||
Dowód: Dowód przeprowadzimy dla szczególnego diagramu: | Dowód: Dowód przeprowadzimy dla szczególnego diagramu: | ||
[ | [[Grafika:Diag13.0.png]] | ||
(Dowód ogólny jest analogiczny lecz wymaga bardziej ''technicznego'' zapisu, wiec go pominiemy.) Pokażemy, że granica powyższego diagramu jest dana jako | (Dowód ogólny jest analogiczny lecz wymaga bardziej ''technicznego'' zapisu, wiec go pominiemy.) Pokażemy, że granica powyższego diagramu jest dana jako | ||
<math> D = \{(x_0, x_1, ... )\mid (\forall n\in \omega)(f_n(x_{n+1}) = x_n)\} | <math>D = \{(x_0, x_1, ... )\mid (\forall n\in \omega)(f_n(x_{n+1}) = x_n)\}</math>. | ||
Zauważmy, że zbiór <math>D </math> jest posetem, w którym elementy są uporządkowane ''po współrzędnych'' (to znaczy, że porządek jest ''dziedziczony'' z produktu <math>\Pi_{n\in \omega} D_n</math>. Jeśli <math>G\subseteq D</math> jest zbiorem skierowanym, to dla każdego <math>n\in \omega </math>zbiór <math>\pi_n[G]= \{x_n\mid x\in G\}</math>jest skierowanym podzbiorem <math>D_n </math>. Niech <math>y_n = \bigvee \{x_n\mid x\in G\} </math>. Z ciągłości funkcji tworzących diagram mamy: <math>f_n(y_{n+1}) = \bigvee f_n(\{x_{n+1}\mid x\in G\})= \bigvee \{x_{n}\mid x\in G\} = y_n</math>. To znaczy, że <math>(y_0, y_1, ...)\in D </math> i, jak łatwo zauważyć, element ten jest supremum skierowanym zbioru <math>G</math>. Pokazaliśmy więc, że <math>D\in</math> '''Dcpo'''. | Zauważmy, że zbiór <math>D</math> jest posetem, w którym elementy są uporządkowane ''po współrzędnych'' (to znaczy, że porządek jest ''dziedziczony'' z produktu <math>\Pi_{n\in \omega} D_n</math>. Jeśli <math>G\subseteq D</math> jest zbiorem skierowanym, to dla każdego <math>n\in \omega</math>zbiór <math>\pi_n[G]= \{x_n\mid x\in G\}</math>jest skierowanym podzbiorem <math>D_n</math>. Niech <math>y_n = \bigvee \{x_n\mid x\in G\}</math>. Z ciągłości funkcji tworzących diagram mamy: <math>f_n(y_{n+1}) = \bigvee f_n(\{x_{n+1}\mid x\in G\})= \bigvee \{x_{n}\mid x\in G\} = y_n</math>. To znaczy, że <math>(y_0, y_1, ...)\in D</math> i, jak łatwo zauważyć, element ten jest supremum skierowanym zbioru <math>G</math>. Pokazaliśmy więc, że <math>D\in</math> '''Dcpo'''. | ||
Udowodnimy teraz, że <math>D</math> wraz z projekcjami <math>\{\pi_n\colon D\to D_n\mid n\in \omega\}</math> jest granicą. Po pierwsze, dla <math>G\subseteq D</math> mamy | Udowodnimy teraz, że <math>D</math> wraz z projekcjami <math>\{\pi_n\colon D\to D_n\mid n\in \omega\}</math> jest granicą. Po pierwsze, dla <math>G\subseteq D</math> mamy | ||
<math>\pi_n(\bigvee G) = y_n = \bigvee \{x_{n}\mid x\in G\} = \bigvee \pi_n[G] | <math>\pi_n(\bigvee G) = y_n = \bigvee \{x_{n}\mid x\in G\} = \bigvee \pi_n[G]</math> | ||
a więc projekcje są ciągłe. Po drugie, jeśli <math>\{g_k\colon E\to D_k\mid k\in \omega\}</math> jest dowolną inną granicą, to zdefiniujmy <math>h\colon E\to D </math> jako <math>h(x) = (g_0(x), g_1(x), ...)</math>. Z definicji powyższej wynika, że dla każdego <math>k\in \omega</math> mamy $\pi_k \circ h = g_k</math>. Zauważmy, że to świadczy o jednoznaczności | a więc projekcje są ciągłe. Po drugie, jeśli <math>\{g_k\colon E\to D_k\mid k\in \omega\}</math> jest dowolną inną granicą, to zdefiniujmy <math>h\colon E\to D</math> jako <math>h(x) = (g_0(x), g_1(x), ...)</math>. Z definicji powyższej wynika, że dla każdego <math>k\in \omega</math> mamy $\pi_k \circ h = g_k</math>. Zauważmy, że to świadczy o jednoznaczności | ||
wyboru <math>h</math>. A zatem <math>D</math> jest granicą omawianego diagramu. Co więcej, z jednoznaczności granicy wnioskujemy, że <math>D\cong E </math>. QED | wyboru <math>h</math>. A zatem <math>D</math> jest granicą omawianego diagramu. Co więcej, z jednoznaczności granicy wnioskujemy, że <math>D\cong E</math>. QED | ||
Uwaga! Powyższe twierdzenie nie zachodzi dla klas dziedzin ciągłych i algebraicznych w ogólności. Aby granica była również posetem odpowiedniej klasy, musimy nałożyć poewne restrykcje zarówno na kształ diagramów, jak i na własności funkcji tworzących diagram. | Uwaga! Powyższe twierdzenie nie zachodzi dla klas dziedzin ciągłych i algebraicznych w ogólności. Aby granica była również posetem odpowiedniej klasy, musimy nałożyć poewne restrykcje zarówno na kształ diagramów, jak i na własności funkcji tworzących diagram. | ||
| Linia 33: | Linia 33: | ||
'''Twierdzenie'''. Rozważmy diagram <math>F</math> w kategorii '''Dcpo''' taki, że: | '''Twierdzenie'''. Rozważmy diagram <math>F</math> w kategorii '''Dcpo''' taki, że: | ||
1. Wierzchołkami <math>F</math> są posety <math>D_0, D_1, D_2, | 1. Wierzchołkami <math>F</math> są posety <math>D_0, D_1, D_2, ..</math>.; | ||
2. Dla <math>n\leq m</math> istnieją funkcje <math>e_{mn}\colon D_n\to D_m</math> i <math>p_{nm}\colon D_m\to D_n</math> tworzące parę e-p; | 2. Dla <math>n\leq m</math> istnieją funkcje <math>e_{mn}\colon D_n\to D_m</math> i <math>p_{nm}\colon D_m\to D_n</math> tworzące parę e-p; | ||
| Linia 42: | Linia 42: | ||
Zdefiniujmy: | Zdefiniujmy: | ||
<math>D = \{ (x_0, x_1, ...)\mid (\forall n\leq m)(x_n=p_{nm}(x_m)) \} | <math>D = \{ (x_0, x_1, ...)\mid (\forall n\leq m)(x_n=p_{nm}(x_m)) \}</math> | ||
<math>p_m\colon D\to D_m,\ \ (x_0, x_1, ...)\mapsto x_m, \ m\in \omega</math> | <math>p_m\colon D\to D_m,\ \ (x_0, x_1, ...)\mapsto x_m, \ m\in \omega</math> | ||
<math>e_m\colon D_m\to D, \ x\mapsto (\bigvee_{k\geq n,m} p_{nk}\circ e_{km}(x)\mid n\in \omega) | <math>e_m\colon D_m\to D, \ x\mapsto (\bigvee_{k\geq n,m} p_{nk}\circ e_{km}(x)\mid n\in \omega)</math>. | ||
Wtedy: | Wtedy: | ||
| Linia 59: | Linia 59: | ||
będzie dowolne i załóżmy, że <math>n\leq n'</math>. Mamy: | będzie dowolne i załóżmy, że <math>n\leq n'</math>. Mamy: | ||
<math>p_{nn'}(y_{n'}) = p_{nn'}(\bigvee_{k\geq n',m} p_{n'k}\circ e_{km}(x)) = \bigvee_{k\geq n',m} p_{nn'}\circ p_{n'k}\circ e_{km}(x) = \bigvee_{k\geq n',m} p_{nk}\circ e_{km}(x)= y_n | <math>p_{nn'}(y_{n'}) = p_{nn'}(\bigvee_{k\geq n',m} p_{n'k}\circ e_{km}(x)) = \bigvee_{k\geq n',m} p_{nn'}\circ p_{n'k}\circ e_{km}(x) = \bigvee_{k\geq n',m} p_{nk}\circ e_{km}(x)= y_n</math>. | ||
W dowodzie korzystaliśmy kolejno z: definicji <math>y_{n'}</math>, ciągłości <math>p_{nn'}</math> i definicji <math>y_n</math>. A zatem <math>y = (y_0, y_1, ...)\in D</math>. Co więcej, funkcje <math>e_m</math> są ciągłe, gdyż tylko funkcje ciągłe zostały użyte w ich definicji. | W dowodzie korzystaliśmy kolejno z: definicji <math>y_{n'}</math>, ciągłości <math>p_{nn'}</math> i definicji <math>y_n</math>. A zatem <math>y = (y_0, y_1, ...)\in D</math>. Co więcej, funkcje <math>e_m</math> są ciągłe, gdyż tylko funkcje ciągłe zostały użyte w ich definicji. | ||
| Linia 66: | Linia 66: | ||
<math>e_m\circ p_m (x_n\mid n\in \omega) = e_m(x_m) = (\bigvee_{k\geq n,m} p_{nk}\circ e_{km}(x_m)\mid n\in\omega) = (\bigvee_{k\geq n,m} p_{nk}\circ e_{km} \circ p_{mk} (x_k)\mid n\in\omega) \subseteq (\bigvee_{k\geq n,m} p_{nk} (x_k)\mid n\in\omega) = (\bigvee_{k\geq n} p_{nk} (x_k)\mid n\in\omega) = (x_n\mid n\in\omega) | <math>e_m\circ p_m (x_n\mid n\in \omega) = e_m(x_m) = (\bigvee_{k\geq n,m} p_{nk}\circ e_{km}(x_m)\mid n\in\omega) = (\bigvee_{k\geq n,m} p_{nk}\circ e_{km} \circ p_{mk} (x_k)\mid n\in\omega) \subseteq (\bigvee_{k\geq n,m} p_{nk} (x_k)\mid n\in\omega) = (\bigvee_{k\geq n} p_{nk} (x_k)\mid n\in\omega) = (x_n\mid n\in\omega)</math>. | ||
Ponadto, <math>p_m\circ e_m (x) = p_m (\bigvee_{k\geq n,m} p_{nk}\circ e_{km}(x)\mid n\in\omega ) = \bigvee_{k\geq m} p_{mk}\circ e_{km}(x) = x</math>. | Ponadto, <math>p_m\circ e_m (x) = p_m (\bigvee_{k\geq n,m} p_{nk}\circ e_{km}(x)\mid n\in\omega ) = \bigvee_{k\geq m} p_{mk}\circ e_{km}(x) = x</math>. | ||
| Linia 73: | Linia 73: | ||
te elementy ciągu <math>(x_n\mid n\in\omega)</math> gdzie <math>n\leq m</math>: | te elementy ciągu <math>(x_n\mid n\in\omega)</math> gdzie <math>n\leq m</math>: | ||
<math>p_n(e_m\circ p_m (x_n\mid n\in \omega)) = ... = p_n(\bigvee_{k\geq n,m} p_{nk}\circ e_{km} \circ p_{mk} (x_k)\mid n\in\omega) = p_n(\bigvee_{k\geq n,m} p_{nm}\circ p_{mk} \circ e_{km} \circ p_{mk} (x_k)\mid n\in\omega) = p_n(\bigvee_{k\geq n,m} p_{nm}\circ p_{mk} (x_k)\mid n\in\omega) = p_n(\bigvee_{k\geq n} p_{nk} (x_k)\mid n\in\omega) = p_n(\bigvee_{k\geq n} x_n\mid n\in\omega) = p_n(x_n\mid n\in\omega) = x_n | <math>p_n(e_m\circ p_m (x_n\mid n\in \omega)) = ... = p_n(\bigvee_{k\geq n,m} p_{nk}\circ e_{km} \circ p_{mk} (x_k)\mid n\in\omega) = p_n(\bigvee_{k\geq n,m} p_{nm}\circ p_{mk} \circ e_{km} \circ p_{mk} (x_k)\mid n\in\omega) = p_n(\bigvee_{k\geq n,m} p_{nm}\circ p_{mk} (x_k)\mid n\in\omega) = p_n(\bigvee_{k\geq n} p_{nk} (x_k)\mid n\in\omega) = p_n(\bigvee_{k\geq n} x_n\mid n\in\omega) = p_n(x_n\mid n\in\omega) = x_n</math>. | ||
To dowodzi, że <math>\bigvee_n e_n\circ p_n = 1_{D}</math>, czyli (5). | To dowodzi, że <math>\bigvee_n e_n\circ p_n = 1_{D}</math>, czyli (5). | ||
| Linia 79: | Linia 79: | ||
Korzystając z powyższego mamy też natychmiast: | Korzystając z powyższego mamy też natychmiast: | ||
<math>h = 1_D\circ h = \bigvee_n E_n\circ p_n\circ h = \bigvee e_m \circ g_n | <math>h = 1_D\circ h = \bigvee_n E_n\circ p_n\circ h = \bigvee e_m \circ g_n</math> | ||
co kończy dowód (6). | co kończy dowód (6). | ||
| Linia 85: | Linia 85: | ||
Do pokazania pozostała nam (7), czyli fakt, że <math>\{e_n\colon D_n\to D\}</math> jest granicą odwrotną diagramu <math>F</math> Jeśli <math>\{f_n\colon E\to D_n\}</math> jest dowolną inną granicą, to sprawdźmy najpierw czy funkcja <math>f = \bigvee_n f_n\circ p_n</math> jest dobrze zdefiniowana, tj. czy supremum jest nad zbiorem skierowanym. Ale tak jest, ponieważ dla <math>n\leq m</math>: | Do pokazania pozostała nam (7), czyli fakt, że <math>\{e_n\colon D_n\to D\}</math> jest granicą odwrotną diagramu <math>F</math> Jeśli <math>\{f_n\colon E\to D_n\}</math> jest dowolną inną granicą, to sprawdźmy najpierw czy funkcja <math>f = \bigvee_n f_n\circ p_n</math> jest dobrze zdefiniowana, tj. czy supremum jest nad zbiorem skierowanym. Ale tak jest, ponieważ dla <math>n\leq m</math>: | ||
<math>f_n \circ p_n = f_m \circ e_{mn}\circ p_{nm}\circ p_m\sqsubseteq f_m\circ p_m | <math>f_n \circ p_n = f_m \circ e_{mn}\circ p_{nm}\circ p_m\sqsubseteq f_m\circ p_m</math>. | ||
Co więcej, | Co więcej, | ||
<math> f\circ e_m = \bigvee_{n\leq m} f_n\circ p_n\circ e_m = \bigvee_{n\leq m} f_n\circ p_n\circ e_n\circ e_{nm} = \bigvee_{n\leq m} f_n\circ e_{nm} = \bigvee_{n\leq m} f_m = f_m. </math> | <math>f\circ e_m = \bigvee_{n\leq m} f_n\circ p_n\circ e_m = \bigvee_{n\leq m} f_n\circ p_n\circ e_n\circ e_{nm} = \bigvee_{n\leq m} f_n\circ e_{nm} = \bigvee_{n\leq m} f_m = f_m.</math> | ||
W końcu pokażemy, że funkcja <math>f</math> o podanych własnościach jest | W końcu pokażemy, że funkcja <math>f</math> o podanych własnościach jest | ||
tylko jedna. Jeśli dla <math>f'\colon D\to E</math> zachodzi <math>f'\circ e_m = f_m</math>, to <math>f'\circ e_m \circ p_m = f_m\circ p_m</math>, a zatem <math>\bigvee_m f'\circ e_m \circ p_m = \bigvee_m f_m\circ p_m | tylko jedna. Jeśli dla <math>f'\colon D\to E</math> zachodzi <math>f'\circ e_m = f_m</math>, to <math>f'\circ e_m \circ p_m = f_m\circ p_m</math>, a zatem <math>\bigvee_m f'\circ e_m \circ p_m = \bigvee_m f_m\circ p_m</math> czyli z ciągłości <math>f'</math>: <math>f'(\bigvee_m \circ e_m \circ p_m) = \bigvee_m f_m\circ p_m</math>. Ale <math>\bigvee_m \circ e_m \circ p_m = 1_D</math> oraz <math>\bigvee_m f_m\circ p_m = f</math> co daje <math>f'\circ 1_D = f</math> czyli <math>f'=f</math>. QED. | ||
== Kategoria <math>\mathrm{Dcpo}^{EP}_{\bot}</math> == | == Kategoria <math>\mathrm{Dcpo}^{EP}_{\bot}</math> == | ||
| Linia 99: | Linia 99: | ||
pary e-p, o których była mowa na początku wykładu ???. Złożenie morfizmów | pary e-p, o których była mowa na początku wykładu ???. Złożenie morfizmów | ||
[ | [[Grafika:Diag13.1.png]] | ||
definiujemy w naturalny sposób jako morfizm | definiujemy w naturalny sposób jako morfizm | ||
[ | [[Grafika:Diag13.2.png]] | ||
Czy <math>(e_2\circ e_1, p_1\circ p_2)</math> jest parą e-p? Tak, ponieważ: <math>e_2\circ e_1\circ p_1\circ p_2 \sqsubseteq e_2\circ 1_E\circ p_2 = e_2\circ p_2\sqsubseteq 1_F</math> oraz <math>p_1\circ p_2\circ e_2\circ e_1 = p_1\circ 1_E\circ e_1 = p_1\circ e_1 = 1_D | Czy <math>(e_2\circ e_1, p_1\circ p_2)</math> jest parą e-p? Tak, ponieważ: <math>e_2\circ e_1\circ p_1\circ p_2 \sqsubseteq e_2\circ 1_E\circ p_2 = e_2\circ p_2\sqsubseteq 1_F</math> oraz <math>p_1\circ p_2\circ e_2\circ e_1 = p_1\circ 1_E\circ e_1 = p_1\circ e_1 = 1_D</math>. A zatem złożenie par e-p jest dobrze zdefiniowane, a co za tym idzie, i co łatwo już teraz pokazać, <math>Dcpo^{EP}_{\bot}</math> jest kategorią. | ||
'''Definicja'''. Nazwijmy '''<math>\omega</math>-kategorią''' każdą kategorię, w której diagram postaci | '''Definicja'''. Nazwijmy '''<math>\omega</math>-kategorią''' każdą kategorię, w której diagram postaci | ||
[ | [[Grafika:Diag13.3.png]] | ||
posiada granicę odwrotną. | posiada granicę odwrotną. | ||
| Linia 119: | Linia 119: | ||
'''Definicja'''. Funktor <math>F</math> między <math>\omega</math>-kategoriami nazywamy '''ciągłym''', jeśli zachowuje granice odwrotne, t.j. jeśli <math>D_{\infty}</math> jest granicą diagramu ???, to <math>F(D_{\infty})</math> jest granicą diagramu | '''Definicja'''. Funktor <math>F</math> między <math>\omega</math>-kategoriami nazywamy '''ciągłym''', jeśli zachowuje granice odwrotne, t.j. jeśli <math>D_{\infty}</math> jest granicą diagramu ???, to <math>F(D_{\infty})</math> jest granicą diagramu | ||
[ | [[Grafika:Diag13.4.png]] | ||
'''Lemat'''. Niech <math>\mathbf{A}</math> będzie <math>\omega</math>-kategorią, <math>F\colon \mathbf{A}\to \mathbf{A}</math> funktorem ciągłym, <math>f\colon A\to F(A)</math> morfizmem w <math>\mathbf{A}</math> oraz niech diagram | '''Lemat'''. Niech <math>\mathbf{A}</math> będzie <math>\omega</math>-kategorią, <math>F\colon \mathbf{A}\to \mathbf{A}</math> funktorem ciągłym, <math>f\colon A\to F(A)</math> morfizmem w <math>\mathbf{A}</math> oraz niech diagram | ||
[ | [[Grafika:Diag13.5.png]] | ||
posiada granicę odwrotną <math>D_{\infty}</math>. Wówczas <math>D_{\infty}\cong F(D_{\infty})</math>. | posiada granicę odwrotną <math>D_{\infty}</math>. Wówczas <math>D_{\infty}\cong F(D_{\infty})</math>. | ||
| Linia 131: | Linia 132: | ||
???, to | ???, to | ||
[ | [[Grafika:Diag13.6.png]] | ||
komutuje. W szczególności | komutuje. W szczególności | ||
[ | [[Grafika:Diag13.7.png]] | ||
komutuje i jak łatwo zauważyć <math>D_{\infty}</math> jest jego granicą. Ale | komutuje i jak łatwo zauważyć <math>D_{\infty}</math> jest jego granicą. Ale | ||
z ciągłości <math>F</math> mamy, że diagram | z ciągłości <math>F</math> mamy, że diagram | ||
[ | [[Grafika:Diag13.8.png]] | ||
komutuje i <math>F(D_{\infty})</math> jest jego granicą. A zatem <math>D_{\infty} | komutuje i <math>F(D_{\infty})</math> jest jego granicą. A zatem <math>D_{\infty} | ||
| Linia 146: | Linia 147: | ||
'''Przykład'''. Przekątna <math>\Delta\colon \mathbf{Dcpo}\to \mathbf{Dcpo}\times \mathbf{Dcpo}</math>, <math>a\mapsto (a,a)</math>; <math>f\mapsto (f,f)</math> dla <math>a\in \mathbf{Dcpo}_0</math> <math>f\in \mathbf{Dcpo}_1</math> jest ciągłym funktorem. | '''Przykład'''. Przekątna <math>\Delta\colon \mathbf{Dcpo}\to \mathbf{Dcpo}\times \mathbf{Dcpo}</math>, <math>a\mapsto (a,a)</math>; <math>f\mapsto (f,f)</math> dla <math>a\in \mathbf{Dcpo}_0</math> <math>f\in \mathbf{Dcpo}_1</math> jest ciągłym funktorem. | ||
== Lokalna ciągłość funktorów == | == Lokalna ciągłość funktorów == | ||
| Linia 152: | Linia 152: | ||
Ciągłość funktora jest często niełatwa do sprawdzenia. Na szczęście istnieje własność ''mocniejsza'', która jest łatwiej weryfikowalna: lokalna ciągłość. | Ciągłość funktora jest często niełatwa do sprawdzenia. Na szczęście istnieje własność ''mocniejsza'', która jest łatwiej weryfikowalna: lokalna ciągłość. | ||
'''Definicja'''. Funktor <math>F\colon \mathcal{D}\to \mathcal{E}</math> pomiędzy kategoriami posetów <math>\mathcal{D}, \mathcal{E}</math> jest { | '''Definicja'''. Funktor <math>F\colon \mathcal{D}\to \mathcal{E}</math> pomiędzy kategoriami posetów <math>\mathcal{D}, \mathcal{E}</math> jest \mathit{ lokalnie ciągły} jeśli przekształcenia <math>f\mapsto F(f)</math> typu <math>\mathrm{Hom}(D,D')\to \mathrm{Hom}(F(D),F(D'))</math> są ciągłe w sensie Scotta dla każdej pary obiektów <math>D,D'\in \mathcal{D}_0</math>. | ||
Dla przykładu przeczytajmy tę definicję dla bifunktora <math>F\colon \mathbf{Dcpo}^{op}\times \mathbf{Dcpo}\to \mathbf{Dcpo}</math>: funktor <math>F</math> jest lokalnie ciągły, jeśli dla dowolnych zbiorów skierowanych <math>A\subseteq [D_2\to D_1]</math> i <math>B\subseteq [D_3\to D_4]</math>, gdzie <math>D_1, ..., D_4\in \mathbf{Dcpo}_0</math> mamy <math>F(\bigvee A, \bigvee B) = \bigvee_{f\in A, g\in G} F(f,g) | Dla przykładu przeczytajmy tę definicję dla bifunktora <math>F\colon \mathbf{Dcpo}^{op}\times \mathbf{Dcpo}\to \mathbf{Dcpo}</math>: funktor <math>F</math> jest lokalnie ciągły, jeśli dla dowolnych zbiorów skierowanych <math>A\subseteq [D_2\to D_1]</math> i <math>B\subseteq [D_3\to D_4]</math>, gdzie <math>D_1, ..., D_4\in \mathbf{Dcpo}_0</math> mamy <math>F(\bigvee A, \bigvee B) = \bigvee_{f\in A, g\in G} F(f,g)</math>. Zauważmy, że supremum po prawej stronie istnieje w <math>[F(D_1,D_3)\to F(D_2, D_4)]</math>. | ||
'''Przykład'''. Eksponent <math>[\_\to \_]\colon\mathbf{Dcpo}^{op}\times \mathbf{Dcpo}\to \mathbf{Dcpo}</math> jest lokalnie ciągły, ponieważ <math>[f\to g] = curry(g\circ ev\circ (1\times f))</math> jest złożeniem funkcji ciągłych w sensie Scotta. | '''Przykład'''. Eksponent <math>[\_\to \_]\colon\mathbf{Dcpo}^{op}\times \mathbf{Dcpo}\to \mathbf{Dcpo}</math> jest lokalnie ciągły, ponieważ <math>[f\to g] = curry(g\circ ev\circ (1\times f))</math> jest złożeniem funkcji ciągłych w sensie Scotta. | ||
| Linia 164: | Linia 164: | ||
Dowód: Połóżmy <math>\widehat{F}(a,b) = F(a,b)</math>, gdzie <math>a,b</math> są posetami ciągłymi z elementami najmniejszymi. Rozważmy pary e-p: | Dowód: Połóżmy <math>\widehat{F}(a,b) = F(a,b)</math>, gdzie <math>a,b</math> są posetami ciągłymi z elementami najmniejszymi. Rozważmy pary e-p: | ||
[ | [[Grafika:Diag13.9.png]] | ||
Możemy wówczas stworzyć diagram | Możemy wówczas stworzyć diagram | ||
[ | [[Grafika:Diag13.10.png]] | ||
i para morfizmów powyżej jest parą e-p. Rzeczywiście: <math>F(e,s)\circ F(p,j) = F(p\circ e, s\circ j) = F(1_a, 1_b) = 1_{F(a,b))} | i para morfizmów powyżej jest parą e-p. Rzeczywiście: <math>F(e,s)\circ F(p,j) = F(p\circ e, s\circ j) = F(1_a, 1_b) = 1_{F(a,b))}</math>. Wykorzystaliśmy kolejno: kontrawariantność <math>F</math> dla pierwszego argumentu, własności par e-p i definicję funktora. Ponadto, | ||
<math>F(p,j)\circ F(e,s) = F(e\circ p, j\circ s) \sqsubseteq F(1_{a'}, 1_{b'}) = 1_{F(a',b')} | <math>F(p,j)\circ F(e,s) = F(e\circ p, j\circ s) \sqsubseteq F(1_{a'}, 1_{b'}) = 1_{F(a',b')}</math>. | ||
Wykorzystaliśmy kolejno: definicję funktora, monotoniczność <math>F</math>, która wynika z lokalnej ciągłości i w końcu definicję <math>F</math> jeszcze raz. | Wykorzystaliśmy kolejno: definicję funktora, monotoniczność <math>F</math>, która wynika z lokalnej ciągłości i w końcu definicję <math>F</math> jeszcze raz. | ||
Zdefiniujmy zatem <math>\widehat{F}((e,p),(j,s)) = (F(p,j),F(e,s))</math>. Oczywiście,\ <math>\widehat{F}</math> jest funktorem. Aby pokazać ciągłość, załóżmy, że mamy w <math>Dcpo^{EP}_{\bot}\times Dcpo^{EP}_{\bot}</math> diagram | Zdefiniujmy zatem <math>\widehat{F}((e,p),(j,s)) = (F(p,j),F(e,s))</math>. Oczywiście,\ <math>\widehat{F}</math> jest funktorem. Aby pokazać ciągłość, załóżmy, że mamy w <math>Dcpo^{EP}_{\bot}\times Dcpo^{EP}_{\bot}</math> diagram | ||
<math>(A_1,B_1)\to (A_2,B_2)\to (A_3,B_3)\to... | <math>(A_1,B_1)\to (A_2,B_2)\to (A_3,B_3)\to...</math> | ||
który ma granicę odwrotną <math>(D,E)</math>. A to znaczy, że w <math>\mathbf{Dcpo}</math> mamy | który ma granicę odwrotną <math>(D,E)</math>. A to znaczy, że w <math>\mathbf{Dcpo}</math> mamy | ||
dwa diagramy: | dwa diagramy: | ||
<math>A_1\to A_2\to A_3\to | <math>A_1\to A_2\to A_3\to..</math>. | ||
i | i | ||
<math>B_1\to B_2\to B_3\to... | <math>B_1\to B_2\to B_3\to...</math> | ||
których granicami są odpowienio <math>D</math> i <math>E</math> Z twierdzenia o koincydencji granicy prostej i odwrotnej (Twierdzenie ???) wiemy, że zachodzi <math>1_D = \bigvee_n e_n\circ p_n</math> oraz <math>1_E = \bigvee_n j_n\circ s_n</math>, a więc <math>1_{(D,e)} = \bigvee (e_n\circ p_n, j_n\circ s_n)</math>. Aplikując lokalną ciągłość <math>F</math> do ostatniej równości mamy | których granicami są odpowienio <math>D</math> i <math>E</math> Z twierdzenia o koincydencji granicy prostej i odwrotnej (Twierdzenie ???) wiemy, że zachodzi <math>1_D = \bigvee_n e_n\circ p_n</math> oraz <math>1_E = \bigvee_n j_n\circ s_n</math>, a więc <math>1_{(D,e)} = \bigvee (e_n\circ p_n, j_n\circ s_n)</math>. Aplikując lokalną ciągłość <math>F</math> do ostatniej równości mamy | ||
<math>1_{\widehat{F}(D,E)} = \widehat{F}(1_{(D,e)}) = (F(1_D,1_E),F(1_D,1_E)) = \bigvee (F(e_n\circ p_n, j_n\circ s_n),F(e_n\circ p_n, j_n\circ s_n)) | <math>1_{\widehat{F}(D,E)} = \widehat{F}(1_{(D,e)}) = (F(1_D,1_E),F(1_D,1_E)) = \bigvee (F(e_n\circ p_n, j_n\circ s_n),F(e_n\circ p_n, j_n\circ s_n))</math>. | ||
Ale Twierdzenie ??? mówi, że ostatnia równość charakteryzuje granicę odwrotną diagramu w <math>Dcpo^{EP}_{\bot}</math>: | Ale Twierdzenie ??? mówi, że ostatnia równość charakteryzuje granicę odwrotną diagramu w <math>Dcpo^{EP}_{\bot}</math>: | ||
<math>\widehat{F}(A_1,B_1)\to \widehat{F}(A_2,B_2)\to \widehat{F}(A_3,B_3)\to | <math>\widehat{F}(A_1,B_1)\to \widehat{F}(A_2,B_2)\to \widehat{F}(A_3,B_3)\to ..</math>. | ||
a zatem <math>\widehat{F}(D,E)=F(D,E)</math> jest tą szukaną granicą odwrotną, co należało pokazać. QED. | a zatem <math>\widehat{F}(D,E)=F(D,E)</math> jest tą szukaną granicą odwrotną, co należało pokazać. QED. | ||
| Linia 201: | Linia 201: | ||
Zgodnie z poprzednim twierdzeniem możemy zdefiniować Eksponent <math>Exp\colon Dcpo^{EP}_{\bot}\times Dcpo^{EP}_{\bot} \to Dcpo^{EP}_{\bot}</math> jako <math>\widehat{[\_\to\_ ]}</math>, który jest ciągły (ponieważ eksponent <math>[\_\to\_ ]</math> jest lokalnie ciągły). Rozważmy złożenie: | Zgodnie z poprzednim twierdzeniem możemy zdefiniować Eksponent <math>Exp\colon Dcpo^{EP}_{\bot}\times Dcpo^{EP}_{\bot} \to Dcpo^{EP}_{\bot}</math> jako <math>\widehat{[\_\to\_ ]}</math>, który jest ciągły (ponieważ eksponent <math>[\_\to\_ ]</math> jest lokalnie ciągły). Rozważmy złożenie: | ||
[ | [[Grafika:Diag13.11.png]] | ||
Definiuje ono funktor ciągły <math>F</math> (jako złożenie dwóch funktorów ciągłych). Jak on działa? Rozważmy parę: | Definiuje ono funktor ciągły <math>F</math> (jako złożenie dwóch funktorów ciągłych). Jak on działa? Rozważmy parę: | ||
[ | [[Grafika:Diag13.12.png]] | ||
Mamy <math>F(P) = Exp\circ \Delta(P) = Exp(P,P) = [\_\to\_ ](P,P) = [P\to P]</math> Podobnie <math>F(Q) = [Q\to Q]</math> Działanie na morfizmach: | Mamy <math>F(P) = Exp\circ \Delta(P) = Exp(P,P) = [\_\to\_ ](P,P) = [P\to P]</math> Podobnie <math>F(Q) = [Q\to Q]</math> Działanie na morfizmach: | ||
<math>F(e,p) = Exp((e,p),(e,p)) = ([\_\to\_ ](p,e), [\_\to\_ ](e,p)) = ([p\to e], [e\to p]) | <math>F(e,p) = Exp((e,p),(e,p)) = ([\_\to\_ ](p,e), [\_\to\_ ](e,p)) = ([p\to e], [e\to p])</math>. | ||
A zatem otrzymujemy: | A zatem otrzymujemy: | ||
[ | [[Grafika:Diag13.13.png]] | ||
Wiemy już, że para funkcji powyżej tworzy parę e-p! Przypomnijmy jeszcze raz jak działają funkcje <math>[p\to e]</math> i <math>[e\to p]</math> na elementy z odpowiednio <math>[P\to P]</math> i <math>[Q\to Q]</math>: przykładowo, dla <math>f\in [P\to P]</math> mamy dla <math>q\in Q</math> | Wiemy już, że para funkcji powyżej tworzy parę e-p! Przypomnijmy jeszcze raz jak działają funkcje <math>[p\to e]</math> i <math>[e\to p]</math> na elementy z odpowiednio <math>[P\to P]</math> i <math>[Q\to Q]</math>: przykładowo, dla <math>f\in [P\to P]</math> mamy dla <math>q\in Q</math> | ||
<math>[p\to e](f)(q) = curry(e\circ ev\circ (1\times p))(f)(q) = (e\circ ev\circ (1\times p))(f,q) = e(ev((f,p(q)))) = e(f(p(q))) = e\circ f\circ p (q) | <math>[p\to e](f)(q) = curry(e\circ ev\circ (1\times p))(f)(q) = (e\circ ev\circ (1\times p))(f,q) = e(ev((f,p(q)))) = e(f(p(q))) = e\circ f\circ p (q)</math> | ||
to znaczy <math>[p\to e](f) = e\circ f\circ p</math> Podobnie <math>[e\to p](g) = p\circ g\circ e</math> dla <math>g\in [Q\to Q]</math>. | to znaczy <math>[p\to e](f) = e\circ f\circ p</math> Podobnie <math>[e\to p](g) = p\circ g\circ e</math> dla <math>g\in [Q\to Q]</math>. | ||
| Linia 227: | Linia 227: | ||
'''Twierdzenie (Dana Scott)'''. Niech <math>P</math> będzie posetem zupełnym z elementem najmniejszym <math>\bot</math>. Zdefiniujmy diagram w <math>\mathbf{Dcpo}</math> jak następuje: | '''Twierdzenie (Dana Scott)'''. Niech <math>P</math> będzie posetem zupełnym z elementem najmniejszym <math>\bot</math>. Zdefiniujmy diagram w <math>\mathbf{Dcpo}</math> jak następuje: | ||
[ | [[Grafika:Diag13.14.png]] | ||
gdzie | gdzie | ||
| Linia 241: | Linia 241: | ||
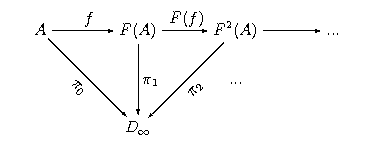
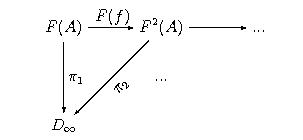
Niech <math>D_{\infty}</math> będzie granicą diagramu | Niech <math>D_{\infty}</math> będzie granicą diagramu | ||
[ | [[Grafika:Diag13.15a.png]] | ||
w <math>\mathbf{Dcpo}</math>. Wówczas <math>D_{\infty}\cong [D_{\infty}\to D_{\infty}]</math>. | w <math>\mathbf{Dcpo}</math>. Wówczas <math>D_{\infty}\cong [D_{\infty}\to D_{\infty}]</math>. | ||
Aktualna wersja na dzień 22:18, 11 wrz 2023
Twierdzenie o istnieniu granic w Dcpo
Udowodnijmy teraz podstawowe twierdzenie na temat diagramów w kategorii Dcpo.
Twierdzenie. W Dcpo istnieją granice dowolnych diagramów.
Dowód: Dowód przeprowadzimy dla szczególnego diagramu:
(Dowód ogólny jest analogiczny lecz wymaga bardziej technicznego zapisu, wiec go pominiemy.) Pokażemy, że granica powyższego diagramu jest dana jako
.
Zauważmy, że zbiór jest posetem, w którym elementy są uporządkowane po współrzędnych (to znaczy, że porządek jest dziedziczony z produktu . Jeśli jest zbiorem skierowanym, to dla każdego zbiór jest skierowanym podzbiorem . Niech . Z ciągłości funkcji tworzących diagram mamy: . To znaczy, że i, jak łatwo zauważyć, element ten jest supremum skierowanym zbioru . Pokazaliśmy więc, że Dcpo.
Udowodnimy teraz, że wraz z projekcjami jest granicą. Po pierwsze, dla mamy
a więc projekcje są ciągłe. Po drugie, jeśli jest dowolną inną granicą, to zdefiniujmy jako . Z definicji powyższej wynika, że dla każdego mamy $\pi_k \circ h = g_k</math>. Zauważmy, że to świadczy o jednoznaczności wyboru . A zatem jest granicą omawianego diagramu. Co więcej, z jednoznaczności granicy wnioskujemy, że . QED
Uwaga! Powyższe twierdzenie nie zachodzi dla klas dziedzin ciągłych i algebraicznych w ogólności. Aby granica była również posetem odpowiedniej klasy, musimy nałożyć poewne restrykcje zarówno na kształ diagramów, jak i na własności funkcji tworzących diagram.
Twierdzenie o zgodności granicy prostej i odwrotnej
Przedstawimy teraz twierdzenie o zgodności granicy prostej i odwrotnej pewnych szczególnych diagramów w kategorii posetów zupełnych. Wynik ten jest znany w literaturze angielskojęzycznej jako limit-colimt coincidence i jest jednym z kamieni milowych w teorii dziedzin. Twierdzenie to wykorzystuje się przede wszystkim przy rozwiązywaniu tak zwanych rekursywnych równań dziedzinowych (ang. recursive domain equations). Przykładem takiego równania jest . Okazuje się, że jego nietrywialne rozwiązania istnieja! Tak więc istnieją posety, które są izomorficzne z przestrzenią swoich ciągłych endofunkcji! Jeden z takich częściowych porządków skonstruujemy poniżej, pod koniec wykładu.
Twierdzenie. Rozważmy diagram w kategorii Dcpo taki, że:
1. Wierzchołkami są posety .;
2. Dla istnieją funkcje i tworzące parę e-p; 3. Dla każdego mamy ;
4. Dla mamy oraz .
Zdefiniujmy:
.
Wtedy:
5. Para jest parą e-p i zachodzi ,
6. jest granicą diagramu . Jeśli jest dowolną inną granicą, to izmorfizm jest dany jako lub ;
7. jest granicą odwrotną diagramu . Jeśli jest dowolną inną granicą, to izmorfizm jest dany jako lub .
Dowód: W Twierdzeniu ??? pokazaliśmy już, że granicą diagramu jest i że izomorfizm ma (pierwszą z) postulowanych postaci. Pokażmy teraz, że funkcje są dobrze zdefiniowane, tj. że należy do dla dowolnego . Niech będzie dowolne i załóżmy, że . Mamy:
.
W dowodzie korzystaliśmy kolejno z: definicji , ciągłości i definicji . A zatem . Co więcej, funkcje są ciągłe, gdyż tylko funkcje ciągłe zostały użyte w ich definicji.
Przejdźmy do dowodu (5). Niech . Mamy:
.
Ponadto, .
Bliższa analiza pokazuje, że pozostawi niezmienione te elementy ciągu gdzie :
.
To dowodzi, że , czyli (5).
Korzystając z powyższego mamy też natychmiast:
co kończy dowód (6).
Do pokazania pozostała nam (7), czyli fakt, że jest granicą odwrotną diagramu Jeśli jest dowolną inną granicą, to sprawdźmy najpierw czy funkcja jest dobrze zdefiniowana, tj. czy supremum jest nad zbiorem skierowanym. Ale tak jest, ponieważ dla :
.
Co więcej,
W końcu pokażemy, że funkcja o podanych własnościach jest tylko jedna. Jeśli dla zachodzi , to , a zatem czyli z ciągłości : . Ale oraz co daje czyli . QED.
Kategoria
W tej kategorii obiektami są posety zupełne posiadające element najmniejszy, zaś morfizmami są pary e-p, o których była mowa na początku wykładu ???. Złożenie morfizmów
definiujemy w naturalny sposób jako morfizm
Czy jest parą e-p? Tak, ponieważ: oraz . A zatem złożenie par e-p jest dobrze zdefiniowane, a co za tym idzie, i co łatwo już teraz pokazać, jest kategorią.
Definicja. Nazwijmy -kategorią każdą kategorię, w której diagram postaci
posiada granicę odwrotną.
Zauważmy, że twierdzenie o zgodności granicy prostej i odwrotnej (Twierdzenie ???) mówi, że jest -kategorią!
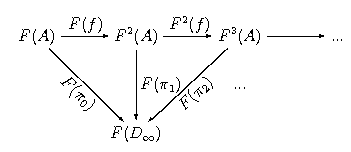
Definicja. Funktor między -kategoriami nazywamy ciągłym, jeśli zachowuje granice odwrotne, t.j. jeśli jest granicą diagramu ???, to jest granicą diagramu
Lemat. Niech będzie -kategorią, funktorem ciągłym, morfizmem w oraz niech diagram
posiada granicę odwrotną . Wówczas .
Dowód: Skoro jest granicą odwrotną diagramu
???, to
komutuje. W szczególności
komutuje i jak łatwo zauważyć jest jego granicą. Ale z ciągłości mamy, że diagram
komutuje i jest jego granicą. A zatem wynika z Lematu ???. QED.
Przykład. Przekątna , ; dla jest ciągłym funktorem.
Lokalna ciągłość funktorów
Ciągłość funktora jest często niełatwa do sprawdzenia. Na szczęście istnieje własność mocniejsza, która jest łatwiej weryfikowalna: lokalna ciągłość.
Definicja. Funktor pomiędzy kategoriami posetów jest \mathit{ lokalnie ciągły} jeśli przekształcenia typu są ciągłe w sensie Scotta dla każdej pary obiektów .
Dla przykładu przeczytajmy tę definicję dla bifunktora : funktor jest lokalnie ciągły, jeśli dla dowolnych zbiorów skierowanych i , gdzie mamy . Zauważmy, że supremum po prawej stronie istnieje w .
Przykład. Eksponent jest lokalnie ciągły, ponieważ jest złożeniem funkcji ciągłych w sensie Scotta.
Lemat. Niech funktor będzie lokalnie ciągły. Wtedy istnieje ciągły funktor którego działanie na obiekty jest takie samo, jak funktora .
Dowód: Połóżmy , gdzie są posetami ciągłymi z elementami najmniejszymi. Rozważmy pary e-p:
Możemy wówczas stworzyć diagram
i para morfizmów powyżej jest parą e-p. Rzeczywiście: . Wykorzystaliśmy kolejno: kontrawariantność dla pierwszego argumentu, własności par e-p i definicję funktora. Ponadto, . Wykorzystaliśmy kolejno: definicję funktora, monotoniczność , która wynika z lokalnej ciągłości i w końcu definicję jeszcze raz.
Zdefiniujmy zatem . Oczywiście,\ jest funktorem. Aby pokazać ciągłość, załóżmy, że mamy w diagram
który ma granicę odwrotną . A to znaczy, że w mamy dwa diagramy:
.
i
których granicami są odpowienio i Z twierdzenia o koincydencji granicy prostej i odwrotnej (Twierdzenie ???) wiemy, że zachodzi oraz , a więc . Aplikując lokalną ciągłość do ostatniej równości mamy
.
Ale Twierdzenie ??? mówi, że ostatnia równość charakteryzuje granicę odwrotną diagramu w :
.
a zatem jest tą szukaną granicą odwrotną, co należało pokazać. QED.
Twierdzenie Scotta
Zgodnie z poprzednim twierdzeniem możemy zdefiniować Eksponent jako , który jest ciągły (ponieważ eksponent jest lokalnie ciągły). Rozważmy złożenie:
Definiuje ono funktor ciągły (jako złożenie dwóch funktorów ciągłych). Jak on działa? Rozważmy parę:
Mamy Podobnie Działanie na morfizmach:
.
A zatem otrzymujemy:
Wiemy już, że para funkcji powyżej tworzy parę e-p! Przypomnijmy jeszcze raz jak działają funkcje i na elementy z odpowiednio i : przykładowo, dla mamy dla
to znaczy Podobnie dla .
Zauważmy w końcu, że dla dowolnego posetu zupełnego , jeśli jako weźmiemy funkcję , zaś jako weźmiemy funkcję , to para jest parą e-p typu .
A zatem otrzymujemy końcowy wniosek:
Twierdzenie (Dana Scott). Niech będzie posetem zupełnym z elementem najmniejszym . Zdefiniujmy diagram w jak następuje:
gdzie
1. ;
2. jest funkcją ; jest funkcją .
3. jest funkcją ; jest funkcją .
Niech będzie granicą diagramu
w . Wówczas .