Laboratorium wirtualne 1/Moduł 5 - ćwiczenie 5: Różnice pomiędzy wersjami
Z Studia Informatyczne
Przejdź do nawigacjiPrzejdź do wyszukiwania
Nie podano opisu zmian |
m Zastępowanie tekstu – „\</math>” na „\ </math>” |
||
| (Nie pokazano 21 wersji utworzonych przez 3 użytkowników) | |||
| Linia 1: | Linia 1: | ||
'''wersja beta''' | |||
<hr width="100%"> | |||
='''''LABORATORIUM WIRTUALNE 1'''''= | |||
=='''Ćwiczenie 5 - Analiza czasowo - częstotliwościowa sygnałów'''== | |||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd1.png]] | |valign="top" width="500px"|[[Grafika:LW1_M5_Slajd1.png]] | ||
| Linia 23: | Linia 32: | ||
{| border="0" cellpadding="4" width="100%" | {| border="0" cellpadding="4" width="100%" | ||
|valign="top" width="500px"|[[Grafika: | |valign="top" width="500px"|[[Grafika:LW1_M5_Slajd4.png]] | ||
|valign="top"|Krótkoczasowa transformata Fouriera (STFT – Short-Time Fourier Transform) stanowi wzorcowy przykład algorytmu analizy czasowo-częstotliwościowej. Umożliwia ona wydobycie z sygnału informacji o tym, jak zmienia się jego widmo w czasie, czyli jednoczesną obserwację jego właściwości zarówno w dziedzinie czasu jak i częstotliwości. Wycinek sygnału (blok próbek o rozmiarze L) przeznaczony do analizy jest sukcesywnie dzielony na segmenty, z których każdy podlega analizie widmowej niezależnie. Podobnie jak w przypadku tradycyjnym, aby usunąć gwałtowne zmiany (cięcia) sygnału na krańcach przedziałów, stosuje się różne okna czasowe w odniesieniu do wspomnianych segmentów. Przesuwając okno w czasie, wzdłuż sygnału, wyznacza się jego zawartość widmową wewnątrz przedziału czasowego, którego długość jest określona szerokością okna. | |valign="top"|Krótkoczasowa transformata Fouriera (STFT – Short-Time Fourier Transform) stanowi wzorcowy przykład algorytmu analizy czasowo-częstotliwościowej. Umożliwia ona wydobycie z sygnału informacji o tym, jak zmienia się jego widmo w czasie, czyli jednoczesną obserwację jego właściwości zarówno w dziedzinie czasu jak i częstotliwości. Wycinek sygnału (blok próbek o rozmiarze L) przeznaczony do analizy jest sukcesywnie dzielony na segmenty, z których każdy podlega analizie widmowej niezależnie. Podobnie jak w przypadku tradycyjnym, aby usunąć gwałtowne zmiany (cięcia) sygnału na krańcach przedziałów, stosuje się różne okna czasowe w odniesieniu do wspomnianych segmentów. Przesuwając okno w czasie, wzdłuż sygnału, wyznacza się jego zawartość widmową wewnątrz przedziału czasowego, którego długość jest określona szerokością okna. | ||
Krótkoczasową transformatę Fouriera sygnału <math>x(t)\ | Krótkoczasową transformatę Fouriera sygnału <math>x(t)\ </math>,, w odniesieniu do okna <math>\varphi(t)\ </math>, rozmieszczonego w pozycji <math>(\tau, \xi)\ </math>, na płaszczyźnie t/f zdefiniować można jako (1). W odróżnieniu od tradycyjnej transformaty Fouriera, dla której do wyznaczenia pojedynczej składowej konieczna jest znajomość funkcji <math>x(t)\ </math>, na całej osi czasu, w tym przypadku, wymagana jest znajomość <math>x(t)\ </math>, tylko w przedziale określonym przez położenie <math>\varphi (t-\tau)\ </math>,. | ||
Dyskretna wersja powyższego równania przyjmuje postać: | Dyskretna wersja powyższego równania przyjmuje postać: | ||
<math>X(\tau_n ,\xi_k)=T_p \sum_{i=0}^{N-1} {x(t_i)\varphi(t_i-\tau_n)e^{-j\xi_k t_i}}</math> | |||
gdzie <math>T_p\ </math>, oznacza okres próbkowania sygnału. Dla przypadku unormowanego, gdy <math>T_p=1\ </math>, otrzymujemy zależność (2). | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd5.png]] | |||
|valign="top"|Kształt okna czasowego <math>\varphi(t)\ </math>, rozmieszczonego w pozycji <math>(\tau, \xi)\ </math>, na płaszczyźnie t/f odgrywa kluczową rolę w przypadku STFT. Iloczyn szerokości okna w dziedzinie czasu <math>\Delta_t\ </math>, i szerokości okna w dziedzinie częstotliwości <math>\Delta_{\omega}\ </math>, jest wielkością stałą dla danego okna. Stąd też, poprawiając rozdzielczość w dziedzinie czasu, będziemy ją pogarszać w dziedzinie częstotliwości i odwrotnie. Zatem szerokość okna wybierana jest na drodze kompromisu. Interpretacja położenia okna czasowo-częstotliwościowego na płaszczyźnie t/f przedstawiona jest na rysunku 1. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd6.png]] | |||
|valign="top"|Na rysunku 2 pokazany jest przykład zastosowania rozkładu STFT do sygnału o postaci: | |||
<math>x(t)=sin2\pi f_1t+sin2\pi f_2t+\alpha [\delta(t-t_1)+\delta(t-t_2)]</math> | |||
dla różnych szerokości (promieni) <math>\Delta_t\ </math>, okna czasowego <math>\varphi(t)\ </math>,. W przypadku zastosowania szerokiego okna czasowego, otrzymuje się bardzo dużą rozdzielczość częstotliwościową i bardzo małą rozdzielczość czasową. W miarę zwężania okna czasowego poprawia się rozdzielczość czasowa kosztem częstotliwościowej. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd7.png]] | |||
|valign="top"|Znany jest pewien przypadek szczególny, w którym okno czasowe ma kształt gaussowski opisany wzorem (3). Okazuje się, że widmo tego okna ma również kształt gaussowski: | |||
<math>\Phi (\omega)=G_{\alpha}(\omega)=e^{-\alpha \omega^2}, \alpha>0</math> | |||
Okno to, od nazwiska pierwszego użytkownika, nosi miano okna Gabora. Iloczyn szerokości okna Gabora w dziedzinie czasu <math>\Delta_t\ </math>, i szerokości okna w dziedzinie częstotliwości <math>\Delta_{\omega}\ </math>, osiąga minimum i wynosi: | |||
: <math>\Delta_t \Delta_{\omega}=\frac{1}{2}</math> | |||
Analityczny zapis transformaty Gabora przedstawia zależność (4). Inaczej: | |||
<math>G(\tau, \xi)=\left \langle x(t), g_{\alpha} (t-\tau)e^{j\xi t}\right \rangle</math> | |||
Do celów obliczeń numerycznych wprowadza się pojęcie dyskretnej transformaty Gabora, określanej w skończonym zbiorze punktów na płaszczyźnie t/f. Zdyskretyzowana wersja transformaty (w sensie położenia okna na płaszczyźnie t/f) jest opisana następującą zależnością: | |||
<math>G(\tau_n, \xi_k)=\int_{-\infty}^{+\infty} {x(t){g_{\alpha}^{*}(t-\tau_n)e^{-j\xi_k t}}\, dt</math> | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd8.png]] | |||
|valign="top"|Praktyczny algorytm obliczeniowy dyskretnego rozkładu Gabora ma postać określoną wzorem (5). Współczynniki rozkładu Gabora są wyznaczane za pomocą algorytmu STFT z równania (6) gdzie <math>N\ </math>, oznacza liczbę przedziałów częstotliwości, <math>T_p\ </math>, okres próbkowania, <math>\gamma [n]\ </math>, funkcję dualną do <math>g_{\alpha}[n]\ </math>,. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd9.png]] | |||
|valign="top"|Rysunek 3 przedstawia panel czołowy wirtualnego przyrządu pomiarowego JTFA (Joint Time-Frequency Analyser) skonstruowanego przez autorów. Przyrząd ten jest udostępniony w sieci jako aplet poprzez dowolną przeglądarkę WWW Przyrząd JTFA może być wykorzystywany do analizy czasowo-częstotliwościowej dowolnych sygnałów jednowymiarowych zapisanych uprzednio w plikach. Istnieje też możliwość wczytania sygnału przy pomocy karty zbierania danych zainstalowanej w komputerze. Jeśli używamy karty zbierania danych musimy określić parametry związane z pobraniem sygnału. W szczególności są to parametry sygnału: częstotliwość próbkowania (''Sampling Rate'') i ilość próbek (''# of Samples'') oraz parametry związane z kartą: numer kanału (''Channel''), z którego odczytujemy dane i wzmocnienie w kanale (''Gain''). Po wybraniu opcji ''ACQ SIGNAL'' nastąpi pobranie sygnału. Zakres częstotliwości analizy jest zawarty w przedziale od składowej stałej do częstotliwości Nyquista, tj. połowy częstotliwości próbkowania. Najwyższa możliwa do uzyskania częstotliwość próbkowania zależy od użytej karty zbierania danych i od możliwości komputera. Częstotliwość próbkowania nie wpływa na wyniki obliczeń, ale jest odzwierciedlana jako oś y widma mocy i spektrogramu. Sygnał wczytany poprzez kartę można zapisać w pliku w celu późniejszego jego wykorzystania (opcja ''SAVE''). Z kolei wybranie polecenia ''READ FILE'' umożliwia wczytanie sygnału zapisanego w pliku. Dane w pliku powinny mieć format wektora kolumnowego liczb (znaki ASCII). Nazwa wczytanego pliku jest zawsze widoczna w polu ''File Name''. | |||
Wirtualny przyrząd pomiarowy JTFA wykorzystuje następujące pola wyświetlania danych (rys.3): | |||
* wyświetlacz widmo mocy / widmo chwilowe (''power spectrum / instantenous spectrum'') pokazuje klasyczne widmo mocy albo widmo chwilowe w zależności od ustawień, | |||
* wyświetlacz spektrogramu pokazuje widmo w skali czasu dla wybranej metody analizy; wartości widma są w tym przypadku symbolizowane przy użyciu kolorów, | |||
* wyświetlacz sygnału analizowanego w czasie. | |||
Sposób wyświetlania danych można zmienić przez przestawienie przełącznika ''Linear/dB'' i/lub ''Cursor''. Przełączenie ''Linear/dB'' zmienia sposób prezentowania spektrogramu ze skali liniowej na decybelową i odwrotnie. Przełącznik ''Cursor'' włącza lub wyłącza wyświetlanie kursorów. Jeśli kursory są włączone wyświetlacz widma mocy zamienia się w wyświetlacz widma chwilowego. Widmo chwilowe jest liczone dla czasu wskazywanego przez kursor (oś x). Do trybu wyświetlania widma mocy można w dowolnej chwili powrócić wciskając przycisk ''Power Spectrum''. | |||
W opisywanym przyrządzie wirtualnym do analizy czasowo-częstotliwościowej sygnału jednowymiarowego można wykorzystać jeden z algorytmów: | |||
* krótkoczasową transformatę Fouriera (STFT) | |||
* transformację Gabora | |||
* i inne | |||
Najprostszą z tych metod jest STFT (''Short Time Fourier Transform''). Przed jej użyciem należy określić okno analizy (''Window Type'') oraz długość okna (''Window Length''), tak aby uzyskać najlepszy kompromis pomiędzy rozdzielczością w czasie i częstotliwości. Można wybrać okna: prostokątne, Hanninga, Hamminga, Blackmana-Harris’a, Blackmana. Jeśli wydłużamy okno uzyskujemy lepszą rozdzielczość w częstotliwości, ale rozdzielczość w czasie staje się gorsza i na odwrót. | |||
Transformacja Gabora jest bardziej skomplikowana obliczeniowo, ale w wyniku uzyskujemy lepszą rozdzielczość czasowo-częstotliwościową. Przed wybraniem tej metody musimy podać wartości: ''Order, Var i Window Length''. Oknem stosowanym w metodzie Gabora jest optymalne okno Gaussa opisane przez podanie długości (''Length'') i wariancji (''Var''). Wartość rządu (''Order'') określa rozdzielczość, ale jednocześnie poziom niepożądanych interferencji pomiędzy elementami analizowanego sygnału. Im wyższy jest rząd tym lepsza jest rozdzielczość czasowo-częstotliwościowa. Jednocześnie ze zwiększaniem rzędu coraz bardziej widoczne są pasożytnicze interferencje. Także czas obliczeń jest proporcjonalny do rzędu. Zwykle wybranie rzędu na poziomie trzy do pięciu daje najlepszy kompromis pomiędzy rozdzielczością i zawartością pasożytniczych interferencji. Pewną eliminację pasożytniczych interferencji można również uzyskać zmniejszając wariancję okna Gaussa (''Var''), ale jednocześnie ulega pogorszeniu rozdzielczość czasowo-częstotliwościowa. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd10.png]] | |||
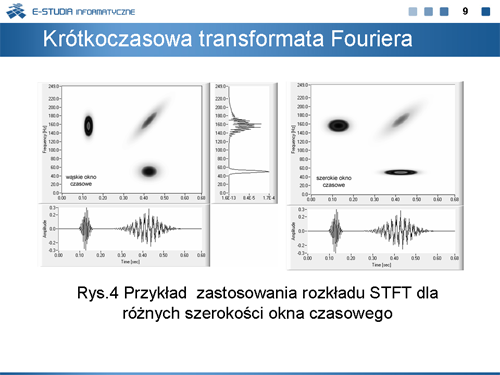
|valign="top"|Na rysunku 4 pokazane są wyniki analizy STFT otrzymane przy wykorzystaniu opisywanego wyżej wirtualnego przyrządu pomiarowego do przeprowadzania analiz czasowo-częstotliwościowych. Sygnał badany, spróbkowany z częstotliwością 500Hz, składa się z dwóch części wyciętych oknami Gaussa (przedziały czasowe <math>0.08 \div 0.15sek.\ </math>, i <math>0.25\div 0.58sek.\ </math>,). Część pierwszą stanowi sygnał sinusoidalny o częstotliwości 156Hz, część druga to złożenie dwóch sygnałów: sinusoidalnego o częstotliwości 50Hz oraz sinusoidalnego o częstotliwości liniowo zmiennej w zakresie <math>90\div 240Hz\ </math>,. Na dole rysunku 11 pokazany jest przebieg czasowy tego sygnału. Po środku przedstawiony jest obraz widma mocy badanego sygnału. Z widma mocy można wywnioskować, jakie składowe częstotliwościowe występują w sygnale badanym, ale nic nie można powiedzieć o chwilach czasu występowania składowych sygnału związanego z tymi częstotliwościowymi. Równie trudno jest określić charakter zmian częstotliwościowych. Natomiast obserwując rozkład na płaszczyźnie t/f, możemy podać zarówno czas występowania składowych sygnału o określonej zawartości częstotliwościowej, jak i charakter zmian częstotliwościowych. Niestety wartości czasu i częstotliwości można określić tylko z pewnym prawdopodobieństwem wyznaczonym przez parametry okna. Zastosowanie wąskiego okna czasowego (i tym samym szerokiego w dziedzinie częstotliwości) objawia się dużym rozmyciem umiejscowienia prążków w dziedzinie częstotliwości i stosunkowo dobrym umiejscowieniem prążków w czasie (rysunek z prawej). Zastosowanie szerokiego okna czasowego (rysunek z lewej) daje dobrą lokalizację częstotliwościową i złą czasową. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd11.png]] | |||
|valign="top"|Na rysunku 5 pokazano wyniki analizy czasowo-częstotliwościowej opisanego poprzednio sygnału, przeprowadzonej tym razem z użyciem transformaty Gabora. Zastosowanie okna Gabora umożliwia osiągnięcie optymalnych rozdzielczości zarówno w dziedzinie czasu, jak i częstotliwości. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd12.png]] | |||
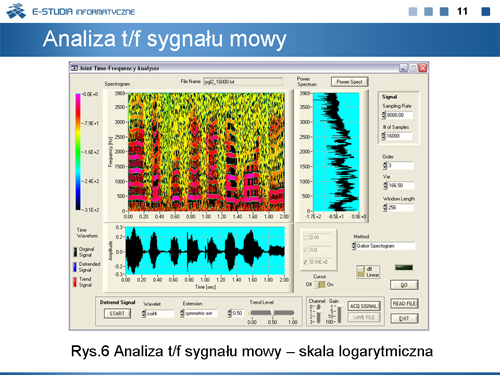
|valign="top"|Na rysunku 6 zaprezentowany jest przykład użycia analizy czasowo-częstotliwościowej do sygnału mowy. Obserwacja spektrogramu pozwala zilustrować mechanizm mowy ludzkiej. Rysunek u góry (część górna lewa) obrazuje energię sygnału jako funkcję czasu i częstotliwości. Można z niego łatwo odczytać, jakie składowe częstotliwościowe występują w poszczególnych dźwiękach. Odpowiadające częstotliwościom kolory odzwierciedlają intensywności poszczególnych składowych. Rysunek u góry po prawej to widmo mocy przetwarzanego sygnału. Od razu widać, że niesie ono dużo mniej informacji niż spektrogram. Spektrogram wykreślony w skali logarytmicznej lepiej obrazuje duże różnice amplitud poszczególnych składowych częstotliwościowych. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd13.png]] | |||
|valign="top"|Innym zastosowaniem analizy czasowo-częstotliwościowej jest detekcja mocno zaszumionych sygnałów. W ogólności szumy równomiernie rozprzestrzeniają energię zarówno w dziedzinie czasu jak i częstotliwości. Sygnały użyteczne z kolei, często koncentrują swoją energię w relatywnie krótkich zakresach czasowych, albo wąskich zakresach częstotliwościowych. Konwersja zaszumionego sygnału do domeny czas-częstotliwość zwykle znacząco poprawia lokalną wartość współczynnika SNR (Signal-to-Noise-Ratio). | |||
Rysunek 7 przedstawia zaszumiony sygnał o częstotliwości zmiennej wykładniczo. Szumy dominują zarówno w przebiegu czasowym, jak i widmie mocy. Analizując te przebiegi praktycznie niemożliwe jest wykrycie właściwego sygnału. Jednak po przejściu do dziedziny czas-częstotliwość od razu można go wykryć, oraz podać zarówno umiejscowienie w czasie jak i charakter zmian częstotliwości. Co więcej bazując na reprezentacji czasowo-częstotliwościowej danego sygnału można zamaskować współczynniki związane z szumem i, korzystając z transformacji odwrotnej, odtworzyć postać sygnału bez szumu. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd14.png]] | |||
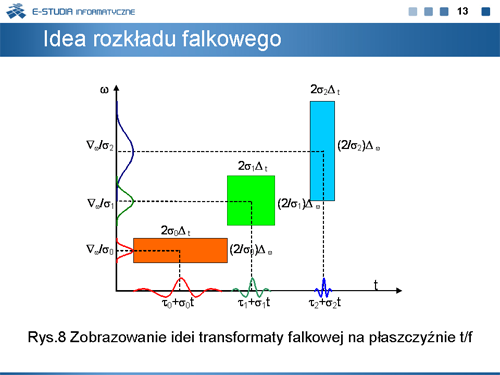
|valign="top"|W przypadku rozkładu falkowego iloczyn promieni okien, czasowego i częstotliwościowego, ma wartość stałą na całej płaszczyźnie. Położenie okna czasowo-częstotliwościowego na płaszczyźnie t/f, dla transformaty falkowej, jest przedstawione na rysunku 8 (proszę porównać położenie okna na płaszczyźnie t/f dla STFT – rys.1). | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd15.png]] | |||
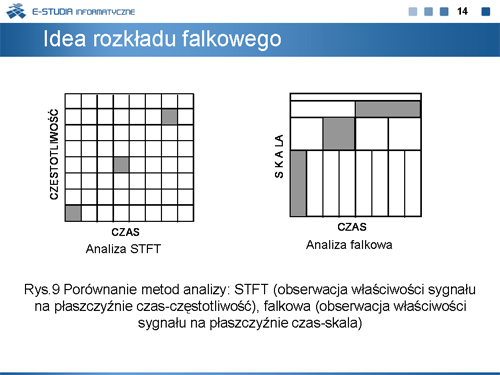
|valign="top"|Na rysunku 9, dla celów porównawczych, zilustrowano ideę czasowo-częstotliwościowej (STFT) oraz falkowej metody analizy sygnałów. Widać na nim wyraźnie, że w odróżnieniu od metody STFT, gdzie rozdzielczość czasowo-częstotliwościowa jest ustalona na całej płaszczyźnie t/f, w metodzie falkowej rozmiary okna czasowo-częstotliwościowego są funkcją jego położenia na tej płaszczyźnie. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd16.png]] | |||
|valign="top"|Na rysunku 10 zamieszczono przykłady skalowania funkcji dla pewnej (typowej) falki. Proces skalowania falki może przebiegać w dwu kierunkach, określa się je mianem kompresji (ściskania) i rozciągania. W przykładzie zamieszczonym na rysunku 10 do skalowania falki zastosowano kompresję. | |||
Drugi parametr rozkładu falkowego to przesunięcie. Sposób przesuwania falki w czasie przedstawia rysunek 11. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd17.png]] | |||
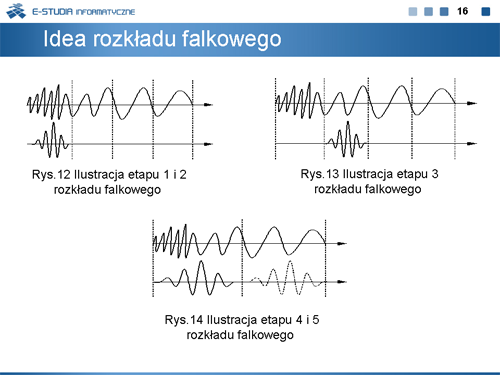
|valign="top"|Można w opisowy sposób zdefiniować proces rozkładu falkowego. Zawiera on 5 charakterystycznych kroków. | |||
#Wybraną falkę ustawić na początku fragmentu sygnału przeznaczonego do analizy. | |||
#Wyznaczyć umowną wartość liczbową odpowiadającą korelacji między bieżącą falką i odpowiadającym jej segmentem sygnału (rys.12).Uwaga! – w przypadku unormowania energii sygnału w aspekcie użytej falki, wspomniana liczba będzie równoważna wartości współczynnika korelacji wzajemnej między falką, a wybranym segmentem sygnału. | |||
#Przesunąć falkę o jeden cykl w prawo i powtórzyć działanie opisane w kroku 2. Sekwencję kroków 3, 2 powtarzać aż do końca trwania sygnału (rys.13). | |||
#Rozciągnąć falkę i powtórzyć kroki od 1 do 3. | |||
#Powtórzyć kroki od 1 do 4 aż do wyczerpania wszystkich skal (rys.14). | |||
Powyższy przykład operuje w zakresie tzw. diadycznego charakteru zmian w obrębie skali i przesunięcia charakterystycznych dla dyskretnej transformaty falkowej (DWT). Pod pojęciem ciągłej transformaty falkowej (CWT) kryje się sposób umożliwiający użycie dowolnej, zmienianej w sposób ciągły, skali oraz ciągłego przesunięcia w czasie. Oczywiście, w kontekście sygnałów dyskretnych ciągłość, w obydwu wskazanych przypadkach, oznacza zmiany w obrębie jednej próbki sygnału (co jedną próbkę). | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd18.png]] | |||
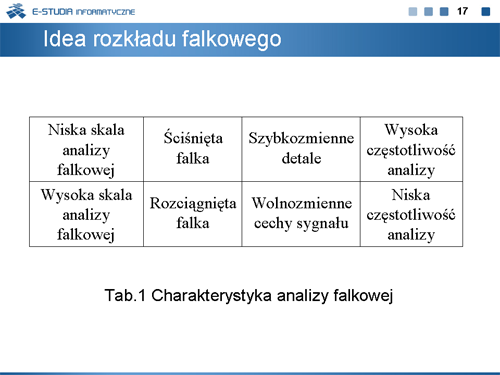
|valign="top"|Należy zauważyć, że w analizie falkowej wyższa skala równoważna jest bardziej rozciągniętej falce. Im bardziej rozciągnięta falka (wyższa skala) tym większa sekcja sygnału, z którą jest porównywana i tym bardziej zgrubne cechy sygnału wyeksponowane są za pomocą odpowiadającego jej współczynnika. Podsumowanie tego spostrzeżenia zawarto w tabeli 1. Fakt, że analiza falkowa nie obrazuje cech sygnału na płaszczyźnie czas-częstotliwość, lecz czas-skala nie stanowi o słabości metody, a wręcz przeciwnie – o jej sile. Okazuje się, że jest to naturalna metoda opisu wielu zjawisk fizycznych odbieranych przez zmysły człowieka. Trzeba się z nią pogodzić i do niej przyzwyczaić. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd19.png]] | |||
|valign="top"|Bardzo efektywna metoda implementacji algorytmu DWT dokonanej z użyciem filtrów opracowana została w 1988 roku przez Mallata. Nawiązuje ona do, znanej z analizy częstotliwościowej, metody kodowania w podpasmach i realizuje tzw. szybką transformatę falkową (Fast Wavelet Transform: FWT). Do analizy falkowej wprowadzono dwa pojęcia: aproksymacji i detalu. Pod pojęciem aproksymacji rozumie się niskoczęstotliwościowe składowe sygnału. Detale to składowe wysokoczęstotliwościowe. Wspomniany proces filtracji, obejmuje dwa filtry: dolnopasmowy (H) i górnopasmowy (G). Oryginalny sygnał S przechodzi przez parę komplementarnych filtrów, które rozdzielają go na dwie składowe <math>a_1\ </math>, (aproksymacja) i <math>d_1\ </math>, (detal) (rys.15). W przypadku filtracji cyfrowej podwaja się liczba danych, przeznaczonych do dalszego przetwarzania. Wygodnym sposobem ograniczenia tej liczby w metodzie falkowej jest decymacja, polegająca na odrzuceniu co drugiej próbki danych. Pełny proces dekompozycji zawiera szereg członów tworzących tzw. drzewo dekompozycji falkowej. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd20.png]] | |||
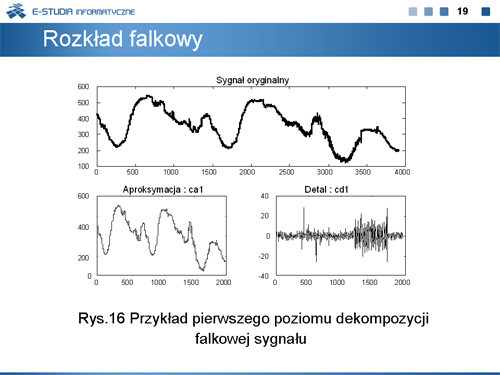
|valign="top"|Przykład pierwszego poziomu dekompozycji falkowej pewnego rzeczywistego sygnału pomiarowego zamieszczono na rysunku 16. | |||
Należy zauważyć, że dobór charakterystyk filtrów rozkładu falkowego jest podyktowany doborem kształtu falki tego rozkładu. Ściśle rzecz ujmując, kształt falki <math>\psi(t)\ </math>, jest jednoznacznie związany z charakterystyką filtru górnopasmowego wyodrębniającego detal w rozkładzie falkowym. Istnieje jeszcze jedna bardzo charakterystyczna funkcja związana ze zbiorami falek. Jest to tzw. funkcja skalująca, oznaczana symbolem <math>\varphi(t)\ </math>,. Jej kształt związany jest z charakterystykami dolnopasmowych kwadraturowych filtrów lustrzanych odpowiedzialnych za wyodrębnienie aproksymacji sygnału. Kształt funkcji skalującej jest zbliżony do kształtu odpowiadającej jej falki, z tym że zawiera ona składową stałą. Definiuje się ją w rekurencyjnym zapisie matematycznym za pomocą równania dylatacyjnego: | |||
<math>\varphi(t)=\sqrt{2}\sum_{k=0}^{N-1} {h_k \varphi (2t-k)}</math> | |||
W kontekście funkcji skalującej falka zdefiniowana jest za pomocą tego samego równania dylatacyjnego opisanego za pomocą innego zestawu współczynników: | |||
<math>\psi(t)=\sqrt{2}\sum_{k=0}^{N-1} {g_k \varphi (2t-k)}</math> | |||
Współczynniki <math>H=\left \{h_k \right \}\ </math>,, oraz <math>G=\left \{g_k \right \}\ </math>, są rozumiane jako współczynniki pary kwadraturowych filtrów lustrzanych. W przypadku bazy ortonormalnej związane są zależnością wzajemną: | |||
<math>g_k=(-1)^k h_{N-k}</math>. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd21.png]] | |||
|valign="top"|Istnieje nieograniczona wręcz liczba możliwych do utworzenia falek, jak i tzw. banków filtrów. Która z nich jest najlepsza zależy od konkretnej implementacji. Nazwy konkretnych rozwiązań pochodzą zwykle od kształtów lub nazwisk osób, które je po raz pierwszy użyły i opublikowały wyniki. Przykładowe nazwy to: Daubechies, Haar, Coiflets, Symlet, Spline, Battle-Lemarie. | |||
Na rysunku 17 pokazano funkcja skalująca i falkowa Daubechies 4 rzędu oraz widma funkcji skalującej i falkowej. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd22.png]] | |||
|valign="top"|Rysunek 18 pokazuje funkcję skalującą i falkową Daubechies 20 rzędu oraz widma tych funkcji. | |||
Przy doborze określonych funkcji falkowych do konkretnych zastosowań należy zwrócić uwagę na te właściwości, które mogą wpłynąć na jakość pożądanego rozwiązania. Należą do nich: | |||
* zakres działania – nośnik (nośnikiem nazywamy zakres zmiennej niezależnej, przy którym funkcja falkowa przyjmuje wartości niezerowe) funkcji skalującej i macierzystej funkcji falkowej oraz ich transformacji Fouriera, który decyduje o ich właściwościach lokalizacyjnych w dziedzinie czasu i częstotliwości, | |||
* symetria, która warunkuje uniknięcie zniekształceń fazowych, | |||
* liczba momentów statystycznych tożsamościowo równych zeru – decyduje ona o jakości kompresji sygnałów (współczynniku kompresji oraz zniekształceniach wprowadzonych przy kompresji); większa liczba momentów równych zeru oznacza większą liczbę współczynników falkowych bliskich zeru odpowiadających na przykład obszarom o podobnym współczynniku szarości, | |||
* regularność umożliwiająca bardziej lub mniej ciągłe odwzorowanie danych, | |||
* ortogonalność lub biortogonalność, | |||
* istnienie opisu jawnego, | |||
* istnienie funkcji skalującej. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd23.png]] | |||
|valign="top"|Skonstruowany przez autorów wirtualny przyrząd pomiarowy służy do wyznaczania dyskretnej transformaty falkowej sygnałów jednowymiarowych zapisanych uprzednio w plikach, bądź też wczytanych przy pomocy karty zbierania danych zainstalowanej w komputerze. Jeśli wykorzystujemy kartę zbierania danych musimy określić parametry związane z pobraniem sygnału. W szczególności są to parametry sygnału: częstotliwość próbkowania (''Sampling Rate'') i ilość próbek (''# of Samples'') oraz parametry związane z kartą: numer kanału (''Channel''), z którego odczytujemy dane i wzmocnienie w kanale (''Gain''). Po wybraniu opcji ''ACQ SIGNAL'' nastąpi pobranie sygnału. Sygnał wczytany poprzez kartę można zapisać w pliku w celu późniejszego jego wykorzystania (opcja SAVE SIGNAL). Z kolei wybranie polecenia ''READ FILE'' umożliwia wczytanie sygnału zapisanego wcześniej w pliku. Dane w pliku powinny mieć format wektora kolumnowego liczb (znaki ASCII). Nazwa wczytanego pliku jest zawsze widoczna w polu ''File Name''. | |||
Dyskretną transformację falkową można wyliczyć przy wykorzystaniu różnych funkcji falkowych. Odpowiednią funkcję falkową należy wybrać za pomocą kontrolki ''Wavelet''. Mamy do wyboru funkcje falkowe Haara, Daubechies, coiflety, biortogonalne i inne. Analiza jest przeprowadzana w zakresie skal podanym w polu ''Level''. Start obliczeń następuje po wciśnięciu przycisku ''GO''. Po chwili wykres współczynników dyskretnego przekształcenia falkowego jest prezentowany na ekranie. | |||
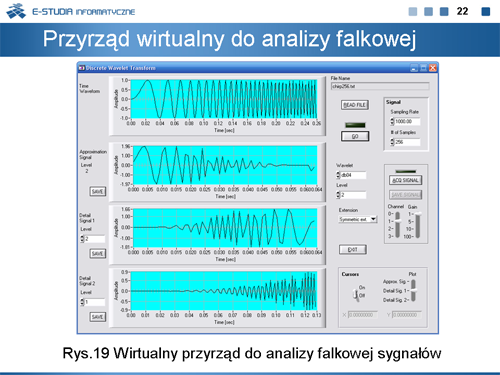
Program wykorzystuje następujące pola wyświetlania danych (rys.19): | |||
* wyświetlacz sygnału analizowanego w czasie (na górze), | |||
* wykres współczynników aproksymacji sygnału będącej wynikiem dyskretnej transformacji falkowej sygnału (drugi od góry), | |||
* dwa ostatnie wykresy prezentują wykresy współczynników dyskretnego przekształcenia falkowego dla określonej skali, którą można określić przy użyciu kontrolki Level (z lewej strony wykresu). | |||
Przełącznik ''Cursors'' włącza lub wyłącza wyświetlanie kursorów przy użyciu których można odczytać dokładne wartości współczynników transformacji falkowej. Wartości współczynników dyskretnego rozkładu falkowego można również zapisać w pliku przy użyciu polecenia ''SAVE''. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd24.png]] | |||
|valign="top"|Na rysunku 20 przedstawiono wyniki dyskretnej analizy falkowej sygnału sinusoidalnego o częstotliwości narastającej liniowo. Analiza została przeprowadzona na trzech poziomach przy wykorzystaniu falki Daubechies 4 rzędu. Widać, że dla niskiej skali, związanej z wysokimi częstotliwościami, współczynniki rozkładu falkowego przyjmują znaczące wartości właśnie dla tej części sygnału, która zawiera wysokie częstotliwości. Z kolei wysoka skale (tutaj 3) związana jest z niskimi częstotliwościami. Sygnał a3 przedstawia natomiast aproksymację sygnału. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd25.png]] | |||
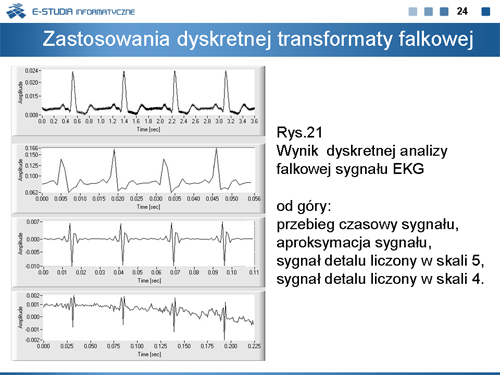
|valign="top"|Na rysunku 21 przedstawiono przykład analizy sygnału EKG za pomocą dyskretnej transformacji falkowej. Zastosowano falkę Daubechies rzędu 4 oraz rozkład falkowy na sześć poziomów. Najciekawsze efekty można zaobserwować w skali 5 i 4. Tego typu analiza może posłużyć do precyzyjnego określenia położenia pewnych charakterystycznych punktów sygnału EKG, ważnych z punktu widzenia diagnostyki medycznej. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd26.png]][[Grafika:LW1_M5_Slajd27.png]] | |||
|valign="top"|Do wykonania zadań należy wykorzystać opisywane wcześniej wirtualne przyrządy pomiarowe umożliwiające przeprowadzenie analizy czasowo-częstotliwościowej oraz dokonanie dyskretnej transformacji falkowej dla podanych sygnałów. | |||
Sygnały dostępne do analizy: | |||
#„hop.txt” – sygnał sinusoidalny, który w określonych chwilach czasowych przyjmuje różne, ale stałe wartości, | |||
#„chirp.txt” – sygnał sinusoidalny o częstotliwości narastającej liniowo w czasie, | |||
#„crosschirp.txt” – suma dwóch sygnałów sinusoidalnych, z których jeden ma częstotliwość liniowo narastającą, a drugi liniowo malejącą w czasie, | |||
#„nlchirp.txt” - sygnał sinusoidalny o częstotliwości narastającej wykładniczo w czasie, | |||
#„doppler.txt” – sygnał obrazujący efekt Dopplera, | |||
#„mowa.txt” – sygnał mowy, | |||
#„breakdown.txt” – sygnał, w którym występuje nieciągłość trudno zauważalne wzrokowo, | |||
#„ekg.txt” – sygnał EKG, | |||
#i inne. | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd28.png]] | |||
|valign="top"| | |||
|} | |||
<hr width="100%"> | |||
{| border="0" cellpadding="4" width="100%" | |||
|valign="top" width="500px"|[[Grafika:LW1_M5_Slajd29.png]] | |||
|valign="top"| | |||
|} | |} | ||
<hr width="100%"> | <hr width="100%"> | ||
Aktualna wersja na dzień 12:05, 5 wrz 2023
wersja beta
LABORATORIUM WIRTUALNE 1
Ćwiczenie 5 - Analiza czasowo - częstotliwościowa sygnałów

|

|

|

|