SW wykład 4 - Slajd6

<<powrót do strony wykładu

Semantyka denotacyjna Dziedziny składniowe i semantyczne Funkcje semantyczne Kompozycjonalność Tiny. Semantyka denotacyjna Tiny. Semantyka denotacyjna, c.d. Pojęcia pomocnicze Pojęcia pomocnicze, c.d. |Tiny. Semantyka denotacyjna, c.d. Tiny. Semantyka denotacyjna, c.d. Problem z while Konstrukcje stałopunktowe Konstrukcje stałopunktowe, c.d. Konstrukcje stałopunktowe, c.d. Przykład Przykład, c.d. Dowód Dowód Zgodność semantyki denotacyjnej

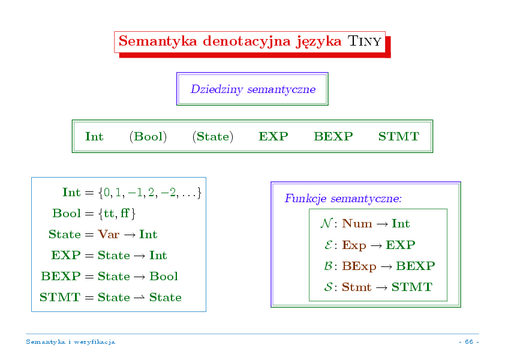
Kolejny krok definiowania semantyki denotacyjnej to definicje dziedzin semantycznych. Dziedziny liczb całkowitych i wartości logicznych nie wymagają komentarza. Dziedzinę stanów (funkcji ze zbioru zmiennych w zbiór liczb całkowitych) wprowadziliśmy już w jednym z poprzednich modułów, podając (wówczas pomocnicze) definicje znaczeń dla wyrażeń. Dziedziny semantyczne dla wyrażeń arytmetycznych i logicznych także pozostawiamy bez zmian: są to zbiory funkcji ze stanów, odpowiednio, liczby całkowite i wartości logiczne. W końcu, dziedzinę znaczeń dla instrukcji tworzą funkcje częściowe z dziedziny stanów w dziedzinę stanów.

Powyżej nazywamy jeszcze funkcje semantyczne dla poszczególnych kategorii składniowych języka. Ich definicje podamy na kolejnych slajdach.

Zwróćmy jeszcze uwagę, że nie będziemy podawać odrębnej dziedziny i funkcji semantycznej dla zmiennych --- w tym sensie odgrywają tu one tylko pomocniczą rolę (albo, jak wskazywaliśmy przy jednym z poprzednich slajdów, są one same swoimi znaczeniami). Także wśród dziedzin semantycznych mogą występować dziedziny pomocnicze, jak tutaj dziedzina stanów, nie będące celem żadnej funkcji semantycznej, a tylko służące definiowaniu bardziej złożonych dziedzin semantycznych zawierających znaczenia dla pewnych kategorii składniowych.

Definicje dziedzin semantycznych dla poszczególnych kategorii składniowych mogą już określać poziom abstrakcji definiowanej semantyki. Na przykład, przyjęliśmy już tu, że znaczeniami instrukcji języka TINY będą funkcje (częściowe) ze stanów w stany. Oznacza to, że z pewnością nie będziemy tu już mówić o obliczeniach, a instrukcje, dla których przebieg obliczeń może być różny, ale ich funkcje wejścia/wyjścia pozostaną takie same, będą względem tej semantyki równoważne.